Download Article
Download Article
A golden rectangle is a rectangle with side lengths that are in the golden ratio (about 1:1.618). This article also explains how to construct a square, which is needed to construct a golden rectangle.
-
1
Draw a square. Let us name the vertices of the square as A, B, C and D.[1]
-
2
Locate the mid-point of any one side of the square by bisecting it. Let us pick the side AB and call its mid-point as point P.[2]
Advertisement
-
3
Connect the mid-point P to a corner of the opposite side. Since P lies on the side AB, the opposite side shall be the side CD. Let’s choose to connect P with C.
-
4
Place the tip of the compass on P and set its width to match the distance PC. Draw a large arc towards the side BC.[3]
-
5
Extend the side AB to cut the arc at some point (say Q).[4]
-
6
Draw a line parallel to the side BC, passing through the point Q.
-
7
Extend the side DC to meet the parallel line at some point (say R).[5]
-
8
Congratulations! You just drew a Golden Rectangle AQRD. Erase any extraneous constructions if you so wish.
- You may verify that the ratio of the measure of the shorter side of the rectangle (QR or AD) to the measure of its longer side (AQ or RD) is very close to 1:1.618.
- You may verify that the ratio of the measure of the shorter side of the rectangle (QR or AD) to the measure of its longer side (AQ or RD) is very close to 1:1.618.
Advertisement
Add New Question
-
Question
What tool is used to draw a rectangle?
You can make rectangles with a stencil, a ruler, or trace around a rectangular object.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
Things You’ll Need
- Compass
- Straightedge (ruler, flat side of protractor, etc.)
References
About This Article
Thanks to all authors for creating a page that has been read 101,193 times.
Did this article help you?
wikiHow Tech Help Pro:
Develop the tech skills you need for work and life
Let’s do this!
Золотое сечение — это особое соотношение сторон фигуры, которое наиболее приятно для созерцания. Это число известно с античных времен, а ученые эпохи Возрождения называли его божественной пропорцией. Число Фи — золотое сечение, приблизительно равное 1,618.
История
Особую красоту деления отрезка на стороны в соотношении 1/1,618 заметили еще античные ученые. Евклид в своих началах использовал этот метод при построении пентагона, а пифогорейцы рассматривали весь мир как царство математической гармонии и уделяли большое внимание соотношению 1/1,618. В 1202 году Леонардо Фибоначчи вывел особую последовательность, отношение членов которой стремилось к числу Фибоначчи. Лука Пачоли, один из величайших алгебраистов Италии, назвал это соотношение божественной пропорцией, связав свойства бога с числом Фи. Именно с этого момента золотое сечение начало активно использоваться в работах художников эпохи Возрождения и получило буквально мистический статус. По словам Кеплера, число Фи — бесценная жемчужина математики.
Число Фи в математике
Золотое сечение часто встречается в геометрии. Золотой прямоугольник — фигура на плоскости, длина и ширина которой соотносятся как 1/1,618. Примечательное свойство такого прямоугольника состоит в том, что при удалении из фигуры любого квадрата образуется новый прямоугольник с точно таким же соотношением сторон. Стоит упомянуть и пентаграмму — звездчатый многоугольник, стороны которого пересекаются в соответствии с правилом золотого сечения.
В арифметике число Фи встречается в упоминаемой выше последовательности Фибоначчи, так как lim(Fn/Fn-1) -> Фи. Кроме того, золотое сечение имеет интересное представление в других формах записи. Так, Фи представляется как бесконечная цепочка квадратных корней из единицы. А если привести Фи к цепному виду, то получится бесконечная дробь вида [1; 1, 1, 1, 1, 1…]
Число Фи в реальности
Мистический ореол вокруг золотого сечения возник благодаря такому явлению как «золотой числизм». Энтузиасты, задавшиеся целью найти эту пропорцию в как можно большем количестве реальных объектов или явлений, часто подгоняли результаты. К примеру, храм Парфенон всегда присутствует в списке объектов, которые построены с учетом божественной пропорции. Однако на деле соотношение ширины храма к его высоте составляет 1,74, а если исключить фронтон, то и вовсе 3.
После придания числу божественных свойств, многие художники и музыканты начали сознательно использовать это соотношение в своих работах. Леонардо да Винчи, Альбрехт Дюрер, Иоганн Бах, Ле Корбюзье, Густав Фехнер намеренно придавали своим произведениям форму, соответствующую числу Фи. Одним из современных примеров использования золотого сечения является мозаика Пенроуза — метод непериодического разбиения плоскости.
Несмотря на явное преувеличение свойств золотой пропорции, она все же встречается в реальности. Большинство спиралевидных объектов связны с числом Фи: раковины моллюсков, атмосферные вихри и даже галактики действительно соответствуют божественной пропорции.
Калькулятор золотого сечения
Если вы хотите использовать божественную пропорцию в своей работе, то наш калькулятор к вашим услугам. Для определения сторон золотого прямоугольника вам понадобится ввести одну из сторон, а программа определит вторую, соответствующую правилу золотого сечения. Прелесть калькулятора состоит в том, что он не просто умножает сторону на 1,618, а подбирает целое значение. Именно поэтому вам потребуется оперировать целыми числами, что удобно на практике.
Пример из реальной жизни
Живопись
Допустим, вы хотите сделать приятную с точки зрения математики картину, следовательно, вам нужно нарисовать ее на золотом прямоугольнике. Вам потребуется заказать холст определенного размера, и чтобы определить его размеры, используйте наш калькулятор. Пусть вы хотите писать на холсте, длина которого составит 120 см. Как узнать необходимую ширину? Введите это значение в ячейку A и получите ответ, равный 74 см.
Заключение
Божественная пропорция — мистическое соотношение, которое занимает умы математиков уже несколько тысячелетий. Возможно, именно число Фи содержит ответы на вечные вопросы о тайнах мироздания. Если вам потребуется создать объекты, соответствующие золотому сечению, используйте наш калькулятор, при помощи которого вы сможете подобрать целые числа.

Золотое сечение или золотая пропорция известна тысячи лет, её применяли ещё в Античной Греции. Это природная закономерность, природная пропорция, можно называть как угодно, но она встречается в природе и окружает нас. Она для нас очень привычна, хотя мы это и не отслеживаем, но наш мозг считывает её как паттерн и воспринимает как что-то хорошее и красивое.
Золотая пропорция — это пропорция асимметрии, но соотношение частей такое, что создает гармонию и выглядит эстетично, что подразумевает для нас «выглядит привычно», «выглядит естественно». Золотая пропорция имеет идеальное соотношение частей, когда отношение меньшей части к большей такое же, как большей части к целому. Это динамическая симметрия и она характерна для роста живой материи.
Я уже писала о золотой пропорции в статье про восприятия человеком красоты, и приводила исследования генетиков и там же рассказывала о том, что все красивые лица на взгляд человека вписываются в пропорцию золотого сечения. Эта тема будоражила деятелей творчества очень много веков. Архитекторы, скульпторы и художники пытались внедрить в свои творения эти пропорции, чтоб достичь красоты. Сегодня происходит все то же самое, и дизайнеры создают свои продукты с учетом этой пропорции.
Давайте разбираться, что такое Золотое сечение
Если опустить всю сложную терминологию и упростить до процентных соотношений, то золотая пропорция будет такой: 100%=62%+38%
Проще говоря, золотая пропорция это деление объекта на две неравные части, где одна часть занимает 62% от целого, а вторая часть занимает 38% от целого.
И получается, что 62% относится к 100%, точно так же как 38% относится к 62%. Отсюда любой объект можно делить бесконечно.
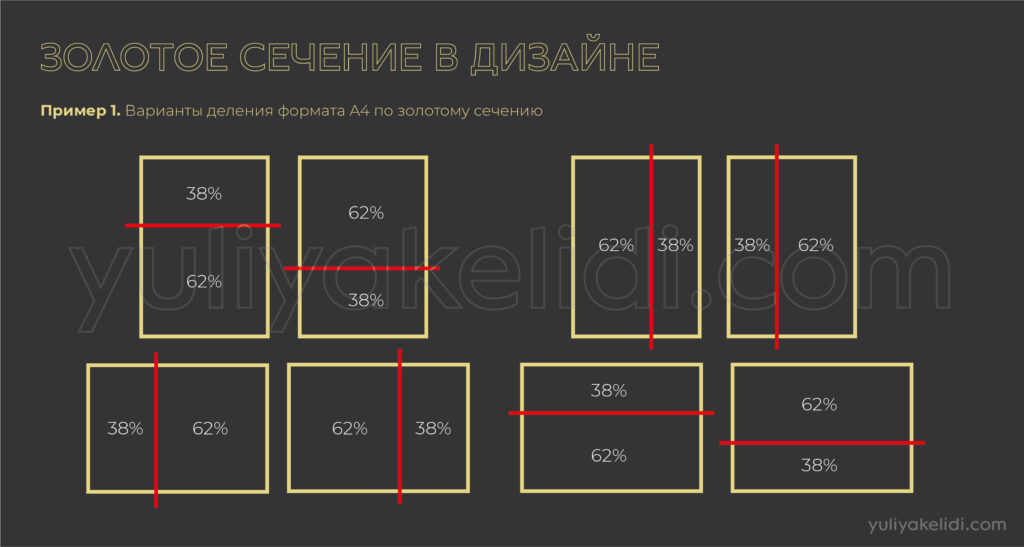
Пример 1. Всё что угодно, целое, мы берём за 100%. Например, формат A4, т.е. вся его площадь это у нас 100%. Чтоб его поделить пополам по золотому сечению мы делим на неравные части, где одна часть занимает 62%, а другая 38%. Все.
Пример 2. У нас есть дорога. Она длиной 2000 м. её надо поделить по золотому сечению. Мы находим, сколько будет 62% от 2000 м. Получается 1240 м. Мы делим нашу дорогу 2000 м. на отметке в 1240 м. И получим деление прямой по золотой пропорции. Все.
Пример 3. Нам надо чтоб общий объем объектов был расположен к целому по золотой пропорции. Например, в плакате мы хотим, чтоб информация была распределена по золотому сечению.
Шаг 1. Формат плаката это наши 100%. Весь текст и картинки мы собираем вместе и они должны занять площадь на плакате в 62%. Остальное будет воздухом.
Шаг 2. Мы в этом объеме 62% подбираем оптимальные размеры для каждого объекта и потом распределяем по плакату.
Итого: наши объекты суммарно займут 62% площади плаката, а 38% площади плаката останется в качестве свободного пространства, т.е. воздуха. Все.
Пример 4. Нам нужно задать ритмический ряд, который будет уменьшаться в золотой пропорции. У нас есть условный объект. Его изначально мы задаем в размерах, допустим 50 мм, которые обозначаем как 100%. Следующая копия этого объекта должна быть 62%, т.е. от 50 мм. мы находим 62%. Это будет 31 мм. Далее, чтоб найти размер следующего объекта, мы берем 31 мм как 100% и от него находим 62%. Получается 19,22. Следующий будет 11,9 мм. Все.
Пример 5. Например, используя золотое сечение, мы можем найти идеальные значения кегля шрифта. Самый крупный текстовый блок у нас идёт 120 pt, чтоб найти размер кегля для меньшего текста, но с золотой пропорцией, мы задаём его в размере 62% от 120. Получаем 74 pt, следующий блок мы уже ищем 62% от 74. Получаем 46 pt. Это и будет уменьшение кегля текста с учетом золотого сечения.
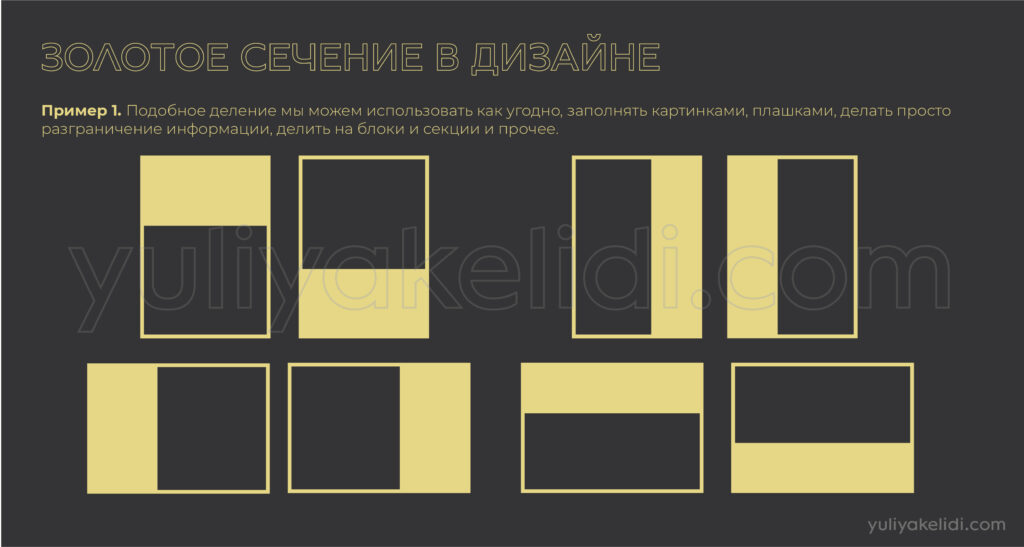
Вариантов применения очень и очень много!
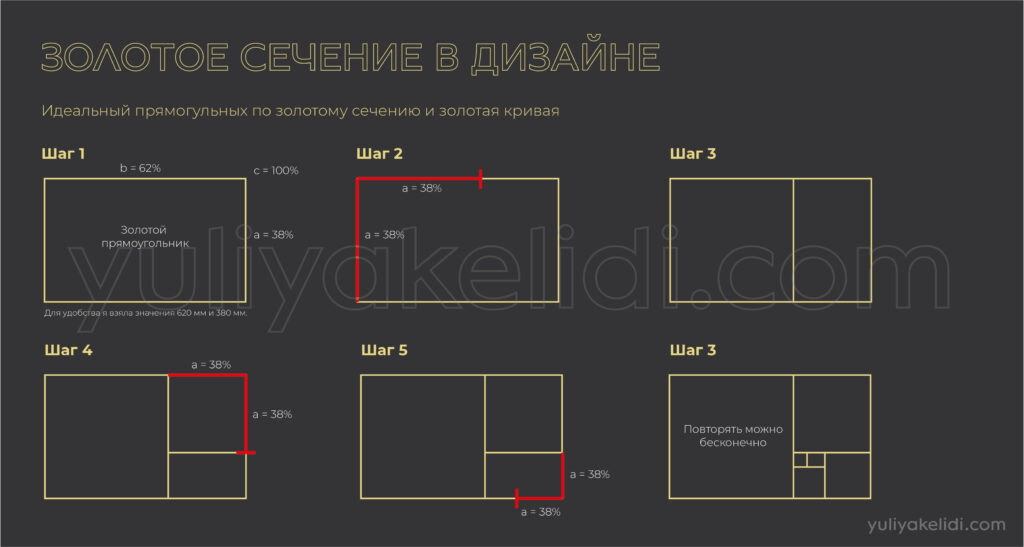
Идеальный прямоугольник по золотому сечению
Чтоб получить знаменитый золотой прямоугольник, по которому потом строится самая знаменитая кривая, нам надо также построить его в пропорциях 62%-38%.
Одна сторона прямоугольника будет равна 62%, а вторая 38%. В сумме они дают 100%. Получается та самая, знаменитая формула, которую записывают в обозначениях a,b,c.
Как звучит определение золотого сечения:
Золотая пропорция — соотношение двух величин, при котором большая величина относится к меньшей, так же, как сумма величин к большей. И далее невероятно сложное объяснение с кучей формул. Давайте упрощать и разбираться, что это все значит. Потому что дизайнеру, для работы, все эти формулы не нужны.
Итак,
100% — это с,
38% — это а,
62% — это b
Золотая пропорция гласит, что a:b = b:c. В цифрах мы получаем следующее: 38:62 равняется 62:100. Да, действительно, если мы поделим 38 на 62, то получим 0,62, и если мы 62 поделим на 100, то получим также 0,62.
Золотая пропорция продолжается и гласит, что c:b = b:a. Давайте снова в цифрах: 100:62 и 62:38. И в одном и во втором случае мы получаем 1,61.
Вот цифра 1,61 это число Фибоначчи, это число золотой пропорции, число золотого сечения, называйте, как хотите, это одно и то же. По-гречески называют «фи» —φ. Его округляют до 1,62. Что в целом и означает 62% от 100%.
И получается пропорция, которую записывают как соотношение 62%-38%!
У золотого прямоугольника короткая сторона а — 38%, а длинная b — 62%. Для удобства, давайте и зададим числа 38 мм и 62 мм. Получим золотой прямоугольник.
Сторону b мы берем как 100 и делим её на 62% и 38%. К слову 62% от стороны b будут равняться 38 мм, т.е. стороне а. Таким образом мы получаем квадрат.
Дальше каждую сторону мы делим на пропорцию 62 и 38 и наш прямоугольник будет уменьшаться до бесконечности.
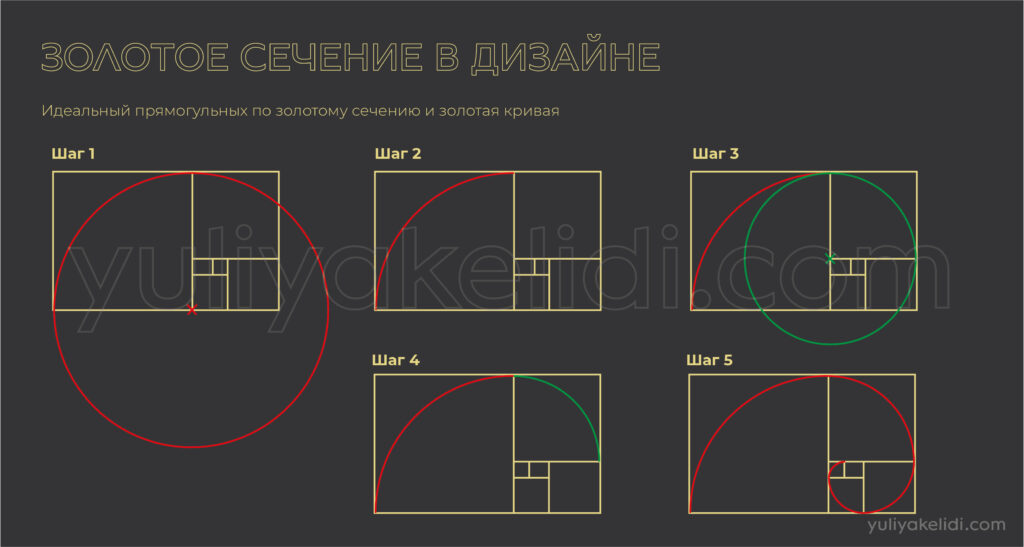
В получившиеся квадраты мы вписываем окружность. И соединяясь, она рисует нам природную кривую, которая характерна для живой материи.
Вот и всё)
И ещё.
В 2023 году я решила создать youtube-канал, на котором буду размещать обучающие ролики по графическому дизайну, также будут ролики про искусство.
Начала я записывать с уроков по изучению программы Adobe Illustrator.
Если вам интересно то, что я делаю, вы можете поддержать меня. Вот ссылка на канал, подпишитесь, пожалуйста.
Также мне важна любая обратная связь, чтоб создавать материалы ещё качественнее.
Теперь у меня появилась страница на Facebook. Если вам интересна эта тема, можете присоединиться и следить за выходом новых статей. Буду рада вас видеть 🙂
Золотое Сечение в Дизайне
20.05.2017
Золотое сечение – это то, о чем должен знать каждый дизайнер. Мы объясним, что это такое, и как вы можете его использовать.
Существует общее математическое соотношение, найденное в природе, которое может быть использовано в дизайне для создания приятных, натурально-выглядящих композиций. Его называют Золотым Сечением или греческой буквой “фи”. Если вы иллюстратор, арт директор или графический дизайнер, вам определенно стоит использовать Золотое Сечение в каждом проекте.
В этой статье мы объясним, как его использовать, а также поделимся несколькими отличными инструментами для дальнейшего вдохновения и изучения.
Тесно связанная с Последовательностью Фибоначи (Fibonacci Sequence), которую вы, возможно, помните из уроков математики или романа Дэна Брауна “Код Да Винчи”, Золотое Сечение описывает идеально симметричное взаимоотношение между двумя пропорциями.
Приблизительно равное соотношению 1 : 1.61, Золотое Сечение может быть иллюститровано как Золотой Прямоугольник: большой прямоугольник, включающий квадрат (в котором стороны равны длине самой короткой стороны прямоугольника) и прямоугольник поменьше.
Если убрать квадрат из прямоугольника, останется другой, маленький Золотой Прямоугольник. Этот процесс может продолжаться до бесконечности, как и цифры Фибоначи, которые работают в обратном порядке. (Добавление квадрата со сторонами, равными длине самой длинной стороны прямоугольника, приближает вас к Золотому Прямоугольнику и Золотому Сечению.)
Золотое Сечение в действии
Считается, что Золотое Сечение используется уже около 4000 лет в искусстве и дизайне. Однако, многие люди соглашаются, что при строительстве Египетских Пирамид также использовался этот принцип.
В более современные времена это правило может быть замечено в музыке, искусстве и дизайне вокруг нас. Применяя аналогичную рабочую методологию, вы можете привнести в свою работу те же особенности дизайна. Давайте взглянем на несколько вдохновляющих примеров.
Греческая архитектура
В древнегреческой архитектуре Золотое Сечение использовалось для определения приятных пространственных отношений между шириной здания и его высотой, размером портика и даже положением колонн, поддерживающих структуру.
В результате получается идеально пропорциональное строение. Движение неоклассической архитектуры также использовало эти принципы.
Тайная вечеря
Леонардо Да Винчи, как и многие другие художники прошлых лет, часто использовал Золотое Сечение для создания приятных композиций.
В Тайной вечере фигуры расположены в нижних двух третях (самая большая из двух частей Золотого Сечения), а Иисус идеально зарисован между золотых прямоугольников.
Золотое сечение в природе
Существует множество примеров Золотого Сечения в природе – их вы можете обнаружить вокруг себя. Цветы, морские раковины, ананасы и даже пчелиные соты демонстрируют одинаковое соотношение.
Как рассчитать Золотое Сечение
Рассчет Золотого Сечения достаточно прост, и начинается с простого квадрата:
01. Нарисуйте квадрат
Он образует длину короткой стороны прямоугольника.
02. Разделите квадрат
Разделите квадрат пополам с помощью вертикальной линии, образуя два прямоугольника.
03. Проведите диагональ
В одном из прямоугольников проведиде линию из одного угла в противоположный.
04. Поверните
Поверните эту линию так, чтобы она легла горизонтально по отношению к первому прямоугольнику.
05. Создайте новый прямоугольник
Создайте прямоугольник, используя новую горизонтальную линию и первый прямоугольник.
Как использовать Золотое Сечение
Использовать этот принцип проще, чем вы думаете. Существует пара быстрых трюков, которые вы можете использовать в своих макетах, или потратить немного больше времени и полностью раскрыть концепт.
Быстрый способ
Если вы когда-нибудь сталкивались с “Правилом третей”, то вам будет знакома идея разделения пространства на равные трети по вертикали и горизонтали, при этом места пересечения линий создают естественные точки для объектов.
Фотограф размещает ключевой объект на одной из этих пересекающихся линий, чтобы создать приятную композицию. Этот прицип может также использоваться в вашей разметке страниц и дизайне постеров.
Правило третей можно применять к любой форме, но если вы примените его к прямоугольнику с пропорциями примерно 1 : 1.6, вы окажетесь очень близко к золотому прямоугольнику, что сделает композицию более приятной для глаз.
Полная реализация
Если вы хотите реализовать Золотое Сечение в вашем дизайне в полной мере, то просто расположите основной контент и сайдбар (в веб дизайне) в соотношении равном 1 : 1.61.
Можно округлить значения в меньшую или большую стороны: если контент-зона равна 640px, а сайдбар 400px, то эта разметка вполне подойдет под Золотое Сечение.
Разумеется, вы также можете разделить области контента и боковой панели на одно и то же отношение, а связь между заголовком веб-страницы, областью содержимого, футером и навигацией также может быть спроектирована с использованием того же приципа.
Полезные инструменты
Вот несколько инструментов, которые помогут вам в использовании Золотого Сечения в дизайне и создании пропорциональных проектов.
01. goldenRATIO
GoldenRATIO – это приложение для создания дизайна веб сайтов, интерфейсов и шаблонов, подходящих под Золотое Сечение. Доступно в Mac App Store за 2,99$. Включает визуальный калькулятор Золотого Сечения.
Так же в приложении есть функция “Избранное”, которое сохраняет настройки для повторяющихся задач и “Click-thru” мод, позволяющий сворачивать приложение в Photoshop.
02. Golden Ratio Typography Calculator
Этот калькулятор Золотого Сечения от Pearsonified помогает в создании идеальной типографики для вашего сайта. Введите размер шрифта, ширину контейнера в поле, и нажмите кнопку Set my type! Если вам нужно оптимизировать количество букв в строчке, вы можете дополнительно ввести значение CPL.
03. Phicalculator
Это простое, полезное и бесплатное приложение доступно для Mac и PC. Введите любое число, и приложение вычислит вторую цифру в соответствии с приципом Золотого Сечения.
04. Atrise Golden Section
Это приложение позволяет проектировать с золотыми пропорциями, экономя кучу времени на вычислениях.
Вы можете менять формы и размеры, фокусируясь на работе над своим проектом. Постоянная лицензия стоит 49$, но вы можете скачать бесплатную версию на месяц.
Обучение Золтому Сечению
Вот несколько полезных туториалов по Золотому Сечению (английский язык):
01. Graphic design, illustration and art
В этом туториале для Digital Arts Роберто Маррас (Roberto Marras) показывает, как использовать Золотое Сечение в художественной работе.
02. Web design
Туториал от Tuts+, рассказывающий, как использовать золотые принципы в веб дизайн проектах.
03. More web design
Туториал от Smashing Magazine, рассказывающий о пропорциях и правиле третей.
Перевод статьи The designer’s guide to the Golden Ratio
Автор оригинального текста
4.2
5
votes
Article Rating
Наблюдения за природой и попытки раскрыть тайны ее прекрасных созданий принесли немало открытый. Одно из них — золотое сечение. Это некоторая закономерность, которой подчиняется все, что мы называем красивым. Люди, животные, цветы, здания, галактики…
Содержание статьи
- 1 Что такое золотое сечение и как его понимать
- 2 Как построить прямоугольник с идеальными пропорциями
- 3 Как разделить отрезок по правилу золотого сечения
- 4 Идеальный треугольник и пентаграмма
- 5 Применение в строительстве
- 6 Золотое соотношение во внутреннем оформлении
- 7 Золотое сечение в ландшафтном дизайне
Что такое золотое сечение и как его понимать
Часто мы сталкиваемся с домами, предметами, строениями, растениями, которые нас чем-то завораживают. Люди издавна пытались понять, почему одно нам кажется красивым, другое нет, искали закономерности. И вроде нашли. Это некоторое соотношение частей, которое назвали золотым сечением.
О том, кто и когда придумал золотое сечение никто не знает точно. Кто-то приписывает открытие Пифагору, но первое упоминание нашли еще в «Началах» Евклида, а жил он в 3 веке до нашей эры. Так что находка явно давняя. Именно по этому принципу построены древнегреческие и римские храмы. Конечно, это могут быть совпадения, но очень уж странные и очень их много. Так что, скорее всего, они были в курсе идеальных пропорций.
Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.
Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.
На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a. Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.
Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.
Эту закономерность развил дальше математик Фибоначчи. Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.
Как построить прямоугольник с идеальными пропорциями
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.
Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).
Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Как разделить отрезок по правилу золотого сечения
Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т.д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.
Итак, порядок деления отрезка по правилу золотого сечения:
- Берем отрезок, делим его пополам.
- Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC.
- Полученную точку C соединяем прямой с другим концом отрезка (A).
- На отрезке AC ставим точку D. Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
- Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E.
- Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.
Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.
Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.
- Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
- Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
https://youtu.be/c3SVIQBXMnA
Применение в строительстве
Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.
Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.
Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.
Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.
Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.
По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Золотое соотношение во внутреннем оформлении
Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:
- Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
- Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
- При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
- При выборе цвета придерживайтесь примерно тех же правил:
- Основной цвет составляет порядка 2/3, все дополнительные и акцентный — 1/3. Цвета выбирают сочетающиеся по определенным правилам.
- Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.
Пример подбора цвета по правилам правильной пропорциональности
- При использовании горизонтального деления стены (панели), высоту панели можно брать 1/3 или 2/3 от общей высоты комнаты. Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.
Почему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.
Золотое сечение в ландшафтном дизайне
При создании ландшафта на участке, принцип идеальных пропорций применяют, называя его правилом треугольника. В композиции должна быть одна доминанта, остальные ее составляющие лишь подчеркивают, оттеняют ее. Например, на участке есть большое дерево и вы хотите его обыграть. Оно и будет центром композиции — доминантой. Нанесите его на план, расчертите клумбу или рокарий, альпинарий — то, что хотите сделать.
От главенствующего растения или камня, под прямым углом проведите две линии. На этих линиях надо будет высадить более низкие растения. Причем второе по высоте не должно быть выше чем 2/3 от высоты основного объекта. Третий объект — не выше чем 1/3. Дополняют композицию еще более низкорослыми насаждениями. Это коротко о том, как применять золотое сечение в планировке посадок.
Но это не все. Растения надо подбирать по цветам — сочетание зелени разных оттенков, вкрапления цветов и декоративно-лиственных растений — все подчиняется тому же закону. Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.