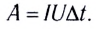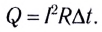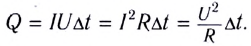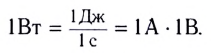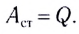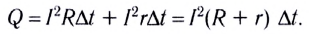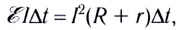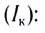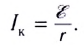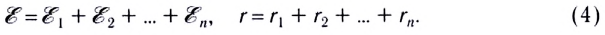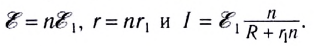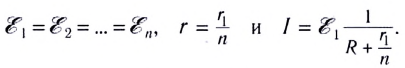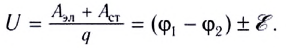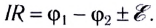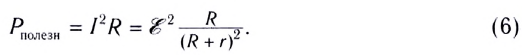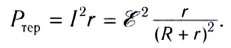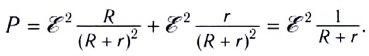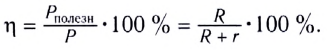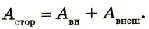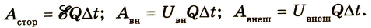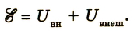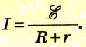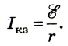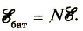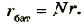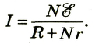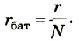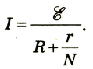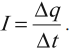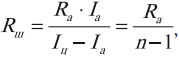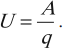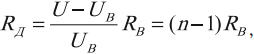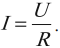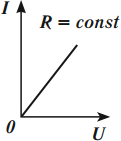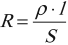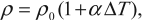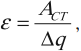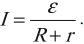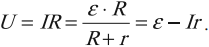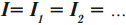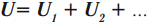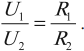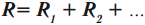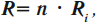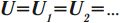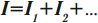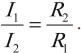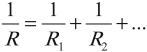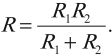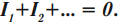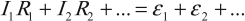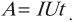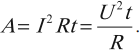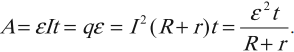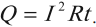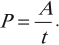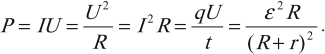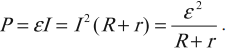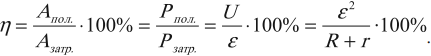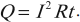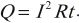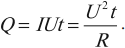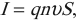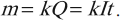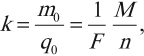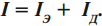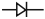Закон Ома для полной цепи:
Работа тока на участке цепи равна произведению силы тока, напряжения па этом участке и промежутка времени, в течение которого совершалась работа:
Закон Джоуля — Ленца:
- количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени прохождения тока по проводнику:
Для однородного участка цепи количество выделившейся теплоты можно вычислить по любой из трех эквивалентных формул:
Мощность, идущая на нагревание проводника, равна работе, которая совершается током за единицу времени:
Единицей мощности электрического тока, так же как и механической мощности, является ватт (1 Вт):
Коэффициент полезного действия (КПД) 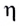
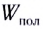
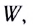
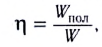
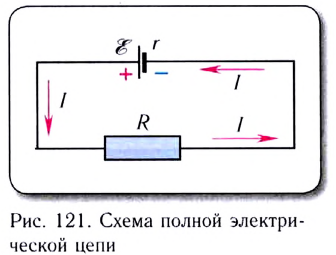
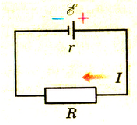
Рассмотрим полную электрическую цепь, содержащую источник ЭДС 
Из определения ЭДС источника тока следует, что совершаемая источником работа
Из закона сохранения энергии следует, что в такой цепи происходит превращение энергии, запасенной источником тока, только в теплоту. При этом работа сторонних сил за промежуток времени 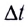
По закону Джоуля — Ленца
Таким образом,
откуда
Полученное выражение представляет собой закон Ома для полной цепи:
сила тока в полной цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна полному сопротивлению цепи.
Заметим, что максимально возможный ток в цепи с данным источником тока возникает в том случае, если сопротивление внешней части цепи стремится к нулю.
Максимально возможный ток через источник называют также током короткого замыкания
Короткое замыкание представляет серьезную опасность для мощных источников тока, поскольку может вывести их из строя.
У гальванических элементов (батареек) сила тока короткого замыкания небольшая, поэтому оно для них не очень опасно.
Внутреннее сопротивление свинцовых аккумуляторов имеет значение от r = 0,1 Ом до r = 0,01 Ом, и сила тока короткого замыкания в них может быть от 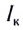
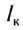
В быту, в осветительных сетях, на распределительных станциях ЭДС имеет величины свыше 100 В, а внутреннее сопротивление цепи очень мало, и согласно закону Ома для замкнутой цепи сила тока короткого замыкания может доходить до 1000 А. Вследствие этого короткое замыкание может привести к пожару. Для зашиты от пожаров в электрические цепи включаются плавкие предохранители, которые плавятся при определенной силе тока и размыкают цепь.
Короткое замыкание может возникнуть из-за плохой изоляции, когда два токоведущих провода соединяются между собой (закорачиваются). Внешнее сопротивление цепи в этом случае стремится к нулю, и сила тока резко возрастает.
Короткое замыкание электропроводки в быту может стать причиной пожара, поэтому ни в коем случае не занимайтесь ремонтом электрических сетей самостоятельно!
Закон Ома для полной цепи можно записать в следующем виде:
Таким образом, ЭДС источника равна сумме падений напряжений на внешнем и внутреннем участках замкнутой цепи.
Закон Ома для полной цепи наглядно можно показать с помощью рисунка 122, где в качестве источника тока взят гальванический элемент Вольта (Сu—Zn).
Потенциал клеммы у цинковой пластины условно принят за нуль. Длина перпендикуляра к проводнику АВС в данной точке цепи пропорциональна ее потенциалу.
Падение напряжения на внешнем участке цепи равно IR, внутри источника — Ir.
Скачки потенциалов на цинковой и медной пластинах 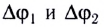
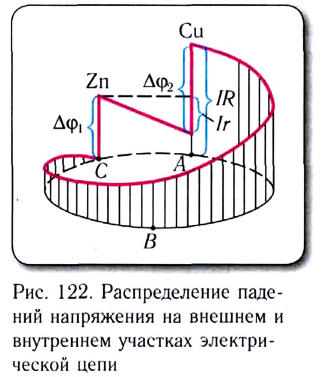
Для лучшего понимания процессов, происходящих в замкнутой электрической цепи рассмотрим аналогичную механическую модель (рис. 123).
Подобно тому как шарик скатывается по винтовой наклонной плоскости под действием силы тяжести из положения 2 в положение 3, так электроны движутся на внешнем участке цепи под действием сил электрического поля.
Для того чтобы поднять шарик в исходное положение 2, необходимо совершить работу против силы тяжести, которая в случае электрической цепи аналогична работе сторонних сил внутри источника тока.
В данном случае пружинное устройство 1, совершающее работу за счет энергии упругой деформации, является механическим аналогом источника ЭДС в замкнутой цепи.
Для работы различных устройств мы используем батарейки (гальванические элементы), которые включаем последовательно с соблюдением полярности.
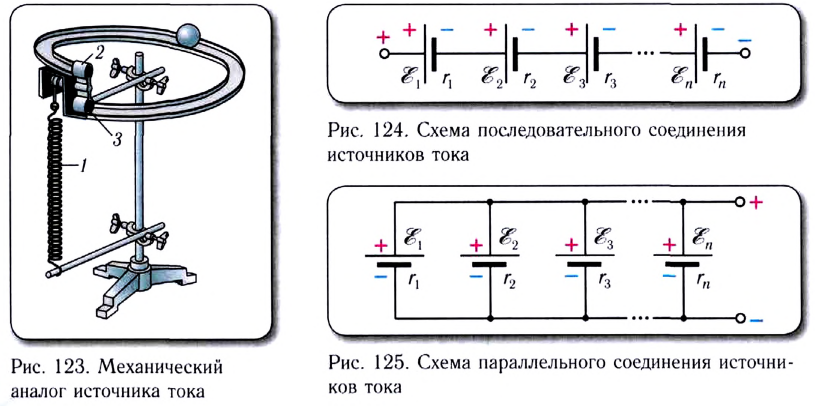
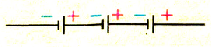
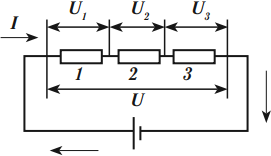
При последовательном соединении n источников тока, когда «минус» первого источника соединяется с «плюсом» второго и т. д. (рис. 124), их ЭДС и внутренние сопротивления суммируются:
В частном случае, если 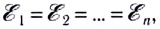
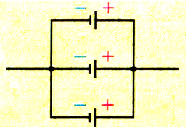
Параллельное соединение источников тока, когда «плюсы» всех источников соединяются в один узел, а «минусы» — в другой (рис. 125), используется значительно реже для повышения надежности электропитания. Можно показать, что при параллельном соединении п одинаковых источников тока суммарная ЭДС батареи равна ЭДС одного источника, а внутреннее сопротивление рассчитывается по законам параллельного соединения:
Работа по перемещению зарядов на неоднородном участке цепи равна сумме работ, совершаемых сторонними силами источника тока и силами электрического поля.
Поскольку напряжение на участке цепи равно отношению работы к перенесенному заряду 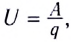
Знак перед 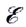
С учетом того, что U = IR (R — полное сопротивление резисторов и источников ЭДС на участке цепи), находим силу тока на участке цепи:
Эта формула выражает закон Ома для неоднородного участка цепи: падение напряжения на неоднородном участке цепи — произведение силы тока I и сопротивления участка цепи R:
Отметим, что падение напряжения пропорционально суммарной работе всех сил, в то время как напряжение U пропорционально работе только электростатических сил.
Мощность, выделяемая на внешнем участке цепи, в которую включены тепловые потребители энергии, называется полезной мощностью. Для ее вычисления используются формулы:
Мощность, выделяемая на внутреннем сопротивлении источника тока, называется теряемой мощностью и вычисляется по формулам:
Сумма полезной и теряемой мощностей равна полной мощности источника тока, которая учитывает выделение энергии как на внешнем, так и на внутреннем участках цепи:
Коэффициент полезного действия источника тока, определяемый как отношение полезной мощности к полной, зависит от сопротивления нагрузки и внутреннего сопротивления источника тока:
Наибольшую полезную мощность от данного источника можно получить тогда, когда внешнее сопротивление равно внутреннему (R = r), и в этом случае максимальный КПД 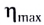
- Заказать решение задач по физике
Закон Ома для полной цепи
Открытый Г. Омом закон для участка цени в общем случае справедлив и для полной цепи, если принимать во внимание как внешнюю, так и внутреннюю части цепи. Математическую запись закона Ома для этого случая можно получить на основании закона сохранения энергии, универсального для всех процессов в природе.
Пусть электрическая цепь состоит из источника тока, имеющего ЭДС и внутреннее сопротивление г, и проводника сопротивлением R (рис. 1.51).
Pиc. 151. Замкнутая электрическая цепь
Согласно закону сохранения энергии работа сторонних сил равна сумме работ электрического тока во внешней и внутренней частях цепи:
По определению
Отсюда
Если учесть, что по закону Ома для участка цепи U =IR, то получим формулу этого закона для полной цепи:
Таким образом, сила тока в полной цепи пропорциональна электроднижущей силе источника и обратно пропорциональна полному сопротивлению цепи.
Сила тока в полной цепи пропорциональна электродвижущей силе источника и обратно пропорциональна полному сопротивлению цепи:
Пользуясь законом Ома для полной цепи, можно рассчитать два экстремальных случая н электрической цепи — короткое замыкание и разомкнутую цепь. Если сопротивление внешней цепи стремится к нулю (короткое замыкание), то сила тока в цепи
Это будет максимальное значение силы тока для данной цепи.
Если цепь разорвана (R→∞ ), то ток в цени прекращается при любых значениях ЭДС и внутреннего сопротивления. В последнем случае напряжение нм полюсах источника тока будет равно электродвижущей силе. Поэтому иногда дают упрощенное определение ЭДС: это величина, равная напряжению на клеммах источника при разомкнутой цепи.
Источники тока могут соединяться в батареи. Существуют несколько способов соединения источников тока.
Последовательным называют соединение, при котором соединяются друг с другом разноименные полюса источников: положительный предыдущего с отрицательным следующего и т. д. (рис. 1.52). Чаще всего соединяют источники с одинаковыми характеристиками, поэтому при последовательном соединении N источников ЭДС батареи будет в N раз больше, чем ЭДС одного источника:
Внутреннее сопротивление такой батареи будет также в N раз больше:
Рис. 152. Схема последовательного соединения источников тока
Для последовательного соединения источников тока закон Ома для полной цепи будет записываться:
Последовательное соединение источников τoιca удобно в том случае, когда сопротивление потребителя значительно больше внутреннего сопротивления одного источника тока.
Параллельным является соединение, при котором все одноименные полюса соединяется в один узел (рис. 1.53).
Pиc. 153. Схема параллельного соединения источников тока
Параллельное соединение применяют тогда, когда в цепи необходимо получить большое значение силы тока при небольшом напряжении.
Электродвижущая сила батареи параллельно соединенных одинаковых источников равна ЭДС одного источника:
Формула закона Ома для параллельного соединения источников имеет вид:
Параллельное соединения удобно тогда» когда сопротивление внешней части цепи значительно меньше внутреннего сопротивления одного источника.
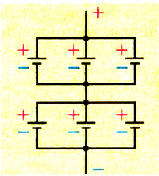
При смешанном соединении батареи источников тока (параллельно или последовательно) в свою очередь соединяют последовательно или параллельно (рис. 1.54).
Pиc. 1.54. Смешанное соединение источников тoκa
- Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
- Сила и закон Ампера
- Закон взаимодействия прямолинейных параллельных проводников с током
- Сила Лоренца
- Звуковые волны в физике
- Электрическое поле в физике
- Работа по перемещению заряда в электростатическом поле
- Закон Ома для однородного участка электрической цепи
При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу. Ее принято называть работой тока.
Рассмотрим произвольный участок цепи. Это может быть однородный проводник, к примеру, обмотка электродвигателя или нить лампы накаливания. Пусть за время ∆t через поперечное сечение проводника проходит заряд ∆q. Тогда электрическое поле совершит работу:
A=ΔqU
Но сила тока равна:
I=ΔqΔt
Выразим заряд:
Δq=IΔt
Тогда работа тока равна:
A=IUΔt
Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого совершалась работа.
Выражая через закон Ома силу тока и напряжение, получим следующие формулы для вычисления работы тока:
A=I2RΔt=U2RΔt
Работа тока измеряется в Джоулях (Дж).
Пример №1. Определите работу тока, совершенную за 10 секунд на участке цепи напряжением 200В и силой тока 16 А.
A=IUΔt=16·220·10=35200 (Дж)=35,2 (кДж)
Закон Джоуля-Ленца
В случае, когда на участке цепи не совершается механическая работа, и ток не производит химических действий, происходит только нагревание проводника. Нагретый проводник отдает теплоту окружающим телам.
Закон, определяющий количество теплоты, которое выделяет проводник с током в окружающую среду, был впервые установлен экспериментально английским ученым Д. Джоулем (1818—1889) и русским Э.Х. Ленцем (1804—1865). Закон Джоуля—Ленца сформулирован следующим образом:
Закон Джоуля—Ленца
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
Q=I2RΔt
Количество теплоты измеряется в Джоулях (Дж).
Пример №2. Определить, какое количество теплоты было выделено за 2 минуты проводником при напряжении 12 В и сопротивлении 2 Ом.
Используем закон Ома и закон Джоуля—Ленца:
Q=I2RΔt=(UR)2Δt=U2RΔt=1222=72 (Дж)
Мощность тока
Любой электрический прибор (лампа, электродвигатель и пр.) рассчитан на потребление определенной энергии в единицу времени. Поэтому наряду с работой тока очень важное значение имеет понятие мощности тока.
Определение
Мощность тока — это работа, производимая за 1 секунду. Обозначается как P. Единица измерения — Ватт (Вт).
Численно мощность тока равна отношению работы тока за время ∆t к этому интервалу времени:
P=AΔt
Это выражение для мощности можно переписать в нескольких эквивалентных формах, если использовать закон Ома для участка цепи:
P=IU=I2R=U2R
Пример №3. При силе тока в электрической цепи 0,3 А сопротивление лампы равно 10 Ом. Определите мощность электрического тока, выделяющуюся на нити лампы.
P=I2R=0,32·10=0,9 (Вт)
Выразив силу тока через заряд, прошедший за единицу времени, получим:
P=qUt
Мощность тока равна мощности на внешней цепи. Ее также называют мощностью на нагрузке, полезной мощностью или тепловой мощностью. Ее можно выразить через ЭДС:
P=(εR+r)2R
Мощность тока на внешней цепи будет максимальная, если сопротивление внешней цепи равно внутреннему сопротивлению: R = r.
Pmax=(εr+r)2r=ε24r
Мощность тока внутренней цепи:
Pвнутр=I2r=(εR+r)2r
Полная мощность:
Pполн=I2(R+r)=ε2R+r
Пример №4. ЭДС постоянного тока ε = 2 В, а его внутреннее сопротивление r = 1 Ом. Мощность тока в резисторе, подключенном к источнику, P0 = 0,75 Вт. Чему равно минимальное значение силы тока в цепи?
Используем формулу для нахождения полезной мощности:
P=(εR+r)2R
Применим закон Ома для полной цепи:
I=εR+r
Выразим сопротивление внешней цепи:
R=εI−r
Отсюда:
P=(εεI−r+r)2(εI−r)=I2(εI−r)=Iε−rI2
Так как внутреннее сопротивление равно единице, получаем квадратное уравнение следующего вида:
rI2−Iε+P=0
I2−1I+0,75=0
Решив это уравнение, получим два корня: I = 0,5 и I = 1,5 А. Следовательно, наименьшая сила тока равна 0,5 А.
Подсказки к задачам
| Объем проводника цилиндрической формы |
V=Sl |
| Масса проводника цилиндрической формы |
m=ρV=ρSl |
| Количество теплоты и изменение температуры |
Q=cmΔT |
Конденсатор в цепи постоянного тока
Постоянный ток через конденсатор не идет, но заряд на нем накапливается, и напряжение между обкладками поддерживается. Напряжение на конденсаторе такое же, как на параллельном ему участке цепи.
Ток не проходит через те резисторы, что соединены с конденсатором последовательно. При расчете электрической цепи их сопротивления не учитывают.
Подсказки к задачам
| Электроемкость, заряд и напряжение |
C=qU |
| Напряженность и напряжение |
E=Ud |
| Энергия конденсатора |
W=q22C=CU22 |
| Количество теплоты |
Q=ΔW |
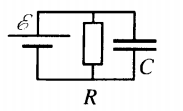
Пример №5. К источнику тока с ЭДС ε = 9 В и внутренним сопротивлением r = 1 Ом подключили параллельно соединенные резистор с сопротивлением R = 8 Ом и плоский конденсатор, расстояние между пластинами которого d = 0,002 м. Какова напряженность электрического поля между пластинами конденсатора?
Напряжение на конденсаторе равно напряжению на резисторе, так как он подключен к нему последовательно. Чтобы найти это напряжение, сначала выразим силу тока на этом резисторе:
I=εR+r
Применим закон Ома:
I=UR
Приравняем правые части выражений и получим:
εR+r=UR
Отсюда напряжение на конденсаторе равно:
U=εRR+r
Напряженность электрического поля равна:
E=Ud=εRd(R+r)=9·80,002(8+1)=720,018=4000 (Вм)
Задание EF17564
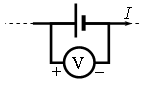
Ответ:
а) 5 Дж
б) 4 Дж
в) 3 Дж
г) 1 Дж
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу для нахождения количества теплоты, выделенной внутри источника тока.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε = 3 В.
• Внутреннее сопротивление источника тока: r = 1 Ом.
• Сила тока в цепи: I = 2 А.
• Напряжение на внешней цепи: U = 5 В.
Количество теплоты, выделенной внутри источника тока, равно:
Q=I2rt=22·1·1=4 (Дж)
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17573
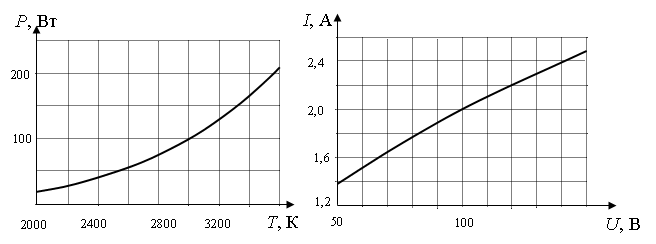
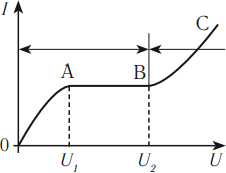
При нагревании спирали лампы накаливания протекающим по ней электрическим током основная часть подводимой энергии теряется в виде теплового излучения. На рисунке изображены графики зависимости мощности тепловых потерь лампы от температуры спирали P=P(T) и силы тока от приложенного напряжения I=I(U). При помощи этих графиков определите примерную температуру спирали лампы при силе тока I=2 A.
Ответ:
Алгоритм решения
1.Записать исходные данные.
2.С помощью графика зависимости силы тока от напряжения вычислить мощность.
3.С помощью графика зависимости мощности от температуры спирали определить ее температуру.
Решение
Нас интересует сила тока, равная 2 А. По графику зависимости силы тока от напряжения этому значение соответствует U = 100 В. Мощность определяется формулой:
P=IU=2·100=200 (Вт)
Этой мощности соответствует температура, равная около 3600 К.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17608
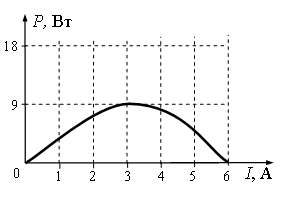
Какое из утверждений соответствует результатам опыта?
А. При коротком замыкании в цепи сила тока будет равна 6 А.
Б. При силе тока в цепи 3 А на реостате выделяется минимальная мощность.
Ответ:
а) только А
б) только Б
в) и А, и Б
г) ни А, ни Б
Алгоритм решения
- Проверить истинность каждого из утверждений.
- Выбрать верный ответ.
Решение
Согласно первому утверждению, при коротком замыкании в цепи сила тока будет равна 6 А. Это действительно так, потому что при этом значении силы тока мощность равна нулю. А это значит, что сопротивление на внешней цепи было нулевым.
Согласно второму утверждению, при силе тока в цепи 3 А на реостате выделяется минимальная мощность. Это не так. На графике этой силе тока соответствует максимальная мощность.
Верно только первое утверждение «А».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 8.5k
В этой статье я объясню, что такое работа электрического тока, какие единицы измерения для нее используются и какие важные формулы необходимо знать.
Что такое работа электрического тока?
Давайте рассмотрим обычную батарейку. По сути, батарейка преобразует химическую энергию в электрическую энергию электронов. Если теперь подключить её в электрическую цепь, то электроны могут совершать работу, используя свою электрическую энергию, например, зажигать лампочку.
Если вы хотите узнать, сколько электрической энергии было преобразовано в другой вид энергии, то вам нужно рассчитать работу электрического тока.
Определение понятия «электрическая работа» и её единицы измерения.
Работа электрического тока [A] позволяет определить, сколько электрической энергии было или может быть преобразовано в другие виды энергии.
Когда вы рассчитываете работу электрического тока, вы знаете, сколько электрической энергии было преобразовано в другие формы энергии. А уже какие другие формы энергии могут быть — это зависит от ситуации (несколько примеров в списке ниже):
- Ваш тостер преобразует электрическую энергию в тепловую;
- Когда вы включаете лампочку, электрическая энергия преобразуется в световую;
- Электродвигатель преобразует электрическую энергию в механическую.
Единицей измерения работы электрического тока в СИ является Джоуль [Дж], также часто используется в качестве единицы измерения Ватт-секунда [Вт·с]. Один джоуль всегда соответствует одной ватт-секунде. То есть 1 Дж = 1 Вт·с .
Другой важной единицей измерения является киловатт-час [кВт·ч]. Один киловатт-час равен 3 600 000 ватт-секунд или джоулей.
1 кВт·ч = 1 * 103 Вт·ч = 1 * 103 * 3600 Вт·с = 3,6 * 106 Вт·с = 3,6 * 106 Дж.
Полезный факт: а вы знали, что именно электрическую работу измеряют электросчётчики установленные в наших домах и квартирах! Электросчётчики измеряют работу электрического тока в кВт·ч.
По какой формуле вычисляется работа электрического тока?
Если вы на каком-либо участке электрической цепи под действием электрического напряжения U привели в движение заряд q, то вы можете рассчитать электрическую работу A как напряжение U, приложенное на концах этого участка цепи, умноженное на электрический заряд q, который прошёл по нему, то есть: A = U * q .
Зная, что электрический заряд, прошедший по участку цепи, можно определить, измерив силу тока и время его прохождения: q = I * t. Тогда электрическую работу A [Дж] можно определить как напряжение U [В], умноженное на силу тока I [А] и умноженное на время t [с], то есть: A = U * I * q .
Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.
Чуть ниже в статье мы разберем два практических примера, которые покажут применение данных формул. Однако перед этим мы кратко рассмотрим еще несколько важных формул.
Примечание: Вы обязательно должны запомнить первые две формулы. Следующие ниже формулы менее важны, но могут быть полезны для вас при решении тех или иных задач.
Другие формулы для определения работы электрического тока.
Закон Ома для участка цепи связывает напряжение U и ток I. Это позволяет нам рассчитать электрическую работу A другим способом.
Итак, согласно закона Ома, U = I * R или I = U / R , где R — это электрическое сопротивление.
Тогда вы можете подставить эти формулы в A = U * I * t. В итоге получатся другие формулы для нахождения работы электрического тока:
- A = I2 * R * t ;
- A = (U2 * t ) / R .
Примеры задач
Пример 1.
У вас есть батарея, подающая постоянное напряжение 12 В и ток 2,3 А. Вы используете эту батарею для освещения лампочки в течение 1 часа. Теперь вы хотите знать, какая работа электрического тока была произведена.
Мы знаем формулу для определения работы электрического тока: A = U * I * q, тогда получаем:
A = 12 В * 2,3 А * 1 ч = 27,6 Вт·ч .
Чтобы дать вам представление о единицах измерения, давайте переведем результат в ватт-секунды и джоули
27,6 Вт·ч = 27,6 * 3600 Вт·с = 99360 Вт·с = 99360 Дж.
Пример 2.
У вас есть батарейка с напряжением 5 В. Эта батарейка совершает электрическую работу в 10*10-2 Вт·с. Нам нужно рассчитать рассчитать количество электрического заряда q, перемещенного между полюсами батареи.
Мы знаем формулу для определения работы электрического тока: A = U * q, тогда q = A / U. Подставляя значения в формулу получаем:
q = 10*10-2 Вт·с / 5 В = 0,02 Кл.
Законы постоянного тока
Содержание
- Постоянный электрический ток. Сила тока
- Постоянный электрический ток. Напряжение
- Закон Ома для участка цепи
- Электрическое сопротивление. Удельное сопротивление вещества
- Электродвижущая сила. Внутреннее сопротивление источника тока
- Закон Ома для полной электрической цепи
- Параллельное и последовательное соединение проводников
- Смешанное соединение проводников
- Работа электрического тока. Закон Джоуля–Ленца
- Мощность электрического тока
- Носители свободных электрических зарядов в металлах, жидкостях и газах
- Полупроводники. Собственная и примесная проводимость полупроводников. Полупроводниковый диод
- Основные формулы раздела «Законы постоянного тока»
Постоянный электрический ток. Сила тока
Электрический ток – это упорядоченное движение заряженных частиц.
Условия существования электрического тока в проводнике:
- наличие свободных заряженных частиц;
- наличие электрического поля.
Напряженность электрического поля должна быть постоянной.
Цепь постоянного тока должна быть замкнутой.
Важно!
Тепловое движение заряженных частиц нельзя назвать электрическим током, так как оно беспорядочное.
Электрический ток можно обнаружить по его действиям:
- тепловому – при протекании тока проводник нагревается;
- химическому – изменяется состав вещества при прохождении электрического тока (электролиз);
- магнитному – электрический ток создает магнитное поле.
За направление тока принимают направление движения положительно заряженной частицы.
Сила тока – это скалярная физическая величина, равная отношению заряда, прошедшего через поперечное сечение проводника, ко времени, за которое этот заряд переносится.
Обозначение – ( I ), единица измерения в СИ – ампер (А) (является основной).
Вычисляется по формуле:
Если за одинаковые промежутки времени через поперечное сечение проводника проходит одинаковый заряд, то ток постоянный.
Для измерения силы тока используют амперметр.
Условное обозначение на схемах:
Амперметр – измерительный прибор для определения силы тока в электрической цепи.
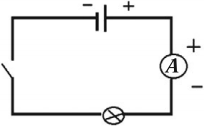
При измерении силы тока амперметр включают в цепь последовательно с тем прибором, силу тока в котором измеряют, и с соблюдением полярности. Клемму амперметра со знаком «+» нужно обязательно соединять с проводом, идущим от положительного полюса источника тока.
Для того чтобы включение амперметра не влияло на величину измеряемого тока, его сопротивление по сравнению с сопротивлением нагрузки должно быть как можно меньшим. Каждый амперметр рассчитывается на некоторое определенное максимальное значение измеряемой величины. Но возникают ситуации, когда необходимо выполнить измерение силы тока больше предельно допустимого значения силы тока.
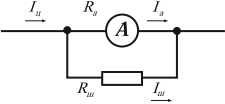
Для этого параллельно амперметру присоединяют проводник (шунт), по которому проходит часть измеряемого тока. Значение сопротивления этого проводника рассчитывается так, чтобы сила тока, проходящего через амперметр, не превышала его максимально допустимого значения.
Сопротивление шунта рассчитывается по формуле:
где ( I_ц ) – сила тока в цепи, ( I_а ) – максимально допустимая для данного амперметра сила тока, ( R_а ) – сопротивление амперметра, ( n=frac{I_ц}{I_а} ).
При этом цена деления прибора увеличивается в n раз, а точность измерений во столько же раз уменьшается.
Работающим с электрическими цепями надо знать, что для человеческого организма безопасной считается сила тока до 1 мА. Сила тока больше 100 мА приводит к серьезным поражениям организма.
Постоянный электрический ток. Напряжение
В проводнике, по которому протекает ток, заряды движутся под действием сил электростатического поля. Работу электростатических сил характеризуют разностью потенциалов или напряжением.
Электрическое напряжение – скалярная физическая величина, равная отношению работы по перемещению электрического заряда между двумя точками цепи к величине этого заряда.
Обозначение – ( U ), единица измерения в СИ – вольт (В).
Формула для вычисления:
Напряжение равно разности потенциалов только в том случае, если рассматриваемый участок цепи не содержит источник тока (ЭДС = 0).
Измеряют напряжение вольтметром.
Изображение вольтметра на схеме:
При измерении напряжения вольтметр включают в цепь параллельно с тем прибором, напряжение на котором измеряют, и с соблюдением полярности. Клемму вольтметра со знаком «+» нужно обязательно соединять с проводом, идущим от положительного полюса источника тока. Для того чтобы включение вольтметра не влияло на измерение напряжения, его сопротивление должно быть большим.
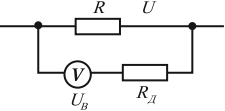
Для измерения напряжения больше, чем допустимое для данного вольтметра, используют добавочное сопротивление – резистор, включаемый последовательно с вольтметром.
Величина добавочного сопротивления рассчитывается по формуле:
где ( U ) – напряжение, которое нужно измерить, ( U_В ) – напряжение, на которое рассчитан вольтметр, ( n=frac{U}{U_В} ), ( R_В ) – сопротивление вольтметра.
При этом цена деления прибора увеличивается в ( n ) раз, а точность измерений во столько же раз уменьшается.
Закон Ома для участка цепи
Взаимосвязь между силой тока, протекающей по проводнику, и напряжением на его концах была экспериментально установлена Г. Омом и носит название закона Ома для участка цепи.
Закон Ома для участка цепи
Сила тока прямо пропорциональна напряжению на концах участка и обратно пропорциональна его сопротивлению:
График зависимости силы тока от напряжения называется вольт-амперной характеристикой. Из закона Ома для участка цепи следует, что при постоянном сопротивлении сила тока прямо пропорциональна напряжению. Следовательно, вольт-амперная характеристика для металлического проводника представляет собой прямую линию, проходящую через начало координат.
Проводник с такими свойствами называется резистором.
Угол наклона графика к оси напряжений зависит от сопротивления проводника. Тангенс угла наклона графика равен проводимости резистора.
Электрическое сопротивление. Удельное сопротивление вещества
Электрическое сопротивление – свойство материала проводника препятствовать прохождению через него электрического тока.
Обозначение – ( R ), единица измерения в СИ – Ом.
Объяснить наличие сопротивления можно на основе строения металлических проводников. Свободные электроны при движении по проводнику встречают на своем пути ионы кристаллической решетки и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.
Чем больше сопротивление проводника, тем хуже он проводит электрический ток.
Сопротивление различных проводников зависит от материала, из которого они изготовлены, их длины, геометрической формы и температуры. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.
Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 м2.
Обозначение – ( rho ), единица измерения в СИ – Ом·м.
Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.
Например, удельное сопротивление меди равно 1,7·10-8 Ом·м, т. е. медный проводник длиной 1 м и сечением 1 м2 обладает сопротивлением 1,7·10-8 Ом. На практике часто используют единицу удельного сопротивления (Ом·мм2)/м.
Электрическое сопротивление проводника прямо пропорционально длине проводника и обратно пропорционально площади поперечного сечения проводника.
Формула для вычисления:
Сопротивление проводника увеличивается с ростом температуры. Удельное сопротивление зависит от температуры:
где ( rho_0 ) – удельное сопротивление при ( T_0 ) = 293 К (20°С), ( Delta T=T-T_0 ), ( alpha ) – температурный коэффициент сопротивления.
Единица измерения температурного коэффициента сопротивления – К-1.
При нагревании увеличивается интенсивность движения частиц вещества. Это создает трудности для направленного движения электронов. Увеличивается число столкновений свободных электронов с ионами кристаллической решетки.
Свойство изменения сопротивления при изменении температуры используется в термометрах сопротивления. Эти приборы могут измерять температуру, основываясь на зависимости сопротивления от температуры. У термометров сопротивления высокая точность измерений.
Электродвижущая сила. Внутреннее сопротивление источника тока
Для создания электрического поля в проводниках используют источник тока. Внутри источника тока происходит перераспределение зарядов, в результате которого на полюсах источника возникает избыток зарядов разных знаков.
Виды источников тока:
- электрофорная машина;
- термопара;
- фотоэлемент;
- аккумулятор;
- гальванический элемент.
Сторонними называются силы неэлектрической природы, действующие внутри источника тока.
Когда проводник соединяют с полюсами источника, то на внешнем участке цепи заряженные частицы движутся под действием электростатической силы. А внутри источника на заряды действуют сторонние и электростатические силы.
Под действием этих сил внутри источника происходит перемещение положительных зарядов от отрицательного полюса источника к положительному. Это перемещение происходит до тех пор, пока сторонние силы не станут равными электростатическим. При переносе заряда эти силы совершают работу. Работа сторонних сил по перемещению заряда компенсирует потери энергии заряженными частицами при их движении по цепи.
Электродвижущей силой (ЭДС) называется отношение работы сторонних сил по перемещению положительного заряда к величине этого заряда.
Обозначение – ( varepsilon ), единица измерения в СИ – вольт (В).
Формула для вычисления:
где ( Delta q ) – модуль перенесенного заряда.
Если электрическая цепь содержит несколько источников тока с ЭДС ( varepsilon_1,varepsilon_2,,…,varepsilon_T ), то суммарная ЭДС ( varepsilon=varepsilon_1+varepsilon_2+…,varepsilon_T ).
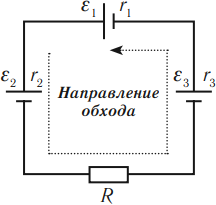
ЭДС считается положительной, если направление обхода цепи против часовой стрелки совпадает с переходом внутри источника тока от отрицательного полюса источника к положительному полюсу.
На рисунке: ( varepsilon_1>0,,varepsilon_2<0,,varepsilon_3>0. )
Суммарная ЭДС: ( varepsilon=varepsilon_1-varepsilon_2+varepsilon_3. )
При подключении проводника к полюсам источника тока происходит перераспределение заряда на поверхности проводника, а внутри проводника возникает постоянное электрическое поле. Заряды начинают перемещаться по замкнутой цепи, в которой устанавливается постоянная сила тока.
Сопротивление источника тока называется внутренним сопротивлением.
Обозначение внутреннего сопротивления – ( r ). Единица измерения в СИ – Ом.
Закон Ома для полной электрической цепи
Полная электрическая цепь состоит из источника тока и проводников, представляющих внешнее сопротивление.
Закон Ома для полной электрической цепи
Сила тока в полной цепи прямо пропорциональна ЭДС, действующей в цепи, и обратно пропорциональна полному сопротивлению цепи:
Полное сопротивление – это сумма внутреннего сопротивления источника и сопротивления внешней цепи. Во внешней цепи ток идет по направлению электрического поля, внутри источника тока – против поля.
Напряжение на внешней цепи (падение напряжения):
Если цепь разомкнута, то ток внутри источника не проходит и ( varepsilon=U ).
ЭДС численно равна напряжению на зажимах источника тока (разности потенциалов на полюсах источника).
Сопротивление внешней цепи больше внутреннего сопротивления источника.
Если сопротивление внешней цепи мало ( (R=0) ), то возможно короткое замыкание. Сила тока короткого замыкания: ( I_{кз}=frac{varepsilon}{r} )Возрастание силы тока приводит к резкому увеличению количества теплоты и может стать причиной пожара. Для предотвращения возгорания в электрическую цепь последовательно включают предохранители.
Соединение источников тока
Источники тока можно соединять между собой последовательно и параллельно.
При параллельном соединении положительные полюсы элементов соединяют между собой, отрицательные – между собой. Если ЭДС источников одинаковы, то общая ЭДС ( varepsilon=varepsilon_1 ) (( varepsilon_1 ) – ЭДС одного источника). Величина, обратная общему внутреннему сопротивлению, равна сумме величин, обратных внутренним сопротивлениям элементов: ( frac{1}{r}=frac{1}{r_1}+frac{1}{r_2}+… ) Если внутренние сопротивления источников одинаковы, то ( r_{общ}=frac{r_1}{n} ), ( r_1 ) – сопротивление одного источника, ( n ) – число источников. Сила тока: ( frac{varepsilon}{R+frac{r}{n}} ).
При последовательном соединении положительный полюс источника соединяется с отрицательным полюсом следующего. Общая ЭДС батареи ( varepsilon=varepsilon_1+varepsilon_2+… ), а общее внутреннее сопротивление равно сумме внутренних сопротивлений отдельных источников: ( r=r_1+r_2+… ) Если внутренние сопротивления источников одинаковы, то ( r_{общ}=nr_1 ). Сила тока: ( I=frac{nvarepsilon}{R+nr} ).
Параллельное и последовательное соединение проводников
Проводники в электрических цепях могут соединяться последовательно и параллельно.
Последовательное соединение проводников
При последовательном соединении начало одного проводника соединяется с концом другого.
При последовательном соединении сила тока во всех проводниках одинакова:
Общее напряжение ( U ) на проводниках равно сумме напряжений на отдельных проводниках:
Напряжение на проводниках прямо пропорционально их сопротивлениям:
Общее сопротивление равно сумме сопротивлений проводников, образующих цепь:
Если проводники имеют одинаковое сопротивление, то общее сопротивление находится по формуле:
где ( n ) – число проводников, ( R_i ) – сопротивление проводника.
Параллельное соединение проводников
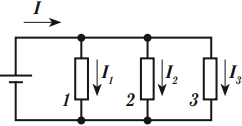
При параллельном соединении проводники подключаются между одной и той же парой точек. Если в этой точке соединяются три и более проводников, то она называется узлом электрической цепи.
При параллельном соединении напряжение на всех проводниках одинаково:
Сумма сил токов, протекающих по проводникам, равна силе тока в неразветвленной цепи:
Это следствие того факта, что в точках разветвления цепи заряды не могут накапливаться.
Силы токов в разветвленных частях цепи обратно пропорциональны их сопротивлениям:
Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников:
Если проводники имеют одинаковое сопротивление, то общее сопротивление находится по формуле:
где ( n ) – число проводников, ( R_1 ) – сопротивление проводника.
Если параллельно соединены два проводника, от общее сопротивление вычисляется по формуле:
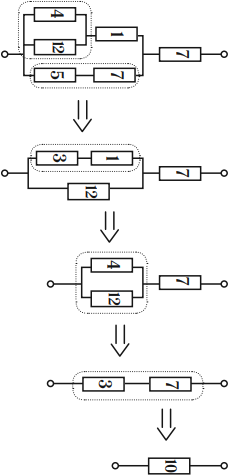
Смешанное соединение проводников
Смешанное соединение проводников – соединение, при котором часть проводников соединена последовательно, а часть – параллельно.
Важно!
Чтобы рассчитать общее сопротивление такого участка или найти силу тока и напряжение при таком соединении, нужно:
- разбить его на простые участки с последовательно или параллельно соединенными проводниками;
- найти общее (эквивалентное) сопротивление каждого из этих участков;
- составить эквивалентную схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений;
- рассчитать сопротивление полученной схемы.
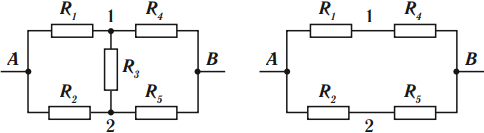
Если в схеме не удается выделить участки с последовательным или параллельным соединением проводников, то можно использовать такое правило: точки с одинаковыми потенциалами можно соединять и разъединять, ток между такими точками не идет.
На рисунке, если ( R_1=R_2,R_4=R_5, ) то потенциалы точек 1 и 2 равны. Резистор ( R_3 ) можно убрать на эквивалентной схеме – ток по нему не идет.
Точки с одинаковыми потенциалами есть в схемах с осью или плоскостью симметрии относительно точек подключения источника тока.
Если схема симметрична относительно оси, проходящей через точки входа и выхода тока, то точки равного потенциала находятся на концах симметричных сопротивлений (по ним идут одинаковые токи).
Если схема симметрична относительно оси, перпендикулярной линии, на которой лежат точки входа и выхода тока, то точки равного потенциала находятся на пересечении этой оси с проводниками.
Если в схеме нет участков с известным видом соединения и нет точек с равным потенциалом, то для расчета таких цепей используют правила Кирхгофа.
Правила Кирхгофа:
- Алгебраическая сумма сил токов, сходящихся в узле, равна нулю:
Положительными считают токи, входящие в узел, отрицательными – выходящие из узла.
- В любом замкнутом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС, имеющихся в контуре:
Порядок расчета цепи:
- выбрать направление токов во всей цепи;
- записать уравнения токов для узлов;
- записать уравнения для выделенных контуров. Произвольные замкнутые контуры выделяются так, чтобы каждый новый контур содержал хотя бы один участок, не входящий в ранее рассмотренные контуры;
- решить полученную систему уравнений.
Алгоритм решения задач на определение силы тока, напряжения или сопротивления на участке цепи:
- начертить схему цепи и указать на ней все элементы;
- установить, какие элементы цепи включены последовательно, какие – параллельно;
- расставить токи и напряжения на каждом участке цепи и записать для каждой точки разветвления (если они есть) уравнения токов и уравнения, связывающие напряжения на участках цепи;
- используя закон Ома, установить связь между токами, напряжениями и ЭДС;
- если в схеме делают какие-либо переключения сопротивлений или источников, уравнения составить для каждого режима работы цепи;
- решить полученную систему уравнений относительно неизвестной величины;
- решение проверить.
Работа электрического тока. Закон Джоуля–Ленца
Работа тока – работа сил электрического поля, создающего электрический ток.
Работа тока на участке цепи вычисляется по формуле:
Используя формулу закона Ома для участка цепи, можно работу тока вычислить так:
Работа тока в замкнутой цепи находится по формуле:
При протекании постоянного тока по металлическому проводнику электроны сталкиваются с положительными ионами, расположенными в узлах кристаллической решетки. При этом электроны передают им энергию. Это приводит к нагреванию проводника. Количество теплоты, выделяющееся в проводнике за время ( t ), равно:
Эта формула выражает закон Джоуля–Ленца: количество теплоты, выделяющееся при прохождении тока по проводнику, прямо пропорционально квадрату силы тока, времени его прохождения и сопротивлению проводника.
Мощность электрического тока
Мощность электрического тока равна отношению работы тока ко времени, в течение которого она совершается.
Обозначение – ( P ), единица измерения в СИ – ватт (Вт).
Вычисляется по формуле:
Можно записать еще несколько формул для вычисления мощности электрического тока на участке цепи:
Полная мощность источника тока:
Коэффициент полезного действия источника тока:
При решении задач на тепловое действие тока нужно учитывать следующее:
1. Если на участке есть источник тока, то необходимо использовать для решения формулу закона Джоуля–Ленца:
2. Если сила тока в цепи постоянна, то удобно использовать формулу закона Джоуля–Ленца:
3. Если постоянно напряжение, то формулу:
4. Количество теплоты можно находить, используя формулы термодинамики.
Носители свободных электрических зарядов в металлах, жидкостях и газах
Одним из условий существования электрического тока является наличие свободных заряженных частиц.
Носители электрического тока: в металлах – свободные электроны; в электролитах – положительные и отрицательные ионы; в газах – электроны и положительные ионы; в полупроводниках – электроны и дырки; в вакууме – любые заряженные частицы, но чаще всего это электроны.
Электрический ток в металлах
Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. При протекании тока по металлическому проводнику не происходит переноса вещества (опыт Рикке). Это значит, что ионы металла не принимают участия в переносе электрического заряда. Носителями заряда являются частицы одинаковые для всех металлов – электроны.
Сила тока в металлическом проводнике с площадью поперечного сечения ( S ):
где ( q ) – элементарный электрический заряд (заряд электрона), ( n ) – концентрация электронов проводимости, ( v ) – средняя скорость упорядоченного движения электронов.
Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов (опыты Мандельштама и Папалекси, Стюарта и Толмена). Катушка с большим числом витков проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному гальванометру. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременный ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра. На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона.
Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема. Электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между положительными ионами, образующими кристаллическую решетку металла.
У некоторых металлов и сплавов обнаружено явление сверхпроводимости. Это явление открыто в 1911 г. Камерлинг-Оннесом. При температурах ниже критической сопротивление проводника становится равным нулю. Значения критической температуры для чистых металлов изменяются в диапазоне от долей кельвина до 30 К. В настоящее время получены вещества с критической температурой 125 К. Сверхпроводящие свойства наблюдаются у ртути, свинца, олова.
Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово-механических представлений.
Явление сверхпроводимости используется для получения сильных магнитных полей
Электрический ток в жидкостях
Жидкости, проводящие электрический ток, называют электролитами. К электролитам относятся водные растворы неорганических кислот, солей и оснований, многие соединения металлов в расплавленном состоянии. Носителями свободных зарядов в электролитах являются положительно и отрицательно заряженные ионы.
В результате электролитической диссоциации (распада нейтральных молекул на ионы) образуются положительные и отрицательные ионы. При подключении электродов к источнику тока ионы под действием электрического поля начинают упорядоченное движение. Электрический ток в электролитах представляет собой перемещение ионов обоих знаков в противоположных направлениях. Положительные ионы движутся к отрицательному электроду (катоду), отрицательные ионы – к положительному электроду (аноду).
Электролиз – явление прохождения электрического тока через электролит, сопровождающееся выделением веществ на электродах.
Закон электролиза был экспериментально установлен английским физиком М. Фарадеем в 1833 году.
Масса ( m ) вещества, выделившегося на электроде, прямо пропорциональна заряду ( Q ), прошедшему через электролит:
Величину ( k ) называют электрохимическим эквивалентом.
Электрохимический эквивалент ( k ) равен отношению массы ( m_0 ) иона данного вещества к его заряду ( q_0 ):
где ( M ) – молярная масса вещества, ( n ) – валентность вещества, ( F=eN_A ) – постоянная Фарадея. ( F ) = 96,5·103 Кл/моль.
Постоянная Фарадея численно равна заряду, который нужно пропустить через раствор любого электролита для получения одного моля одновалентного вещества.
Явление электролиза широко применяется в современном промышленном производстве: получение чистых металлов (меди, алюминия), нанесение металлических покрытий (гальваностегия), изготовление копий с матриц (гальванопластика).
Электрический ток в газах
В обычных условиях газы являются диэлектриками, но при определенных условиях газ может стать проводником. Процесс протекания электрического тока через газ называется газовым разрядом. Носители заряда в газе – свободные электроны и ионы. Проводимость в газах смешанная – электронно-ионная.
Свободные носители заряда в газах появляются в процессе ионизации. Ионизация – процесс вырывания электрона из атома. Наряду с процессом ионизации в газе происходит и обратный процесс – рекомбинация заряженных частиц.
Ионизацию вызывают нагревание газа, излучение (ультрафиолетовое, рентгеновское или гамма-излучение).
Выделяют два вида разрядов в газе: несамостоятельный и самостоятельный разряды.
Несамостоятельный разряд происходит под действием внешнего ионизатора и прекращается, как только ионизатор перестает действовать. Самостоятельный разряд происходит без действия внешнего ионизатора под действием электрического поля, существующего между электродами. С ростом напряженности электрического поля скорости свободных заряженных частиц растут. Достигая катода, такие частицы выбивают из него электроны (вторичная электронная эмиссия). Эти электроны, разгоняясь полем, вызывают ионизацию других молекул (ионизация электронным ударом). Число заряженных частиц нарастает лавинообразно, и внешний ионизатор не нужен для поддержания тока.
На рисунке участок ОАВ соответствует несамостоятельному разряду, участок ВС – самостоятельному разряду.
Виды самостоятельного разряда:
- тлеющий;
- дуговой;
- коронный;
- искровой.
Тлеющий разряд происходит в разреженном газе при низком давлении. Применяется в газосветных трубках, лампах дневного света, цифровых индикаторах, ртутных лампах низкого давления.
Дуговой разряд – разряд между электродами, нагретыми до высокой температуры при атмосферном или повышенном давлении. Применяется в ртутных лампах высокого давления, при сварке металлов, в электропечах, в источниках света (прожекторах).
Коронный разряд возникает при нормальном и повышенном давлении у заостренных электродов. У острия электрода напряженность электрического поля велика, и в этой области возникает ударная ионизация при атмосферном давлении. Коронный разряд может возникнуть в тонких проводах, находящихся под высоким напряжением. Это приводит к утечке электроэнергии. Применяется в электрофильтрах, громоотводах, счетчике Гейгера–Мюллера.
Искровой разряд – это прерывистый самостоятельный разряд при нормальном или повышенном атмосферном давлении газа в электрическом поле очень большой напряженности. Применяется при обработке металлов. Пример такого разряда в природе – молния.
Плазма – частично или полностью ионизированный газ, в котором плотности отрицательных и положительных зарядов одинаковы. При сильном нагревании любое вещество испаряется, превращается в газ. Если увеличивать температуру и далее, резко усиливается процесс термической ионизации. Молекулы газа начнут распадаться на составляющие их атомы, которые затем превращаются в ионы.
В состоянии плазмы находится подавляющая часть вещества Вселенной: звезды, галактические туманности и межзвездная среда. Около Земли плазма существует в виде солнечного ветра и ионосферы. Плазму можно наблюдать в рекламных газовых трубках, кварцевых лампах. За последние годы применение плазмы существенно расширилось. Высокотемпературная плазма (Т ∼ 106–108 К) из смеси дейтерия с тритием используется для осуществления управляемого термоядерного синтеза; низкотемпературная плазма (Т ≤ 105 К) – в различных газоразрядных приборах: газовых лазерах, ионных приборах.
Полупроводники. Собственная и примесная проводимость полупроводников. Полупроводниковый диод
В природе существует большая группа веществ, занимающих промежуточное положение между проводниками и диэлектриками по величине электропроводности.
Полупроводниками называют вещества, удельное сопротивление которых находится в интервале от 10-3 до 107 Ом·м. К типичным полупроводникам относятся германий и кремний, селен, теллур, мышьяк.
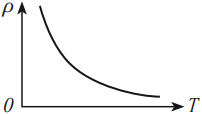
Удельное сопротивление полупроводника зависит от внешних факторов: температуры, освещенности, электрического поля. С ростом температуры удельное сопротивление полупроводника уменьшается. С ростом освещенности также происходит уменьшение сопротивления полупроводника.
Такой ход зависимости удельного сопротивления от температуры ( rho(T) ) показывает, что у полупроводников концентрация свободных носителей заряда не остается постоянной, а увеличивается с ростом температуры. Объясним такую зависимость на примере германия.
Атомы германия на внешней оболочке имеют четыре валентных электрона. В кристаллической решетке каждый атом окружен четырьмя ближайшими соседями. Связь между атомами в кристалле германия является ковалентной, т. е. осуществляется парами валентных электронов. Каждый валентный электрон принадлежит двум разным атомам. Валентные электроны в кристалле германия связаны с атомами гораздо сильнее, чем в металлах, поэтому концентрация электронов проводимости при комнатной температуре в полупроводниках значительно меньше, чем у металлов. Вблизи абсолютного нуля температуры в кристалле германия все электроны заняты в образовании связей. Такой кристалл электрического тока не проводит.
При повышении температуры некоторая часть валентных электронов может получить энергию, достаточную для разрыва ковалентных связей. Тогда в кристалле возникнут свободные электроны (электроны проводимости). Одновременно в местах разрыва связей образуются вакансии, которые не заняты электронами. Эти вакансии получили название дырок. Вакантное место может быть занято валентным электроном из соседней пары, тогда дырка переместится на новое место в кристалле. При заданной температуре полупроводника в единицу времени образуется определенное количество электронно-дырочных пар. В то же время идет обратный процесс – при встрече свободного электрона с дыркой восстанавливается электронная связь между атомами германия. Этот процесс называется рекомбинацией. Электронно-дырочные пары могут появляться также при освещении полупроводника за счет энергии электромагнитного излучения. В отсутствие электрического поля электроны проводимости и дырки участвуют в хаотическом тепловом движении.
Если полупроводник поместить в электрическое поле, то в упорядоченном движении участвуют свободные электроны и дырки, которые ведут себя как положительно заряженные частицы. Поэтому ток ( I ) в полупроводнике складывается из электронного ( I_Э ) и дырочного ( I_Д ) токов:
Концентрация электронов проводимости в полупроводнике равна концентрации дырок.
Электронно-дырочный механизм проводимости проявляется только у чистых (т. е. без примесей) полупроводников. Он называется собственной электрической проводимостью полупроводников.
Собственный полупроводник — полупроводник, не содержащий примесей, влияющих на его электропроводность.
При наличии примесей электрическая проводимость полупроводников сильно изменяется. Например, добавка в кристалл кремния примесей фосфора в количестве 0,001 атомного процента уменьшает удельное сопротивление более чем на пять порядков.
Важно!
Необходимым условием резкого уменьшения удельного сопротивления полупроводника при введении примесей является отличие валентности атомов примеси от валентности основных атомов кристалла.
Примесной проводимостью называют проводимость полупроводников при наличии примесей.
Различают два типа примесной проводимости – электронную и дырочную.
Электронная проводимость
Электронная проводимость возникает при введении в кристалл германия с четырехвалентными атомами пятивалентных атомов (например атомов мышьяка, ( As )).
Четыре валентных электрона атома мышьяка включены в образование ковалентных связей с четырьмя соседними атомами германия. Пятый валентный электрон оказывается лишним, он легко отрывается от атома мышьяка и становится свободным.
Атом, потерявший электрон, превращается в положительный ион, расположенный в узле кристаллической решетки. Примесь из атомов с валентностью, превышающей валентность основных атомов полупроводникового кристалла, называется донорной примесью. В результате ее введения в кристалле появляется значительное число свободных электронов. Это приводит к резкому уменьшению удельного сопротивления полупроводника.
Основными носителями заряда являются электроны. Концентрация свободных электронов намного больше концентрации дырок. Такая проводимость называется электронной, а полупроводник, обладающий электронной проводимостью, называется полупроводником ( n )-типа.
Дырочная проводимость
Дырочная проводимость возникает при введении в кристалл германия трехвалентных атомов (например атомов индия, ( In )). Атом индия с помощью своих валентных электронов создал ковалентные связи лишь с тремя соседними атомами германия. На образование связи с четвертым атомом германия у атома индия нет электрона. Этот недостающий электрон может быть захвачен атомом индия из ковалентной связи соседних атомов германия. В этом случае атом индия превращается в отрицательный ион, расположенный в узле кристаллической решетки, а в ковалентной связи соседних атомов образуется вакансия.
Примесь атомов, способных захватывать электроны, называется акцепторной примесью. В результате введения акцепторной примеси в кристалле разрывается множество ковалентных связей и образуются вакантные места – дырки. На эти места могут переходить электроны из соседних ковалентных связей, что приводит к движению дырок по кристаллу.
Наличие акцепторной примеси резко снижает удельное сопротивление полупроводника за счет появления большого числа свободных дырок. Концентрация дырок в полупроводнике с акцепторной примесью значительно превышает концентрацию электронов.
Проводимость такого типа называется дырочной проводимостью. Примесный полупроводник с дырочной проводимостью называется полупроводником p-типа. Основными носителями заряда в полупроводниках p-типа являются дырки.
p-n переход (электронно-дырочный переход) – это область контакта двух полупроводников с разными типами проводимости.
При контакте двух полупроводников n- и p-типов начинается процесс диффузии: дырки из p-области переходят в n-область, а электроны, наоборот, из n-области в p-область. В результате в n-области вблизи зоны контакта уменьшается концентрация электронов и возникает положительно заряженный слой. В p-области уменьшается концентрация дырок и возникает отрицательно заряженный слой. Таким образом, на границе полупроводников образуется двойной электрический слой, поле которого препятствует процессу диффузии электронов и дырок. Пограничная область раздела полупроводников с разными типами проводимости называется запирающим слоем. Объемные заряды этого слоя создают между p- и n-областями запирающее напряжение ( U_З ), приблизительно равное 0,35 В для германиевых n-p-переходов и 0,6 В для кремниевых.
p-n-переход обладает свойством односторонней проводимости. Если полупроводник с p-n-переходом подключен к источнику тока так, что положительный полюс источника соединен с n-областью, а отрицательный – с p-областью, то напряженность поля в запирающем слое возрастает. Дырки в p-области и электроны в n-области будут смещаться от p-n-перехода, увеличивая тем самым концентрации неосновных носителей в запирающем слое. Ток через p-n-переход практически не идет. Напряжение, поданное на p-n-переход, в этом случае называют обратным. Незначительный обратный ток обусловлен только собственной проводимостью полупроводниковых материалов.
Если p-n-переход соединить с источником так, чтобы положительный полюс источника был соединен с p-областью, а отрицательный с n-областью, то напряженность электрического поля в запирающем слое будет уменьшаться, что облегчает переход основных носителей через контактный слой. Дырки из p-области и электроны из n-области, двигаясь навстречу друг другу, будут пересекать p-n-переход, создавая ток в прямом направлении. Сила тока через p-n-переход в этом случае будет возрастать при увеличении напряжения источника.
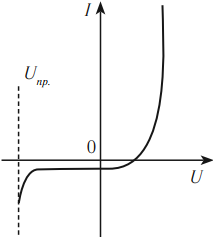
Способность p-n-перехода пропускать ток практически только в одном направлении используется в приборах, которые называются полупроводниковыми диодами.
Обозначение на схемах полупроводникового диода:
Полупроводниковые диоды изготавливают из кристаллов кремния или германия. Они используются в выпрямителях для преобразования переменного тока в постоянный. Вольт-амперная характеристика полупроводникового диода приведена на рисунке.
Полупроводниковые диоды имеют малые размеры, длительный срок службы, механическую прочность. Существенным недостатком полупроводниковых диодов является зависимость их параметров от температуры.
Основные формулы раздела «Законы постоянного тока»
Законы постоянного тока
3.1 (61.94%) 72 votes
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more