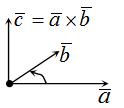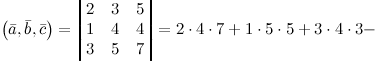Задачи как найти векторное произведение - Avtoru.top

Решения типовых задач по теме: «Векторное произведение векторов»
Задача № 1. Даны модули векторов vec{a} и vec{b} , left|vec{a} right|=8,; left|vec{b} right|=15 , и их скалярное произведение vec{a}vec{b}=96. Вычислить модуль векторного произведения left|[vec{a}vec{b}] right| .
Решение. Так как модуль векторного произведения двух векторов равен произведению модулей данных векторов, умноженному на синус угла между векторами, то необходимо знать синус угла между векторами vec{a} и vec{b} .
Воспользуемся скалярным произведением данных векторов:

vec{a}vec{b}=left|vec{a} right|left|vec{b} right|cos hat{(vec{a}vec{b})},

откуда

$cos hat{(vec{a}vec{b})}=frac{vec{a}vec{b}}{|vec{a}||vec{b}|}=frac{96}{8cdot 15}=frac{4}{5}.$

Тогда

$sin hat{(vec{a}vec{b})}=sqrt{1-frac{16}{25}}=frac{3}{5}.$

Следовательно,

$left|[vec{a}vec{b}] right|=left|vec{a} right|left|vec{b} right|sin hat{(vec{a}vec{b})}=8cdot 15cdot frac{3}{5}=72.$

Ответ: left|[vec{a}vec{b}] right|=72.
Задача № 2. Какому условию должны удовлетворять векторы vec{a} и vec{b} , чтобы векторы 3vec{a}+vec{b} и vec{a}-3vec{b} были коллинеарны?
Решения этих задач подробно изложено в следующем видео

Задача № 3. Векторы vec{a} , vec{b} и vec{c} удовлетворяют условию vec{a}+vec{b}+vec{c} . Доказать, что left[vec{a}vec{b} right]=left[vec{c} vec{a}right]=left[vec{b}vec{c} right] .
Задача № 4. Вычислить площадь параллелограмма, построенного на векторах vec{AB}=6vec{a}-3vec{b} и vec{AD}=3vec{a}+2vec{b} , если left|vec{a} right|=3,; left|vec{b} right|=5 и $left(hat{vec{a}vec{b}} right)=frac{pi }{6}.$
Указания. Площадь параллелограмма численно равна длине вектора, полученного в результате векторного умножения двух данных векторов, т. е.

$S_{ABCD}=left|vec{AB}times vec{AD} right|=left|(6vec{a}-3vec{b})(3vec{a}+2vec{b}) right|.$

Ответ: S параллелограмма= 157,5 кв. ед.
Решения этих задач подробно изложено в следующем видео

Задача № 5. Зная стороны треугольника vec{AB} ={-3; -2; 6} и vec{BC} = {- 2; 4; 4}, вычислить длину высоты vec{AD} .
Решение. I способ приведен в видеоуроке
II способ. Указания. Найти Пр $_{vec{BO}}vec{BA}$ и затем по теореме Пифагора вычислить высоту vec{AD} .
Ответ: $AD=frac{8}{3}sqrt{5}$ ед. длины.
Решение этой задачи подробно изложено в следующем видео

Задача № 6. Решить самостоятельно. Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах: vec{a} {6;0;2} и vec{b} {1,5; 2; 1}.
Указания. Одна из диагоналей параллелограмма будет равна сумме векторов сторон, а другая — разности векторов сторон параллелограмма (рис.1).
vekt090

Рис.1

vec{OC}=vec{a}+vec{b},; vec{AB}=vec{b}-vec{a}.; S=left|vec{a}times vec{b} right|.

Ответ: длины диагоналей $frac{1}{2}sqrt{277}$ и $frac{1}{2}sqrt{101}$ , площадь параллелограмма 13 кв.ед.
Задача № 7. Зная, что векторы vec{a}=alpha vec{i}+7vec{j}+3vec{k} и vec{b}= vec{i}+beta vec{j}+2vec{k} коллинеарны, вычислить коэффициенты α и β.
Указания. Если векторы а и b коллинеарны, то их векторное произведение равно нулю, vec{a}times vec{b}=0 .
Ответ: $alpha =frac{3}{2};; beta =frac{14}{3}$
Решения этих задач подробно изложено в следующем видео

Источник

Векторное произведение векторов

Определение

Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $.

Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.

Формула

Формула 1

Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле:

$$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$

Формула 2

В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$

где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $.

Определитель во второй формуле можно раскрыть по первой строке:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 — a_3 b_2) — overline{j} (a_1 b_3 — a_3 b_1) + overline{k} (a_1 b_2 — a_2 b_1) $$

Итого вторая формула приобретает окончательный короткий вид:

$$ overline{a} times overline{b} = (a_2 b_3 — a_3 b_2; a_3 b_1 — a_1 b_3; a_1 b_2 — a_2 b_1) $$

Свойства

При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
$$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$

Примеры решений

Пример 1

Найти векторное произведение векторов, заданных координатами

$$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$

Решение

Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) — overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} — overline{j} + 3overline{k} $$

Полученный ответ можно записать в удобном виде:

$$ overline{a} times overline{b} = (5, -1, 3) $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ overline{a} times overline{b} = (5, -1, 3) $$

Геометрический смысл

Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.

Пример 2

Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$

Решение

Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов.

Находим определитель:

$$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) — overline{j}(2+3) + overline{k}(4+1) = -5overline{i} — 5overline{j} + 5overline{k} $$

Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора:

$$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$

По формуле нахождения площади треугольника имеем:

$$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$

Ответ

$$ S_Delta = 4.33 $$

Источник

Примеры
решения задач с векторами

Вектора
применяются во многих науках,
таких как: математика, физика, геометрия
и многих других прикладных науках. На
практике, они позволяют не делать лишних
операций и сократить время выполнения
задач. Поэтому, будущим специалистам
очень важно понять теорию векторов и
научиться решать задачи с ними.

Перед
изучением примеров решения задач
советуем изучить теоретический материал
по векторам, прочитать все определения
и свойства. Список тем находится в правом
меню.

Координаты
вектора

Теоретический
материал по теме — координаты
вектора.

Пример

Запись
означает,
что вектор
имеет
следующие координаты: абсцисса равна
5, ордината равна -2.

Пример

Задание.
Заданы векторы
и
.
Найти координаты вектора

Решение.

Пример

Задание.
Вектор
.
Найти координаты вектора

Решение.

Пример

Задание.
Найти координаты вектора
,
если

Решение.

Длина
(модуль) вектора

Теоретический
материал по теме — длина
вектора.

Пример

Задание.
Найти длину вектора

Решение.
Используя формулу, получаем:

Пример

Задание.
Найти длину вектора

Решение.
Используя формулу, получаем:

Угол
между векторами

Теоретический
материал по теме — угол
между векторами.

Пример

Задание.
Известно, что скалярное произведение
двух векторов
,
а их длины
.
Найти угол между векторами
и
.

Решение.
Косинус искомого угла:

Пример

Задание.
Найти угол между векторами
и

Решение.
Косинус искомого угла

Пример

Задание.
Найти угол между векторами
и

Решение.
Косинус искомого угла:

Разложение
вектора по ортам координатных осей

Теоретический
материал по теме — разложение
вектора по ортам.

Пример

Задание.
Зная разложения вектора
по
базисной системе векторов:
,
записать координаты этого вектора в
пространстве.

Решение.
Коэффициенты при ортах и есть координатами
вектора, поэтому из того, что
,
получаем, что

Пример

Задание.
Вектор
задан
своими координатами:
.
Записать разложение данного вектора
по ортам осей координат.

Решение.
Координаты вектора — это коэффициенты
при ортах координатных осей в разложении
вектора по базисной системе векторов,
поэтому искомое разложение:

Скалярное
произведение векторов

Теоретический
материал по теме — скалярное
произведение векторов.

Пример

Задание.
Вычислить скалярное произведение
векторов
и
,
если их длины соответственно равны 2 и
3, а угол между ними 60°.

Решение.
Так как из условия
,
,
а
,
то

Пример

Задание.
Найти скалярное произведение векторов
и

Решение.
Скалярное произведение

Векторное
произведение векторов

Теоретический
материал по теме — векторное
произведение векторов.

Пример

Задание.
Найти векторное произведение векторов
и

Решение.
Составляем определитель и вычисляем
его:

Смешанное
произведение векторов

Теоретический
материал по теме — смешанное
произведение векторов.

Пример

Задание.
Вычислить объем пирамиды, построенной
на векторах
,
,

Решение.
Найдем смешанное произведение заданных
векторов, для это составим определитель,
по строкам которого запишем координаты
векторов
,
и
:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание:

Координаты вектора
Длина (модуль) вектора
Угол между векторами
Разложение вектора по ортам координатных осей
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов

Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других
прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач.
Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.

Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать
все определения и свойства. Список тем находится в правом меню.

Координаты вектора

Теоретический материал по теме — координаты вектора.

Пример

Запись $overline{a}=(5 ;-2)$ означает, что вектор $overline{a}$
имеет следующие координаты: абсцисса равна 5, ордината равна -2.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Заданы векторы $overline{a}=(-3 ; 5)$
и $overline{b}=(0 ;-1)$. Найти координаты вектора $overline{c}=overline{a}+overline{b}$

Решение. $overline{c}=overline{a}+overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$

Пример

Задание. Вектор $overline{a}=(3 ;-2)$.
Найти координаты вектора 2$overline{a}$

Решение. $2 overline{a}=2 cdot(3 ;-2)=(2 cdot 3 ; 2 cdot(-2))=(6 ;-4)$

Пример

Задание. Найти координаты вектора $overline{A B}$,
если $A(-4 ; 2), B(1 ;-3)$

Решение. $overline{A B}=(1-(-4) ;-3-2)=(5 ;-5)$

Длина (модуль) вектора

Теоретический материал по теме — длина вектора.

Пример

Задание. Найти длину вектора $overline{a}=(-4 ; 3)$

Решение. Используя формулу, получаем:

$|overline{a}|=sqrt{(-4)^{2}+3^{2}}=sqrt{16+9}=sqrt{25}=5$

Пример

Задание. Найти длину вектора $overline{a}=(1 ; 0 ;-4)$

Решение. Используя формулу, получаем:

$|overline{a}|=sqrt{1^{2}+0^{2}+(-4)^{2}}=sqrt{1+0+16}=sqrt{17}$

Угол между векторами

Теоретический материал по теме — угол между векторами.

Пример

Задание. Известно, что скалярное произведение двух векторов $(overline{a} ; overline{b})=2$,
а их длины $|overline{a}|=2,|overline{b}|=2$.
Найти угол между векторами $overline{a}$ и
$overline{b}$.

Решение. Косинус искомого угла:

$$cos (bar{a}, bar{b})=frac{(bar{a} ; bar{b})}{|bar{a}| cdot|bar{b}|}=frac{2}{2 cdot 2}=frac{1}{2} Rightarrow(bar{a}, bar{b})=60^{circ}$$

Пример

Задание. Найти угол между векторами $overline{a}=(1 ; sqrt{3})$ и
$overline{b}=(1 ; 0)$

Решение. Косинус искомого угла

$$cos (bar{a}, bar{b})=frac{1 cdot 1+sqrt{3} cdot 0}{sqrt{1^{2}+(sqrt{3})^{2}} cdot sqrt{1^{2}+0^{2}}}=frac{1}{2}$$
$$(bar{a}, bar{b})=arccos frac{1}{2}=60^{circ}$$

Пример

Задание. Найти угол между векторами $overline{a}=(1 ; 3)$
и $overline{b}=(2 ; 1)$

Решение. Косинус искомого угла:

$$cos (bar{a}, bar{b})=frac{1 cdot 2+3 cdot 1}{sqrt{1^{2}+3^{2}} cdot sqrt{2^{2}+1^{2}}}=frac{5}{sqrt{10} cdot sqrt{5}}=sqrt{frac{1}{2}}=frac{sqrt{2}}{2}$$
$$(bar{a}, bar{b})=arccos frac{sqrt{2}}{2}=45^{circ}$$

Разложение вектора по ортам координатных осей

Теоретический материал по теме — разложение вектора по ортам.

Пример

Задание. Зная разложения вектора $overline{a}$
по базисной системе векторов: $overline{a}=3 overline{i}-overline{k}$, записать координаты этого вектора в пространстве.

Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что $overline{a}=3 overline{i}-0 cdot overline{j}-overline{k}$,
получаем, что $overline{a}=(3 ; 0 ;-1)$

Пример

Задание. Вектор $overline{a}$ задан
своими координатами: $overline{a}=(2 ;-1 ; 5)$. Записать разложение данного вектора по ортам осей координат.

Решение. Координаты вектора — это коэффициенты при ортах координатных осей в разложении вектора
по базисной системе векторов, поэтому искомое разложение:

$overline{a}=2 overline{i}-overline{j}+5 overline{k}$

Скалярное произведение векторов

Теоретический материал по теме — скалярное произведение векторов.

Пример

Задание. Вычислить скалярное произведение векторов $overline{a}$ и
$overline{b}$ , если их длины соответственно равны 2 и 3,
а угол между ними 60°.

Решение. Так как из условия $|overline{a}|=2$,
$|overline{b}|=3$, а 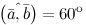, то

$overline{a} cdot overline{b}=(overline{a}, overline{b})=2 cdot 3 cdot cos 60^{circ}=6 cdot frac{1}{2}=3$

Пример

Задание. Найти скалярное произведение векторов $overline{a}=(3 ;-1)$ и
$overline{b}=(-2 ; 7)$

Решение. Скалярное произведение

$overline{a} overline{b}=3 cdot(-2)+(-1) cdot 7=-6-7=-13$

Векторное произведение векторов

Теоретический материал по теме — векторное произведение векторов.

Пример

Задание. Найти векторное произведение векторов $overline{a}=(6 ; 7 ; 10)$ и
$overline{b}=(8 ; 5 ; 9)$

Решение. Составляем определитель и вычисляем его:

$overline{a} times overline{b}=left| begin{array}{ccc}{overline{i}} & {overline{j}} & {overline{k}} \ {6} & {7} & {10} \ {8} & {5} & {9}end{array}right|=overline{i} left| begin{array}{cc}{7} & {10} \ {5} & {9}end{array}right|-overline{j} left| begin{array}{cc}{6} & {10} \ {8} & {9}end{array}right|+overline{k} left| begin{array}{cc}{6} & {7} \ {8} & {5}end{array}right|=$

$=overline{i}(7 cdot 9-5 cdot 10)-overline{j}(6 cdot 9-8 cdot 10)+overline{k}(6 cdot 5-8 cdot 7)=$

$=13 overline{i}+26 overline{j}-26 overline{k}=(13 ; 26 ;-26)$

Смешанное произведение векторов

Теоретический материал по теме — смешанное произведение векторов.

Пример

Задание. Вычислить объем пирамиды, построенной на векторах $overline{a}=(2 ; 3 ; 5)$,
$overline{b}=(1 ; 4 ; 4)$,
$overline{c}=(3 ; 5 ; 7)$

Решение. Найдем смешанное произведение заданных векторов, для это составим определитель,
по строкам которого запишем координаты векторов $overline{a}$,
$overline{b}$ и $overline{c}$:

$(overline{a}, overline{b}, overline{c})=left| begin{array}{lll}{2} & {3} & {5} \ {1} & {4} & {4} \ {3} & {5} & {7}end{array}right|=2 cdot 4 cdot 7+1 cdot 5 cdot 5+3 cdot 4 cdot 3-$

$-3 cdot 4 cdot 5-5 cdot 4 cdot 2-1 cdot 3 cdot 7=-4$

$$V_{пир}=frac{1}{6}|(overline{a}, overline{b}, overline{c})|=frac{1}{6} cdot 4=frac{2}{3}$$

Читать первую тему — операции над векторами,
раздела векторы.

Источник

Векторное произведение векторов

Определение

Формула

Свойства

Примеры решений

Геометрический смысл

Координаты вектора

Длина (модуль) вектора

Угол между векторами

Разложение вектора по ортам координатных осей

Скалярное произведение векторов

Векторное произведение векторов

Смешанное произведение векторов

Не пропустите также: