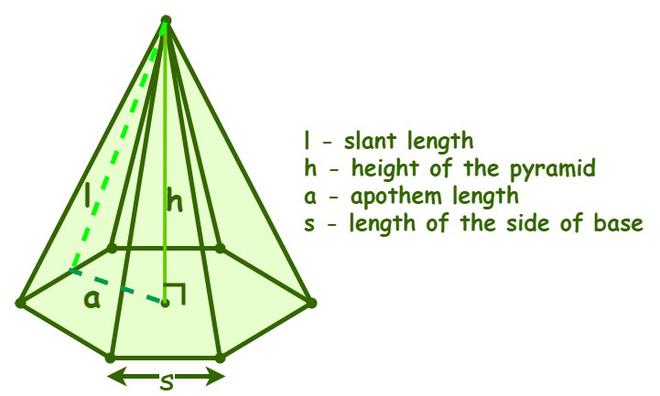
Обозначения
- $SABCDEF$ — правильная шестиугольная пирамида
- $O$ — центр основания пирамиды
- $a$ — длина стороны основания пирамиды
- $h$ — длина бокового ребра пирамиды
- $S_{text{осн.}}$ — площадь основания пирамиды
- $V_{text{пирамиды}}$ — объем пирамиды
Площадь основания пирамиды
В основаниях пирамиды находится правильный шестиугольник со стороной $a$. По свойствам правильного шестиугольника, площадь основания пирамиды равна $$ S_{text{осн.}}=frac{3sqrt{3}}{2}cdot a^2 $$
Правильный шестиугольник в основании пирамиды

Находим $SO$
Прямая $SO$ является высотой пирамиды, поэтому $angle SOF=90^{circ}$. Треугольник $SOF$ прямоугольный, в нем $FO=a, FS=h$. По свойствам прямоугольного треугольника $$ SO=sqrt{FS^2-FO^2}=sqrt{h^2-a^2} $$
Объем пирамиды
Объем пирамиды вычисляется как треть произведения площади ее основания на ее высоту. Высотой правильной пирамиды является отрезок $SO$. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем $$ V_{text{пирамиды}}=frac{1}{3}cdot S_{text{осн.}}cdot SO=frac{sqrt{3}}{2}cdot a^2 cdot sqrt{h^2-a^2} $$
Находим $ST$ и $TO$

A hexagonal pyramid is a three-dimensional shaped pyramid that has a hexagonal base along with the sides or faces in the shape of isosceles triangles that meet at the apex or the top of the pyramid. A hexagonal pyramid is one of the different types of pyramids, which are classified based on the shape of the base of a pyramid. It is also known as a heptahedron since a hexagonal pyramid consists of 7 faces, which includes a hexagonal base and 6 isosceles triangular lateral faces. It has a total of seven faces, twelve edges, and seven vertices. One of the seven vertices is the apex, which is at the top, and the other six are at the base of the pyramid. Out of the twelve edges, six edges connect the triangle edges that meet at the apex, and the other six are the edges of the base.
Regular Hexagonal Pyramid
A regular hexagonal pyramid is a pyramid whose hexagonal base is regular and the pyramid is straight, whereas an irregular hexagonal pyramid is a pyramid whose hexagonal base is irregular and the pyramid is oblique. A right regular pyramid is a hexagonal pyramid with a regular hexagonal base and, the apex of the pyramid is right above the center of the base, such that the apex forms a right angle with the center of the base and any other vertex.
Regular Hexagonal Pyramid formula
There are two formulas for a regular hexagonal pyramid, i.e., the surface area of a regular hexagonal pyramid and the volume of a regular hexagonal pyramid. To calculate the surface area or the volume of a regular hexagonal pyramid, we need to know its four major aspects, i.e., the length of the side of the base; the apothem, which is the distance from the center of the base to any point on the side of the base; the height of the pyramid, which is the perpendicular distance from the apex to the center of the base; and finally the slant height of the pyramid, which is the height of the triangular faces or the perpendicular distance from the apex to any point on the boundary of the base of the pyramid.
Lateral surface area (LSA)
The lateral surface area is the region occupied by the lateral surfaces or triangular faces of a regular hexagonal pyramid. The formula to determine the lateral surface area of the regular hexagonal pyramid (LSA) is given as follows,
The lateral surface area of the regular hexagonal pyramid = The sum of areas of the lateral surfaces (triangles) of the pyramid
= 6 × [½ × base × height] =3 (s × l)
Lateral surface area of the regular hexagonal pyramid = 3(s × l)
Where,
“s” is the side length of the base, and
“l” is the slant height of the pyramid.
Total surface area (TSA)
The total surface area is the total region occupied by all the surfaces of a regular hexagonal pyramid, i.e., the area occupied by the lateral surfaces, or triangular faces, and also is hexagonal base.
Total surface area of a pyramid (TSA) = Lateral surface area of the pyramid + Base area
The surface area of the hexagonal pyramid can be calculated when we have the slant height of the pyramid which is the height from the apex to any point on the boundary of the base of the pyramid. Hence, let us see both the formula of the hexagonal pyramid – base area and surface area.
Base area = 3as
Where,
“a” is the apothem length, and
“s” is the side length of the base.
TSA = LSA + Base area
TSA = 3sl + 3as
Hence,
Total surface area of the regular hexagonal pyramid (TSA) = 3sl + 3as
Where,
“s” is the side length of the base,
“l” is the slant height, and
“a” is the apothem length.
When the apothem of the regular hexagonal pyramid is not mentioned and the triangular faces are equilateral, there is another alternative formula to calculate its surface area, i.e.,
Total surface area of the hexagonal pyramid = 3(s × l) + 3√3/2 (s)2
Where,
“s” is the side length of the base, and
“l” is the slant height of the pyramid.
Area of the hexagonal base = 3√3/2 (s)2
Volume of the regular hexagonal pyramid
The volume is the total space enclosed between all the faces of a regular hexagonal pyramid. The general formula for calculating the volume of a pyramid is equal to one-third of the product of the base area and the height of the pyramid.
Volume (V) = (1/3) × Base area × Height cubic units
Now, by substituting the values of the base area and the height, we get
Volume of the regular hexagonal pyramid = (a × s × h) cubic units
Where,
“a” is the apothem length,
“s” is the side length of the base, and
“h” is the height of the pyramid.
When the apothem of the regular hexagonal pyramid is not mentioned and the triangular faces are equilateral, there is another alternative formula to calculate its volume, i.e.,
Volume of the regular hexagonal pyramid (V)= (√3/2) × s2 × h cubic units
Where,
“s” is the side length of the base, and
“h” is the height of the pyramid.
Practice Problems based on Regular Hexagonal Pyramid
Problem 1: What is the volume of a regular hexagonal pyramid whose apothem length is 5 cm, length of the side of the base is 10 cm, and height is 13 cm?
Solution:
Given data,
Apothem length (a) = 5 cm
The length of the side of the base = 10 cm,
The height of the pyramid = 13 cm
We know that,
The volume of a regular hexagonal pyramid (V) = (a × s × h) cubic units
V = 5 × 10 × 13
Volume = 650 cm3
Therefore, the volume of the given hexagonal pyramid is 650 cu. cm.
Problem 2: What is the surface area of a regular hexagonal pyramid if its apothem length is 6 inches, the length of the side of the base is 8 inches, and the slant height is 15 inches?
Solution:
Given data,
Apothem length (a) = 6 inches
The length of the side of the base (s) = 8 inches
The slant height of the pyramid (l) = 15 inches
We know that,
The surface area of the hexagonal pyramid = 3as + 3sl square units
= 3 × 6 × 8 + 3 × 8 × 15
= 144 + 360 = 504 sq. in
Therefore, the surface area of the given pyramid is 504 sq. in.
Problem 3: Find the height of a regular hexagonal pyramid if its volume is 576 cu. cm, the length of the side of the base is 8 cm, and the apothem length is 8 cm.
Solution:
Given data,
Apothem length (a) = 8 cm
The length of the side of the base (s) = 8 cm
Volume = 576 cu. cm
We know that,
The volume of a regular hexagonal pyramid (V) = (a × s × h) cubic units
⇒ 8 × 8 × h = 576
⇒ 64h = 576
⇒ h = 576/64 = 9 cm
Hence, the height of a regular hexagonal pyramid is 9 cm.
Problem 4: What is the volume of a regular hexagonal pyramid if the sides of a base are 7 cm each and the height of the pyramid is 14 cm?
Solution:
Given data,
Height of the pyramid (h) = 14 cm
The length of the side of the base (s) = 7 cm
Area of the hexagonal base (A) = 3√3/2 b2 = 3√3/2 (7)2 = 147√3/2 sq. cm
The volume of a regular hexagonal pyramid (V) = 1/3 × A × h
V = 1/3 × (147√3/2) × 14 = 594.09 cm3
Hence, the volume of the given pyramid is 594.09 cm3.
Problem 5: Determine the lateral surface area of a regular hexagonal pyramid if the side length of the base is 15 inches and the pyramid’s slant height is 21 inches.
Solution:
Given data,
The length of the side of the base (s) = 15 inches, and
Slant height (l) = 21 inches
The perimeter of the square base (P) = 6s = 6(15) = 90 inches
We know that,
The lateral surface area (LSA) = (½) Pl
= (½ ) × (90) × 21 = 945 sq. in
Therefore, the lateral surface area of the given pyramid is 945 sq. in.
FAQs based on Regular Hexagonal Pyramid
Question 1: What is a Hexagonal Pyramid?
Answer:
A hexagonal pyramid is a 3D shape with hexagonal base combined with 6 triangles faces against each sides of the hexagonal base erected in such a way to form a pyramid at its apex. These triangles may be either isosceles triangles or equilateral triangles and these triangles are called as lateral faces. A hexagonal pyramid contains 7 vertices, 7 faces, and 12 edges.
Question 2: What is the formula for finding the volume of the Hexagonal Pyramid?
Answer:
The formula for calculating the volume of the hexagonal pyramid is given by,
Volume of Hexagonal Pyramid(V) = (abh) cubic units
where,
a is the apothem of the pyramid,
b is the base, and h is the height.
Question 3: What is the formula for finding the Surface Area of a Hexagonal Pyramid?
Answer:
Formula for finding the surface area of a hexagonal pyramid is given by,
Surface Area of Hexagonal Pyramid (TSA)= (3ab + 3bs) square units,
where,
a is the apothem of the pyramid,
b is the base, and
s is the slant height of the pyramid.
Высота пирамиды: определение, формулы, расчеты
23.11.2018 18:31
Одной из объемных фигур, изучаемых в курсе пространственной геометрии, является пирамида. Важной характеристикой этой фигуры является ее высота. В статье дадим определение высоты пирамиды и приведем формулы, через которые она связана с другими линейными характеристиками.
Что собой представляет пирамида
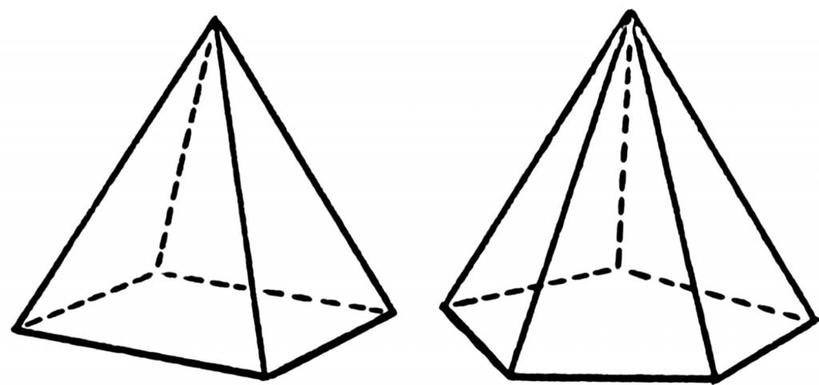
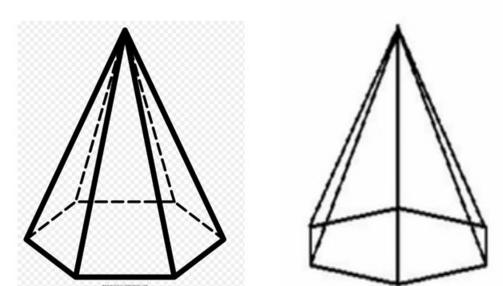
Под пирамидой понимают геометрическую фигуру пространственную, которая получается в результате соединения всех углов многоугольника с одной точкой пространства. Рисунок ниже демонстрирует расположение линий (ребер) для четырехугольной и пятиугольной пирамид.
Многоугольная грань фигуры называется ее основанием. Точка, где все треугольные грани соединяются, называется вершиной. Для определения высоты пирамиды отмеченные элементы являются важными.
Высота фигуры
Высотой пирамиды называется перпендикуляр, который из ее вершины опущен на плоскость основания. Важно понимать, что из каждой вершины, принадлежащей основанию фигуры, тоже можно провести перпендикуляр к соответствующей треугольной грани, однако он высотой не будет являться. Высота пирамиды — это единственный перпендикуляр, который является одной из важных ее линейных характеристик.
Каждому школьнику известно, что любая плоская фигура обладает геометрическим центром (в физике ему соответствует центр масс). Например, геометрический центр для произвольного треугольника определяется точкой пересечения его медиан, для параллелограмма — точкой пересечения диагоналей. Если высота пирамиды пересекает ее основание в геометрическом центре, то фигура называется прямой. Пирамида прямая, имеющая в основании многоугольник с одинаковыми сторонами и углами, называется правильной.
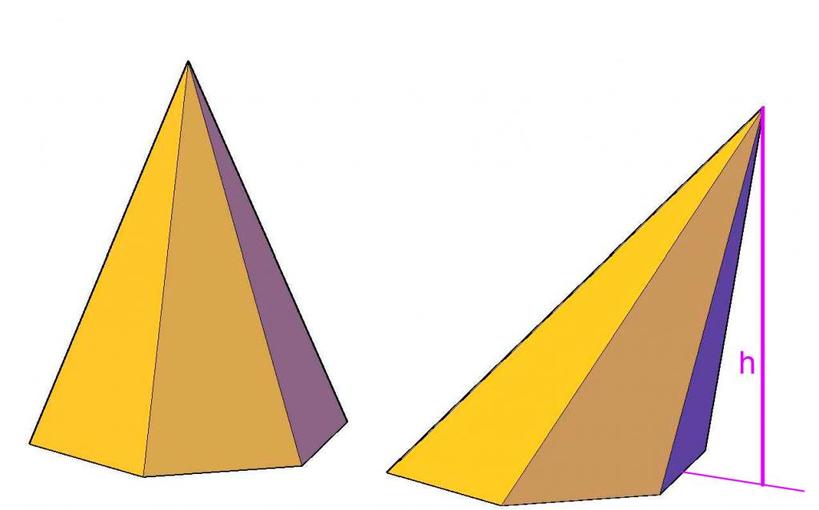
Рисунок выше показывает, чем отличается неправильная пирамида от правильной. Видно, что высота неправильной фигуры лежит за пределами ее основания, в то время как у правильной шестиугольной пирамиды высота находится внутри фигуры, пересекая ее основание в центре геометрическом.
Важными свойствами всех правильных пирамид являются следующие:
- все боковые грани представляют собой равнобедренные треугольники и равны друг другу;
- длины боковых ребер и апофем являются одинаковыми.
Формулы для высоты правильной пирамиды
Существует четыре основных линейных характеристики для любой пирамиды правильной:
- сторона основания;
- боковое ребро;
- апофема боковой грани;
- высота фигуры.
Все они связаны математически друг с другом. Обозначим длину стороны основания символом a, высоту — h, апофему — hb и ребро — b. Формулы, которые эти величины связывают, имеют индивидуальный вид для соответствующей n-угольной пирамиды. Например, для правильной пирамиды четырехугольной высоту можно определить по формулам:
h = √(ab2 — a2/4);h = √(b2 — a2/2).
Эти формулы следуют из теоремы Пифагора при рассмотрении соответствующих прямоугольных треугольников внутри пирамиды.
Если рассматривается фигура с треугольным основанием, тогда справедливы следующие формулы для высоты правильной пирамиды:
h = √(ab2 — a2/12);h = √(b2 — a2/3).
Решение задачи с шестиугольной пирамидой
Предположим, что нам дана пирамида правильная с шестиугольным основанием. Известно, что высота основания пирамиды равна 13 см. Зная, что длина ее бокового ребра равна 10 см, необходимо вычислить объем и высоту правильной шестиугольной пирамиды.
Рисунок ниже показывает, как выглядит правильный шестиугольник.
Расстояние между любыми его двумя параллельными сторонами называется высотой. Не сложно показать, что эта высота ha связана с длиной стороны фигуры следующей формулой:
ha = a*√3
Подставляя в выражение значение ha, находим, что сторона основания a равна 7,51 см.
Высоту h фигуры можно определить, если рассмотреть прямоугольный треугольник, находящийся внутри пирамиды и состоящий из двух катетов (высота пирамиды и половина диагонали шестиугольного основания) и гипотенузы (боковое ребро). Тогда значение h будет равно:
h = √(b2 — a2) = √(100 — 56,4) = 6,6 см.
Объем пирамиды определяется как третья часть от произведения высоты фигуры на площадь ее основания. Площадь правильного шестиугольника равна:
S6 = n/4*a2*ctg(pi/n) = 6/4*a2*ctg(pi/6) = 3*√3/2*a2 = 3*√3/2*56,4 ≈ 146,53 см2.
Использованная для вычисления S6 формула является универсальной для произвольного правильного n-угольника.
Для определения объема фигуры остается подставить в соответствующую формулу найденные параметры:
V = 1/3*h*S6 = 1/3*6,6*146,53 = 322,366 см3.
Мы получили значение высоты пирамиды и рассчитали ее объем. Таким образом, поставленная задача решена.
Определение
Пирамида – это многогранник, составленный из многоугольника (A_1A_2…A_n) и (n) треугольников с общей вершиной (P) (не лежащей в плоскости многоугольника) и противолежащими ей сторонами, совпадающими со сторонами многоугольника.
Обозначение: (PA_1A_2…A_n).
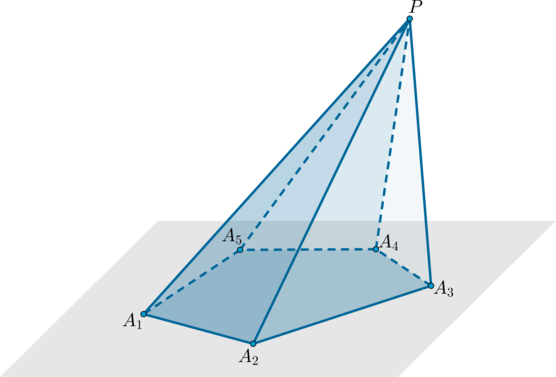
Пример: пятиугольная пирамида (PA_1A_2A_3A_4A_5).
Треугольники (PA_1A_2, PA_2A_3) и т.д. называются боковыми гранями пирамиды, отрезки (PA_1, PA_2) и т.д. – боковыми ребрами, многоугольник (A_1A_2A_3A_4A_5) – основанием, точка (P) – вершиной.
Высота пирамиды – это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамида, в основании которой лежит треугольник, называется тетраэдром.
Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено одно из условий:
((a)) боковые ребра пирамиды равны;
((b)) высота пирамиды проходит через центр описанной около основания окружности;
((c)) боковые ребра наклонены к плоскости основания под одинаковым углом.
((d)) боковые грани наклонены к плоскости основания под одинаковым углом.
Правильный тетраэдр – это треугольная пирамида, все грани которой – равные равносторонние треугольники.
Теорема
Условия ((a), (b), (c), (d)) эквивалентны.
Доказательство
Проведем высоту пирамиды (PH). Пусть (alpha) – плоскость основания пирамиды.
1) Докажем, что из ((a)) следует ((b)). Пусть (PA_1=PA_2=PA_3=…=PA_n).
Т.к. (PHperp alpha), то (PH) перпендикулярна любой прямой, лежащей в этой плоскости, значит, треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) – прямоугольные. Значит, эти треугольники равны по общему катету (PH) и гипотенузам (PA_1=PA_2=PA_3=…=PA_n). Значит, (A_1H=A_2H=…=A_nH). Значит, точки (A_1, A_2, …, A_n) находятся на одинаковом расстоянии от точки (H), следовательно, лежат на одной окружности с радиусом (A_1H). Эта окружность по определению и есть описанная около многоугольника (A_1A_2…A_n).
2) Докажем, что из ((b)) следует ((c)).
Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) прямоугольные и равны по двум катетам. Значит, равны и их углы, следовательно, (angle PA_1H=angle PA_2H=…=angle PA_nH).
3) Докажем, что из ((c)) следует ((a)).
Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) прямоугольные и по катету и острому углу. Значит, равны и их гипотенузы, то есть (PA_1=PA_2=PA_3=…=PA_n).
4) Докажем, что из ((b)) следует ((d)).
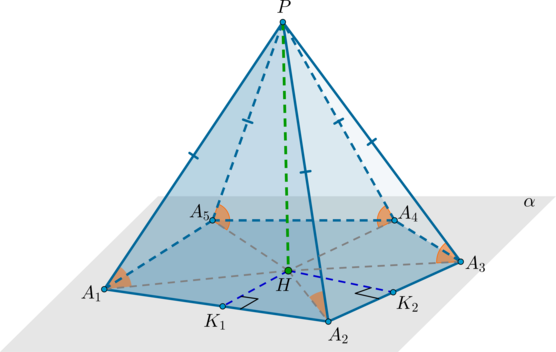
Т.к. в правильном многоугольнике совпадают центры описанной и вписанной окружности (вообще говоря, эта точка называется центром правильного многоугольника), то (H) – центр вписанной окружности. Проведем перпендикуляры из точки (H) на стороны основания: (HK_1,
HK_2) и т.д. Это – радиусы вписанной окружности (по определению). Тогда по ТТП ((PH) – перпендикуляр на плоскость, (HK_1, HK_2) и т.д. – проекции, перпендикулярные сторонам) наклонные (PK_1, PK_2) и т.д. перпендикулярны сторонам (A_1A_2, A_2A_3) и т.д. соответственно. Значит, по определению (angle PK_1H, angle PK_2H) равны углам между боковыми гранями и основанием. Т.к. треугольники (PK_1H, PK_2H, …) равны (как прямоугольные по двум катетам), то и углы (angle PK_1H, angle PK_2H, …) равны.
5) Докажем, что из ((d)) следует ((b)).
Аналогично четвертому пункту треугольники (PK_1H, PK_2H, …) равны (как прямоугольные по катету и острому углу), значит, равны отрезки (HK_1=HK_2=…=HK_n). Значит, по определению, (H) – центр вписанной в основание окружности. Но т.к. у правильных многоугольников центры вписанной и описанной окружности совпадают, то (H) – центр описанной окружности. Чтд.
Следствие
Боковые грани правильной пирамиды – равные равнобедренные треугольники.
Определение
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Апофемы всех боковых граней правильной пирамиды равны между собой и являются также медианами и биссектрисами.
Важные замечания
1. Высота правильной треугольной пирамиды падает в точку пересечения высот (или биссектрис, или медиан) основания (основание – правильный треугольник).
2. Высота правильной четырехугольной пирамиды падает в точку пересечения диагоналей основания (основание – квадрат).
3. Высота правильной шестиугольной пирамиды падает в точку пересечения диагоналей основания (основание – правильный шестиугольник).
4. Высота пирамиды перпендикулярна любой прямой, лежащей в основании.
Определение
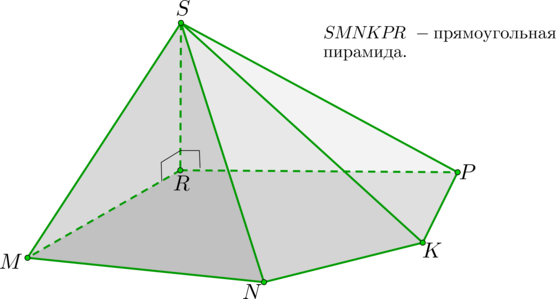
Пирамида называется прямоугольной, если одно ее боковое ребро перпендикулярно плоскости основания.
Важные замечания
1. У прямоугольной пирамиды ребро, перпендикулярное основанию, является высотой пирамиды. То есть (SR) – высота.
2. Т.к. (SR) перпендикулярно любой прямой из основания, то (triangle SRM, triangle SRP) – прямоугольные треугольники.
3. Треугольники (triangle SRN, triangle SRK) – тоже прямоугольные.
То есть любой треугольник, образованный этим ребром и диагональю, выходящей из вершины этого ребра, лежащей в основании, будет прямоугольным.
[{Large{text{Объем и площадь поверхности пирамиды}}}]
Теорема
Объем пирамиды равен трети произведения площади основания на высоту пирамиды: [V_{text{пирамиды}}=dfrac13 S_{text{осн}}cdot h]
Следствия
Пусть (a) – сторона основания, (h) – высота пирамиды.
1. Объем правильной треугольной пирамиды равен (V_{text{прав.треуг.пир.}}=dfrac{sqrt3}{12}a^2h),
2. Объем правильной четырехугольной пирамиды равен (V_{text{прав.четыр.пир.}}=dfrac13a^2h).
3. Объем правильной шестиугольной пирамиды равен (V_{text{прав.шест.пир.}}=dfrac{sqrt3}{2}a^2h).
4. Объем правильного тетраэдра равен (V_{text{прав.тетр.}}=dfrac{sqrt3}{12}a^3).
Теорема
Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему.
[{Large{text{Усеченная пирамида}}}]
Определение
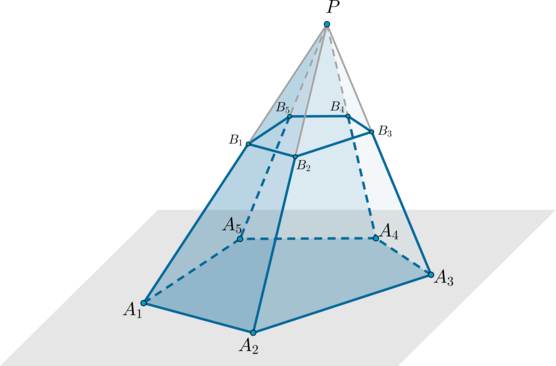
Рассмотрим произвольную пирамиду (PA_1A_2A_3…A_n). Проведем через некоторую точку, лежащую на боковом ребре пирамиды, плоскость параллельно основанию пирамиды. Данная плоскость разобьет пирамиду на два многогранника, один из которых – пирамида ((PB_1B_2…B_n)), а другой называется усеченная пирамида ((A_1A_2…A_nB_1B_2…B_n)).
Усеченная пирамида имеет два основания – многоугольники (A_1A_2…A_n) и (B_1B_2…B_n), которые подобны друг другу.
Высота усеченной пирамиды – это перпендикуляр, проведенный из какой-нибудь точки верхнего основания к плоскости нижнего основания.
Важные замечания
1. Все боковые грани усеченной пирамиды – трапеции.
2. Отрезок, соединяющий центры оснований правильной усеченной пирамиды (то есть пирамиды, полученной сечением правильной пирамиды), является высотой.
ЭСО
→ МНОГОГРАННИКИ
→ Геометрическое тело
→ Многогранник
→ Пирамида
Пред. ←
Содержание
→ След.
Правильная пирамида
ОПРЕДЕЛЕНИЕ:
Пирамида называется правильной, если её
основание — правильный n-угольник, а все
боковые рёбра равны.
ТЕОРЕМА
О высоте правильной пирамиды
В правильной пирамиде отрезок, соединяющий вершину
пирамиды с центром её основания, является
высотой пирамиды.
Для определённости проведём доказательство для правильной шестиугольной
пирамиды SABCDEF:
Пусть точка O — центр шестиугольника ABCDEF. Докажем, что
отрезок SO есть высота пирамиды. Рассмотрим какие-нибудь
два диагональных сечения, проходящие через отрезок SO,
например треугольники ASD и CSF. Указанные теругольники
являются равнобедренными (все боковые ребра правильной пирамиды
равны), следовательно, в каждом из них медиана SO является
высотой, т.е. SO ⊥ FC, SO ⊥ AD
Таким образом, прямая SO перпендикулярна двум пересекающимся
прямым FC и AD плоскости основания, а значит она перпендикулярная
этой плоскости. Таким образом отрезок SO перпендикулярен
плоскости основания, т.е. является высотой пирамиды.
В случае правильной пирамиды, основанием которой
служит n-угольник с чётным числом вершин, доказательство
аналогично. В случае, когда основанием пирамиды служит
многоугольник с нечётным числом вершин, для доказательства
можно воспользоваться тем, что основание высоты
правильной пирамиды совпадает с центром окружности,
описанной около его основания.
ТЕОРЕМА
О площади боковой поверхности правильной пирамиды
Площадь боковой поверхности правильной пирамиды равна половине
произведения периметра основания на апофему
Sбок = ½ Pоснℓ
Доказательство проведём для правильной шестиугольной пирамиды
TABCDEF:
В случае правильной n-угольной пирамиды доказательство аналогично
Пусть периметр основания пирамиды Pосн, апофему обозначим
буквой ℓ. Боковые грани правильной пирамиды являются равнобедренными
треугольниками, основания которых — стороны основания пирамиды,
а высоты равны апофеме ℓ.
Площадь боковой поверхности равна сумме указанных
равнобедренных треугольников, т.е.:
Sбок =
½ ABℓ + ½ BCℓ + ½ CDℓ + ½ DEℓ +
½ EFℓ + ½ FAℓ = ½ ℓ(AB + BC + CD + DE + EF + FA) =
½ Pоснℓ.
- Апофема правильной пирамиды
Пред. ←
Содержание
→ След.