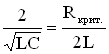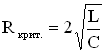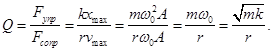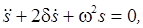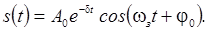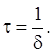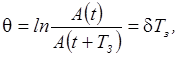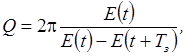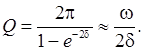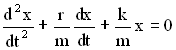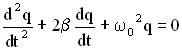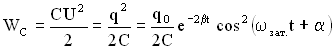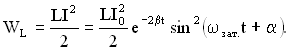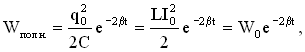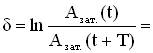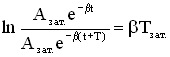Время релаксации затухающих колебаний как найти

Затухающие
колебания. Декремент затухания,
коэффициент затухания, время релаксации

Свободные колебания
технических систем в реальных условиях
протекают, когда на них действуют силы
сопротивления. Действие этих сил приводит
к уменьшению амплитуды колеблющейся
величины.

Колебания,
амплитуда которых из-за потерь энергии
реальной колебательной системы
уменьшается с течением времени,
называются затухающими.

Наиболее часто
встречается случаи, когда сила
сопротивления пропорциональна скорости
движения

где r —
коэффициент сопротивления среды. Знак
минус показывает, что F_C направлена
в сторону противоположную скорости.

Запишем
уравнение колебаний в точке, колеблющийся
в среде, коэффициент сопротивлений
которой r. По
второму закону Ньютона

где β — коэффициент
затухания. Этот коэффициент характеризует
скорость затухания колебаний, При
наличии сил сопротивления энергия
колеблющейся системы будет постепенно
убывать, колебания будут затухать.

— дифференциальное
уравнение затухающих колебаний.

— уравнение
затухающих колебаний.

ω – частота затухающих
колебаний:

Период затухающих
колебаний:

Затухающие
колебания при строгом рассмотрении не
являются периодическими. Поэтому о
периоде затухаюших колебаний можно
гово­рить, когда β мало.

Если
затухания выражены слабо (β→0), то .
Затухающие колебания можно

рассматривать как
гармонические колебания, амплитуда
которых меняется по экспоненциальному
закону

В
уравнении (1) А₀ и
φ₀ —
произвольные константы, зависящие от
выбора момента времени, начиная е
которого мы рассматриваем колебания

Рассмотрим
колебание в течение, некоторого времени 
τ, за которое амплитуда уменьшится
в е раз

τ — время релаксации.

Коэффициент
затихания β обратно пропорционален
времени, в течение которого амплитуда
уменьшается в е раз.
Однако коэффициента затухания недостаточна
для характеристики затуханий колебаний.
Поэтому необходимо ввести такую
характеристику для затухания колебаний,
в которую входит время одного колебаний.
Такой характеристикой
является декремент (по-русски:
уменьшение) затуханияD,
который равен отношению амплитуд,
отстоящих по времени на период:       

Логарифмический
декремент затухания равен
логарифму D:

Логарифмический
декремент затухания обратно пропорционален
числу колебаний, в результате которых
амплитуда колебаний умень­шилась
в е раз.
Логарифмический декремент затухания
— постоянная для данной системы величина.

Еще
одной характеристикой колебательной
система является добротность Q.

Добротность
пропорциональна числу колебаний,
совершаемых системой, за время релаксации
τ.

Добротность Q колебательной
системы является мерой относительной
диссипации (рассеивания) энергии.

Добротность Q колебательной
системы называется число, показывающее
во сколько раз сила упругости больше
силы сопротивления.

Чем больше добротность,
тем медленнее происходит затухание,
тем затухающие колебания ближе к
свободным гармоническим.

Вынужденные
колебания.

Резонанс

В целом ряде случаев
возникает необходимость создания
систем, совершающих незатухающие
колебания. Получить незатухающие
колебания в системе можно, если
компенсировать потери энергии,
 воздействуя на систему периодически
изменяющейся силой.

Пусть

Запишем
выражение для уравнения движения
материальной точки, совершающей
гармоническое колебательное движение
под действием вынуждающей силы.

По второму закону
Ньютона:

                                                            (1)

— дифференциальное
уравнение вынуж­денных колебаний.

Это дифференциальное
уравнение является линейным неоднородным.

Его решение равно
сумме общего решения однородного
уравнения и частного решения неоднородного
уравнения:

Найдем частное
решение неоднородного уравнения. Для
этого перепишем уравнение (1) в следующем
виде:

                                                                            (2)

Частное решение
этого уравнения будем искать в виде:

Тогда

Подставим в (2):

т.к.
выполняется для любого t ,
то должно выполняться равенство  γ
= ω , следовательно,

Это комплексное
число удобно представить в виде

где А определяется
по формуле (3 ниже), а φ — по формуле (4),
следовательно, решение (2),в комплексной
форме имеет вид

Его вещественная
часть, являвшаяся решением уравнения
(1) равна:

где

                                                                    (3)

                                                                               (4)

Слагаемое
Х_о.о. играет
существенную роль только в начальной
стадии при установлении колебаний до
тех пор, пока амплитуда вынужденных
колебаний не достигнет значения
определяемого равенством (3). В
установившемся режиме вынужденные
колебания происходят с частотой ω и
являются гармоническими. Амплитуда (3)
и фаза (4) вынужденных колебаний зависят
от частоты вынуждающей силы.  При
определенной частоте вынуждающей силы
амплитуда может достигнуть очень больших
значений. Резкое возрастание амплитуды
вынужденных колебаний при приближении
частоты вынуждающей силы к собственной
частоте механи­ческой системы,
называется резонансом.

Частота
ω вынуждающей силы,  при которой
наблюдается резонанс, называется
резонансной. Для того чтобы найти
значение ω_рез,
необходимо найти условие максимума
амплитуды. Для этого нужно определить
условие минимума знаменателя в (3) (т.е.
исследовать (3) на экстремум).

Зависимость
амплитуды колеблющейся величины от
частоты вынуждающей силы называется резонансной
кривой.
Резонансная кривая будет тем выше, чем
меньше коэффициент затухания β и с
уменьшением β, максимум резонансных
кривых смешается вправо. Если β = 0, то

ω_рез =
ω₀.

При ω→0
все кривые приходят к значению          
— статическое отклонение.

Параметрический
резонанс возникает в том случае, когда
периодическое изменение одного из
параметров система приводит к резкому
увеличению амплитуды колеблющейся
системы. Например, кабины, делающие
«солнышко» за счет изменения
положения центра тяжести система.(То
же в «лодочках».) См. §61 .т. 1 Савельев
И.В.

 Автоколебаниями
называются такие колебания, энергия
которых периодически пополняется в
результате воздействия самой системы
за счет источника энергии, находящегося
в этой же системе. 

Соседние файлы в папке Физика_1

• #
• #
• #
• #
• #
• #

  21.05.2015145.41 Кб3116.doc

• #
• #

  21.05.2015184.41 Кб2019.pdf

• #

  21.05.201599.84 Кб122.doc

• #

  21.05.2015112.13 Кб1020.doc

• #

Если на колеблющееся тело действует сила трения, то энергия системы, амплитуда смещения и амплитуда скорости не остаются постоянными, а убывают, энергия расходуется на преодоление сил трения и превращается в тепло. Происходит затухание колебаний. Такие колебания не являются гармоническими, и дифференциальное уравнение движения, как это было показано в начале раздела, имеет вид:

,

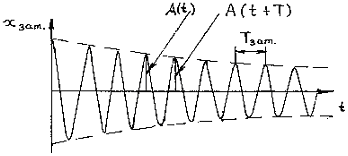
где b = r/2m – коэффициент затухания,  – собственная частота (угловая) колебаний системы при отсутствии затухания и m – масса колеблющейся системы. При условии, что затухание мало β << ω₀, этому уравнению в качестве решения удовлетворяет функция (рис. 48):

,

где е = 2,71 – основание натуральных логарифмов; A₀ и a₀ – постоянные  величины, зависящие от начальных условий;  – угловая частота затухающих колебаний, которая всегда меньше собственной частоты ω₀.

 Периодом затухающих колебаний принято называть время T, за которое система дважды проходит через среднее положение в одном и том же направлении, или время, за которое отклонение в одну и ту же сторону дважды достигает максимального значения. Силы трения замедляют движение системы. Поэтому период затухающих колебаний всегда несколько больше, чем период тех собственных колеба­ний, которые совершала бы система, если бы трение отсутствовало. При малом трении β << w₀ можно считать, что период затухающих колебаний Т = 2p/w практически равен периоду колебаний в отсутствии трения Т₀ = 2p/w₀, и угловая частота затухающих колебаний w = 2p/T совпадает с угловой частотой в отсутствии трения w₀ = 2p/Т₀.

Роль  амплитуды  колебаний в условно периодическом движении играет величина, которая убывает с течением времени по экспоненциальному закону:

.

Коэффициентом затухания β определяется быстрота (скорость), с которой убывает амплитуда. Величина τ_с, обратная β, называется временем затухания или временем релаксации τ_с = 1/β. Время релаксации – это то время, в течение которого амплитуда уменьшается в е = 2,71 раз. В самом деле, при t = t_c имеем

A(0)/A(t_c) = A₀/(A₀e^–1) = e.

Отношение амплитуд, соответствующих различным моментам времени, отличающимся на период, называется декрементом затухания:

D = A(t)/A(t + T) = A₀ e^{–b t} /A₀ e^{–b (t + T )} = e ^{b T}

Натуральный логарифм этого отношения называется логарифмическим декрементом затухания:

J = ln D = ln e ^{b T} = b T =  T / t_c .

Показатель затухания β характеризует затухание колебаний за единицу времени, а логарифмический декремент – за период. Величина, обратная логарифмическому декременту затухания, равна числу колебаний N_e, совершающихся за время релаксации: J^–1 = t_c / T = N_e , причем за это время t_c амплитуда уменьшается в е раз. Для характеристики колебательной системы часто употребляется также величина

Q = π /J = π N_e ,

называемая добротностью колебательной системы. Добротность пропорцио­нальна числу колебаний N_e , совершаемых системой за время релаксации.

Параметры затухания b, t_с, J и Q связаны между собой взаимно-однозначными соотношениями, а именно:

J = p / Q = b Т = Т / t_с , b = 1 /t_с = J / Т = p / Q Т,

t_с = 1 / b = Т / J =  Q Т / p   и  Q = p / J = p /b Т = pt_с / Т.

                          Рис. 48                                                         Рис. 49

Чем медленнее затухают колебания Т << t_с, тем выше добротность контура. Добротность – это характеристика качества колеблющейся системы. Для справки, добротность электрического колебательного контура обычно не превышает значения 10³, камертона составляет примерно 10⁴, кристалла кварца может достигать значения 10⁸, и наивысшей добротностью обладает резонатор лазера (10¹² и выше).

Затуханием называется постепенное ослабление
колебаний с течением времени, обусловленное потерей энергии колебательной
системой. При механических колебаниях причиной затухания является действие сил
трения и излучение энергии колебаний в окружающую среду в виде упругих волн.
Свободные колебания всех реальных колебательных систем являются
затухающими.

Рассмотрим затухающие колебания линейной системы.
Система называется линейной, если параметры,
характеризующие существенные в рассматриваемом процессе физические свойства
системы, не изменяются в ходе процесса.

Дифференциальное уравнение затухающих
колебаний в
линейной системе:

где ω – циклическая частота незатухающих собственных
колебаний системы, δ (с^-1) – коэффициент
затухания.

Решение этого уравнения имеет вид:

Здесь —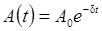
амплитуда затухающих колебаний, —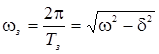
циклическая частота затухающих колебаний.

В экспоненциальной форме уравнение затухающих колебаний
записывается как:

.

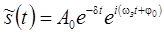
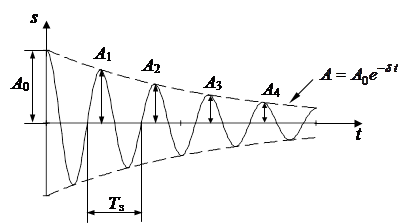
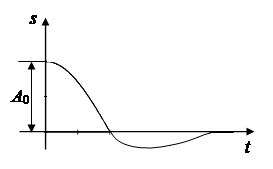
График затухающих колебаний приведен на
рисунке: 

Промежуток времени τ, в течение которого амплитуда
затухающих колебаний уменьшается в e раз,
называется временем
релаксации:

Величина,
равная

называется логарифмическим
декрементом затухания.

Еще
одна характеристика системы, совершающей затухающие колебания, —
ее добротность, равная:

где E(t) –
полная энергия системы в момент времени t. Чем выше добротность системы, тем медленнее
происходит в ней процесс затухания колебаний. Можно показать,
что:

При
увеличении коэффициента затухания циклическая частота затухающих колебаний
уменьшается, и при δ ≥ ω процесс затухания
становится апериодическим: выведенная из
положения равновесия колебательная система постепенно (без колебаний)
возвращается в него:

< Предыдущая                     Оглавление                      Следующая >

Уравнение затухающих колебаний имеет вид найти время релаксации

§6 Затухающие колебания

Декремент затухания. Логарифмический декремент затухания.

Добротность

Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.

Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.

Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения

где r — коэффициент сопротивления среды. Знак минус показывает, что F_C направлена в сторону противоположную скорости.

Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r . По второму закону Ньютона

где β — коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.

— дифференциальное уравнение затухающих колебаний.

— у равнение затухающих колебаний.

ω – частота затухающих колебаний:

Период затухающих колебаний:

Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно гово­рить, когда β мало.

Если затухания выражены слабо (β→0), то . Затухающие колебания можно

рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону

В уравнении (1) А₀ и φ₀ — произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания

Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз

τ — время релаксации.

Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D , который равен отношению амплитуд, отстоящих по времени на период:

Логарифмический декремент затухания равен логарифму D :

Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний умень­шилась в е раз. Логарифмический декремент затухания — постоянная для данной системы величина.

Еще одной характеристикой колебательной система является добротность Q .

Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.

Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.

Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.

Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.

§7 Вынужденные колебания.

Резонанс

В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.

Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.

По второму закону Ньютона:

(1)

— дифференциальное уравнение вынуж­денных колебаний.

Это дифференциальное уравнение является линейным неоднородным.

Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения:

Найдем частное решение неоднородного уравнения. Для этого перепишем уравнение (1) в следующем виде:

(2)

Частное решение этого уравнения будем искать в виде:

т.к. выполняется для любого t , то должно выполняться равенство γ = ω , следовательно,

Это комплексное число удобно представить в виде

где А определяется по формуле (3 ниже), а φ — по формуле (4), следовательно, решение (2),в комплексной форме имеет вид

Его вещественная часть, являвшаяся решением уравнения (1) равна:

(3)

(4)

Слагаемое Х_о.о. играет существенную роль только в начальной стадии при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения определяемого равенством (3). В установившемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механи­ческой системы, называется резонансом.

Частота ω вынуждающей силы, при которой наблюдается резонанс, называется резонансной. Для того чтобы найти значение ω_рез, необходимо найти условие максимума амплитуды. Для этого нужно определить условие минимума знаменателя в (3) (т.е. исследовать (3) на экстремум).

Зависимость амплитуды колеблющейся величины от частоты вынуждающей силы называется резонансной кривой. Резонансная кривая будет тем выше, чем меньше коэффициент затухания β и с уменьшением β, максимум резонансных кривых смешается вправо. Если β = 0, то

При ω→0 все кривые приходят к значению — статическое отклонение.

Параметрический резонанс возникает в том случае, когда периодическое изменение одного из параметров система приводит к резкому увеличению амплитуды колеблющейся системы. Например, кабины, делающие «солнышко» за счет изменения положения центра тяжести система.(То же в «лодочках».) См. §61 .т. 1 Савельев И.В.

Основные сведения о затухающих колебаниях в физике

Определение затухающих колебаний

Колебания бывают незатухающими и затухающими.

Затухающие колебания — это колебания, амплитуда которых уменьшается с течением времени (пока не станет равна нулю), так как колебательная система теряет энергию. Энергия может расходоваться на преодоление сопротивления воздуха, на увеличение внутренней энергии, на преодоление сил трения (в механической системе). В электромагнитном контуре энергия уменьшается из-за тепловых потерь.

Вывод: когда запас энергии закончится, колебания прекратятся.

Характеристики затухающих колебаний

Общие признаки затухающих колебаний:

1. Дифференциальное уравнение получено с учетом убывания в процессе колебаний колебательной энергии.
2. Уравнение колебаний — это решение дифференциального уравнения.
3. Амплитуда зависит от времени.
4. Частота и период зависят от степени затухания колебаний.

Дифференциальное уравнение, которое описывает затухающие колебания, имеет вид:

• β=r/2m — коэффициент затухания;
• ω0=√k/m — собственная частота (угловая) колебаний системы при отсутствии затухания;
• m — масса колеблющейся системы.

Основные параметры:

1. Скоростью затухания колебаний принято называть величину, которая прямо пропорциональна силе затухания колебаний.

2. Период затухающих колебаний — это минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении.

Т = 2 π / ω — без потерь энергии.

Т = 2 π / √ ( ω 0 ² — β ² ) — с потерями.

3. Амплитуда затухающих колебаний (при небольших затуханиях) — это наибольшее отклонение от положения равновесия за период. Амплитуда затухающих колебаний постоянно изменяется со временем. И убывает по экспоненциальному закону:

• ω0=2π/T, в отсутствии потерь энергии;
• при потерях: ω=√(ω0²-β²).

5. Коэффициент затухания — величина, которой определяется быстрота (скорость) убывания амплитуды. Данный коэффициент характеризует затухание колебаний за единицу времени. Измеряется в герцах (Гц) или обратных секундах ( с ( — 1 ) ) .

6. Время затухания (время релаксации) — величина, обратная коэффициенту затухания; время, в течение которого амплитуда уменьшается.

7. Число колебаний.

8. Добротность колебаний.

Для затухающих свободных колебаний добротность характеризует скорость убывания энергии при малых затуханиях.

Для того чтобы управлять затуханием колебаний, нужно:

1. Уменьшить потери энергии в системе.
2. Обеспечить приток энергии для компенсации потерь.

Примеры решения задач

Дан график зависимости амплитуды колебаний от времени. Определить по графику время релаксации и коэффициент затухания.

Время релаксации (время, за которое амплитуда уменьшается в е=2,7 раз) находим по графику: τ=6mc.

Коэффициент затухания находим по формуле: τ = 1 / β ⇒ β = 1 / τ = 1 / 6 * 10 ( — 3 ) = 170 с ( — 1 ) .

Ответ: 6 m c , 170 с ( — 1 ) .

За время релаксации, равное 7 секунд, произошло 10 колебаний. Найти период колебаний.

Найдем период по формуле: N e = τ c / T ⇒ T = τ c / N e = 7 / 10 = 0 , 7 с .

Затухающие колебания

4.2 Затухающие колебания

4.2.1 Дифференциальное уравнение затухающих колебаний

Если кроме возвращающей силы на систему действует ещё и сила сопротивления (например, сила трения в механической системе или сопротивление проводника в контуре), то энергия колебательной системы будет расходоваться на преодоление этого сопротивления. Вследствие этого амплитуда колебаний будет уменьшаться и колебания будут затухать. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.

Рассмотрим затухание на примере пружинного маятника с коэффициентом упругости k, массой m, колеблющегося в среде, например, в жидкости, с коэффициентом сопротивления r. Предположим, что колебания малы и что маятник испытывает вязкое трение. В этом случае можно считать, что сила сопротивления пропорциональна скорости:

Знак минус указывает на противоположные напра­вления силы трения и скорости. Закон движения маятника при данных условиях будет иметь вид:

Преобразуем это выражение:

(51)

Обозначим: w02 = = d, где w0 — циклическая частота собственных колебаний пружинного маятника при отсутствии сил сопротивления, d — коэффициент затухания. Дифференциальное уравнение затухающих коле­баний маятника примет вид:

(52)

Получили однородное дифференциальное уравнение, второго порядка, описывающее малые затухающие колебания в системе с вязким трением. Его решение имеет вид:

где ω — частота затухающих колебаний:

w = . (54)

Уравнение (52) справедливо для любой системы, как механической, так и немеханической, например, для электромагнитного контура. Действительно, для колебательного контура с сопротивлением R второе правило Кирхгофа имеет вид уравнения (29), которое после преобразований принимает вид:

.

Из сравнения с уравнением (52) следует:

Таким образом, дифференциальное уравнение затухающих колебаний

любой линейной системы в общем виде задается уравнением:

+ 2d+w02S = 0. (55)

где S — колеблющаяся величина, описывающая тот или иной физический процесс, d = const – коэффициент затухания, w0 — собственная циклическая частота колебательной системы, т. е. частота свободных незатуха­ющих колебаний той же колебательной системы (при отсутствии потерь энергии) Решение уравнения (55) имеет вид:

амплитуда затухающих колебаний; A0 — начальная амплитуда.

Таким образом, затухающие колебания описываются функцией с экспоненциально убывающей амплитудой, т. е. затухающие колебания не являются гармоническими.

Зависимость (56) показана на рисунке 10 сплошной линией, а зависимость (57) — штриховыми линиями. Если пропорциональность силы трения и скорости не выполняются, то и закон убывания амплитуды будет другим. Например при сухом трении Fтр ≠ ƒ(t), Fтр = const и амплитуда убывает согласно геометрической прогрессии. Во многих измерительных приборах наряду с вязким трением (наличие смазки) присутствует и сухое трение (напр. в подшипниках). Пока амплитуды колебаний велики, в затухании доминирует вязкое трение. При малых амплитудах преобладает влияние сухого трения.

4.2.2 Параметры затухающих колебаний

1) Период затухающих колебаний:

Т = (58)

При δ β2 , согласно формуле (58) Т → 2π/ ωo. Такой режим затухания называют периодическим или колебательным (рисунок 10). В этом случае для характеристики процессов в системе можно использовать параметры гармонических колебаний.

2) При ωo2 ≈ β2 наступает критический режим колебаний. В формуле (58) ω → 0, Т → ∞. Наличие большого затухания в системе приводит к большим потерям энергии, поэтому, перейдя положение равновесия, система не в состоянии отойти от него на сколь-нибудь заметное расстояние и возвращается к равновесию (рисунок 11). Условие наблюдения критического режима можно получить из соотношений:

а) для механической системы

rk = 2 (67)

в) по аналоги для электрической системы

. (68)

3) При ωo2 wо2) выражение для резонансной частоты становится мнимым. Это означает, что при этих условиях резонанс не наблюдается — с увеличением частоты амплитуда вынужденных колебаний монотонно убывает. Изображенная на рисунке 13 совокупность графиков функции (79), соответствующих различным значениям параметра d, называется резонансными кривыми.

По поводу резонансных кривых можно сделать еще следующие замечания. При стремлении wо к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному fо/wо2, т. е. Fo/k. Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины Fo. При w → ∞ все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия. Наконец, отметим, что чем меньше d, тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» по­лучается максимум. Из формулы (79) вытекает, что при малом зату­хании (т. е. при d > w 0, tgj = -2δ/ω и сдвиг фаз становится равным p. Зависимость j от w при разных значениях d показана графически на рисунке 14.

При слабом затухании wрез» w0, и значение j при резонансе можно считать равным p/2.Сдвиг фаз на p/2 при резонансе означает, что вынуждающая сила опережает смещение на Т/4. При этом условии работа вынуждающей силы всегда положительна и приток энергии к колебательной системе максимален.

С явлением резонанса приходится считаться при конструировании машин и различного рода сооружений. Собственная частота колебаний этих устройств ни в коем случае не должна быть близка к частоте возможных внешних воздействий. В противном случае возникают вибра­ции, которые могут вызвать катастрофу. Известны слу­чаи, когда обрушивались мосты при прохождении по ним марширующих колонн солдат. Это происходило потому, что собственная частота колебаний моста оказывалась близкой к частоте, с которой шагала колонна.

Вместе с тем явление резонанса часто оказывается весьма полезным, особенно в акустике, радиотехнике и т. д.

4.4 Автоколебания

Огромный интерес для техники представляет возможность поддерживать колебания незатухающими. Для этого необходимо восполнять потери энергии реальной колебательной системы. Особенно важны и широко применимы так называемые автоколебания — незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний определяются самой системой.

Автоколебания принципиально отличаются от свободных незатухающих колебаний, происходящих без действия сил, а также от вынужденных колебаний, происходящих под действием периодической силы. Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени (в такт с ее колебаниями).

Примером автоколебательной системы могут служить часы. Храповой механизм подталкивает маятник в такт с его колебаниями. Энергия, передаваемая при этом маятнику, берется либо за счет раскручивающейся пружины, либо за счет опускающегося груза. Колебания воздуха в духовых инструментах и органных трубах также возникают вследствие автоколебаний, поддерживаемых воздушной струёй.

Автоколебательными системами являются также двигатели внутреннего сгорания, паровые турбины, ламповый генератор и т. д.

4.5 Переменный ток

4.5.1 Вынужденные электромагнитные колебания. Закон Ома для переменного тока.

Переменный ток можно рассматривать как установившиеся вынужденные электромагнитные колебания в цепи, содержащей резистор, катушку индуктивности и конденсатор. Мы будем рассматривать квазистационарные токи, для которых мгновенные значения силы тока во всех сечениях цепи практически одинаковы. Для мгновенных значений квазистационарных токов выполняются закон Ома и вытекающие из него правила Кирхгофа.

Рассмотрим процессы, происходящие в цепи, содержащей последовательно включённые резистор, катушку индуктивности, конденсатор и источник переменной Э. Д.С., изменяющейся по гармоническому закону:

где εo — амплитуда электродвижущей силы.

В цепи возникнет переменный ток, который вызовет на всех элементах цепи соответствующие падения напряжения UR, UL, UC . Будем считать, что внутреннее сопротивление источника э. д.с. пренебрежимо мало по сравнению с R. По закону Ома для участка цепи 1- L— R-2 имеем:

где φ2 — φ1 = q/C — мгновенное значение разности потенциалов обкладок

конденсатора, q — его заряд в этот же момент времени, — L(dI/dt) — э. д.с. самоиндукции в контуре. Возьмём производную по времени от обеих частей равенства (145). Учитывая, что dq/dt = I — ток в контуре, получим:

Учитывая, что R/L = 2δ, 1/ (ωC) = ωo2 и введя обозначение — εoω/L = еo уравнение (84) запишем в виде:

Решение уравнения (85) аналогично решению ранее рассмотренного уравнения (71). Ищем решение уравнения (84) для установившегося режима в виде:

где Iо — амплитуда переменного тока в контуре, j — сдвиг фаз между э. д.с. источника тока и силой тока. По аналогии с определением формул (74) и (75) найдём выражения для Iо и j :

(86)

(87)

Соотношение (86) называется законом Ома для переменного тока. Величина

(88)

называется полным сопротивлением цепи.

RL = ωL — индуктивное сопротивление;

RC = 1/ (ωC) — ёмкостное сопротивление;

— реактивное сопротивление. Реактивное сопротивление не вызывает тепловых потерь в цепи переменного тока. Оно создаёт сдвиг фаз между током и вынуждающей э. д.с.

R — активное сопротивление; за счёт него возникают тепловые потери в контуре.

Падение напряжения на отдельных участках цепи, представленной на рис. 15, можно получить, используя выражение (85):

UC = q/ С = U0C cos(ωt — φ — π/2);

По второму правилу Кирхгофа:

На рисунке 16 представлена векторная диаграмма амплитуд колебаний на всех элементах рассматриваемой цепи (см. рис. 15).

Из выражения (86) следует, что амплитуда тока зависит от частоты вынуждающей э. д.с. (рисунок 18). Максимального значения I0 достигает при частоте ωрез, равной:

(89)

Явление достижения током максимального значения I0рез при ω = ωрез называется резонансом напряжений. Это вызвано тем, что при ω = ωрез падения напряжений на индуктивном и ёмкостном сопротивлениях достигают максимальных значений равных по модулю и противоположных по фазе, поэтому суммарное падение напряжение на реактивном сопротивлении равно нулю. Падение напряжения на активном сопротивлении максимально, его амплитудное значение

Векторная диаграмма для резонанса напряжений при­ведена на рис.17.

Подставив в формулу (91) значения резонансной частоты и амплитуды напряжений на катушке индуктивности и конденсаторе, получим:

( UL )рез= ( UС )рез= I0 = U0 = Q U0, (92)

где Q — добротность контура.

Так как доброт­ность обычных колебательных контуров больше единицы, то напряжение как на катушке индуктивности, так и на конденсаторе превышает напряжение, приложенное к цепи. Поэтому явление резонанса напряжений используется в технике для усиления колебания напряжения какой-либо определенной частоты. Например, в случае резонан­са на конденсаторе, можно получить напряжение с амплитудой QUm ( в данном случае Q — добротность контура, которая может быть значительно больше Um. Это усиление напряжения возможно только для узкого интервала частот вблизи резонанс­ной частоты контура, что позволяет выделить из многих сигналов одно колебание определенной частоты, т. е. на радиоприемнике настроиться на нужную длину волны. Явление резонанса напряжений необходимо учитывать при расчете изоляции элект­рических линий, содержащих конденсаторы и катушки индуктивности, так как иначе может наблюдаться их пробой.

4.5.2 Мощность, выделяемая в цепи переменного тока

Полное мгновенное значение мощности переменного тока равно произведению мгновенных значений э. д.с. и силы тока. P(t) = ε(t) I(t), где

Практический интерес представляет не мгновенное значение мощности, а ее среднее значение за период колебания. Учитывая, что =1/2, sinw t.cosw t = 0, получим

= I0 ε0 cosj (93)

Из векторной диаграммы (см. рис. 16) следует, что ε0 cosj = RI0. Поэтому

.

Такую же мощность развивает постоянный ток . Величины Iэф = I0 /, Uэф = U0 / называются соответственно действующими (или эффективными) значениями тока и на­пряжения. Все амперметры и вольтметры градуируются по действующим значениям тока и напряжения. Учитывая действующие значения тока и напряжения, выражение средней мощности можно записать в виде:

(94)

где множитель cosj называется коэффициентом мощности,

Формула (94) показывает, что мощность, выделяемая в цепи переменного тока, в общем случае зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Если в цепи реактивное сопротивление отсутствует, то cosj =1 и P = Iэф εэф. Если цепь содержит только реактивное сопротивление (R=0), то cosj = 0 и средняя мощ­ность равна нулю, какими бы большими ни были ток и напряжение. Если cosj имеет значения, существенно меньшие единицы, то для передачи заданной мощности при данном напряжении генератора нужно увеличивать силу тока I, что приведет либо к выделению джоулевой теплоты, либо потребует увеличения сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся увеличить cosj, наименьшее допустимое значение которого для промышленных уста­новок составляет примерно 0,85.

3.1. Механические затухающие колебания

3.2. Электромагнитные затухающие колебания

3.3. Характеристики затухающих колебаний

Затуханием колебаний называется постепенное уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой.

Собственные колебания без затухания – это идеализация. Причины затухания могут быть разные. В механической системе к затуханию колебаний приводит наличие трения. В электромагнитном контуре к уменьшению энергии колебаний приводят тепловые потери в проводниках, образующих систему. Когда израсходуется вся энергия, запасенная в колебательной системе, колебания прекратятся. Поэтому амплитуда затухающих колебаний уменьшается, пока не станет равной нулю.

Затухающие колебания, как и собственные, в системах, разных по своей природе, можно рассматривать с единой точки зрения – общих признаков. Однако, такие характеристики, как амплитуда и период, требуют переопределения, а другие – дополнения и уточнения по сравнению с такими же признаками для собственных незатухающих колебаний. Общие признаки и понятия затухающих колебаний следующие:

Дифференциальное уравнение должно быть получено с учетом убывания в процессе колебаний колебательной энергии.

Уравнение колебаний – решение дифференциального уравнения.

Амплитуда затухающих колебаний зависит от времени.

Частота и период зависят от степени затухания колебаний.

Фаза и начальная фаза имеют тот же смысл, что и для незатухающих колебаний.

3.1. Механические затухающие колебания

Механическая система: пружинный маятник с учетом сил трения. Силы, действующие на маятник:

Упругая сила. , где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.

Сила сопротивления. Рассмотрим силу сопротивления, пропорциональную скорости v движения (такая зависимость характерна для большого класса сил сопротивления): . Знак «минус» показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:

Закон движения пружинного маятника – это второй закон Ньютона: ma = F_упр. + F_сопр.

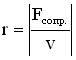
Учитывая, что и , запишем второй закон Ньютона в виде:

.

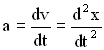
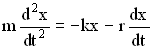
Разделив все члены уравнения на m, перенеся их все в правую часть, получим дифференциальное уравнение затухающих колебаний:

Обозначим , где β – коэффициент затухания, , где ω₀ – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.

В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид:

. Это линейное дифференциальное уравнение второго порядка. Уравнение затухающих колебаний есть решение такого дифференциального уравнения: .

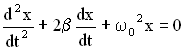
В приложении 1 показано получение решения дифференциального уравнения затухающих колебаний методом замены переменных.

Частота затухающих колебаний:

(физический смысл имеет только вещественный корень, поэтому ).

Период затухающих колебаний: .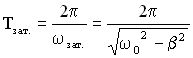

Смысл, который вкладывался в понятие периода для незатухающих колебаний, не подходит для затухающих колебаний, так как колебательная система никогда не возвращается в исходное состояние из-за потерь колебательной энергии. При наличии трения колебания идут медленнее: .

Периодом затухающих колебаний называется минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении.

Для механической системы пружинного маятника имеем:

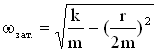
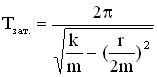
, . Амплитуда затухающих колебаний: , для пружинного маятника .

Амплитуда затухающих колебаний – величина не постоянная, а изменяющаяся со временем тем быстрее, чем больше коэффициент β. Поэтому определение для амплитуды, данное ранее для незатухающих свободных колебаний, для затухающих колебаний надо изменить.

При небольших затуханиях амплитудой затухающих колебаний называется наибольшее отклонение от положения равновесия за период.

Графики зависимости смещения от времени и амплитуды от времени представлены на Рисунках 3.1 и 3.2.

Рисунок 3.1 – Зависимость смещения от времени для затухающих колебаний

Рисунок 3.2 – Зависимости амплитуды от времени для затухающих колебаний

3.2. Электромагнитные затухающие колебания

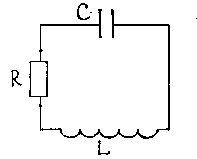
Электромагнитные затухающие колебания возникают в электромагнитной колебательной систему, называемой LCR – контур (Рисунок 3.3).

Рисунок 3.3.

Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура:

Падение напряжения:

— на активном сопротивлении: , где I – сила тока в контуре;

— на конденсаторе (С): , где q – величина заряда на одной из обкладок конденсатора.

ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение: (закон Фарадея).

Подставим значения U_R, U_C, в уравнение, отражающее закон Кирхгофа, получим:

.

Сила тока определяется как производная от заряда , тогда , и дифференциальное уравнение примет вид:

.

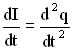
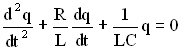
Обозначим , , получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:

Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид:

или

.

Амплитуда затухающих колебаний заряда имеет вид:

, где .

Частота затухающих колебаний в LCR – контуре:

.

Период затухающих электромагнитных колебаний:

.

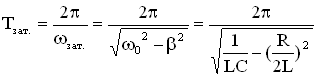
Возьмем уравнение для заряда в виде , тогда уравнение для напряжения на обкладках конденсатора можно записать так .

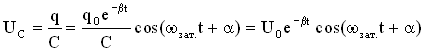
Величина 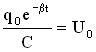называется амплитудой напряжения на конденсаторе.

Ток в контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение и векторную диаграмму.

Окончательное уравнение для силы тока таково:

,

где 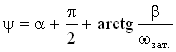— начальная фаза.

Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу.

Энергия колебаний в контуре складывается из энергии электрического поля

и энергии магнитного поля

Полная энергия в любой момент времени:

где W₀ – полная энергия контура в момент времени t=0.

1. Коэффициент затухания β. Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону: .

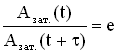
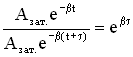
Пусть за время τ амплитуда колебаний уменьшится в «e » раз («е» – основание натурального логарифма, е ≈ 2,718). Тогда, с одной стороны, , а с другой стороны, расписав амплитуды А_зат.(t) и А_зат.(t+τ), имеем . Из этих соотношений следует βτ = 1, отсюда

.

Промежуток времени τ, за который амплитуда уменьшается в «е» раз, называется временем релаксации.

Коэффициент затухания β – величина, обратно пропорциональная времени релаксации.

2. Логарифмический декремент затухания δ — физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период .

Если затухание невелико, т.е. величина β мала, то амплитуда незначительно изменяется за период, и логарифмический декремент можно определить так:

,

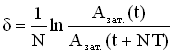
где А_зат.(t) и А_зат.(t+NT) – амплитуды колебаний в момент времени е и через N периодов, т.е.в момент времени (t + NT).

3. Добротность Q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) νа отношение энергии W(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:

. Так как энергия пропорциональна квадрату амплитуды, то .

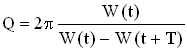
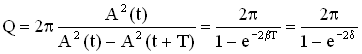
При малых значениях логарифмического декремента δ добротность колебательной системы равна

,

где N_e – число колебаний, за которое амплитуда уменьшается в «е» раз.

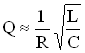
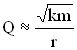
Так, добротность электромагнитной системы LCR – контура при малом затухании колебаний равна , а добротность пружинного маятника — .Чем больше добротность колебательной системы, тем меньше затухание, тем дольше будет длиться периодический процесс в такой системе.

4. При увеличении коэффициента β, частота затухающих колебаний уменьшает-ся, а период увеличивается. При ω₀ = β частота затухающих колебаний становится равной нулю ω_зат. = 0, а Т_зат. = ∞. При этом колебания теряют периодический характер и называются апериодическими.

При ω₀ = β параметры системы, ответственные за убывание колебательной энергии, принимают значения, называемые критическими. Для пружинного маятника условие ω₀ = β запишется так: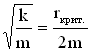, откуда найдем величину критического коэффициента сопротивления:

.

Для LCR – контура условие позволяет вычислить критическое сопротивление контура, при котором колебания потеряют свою периодичность:

.