Ускорение свободного падения характеризует то, как быстро будет увеличиваться скорость тела при свободном падении. Свободным падением называется ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести. Из физики известно, что ускорение свободного падения на Земле составляет (9,8)
мс2
.
Вопрос, почему эта величина именно такая, мы рассмотрим в этой теме.
Ускорение свободного падения в упрощённом виде можно рассчитать по формуле
g=Fm
, которая получается из формулы
F=m⋅g
, где (F) — сила тяжести либо вес тела в состоянии покоя или равномерного прямолинейного движения, (m) — масса тела, которое притягивает планета, (g) — ускорение свободного падения.
Сила тяжести, действующая на тело, зависит от массы тела, массы планеты, притягивающей тело, и от расстояния, на котором находится тело от центра массы планеты.
(F) — сила тяжести, Н;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
(R) — расстояние между центрами планеты и объекта в метрах. Если притягиваемое тело находится на поверхности планеты, тогда (R) равен радиусу планеты (если планета имеет сферическую форму);
m1 и
m2
— масса планеты и притягиваемого тела, выраженные в кг.
Обрати внимание!
Если мы объединим обе формулы, тогда получим формулу
g=G⋅mR2
, с помощью которой можно вычислить ускорение свободного падения на любом космическом объекте — на планете или звезде.
Пример:
ускорение свободного падения у поверхности Земли вычисляют таким образом:
, где
(g) — ускорение свободного падения;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
Практически на Земле ускорение свободного падения на полюсах немного больше ((9,832)
мс2
), чем на экваторе ((9,78)
мс2
), так как Земля не имеет форму идеального шара, а на экваторе скорость вращения больше, чем на полюсах. Среднее значение ускорения свободного падения у поверхности Земли равно (9,8)
мс2
.
Ускорение свободного падения у поверхности любого космического тела — на планете или звезде — зависит от массы этого тела и квадрата его радиуса. Таким образом, чем больше масса звезды и чем меньше её размеры, тем больше значение ускорения свободного падения у её поверхности.
При помощи формулы расчёта ускорения свободного падения и измерений, проведённых для удалённых объектов, учёные-физики могут определить величину ускорения свободного падения на любой планете или звезде.
Рис. (1). Планеты Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун; и карликовые планеты: Церера, Плутон, Эрида ((2003) UB (313))
Таблица (1). Ускорение свободного падения и другие характеристики планет Солнечной системы и карликовых планет
|
Небесное тело |
Ускорение свободного падения, мс2 |
Диаметр, км |
Расстояние до Солнца, миллионы км |
Масса, кг |
Соотношение с массой Земли |
|
Меркурий |
(3,7) |
(4878) |
(58) |
(3,3*) 1023 |
(0,055) |
|
Венера |
(8,87) |
(12103) |
(108) |
(4,9*) 1024 |
(0,82) |
|
Земля |
(9,8) |
(12756,28) |
(150) |
(6,0*) 1024 |
(1) |
|
Марс |
(3,7) |
(6794) |
(228) |
(6,4*) 1023 |
(0,11) |
|
Юпитер |
(24,8) |
(142984) |
(778) |
(1,9*) 1027 |
(317,8) |
|
Сатурн |
(10,4) |
(120536) |
(1427) |
(5,7*) 1026 |
(95,0) |
|
Уран |
(8,87) |
(51118) |
(2871) |
(8,7*) 1025 |
(14,4) |
|
Нептун |
(10,15) |
(49532) |
(4498) |
(1,02*) 1026 |
(17,1) |
|
Плутон |
(0,66) |
(2390) |
(5906) |
(1,3*) 1022 |
(0,0022) |
|
Луна |
(1,62) |
(3473,8) |
(0,3844 ) (до Земли) |
(7,35*) 1022 |
(0,0123) |
|
Солнце |
(274,0) |
(1391000) |
— |
(2,0*) 1030 |
(332900) |
Нейтронные звёзды имеют малый диаметр — порядка десятков километров, — а масса их сопоставима с массой Солнца. Поэтому гравитационное поле у них очень сильное.
Пример:
если диаметр нейтронной звезды равен (20) км, а масса её в (1,4) раза больше массы Солнца, тогда ускорение свободного падения будет в (200000000000) раз больше, чем у поверхности Земли.
Его величина приблизительно равна
2⋅1012 мс2
. Значение ускорения свободного падения для нейтронной звезды может достигать значения
7⋅1012 мс2
.
Ускорение свободного падения
Ускорение свободного падения — движение объекта, который получает ускорение из-за действующей на него силы тяжести; обозначается буквой g и измеряется в м/с². На поверхности Земли ускорение свободного падения примерно равно 9,81 м/с².
На полюсах (Южном и Северном) ускорение свободного падения будет больше, а на экваторе — меньше. Это происходит из-за двух фактов:
- Земля — не идеальный круг, а приплюснутый шар и её радиус на полюсах меньше, чем на экваторе (ускорение зависит от радиуса),
- центробежные силы (при вращении Земли) минимально компенсируют гравитацию больше на экваторе, чем на полюсах.
В вакууме тела падают с одинаковой скоростью потому, что ускорение свободного падения не зависит от массы.
Таблица ускорения свободного падения небесных тел
| Небесное тело | g (в м/с²) |
|---|---|
| Луна | 1,62 |
| Солнце | 274 |
| Меркурий | 3,72 |
| Венера | 8,87 |
| Земля | 9,81 |
| Марс | 3,711 |
| Юпитер | 24,79 |
| Сатурн | 10,44 |
| Уран | 8,87 |
| Нептун | 11,15 |
От чего зависит ускорение свободного падения?
Ускорение свободного падения зависит от массы планеты и радиуса планеты — чем она тяжелее, тем сильнее притягивает тела (т.е. масса тела не влияет на ускорение).
Возможно для будущих вычислений нужны будут эти данные:
- Масса Земли = 5,98 × (10^24) кг (или 5,972E24 кг)
- Радиус Земли = 6 371 км = 6,37×(10^6) м.
Как найти ускорение свободного падения?
Формула ускорения свободного падения

g — ускорение свободного падения
G — гравитационная постоянная
M — масса планеты
R — радиус планеты
Гравитационная постоянная («G», не путайте с «g») — это фундаментальная физическая константа, которая примерно равна
и связывает силы гравитационного притяжения между двумя телами (G) с их массами (m1 и m2) и расстоянием между ними (R) в формуле:
Пример расчёта ускорения свободного падения (для Земли):
Вспомним формулу:

G — гравитационная постоянная
M — масса планеты
R — радиус планеты
Как узнать время падения тела?
Формула времени свободного падения (когда тело падает вертикально):
t = V / g = √(2h/g)
Где:
- t — время
- V — скорость тела
- g — ускорение ≈ 9,8 м/с²
- h — расстояние
Пример:
Высота (h) = 20 м
Нужно найти скорость и время падения.
Решение:
Формула скорости:
V0 = 0
g ≈ 9,8 м/с²
h = 20 м
V² = 0² + 2 × 9,8 м/с² × 20 м ⇔ V = √392 м/с ≈ 19,8 м/с
Зная скорость, применяем эту формулу:
t = V / g = (19,8 м/с) / (9,8 м/с²) ≈ 2,02 с
Либо используя только высоту и ускорение:
t = √(2h/g) = √(2 × 20 м / 9,8 м/с²) ≈ 2,02 с
Где нужны знания о свободном падении?
Они могут понадобиться:
- в авиации,
- в космонавтике,
- при поиске полезных ископаемых (там, где есть залежи тяжёлых ископаемых, g меняется),
- при разработке новых лыжных трамплинов и полос приземления,
- при разработке новых автомобилей (рассчитываются наилучшие показатели для экономии топлива).
Узнайте также про Закон сохранения энергии, Силу Архимеда, Законы Ньютона и Космологию.
Сила всемирного тяготения. Искусственные спутники
- Гравитационное взаимодействие
- Закон всемирного тяготения
- Ускорение свободного падения на поверхности для различных планет
- Космические скорости
- Искусственные спутники Земли
- Задачи
п.1. Гравитационное взаимодействие
Согласно современным представлениям, все тела, обладающие массой, притягиваются друг к другу. Это взаимодействие называется гравитационным.
Таким образом, масса проявляется в природе двумя качественно разными способами.
Инертная масса — мера инертности тел (второй закон Ньютона), дающая связь между силой и вызываемым ею ускорением.
Гравитационная масса — мера гравитационного взаимодействия тел (закон всемирного тяготения), определяющая силу взаимного притяжения.
Нужно подчеркнуть, что инертная масса и гравитационная масса возникают в механике при рассмотрении совершенно разных явлений, и ниоткуда не следует, что они должны быть равны.
Тем не менее, уже сам Ньютон доказал равенство этих масс с точностью 10-3.
На сегодняшний день (эксперимент 2009 г.) этот факт подтвержден с точностью 10-13.
Принцип эквивалентности
Значения инертной и гравитационной массы одного и того же тела равны.
п.2. Закон всемирного тяготения
Закон всемирного тяготения
Две материальные точки массами (m_1) и (m_2) притягиваются по направлению друг к другу с силой (F), прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния (r) между ними: $$ F=Gfrac{m_1m_2}{r^2} $$ Коэффициент пропорциональности называется гравитационной постоянной;
она одинакова для всех тел природы и в системе СИ равна $$ G=6,67cdot 10^{-11}frac{text{Н}cdot text{м}^2}{text{кг}^2} $$
Физический смысл гравитационной постоянной
Если два тела массой по 1 кг находятся на расстоянии 1 м друг от друга, сила гравитационного взаимодействия между ними равна $$ F=Gcdot 1frac{text{кг}^2}{text{м}^2}=6,67cdot 10^{-11} text{Н} $$
Закон всемирного тяготения выполняется для тел, размерами которых можно пренебречь, т.е. для материальных точек. Но его применение можно расширить.
При рассмотрении небесных тел (Солнца, планет и их спутников) в первом приближении их можно считать однородными идеальными сферами с одинаковой плотностью вещества внутри. Как показывает теория, в такой модели небесное тело можно заменить материальной точкой, совпадающей с его центром, с массой полностью сосредоточенной в этом центре.
В этом случае для применения закона всемирного тяготения открываются дополнительные возможности. Например, можно описывать движение небольшого тела на поверхности планеты, «сжимая» всю планету в материальную точку, от которой тело удалено на расстояние, равное радиусу планеты.
п.3. Ускорение свободного падения на поверхности для различных планет
Найдем силу, с которой Земля притягивает небольшое тело массой m, расположенное на её поверхности.
 |
Будем считать Землю сферическим однородным телом. Масса Земли (M_oplus=5,97cdot 10^{24} text{кг}), радиус Земли (R_oplus=6370 text{км}). Допущение об однородности позволяет перейти к модели, в которой вся масса Земли сосредоточена в её центре. Расстояние от центра до поверхности, на которой находится тело, – это радиус Земли. |
Получаем, что сила притяжения между Землей и телом: $$ F=Gfrac{M_oplus m}{R^2_oplus} $$
По своей природе, полученная сила является ничем иным, как силой тяжести (F=mg), с которой мы уже знакомы (см. §22 данного справочника).
Значит, (Gfrac{M_oplus m}{R^2_oplus}=mg), и ускорение свободного падения begin{gather*} g=Gfrac{M_oplus}{R^2_oplus}\[6pt] g=6,67cdot 10^{-11}cdot frac{5,97cdot 10^{24}}{(6,37cdot 10^6)^2}approx 9,81 (text{м/с}^2) end{gather*} Что полностью согласуется с многочисленными экспериментами.
Полученный результат можно обобщить и применить к любому другому небесному телу.
Ускорение свободного падения на поверхности сферической однородной планеты или звезды массой (M) и радиусом (R) прямо пропорционально массе и обратно пропорционально квадрату радиуса: $$ g=Gfrac{M}{R^2} $$
Например, для Луны (g_{text{Л}}=1,62frac{text{м}}{text{с}^2}approx 0,165g_0); для Юпитера (g_{text{Ю}}=23,95frac{text{м}}{text{с}^2}approx 2,442g_0); для Солнца (g_{text{С}}=273,1frac{text{м}}{text{с}^2}approx 27,85g_0). Здесь, (g_0) — ускорение свободного падения у поверхности Земли.
Заметим, что в задачах на гравитационное взаимодействие часто оказывается полезной замена (GM=gR^2).
п.4. Космические скорости
Если тело находится на поверхности Земли, то расстояние между центром планеты, где сосредоточена вся масса, и этим телом равно радиусу Земли (R_oplus).
Если подняться над поверхностью на некоторую высоту (h), расстояние станет равным ((R_oplus+h)). Сила всемирного тяготения (она же – сила тяжести) на этой высоте: $$ F_h=Gfrac{M_oplus m}{(R_oplus+h)^2} $$
Т.к. (GM_oplus=gR^2_oplus), где (g=9,81 (text{м/с})^2), можем также записать удобное на практике выражение: $$ F_h=mgleft(frac{R_oplus}{(R_oplus+h)}right)^2 $$
Пусть мы хотим запустить спутник, который будет летать на высоте (h) по круговой орбите с постоянной скоростью (v). При равномерном движении по окружности ускорение равно отношению квадрата скорости к радиусу орбиты. Получаем: $$ F_h=Gfrac{M_oplus m}{(R_oplus +h)^2}=ma=mfrac{v^2_h}{(R_oplus + h)} $$
Скорость вращения спутника на высоте (h): $$ v_h=sqrt{frac{GM_oplus}{R_oplus + h}} $$
Зная ускорение свободного падения у поверхности Земли (g), можем также записать: $$ v_h=sqrt{frac{gR^2_oplus}{R_oplus + h}} $$
В общем случае:
Чтобы запустить тело на круговую орбиту на высоте (h) над поверхностью сферической однородной планеты или звезды массой (M) и радиусом (R), нужно на этой высоте сообщить телу в горизонтальном направлении скорость $$ v_h=sqrt{frac{GM}{R+h}} $$
Скорости, достаточные для запуска околоземного спутника, межпланетной станции и вылета за пределы Солнечной системы, называют космическими скоростями для Земли.
Первая космическая скорость
Скорость, достаточная для того, чтобы тело, запускаемое с Земли на уровне моря ((h=0)), стало её искусственным спутником, равна $$ v_1=sqrt{frac{GM_oplus}{R_oplus}}=sqrt{gR_oplus}approx 7,92 text{км/с} $$
Вторая космическая скорость
Скорость, достаточная для того, чтобы тело, запускаемое с Земли на уровне моря ((h=0)), преодолело земное притяжение и смогло осуществить межпланетный полет в пределах Солнечной системы, равна $$ v_2=sqrt{frac{2GM_oplus}{R_oplus}}=sqrt{2gR_oplus}approx 11,18 text{км/с} $$
Аналогичные формулы для первой и второй космических скоростей можно получить для любой планеты, как в Солнечной системе, так и за ее пределами.
Нужно только знать массу и радиус планеты.
Можно также рассчитать скорость, необходимую для межзвездных полетов при старте с Земли. Это задача непростая, т.к. необходимо учесть относительное движение трех тел: космического корабля, Земли и Солнца.
Третья космическая скорость
Скорость, достаточная для того, чтобы тело, запускаемое с Земли на уровне моря ((h=0)), преодолело притяжение Земли и Солнца и смогло осуществить межзвездный полет за пределы Солнечной системы, равна $$ v_3=sqrt{(sqrt{2}-1)^2frac{GM_odot}{R_odot}+frac{2GM_oplus}{R_oplus}} approx 16,65 text{км/с} $$
В этой формуле, (M_odot) — масса Солнца, (R_odot) — радиус орбиты вращения Земли вокруг Солнца.
п.5. Искусственные спутники Земли
Искусственный спутник Земли – это космический летательный аппарат, вращающийся вокруг Земли по геоцентрической орбите (эллипсу, в одном из фокусов которого находится Земля).
Круговая орбита спутника в плоскости экватора Земли, двигаясь по которой он находится всё время над одной и той же точкой экватора, называется геостационарной. Такие спутники имеет большое значение для создания систем связи.
Чтобы запустить спутник на орбиту, ему необходимо сообщить скорость, больше чем первая космическая, но меньше чем вторая космическая: $$ 7,92frac{text{км}}{text{с}}lt vlt 11,18frac{text{км}}{text{с}} $$
На практике, получение соответствующей силы тяги ракетного двигателя, способного разогнать ракету до таких скоростей, является сложной технической проблемой.
Вывод спутников на орбиту осуществляется с помощью многоступенчатых ракет-носителей в несколько этапов. На первом этапе ракета стартует и, двигаясь вертикально вверх, проходит плотные слои атмосферы на относительно небольшой скорости, после чего отработавшие двигатели первой ступени отделяются (у Илона Маска — аккуратно возвращаются на Землю). На втором этапе ракета постепенно разворачивается параллельно к поверхности Земли и начинает ускоряться. Когда скорость достигает определенной величины и направления, работа двигателей прекращается, отделяется вторая ступень. Спутник начинает самостоятельное движение по расчетной орбите.
Искусственные спутники Земли используются для решения разнообразных научных и прикладных задач.
В апреле 2020 года на орбите находилось 1388 спутников США, 356 Китая, 167 России, 138 Британии, 78 Японии и 627 других стран. Из них: 1007 спутников связи, 446 спутников для исследования Земли, 97 спутников навигации и GPS, 87 научно-исследовательских спутников и другие космические аппараты.
п.6. Задачи
Задача 1. С какой силой Земля притягивает Луну? Масса Земли (M_oplus=5,97cdot 10^{24} text{кг}), масса Луны (m_{text{л}}=7,36cdot 10^{22} text{кг}), средний радиус лунной орбиты (R=384 text{тыс.км}). А с какой силой Луна притягивает Землю?
Дано:
(M_oplus=5,97cdot 10^{24} text{кг})
(m_{text{л}}=7,36cdot 10^{22} text{кг})
(R=384 text{тыс.км}=3,84cdot 10^8 text{м})
__________________
(F_{text{ЗЛ}}, F_{text{ЛЗ}}-?)
По закону всемирного тяготения $$ F_{text{ЗЛ}}=Gfrac{M_oplus m_{text{л}}}{R^2} $$ Получаем begin{gather*} F_{text{ЗЛ}}=6,67cdot 10^{-11}cdot frac{5,97cdot 10^{24}cdot 7,36cdot 10^{22}}{(3,84cdot 10^8)^2}approx \[6pt] approx 19,9cdot 10^{-11+24+22-16}=1,99cdot 10^{20} (text{Н}) end{gather*} Эта сила направлена от центра Луны к центру Земли.
По третьему закону Ньютона, Луна притягивает Землю с такой же по величине силой, которая направлена противоположно, от центра Земли к центру Луны: $$ overrightarrow{F_{text{ЗЛ}}}=-overrightarrow{F_{text{ЛЗ}}} $$ Ответ: 1,99·1020 Н
Задача 2. Самая высокая гора на Земле – Эверест (8848 м). Во сколько раз сила тяжести на уровне моря больше силы тяжести на вершине Эвереста? Радиус Земли (R_oplus=6370 text{км}).
Дано:
(R_oplus=6370 text{км}=6,37cdot 10^6 text{м})
(h=8848 text{м})
__________________
(frac{F}{F_h}-?)
Сила тяжести для тела массой (m) на уровне моря begin{gather*} F=Gfrac{M_oplus m}{R_oplus^2} end{gather*} На вершине Эвереста begin{gather*} F_h=Gfrac{M_oplus m}{(R_oplus +h)^2} end{gather*} Отношение сил: begin{gather*} frac{F}{F_h}=Gfrac{M_oplus m}{R_oplus^2}:Gfrac{M_oplus m}{(R_oplus +h)^2}= frac{(R_oplus+h)^2}{R^2_oplus}=left(frac{R_oplus+h}{R_oplus}right)^2 =left(1+frac{h}{R_oplus}right)^2 end{gather*} Получаем: begin{gather*} frac{F}{F_h}=left(1+frac{8848}{6,37cdot 10^6}right)^2approx 1,003 end{gather*} Ответ: в 1,003 раза
Задача 3. На поверхности Земли на тело действует силы тяжести (F=54 text{Н}).
Чему будет равна сила тяжести, действующая на это тело на высоте, равной двум радиусам Земли?
Дано:
(F=54 text{Н})
(h=2R_oplus )
__________________
(F_h-?)
Сила тяжести на поверхности Земли begin{gather*} F=Gfrac{M_oplus m}{R_oplus^2} end{gather*} Сила тяжести на высоте (h) begin{gather*} F_h=Gfrac{M_oplus m}{(R_oplus +h)^2}=Gfrac{M_oplus m}{(R_oplus+2R_oplus)^2}=Gfrac{M_oplus m}{9R^2_oplus} end{gather*} Отношение сил: begin{gather*} frac{F}{F_h}=Gfrac{M_oplus m}{R_oplus^2}:Gfrac{M_oplus m}{9R^2_oplus}=9, F_h=frac{F}{9}\[6pt] F_h=frac{54}{9}=6 (text{Н}) end{gather*} Ответ: 6 Н
Задача 4*. Чему равны первая и вторая космические скорости вблизи поверхности Луны? Сравните их со значениями первой и второй космических скоростей у поверхности Земли.
Радиус Луны (R=1740 text{км}), масса Луны (M=7,36cdot 10^{22} text{кг}).
Дано:
(R=1740 text{км}=1,74cdot 10^6 text{м})
(M=7,36cdot 10^{22} text{кг})
__________________
(v_1, v_2-?)
(frac{v_{text{1З}}}{v_{text{1Л}}}, frac{v_{text{2З}}}{v_{text{2Л}}}-?)
Первая и вторая космические скорости $$ v_1=sqrt{frac{GM}{R}}, v_2=sqrt{frac{2GM}{R}}=sqrt{2}v_1 $$ Получаем: begin{gather*} v_1=sqrt{frac{6,67cdot 10^{-11}cdot 7,36cdot 10^{22}}{1,74cdot 10^6}}approx sqrt{2,82cdot 10^6}approx\[6pt] approx 1,68cdot 10^3frac{text{м}}{text{с}}=1,68frac{text{км}}{text{с}}\[6pt] v_2=sqrt{2}cdot 1,68approx 2,37frac{text{км}}{text{с}} end{gather*} Сравним со скоростями для Земли: begin{gather*} frac{v_{text{1З}}}{v_{text{1Л}}}=frac{7,92}{1,68}approx 4,7 text{раз}, frac{v_{text{2З}}}{v_{text{2Л}}}=frac{sqrt{2}v_{text{1З}}}{sqrt{2}v_{text{1Л}}}=frac{v_{text{1З}}}{v_{text{1Л}}}approx 4,7 text{раз} end{gather*} Космические скорости для Луны в 4,7 раз меньше земных.
Ответ: 1,68 км/с; 2,37 км/с; в 4,7 раз меньше
Задача 5*. Рассчитайте радиус геостационарной орбиты спутника и высоту такого спутника над Землей. Масса Земли (M_oplus=5,97cdot 10^{24} text{кг}), радиус Земли (R_oplus =6400 text{км}).
Ответ запишите в км.
Дано:
(M_oplus=5,97cdot 10^{24} text{кг})
(T=24 text{ч}=8,64cdot 10^4 text{с})
(R_oplus =6400 text{км}=6,4cdot 10^6 text{м})
__________________
(R, h-?)
На геостационарной орбите спутник «зависает» над Землей, его линейная скорость равна отношению длины окружности орбиты к периоду вращения (сутки): begin{gather*} v=frac{2pi R}{T}=sqrt{frac{GM_oplus}{R}}Rightarrow frac{4pi ^2R^2}{T^2}=frac{GM_oplus}{R}Rightarrow R^3=frac{GM_oplus T^2}{4pi ^2}\[6pt] R=sqrt[{3}]{frac{GMT^2}{4pi ^2}} end{gather*} Получаем: begin{gather*} R=sqrt[{3}]{frac{6,67cdot 10^{-11}cdot 5,97cdot 10^{24}cdot (8,64cdot 10^4)^2}{4pi ^2}}approx sqrt[{3}]{75,3cdot 10^{-11+24+8}}approx\[6pt] approx 4,22cdot 10^7 (text{м})=42200 (text{км})\[6pt] h=R-R_oplus=42200-6400=35800 (text{км}) end{gather*} Ответ: 42200 км; 35800 км
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Ускоре́ние свобо́дного паде́ния g (обычно произносится как «Жэ» или «Жи»), — ускорение, сообщаемое телу под действием притяжения планеты или другого астрономического тела в безвоздушном пространстве — вакууме. Его значение для Земли обычно принимают равным 9,8 или 10 м/с². Стандартное («нормальное») значение, принятое при построении систем единиц, g = 9,80665 м/с², а в технических расчетах обычно принимают g = 9,81 м/с².
| Луна | 1,62 | Сатурн | 10,44 |
| Меркурий | 3,68 — 3,74 | Земля | 9,81 |
| Марс | 3,86 | Нептун | 11,09 |
| Уран | 8,86 | Юпитер | 23,95 |
| Венера | 8,88 | Солнце | 273,1 |
Значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте 45,5° на уровне моря.
Реальное ускорение свободного падения на поверхности Земли зависит от широты и варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах[1]. Оно может быть вычислено по эмпирической формуле:
,
где φ — широта рассматриваемого места, h — высота над уровнем моря.[2]
[править] Вычисление ускорения свободного падения
| h, км | g, м/с2 | h, км | g, м/с2 |
|---|---|---|---|
| 0 | 9.8066 | 20 | 9.7452 |
| 1 | 9.8036 | 50 | 9.6542 |
| 2 | 9.8005 | 80 | 9.5644 |
| 3 | 9.7974 | 100 | 9.505 |
| 4 | 9.7943 | 120 | 9.447 |
| 5 | 9.7912 | 500 | 8.45 |
| 6 | 9.7882 | 1000 | 7.36 |
| 8 | 9.7820 | 10 000 | 1.50 |
| 10 | 9.7759 | 50 000 | 0.125 |
| 15 | 9.7605 | 400 000 | 0.0025 |
Ускорение свободного падения состоит из двух слагаемых: гравитационного ускорения и центростремительного ускорения.
Значение гравитационного ускорения на поверхности планеты можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R:
,
где G — гравитационная постоянная (6,6742×10-11 м3с-2кг-1).
Если применить эту формулу для вычисления гравитационного ускорения на поверхности Земли, мы получим
м/с²
Полученное значение приблизительно совпадает с ускорением свободного падения. Отличия обусловлены:
- центростремительным ускорением в системе отсчёта, связанной с вращающейся Землёй;
- неточностью формулы из-за того, что масса планеты распределена по объёму, который имеет нешарообразную форму(см. геоид);
- неоднородностью Земли, что используется для поиска полезных ископаемых по гравитационным аномалиям;
| Город | Географические координаты (по Гринвичу) | Высота над уровнем моря, м | Ускорение свободного падения, м/с2 | |
|---|---|---|---|---|
| Долгота | Широта | |||
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80112 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Киев | 30,30 в.д. | 50,27 с.ш. | 179 | 9,81054 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 655 | 9,79981 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Исторически масса Земли была впервые определена Генри Кавендишем, исходя из известного ускорения свободного падения и радиуса Земли, и впервые измеренной им гравитационной постоянной.
[править] Перегрузки
Термин «жэ» используется в космонавтике и авиации для обозначения перегрузок — увеличения веса тела, вызванного его ускоренным движением. Допустимое значение перегрузок для гражданских самолетов составляет 4,33 g. Обычный человек может выдерживать перегрузки до 5 g. Тренированные пилоты в антиперегрузочных костюмах могут переносить перегрузки до 9 g. Сопротивляемость к отрицательным, направленным вверх перегрузкам, значительно ниже. Обычно при 2-3 g в глазах «краснеет» и человек теряет сознание из-за прилива крови к голове.
В этом вопросе существует небольшая терминологическая путаница: к примеру, определение перегрузки выше даёт для стоящего неподвижно человека перегрузку в 0g, но в таблице ниже этот же случай рассматривается как перегрузка в 1g. Похожий казус происходит при измерении давления: мы говорим — давление 0, подразумевая давление в одну атмосферу вокруг нас, учёный скажет — давление 0, подразумевая полное отсутствие молекул в данном объёме.
| Человек, стоящий неподвижно | 1 g |
| Пассажир в самолете при взлете | 1,5 g |
| Парашютист при приземлении со скоростью 6 м/с | 1,8 g |
| Парашютист при раскрытии парашюта (при изменении скорости от 60 до 5 м/с) | 5,0 g |
| Космонавты при спуске в космическом корабле «Союз» | до 3,0—4,0 g |
| Летчик при выполнении фигур высшего пилотажа | до 5 g |
| Летчик при выведении самолета из пикирования | 8,0—9 g |
| Перегрузка (длительная), соответствующая пределу физиологических возможностей человека | 8,0—10,0 g |
| Наибольшая (кратковременная) перегрузка автомобиля, при которой человеку удалось выжить[3] | 179,8 g |
[править] Примечания
- ↑ «Свободное падение тел. Ускорение свободного падения»
- ↑ g-Extractor на сайте Physikalisch-Technische Bundesanstalt (PTB).
- ↑ Авария в предквалификации Гран-при Великобритании
[править] Литература
- А. С. Енохович Краткий справочник по физике. — М.: «Высшая школа», 1976. — 288 с.
Ускорение свободного падения, теория и онлайн калькуляторы
Ускорение свободного падения
Определение ускорения свободного падения
Определение
Ускорением свободного падения называют ускорение, которое телу придает сила тяжести, если другие силы на рассматриваемое тело не действуют или их
действие взаимно компенсируется.
Ускорение свободного падения обозначают буквой $g$. На поверхности Земли оно изменяется пределах от $9,78 frac{м}{с^2}$ до $9,832 frac{м}{с^2}$. На полюсах Земли ускорение свободного падения максимально, на экваторе минимально. Средним (стандартным или нормальным) значением ускорения свободного падения на Земле принято считать его величину, равную $g=9,80665 frac{м}{с^2} $. В задачах величину ускорения свободного падения считают равной $g=9,81frac{м}{с^2}$ или часто даже полагают $g=10frac{м}{с^2}$, если расчеты приблизительные.
В соответствии с обобщенным законом Галилея все тела, находящиеся в одном и том же поле тяготения падают с одинаковыми ускорениями. Это означает, что в данной точке Земли ускорение свободного падения одинаково для всех тел. Изменение величины ускорения свободного падения около поверхности Земли в зависимости от широты связано с суточным вращением нашей планеты вокруг своей оси и тем, что форма Земли отличается от формы шара (Земля сплюснута).
Зависимость ускорения свободного падения от высоты над уровнем Земли
Если суточным вращением Земли пренебречь, то сила тяжести ($P=mg$) равна по величине силе тяготения (F):
[P=mg=F=gamma frac{mM}{R^2}left(1right),]
где $M$ — масса Земли; $R$ — расстояние от центра Земли, до рассматриваемого тела; $gamma $- гравитационная постоянная. Формула (1) справедлива, если тело находится около поверхности Земли, тогда ускорение свободного падения равно:
[g=gamma frac{M}{R^2}left(2right).]
Ускорение, вычисляемое при помощи формулы (2) называют ускорением свободного падения на уровне моря.
Допустим, что тело находится на высоте $h$ над уровнем Земли, тогда сила тяжести, действующая на тело равна:
[P=gamma frac{mM}{{left(R_Z+hright)}^2}left(3right),]
где $R_Z$ — радиус Земли. В таком случае ускорение свободного падения зависит от высоты, на которой находится рассматриваемое тело:
[g=gamma frac{M}{{left(R_Z+hright)}^2}left(4right).]
Изменениями ускорения свободного падения на высотах, которые много меньше, чем радиус Земли обычно пренебрегают. При этом считают, что ускорение свободного падения постоянная величина.
Влияние вращения Земли на ускорение свободного падения
Как уже отмечалось, на ускорение свободного падения оказывает влияние вращение нашей планеты вокруг своей оси. Допустим, что тело массой $m$ находится в точке с географической широтой $varphi $. Вместе в планетой тело движется и при этом траекторией его движения является окружность радиуса $r$, равного:
[r=R_Z{cos varphi left(5right), }]
где $R_Z$ — радиус Земли. Центростремительное ускорение ($a_n$) нашего тела при этом будет составлять величину:
[a_n=frac{v^2}{r}=frac{4{pi }^2R_Z{cos varphi }}{T^2} left(6right),]
где $T$ — период вращения Земли. Силу тяготения ($F$) можно разложить на две составляющие: центростремительную силу ($F_n$) и силу тяжести ($P$). Сила тяжести везде кроме полюсов, меньше силы тяготения. Везде, кроме экватора и полюсов, сила тяжести направлена не точно в центр Земли, а немного в сторону от него.
За счет вращения Земли сила тяжести на полюсах больше, чем у экватора, наша планета сплюснута.
Ускорение свободного падения на полюсе ($g_p$) максимально. Так как центростремительное ускорение равно нулю, полярный радиус ($R_p$) минимален:
[g_p=frac{gamma M}{R^2_p}left(7right).]
Ускорение свободного падения ($g_e$) на экваторе равно разности:
[g_e=frac{gamma M}{R^2_e}-a^e_n=frac{gamma M}{R^2_e}-frac{4{pi }^2R_e}{T^2}left(8right),]
где $R_e$ — экваториальный радиус Земли. Величину $frac{gamma M}{R^2_e}$ называют напряженностью гравитационного поля Земли.
Примеры задач с решением
Пример 1
Задание. Радиус некоторой планеты равен R, ее средняя плотность составляет $rho $, считая, что масса планеты распределена равномерно, определите ускорение свободного падения около поверхности этой планеты.
Решение. Ускорение свободного падения около поверхности планеты можно найти как:
[g=gamma frac{M}{R^2}left(1.1right),]
где $R$ — радиус планеты; $M$ — масса планеты. Массу планеты найдем, считая ее шаром:
[M=frac{4}{3}pi R^3rho left(1.2right).]
Тогда ускорение свободного падения около поверхности этой планеты равно:
[g=gamma frac{frac{4}{3}pi R^3rho }{R^2}=frac{4}{3}gamma pi rho R.]
Ответ. $g=frac{4}{3}gamma pi rho R.$
Пример 2
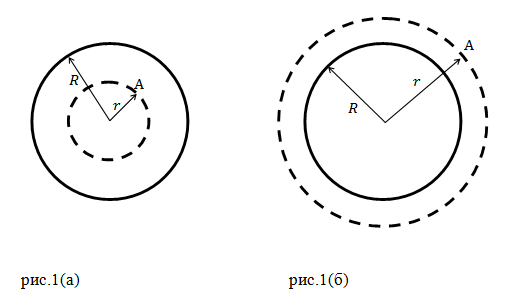
Задание. Какова зависимость ускорения свободного падения от расстояния от центра планеты$ ( r)$, если планета — однородный шар, плотность которого равна $rho ?$ Радиус планеты R. Изобразите график $gleft(rright).$
Решение. Рассмотрим случай, когда расстояние от центра планеты меньше ее радиуса ($r$ меньше $R$) (рис.1 (а)).
Расположим тело массы $m$ на расстоянии $r$ от центра планеты (в точке А). Тогда тело притягивается к планете с силой:
[mg=frac{gamma M’m}{r^2}left(2.1right),]
где $M’=frac{4}{3}pi r^3rho $ — масса планеты, которая ограничена сферической поверхностью радиуса $r$. При этом, ускорение свободного падения равно:
[g_1(r)=frac{gamma frac{4}{3}pi r^3rho }{r^2}=frac{4}{3}pi gamma rho r.]
Расположим материальную точку массы $m$ в точке А за пределами планеты (рис.1 (б)), тогда по закону всемирного тяготения на точечную массу действует сила, равная:
[mg=gamma frac{mM’}{r^2} left(2.2right),]
где $M’=frac{4}{3}pi R^3rho $, в этом случае ускорение свободного падения равно:
[g_2(r)=gamma frac{4}{3}pi R^3frac{rho }{r^2}.]
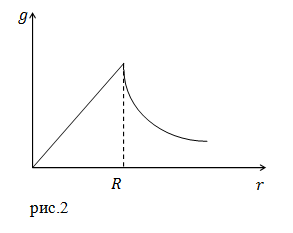
В результате получаем:
[left{ begin{array}{c}
g_1left(rright)=frac{4}{3}pi gamma rho r при rle R \
g_2left(rright)=gamma frac{4}{3}pi R^3frac{rho }{r^2}при rge R. end{array}
right. ]
Читать дальше: центростремительное ускорение.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!







![g=9{,}780327left[1+0{,}0053024,sin^2(phi) - 0{,}0000058,sin^2(2phi)right] - 3,086cdot 10^{-6},h](https://web.archive.org/web/20100405053211im_/http://upload.wikimedia.org/math/6/5/8/658a780a8a3581d0f61972536d368ba5.png) ,
, ,
, м/с²
м/с²