Статика — раздел механики, изучающий условия равновесия тел.
Виды равновесия
Устойчивое равновесие |
|
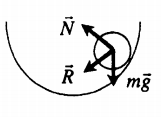 |
Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (Ep min). |
Неустойчивое равновесие |
|
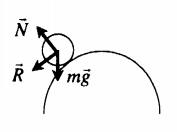 |
Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (Ep max). |
Безразличное равновесие |
|
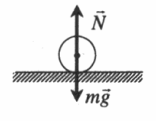 |
При выведении тела из положения безразличного равновесия дополнительных сил не возникает. |
Момент силы
Определение
Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:
M = Fd
M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).
Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.
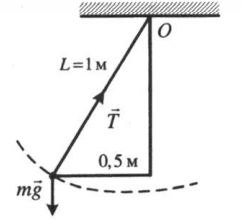
Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?
Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:
M = Fd = mgd = 2∙10∙0,5 = 10 (Н∙м)
Момент силы может быть положительным и отрицательным.
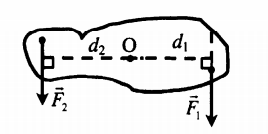
Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:
M1 = F1d1
Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:
M2 = F2d2
Правило моментов
Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
∑Mi=0
Иначе правило моментов можно сформулировать так:
Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.
∑Mпо час. стр.=∑Mпр. час. стр.
Условия равновесия тел
| Тело не участвует в поступательном движении: |
∑→Fi=0; →vo=0 |
| Тело не участвует во вращательном движении: |
∑Mi=0; ω0=0 |
| Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении) |
∑→Fi=0; →vo=0 и ∑→Fi=0; →vo=0 |
Простые механизмы
Определение
Простые механизмы — приспособления, служащие для преобразования силы. К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.
Наклонная плоскость |
|
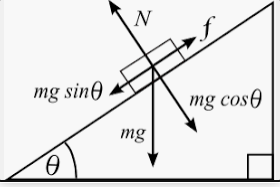 |
Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: mgsinθ<mg |
Рычаг |
|
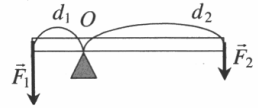 |
Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F1F2=d2d1 |
Неподвижный блок |
|
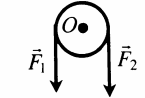 |
Изменяет направление действия силы. Модули и плечи сил при этом равны: F1 = F2 M1 = M2 |
Подвижный блок |
|
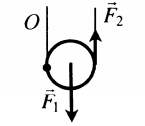 |
Дает выигрыш в силе в 2 раза:
d1 = R d2 = 2R F1 = 2F2 |
Клин |
|
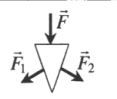 |
Делит силу на две равные части, направление которых зависит от формы клина: →F=→F1+→F2 |
Золотое правило механики
При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.
Задание EF22660
Алгоритм решения
1.Записать исходные данные.
2.Записать правило моментов и выполнить решение в общем виде.
3.Подставить известные данные и вычислить искомую величину.
Решение
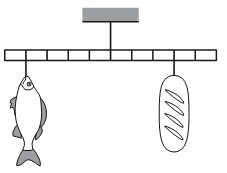
Известна лишь масса батона: m1 = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:
d1 = 0,3
d2 = 0,4
Запишем правило моментов:
F1 d1 = F2 d2
Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:
m1gd1 = m2gd2
m1d1 = m2d2
Отсюда масса рыбы равна:
m2=m1d1d2=0,8·0,30,4=0,6 (кг)
Ответ: 0,6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18706
Ответ:
а) 0
б) О2О3
в) О2В
г) О3В
Алгоритм решения
- Сформулировать определение плеча силы.
- Найти плечо силы трения и аргументировать ответ.
Решение
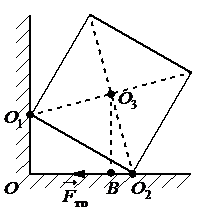
Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О3В.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 9.7k
Моменты импульса и силы связаны между
собой важным соотношением, которое
называется уравнением моментов. Вначале
получим это соотношение для одной
материальной точки. С этой целью
продифференцируем момент импульса
(5.5) по времени
.
(5.9)
Учитывая, что
и
,
с учетом (5.1), получим
.
(5.10)
Это и есть уравнение моментов для одной
материальной точки.
Распространим теперь уравнение (5.10) на
систему материальных точек. Для этого
сложим все уравнения (5.10) для каждой
точки, понимая под М момент всех
действующих на нее сил, как внешних, так
и внутренних
.
(5.11)
Суммарный момент всех внутренних сил
равен нулю. Действительно, внутренние
силы входят в систему попарно. Эти силы
направлены противоположно и действуют
вдоль одной и той же прямой, поэтому
момент таких двух сил, а значит и момент
всех внутренних сил равны нулю. В
результате получаем уравнение моментов
для системы материальных точек:
,
(5.12)
где
— суммарный момент всех внешних сил,
—
момент импульса системы.
Таким образом, скорость изменения
момента импульса системы относительно
неподвижной точки (полюса) равна
результирующему моменту относительно
той же точки всех внешних сил, действующих
на систему.
Соотношение (5.12) справедливо, в частности,
для твердого тела, закрепленного в одной
точке. В этом случае оно выражает основной
закон динамики для тела, вращающегося
вокруг неподвижной точки. Из него
следует, что момент импульса является
основной динамической характеристикой
тела, вращающегося вокруг неподвижной
точки.
Из уравнения моментов (5.12) непосредственно
вытекает закон сохранения момента
импульса механической системы. Если
момент внешних сил равен нулю (),
то момент импульса системы остается
постоянным ().
Таким образом, момент импульса замкнутой
системы относительно произвольного
центра остается постоянным во времени.
Такова формулировка закона сохранения
момента импульса механической системы.
Этот закон, наряду с законами сохранения
импульса и энергии, является одним из
фундаментальных законов природы. В
теоретической механике, изучающей самые
общие законы движения, закон сохранения
момента импульса связывается с
изотропностью пространства, т.е. с
инвариантностью относительно вращений
пространства.
5.3. Момент силы и момент импульса относительно неподвижной оси
Следует различать и никоим образом не
смешивать понятия момента импульса и
момента силы относительно точки и
относительно оси. Момент вектора
относительно точки сам есть вектор,
тогда как момент вектора относительно
оси уже не является вектором.
М
Рис.5.4
оментом импульса
и моментом силы
относительно произвольной оси Z
называют проекции векторов
и
на эту ось в предположении, что точка О
(полюс) лежит на рассматриваемой оси
(рис.5.4).
Покажем на примере момента силы, что
выбор точки на оси влияет на значение
,
но не влияет на значение
.
Будем полагать, что точка О, относительно
которой определен момент силы
,
расположена в произвольной точке на
оси вращения (рис.5.5). Разложим вектор
силы на три взаимно перпендикулярные
составляющие, две из которых,
||
и
,
параллельная и перпендикулярная оси
вращения, лежат в плоскости, проходящей
через ось вращения и точку приложения
силы, а третья
— перпендикулярна к этой плоскости
(обозначена на рисунке крестиком). Момент
силы
относительно
точки О равен сумме моментов составляющих:
.
В
Рис.5.5
екторное произведение направлено
перпендикулярно плоскости, в которой
лежат образующие его векторы. Векторы
||
и
перпендикулярны оси, и следовательно,
их проекции на эту ось равны нулю. Поэтому
.
(5.13)
Здесь
,
а
.
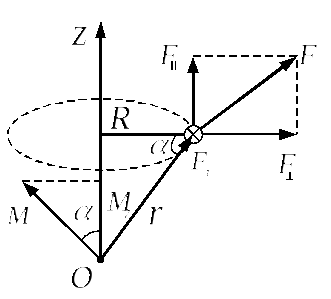
Окончательно, для момента силы относительно
оси вращения получаем:
,
(5.14)
где
—
радиус окружности с центром на оси OZ,
а
— касательная составляющая силы к этой
окружности.
Таким образом, момент силы относительно
оси характеризует способность силы
вращать тело вокруг этой оси. В соответствии
с правилом винта величина
положительна,
когда сила приводит к вращению тела
вокруг направления оси против часовой
стрелки, и отрицательна – при вращении
в противоположном направлении.
Проектируя векторное уравнение (5.12) на
ось ОZ, получим
.
(5.15)
Это уравнение называется уравнением
моментов относительно неподвижной оси.
Когда момент внешних сил относительно
какой-либо оси равен нулю, то момент
импульса системы относительно той же
оси остается постоянным. Это закон
сохранения момента импульса относительно
неподвижной оси.
Этот закон в сочетании с законом
сохранения механической энергии
эффективно используется при решении
задач на вращательное движение твердого
тела (см.5.8).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание книги
Предыдующая страница
§4. Основные законы динамики
4.6 Вращательное движение твердого тела. Момент силы.
Конечно, положение одной, даже «особой», точки далеко не полностью описывает движение всей рассматриваемой системы тел, но все-таки, лучше знать положение хотя бы одной точки, чем не знать ничего. Тем не менее, рассмотрим применение законов Ньютона к описанию вращения твердого тела вокруг фиксированной оси [1].
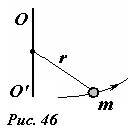
Начнем с простейшего случая: пусть материальная точка массы m прикреплена с помощью невесомого жесткого стержня длиной r к неподвижной оси OO’ (рис. 46). Материальная точка может двигаться вокруг оси, оставаясь от нее на постоянном расстоянии, следовательно, ее траектория будет являться окружностью с центром на оси вращения.
Безусловно, движение точки подчиняется уравнению второго закона Ньютона (~m vec a = vec F_0). Однако, непосредственное применение этого уравнения не оправдано: во-первых, точка обладает одной степенью свободы, поэтому в качестве единственной координаты удобно использовать угол поворота, а не две декартовые координаты; во-вторых, на рассматриваемую систему действуют силы реакции в оси вращения, а непосредственно на материальную точку – сила натяжения стержня. Нахождение этих сил представляет собой отдельную проблему, решение которой излишне для описания вращения. Поэтому имеет смысл получить на основании законов Ньютона специальное уравнение, непосредственно описывающее вращательное движение.
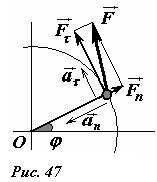
Пусть в некоторый момент времени на материальную точку действует некоторая сила (~vec F), лежащая в плоскости перпендикулярной оси вращения (рис. 47). При кинематическом описании криволинейного движения вектор полного ускорения (~vec a) удобно разложить на две составляющих: нормальную (~vec a_n), направленную к оси вращения, и тангенциальную (~vec a_{tau}) , направленную параллельно вектору скорости. Значение нормального ускорения для определения закона движения нам не нужно. Конечно, это ускорение также обусловлено действующими силами, одна из которых неизвестная сила натяжения стержня.
Запишем уравнение второго закона в проекции на тангенциальное направление:
(~m a_{tau} = F_{tau}) , (1)
заметим, что сила реакции стержня не входит в это уравнение, так как она направлена вдоль стержня и перпендикулярна выбранной проекции. Изменение угла поворота φ непосредственно определяется угловой скоростью (~omega = frac{Delta varphi}{Delta t}) , изменение которой в свою очередь описывается угловым ускорением (~varepsilon = frac{Delta omega}{Delta t}) . Угловое ускорение связано с тангенциальной составляющей ускорения соотношением aτ = rε. Если подставить это выражение в уравнение (9), то получим уравнение, пригодное для определения углового ускорения. Удобно ввести новую физическую величину, определяющую взаимодействие тел при их повороте. Для этого умножим обе части уравнения (1) на r
(~m r^2 varepsilon = F_{tau} r) . (2)
и рассмотрим выражение в его правой части Fτr, имеющего смысл произведения тангенциальной составляющей силы, на расстояние от оси вращения до точки приложения силы. Это же произведение можно представить несколько иной форме (см. рис. 48)
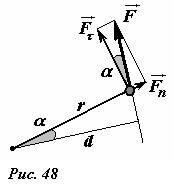
M = Fτr = Fr cos α = Fd, здесь d — расстояние от оси вращения до линии действия силы, которое также называют плечом силы. Эта физическая величина, произведение модуля силы на расстояние от линии действия силы до оси вращения (плечо силы) M = Fd называется моментом силы. Действие силы может приводить к вращению, как по часовой стрелке, так и против часовой стрелки. В соответствии с выбранным положительным направлением вращения следует определять и знак момента силы. Заметьте, что момент силы определяется той составляющей силы, которая перпендикулярна радиус-вектору точки приложения. Составляющая вектора силы, направленная вдоль отрезка, соединяющего точку приложения и ось вращения, не приводит к раскручиванию тела. Эта составляющая при закрепленной оси компенсируется силой реакции в оси, поэтому она не влияет на вращение тела.
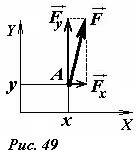
Запишем еще одно полезное выражения для момента силы. Пусть сила (~vec F) приложена к точке А, декартовые координаты которой равны x,y (рис. 49). Разложим силу (~vec F) на две составляющие (~vec F_x, vec F_y) , параллельные соответствующим осям координат. Момент силы (~vec F) относительно оси, проходящей через начало координат, очевидно равен сумме моментов составляющих (~vec F_x, vec F_y) , то есть M = xFy — yFx.
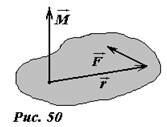
Аналогично, тому, как нами было введено понятие вектора угловой скорости, можно определить также и понятие вектора момента силы. Модуль этого вектора соответствует данному выше определению, направлен же он перпендикулярно плоскости, содержащей вектор силы и отрезок, соединяющий точку приложения силы с осью вращения. Вектор момента силы также может быть определен как векторное произведение радиус-вектора точки приложения силы на вектор силы
(~vec M = vec r times vec F) .
Заметим, что при смещении точки приложения силы вдоль линии ее действия момент силы не изменяется.
Обозначим произведение массы материальной точки на квадрат расстояния до оси вращения mr2 = I (эта величина называется моментом инерции материальной точки относительно оси). С использованием этих обозначений уравнение (2) приобретает вид, формально совпадающий с уравнением второго закона Ньютона для поступательного движения
(~I varepsilon = M) . (3)
Это уравнение называется основным уравнением динамики вращательного движения. Итак, момент силы во вращательном движении играет такую же роль, как и сила в поступательном движении, именно он определяет изменение угловой скорости. Оказывается, (и это подтверждает наш повседневный опыт) влияние силы на скорость вращения определяет не только величина силы, но и точка его приложения. Момент инерции определяет инерционные свойства тела по отношению к вращению (говоря простым языком – показывает, легко ли раскрутить тело) — чем дальше от оси вращения находится материальная точка, тем труднее привести ее во вращение.
Уравнение (3) допускает обобщение на случай вращения произвольного тела. При вращении тела вокруг фиксированной оси угловые ускорения всех точек тела одинаковы. Поэтому, аналогично тому, как мы проделали при выводе уравнения Ньютона для поступательного движения тела, можно записать уравнения (3) для всех точек вращающегося тела и затем их просуммировать. В результате мы получим уравнение, внешне совпадающее с (3), в котором I — момент инерции всего тела, равный сумме моментов составляющих его материальных точек, M — сумма моментов внешних сил, действующих на тело.
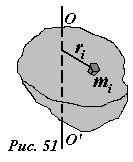
Покажем, каким образом вычисляется момент инерции тела. Важно подчеркнуть, момент инерции тела зависит не только от массы, формы и размеров тела, но и от положения и ориентации оси вращения. Формально процедура расчета сводится к разбиению тела на малые части, которые можно считать материальными точками (рис. 51), и суммированию моментов инерций этих материальных точек, которые равны произведению массы на квадрат расстояния до оси вращения
(~I = m_1 r^2_1 + m_2 r^2_2 + m_3 r^2_3 + ldots) .
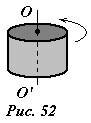
Для тел простой формы такие суммы давно подсчитаны, поэтому часто достаточно вспомнить (или найти в справочнике) соответствующую формулу для нужного момента инерции. В качестве примера: момент инерции кругового однородного цилиндра массы m и радиуса R для оси вращения совпадающей с осью цилиндра равен (~I = frac{1}{2} m R^2) .
Примечания
- ↑ В данном случае мы ограничиваемся рассмотрением вращения вокруг фиксированной оси, потому, что описание произвольного вращательного движения тела представляет собой сложную математическую проблему, далеко выходящую за рамки курса математики средней школы. Знания же других физических законов, кроме рассматриваемых нами, это описание не требует.
Следующая страница
Уравнение моментов
Определение и уравнение моментов
Пусть O — любая неподвижная точка в инерциальной системе отсчета. Это называется началом или полюсом. Обозначим через
радиус-вектор, взятый от этой точки до точки приложения силы
(рис.1).
рис 1.
ОПРЕДЕЛЕНИЕ
Момент силы относительно точки O является векторным произведением радиус-вектора
и силы
:
направление выбрано так, что последовательность векторов
образует правую систему, т. е. если вы посмотрите вдоль вектора
,то поворот вдоль кратчайшего пути от первого фактора в (1) до вторая выполняется по часовой стрелке, таким образом
совпадает с направлением поступательного движения правого штыря, ручка которого вращается от
до
вдоль кратчайшего пути.
Моментом нескольких сил относительно точки является векторная сумма моментов этих сил относительно одной и той же точки:
Момент импульса материальной точки
ОПРЕДЕЛЕНИЕ
Момент импульса материальной точки относительно точки O является векторным произведением радиус-вектора и импульса
:
где J — момент инерции, — угловая скорость вращения тела.
Система из n материальных точек — это момент количества движения относительно некоторой точки O — векторная сумма моментов импульсов этих точек относительно того же начала:
Временная производная от момента импульса механической системы относительно неподвижной точки (полюса О) равна сумме внешних силовых моментов
, действующих на систему:
Для материальной точки уравнение момента написано:
Уравнение (6) называется моментом для системы материальных точек. Это основной закон динамики твердого тела, вращающегося вокруг неподвижной точки.
В проекциях на оси фиксированной декартовой системы координат с началом на полюсе O уравнение моментов системы записывается в виде:
где — проекция момента количества движения на соответствующей оси;
— проекции полного момента сил на соответствующую ось.
Уравнение моментов позволяет получить ответ на следующие вопросы:
1. найти момент силы (общий момент внешних сил) относительно интересующей нас точки в любой момент времени, если известна зависимость момента количества движения частицы (системы частиц) от одной и той же точки;
2. определить приращение углового момента частицы (системы частиц) относительно точки O для любого периода времени, если временная зависимость силового момента (полного момента внешних сил), действующего на эту частицу (система частиц) относительно одной и той же точки.
Примеры решения проблем
ПРИМЕР 1
Сравните угловые скорости, полученные материальной точкой под действием крутящих моментов, графики (a, b) которых показаны на рисунках.
рис 2.
В соответствии с уравнением моментов для материальной точки мы имеем:
где
поскольку мы имеем дело с материальной точкой, соответственно, J не зависит от времени, получаем:
откуда
Вспомните геометрический смысл интеграла.
Вычислить и сравнить площадь треугольников OAB и OCD.
Области треугольников равны соответственно
Угловые скорости, полученные материальной точкой, равны в первом и втором случаях.
ПРИМЕР 2
Горизонтальный диск с радиусом R = 0,2 м и массой m = 5 кг вращается вокруг оси, проходящей через ее центр. Зависимость угловой скорости вращения диска от времени определяется уравнением w = A + 8t. Найдите значение касательной силы, приложенной к ободу диска. Трение пренебрегалось.
Мы делаем рисунок
рис 3.
Запишем уравнение моментов:
где — искомая сила. Перепишите (2.2), найдите модуль:
— угол между вектором
и
равен
, так как силы, касательные к диску,
направлены вдоль радиуса диска в точку касания, следовательно, M = RF.
Поскольку мы имеем дело с телом, который не меняет момент инерции со временем, мы имеем:
Где — момент инерции диска относительно оси, проходящей через его центр.
, получим:
Подставим числовые значения, получим:
Величина (модуль) касательной силы, приложенной к краю диска, равна 4 N.