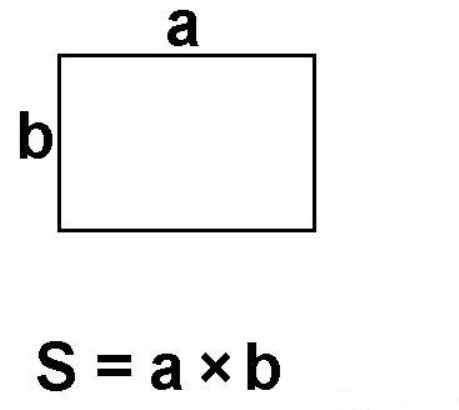Содержание
- Какую формулу можно применить для расчета размера жилой зоны в частном доме
- С чего начинать
- В каком классе изучают площадь прямоугольника?
- Обозначение площади
- Треугольник
- 1. Если известна сторона и высота.
- 2. Если известны две стороны и синус угла.
- 3. Если есть радиус описанной окружности.
- Прямоугольник
- Квадрат
- Трапеция
Если помещение обычное и не имеет выступающих частей, вычислить площадь помещения несложно. Измерьте длину и ширину и отметьте их на листе бумаги. Напишите данные измерений с десятичной запятой в сантиметрах.
Например, длина составляет 4,35 метра (430 см), а ширина — 3,25 метра (325 см). Как рассчитать площадь комнаты. Перемножьте полученные числа, чтобы получить площадь комнаты в квадратных метрах.
Возвращаясь к нашему примеру, мы имеем: 4. 35 м * 3. 25 м = 14, 1375 кв.
м. Это значение обычно округляется, так как после запятой остается две цифры.
Отвечает Климова Г. 09. 03. 22.
Какую формулу можно применить для расчета размера жилой зоны в частном доме
Чтобы определить площади, имеющиеся в вашем доме, нужны размеры всех помещений, предназначенных для жилья.
Чтобы знать, какие площади дома следует считать пригодными для жилья, можно тщательно пересмотреть и изучить проект дома и его технический паспорт. Размеры площадей и категории каждого помещения приведены в подробном перечне
Жилая комната: гостиная.
- Главная спальня.
- Гардеробная.
- Чтобы правильно измерить жилую комнату, необходимо тщательно измерить длину и ширину всех существующих стен в каждой комнате, предназначенной для постоянного использования. Это можно сделать с помощью строительного метра. Рекомендуется проводить измерения точно и аккуратно. Перед проведением измерений следует убрать из комнаты все лишние предметы, а измерять удобнее вдоль кирпичей пола, отведя место у каждой стены. Все проведенные замеры следует записать, а также зафиксировать помещение, в котором они были произведены.
После того как проведены замеры жилого помещения и все точно записано, можно приступать к расчету необходимых величин. Для точных расчетов можно применять следующие типы
e (длина) комнаты x w (ширина) = p (площадь) комнаты.
Результаты полученных измерений следует записывать и комментировать. Это облегчит выполнение большего объема работы в домашних условиях в будущем. Далее сложите все измерения, которые вы сделали для каждой комнаты. Это даст вам представление о жилой площади вашей недвижимости.
Самое время вспомнить школьную математику — для вычисления площади вам понадобятся три вещи
С чего начинать
Длина — обычно 4 или 4,5 метра.
- Ширина — стандартное значение для большинства домов составляет 3 или 3,5 метра.
- Высота — в новых зданиях она обычно составляет 2,5 метра. Однако в сталинских зданиях этот показатель может достигать 3 метров.
- Решая задачу по вычислению площади, не делайте этого без соответствующих инструментов.
Рулетка, рулетка
- Угол строения,
- карандаш
- Компьютер,.
- Нивелир.
- Если вы планируете много писать, предпочтительнее использовать блокнот или тетрадь вместо бумаги. Листки имеют тенденцию теряться, и не всегда их можно найти позже, когда они необходимы. Ленты нуждаются в приспособлении для фиксации. В противном случае возникают сложности, и расчеты могут превратиться в настоящую пытку.
Математика 3 класс Урок 22 — Площадь прямоугольника. Вы узнаете: как вычислить площадь прямоугольника. Вы узнаете: как сравнивать геометрические фигуры по площади.
Вычислите площадь прямоугольника. Площадь — это внутренняя часть геометрической фигуры. Площадь измеряется в квадратных сантиметрах.
Чтобы найти площадь прямоугольника, его длину нужно умножить на ширину. Интересные факты о геометрических фигурах Первые упоминания о геометрических фигурах встречаются у древних египтян и древних шумеров.
В каком классе изучают площадь прямоугольника?
В геометрии фигура определяется как плоскость, отрезок плоскости или набор точек в пределах криволинейной поверхности, ограниченной со всех сторон. В реальной жизни нас окружают различные объекты, характеризующиеся как фигуры, например, мобильные телефоны, холодильники и летающие змеи. В этой статье описано несколько способов определения местоположения области.
Обозначение площади
Если параметр фигуры задан в разных единицах длины, решить задачу невозможно. Поэтому для правильного решения задачи все данные должны быть переведены в одну единицу измерения.
Общие единицы измерения для площади :
Квадратные миллиметры (мм 2 ),
- квадратный сантиметр (см 2 ),.
- квадратный десятичный метр (дм 2 ), квадратный метр (м2 ), квадратный метр (м2 ), квадратный метр (м2 ).
- квадратный метр (м 2 ), квадратный километр (км 2 )
- квадратный километр (км 2 ), гектар (га)
- гектар (га).
- Советы, статьи, видео и контрольные списки по обучению доставляются в ваш почтовый ящик
Круг — это множество точек на плоскости, равноудаленных от центра и заключенных в окружность. Радиусом обычно называют отрезок прямой, соединяющий центр окружности с любой точкой.
S = π × r 2 , где r — радиус, а π — константа, равная отношению окружности круга к его диаметру, которое всегда равно 3. 14.
S = & amp; pi × d 2 : 4, где d — диаметр.
S = L 2 : (4 × pi), где L — длина окружности.
Нужно быстро подтянуть знания перед экзаменом? Запишитесь на курс ЕГЭ по математике от Skysmart!
Треугольник — это геометрическая фигура, которая не лежит на прямой линии, а состоит из трех точек, соединенных тремя отрезками прямых. Эти три точки называются вершинами, а отрезки прямых — ребрами. Площадь треугольника может быть вычислена из исходных данных несколькими способами. Давайте рассмотрим их.
Треугольник
S = 0. 5 × a × h, где a — длина основания, а h — высота до основания.
1. Если известна сторона и высота.
Основания могут располагаться в различных положениях, например
Для тупых углов высота отражается на продолжении основания.
В случае прямого угла основание и высота являются его катетами: s
s = 0. 5 x α x β * sina, где a и b — две стороны, а sina — полутонна между ними.
2. Если известны две стороны и синус угла.
s = (a x b x c) : (4 x r), где a, b и c — стороны треугольника, а r — радиус контура.
3. Если есть радиус описанной окружности.
s = p×r, где p — половина лимперметра треугольника, а r — радиус записанного контура.
Прямоугольник
s = a × b, где a и b — длина и ширина прямоугольника.
s = a x √ (d 2-a 2), где a — известная сторона, а d — диагональ.
Диагональ — это отрезок, соединяющий противоположные углы. Она присутствует во всех геометриях, где число вершин превышает 3.
s = 0. 5 x d 2 x ( ), где d — диагональ, а a — угол между диагоналями.
Квадрат — это то же самое, что и прямоугольник, но все стороны могут быть равны. Найти его площадь просто: s
Квадрат
s = a 2, где a — сторона квадрата.
s = d 2:2, где d — диагональ.
Таблица представляет собой четырехугольник с двумя параллельными и двумя непараллельными сторонами.
Трапеция
S = 0. 5 x (A + B) x H, где A и B — два разных основания, а H — высота трапеции.
Высоту трапеции можно построить, проведя отрезки, соединяющие параллельные стороны под прямым углом.
Прямоугольник — это четырехугольник, противоположные стороны которого параллельно-параллельны.
Содержание материала
- Площадь застройки
- Видео
- Как высчитывается площадь помещения?
- Какую формулу можно применить для расчета размера жилой зоны в частном доме
- С чего начинать
- В каком классе изучают площадь прямоугольника?
Площадь застройки
Площадь застройки — площадь горизонтального сечения здания на уровне цоколя, включая его выступающие части. Крыльцо и пандус также включаются в площадь застройки, а выступающие части крыши — нет. Логика такая: на площади участка выделяются площадь застройки, отмостки, площадок, проездов, дорожек и т.д. Балкон на втором этаже, выступающий за пределы цоколя, не будет включен в площадь застройки, если только он не расположен на несущих столбах. Для владельца земельного участка существенным является «разрешенная площадь застройки», которая обычно не может превышать 30% общей площади участка.
Как высчитывается площадь помещения?
Автор вопроса: Создано:
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см). Как высчитать площадь комнаты. Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем.
Ответил(а): Климова Г. 09.03.22
Видео
Какую формулу можно применить для расчета размера жилой зоны в частном доме
С целью определения площади отведённой под жилую, нужно иметь размеры всех зон, предназначенных для жилья в данном доме.
Для того, чтобы выяснить, какие именно зоны в конкретном частном домовладении необходимо считать жилыми, достаточно развернуть и внимательно изучить проект дома и его технический паспорт. В экспликации к техпаспорту можно конкретно увидеть как величину площади, так и категорию каждой из комнат.
К комнатам, предназначенным для жилья можно отнести:
- Зал-гостиную.
- Комнаты -спальни.
- Гардеробную.
Для того, чтобы правильно замерить жилую площадь помещения, требуется тщательно замерить длину и ширину всех имеющихся стен в каждой из комнат, предусмотренных для постоянного в них нахождения. Это можно сделать при помощи строительной рулетки. Все измерения рекомендуется делать точно и аккуратно. Удобнее будет если перед снятием замеров вынести из комнат все ненужное, чтобы место у каждой из стен было в свободном доступе и после этого произвести измерения вдоль полового плинтуса. Все полученные результаты измерений с обязательной пометкой зоны, в которой они производились надо зафиксировать.
Когда измерения жилых помещений подойдут к концу и все точно записано, можно заняться подсчётом необходимой величины. Для её точного вычисления можно применить следующую формулу:
Д (длина) одной комнаты х Ш (ширина) одной комнаты =П (площадь) одной комнаты.
Результаты полученных измерений нужно записать, сделав пометки — такой шаг облегчит задачу в том случае, если вы в будущем соберётесь предпринять ещё какие-либо работы в доме. После этого, надо сложить все результаты замеров, полученные вами для каждой комнаты. Вычисленная величина и станет показателем жилой площади вашего домовладения.
С чего начинать
Самое время вспомнить школьную математику – чтобы рассчитать площадь, необходимы три параметра:
- Длина – обычно она бывает 4 либо 4,5 метра.
- Ширина – стандартное значение для большинства домов это 3 или 3,5 метра.
- Высота – в новостройках она обычно равна 2,5 метрам. А вот в постройках сталинской эпохи может составлять до 3 метров.
В решении задачи, как рассчитать площадь, не обойтись и без соответствующих инструментов:
- рулетки;
- строительного угольника;
- карандаша;
- калькулятора;
- строительного уровня.
Если планируются много писать, то вместо листка бумаги лучше взять блокнот либо тетрадь. Листики имеют свойство теряться, причём, когда нужно не всегда найдёшь их потом. Рулетка обязательно должна быть с фиксатором, иначе возникнуть сложности и процедура расчётов превратится в настоящее мучение.
В каком классе изучают площадь прямоугольника?
Автор вопроса: Создано:
Математика 3 класс Урок№22 — Площадь прямоугольника. мы узнаем: способ вычисления площади прямоугольника; мы научимся: сравнивать геометрические фигуры по площади; мы сможем: вычислять площадь прямоугольника. Площадь – внутренняя часть геометрической фигуры. Площадь измеряется в квадратных сантиметрах. Чтобы найти площадь прямоугольника, надо его длину умножить на ширину. Интересные факты о геометрических фигурах Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров.
Ответил(а): Щукин Д. 22.03.22
Теги
Площадь
В школьном курсе математики 4-5 класса рассматривается понятие площади. Это значение часто встречается как в реальной жизни, где мы постоянно интересуемся площадью квартиры, так и при решении задач.
Определение понятия
Площадь указывает на размер плоскости, которую занимает фигура. Если вырезать любую фигуру из листа бумаги, положить на поверхность, а потом обвести карандашом, мы получим визуальное воплощение характеристики площади.
Площади двух абсолютно разных фигур могут быть одинаковыми. Почему так происходит? Потому что площадь – это характеристика. Можно провести простую аналогию с деньгами: сто грамм конфет и полкилограмма крупы стоят одинаково, но это совершенно разные вещи. Так треугольник и прямоугольник могут иметь одинаковую площадь. Фигуры, имеющие одинаковую площадь, называют равновеликими.
Характеристики понятия
Площадь имеет несколько характеристик:
- Положительность. Площадь не может быть отрицательной, как не может быть отрицательным пространство. Есть единственный случай, когда площадь стремится к нулю: измерение площади точки.
- Нормируемость.
На практике площадь можно определять с помощью палетки или специального измерительного прибора – планиметра.
Площади простых фигур
Формула для определения площади зависит от фигуры. Обозначение площади, чаще всего, остается неизменным – это латинская заглавная буква “S”. Это не правило, просто одна из традиций обозначения площади. В высшей математике, теплотехнике и многих других дисциплинах площадь могут обозначать другими буквами.
Рассмотрим наиболее популярные формулы определения площадей:
- Прямоугольник. S=a*b – произведение длины на ширину.
- Треугольник. $S=<1over2>a*h$ – половина произведения основания на высоту, проведенную к этому основанию.
- Круг. $S=pi*r^2$ – отдельно нужно отметить, что окружность площади иметь не может. Только круг.
Предварительно нужно убедиться в том, что параметры фигуры находятся в одинаковых единицах измерения. Например, когда ширина прямоугольника представлена в миллиметрах, а длина в сантиметрах, следует перевести сантиметры в миллиметры и только потом использовать формулу.
Рис. 2. Площадь прямоугольника.
Что такое площадь квадрата? Это сторона фигуры, возведенная в квадрат. Потому что квадрат это прямоугольник, длина и ширина которого равны:
Если у квадрата одна сторона равняется 100 м, то его площадь равна одному гектару. Эту единицу используют, когда необходимо оценить размеры земной поверхности при распределении сельскохозяйственных угодий:
Площади полей могут также измерять в арах, что в народе называют «соткой», потому что один ар – это квадрат, сторона которого равняется 10 м, а его площадь соответственно 100 $м^2$.
Площадь произвольной фигуры
Площадь сложной фигуры можно определить, просуммировав площади ее частей. Для этого нужно просто разделить произвольную геометрическую фигуру на простые составляющие так, чтобы можно было легко определить их квадратуры.
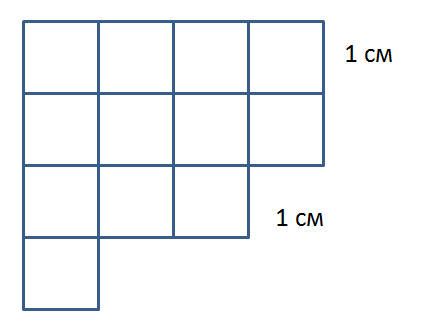
Рис. 3. Площадь сложной фигуры.
Фигуру на рисунке 3 можно разбить на 12 квадратов со сторонами 1 см. Тогда площадь каждого квадрата будет равняться $1см^2$. Получается, что площадь рассматриваемой фигуры будет $12 см^2$.
Что мы узнали?
Мы познакомились с понятием площади. Узнали, что для каждой фигуры есть свой метод определения площади. Важно, чтобы основные параметры фигуры были выражены в одних и тех же единицах.
Определение площади
Определение
Площадь S — это положительная величина, численное значение которой обладает следующими свойствами:
Главная 


Площадь квадрата
Квадрат – это правильный четырехугольник, в котором все углы и стороны равны между собой.
Довольно часто эту фигуру рассматривают, как частный случай ромба или прямоугольника. Диагонали квадрата равны между собой и используются в формуле площади квадрата через диагональ.
Для расчета площади рассмотрим формулу площади квадрата через диагонали:
Рассмотрим пример расчета площади квадрата через диагональ. Пусть дан квадрат с диагональю d = 3 см. Необходимо вычислить его площадь:
Так как в предыдущем примере расчета площади квадрата мы рассчитали значение по диаметру, теперь попробуем найти длину стороны:

Диаметр описанной окружности будет равен диаметру квадрата. Так как квадрат считается правильным ромбом, можно использовать формулу расчета площади ромба. Она равна половине произведения его диагоналей. Диагонали квадрата равны, значит формула будет выглядеть так: Дан квадрат, вписанный в окружность. Диагональ окружности равна d = 6 см. Найдите площадь квадрата.
Мы помним, что диагональ окружности равна диагонали квадрата. Подставляем значение в формулу расчета площади квадрата через его диагонали: 


Рассмотрим пример расчета площади квадрата через периметр.
Дан квадрат с периметром P = 16 см. Найдите его площадь.
Находим сторону: 
Теперь рассчитаем площадь: 
Площадь данного квадрата равна 16 
Загрузить PDF
Загрузить PDF
Площадь поверхности – это суммарная площадь всех поверхностей, которые составляют объемную фигуру. Площадь поверхности является числовой характеристикой поверхности.[1]
Вычислить площадь поверхности объемной (трехмерной) фигуры довольно просто, если знать соответствующую формулу. Существует определенная формула для каждой фигуры, поэтому сначала нужно определить, какая фигура дана. Чтобы быстро вычислять площадь поверхности, запомните соответствующие формулы для разных фигур. В данной статье рассматриваются наиболее распространенные фигуры.
-
1
Запишите формулу для вычисления площади поверхности куба. У куба шесть равных квадратных граней. Так как стороны квадрата равны, площадь квадрата равна a2, где а – сторона. Так как у куба шесть равных квадратных граней, чтобы найти площадь поверхности, умножьте площадь одной грани (квадрата) на 6. Формула для вычисления площади поверхности (SA) куба: SA = 6а2, где а – ребро куба (сторона квадрата).[2]
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте ребро куба. Ребра куба равны, поэтому можно измерить только одно (любое) ребро. Ребро измерьте с помощью линейки (или рулетки). Обратите внимание на используемые единицы измерения.
- Запишите значение, обозначив его через а.
- Например: а = 2 см
-
3
Значение а возведите в квадрат. То есть возведите в квадрат длину ребра куба. Для этого умножьте значение на себя. Если вы только приступили к изучению формул с квадратами, запишите формулу так: SA = 6*а*а.
- Сейчас вы вычислили значение площади одной из граней куба.
- Например: а = 2 см
- a2 = 2 х 2 = 4 см2
-
4
Вычисленное значение умножьте на шесть. Помните, что у куба шесть равных граней. Вычислив площадь одной из граней, умножьте полученное значение на 6, чтобы включить все грани куба.
- Это последний шаг в процессе вычисления площади поверхности куба.
- Например: а 2 = 4 см2
- SA = 6 х а2 = 6 х 4 = 24 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности прямоугольной призмы. У прямоугольной призмы шесть граней, причем равными являются только противоположные грани.[3]
Поэтому формула для вычисления площади поверхности прямоугольной призмы включает значения трех разных ребер: SA = 2ab + 2bc + 2ac.- Здесь а – ширина, b – высота, с – длина призмы.
- Если проанализировать формулу, можно понять, что она суммирует площади всех граней.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Найдите значения высоты, ширины и длины призмы. Три ребра не являются равными, поэтому нужно выполнить три измерения. Измерьте соответствующие ребра с помощью линейки (или рулетки). Ребра измеряйте в одной единице измерения.
- Измерьте длину грани, которая лежит в основании призмы; длину обозначьте через с.
- Например: с = 5 см
- Измерьте ширину грани, которая лежит в основании призмы; ширину обозначьте через а.
- Например: а = 2 см
- Измерьте высоту призмы; высоту обозначьте через b.
- Например: b = 3 см
-
3
Вычислите площадь одной грани призмы, а затем полученное значение умножьте на два. Помните, что у прямоугольной призмы шесть граней, причем равными являются только противоположные грани. Умножьте длину на высоту (с на а), чтобы найти площадь одной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[4]
- Например: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 см2
-
4
Вычислите площадь другой грани призмы, а затем полученное значение умножьте на два. Умножьте ширину на высоту (а на b), чтобы найти площадь другой грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[5]
- Например: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 см2
-
5
Вычислите площадь фронтальной грани, а затем полученное значение умножьте на два. Умножьте длину на ширину (с на b), чтобы найти площадь фронтальной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[6]
- Например: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 см2
-
6
Сложите три значения. Так как площадь поверхности – это суммарная площадь всех граней фигуры, сложите найденные значения площадей отдельных граней. Вы получите площадь поверхности прямоугольной призмы.[7]
- Например: SA = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности треугольной призмы. Треугольная призма имеет две равные треугольные грани и три прямоугольные грани. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти площади всех граней и сложить их. Формула для вычисления площади поверхности треугольной призмы: SA = 2S + РH, где S – площадь треугольной грани, Р – периметр треугольной грани, H – высота призмы.[8]
- Здесь S – это площадь треугольника (треугольной грани), которая вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание).
- Р – периметр треугольника (треугольной грани), который равен сумме всех сторон треугольника.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Вычислите площадь треугольной грани и умножьте ее на два. Площадь треугольника вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание). Так как треугольная призма имеет две равные треугольные грани, эту формулу можно умножить на два. Поэтому, чтобы вычислить площади двух треугольных граней, просто перемножьте основание и высоту треугольника (b*h).[9]
- Основание треугольника b – это его нижняя сторона.
- Например: b = 4 см
- Высота треугольника h – это перпендикуляр, опущенный на основание из противоположной вершины.
- Например: h = 3 см
- Площадь двух треугольных граней равна: 2(1/2)b*h = b*h = 4*3 =12 см.
-
3
Измерьте каждую сторону треугольника и высоту призмы. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти значение каждой стороны треугольника и высоты призмы. Высота призмы – это расстояние между треугольными гранями.
- Например: Н = 5 см
- Стороны треугольника – это три ребра одной (любой) из треугольных граней.
- Например: а = 2 см, b = 4 см, с = 6 см
-
4
Вычислите периметр треугольника. Для этого сложите все стороны треугольника: Р = а + b + с.
- Например: P = а + b + с = 2 + 4 + 6 = 12 см
-
5
Перемножьте периметр треугольной грани и высоту призмы. Помните, что высота призмы – это расстояние между треугольными гранями. Таким образом, Р умножьте на Н.
- Например: Р х Н = 12 х 5 = 60 см2
-
6
Сложите полученные значения. Чтобы найти площадь поверхности треугольной призмы, сложите два значения, вычисленные ранее.[10]
- Например: 2S + PH = 12 + 60 = 72 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности шара. Шар имеет изогнутую поверхность, поэтому формула включает математическую константу π (число Пи). Чтобы вычислить площадь поверхности шара, воспользуйтесь формулой SA = 4π*r2.[11]
- Здесь r – радиус шара, π ≈ 3,14.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус шара. Радиус шара равен половине его диаметра, то есть половине отрезка, который проходит через центр шара и соединяет две точки, лежащие на его поверхности.[12]
- Например: r = 3 см
-
3
Радиус шара возведите в квадрат. Для этого умножьте значение радиуса (r) на себя. Помните, что формулу можно записать так: SA = 4π*r*r.[13]
- Например: r2 = r x r = 3 x 3 = 9 см2
-
4
Перемножьте квадрат радиуса и приблизительное значение числа Пи. Число Пи является математической константой, которая равна отношению длины окружности к ее диаметру.[14]
Это иррациональное число со множеством цифр после десятичной запятой. Зачастую число Пи округляется до 3,14. Квадрат радиуса умножьте на π (на 3,14), чтобы вычислить площадь круглого сечения шара. [15]
- Например: π*r2 = 3,14 x 9 = 28,26 см2
-
5
Полученное значение умножьте на четыре. Чтобы найти значение площади поверхности сферы, площадь круглого сечения умножьте на 4.[16]
- Например: 4π*r2 = 4 x 28,26 = 113,04 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности цилиндра. Цилиндрическая поверхность этой фигуры ограничена двумя круглыми параллельными плоскостями, которые называются основаниями. Формула для вычисления площади поверхности цилиндра: SA = 2π*r2 + 2π*rh, где r – радиус основания, h – высота цилиндра, π ≈ 3,14.[17]
- 2π*г2 – это площадь двух оснований, а 2πrh – это площадь цилиндрической поверхности.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус основания и высоту цилиндра. Радиус окружности равен половине ее диаметра, то есть половине отрезка, который проходит через центр окружности и соединяет две точки, лежащие на ней.[18]
Высота цилиндра – это расстояние между его основаниями. Измерьте и запишите радиус основания и высоту цилиндра.- Например: r = 3 см
- Например: h = 5 см
-
3
Вычислите площадь основания и умножьте ее на два. Чтобы найти площадь основания, воспользуйтесь формулой для вычисления площади круга: S = π*г2. Сначала радиус возведите в квадрат, а затем полученное значение умножьте на число Пи. Результат умножьте на два, чтобы учесть второе равное основание.[19]
- Например: площадь основания = π*r2 = 3,14 х 3 х 3 = 28,26 см2
- Например: 2π*r2 = 2 x 28,26 = 56,52 см2
-
4
Вычислите площадь цилиндрической поверхности. Для этого воспользуйтесь формулой S = 2π*rh, по которой можно найти площадь поверхности трубы. Здесь труба – это поверхность между двумя основаниями цилиндра. Перемножьте двойку, число Пи, радиус и высоту.[20]
- Например: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 см2
-
5
Сложите полученные значения. Сложите площади двух оснований и площадь цилиндрической поверхности (между двумя основаниями), чтобы вычислить общую площадь поверхности цилиндра. Обратите внимание, что при сложении этих величин получится исходная формула: SA = 2π*r2 + 2π*rh.[21]
- Например: 2π*r2 + 2π*rh = 56,52 + 94,2 = 150,72 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности квадратной пирамиды. Квадратная пирамида имеет одно квадратное основание и четыре треугольные грани. Помните, что площадь квадрата равна квадрату его стороны. Площадь треугольника равна 1/2sl (половина основания треугольника, умноженная на его высоту). Так как пирамида имеет четыре треугольные грани, нужно площадь треугольника умножить на 4. Таким образом, площадь поверхности квадратной пирамиды вычисляется по формуле: SA = s2 + 2sl.[22]
- В этой формуле s – ребро квадратной грани (сторона квадрата), l – апофема пирамиды.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Найдите значения апофемы и ребра квадратной грани. Апофема (l) – это высота треугольной грани, то есть расстояние между основанием треугольника и его вершиной. Ребро квадратной грани (s) – это сторона квадрата. Помните, что у квадрата все стороны равны, поэтому измерьте любое ребро квадратной грани, а также измерьте апофему пирамиды.[23]
- Например: l = 3 см
- Например: s = 1 см
-
3
Найдите площадь квадратной грани. Для этого возведите в квадрат ребро этой грани (сторону квадрата), то есть умножьте значение s на себя.[24]
- Например: s2 = s х s = 1 х 1 = 1 см2
-
4
Вычислите общую площадь четырех треугольных граней. Вторая часть формулы включает суммарную площадь четырех треугольных граней. Согласно формуле 2ls, перемножьте 2, s и l. Так вы найдете суммарную площадь 4-х треугольных граней.[25]
- Например: 2 х s х l = 2 х 1 х 3 = 6 см2
-
5
Сложите полученные значения. Сложите площадь квадратной грани и общую площадь четырех треугольных граней, чтобы вычислить площадь поверхности пирамиды.[26]
- Например: s2 + 2sl = 1 + 6 = 7 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности конуса. Конус имеет круглое основание и закругленную боковую поверхность, которая сужается в вершине этой фигуры. Чтобы найти площадь поверхности конуса, нужно вычислить значения площади круглого основания и площади боковой поверхности, а затем сложить эти значения. Формула для вычисления площади поверхности конуса: SA = π*r2 + π*rl, где r – радиус круглого основания, l – образующая (расстояние между вершиной конуса и точкой, которая лежит на окружности круга), π ≈ 3,14.[27]
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус основания и высоту конуса. Радиус – это отрезок, соединяющий центр круга и точку, которая лежит на его окружности. Высота – это расстояние между центром круга и высотой конуса.[28]
- Например: r = 2 см
- Например: h = 4 см
-
3
Найдите значение образующей конуса (l). Образующая конуса является гипотенузой треугольника, поэтому воспользуйтесь теоремой Пифагора, чтобы вычислить образующую: l = √(r2 + h2), где r – радиус круглого основания, h – высота конуса.[29]
- Например: l = √(r2 + h2) = √(2 х 2 + 4 х 4) = √(4 + 16) = √(20) = 4,47 см
-
4
Вычислите площадь круглого основания. Площадь круга вычисляется по формуле S = π*r2. Измерив радиус, возведите его в квадрат (умножьте r на себя), а затем квадрат радиуса умножьте на число Пи.[30]
- Например: π*r2 = 3,14 x 2 x 2 = 12,56 см2
-
5
Вычислите площадь боковой поверхности конуса. Сделайте это по формуле S = π*rl, где r – радиус круга, l – образующая, которая найдена ранее.[31]
- Например: π*rl = 3,14 x 2 x 4,47 = 28,07 см
-
6
Сложите полученные значения, чтобы найти площадь поверхности конуса. Площадь поверхности конуса равна сумме площади круглого основания и площади боковой поверхности конуса.[32]
- Например: π*r2 + π*rl = 12,56 + 28,07 = 40,63 см2
Реклама
Что вам понадобится
- Линейка
- Ручка или карандаш
- Бумага
Об этой статье
Эту страницу просматривали 70 452 раза.
Была ли эта статья полезной?
Изучая варианты квартир для аренды или покупки, вы сравниваете не только такие параметры, как ремонт, локация, вид из окна, планировка, но и общую площадь. Как определяется этот показатель и на что он влияет?
Из чего состоит общая площадь квартиры
Общая площадь квартиры — это, согласно Жилищному кодексу, сумма площадей всех частей объекта недвижимости, за исключением балконов, лоджий, веранд и террас (до 1 марта 2005 года их учитывали). То есть в общую площадь входят комнаты, санузлы, кухня, кладовка, гардеробная, коридор, стены, перегородки.
Узнать, какая у квартиры общая площадь, можно в выписке из Единого государственного реестра прав на недвижимое имущество (ЕГРН). Еще один способ — сервис Росреестра. Достаточно ввести адрес объекта или его кадастровый номер.
На что влияет общая площадь
Значение общей площади квартиры используется для расчета налога на имущество, коммунальных начислений, компенсаций, для выделения долей и определения размера нового жилого помещения, предоставляемого взамен старого (например, аварийного). Общая площадь влияет на стоимость объекта недвижимости.
Что такое кадастровая стоимость квартиры и чем она отличается от рыночной
Как считать общую площадь
Для расчета общей площади нужно суммировать площадь всех входящих в нее помещений. Понадобятся рулетка и калькулятор. Если помещение прямоугольное или квадратное, длины двух стыкующихся между собой стен нужно умножить. Если одна стена — 5 метров, другая — 3 метра, общая площадь будет 15 кв. м.
Нестандартные по форме помещения нужно мысленно разделить на треугольники и прямоугольники. Посчитать их площадь можно по аналогии с предыдущим вариантом и сложить. Площадь стен можно высчитать, умножив толщину на длину.
Что такое жилая, полезная и приведенная площадь квартиры
К жилой площади относятся только те помещения, которые пригодны для проживания: гостиная, спальня, детская. Сюда не относятся: кухня, санузлы, коридор, кладовые и гардеробные.
В полезную площадь включают все используемые помещения. Сюда могут войти балкон и терраса с отоплением, которые не вошли в общую площадь.
Общая приведенная площадь нужна для определения стоимости объекта в договоре долевого участия. В ней учитывают общую площадь квартиры вместе с лоджиями, верандами, террасами, но считают их по понижающим коэффициентам:
- 0,5 — для лоджий
- 0,3 — для балконов
- 0,3 — для террас
- 1,0 — для веранд
То есть если в квартире общей площадью 42 кв. м. есть балкон площадью 3 кв. м., то общую приведенную площадь нужно рассчитывать так:
ОПП = общая площадь + площадь балкона * 0,3 = 42 + 3 * 0,3 = 42,9
Выбор пользователей Банки.ру
| Название | Мин. ставка | |
|---|---|---|
|
Ипотека для IT-специалистов на строящуюся квартиру Росбанк |
от 4.45% |
Подробнее Подать заявку |
|
Семейная ипотека Альфа-Банк |
от 5.6% |
Подробнее Подать заявку |
|
Семейная ипотека Газпромбанк |
от 5.45% |
Подробнее Подать заявку |
|
Семейная ипотека ВТБ |
от 5.5% |
Подробнее Подать заявку |
|
С господдержкой Банк «Открытие» |
от 7.3% |
Подробнее Подать заявку |
Площадь влияет на стоимость квартиры. Но важно также и то, как используются квадратные метры.
«Часто бывает, что квартира евроформата с кухней-гостиной площадью 38 кв. м пользуется бо́льшим спросом, чем классическая однушка 45 кв. м, где большой коридор», — говорит Виктор Зубик, основатель управляющей компании Smarent.
Почитайте о том, как эффективно использовать площадь, быстро и недорого преобразить квартиру, подготовить ее к продаже и получить больше денег.
Как подготовить квартиру к продаже и получить больше денег: советы экспертов