Методы Оптимизации. Даниил Меркулов. Сопряженная функция
Conjugate function
Сопряженная Функция
Пусть $f: mathbb{R}^n to mathbb{R}$.
Функция $f^*: mathbb{R}^n to mathbb{R}$ называется сопряжённой функцией к функции $f(x)$ и определена как
$$
f^(y) = suplimits_{x in mathbf{dom} ; f} left( langle y,xrangle — f(x)right).
$$
Область определения $f^$ это множество таких $y$, что супремум конечен.
Свойства сопряженной функции
- $f^*(y)$ — выпуклая функция как поточечный супремум функций выпуклых по $y$
- Неравенство Фенхеля — Юнга:
$$
f(x) + f^*(y) ge langle y,x rangle
$$ - Пусть функции $f(x). f^*(y), f^{}(x)$ определены на $mathbb{R}^n$. Тогда $f^{}(x) = f(x)$ тогда и только тогда, когда $f(x)$ — выпуклая функция.
- Частный случай сопряжения, когда функция дифференцируема называется преобразованием Лежандра. Пусть $f(x)$ — выпукла и дифференцируема, $mathbf{dom}; f = mathbb{R}^n$. Тогда $x^* = underset{x}{operatorname{argmin}} langle x,yrangle — f(x)$. В этом случае $y = nabla f(x^)$. Стало быть:
$$
f^(y) = langle nabla f(x^), x^ rangle — f(x^*)
$$
$$
f^*(y) = langle nabla f(z), z rangle — f(z), ;;;;;; y = nabla f(z), ;; z in mathbb{R}^n
$$
- Пусть $f(x,y) = f_1(x) + f_2(y)$, где $f_1, f_2$ — выпуклые функции, тогда
$$
f^(p,q) = f_1^(p) + f_2^*(q)
$$ - Пусть $f(x) le g(x);; forall x in X$. Пусть так же $f^(y), g^(y)$ определены на $Y$. Тогда $forall x in X, forall y in Y$
$$
f^(y) ge g^(y) ;;;;;; f^{}(y) le g^{}(y)
$$
Примеры
Схема поиска сопряженной функции, в целом, стандартна:
- Запись $f^*(y) = suplimits_{x in mathbf{dom} ; f} left( langle y,xrangle — f(x)right) = suplimits_{x in mathbf{dom} ; f} f(x,y)$
- Поиск тех значений $y$, при которых $ suplimits_{x in mathbf{dom} ; f} f(x,y)$ конечен. Эти значения составляют область определения сопряженной функции $f^*(y)$
- Поиск $x^$, при котором $f(x,y)$ достигает своего максимального значения как функция по $x$. $f^(y) = f(x^*, y)$
Пример 1
Найти $f^*(y)$, если $f(x) = ax + b$
Решение:
- Рассмотрим функцию, супремумом которой является сопряженная: $langle y,xrangle — f(x) = yx — ax — b$
- Построим область определения (т.е. те $y$, для которых $sup$ конечен). Это одна точка $y = a$
- Значит, $f^*(a) = -b$
Пример 2
Найти $f^*(y)$, если $f(x) = -log x, ;; xin mathbb{R}_{++}$
Решение:
- Рассмотрим функцию, супремумом которой является сопряженная: $langle y,xrangle — f(x) = yx + log x$.
- Эта функция не ограничена сверху при $y ge 0$. Значит, $mathbf{dom} ; f^* = {y < 0}$
- Её максимум достигается при $x = -1/y$. Значит, $f^*(y) = -log(-y) — 1$
Пример 3
Найти $f^*(y)$, если $f(x) = e^x$
Решение:
- Рассмотрим функцию, супремумом которой является сопряженная: $langle y,xrangle — f(x) = yx -e^x$.
- Эта функция не ограничена сверху при $y < 0$. Значит, $mathbf{dom} ; f^* = {y ge 0}$ (с нулем лучше поработать аккуратнее)
- Её максимум достигается при $x = log y$. Значит, $f^*(y) = y log y — y$. Полагая, что $0 log 0 = 0$.
Пример 4
Найти $f^*(y)$, если $f(x) = x log x, x neq 0, ;;; f(0) = 0, ;;; x in mathbb{R}_+$
Решение:
- Рассмотрим функцию, супремумом которой является сопряженная: $langle y,xrangle — f(x) =xy — x log x$.
- Эта функция ограничена сверху при всех $y$. Значит, $mathbf{dom} ; f^* = mathbb{R}$ (с нулем лучше поработать аккуратнее)
- Её максимум достигается при $x = e^{y-1}$. Значит, $f^*(y) = e^{y-1}$.
Пример 5
Найти $f^*(y)$, если $f(x) =frac{1}{2} x^T A x, ;;; A in mathbb{S}^n_{++}$
Решение:
- Рассмотрим функцию, супремумом которой является сопряженная: $langle y,xrangle — f(x) =y^Tx — frac{1}{2}x^TAx$.
- Эта функция ограничена сверху при всех $y$. Значит, $mathbf{dom} ; f^* = mathbb{R}$ (с нулем лучше поработать аккуратнее)
- Её максимум достигается при $x = A^{-1}y$. Значит, $f^*(y) = frac{1}{2}y^TA^{-1}y$.
Пример 6
Найти $f^*(y)$, если $f(x) =maxlimits_{i} x_i, ;;; x in mathbb{R}^n$
Решение:
- Рассмотрим функцию, супремумом которой является сопряженная: $langle y,xrangle — f(x) =y^Tx — maxlimits_{i}x_i$.
- Заметим, что если вектор $y$ имеет хотя бы одну отрицательную компоненту, то эта функция не ограничена по $x$.
- Пусть теперь $y succeq 0, ;;; 1^T y > 1$. $y notin mathbf{dom ; f^*(y)}$
- Пусть теперь $y succeq 0, ;;; 1^T y < 1$. $y notin mathbf{dom ; f^*(y)}$
- Остается только $y succeq 0, ;;; 1^T y = 1$. Тогда $x^Ty le maxlimits_i x_i$
- Значит, $f^*(y) = 0$.
Домашнее задание 8
- Найти $f^*(y)$, если $f(x) = -dfrac{1}{x}, ;; xin mathbb{R}_{++}$
- Найти $f^*(y)$, если $f(x) = -0,5 — log x, ;; x>0$
- Найти $f^*(y)$, если $f(x) = log left( sumlimits_{i=1}^n e^{x_i} right)$
- Найти $f^*(y)$, если $f(x) = — (a^2 — x^2)^{1/2}, ;;; |x| le a, ;;; a>0$
В какой области?
[math]u(x,y)=frac{x}{x^2+y^2}[/math]
Условия Коши — Римана:
[math]frac{partial u}{partial x}=frac{partial v}{partial y}hspace{14mm}(1)[/math]
[math]frac{partial u}{partial y}=-frac{partial v}{partial x}hspace{12mm}(2)[/math]
Имеем
[math]frac{partial u}{partial y}=-frac{2xy}{(x^2+y^2)^2}[/math]
Используя (2) получаем
[math]v(x,y)=-intfrac{-2xy}{(x^2+y^2)^2}dx=yintfrac{2x}{(x^2+y^2)^2}dx=-frac{y}{x^2+y^2}+k(y)[/math]
Находим производную [math]v[/math] по [math]y[/math]
[math]frac{partial v}{partial y}=frac{partial}{partial y}left(-frac{y}{x^2+y^2}+k(y)right)=frac{y^2-x^2}{(x^2+y^2)^2}+k'(y)[/math]
и производную [math]u[/math] по [math]x[/math]
[math]frac{partial u}{partial x}=frac{y^2-x^2}{(x^2+y^2)^2}[/math]
Из (1) получаем теперь
[math]frac{y^2-x^2}{(x^2+y^2)^2}=frac{y^2-x^2}{(x^2+y^2)^2}+k'(y)[/math]
Оттуда
[math]k'(y)=0[/math]
следовательно
[math]k(y)=C[/math]
Окончательно получаем
[math]v(x,y)=-frac{y}{x^2+y^2}+C[/math]
Дважды
непрерывно дифференцируемая функция
называетсягармонической
в
области D
плоскости
(Z),
если во всех точках этой области
выполняется равенство
(6).
Отметим,
что уравнение (6) называют уравнением
Лапласа
и коротко записывают
(7).
Две
функции u(x,y)
и v(x,y)
области D
плоскости
(Z)
называются сопряженными
гармоническими функциями
в этой области, если во всех точках этой
области выполняются условия Коши-Римана
,
.
Мы
покажем, что действительная и мнимая
части u(x,y),
v(x,y)
в аналитической области D
функции W
= f(Z)
являются сопряженными гармоническими
функциями. Так как у аналитической
функции действительная и мнимая части
удовлетворяют условиям Коши-Римана, то
нам достаточно доказать гармоничность
функций u(x,
y),
v(x,
y)
в области D.
Отметим,
что аналитическая в области D
функция f(Z)
имеет производную всех порядков (без
доказательства). Поэтому действительная
и мнимая части этой функции имеют в
области D
производные всех порядков по всем
переменным, и эти производные непрерывны.
Поэтому в частности будут существовать
все непрерывные производные 1го
и 2го
порядка. То есть эти функции будут дважды
непрерывно дифференцируемы.
Воспользуемся
теперь условием Коши-Римана
,
.
Продифференцируем
первое равенство по x,
а второе – по y,
и сложим. Получим
(так как смешанные производные, когда
непрерывны, равны). Следовательно,u-гармоническая
функция, аналогично доказывается, что
v
гармоническая функция, следовательно,
u
и v
– сопряженные гармонические функции.
Построение мнимой части аналитической функции по ее действительной части
Пусть
в некоторой области D
плоскости известна действительная
часть u(x,y)
аналитической функции. Требуется
построить ее мнимую часть v(x,y)
в этой области. Как мы знаем
;
.
Составим
выражение
.
Очевидно,,
так как(Лапласиян).
Следовательно, выражение
будет полным дифференциалом некоторой
функции.
Пусть
D
– это односвязная область, тогда
криволинейный интеграл
не будет зависеть от формы и пути,
соединяющего точки ()
и (x,y),
принадлежащие D
(лежащие в D)
и, следовательно, будет представлять
собой некоторую функцию
верхнего предела. Как мы знаем из теории
криволинейных интегралов, эта функция
дифференцируема в областиD,
и ее частные производные
и
соответственно равныp(x,y),
Q(x,y).
Следовательно, в области D
частные производные функций v(x,y)
и
совпадают. Поэтому эти функции могут
отличаться лишь на константу, следовательно,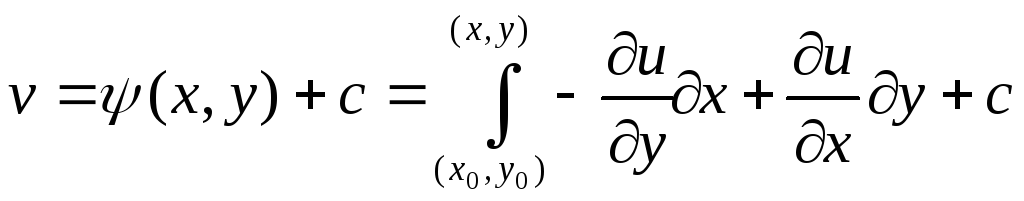
Как видно, мнимая часть аналитической
функции определяется с точностью до
постоянной.
Отметим,
что, если известно значение аналитической
функции W
= f(Z)
в
какой-нибудь одной точке
(
),
то мнимая частьv(x,y)
этой функции и, следовательно, сама
аналитическая функция f(Z)
определяется однозначно по действительной
части u(x,y).
В
случае многосвязной области D
криволинейный интеграл
Поэтому мнимая частьv(x,y)
будет также, вообще говоря, многозначной
функцией. Действительная часть по мнимой
части строится аналогичным образом.
Отметим,
что мнимая часть v(x,y)
функции
является действительной частью функции
.
Отметим, что мнимая часть по действительной
находится другим способом. Пишут
уравнения;
.
Интегрируют одно из равенств (первое
поx)
(1),
затем дифференцируют полученное
равенство по переменной y
.
Отсюда находяти подставляют его в (1).
Пример.
Построить
мнимую часть числа по действительной
;
.
Интегрируем по x.
.
Находим производную по y
и приравниваем
,
и теперь интегрируем
.
Таким
образом,
,
,
,
,
следовательно,;
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
$begingroup$
Is there a formula to find the adjoint of a function? For instance I have $T(alpha)=(x+iy)alpha$, how would I compute $T^*(alpha)$?
asked Nov 10, 2014 at 22:32
$endgroup$
$begingroup$
You want $langle Talpha, betarangle=langle alpha, T^*betarangle$. Here the left-hand side is $(x+iy)langle alpha,betarangle$, so in this example $T^*alpha=(x-iy)alpha$.
answered Nov 10, 2014 at 22:34
Kevin ArlinKevin Arlin
50.7k3 gold badges56 silver badges108 bronze badges
$endgroup$
0
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Содержание
- 1 Определения
- 2 Сопряженная функция
- 3 Вспомогательная лемма
- 3.1 Доказательство
- 4 Теорема Фенхеля-Моро
- 4.1 Доказательство
- 5 Приложения теории двойственности
- 5.1 Связь опорной и индикаторной функций множества
- 5.2 Евклидово расстояние от точки до множества
- 5.3 Расстояние по Хаусдорфу между двумя компактами
- 5.4 Опорная функция пересечения множеств
- 6 Список литературы
Определения
Пусть $$X$$ — гильбертово пространство.
Через $$overline{mathbb{R}}$$ будем обозначать расширенную вещественную прямую, $$overline{mathbb{R}} = mathbb{R} cup left{ -infty; +infty right}$$.
Будем рассматривать функции $$f: X to overline{mathbb{R}}$$.
Определение 1.
Надграфиком функции $$f$$ называется множество
[
text{epi} , f = left{ left( x,alpha right) in Xtimes mathbb{R} : f(x) leqslant alpharight}.
]
Определение 2.
Эффективным множеством функции $$f$$ называется множество
[
text{dom} , f = left{ x in X : f(x) lt +infty right}.
]
Определение 3.
Функция $$f$$ называется собственной, если $$text{dom} , f neq varnothing$$ и $$f(x) gt -infty ; forall x$$.
Определение 4.
Функция $$f$$ называется выпуклой, если ее надграфик $$text{epi} , f$$ является выпуклым множеством.
Определение 5.
Функция $$f$$ называется замкнутой, если ее надграфик $$text{epi} , f$$ замкнут.
Сопряженная функция
Определение.
Функцией, сопряженной к $$f$$, называется функция, определенная формулой
[
f^*(x^*) = underset{x in X}{text{sup}}left( leftlangle x^*,x rightrangle — f(x) right),
]
где $$x^*$$ — обозначение для аргумента сопряженной функции.
Из определения сопряженной функции вытекает неравенство Юнга-Фенхеля
[
f^*(x^*) + f(x) geqslant leftlangle x, x^* rightrangle ; forall x,x^* in X.
]
Вторая сопряженная функция $$f^{**}$$ определяется по формуле $$f^{**}=(f^*)^*$$.
Пример 1.
Для аффинной функции $$f(x) = leftlangle a,x rightrangle + b$$ сопряженная функция вычисляется по формуле
[
f^*(x^*) =
begin{cases}
-b, &x^* = a;\
+infty, &x^* neq a.
end{cases}
]
Пример 2.
Для произвольной выпуклой функции $$f$$ умножение на положительный скаляр $$lambda gt 0$$ определяется соотношением
[
left( lambda f right)(x) = lambda f(x), ; forall x in X.
]
Непосредственно вычисляется, что
[
left( lambda f right)^*(x^*) equiv lambda f^*(x^*/lambda), ; x^* in X.
]
Пример 3.
Пусть $$M$$ — евклидово пространство, и пусть $$f: M to mathbb{R}$$ — функция $$f(x) = leftlangle a,x rightrangle$$, где $$a in M$$. Поскольку
[
underset{xin M}{text{sup}}left{ leftlangle s,x rightrangle — leftlangle a,x rightrangle right} = underset{xin M}{text{sup}} leftlangle s-a,x rightrangle =
begin{cases}
0, &s = a;\
+infty, &s neq a.
end{cases}
]
для всех $$s in M$$, то сопряженная функция $$f^*$$ — индикаторная функция $$delta_left{ a right}$$ одноэлементного множества $$left{ a right}$$.
Вспомогательная лемма
Лемма.
Пусть функция $$f$$ — выпуклая, замкнутая, собственная. Тогда $$f^*$$ — также собственная функция.
Доказательство
Докажем, что $$f^∗(x^∗) gt -infty$$ $$forall x^∗ in X$$. Возьмем $$x_0 in text{dom} , f neq varnothing$$. Тогда $$f^∗(x^∗) geqslant leftlangle x_0, x^∗rightrangle − f(x_0) gt -infty$$, так как $$f(x_0) lt +infty$$.
Остается доказать существование вектора $$y^∗ in X$$, для которого $$f^∗(y^∗) lt +infty$$.
Очевидно, точка $$(x_0, f(x_0) − 1)$$ не принадлежит замкнутому выпуклому множеству $$text{epi} , f$$. Следовательно, по теореме об отделимости ее можно строго отделить от выпуклого замкнутого множества $$text{epi} , f$$. Поэтому существуют $$y^∗ in X$$ и $$beta in mathbb{R}$$ такие, что
begin{equation}
label{1}
underset{(x,alpha) in text{epi} , f}{text{sup}}left{ betaalpha + leftlangle y^*,x rightrangle right} lt beta (f(x_0) — 1) + leftlangle y^*, x_0 rightrangle.
end{equation}
Докажем, что $$beta lt 0$$. Действительно, предположим обратное. Случай $$beta gt 0$$ невозможен, так как $$(x_0, alpha) in text{epi} , f;$$ $$forall alpha
geqslant f(x_0) neq +infty$$ и, значит, при $$beta gt 0$$ имеет место $$underset{(x_0,alpha) in text{epi} , f}{text{sup}}beta alpha = +infty$$, что противоречит неравенству ($$ref{1}$$).
Пусть теперь $$beta = 0$$. Тогда
[
underset{(x,alpha) in text{epi} , f}{text{sup}} leftlangle y^*, x rightrangle lt leftlangle y^*, x_0 rightrangle,
] хотя
[
(x_0, f(x_0)) in text{epi} , f implies underset{(x,alpha) in text{epi} , f}{text{sup}} leftlangle y^*, x rightrangle geqslant leftlangle y^*, x_0 rightrangle.
]
Полученное противоречие доказывает, что $$beta lt 0$$. Поэтому, в силу положительной однородности неравенства ($$ref{1}$$) по переменной $$(y^∗, beta)$$,
не теряя общности, будем считать, что $$beta = -1$$.
В силу ($$ref{1}$$) имеем
[
f^*(y^*) = underset{x}{text{sup}} left{ -f(x) + leftlangle y^*,x rightrangle right} = underset{(x,alpha) in text{epi} , f}{text{sup}} left{ -alpha + leftlangle y^*,x rightrangle right} lt -(f(x_0) — 1) + leftlangle y^*, x_0 rightrangle implies f^*(y^*) lt +infty.
]
Значит, функция $$f^*$$ является собственной.$$;;blacksquare$$
Теорема Фенхеля-Моро
Теорема.
Пусть функция $$f$$ — выпуклая, замкнутая, собственная. Тогда $$f^{**} = f$$.
Доказательство
Покажем, что $$f^{**} leqslant f$$. В силу неравенства Юнга-Фенхеля $$forall x in X$$ имеем
[
f(x) geqslant leftlangle x, x^* rightrangle — f^*(x^*) ; forall x^* in X implies f(x) geqslant underset{x^*}{text{sup}}left{ leftlangle x, x^* rightrangle — f^*(x^*) right} = f^{**}(x).
]
Остается показать, что $$f^{**} geqslant f$$.
Предположим противное. Тогда существует $$x_0 in X$$, для которого $$f^{∗∗}(x_0) lt f(x_0)$$. Поэтому точка $$(x_0, f^{∗∗}(x_0))$$ строго отделима от выпуклого замкнутого множества $$text{epi} , f$$. Значит, существуют $$y^∗ in X$$ и $$beta in mathbb{R}$$ такие, что
begin{equation}
label{2}
beta f^{**}(x_0) + leftlangle y^*,x_0 rightrangle gt underset{(y,alpha) in text{epi} , f}{text{sup}}left( betaalpha + leftlangle y^*,y rightrangle right).
end{equation}
Докажем, что $$beta lt 0$$. Действительно, случай $$beta gt 0$$ невозможен, что обосновывается так же, как и при доказательстве вспомогательной леммы, с учетом того, что $$text{dom} , f neq varnothing$$.
Пусть теперь $$beta = 0$$. Тогда
[
gamma = leftlangle y^*, x_0 rightrangle — underset{y in text{dom} , f}{text{sup}} leftlangle y^*, y rightrangle gt 0.
]
В силу леммы функция $$f^*$$ является собственной. Поэтому существует $$y^*_1 in text{dom} , f^* neq varnothing$$. Для $$t gt 0$$ имеем
[
f^*(y^*_1+ty^*) = underset{y in text{dom} , f}{text{sup}} left( leftlangle y^*_1 + ty^*, y rightrangle — f(y) right) leqslant underset{y in text{dom} , f}{text{sup}} left( leftlangle y^*_1, y rightrangle — f(y) right) + t underset{y in text{dom} , f}{text{sup}} leftlangle y^*, y rightrangle = f^*(y^*_1) + t underset{y in text{dom} , f}{text{sup}} leftlangle y^*, y rightrangle.
]
Отсюда в силу неравенства Юнга-Фенхеля для функции $$f^*$$ вытекает
[
f^{**}(x_0) geqslant leftlangle y^*_1 + ty^*, x_0 rightrangle — f^*(y^*_1 + ty^*) geqslant leftlangle y^*_1, x_0 rightrangle + t leftlangle y^*, x_0 rightrangle — f^*(y^*_1) — t underset{y in text{dom} , f}{text{sup}} leftlangle y^*, y rightrangle = leftlangle y^*_1, x_0 rightrangle — f^*(y^*_1) + tgamma, ;forall tgt 0.
]
Получили противоречие, так как $$gamma gt 0$$ и, значит, при больших $$t$$ значение $$tgamma$$ может быть сделано как угодно большим и, следовательно, при достаточно больших $$t gt 0$$ последнее неравенство выполняться не может.
Таким образом, доказано, что $$beta lt 0$$; значит, не теряя общности рассуждений, будем считать, что $$beta = -1$$. В силу неравенства ($$ref{2}$$) имеем
[
-f^{**}(x_0) + leftlangle y^*, x_0 rightrangle gt underset{y in text{dom} , f}{text{sup}} left( -f(y) + leftlangle y^*,y rightrangleright) = f^*(y^*),
]
откуда
[
leftlangle y^*, x_0 rightrangle gt f^*(y^*) + f^{**}(x_0),
]
что противоречит неравенству Юнга–Фенхеля для функции $$f^∗$$. Полученное противоречие доказывает, что $$f^{**} geqslant f$$ и, значит, $$f^{∗∗} = f$$. $$;;blacksquare$$
Приложения теории двойственности
Связь опорной и индикаторной функций множества
Определим опорную функцию множества $$A subset X$$ на $$X$$ соотношением
begin{equation}
label{3}
rho(x^*|A) = underset{y in A}{text{sup}} leftlangle x^*, y rightrangle, x^* in X.
end{equation}
Введем индикаторную функцию следующим образом
[
delta_A(x) =
begin{cases}
0, &x in A;\
+infty, &x notin A.
end{cases}
]
Предложение 1. Пусть $$delta_A(cdot)$$ — индикаторная функция выпуклого замкнутого множества $$A$$. Тогда $$rho^*(cdot|A) = delta_A(cdot)$$.
Доказательство
Функция $$delta_A$$ является выпуклой, замкнутой и собственной. Поэтому по теореме Фенхеля-Моро $$delta_A^{**} = delta_A$$. Кроме того, для произвольного $$x^*$$ имеем
[
delta_A^*(x^*) = underset{x}{text{sup}}left{ leftlangle x, x^* rightrangle — delta_A(x)right} = underset{x in A}{text{sup}} left{ leftlangle x, x^* rightrangle right} = rho(x^*| A).
]
Следовательно, $$delta_A = delta_A^{**} = rho^*(cdot|A)$$. $$;;blacksquare$$
Евклидово расстояние от точки до множества
Для евклидова расстояния
$$d(x,ℳ) = underset{y in ℳ}{text{min}} left| x -y right|$$ от точки $$x$$ до множества $$ℳ$$, $$ℳ in text{conv} ;mathbb{R}^n$$ — выпуклый компакт, справедливы следующие соотношения двойственности
[
d(x,ℳ) = underset{left| l right| leqslant 1}{text{max}} left{ left( l,x right) — rholeft( l|ℳ right) right},
]
[
d^2(x,ℳ) = underset{l}{text{max}} left{ left( l,x right) — rholeft( l|ℳ right) — frac{1}{4} left( l,l right) right},
]
где $$rholeft( l|ℳ right)$$ — опорная функция множества $$ℳ$$.
Покажем справедливость второго соотношения.
Имеем функцию $$varphi(x) = d^2(x,ℳ) = underset{y in ℳ}{text{min}}left( x-y, x-y right)$$. Поскольку функция $$varphi$$ является выпуклой, замкнутой и собственной, по теореме Фенхеля-Моро $$varphi^{**} = varphi$$.
Найдем сопряженную функцию к $$varphi(x)$$
[
varphi^*(l) = underset{x}{text{sup}}left{ left( l,x right) — varphi(x) right} = underset{x}{text{sup}};underset{y in ℳ}{text{max}} left{ left( l,x right) — left( x-y,x-y right)right} = underset{y in ℳ}{text{max}} ;underset{x}{text{sup}} left{ left( l,x right) — left( x-y,x-y right)right} = underset{y in ℳ}{text{max}} left(left( l, frac{l}{2} + y right) — frac{1}{4}left( l,l right)right)= rholeft( l|ℳ right) + frac{1}{4}left( l,l right),
]
откуда, очевидно, следует второе соотношение. $$;;blacksquare$$
Расстояние по Хаусдорфу между двумя компактами
Пусть $$X = mathbb{R}^n$$, $$A$$ и $$B$$ — выпуклые компакты.
Лемма 1.
[
hleft( A, B right) = underset{left| l right| leqslant 1}{text{max}}left| rholeft( l|A right) — rholeft( l|B right)right|,
]
где $$hleft( A, B right)$$ — расстояние по Хаусдорфу между множествами $$A$$ и $$B$$.
Замечание 1. $$dleft( x, B right) = hleft( x, B right) = underset{left| l right| leqslant 1}{text{max}}left| left( l,x right) — rholeft( l|B right)right|$$.
Опорная функция пересечения множеств
Приведем три вспомогательных утверждения без доказательства $$^{[1]}$$.
Лемма 2. Для любых функций $$f_1,{…},f_n$$ имеет место
[
left( f_1 oplus f_2 oplus {…} oplus f_n right)^* = f_1^* + f_2^* + {…} + f_n^*.
]
Предложение 2. Пусть $$f$$ — выпуклая собственная функция и $$X = mathbb{R}^n$$. Тогда ее замыкание $$text{cl} , f$$ также является собственной функцией.
Предложение 3. Для выпуклой функции $$f$$ имеет место
[
(text{cl} , f)^* = f^*.
]
Определим опорную функцию соотношением ($$ref{3}$$).
Предложение 4. Пусть $$A, B$$ — выпуклые ограниченные подмножества $$mathbb{R}^n$$ и $$text{int} , A cap text{int} , B neq varnothing$$. Тогда
[
rholeft( cdot | Acap B right) = text{cl}left( rholeft( cdot |A right) oplus rholeft( cdot |B right) right).
]
Доказательство
Для ограниченного множества опорная функция выпукла и непрерывна на $$mathbb{R}^n$$. Поэтому в силу леммы 2 и предложения 1 для произвольного $$x$$ имеем
[
left( rholeft( cdot |A right) oplus rholeft( cdot |B right) right)^*(x) = rho^*(x| A) + rho^*(x| B) =
delta_A(x) + delta_B(x) = delta_{Acap B}(x) = rho^*( x | Acap B ),
]
откуда в силу предложения 3 имеем
begin{equation}
label{4}
(text{cl} , varphi)^* = rho^*( cdot | Acap B ),
end{equation}
где функция $$varphi$$ определяется соотношением $$varphi(x) = left( rholeft( cdot |A right) oplus rholeft( cdot |B right) right)(x)$$. Здесь мы использовали легко проверяемое свойство индикаторных функций, а именно, что для любых двух множеств $$A, B$$ выполняется $$delta_A + delta_B = delta_{Acap B}$$. Функция $$varphi$$ является собственной, так как она сама не равна тождественно $$+infty$$, и в силу доказанного выше сопряженная к ней функция также не равна тождественно $$+infty$$. Поэтому в силу предложения 2 функция $$text{cl} , varphi$$ также является собственной. Применяя к равенству ($$ref{4}$$) теорему Фенхеля-Моро, имеем $$rholeft( cdot | Acap B right) = text{cl}left( rholeft( cdot |A right) oplus rholeft( cdot |B right) right).$$ $$;;blacksquare$$
Список литературы
- Арутюнов А. В. «Лекции по выпуклому и многозначному анализу», М.: ФИЗМАТЛИТ, 2014.
- Востриков И.В. «Лекции по динамическому программированию и процессам управления», 2022.


