Синус 5пи на 4 как найти

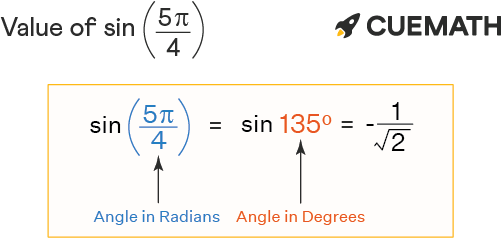
The value of sin 5pi/4 is -0.7071067. . .. Sin 5pi/4 radians in degrees is written as sin ((5π/4) × 180°/π), i.e., sin (225°). In this article, we will discuss the methods to find the value of sin 5pi/4 with examples.

Sin 5pi/4: -(1/√2)
Sin 5pi/4 in decimal: -0.7071067. . .
Sin (-5pi/4): 0.7071067. . . or 1/√2
Sin 5pi/4 in degrees: sin (225°)

What is the Value of Sin 5pi/4?

The value of sin 5pi/4 in decimal is -0.707106781. . .. Sin 5pi/4 can also be expressed using the equivalent of the given angle (5pi/4) in degrees (225°).

We know, using radian to degree conversion, θ in degrees = θ in radians × (180°/pi)
⇒ 5pi/4 radians = 5pi/4 × (180°/pi) = 225° or 225 degrees
∴ sin 5pi/4 = sin 5π/4 = sin(225°) = -(1/√2) or -0.7071067. . .

Explanation:

For sin 5pi/4, the angle 5pi/4 lies between pi and 3pi/2 (Third Quadrant). Since sine function is negative in the third quadrant, thus sin 5pi/4 value = -(1/√2) or -0.7071067. . .
Since the sine function is a periodic function, we can represent sin 5pi/4 as, sin 5pi/4 = sin(5pi/4 + n × 2pi), n ∈ Z.
⇒ sin 5pi/4 = sin 13pi/4 = sin 21pi/4 , and so on.
Note: Since, sine is an odd function, the value of sin(-5pi/4) = -sin(5pi/4).

Methods to Find Value of Sin 5pi/4

The sine function is negative in the 3rd quadrant. The value of sin 5pi/4 is given as -0.70710. . .. We can find the value of sin 5pi/4 by:

Using Trigonometric Functions
Using Unit Circle

Sin 5pi/4 in Terms of Trigonometric Functions

Using trigonometry formulas, we can represent the sin 5pi/4 as:

± √(1-cos²(5pi/4))
± tan(5pi/4)/√(1 + tan²(5pi/4))
± 1/√(1 + cot²(5pi/4))
± √(sec²(5pi/4) — 1)/sec(5pi/4)
1/cosec(5pi/4)

Note: Since 5pi/4 lies in the 3rd Quadrant, the final value of sin 5pi/4 will be negative.

We can use trigonometric identities to represent sin 5pi/4 as,

sin(pi — 5pi/4) = sin(-pi/4)
-sin(pi + 5pi/4) = -sin 9pi/4
cos(pi/2 — 5pi/4) = cos(-3pi/4)
-cos(pi/2 + 5pi/4) = -cos 7pi/4

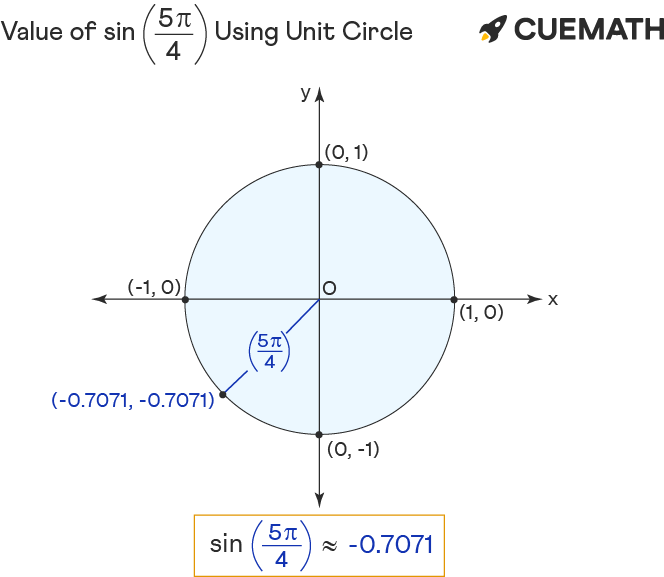
Sin 5pi/4 Using Unit Circle

To find the value of sin 5π/4 using the unit circle:

Rotate ‘r’ anticlockwise to form 5pi/4 angle with the positive x-axis.
The sin of 5pi/4 equals the y-coordinate(-0.7071) of the point of intersection (-0.7071, -0.7071) of unit circle and r.

Hence the value of sin 5pi/4 = y = -0.7071 (approx)

☛ Also Check:

sin 2pi/3
cos 2pi/7
cos 7pi/3
sec 7pi/4
sin pi/12
tan 3pi/8

FAQs on Sin 5pi/4

What is Sin 5pi/4?

Sin 5pi/4 is the value of sine trigonometric function for an angle equal to 5pi/4 radians. The value of sin 5pi/4 is -(1/√2) or -0.7071 (approx).

What is the Value of Sin 5pi/4 in Terms of Sec 5pi/4?

Since the sine function can be represented using the secant function, we can write sin 5pi/4 as √(sec²(5pi/4) — 1)/sec 5pi/4. The value of sec 5pi/4 is equal to -1.414213.

How to Find Sin 5pi/4 in Terms of Other Trigonometric Functions?

Using trigonometry formula, the value of sin 5π/4 can be given in terms of other trigonometric functions as:

± √(1-cos²(5pi/4))
± tan(5pi/4)/√(1 + tan²(5pi/4))
± 1/√(1 + cot²(5pi/4))
± √(sec²(5pi/4) — 1)/sec(5pi/4)
1/cosec(5pi/4)

☛ Also check: trigonometric table

What is the Value of Sin 5pi/4 in Terms of Tan 5pi/4?

We know, using trig identities, we can write sin 5pi/4 as -tan(5pi/4)/√(1 + tan²(5pi/4)). Here, the value of tan 5pi/4 is equal to 1.

How to Find the Value of Sin 5pi/4?

The value of sin 5pi/4 can be calculated by constructing an angle of 5π/4 radians with the x-axis, and then finding the coordinates of the corresponding point (-0.7071, -0.7071) on the unit circle. The value of sin 5pi/4 is equal to the y-coordinate (-0.7071). ∴ sin 5pi/4 = -0.7071.

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

x^{2}-x-6=0
-x+3gt 2x+1
линия:(1,:2),:(3,:1)
f(x)=x^3
доказывать:tan^2(x)-sin^2(x)=tan^2(x)sin^2(x)
frac{d}{dx}(frac{3x+9}{2-x})
(sin^2(theta))’
sin(120)
lim _{xto 0}(xln (x))
int e^xcos (x)dx
int_{0}^{pi}sin(x)dx
sum_{n=0}^{infty}frac{3}{2^n}
Показать больше

Описание

Поэтапное решение задач по алгебре, тригонометрии и исчислению

step-by-step

sinleft(frac{5pi}{4}right)

Блог-сообщения, имеющие отношение к Symbolab

My Notebook, the Symbolab way

Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

1) Вычислитеа) sin 5 п/4=б) tg 7 п/6=в) cos п/6 — сеп 1) Вычислите

а) sin 5 п/4=

б) tg 7 п/6=

в) cos п/6 — сеп п/4=

г) tg 3 п/4 x cos 3 п/4+сtg (-п/6) х sin п/6=

д) sin 510-sin270 ctg270=

2) Упростите выражение

сos^2 — sin^2t/tg (-t) ctgt

3) Решите уравнение:

a) sint=1/2

б) sin (п/2 + t) = — корень из 3/2

4) Известно, что ctg (t-п) = — 3/4 и п/2 п/2

Найдите:

a) cos (3 п/2 — t)

б) cos (п + t)

5) Расположите в порядке возростания:

a=cos6

b=cos7

c=sin6

d=sin 4

Найдите правильный ответ на вопрос ✅ «1) Вычислитеа) sin 5 п/4=б) tg 7 п/6=в) cos п/6 — сеп 1) Вычислите а) sin 5 п/4= б) tg 7 п/6= в) cos п/6 — сеп п/4= г) tg 3 п/4 x cos 3 …» по предмету 📘 Алгебра, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.

Смотреть другие ответы

Главная » Алгебра » 1) Вычислитеа) sin 5 п/4=б) tg 7 п/6=в) cos п/6 — сеп 1) Вычислите а) sin 5 п/4= б) tg 7 п/6= в) cos п/6 — сеп п/4= г) tg 3 п/4 x cos 3 п/4+сtg (-п/6) х sin п/6= д) sin 510-sin270 ctg270=

Источник

1 ) sin 5 * π/4 = sin (4 * π/4 + π/4) = sin (π + π/4) = — sin π/4 = -√2/2;

2 ) cos (- 7 * π/3) = cos 7 * π/3 = cos (6 * π/3 + π/3) = cos (2 * π + π/3) = cos π/3 = 1/2;

3 ) tg 5 * π/3 = tg (6 * π/3 — π/3) = tg (2 * π — π/3) = tg (- π/3) = — tg π/3 = — √3;

4 ) sin 40 * π/3 = sin ( 39 * π/3 + π/3) = sin (13 * π + π/3) = sin (π +π/3) = — sin π/3 = — √3/2;

5) ctg 1 * π/6 = ctg π/6 = √3.

Ответ : 1 ) -√2/2; 2 ) 1/2; 3 ) — √3; 4 ) — √3/2; 5 ) √3.

Источник

Задачи

$sin{fraction{5 pi}{4}} $

-frac{sqrt{2}}{2}approx -0.707106781

Tick mark Image

Подобные задачи из результатов поиска в Интернете

sin(pi +frac{pi }{4})=sin(pi )cos(frac{pi }{4})+sin(frac{pi }{4})cos(pi )

Use sin(x+y)=sin(x)cos(y)+sin(y)cos(x) where x=pi and y=frac{pi }{4} to obtain the result.

0cos(frac{pi }{4})+sin(frac{pi }{4})cos(pi )

Get the value of sin(pi ) from trigonometric values table.

0times left(frac{sqrt{2}}{2}right)+sin(frac{pi }{4})cos(pi )

Get the value of cos(frac{pi }{4}) from trigonometric values table.

0times left(frac{sqrt{2}}{2}right)+frac{sqrt{2}}{2}cos(pi )

Get the value of sin(frac{pi }{4}) from trigonometric values table.

0times left(frac{sqrt{2}}{2}right)+frac{sqrt{2}}{2}left(-1right)

Get the value of cos(pi ) from trigonometric values table.

-frac{sqrt{2}}{2}

Выполните арифметические операции.

Примеры

Источник

What is the Value of Sin 5pi/4?

Methods to Find Value of Sin 5pi/4

Sin 5pi/4 in Terms of Trigonometric Functions

Sin 5pi/4 Using Unit Circle

FAQs on Sin 5pi/4

What is Sin 5pi/4?

What is the Value of Sin 5pi/4 in Terms of Sec 5pi/4?

How to Find Sin 5pi/4 in Terms of Other Trigonometric Functions?

What is the Value of Sin 5pi/4 in Terms of Tan 5pi/4?

How to Find the Value of Sin 5pi/4?

Номер Строки

Задачи

Подобные задачи из результатов поиска в Интернете

Поделиться

Примеры

Не пропустите также: