Сила притяжения как найти работу

1. Работа силы тяжести, потенциальная энергия гравитационного взаимодействия. Вторая и третья космические скорости.

Работа силы
тяжести

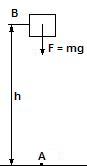
Работу силы тяжести
рассмотрим на примере. Пусть тело падает
под действием силы тяжести F = mg с высоты
h из точки B в точку A. Формула работы
силы:

A = |F||S|cosα

Подставим значения
для нашего примера:

A = mgh

косинус альфа
здесь равен единице.

 Закон, описывающий
эти силы, открытый И. Ньютоном и
опубликованный в 1687 году, получил
название закона
всемирного тяготения:
две материальные точки притягиваются
с силами, пропорциональными произведению
масс этих точек, обратно пропорциональными
квадрату расстояния между точками и
направленными вдоль прямой, соединяющей
эти точки:

 Так как сила
является векторной величиной, то и
формуле, определяющей силу притяжения,
следует придать векторную форму.

 Для этого введем
вектор r12, соединяющий точки 1 и 2 (рис.
112).

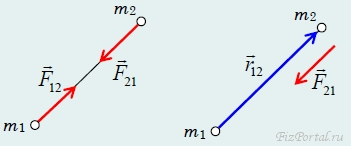
Тогда сила
притяжения, действующая на второе тело,
может быть записана в виде

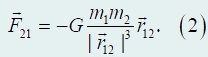
 В формулах (1),
(2) коэффициент пропорциональности в
называется гравитационной постоянной.
Значение этой величины не может быть
найдено из других физических законов
и определено экспериментально. Численное
значение гравитационной постоянной
зависит от выбора системы единиц, так,
в СИ оно равно:

 Впервые
гравитационную постоянную экспериментально
измерил английский физик Генри Кавендиш.
В 1798 году он сконструировал крутильные
весы и измерил с их помощью силу притяжения
двух сфер, подтвердив закон всемирного
тяготения; определил гравитационную
постоянную, массу и среднюю плотность
Земли.

 Вопрос о природе
гравитационного взаимодействия является
чрезвычайно сложным. Сам И. Ньютон на
этот вопрос давал лаконичный ответ:
«Гипотез не измышляю», тем самым
отказываясь даже рассуждать на эту
тему. Достаточно того, что закон всемирного
тяготения с высокой степенью точности
количественно описывает гравитационное
взаимодействие. Громадные успехи
ньютоновской механики почти на два
столетия предопределили подобный подход
ко всей физической науке, не только
механике: достаточно открыть, найти
законы, правильно описывающие физические
явления, и научиться применять их к
количественному описанию этих явлений.

 Так, в изучении
гравитации считалось, что непонятным
образом одно тело может оказывать
влияние на другое, причем это влияние
передается мгновенно, то есть изменение
положения одного из тел мгновенно
изменяет силы, действующие на другие
тела, независимо от того, на каком
расстоянии эти тела расположены. Этот
общий подход к характеру физических
взаимодействий получил название теории
дальнодействия. Подобный взгляд на
взаимодействия тел был распространен
на электрические и магнитные явления,
изучение которых активно проводилось
в течение XVIII − XIX веков. Лишь в 30-х годах
XIX века английским физиком М. Фарадеем
для электромагнитных взаимодействий
были сформулированы основные положения
альтернативной теории близкодействия:
для передачи взаимодействия обязательно
необходим «посредник», некая среда,
передающая эти взаимодействия; сами
взаимодействия не могут передаваться
мгновенно, требуется определенное время
для того, чтобы изменение в положении
одного из тел «почувствовали» другие
взаимодействующие тела. В начале XX
столетия немецкий физик А. Эйнштейн
построил новую теорию гравитации −
общую теорию относительности. В рамках
этой теории гравитационные взаимодействия
объясняются следующим образом: каждое
тело, обладающее массой, изменяет
свойства пространства времени вокруг
себя (создает гравитационное поле),
другие же тела движутся в этом измененном
пространстве времени (в гравитационном
поле), что приводит к появлению наблюдаемых
сил, ускорению и т. д. С этой точки зрения
выражение «находится в гравитационном
поле» эквивалентно выражению «действуют
гравитационные силы».

 К этим вопросам
мы обратимся позднее при изучении
электромагнитного поля.

 Самое поразительное
в явлении тяготения заключается в том,
что гравитационные силы пропорциональны
массам тел. Действительно, ранее мы
говорили о массе как о мере инертности
тела. Оказалось, что масса также определяет
принципиально иное свойство материальных
тел − является мерой способности
участвовать в гравитационных
взаимодействиях. Поэтому можно говорить
о двух массах − инерционной и
гравитационной. Закон всемирного
тяготения утверждает, что эти массы
пропорциональны друг другу. Подтверждением
этого утверждения является давно
известный факт: все тела падают на землю
с одинаковым ускорением. Экспериментально
с высокой точностью пропорциональность
гравитационной и инерционной масс была
подтверждена в работах венгерского
физика Лоранда Этвеша. Впоследствии
пропорциональность инерционной и
гравитационной масс легла в основу
новой теории гравитации − общей теории
относительности А. Эйнштейна.

 В заключение
отметим, что закон всемирного тяготения
может быть положен в основу определения
единицы массы (конечно, гравитационной).
Например: два точечных тела единичной
гравитационной массы, находящиеся на
расстоянии в один метр, притягиваются
с силой в один Н.

 Задание для
самостоятельной работы: определите
массы двух точечных тел, находящихся
на расстоянии 1,0 м друг от друга и
взаимодействующих с силой 1,0 Н.

 Для гравитационных
сил справедлив принцип суперпозиции:
сила, действующая на точечное тело со
стороны нескольких других тел, равна
сумме сил, действующих со стороны каждого
тела. Это утверждение также является
обобщением экспериментальных данных
и фундаментальным свойством гравитационных
взаимодействий.

 Посмотрим на
принцип суперпозиции с математической
точки зрения: по закону всемирного
тяготения сила гравитационного
взаимодействия пропорциональна массе
этих тела. Если бы зависимость от масс
была нелинейна, то и принцип суперпозиции
не выполнялся бы. Действительно, пусть
тело массой mo взаимодействует с двумя
точечными телами массами m1 и m2. Поместим
мысленно тела m1 и m2 в одну точку (тогда
их можно рассматривать как одно тело).
В этом случае сила, действующее на тело
mo, равна:

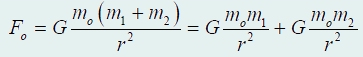
представлена в
виде суммы сил, действующих со стороны
двух тел − m1 и m2.

 В случае нелинейной
зависимости между силой и массой принцип
суперпозиции был бы несправедлив.

Закон всемирного
тяготения для точечных тел и принцип
суперпозиции позволяют, в принципе,
вычислять силы взаимодействия между
телами конечных размеров (рис. 113).

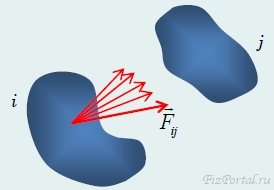
рис. 113

 Для этого
необходимо мысленно разбить каждое из
тел на малые участки, каждый из которых
можно рассматривать как материальную
точку. Затем вычислить двойную сумму
сил взаимодействия между всеми парами
точек. В общем случае вычисление такой
суммы является сложной математической
задачей.

 Подчеркнем, что
сила взаимодействия между телами
конечных размеров вычисляется только
методом разбиения тел и последующего
суммирования. Ошибочно утверждение о
том, что сила взаимодействия между
телами может быть вычислена как сила
взаимодействия, равная силе взаимодействия
точечных тел, расположенных в центрах
масс. Для обоснования этого утверждения
рассмотрим простой пример.

 Пусть одно из
взаимодействующих тел можно считать
материальной точкой массы mo, а второе
тело представимо в виде двух материальных
точек равных масс m, расположенных на
фиксированном расстоянии а друг от
друга (рис. 114).

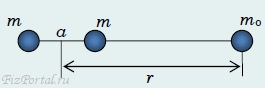
рис. 114

 Все материальные
точки расположены на одной прямой,
расстояние от первого тела до центра
второго обозначим r. Сила притяжения,
действующая на тело mo, равна:

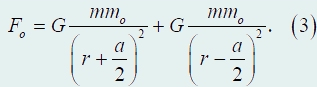
 Если же соединить
материальные точки, составляющие второе
тело, в одну массой 2m, расположенную в
центре тела, то сила взаимодействия
будет равна:

что отличается
от выражения (3). Только при r >> а
выражение (3) переходит в формулу (2).
Заметьте, что в этом случае второе тело
следует рассматривать как материальную
точку.

Первой космической
скорости недостаточно для того, чтобы
тело могло выйти из сферы земного
притяжения. Необходимая для этого
скорость называется второй космической.
Второй
космической
(или параболической)
скоростью
v₂
называют ту наименьшую скорость, которую
надо сообщить телу, чтобы оно могло
преодолеть притяжение Земли и превратиться
в спутник Солнца, т. е. чтобы его орбита
в поле тяготения Земли стала параболической.
Для того чтобы тело (при отсутствии
со­противления среды) могло преодолеть
земное притяжение и уйти в космическое
пространство, необходимо, чтобы его
кинетическая энергия была равна работе,
совер­шаемой против сил тяготения:

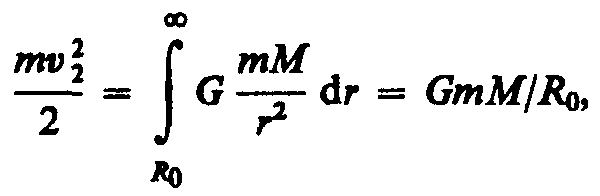
откуда

Третьей космической
скоростью
v₃
называют скорость, которую необходимо
сооб­щить телу на Земле, чтобы оно
покинуло пределы Солнечной системы,
преодолев притяжение Солнца. Третья
космическая скорость v₃=16,7
км/с. Сообщение телам таких больших
начальных скоростей является сложной
технической задачей. Ее первое
теоретическое осмысление начато К. Э.
Циолковским, им была выведена уже
рассмот­ренная нами формула (10.3),
позволяющая рассчитывать скорость
ракет.

Впервые космические
скорости были достигнуты в СССР: первая
— при запуске первого искусственного
спутника Земли в 1957 г., вторая — при
запуске ракеты в 1959 г. После исторического
полета Ю. А. Гагарина в 1961 г. начинается
бурное развитие космонавтики.

Движение
в неинерциальных системах отсчета

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Подробности

Обновлено 30.05.2018 20:11

Просмотров: 707

Задачи по физике — это просто!

Вспомним

Формулы, по которым можно вычислить работу силы:

Не забываем, что решать задачи надо всегда в системе СИ!

А теперь к задачам!

Задача 2

Какую работу совершит сила тяжести при падении мяча массой 0,5 кг на землю из состояния покоя с высоты 5 метров?

Задача 4

Скорость падающего кирпича массой 2 кг на некотором отрезке пути изменилась от 3 м/с до 6 м/с. Определить работу, совершенную силой тяжести.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Совсем недавно, мы
изучили работу силы. Напомним, что работа силы равна произведению модуля силы,
модуля перемещения и косинуса угла между направлениями силы и перемещения:

Рассмотрим теперь частный
случай — работу силы тяжести при перемещении тела с высоты h₁
на высоту h₂.

Первый случай — это
падение тела вертикально вниз.

В этом случае,
перемещение, конечно же, будет равно

Сила тяжести, как мы
знаем, равна

.

Поскольку сила тяжести
направлена вертикально вниз, как и перемещение, косинус угла между
направлениями этих векторов равен единице. Таким образом, мы получим, что
работа силы тяжести равна:

Второй случай — это когда
тело, наоборот, подбрасывают вертикально вверх с высоты h₁
на высоту h₂.

В этом случае, угол между
направлением силы тяжести и направлением перемещения составит 180^о.
Это приводит нас к тому, что работа силы тяжести опять-таки равна:

Наконец, рассмотрим
случай, когда между направлением силы тяжести и перемещением существует
произвольный угол α.

Обозначим модуль
перемещения за s. В этом случае,
работа силы тяжести равна:

Но, исходя из определения
косинуса:

Таким образом, мы в
третий раз получили одинаковый результат.

Более того, если даже мы
рассмотрим криволинейную траекторию, то убедимся, что результат будет тем же.

Любую кривую мы можем
представить в виде ломаной линии, состоящей из очень маленьких горизонтальных и
вертикальных отрезков. На горизонтальных отрезках работа силы тяжести будет
равна нулю, поскольку в этом случае направление перемещения перпендикулярно
направлению силы тяжести. На вертикальных участках работа будет равна: A
= mg(s₁
+ … + s_n).
Очевидно, что эта сумма будет равна (h₁
– h₂):

Таким образом, мы
убедились, что работа силы тяжести не зависит от траектории движения тела.
Имеет значение лишь то, насколько начальное положение тела отличается от
конечного. Это плавно подводит нас к понятию потенциальной энергии, которое
мы рассмотрим немного позже.

Из приведенных примеров
вытекает еще один важный вывод: при движении тела по замкнутой траектории
работа силы тяжести равна нулю. Для начала рассмотрим контур, имеющий форму
прямоугольника. Как мы уже убедились, при движении тела в горизонтальном
направлении, работа силы тяжести равна нулю. Вектор перемещения направлен
перпендикулярно вектору силы тяжести. При перемещении же по противолежащим
вертикальным сторонам контура, сила тяжести совершает работу, равную по
абсолютной величине, но противоположную по знаку.

В одном случае вектор
перемещения направлен так же, как вектор силы тяжести, а в другом — направлен в
противоположную сторону. Это довольно логично, поскольку при движении тела
вниз, сила тяжести ему «помогает», а при движении вверх — наоборот, мешает.

Мы можем сколь угодно
усложнить эту траекторию, получив совершенно произвольный замкнутый контур.

Но опять же, разбив все
кривые на ломаные линии с горизонтальными и вертикальными участками, мы
убедимся, что суммарная работа будет равна нулю.

Силы, обладающие такими
свойствами, называются консервативными. То есть, консервативная сила — это
такая сила, работа которой в замкнутом контуре равна нулю.

Примеры решения задач.

Задача 1. Охотник
стреляет со скалы под углом 40° к горизонту. За время падения пули работа силы
тяжести составила 5 Дж. Если пуля вошла в землю на расстоянии 250 м от скалы,
то какова её масса?

Задача 2. Находясь
на Нептуне, тело совершило перемещение так, как показано на рисунке. При этом
перемещении работа силы тяжести составила 840 Дж. Если масса данного тела равна
5 кг, то каково ускорение свободного падения на Нептуне?

Работа в гравитационном поле, формула

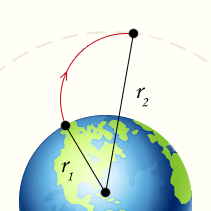
Если тело перемещается в гравитационном поле на значительное расстояние, то совершаемую против сил гравитационного притяжения работу (например, работу для вывода ракеты в космос) нельзя вычислить по формуле W=G·h, потому, что сила тяжести G обратно пропорциональна расстоянию между центрами масс.

Работа, совершаемая при перемещении тела вдоль радиуса в гравитационном поле, определяется как интеграл

[
W = int_{r_1}^{r_2} F dr
= int_{r_1}^{r_2} γ frac{m_a m_b}{r^2} dr
]

[
W = γ m_a m_b int_{r_1}^{r_2} frac{1}{r^2} dr
]

См. Таблицу интегралов

[
W = γ m_a m_b (frac{1}{r_1} — frac{1}{r_2})
]

Здесь:
W — работа против гравитационной силы (Джоуль),
G — гравитационная сила, с которой два тела притягиваются друг к другу (Ньютон),
m_a — масса первого тела (кг),
m_b — масса второго тела (кг),
r — расстояние между центрами масс тел (метр),
r₁ — начальное расстояние между центрами масс тел (метр),
r₂ — конечное расстояние между центрами масс тел (метр),
γ — гравитационная постоянная 6.67 · 10^-11
(м³/(кг · сек²)),

Величина работы W не зависит от формы пути от точки r₁ к r₂, так как в формулу входят только радиальные составляющие dr перемещения, совпадающие с направлением силы притяжения.

формула (3) справедлива в случае любых небесных тел.

Вычислить, найти работу в гравитационном поле по формуле (3)