Резонансная частота.
Параллельный колебательный контур (рисунок 1) или последовательный колебательный контур (рисунок 2) могут использоваться в генераторах синусоидальных колебаний. Если в одной из этих схем зарядить конденсатор то он будет разряжаться заряжая катушку индуктивности, катушка разряжаясь будет заряжать конденсатор, этот процесс будет повторяться с определённым периодом T. Период это время одного колебания. Частота колебаний это величина обратная периоду. Разделив единицу на численное значение периода получим численное значение частоты.
Рисунок 1 — Параллельный колебательный контур
Рисунок 2 — Последовательный колебательный контур
Частота возникших колебаний называется собственной частотой колебаний контура для контуров изображённых на рисунках выше эта частота равна резонансной частоте этих контуров. Резонансная частота контура зависит от индуктивности L и ёмкости C её элементов, для колебательного контура (последовательного или параллельного) её можно найти по формуле:
Где L-индуктивность катушки контура, C-ёмкость конденсатора контура.
Если на параллельный или последовательный колебательный контур подавать переменное синусоидальное напряжение и изменять его частоту то будут меняться реактивные сопротивления элементов контура, если частота увеличивается то сопротивление конденсатора уменьшается а сопротивление катушки увеличивается и наоборот: если частота уменьшается то сопротивление конденсатора увеличивается а сопротивление катушки уменьшается, очевидно что есть такая частота при которой сопротивление катушки и конденсатора равны эта частота и есть резонансная. Сопротивление параллельного колебательного контура при этой частоте будет наибольшим (по сравнению с сопротивлениями этого контура при других частотах) а сопротивление последовательного колебательного контура при такой частоте будет наименьшим. Эти свойства контуров используют для построения фильтров например в полосно-пропускающем фильтре последовательно с нагрузкой ставиться последовательный контур и при подаче на это соединение (нагрузки и контура) переменного напряжения с резонансной частотой ток в нагрузке будет максимальным при других частотах ток будет меньше. Резонанс в параллельном контуре называют — резонансом токов, резонанс в последовательном контуре — резонансом напряжений. Можно простым способом определить каким будет сопротивление контура при резонансной частоте: например допустим что на параллельный колебательный контур подаётся постоянный ток, постоянный ток можно считать частным случаем переменного короче говоря постоянный ток это переменный с наименьшей возможной частотой, известно что при постоянном токе катушка действует как перемычка следовательно сопротивление контура будет равно нулю если резонансная частота не бесконечно мала (т.е. не постоянный ток) и сопротивление есть то оно больше нуля (т.е. сопротивления при постоянном токе) следовательно сопротивление параллельного колебательного контура на резонансной частоте максимальное а у последовательного контура наоборот. Зная то что конденсатор постоянный ток не пропускает, можно аналогично определить каким д.б. сопротивление последовательного контура на резонансной частоте. Выведем формулу для расчёта резонансной частоты зная то что при резонансе реактивные сопротивления элементов (катушки и конденсатора) контура равны:
Для расчёта резонансной частоты и периода колебаний колебательного контура с катушкой и конденсатором можно воспользоваться программой:
Содержание
- 1 Эффект резонанса
- 2 Определение колебательного контура
- 3 Подключение к цепи индуктивной катушки
- 3.1 Параллельный КК
- 3.2 Последовательный КК
- 4 Резонансная частота
- 5 Применение колебательных контуров
- 6 Условие отсутствия резонанса
- 7 Амплитуда резонанса
- 7.1 Амплитуда тока
- 7.2 Амплитуда напряжения
- 8 Видео
Галилео Галилей, исследуя маятники и музыкальные струны, описал явление, которое впоследствии стали называть резонансом. Оно проявляется не только в акустике, но и в механике, электронике, оптике и астрофизике. Резонансный эффект имеет как положительные, так и отрицательные воздействия на колебательные системы.
Резонанс
Эффект резонанса
Ярким примером механического класса резонаторов является пружинный маятник. Профессор из технологического Массачусетского института (в Америке), В. Левин, акцентирует внимание своих студентов на то, что резонанс (resonance) – это эффект, сопряжённый с увеличением амплитуды. Для демонстрации явления используется установка. Она состоит из следующих компонентов:
- электродвигатель;
- механизм, превращающий вращение в возвратно-поступательное движение;
- ЛАТР – лабораторный автотрaнcформатор;
- медная пружина из проволоки с набором грузиков;
- направляющая для пружины.
Направление колебания пружины – вертикальное. Вращение вала мотора заставляет пружину совершать колебания. С помощью автотрaнcформатора присутствует возможность регулировать напряжение. Регулировка позволяет варьировать частоту вращения вала и колебаний маятника. При изменении частоты вращения вала амплитуда возвратно-поступательного движения остаётся неизменной.
Перед опытом замеряется удлинение медной пружины под действием грузиков (для оценки резонансной частоты пружины). Изменение скорости вращения вала заставляет амплитуду колебания конца пружины с грузом изменяться. Амплитуда увеличивается и на 1-м герце частоты становится максимальной (~30 см).
Важно! При дальнейшем увеличении скорости вращения вала амплитуда конца пружины начинает уменьшаться. Это означает, что resonance пройден. Если уменьшать напряжение, а с ним и частоту вращения двигателя, снова можно наблюдать эффект resonance колебания пружины.
Пружинный маятник
Добротность пружины Q определяется как отношение амплитуды колебания пружины Aпр к амплитуде колебания вынуждающей силы Aвс. В этом случае Q = Aпр/Aвс = 30/5 = 6, где Aвс = 5.
Определение колебательного контура
Частота вращения: формула
Резонансные явления, отмеченные в электротехнике, ярко выражены в схемах колебательных контуров (КК). Подобные конструкции представляют собой элементарные системы, способные осуществлять свободные колебания электромагнитной природы. Сам КК в цепи состоит из следующих элементов:
- конденсатора;
- катушки индуктивности;
- источника тока.
Внимание! Выводы элементов схемы могут соединяться друг с другом параллельно или последовательно. Все зависит от того, какого результата нужно добиться от резонанса в КК.
Подключение к цепи индуктивной катушки
Резонанс в электрической цепи
Включение в ёмкостную цепь катушки индуктивности сразу превращает её в КК. В зависимости от схемы подключения, различают два вида КК 1 класса: параллельный и последовательный.
Параллельный КК
В данной схеме конденсатор С соединён с катушкой L параллельно. Если заряженный конденсатор присоединить к катушке, то энергия, запасённая в нём, передастся ей. Через индуктивную катушку L потечёт ток, вызывая электродвижущую силу (ЭДС).
ЭДС самоиндукции L будет направлена на снижение тока в параллельной цепи. Ток, созданный этой ЭДС, и ток разряда ёмкости сначала одинаковы, а их суммарное значение равно нулю. Конденсатор передаст свою энергию Ec в катушку и полностью разрядится. Индуктивность, получив максимальную магнитную энергию EL, начнёт заряжать ёмкость напряжением уже другой полярности. Когда вся энергия из индуктивности перейдёт в ёмкость, конденсатор будет полностью заряжен. В цепи появляются колебания, такой контур называется колебательным.
Параллельный КК
К сведению. Если бы в такой цепи отсутствовали потери, то такие колебания никогда не стали затухать. На пpaктике, продолжительность процесса зависит от потери энергии. Чем больше потери, тем меньше длительность колебаний.
Параллельное соединение C и L вызывает резонанс токов. Это значит, что токи, проходящие через C и L, выше по значению, чем ток через сам контур, в конкретное число раз. Это число носит название добротности Q. Оба тока (емкостной и индуктивный) остаются внутри цепи, потому что они находятся в противофазе, и происходит их обоюдная компенсация.
Стоит отметить! На fрез величина R КК устремляется к бесконечности.
Последовательный КК
В этой схеме соединены последовательно друг с другом катушка и конденсатор.
Последовательный КК
В такой схеме происходит resonance напряжений, R контура устремляется к нулю в случае образования резонансной частоты (fрез). Это позволяет использовать подобную систему резонанса в качестве фильтра.
Резонансная частота
При подаче на два КК (параллельного и последовательного) переменного напряжения с изменяющейся частотой их реактивные сопротивления C и L будут меняться. Изменения происходят следующим образом:
- с увеличением f – ёмкостное сопротивление уменьшается, а индуктивное увеличивается;
- с уменьшением f – ёмкостное сопротивление увеличивается, а индуктивное уменьшается.
Резонанс — что это такое
Частота, при которой реактивные сопротивления обоих элементов контура равны, называется резонансной.
Важно! При fрез сопротивление параллельного КК будет максимальным, а последовательного КК – минимальным.
Резонансная частота формула, которой имеет вид:
fрез = 1/2π*√L*C,
где:
- L – индуктивность, Гн;
- C – ёмкость, Ф.
Подставляя известные значения ёмкости и индуктивности в формулу резонансной частоты колебательного контура любой конфигурации, можно рассчитать этот параметр.
Для определения периода колебаний КК и частоты резонанса можно воспользоваться онлайн калькулятором на соответствующем портале в сети. Профессиональная программа имеет несложный интерфейс.
Пример интерфейса онлайн калькулятора LC-контура
Применение колебательных контуров
Подробный расчет колебательного контура позволяет точно подбирать величину необходимых элементов КК. Это позволяет использовать их в схемах электроники в виде:
- частотных фильтров – в радиоприёмниках, генераторах сигналов, преобразователях и выпрямителях;
- колебательных контуров – для выделения и настройки на определённую частоту станции вещания;
- силовых resonance-фильтров – для формирования напряжения синусоидальной формы.
На самолётах гражданской авиации КК применяется в блоках регулировки частоты генераторов.
Условие отсутствия резонанса
Для того чтобы возник резонанс формула которого для тока равна ω0*C = 1/ ω0*L, необходимо выполнения этого равенства. Существуют условия для невозможности появления этого эффекта, а именно:
- отсутствие у системы собственных колебаний;
- невозможность совпадения частоты внешнего воздействия с собственной частотой системы.
Амплитуда резонанса
В КК при подаче переменного напряжения от внешнего источника наблюдаются два вида резонанса и резкое увеличение двух видов амплитуды: амплитуды тока и амплитуды напряжения.
Амплитуда тока
Амплитуда тока резко возрастает при резонансе напряжений в последовательном контуре (последовательный резонанс). Источник переменной ЭДС включён в цепь, где нагрузкой служат последовательно включённые элементы L и С.
В этом случае в цепь входят сопротивления: активное r и реактивное x, равное:
x = xL – xC.
Так как для внутренних колебаний xL и xC равны, то для тока, поступающего от генератора, при резонансе (когда частоты совпадают) эти значения тоже одинаковы. Поэтому x = 0. В итоге полное сопротивление цепи будет состоять только из небольшого активного сопротивления. Ток при этом получается максимальным.
Схема (а) и резонансные кривые (б) для резонанса напряжений
Амплитуда напряжения
Резонанс токов (параллельный резонанс) является условием резкого возрастания амплитуды напряжения. Источник ЭДС подключается вне контура и нагружен параллельно соединёнными элементами L и С. В этом случае на эффект резонанса влияет внутреннее сопротивление генератора. Амплитуда напряжения на контуре максимальна при малом отличии напряжения контура от напряжения генератора. Это возможно при малом Ri.
Внимание! Изменение частоты генератора меняет ток, а амплитуда напряжения на контуре не отстаёт по величине от напряжения на генераторе. Если, U = Е – I*Ri, где Е – ЭДС, I – ток, то при малом Ri U = Е.
Схема (а) и резонансные кривые (б) для резонанса токов
Формула для определения расчётной резонансной частоты для разных колебательных систем различается по входящим в неё параметрам. Несмотря на все различия, суть остаётся неизменной: эффект резонанса наступает тогда, когда частота внутренних колебаний системы и внешних воздействий становятся равны друг другу.
Видео
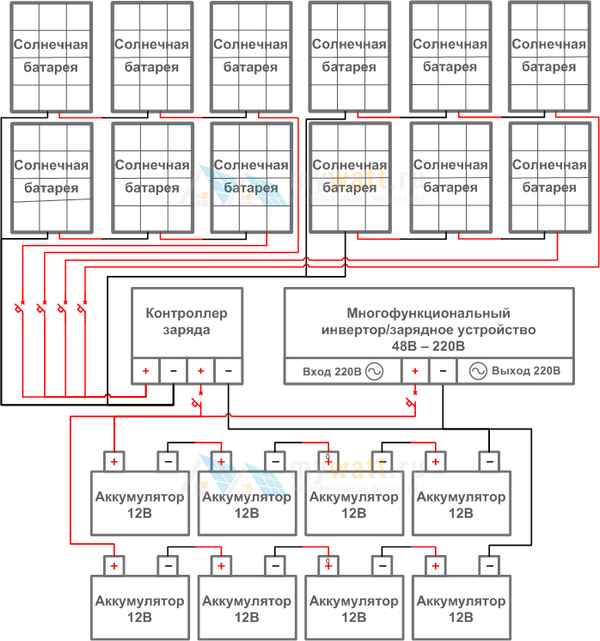
Солнечная батарея: подключение внешних аккумуляторов
Особенности подключения аккумуляторов к солнечным батареям. Как рассчитать основные параметры АКБ для солнечных батарей. Основные виды аккумуляторных батарей для гелиосистем. Гелиосистема с AGM-накопителями….
23 05 2023 0:24:11
О поражении электрическим током:
Воздействие электротока на человеческий организм. Понятие электротравмы. Подразделение степеней тяжести поражения от удара электрическим током. Классификация электротравматизма. Виды местных электротравм….
03 05 2023 22:45:51
Формула расчета частоты вращений
Частота вращения: формула. Синхронные и асинхронные электромашины. Синхронная скорость и скольжение. Расчет и регулировка частоты вращений. Номинальная скорость вращения в двигателях постоянного тока….
29 04 2023 14:46:18
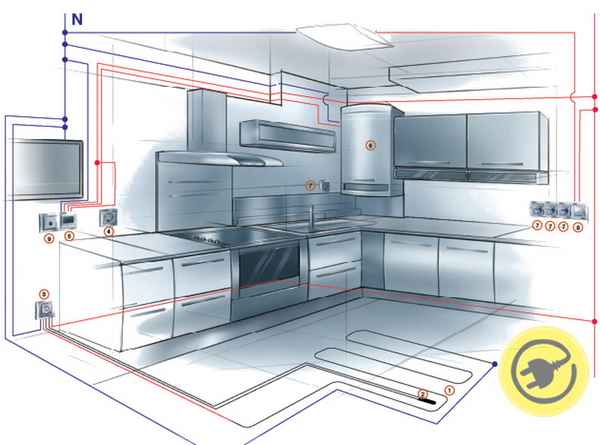
Электроснабжение кухни — советы экспертов
Современная кухня это основной потребитель электроэнергии в квартире, чтобы избежать проблем с электропроводкой нужно правильно произвести её комплектацию….
10 04 2023 14:24:50
The resonant frequency is defined as the frequency of a circuit when the values of capacitive impedance and the inductive impedance become equal. It is defined as the frequency at which a body or system reaches its highest degree of oscillation. A resonant circuit is made up of a parallel-connected capacitor and an inductor. It is mostly employed to create a given frequency or to consider a specific frequency from a complex circuit. The resonant frequency exists only when the circuit is purely resistive.
Formula
The formula for resonant frequency is given by the reciprocal of the product of two times pi and the square root of the product of inductance and capacitance. It is represented by the symbol fo. Its standard unit of measurement is hertz or per second (Hz or s-1) and its dimensional formula is given by [M0L0T-1].
fo = 1/2π√(LC)
where,
fo is the resonant frequency,
L is the inductance of circuit,
C is the capacitance of circuit.
Derivation
Suppose we have a circuit where a resistor, inductor and capacitor are connected in series under an AC source.
The value of resistance, inductance and capacitance is R, L and C.
Now, it is known that the impedance Z of the circuit is given by,
Z = R + jωL – j/ωC
Z =R + j (ωL – 1/ωC)
To satisfy the condition of resonance, the circuit must be purely resistive. Hence, the imaginary part of impedance is zero.
ωL – 1/ωC = 0
ωL = 1/ωC
ω2 = 1/LC
Putting ω = 1/2πfo, we get
(1/2πfo)2 = 1/LC
fo = 1/2π√(LC)
This derives the formula for resonant frequency.
Sample Problems
Problem 1. Calculate the resonant frequency for a circuit of inductance 5 H and capacitance 3 F.
Solution:
We have,
L = 5
C = 3
Using the formula we have,
fo = 1/2π√(LC)
= 1/ (2 × 3.14 × √(5 × 3))
= 1/24.32
= 0.041 Hz
Problem 2. Calculate the resonant frequency for a circuit of inductance 3 H and capacitance 1 F.
Solution:
We have,
L = 3
C = 1
Using the formula we have,
fo = 1/2π√(LC)
= 1/ (2 × 3.14 × √(3 × 1))
= 1/10.86
= 0.092 Hz
Problem 3. Calculate the resonant frequency for a circuit of inductance 4 H and capacitance 2.5 F.
Solution:
We have,
L = 4
C = 2.5
Using the formula we have,
fo = 1/2π√(LC)
= 1/ (2 × 3.14 × √(4 × 2.5))
= 1/6.28
= 0.159 Hz
Problem 4. Calculate the inductance of a circuit if the capacitance is 4 F and the resonant frequency is 0.5 Hz.
Solution:
We have,
fo = 0.5
C = 4
Using the formula we have,
fo = 1/2π√(LC)
=> L = 1/4π2Cfo2
= 1/ (4 × 3.14 × 3.14 × 4 × 0.5 × 0.5)
= 1/39.43
= 0.025 H
Problem 5. Calculate the inductance of a circuit if the capacitance is 3 F and the resonant frequency is 0.023 Hz.
Solution:
We have,
fo = 0.023
C = 3
Using the formula we have,
fo = 1/2π√(LC)
=> L = 1/4π2Cfo2
= 1/ (4 × 3.14 × 3.14 × 3 × 0.023 × 0.023)
= 1/0.0199
= 50.25 H
Problem 6. Calculate the capacitance of a circuit if inductance is 1 H and the resonant frequency is 0.3 Hz.
Solution:
We have,
fo = 0.3
L = 1
Using the formula we have,
fo = 1/2π√(LC)
=> C = 1/4π2Lfo2
= 1/ (4 × 3.14 × 3.14 × 1 × 0.3 × 0.3)
= 1/3.54
= 0.282 F
Problem 7. Calculate the capacitance of a circuit if inductance is 0.1 H and the resonant frequency is 0.25 Hz.
Solution:
We have,
fo = 0.25
L = 0.1
Using the formula we have,
fo = 1/2π√(LC)
=> C = 1/4π2Lfo2
= 1/ (4 × 3.14 × 3.14 × 0.1 × 0.25 × 0.25)
= 1/0.246
= 4.06 F
Last Updated :
15 May, 2022
Like Article
Save Article
Явление
резонанса. Электрическая цепь, содержащая
индуктивность и емкость, может служить
колебательным контуром, где возникает
процесс колебаний электрической
энергии, переходящей из индуктивности
в емкость и обратно. В идеальном
колебательном контуре эти колебания
будут незатухающими. При подсоединении
колебательного контура к источнику
переменного тока угловая частота
источника ? может оказаться равной
угловой частоте ?0, с которой происходят
колебания электрической энергии в
контуре. В этом случае имеет место
явление резонанса, т. е. совпадения
частоты свободных колебаний ?0, возникающих
в какой-либо физической системе, с
частотой вынужденных колебаний ?,
сообщаемых этой системе внешними
силами.
Резонанс
в электрической цепи можно получить
тремя способами: изменяя угловую частоту
? источника переменного тока, индуктивность
L или емкость С. Различают резонанс при
последовательном соединении L и С —
резонанс напряжений и при параллельном
их соединении — резонанс токов. Угловая
частота ?0, при которой наступает
резонанс, называется резонансной, или
собственной частотой колебаний
резонансного контура.
35. Резонанс в последовательном колебательном контуре. Добротность, векторная диаграмма. Характеристическое сопротивление, затухание контура.
Резонанс
напряжений
– явление, при котором цепь содержащая
активные и реактивные сопротивления,
будет только активное сопротивление
(XL — XC = 0). При этом ток в цепи совпадает
по фазе с напряжением. Условие
возникновение резонанса напряжений –
равенство нулю реактивного сопротивления.

характеристическое
сопротивление контура.
Таким
образом:

частота

для парралельного
При
резонансе напряжений ток максимален,
так как сопротивление минимально, а
и
таким образом
Добротностью
контура называется отношение модуля
реактивной составляющей напряжения в
цепи к модулю входного напряжения в
момент резонанса.
Полосу
частот вблизи резонанса, на границах
которой ток снижается до величины
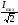
пропускания
резонансного тока.
Чем
больше добротность, тем острее кривая
и уже полоса пропускания
36. Резонанс (определение). Последовательный и параллельный колебательные контуры. Резонансные кривые в относительных единицах для последовательного колебательного контура.
резонанс
напряжений в цепях переменного тока
это такой процесс, при котором на
отдельных элементах цепи возникает
напряжение больше чем питающее. Такой
процесс возникает в цепях, состоящих
из последовательно соединённых емкости
и индуктивности. В так называемом
последовательном колебательном контуре.
Для
наступления резонанса в цепи переменного
тока необходимо чтобы выполнялись
условия. Во-первых, реактивное
сопротивление индуктивности должно
быть равно реактивному сопротивления
емкости. При этом активное сопротивление
такого контура должно быть минимальным.
Рисунок
1 — последовательный колебательный
контур
Во
вторых собственная частота последовательного
колебательного контура состоящего из
индуктивности и емкости должна совпадать
с частотой питающего напряжения. Тогда
в цепи наступает резонанс напряжений.
Энергия, накопленная в магнитном поле,
полностью переходит в энергию
электрического поля в конденсаторе и
наоборот.
А
для источника переменного напряжения
такая цепь становится практически
закороткой и в ней протекает максимально
возможный ток. Ограниченный только
активным сопротивлением контура.
Поскольку реактивные сопротивления
индуктивности и емкости на резонансной
частоте становятся равные нулю и энергия
в них не рассеивается. В отличии от
активного сопротивления в котором по
закону джоуля ленца выделяется тепло.
Рисунок
2 — Зависимость тока и полного реактивного
сопротивления от частоты источника
напряжения
При
изменении частоты питающего напряжения
или параметров контура резонанс
исчезает. Напряжение на элементах цепи
распределяется в соответствии с законом
Ома. То есть падение напряжения на
емкости и индуктивности будет равно
току, умноженному на их реактивные
сопротивления.
В
случае резонанса напряжение на емкости
или индуктивности будет в Q раз больше
чем напряжение источника. Q это добротность
контура величина обратная коэффициенту
затухания колебаний в контуре. Таким
образом, чем выше добротность контура,
тем выше будет увеличение напряжения.
Резона́нс
(фр. resonance, от лат. resono — откликаюсь) —
явление резкого возрастания амплитуды
вынужденных колебаний, которое наступает
при приближении частоты внешнего
воздействия к некоторым значениям
(резонансным частотам), определяемым
свойствами системы
Соседние файлы в предмете Теория электрических цепей
- #
15.06.201438.49 Кб21Лаба 7 7_4 [Вариант 4].mcd
- #
- #
- #
- #
- #
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.