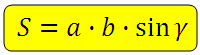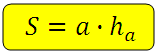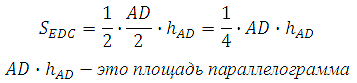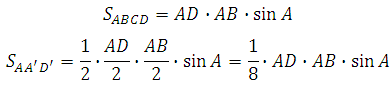Решение задач как найти площадь параллелограмма - Avtoru.top

3. Геометрия на плоскости (планиметрия). Часть I

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Параллелограмм и его свойства

Сумма внутренних углов любого четырехугольника равна (360^circ).

Свойства параллелограмма:

(blacktriangleright) Противоположные стороны попарно равны;

(blacktriangleright) Диагонали точкой пересечения делятся пополам;

(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).

Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:

(blacktriangleright) если противоположные стороны попарно равны;

(blacktriangleright) если две стороны равны и параллельны;

(blacktriangleright) если диагонали точкой пересечения делятся пополам;

(blacktriangleright) если противоположные углы попарно равны.

Площадь параллелограмма

Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.

Задание
1

#1783

Уровень задания: Легче ЕГЭ

Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.

Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 — 32 = 18).

Ответ: 18

Задание
2

#1784

Уровень задания: Равен ЕГЭ

Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.

У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).

Ответ: 1,25

Задание
3

#273

Уровень задания: Равен ЕГЭ

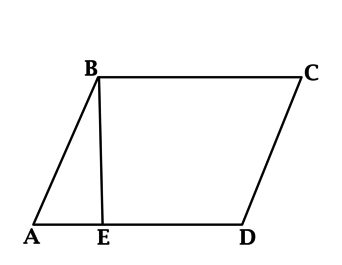
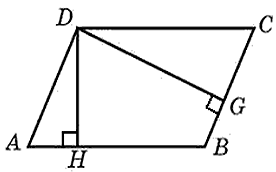
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).

Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).

Ответ: 2

Задание
4

#1785

Уровень задания: Равен ЕГЭ

Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.

В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} — 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).

Ответ: 135

Задание
5

#1686

Уровень задания: Равен ЕГЭ

Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).

По теореме Пифагора находим: (AB^2=AD^2 — BD^2 = 25 — 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).

Ответ: 12

Задание
6

#1685

Уровень задания: Равен ЕГЭ

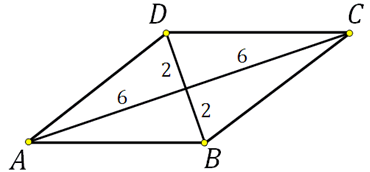
В параллелограмме (ABCD): (P_{triangle AOB} = , (P_{triangle AOD} = 9), а сумма смежных сторон равна (7). Найдите произведение этих сторон параллелограмма (ABCD).

(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} — P_{triangle AOB} = AD — AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).

Ответ: 12

Задание
7

#3617

Уровень задания: Равен ЕГЭ

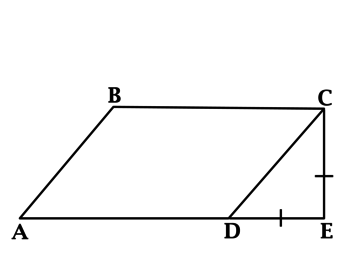
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.

Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]

Ответ: 6

Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.

Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».

Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.

Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

Всего: 116 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Тип 17 № 65

Найдите площадь параллелограмма, изображённого на рисунке.

Тип 17 № 91

Найдите площадь параллелограмма, изображённого на рисунке.

Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов  — 45°. Найдите площадь параллелограмма, делённую на

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов  — 60°. Найдите площадь параллелограмма, делённую на

Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен Найдите площадь параллелограмма.

Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен Найдите площадь параллелограмма.

Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен Найдите площадь параллелограмма.

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 1)

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.5)

В трапеции проведен отрезок, параллельный основаниям и делящий ее на две трапеции одинаковой площади. Найдите длину этого отрезка, если основания трапеции равны см и см.

Источник: ГИА-2012. Математика. Диагностическая работа №2 (2 вар.)

Найдите площадь выпуклого четырёхугольника с диагоналями 3 и 4, если отрезки, соединяющие середины его противоположных сторон, равны.

Источник: Тренировочные работы. Иркутск  — 2013, вариант 1.

Найдите площадь выпуклого четырёхугольника с диагоналями 8 и 5, если отрезки, соединяющие середины его противоположных сторон, равны.

Источник: Тренировочные работы. Иркутск  — 2013, вариант 3.

Найдите площадь параллелограмма, изображённого на рисунке.

Площадь параллелограмма ABCD равна 56. Точка E  — середина стороны CD. Найдите площадь трапеции AECB.

Источник: Банк заданий ФИПИ

Найдите площадь параллелограмма, изображённого на рисунке.

Источник: Банк заданий ФИПИ

В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60° , сторона AB равна 4. Найдите площадь трапеции.

Источник: Банк заданий ФИПИ

Найдите площадь параллелограмма, изображённого на рисунке.

Источник: Банк заданий ФИПИ

Всего: 116 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Найдите площадь параллелограмма. Здравствуйте! В этой статье представлена группа заданий решение которых связанно с площадью параллелограмма. Задачи входят в состав экзамена. Рекомендую посмотреть статью в которой о площади параллелограмма (и треугольника) всё подробно расписано. При решении пригодятся формулы:

*Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.

*Площадь параллелограмма равна произведению параллелограмма на высоту проведённую к этой стороне.

Также рассматриваются задачи с ромбами. Как известно, ромб является параллелограммом и обладает его свойствами, но есть ещё и дополнительные. Нам понадобится это:

— Диагонали ромба взаимно перпендикулярны.

Рассмотрим задачи:

zadacha

27586. Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150⁰.

Используем формулу площади параллелограмма:

Стороны равны 1, а острый угол будет равен 30⁰:

Ответ: 0,5

zadacha

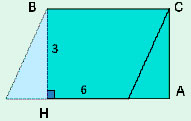
27614. Найдите площадь ромба, если его диагонали равны 4 и 12.

Известно, что диагонали ромба пересекаются под прямым углом, также они точкой пересечения делятся пополам. Построим эскиз следующим образом и отметим на нём размеры половин диагоналей:

Получается, что ромб диагоналями разбивается на 4 равных прямоугольных треугольника с катетами 2 и 6. Можем вычислить площадь этого треугольника:

Так как все четыре треугольника образованные диагоналями равны, то

Ответ: 24

zadacha

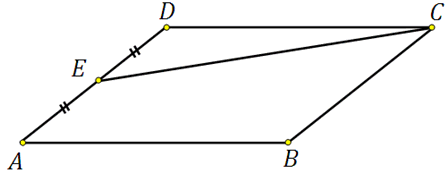
317338. Площадь параллелограмма ABCD равна 189. Точка Е середина стороны AD. Найдите площадь трапеции AECB.

Для того чтобы вычислить площадь трапеции достаточно понимать как определить площадь отсечённого треугольника EDC. *Далее мы из площади параллелограмма просто вычтем площадь треугольника.

Посмотрите! Сторона треугольника ED равна половине стороны параллелограмма, высота у них общая. Что это значит? А то что:

Получается, что площадь треугольника в четыре раза меньше площади параллелограмма:

Таким образом:

Ответ: 141,75

*Какую часть по площади занимает треугольник в параллелограмме можно увидеть разделив параллелограмм диагональю (он делится пополам):

Площадь треугольника ADC составляет ½ от площади параллелограмма, а площадь треугольника EDC равна половине площади ADC, то есть треугольник EDC по площади будет в 4 раза меньше.

zadacha

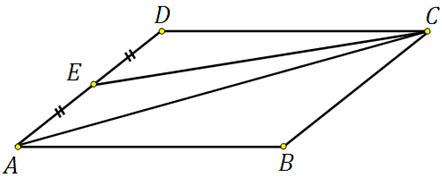
319056. Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A′B′C′D′, вершинами которого являются середины сторон данного параллелограмма.

Построим эскиз:

Нетрудно заметить, что площади треугольников 1, 2, 3 и 4 равны, так как у них есть равные стороны и синусы углов между ними приобретают равные значения.

Вычислим площадь треугольника АA′D′:

Получается, что площадь треугольника будет в восемь раз меньше. Таким образом, искомая площадь равна:

Ответ: 76,5

*Конечно же, «опытный глаз» сразу увидит, что площадь параллелограмма A′B′C′D′ в два раза меньше площади данного параллелограмма, но понимать формальное соотношение площадей фигур необходимо и важно.

**Если вы построите отрезки соединяющие середины противоположных сторон, то сразу наглядно увидите каким образом параллелограмм разбивается на равные по площади треугольники и решение будет очевидно.

zadacha

319057. Площадь параллелограмма ABCD равна 176. Точка E– середина стороны CD. Найдите площадь треугольника ADE.

Площадь треугольника ADE составляет четвёртую часть от площади параллелограмма, посмотрите вше задачу 317338. То есть S_ADE=176/4=44.

Ответ: 44

27585. Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 30⁰.

Посмотреть решение

27610. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Посмотреть решение

27611. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

Посмотреть решение

27612. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Посмотреть решение

27613. Найдите площадь ромба, если его высота равна 2, а острый угол 30⁰.

Посмотреть решение

27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.

Посмотреть решение

27616. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

Посмотреть решение

На этом всё. Успеха вам!

С уважением, Александр

Делитесь информацией о сайте в социальных сетях.

Источник

Инфоурок

›

Геометрия

›Конспекты›Электронный урок по теме: «Решение задач на нахождение площади параллелограмма»

Электронный урок по теме: «Решение задач на нахождение площади параллелограмма»

Скачать материал

Сейчас обучается 143 человека из 50 регионов

Сейчас обучается 246 человек из 63 регионов

Сейчас обучается 353 человека из 69 регионов

Описание презентации по отдельным слайдам:

1 слайд

Урок геометрии в 8 классе с углубленным изучением математики

Автор разработки:
учитель математики МБОУ СШ № 10 г. Павлово
Леонтьева Светлана Ивановна

Чему бы ты ни учился, ты учишься для себя.
(Петроний- сатирик Древней Греции)
2 слайд

Приветствую вас
на уроке геометрии
в 8 классе

Уроки №28
10.11.2016 г.
3 слайд

Успешного усвоения материала
Интересные мысли и высказывания
Чтобы дойти до цели,
надо прежде всего идти.

О.Бальзак
4 слайд

Отчёт
по выполнению
ДР в группе
5 слайд

Проверка ДР №17 на 03.11.19

Теория:
Опросите друг друга в парах
по следующим вопросам:

Чему равна площадь квадрата со стороной а?
Чему равна площадь прямоугольника со сторонами а и b?
Чему равна площадь параллелограмма
со стороной а и высотой h?
6 слайд

Практика:
№459(а,б) — назовите ответы

№ 460
ДР №17
13см
12см
Проговорите краткое решение задачи и ответ
7 слайд

Практика:
№464(а)
а=18см, b=30см, h1=6см
ДР №17
8 слайд

Прокомментируйте решение №462
пошагово:

ДР №17
6см
6см
6см
6см
3см
1.
2.
3.
4.
9 слайд

Практика: дополнительные задачи
А
В
С
D
О
M
N
K
P
10 слайд

Вывод: Площадь ромба равна половине произведения его диагоналей
А
В
С
D
О
где d1 и d2 -диагонали ромба
11 слайд

Решение задачи показать индивидуально
12 слайд

Оцените выполнение
ДР
13 слайд

КР
Решение задач на нахождение площади параллелограмма.
03.11.19г.
14 слайд

Закрепить теорему о площади параллелограмма при решении задач.
Формировать правильную математическую речь, совершенствовать навыки решения задач.
Цели урока:
15 слайд

Работа в парах на оценку
Постройте высоты параллелограмма на готовых чертежах
16 слайд

Решите в паре задачу из Рабочей тетради. Проговорите решение.
17 слайд

Решите в группе задачи.
18 слайд

Решение задач в группе на применение формулы площади параллелограмма
Проверка
19 слайд

Решение задач на применение формулы площади параллелограмма
Н
20 слайд

Решение задач на применение формулы площади параллелограмма
21 слайд

Решение задач на применение формулы площади параллелограмма
22 слайд

Решение задач на применение формулы площади параллелограмма
23 слайд

Подводим итоги:
Площади каких четырехугольников можно найти, умножая сторону на высоту?
Площади каких четырехугольников можно найти перемножив его диагонали и результат поделив пополам?
24 слайд

Критерии оценки за урок:
1. Комментировали ДЗ
2. Активно участвовали в решении устных задач.
3. Привели решение задач, решаемых письменно
Поставьте себе оценку за урок
25 слайд

Назовите ученика, который по вашему мнению был сегодня на уроке лучшим
26 слайд

Решение задач на применение формулы площади параллелограмма

Самостоятельная работа
Индивидуальный зачет.
Записи на листе- кратко.
Ответ выделить
28 слайд

ДР №18 на 10.11.19

Теория:
знать формулы нахождения площади квадрата, прямоугольника, параллелограмма и ромба

Практика: №№ 466, 467, 464(в)
ДР №17
Для индивидуального решения:
29 слайд

ДР №17
Для индивидуального решения:

Краткое описание документа:

Материалы
урока по теме: «Решение задач на нахождение площади параллелограмма» — полный конспект урока в виде
презентации, включающий обязательную проверку домашнего задания с анализом
допущенных ошибок, экспресс-опрос по теории, упражнения на
закрепление основных введенных раннее понятий. На уроке активно
используется материал учебника, позволяющий разобрать теорию
и основные задачи по теме. Учащимся предоставляется возможность поработать
по готовым чертежам и ликвидировать имеющиеся пробелы в знаниях. В
течение всего урока идет процесс самооценки усвоения материала. В конце
урока дается подробное домашнее задание, содержащее как теоретическую, так и
практическую часть. Такое изложение материала урока позволяет ученику пройти
материал урока повторно дома, закрепив и разобрав сложные моменты
темы.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 266 075 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Основы туризма и гостеприимства»
Курс повышения квалификации «Управление финансами: как уйти от банкротства»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Организация маркетинга в туризме»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»
Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»
Курс профессиональной переподготовки «Уголовно-правовые дисциплины: теория и методика преподавания в образовательной организации»

Настоящий материал опубликован пользователем Леонтьева Светлана Ивановна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 7 лет и 10 месяцев
- Подписчики: 1
- Всего просмотров: 521903
- Всего материалов:
  
  408

Источник

Тип урока: изучение нового материала.

Цели:

Повторить площадь прямоугольника.
Вывести формулу площади параллелограмма.
Применять формулу площади параллелограмма при решении задач.

Планируемые результаты:

Предметные:

Познакомиться с формулой площади параллелограмма и ее доказательством.
Научиться выводить формулу площади параллелограмма и находить площадь параллелограмма, используя формулу, решать задачи.

Метапредметные:

Коммуникативные: с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации.
Регулятивные: выделять и осознавать то, что уже усвоено и что еще подлежит усвоению, осознавать качество и уровень усвоения.
Познавательные: сопоставлять характеристики объектов по одному или нескольким признакам; выявлять сходства и различия объектов.

Виды деятельности: формирование у учащихся умений построения и реализации новых знаний, выполнение практических заданий.

Оборудование: доска, мел, линейка, учебник, наглядность, проектор, мультимедийная презентация.

Учебник (УМК): Геометрия 7-9, Л.С.Атанасян, В.Ф.Бутузов, 2015.

1. Приветствие

2. Проверка домашнего задания

Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.

Дано:

АВСД — прямоугольник
Р= 60
АВ:ВС=4:11

Найти: S.

Решение:

Пусть 1 часть равна х, тогда АВ=4х, ВС=11х, составим и решим уравнение:

Р=2(АВ+ВС),
60=2(4х+11х),
60=30х,
х=2.
АВ=4·2=8
ВС=11 ·2=22
S=АВ · ВС=8 ·22=176.

Ответ:176

3. Мотивация на учебную деятельность

Устная работа.

Найти площади фигур:

Какой вывод можно сделать?

(- Все фигуры имеют одинаковую площадь.

— Фигуры № 1,2,3 равны, а у равных фигур равные площади.

— Фигуры №1,4 или 2,4 или 3,4 имеют равные площади, но сами они разные.)

Такие фигуры называются равновеликими. Фигуры № 3,4 называют равновеликими, так как их площади равны, но сами фигуры не равны.

4. Целеполагание. Постановка проблемы. Поиск путей решения проблемы

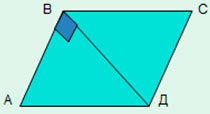
Решим задачу.

Дано:

АВСД — параллелограмм

АД – основание, АД=6

ВН — высота, ВН=3

Найти: S.

Надо 6 · 3?

То есть использовать формулу площади прямоугольника?

А как читается данная формула? (Площадь прямоугольника равна произведению его смежных сторон.)

А ВН и АД разве смежные?

Что можно сделать, чтобы мы получили прямоугольник? (Надо ∆АВН переместить вправо и получим прямоугольник.)

Тогда прямоугольник и параллелограмм будут какими фигурами? (Равновеликими).

Решение:

S=АД · ВН = 6 · 3 = 18.

Мы можем заменить параллелограмм на равновеликую фигуру прямоугольник => можно утверждать, что их площади равны.

Ответ: 18.

5. Тема урока: Площадь параллелограмма

Цели урока:

Вывести формулу площади параллелограмма.
Решить задачи на вычисление площади параллелограмма.

Решение проблемы

Выведем формулу площади параллелограмма.

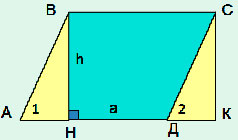
Теорема: площадь параллелограмма равна произведению его основания на высоту.

Дано:

АВСД — параллелограмм
S — площадь,
а — основание,
h – высота.

Доказать: S = аh.

Доказательство:

Дан параллелограмм АВСД:

1) достроим параллелограмм АВСД до трапеции АВСК;

2) рассмотрим ∆АВН и ∆ДСК:

а) АВ=СД (противоположные стороны параллелограмма),

б) 1= 2 (соответственные углы при АВ || СД и АД – секущей), значит ∆АВН = ∆ДСК (по гипотенузе и острому углу) => SАВН=SДСК.

3) SВНКС = аh (по теореме о площади прямоугольника);

4) SАВСД + SСДК = SАВН + SВНКС,

SАВСД = SВНКС (так как ∆АВН = ∆ДСК),

SАВСД = аh.

6. Первичное закрепление

Работа устно.

Дано:

АВСД — параллелограмм
АВ=10
ВД — высота, ВД=12

Найти: S.

Чему равняется площадь параллелограмма? (Произведение основания на высоту.)

А АВ основание? (Нет, но к ней проведена высота, значит можно утверждать, что АВ является основанием.)

Верно, то есть высота всегда проведена к основанию.

Решение:

S=ВД · ВА = 12 · 10 = 120.

Ответ: 120.

7. Письменная работа

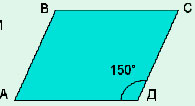
Дано:

АВСД — параллелограмм
АВ=14
ВС=18

Д = 150°

Найти: S.

Решение:

Что надо сделать?

1) Построить высоту ВН.

2) Рассмотрим ∆АВН:

А=180°-Д=180°-150°= 30° (соответственные углы при СВ || АД и АВ – секущей)

ВН =½АВ=½· 14=7 (катет, лежащий напротив угла в 30° равен половине гипотенузы)

3) SАВСД =АД · ВН = 18 · 7 = 126. (АД=ВС как противоположные стороны параллелограмма).

Ответ: 126.

8. Домашнее задание

Открываем дневники и записываем домашнее задание: Выучить формулировку и доказательство теоремы, № 459.

!!! Обратите внимание!!! Вы будете находить не только площадь параллелограмма, но и основание и высоту. Вы будете работать с данной формулой.

9. Рефлексия

Что сегодня я узнал (а)?
Я научился(ась) чему-то новому?
Я понял (а) материал или были затруднения?

10. Резерв

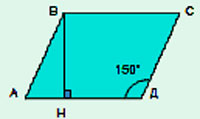
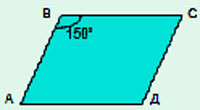
Дано:

АВСД — параллелограмм
АВ=ВС=10
В = 150°

Найти: S.

Решение:

1) Построить высоту ВН.

2) Рассмотрим ∆АВН:

А=180° – Д=180°-150°= 30° (соответственные углы при ВС || АД и АВ – секущей)

ВН=½АВ= ½· 10=5 (катет лежащий напротив угла в 30° равен половине гипотенузы)

3) SАВСД =АД · ВН = 10 · 5 = 50. (АД=ВС как противоположные стороны параллелограмма).

Ответ: 50.

Источник

Параллелограмм и его свойства

Электронный урок по теме: «Решение задач на нахождение площади параллелограмма»

Описание презентации по отдельным слайдам:

Краткое описание документа:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Материал подходит для УМК

Другие материалы

Вам будут интересны эти курсы:

1. Приветствие

2. Проверка домашнего задания

3. Мотивация на учебную деятельность

4. Целеполагание. Постановка проблемы. Поиск путей решения проблемы

5. Тема урока: Площадь параллелограмма

Решение проблемы

6. Первичное закрепление

7. Письменная работа

8. Домашнее задание

9. Рефлексия

10. Резерв

Не пропустите также: