Радиус вписанной окружности в равнобедренный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Содержание
- Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
- Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
- Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
- Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
- Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
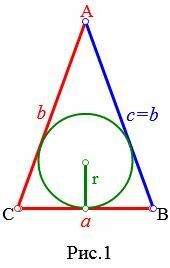
Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.
Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:
где полупериметр p вычисляется из формулы:
Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:
Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:
Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):
Ответ:
2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
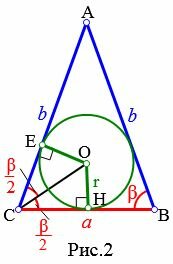
Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac{large beta}{large 2}. ) Для прямоугольного треугольника OCH можно записать:
Откуда получим формулу радиуса вписанной в треугольник окружности:
Учитывая формулы половинного угла тригонометрических функций, формулу (8) можно записать так:
Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):
Ответ:
3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
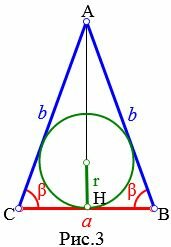
Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:
Откуда:
Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:
или
Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:
Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).
Подставим значения ( small b=9 ,; beta=35° ) в (11):
Ответ:
4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
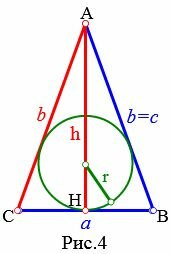
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :
где
Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:
Откуда
Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:
Подставим (15) в (16):
Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:
Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:
Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):
Ответ:
5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
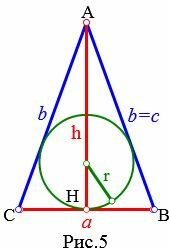
Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.
Из формулы (15) найдем b:
Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:
или
Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):
Ответ:
Смотрите также:
- Окружность, описанная около треугольника
- Радиус описанной окружности около треугольника онлайн
- Радиус описанной окружности около равнобедренного треугольника онлайн
- Радиус описанной окружности около равностороннего треугольника онлайн
- Радиус описанной окружности около прямоугольного треугольника онлайн
- Радиус вписанной в треугольник окружности онлайн
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
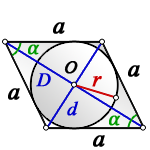
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :
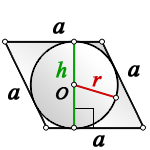
2. Радиус вписанной окружности ромба, равен половине его высоты
a — сторона ромба
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :
Радиус вписанной окружности в равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Радиус окружности, вписанной в равнобедренный треугольник
Свойства равнобедренного треугольника дают возможность получить дополнительные формулы. Рассмотрим некоторые из них.
Поскольку для равнобедренного треугольника полупериметр
Так как формула площади равнобедренного треугольника по формуле Герона равна
Эту формулу можно упростить
Таким образом, радиус окружности, вписанной в равнобедренный треугольник, равен
Если найти площадь по боковой стороне b и высоте, проведенной к основанию ha:
то получим еще одну формулу для нахождения радиуса вписанной в равнобедренный треугольник окружности:
Так как центр вписанной в треугольник окружности является точкой пересечения биссектрис треугольника, если известны углы при вершине и основании
Из прямоугольного треугольника AOF
Если известна боковая сторона и угол при основании, из прямоугольного треугольника ACF найдем AF
а затем из треугольника AOF — OF:
Эти формулы могут помочь ускорить вычисления. Запоминать их необязательно, достаточно повторить рассуждения.
Радиус вписанной окружности в равнобедренный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Открыть онлайн калькулятор
1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.
Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:
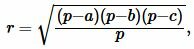 |
(1) |
где полупериметр p вычисляется из формулы:
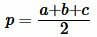 . . |
(2) |
Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:
| ( small p=frac<large a+b+c> <large 2>) ( small =frac<large 2b+a><large 2>, ) | (3) |
| ( small p-a=frac<large 2b+a><large 2>-a ) ( small =frac<large 2b-a><large 2>, ) | (4) |
| ( small p-b=p-c=frac<large 2b+a><large 2>-b ) ( small =frac<large a><large 2>. ) | (5) |
Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:
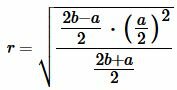
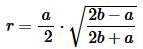 . . |
(6) |
Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):
Ответ:
2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac<large beta><large 2>. ) Для прямоугольного треугольника OCH можно записать:
Откуда получим формулу радиуса вписанной в треугольник окружности:
| ( small r=frac<large a> <large 2>cdot mathrmfrac<large beta> <large 2>.) | (8) |
| ( small r=frac<large a> <large 2>cdot frac<large sin beta> <large 1+cos beta>.) | (9) |
Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):
Ответ:
3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:
( small frac<large CH><large AC>=frac<large frac<2>><large b>= cos beta .)
| ( small a=2b cdot cos beta .) | (10) |
Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:
| ( small r=b cdot cos beta cdot mathrmfrac<large beta> <large 2>) | (11) |
Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:
| ( small r=b cdot frac<large sin beta cdot cos beta> <large 1+ cos beta>) | (12) |
Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).
Подставим значения ( small b=9 ,; beta=35° ) в (11):
Ответ:
4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :
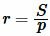 , , |
(13) |
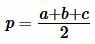 |
(14) |
Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:
( small left( frac<large a><large 2>right)^2=b^2-h^2 )
| ( small a=2 cdot sqrt ) | (15) |
Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:
| ( small S=frac<large 1> <large 2>cdot a cdot h. ) | (16) |
Подставим (15) в (16):
| ( small S=h cdot sqrt ) | (17) |
Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:
| ( small p=frac<large a+b+c> <large 2>) ( small =frac<large a+2b> <large 2>) ( small =frac<large a><large 2>+b )( small =b+ sqrt ) | (18) |
Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:
| ( small r=frac<large S> <large p>) ( small =frac<large h cdot sqrt><large b+ sqrt> ) | (19) |
Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):
Ответ:
5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.
Из формулы (15) найдем b:
( small b^2-h^2=left( frac<large a> <large 2>right)^2 )
( small b^2= frac<large a^2> <large 4>+h^2 )
| ( small b= frac<large 1> <large 2>cdot sqrt< a^2+ 4h^2 >) | (20) |
Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:
| ( small r=large frac< a cdot h >>) | (21) |
Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):
Ответ:
http://matworld.ru/geometry/radius-vpisannoj-okruzhnosti-v-ravnobedrennyj-treugolnik.php
Как найти радиус вписанной окружности треугольника
Содержание:
- Окружность, вписанная в треугольник — как найти радиус
-
Свойства вписанной в треугольник окружности
- Первое свойство
- Второе свойство
- Третье свойство
-
Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Как найти через высоту или стороны, примеры решения
Окружность, вписанная в треугольник — как найти радиус
Определение
Вписанной в треугольник окружностью называют такую окружность, которая занимает внутреннее пространство геометрической фигуры, соприкасаясь со всеми ее сторонами.
В таком случае грани треугольника представляют собой касательные к этой окружности. Сама геометрическая фигура с тремя углами считается описанной вокруг рассматриваемой окружности.
Свойства вписанной в треугольник окружности
Окружность, которую вписали в треугольник, обладает определенными свойствами. Основные из них можно записать таким образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Центр окружности, которую вписали в треугольник, совпадает с точкой пересечения биссектрис этой геометрической фигуры.
- Во внутреннее пространство любого треугольника можно вписать лишь одну окружность.
- Формула радиуса окружности, который вписали во многоугольник с тремя углами, будет иметь такой вид:
В представленной формуле радиуса окружности использованы следующие величины:
- S – является площадью треугольника;
- р – представляет собой полупериметр геометрической фигуры;
- a, b, c – являются сторонами треугольника.
Перечисленные свойства необходимо доказать.
Первое свойство
Требуется доказать, что центр окружности, которую вписали в фигуру с тремя углами, совпадает с точкой пересечения биссектрис.
Доказательство построено в несколько этапов:
- Необходимо опустить из центральной точки окружности перпендикулярные прямые OL, OK и OM, которые опускаются на стороны треугольника АВС. Из вершин треугольника следует провести прямые, соединяющие их с центром фигуры OA, OC и OB.
- Далее можно рассмотреть пару треугольников AOM и AOK. Можно отметить, что они являются прямоугольными, так как OM и OK являются перпендикулярами к сторонам AC и AB. Гипотенуза OA является общей для пары этих фигур.
- Исходя из того, что касательная к окружности является перпендикуляром к радиусу, который проведен в точку касания, согласно свойству касательной к окружности, то катеты OМ и OК представляют собой радиусы окружности и, следовательно, равны.
- Согласно полученным утверждениям, можно сделать вывод о равенстве прямоугольных треугольников AOМ и AOК по гипотенузе и катету. Таким образом, углы OAМ и OAК тоже равны. Получается, что OA является биссектрисой угла BAC.
- Аналогично можно доказать, что OC является биссектрисой угла ACB, а OB – биссектрисой угла ABC.
- Таким образом, биссектрисы треугольника совпадают в одной точке, которая представляет собой центр вписанной окружности.
Данное свойство окружности доказано.
Второе свойство
Необходимо представить доказательства свойства окружности, согласно которому в любой треугольник можно вписать окружность, причем только одну.
Доказательство состоит из нескольких этапов:
- Окружность получится вписать в треугольник в том случае, когда существует точка, удаленная на равные расстояния от сторон геометрической фигуры.
- Можно построить пару биссектрис ОА и ОС. Из точки, в которой они пересекаются, необходимо опустить перпендикулярные прямые OK, OL и OM ко всем граням многоугольника с тремя углами ABC.
- Затем следует рассмотреть пару треугольников AOK и AOM.
- Эти фигуры обладают общей гипотенузой АО. Углы OAK и OAM равны, так как OA является биссектрисой угла KAM. Углы OKA и OMA прямые, то есть также равны, так как OK и OM являются перпендикулярами к сторонам AB и AC.
- Исходя из того, что две пары углов равны, можно сделать вывод о равенстве третьей пары AOM и AOK.
- Таким образом, получилось подтвердить равенство треугольников AOK и AOM по стороне AO и двум углам, которые к ней прилегают.
- Удалось определить равенство сторон ОМ и ОК, то есть они удалены на одинаковое расстояние от сторон геометрической фигуры АС и АВ.
- Аналогично можно доказать, что OM и OL равны, то есть равноудалены от граней AC и BC.
- Таким образом, точка равноудалена от сторон треугольника, что делает ее центром окружности, которая вписана в этот многоугольник.
- Аналогичным способом можно определить точку во внутреннем пространстве любой геометрической фигуры с тремя углами, которая будет удалена на равные расстояния от его сторон, и представляет собой центр окружности, вписанной в этот треугольник.
- Исходя из вышесказанного, можно сделать вывод о том, что в любой треугольник можно вписать окружность.
- Необходимо заметить, что центральная точка окружности совпадает с точкой, в которой пересекаются биссектрисы треугольника.
- Можно допустить ситуацию, при которой в геометрическую фигуру с тремя углами можно вписать две и более окружности.
- Необходимо провести три прямые из вершин геометрической фигуры к центральной точке окружности, вписанной в нее, и опустить перпендикулярные прямые к каждой грани треугольника. Таким образом, будет доказано, что рассматриваемая окружность лежит на пересечении биссектрис треугольника, согласно доказательству ее первого свойства.
- Получим совпадение центральной точки окружности и центра первой окружности, которая уже была вписана в этот треугольник, а ее радиус соответствует перпендикуляру, опущенному на сторону треугольника так же, как и в первом случае. Можно сделать вывод о совпадении этих окружностей.
- Аналогично любая другая окружность, вписанная в геометрическую фигуру с тремя углами, будет совпадать с первой окружностью.
- Таким образом, в треугольник получается вписать лишь одну окружность.
Свойство доказано.
Третье свойство
Требуется доказать, что радиус окружности, которую вписали в геометрическую фигуру с тремя углами, представляет собой отношение площади треугольника к полупериметру:
Кроме того, необходимо представить доказательства следующему равенству:
Доказательство:
- Следует рассмотреть произвольный треугольник АВС, стороны которого соответствуют a, b и c. Для расчета полупериметра данного треугольника целесообразно использовать формулу:
- Центральная точка окружности совпадает с точкой пересечения биссектрис геометрической фигуры с тремя углами. Прямые OA, OB и OC, которые соединяют O с вершинами треугольника АВС, разделяют геометрическую фигуру на три части: AOC, COB, BOA. Площадь треугольника ABC представляет собой сумму площадей этих трех частей.
- Исходя из того, что площадь какого-либо треугольника представляет собой половину произведения его основания на высоту, а высота треугольников AOC, COB, BOA рассчитывается, как радиус окружности r, то площади треугольников AOC, COB и BOA можно определить по формулам:
- Далее необходимо представить площадь S геометрической фигуры АВС, как сумму площадей нескольких треугольников:
- Следует отметить, что второй множитель является полупериметром геометрической фигуры с тремя углами АВС, что можно записать в виде равенства:
- Таким образом, доказано равенство радиуса вписанной окружности и отношения площади треугольника к полупериметру.
- Можно записать формулу Герона, смысл которой заключается в следующем: площадь треугольника (S) равняется квадратному корню из произведения его полупериметра (p) на разности полупериметра и каждой из его сторон (a, b, c)
- Далее следует преобразовать формулу для расчета радиуса:
Свойство окружности доказано.
Формулы вычисления радиуса вписанной окружности
Параметры окружности, которую вписали в геометрическую фигуру с тремя углами, можно рассчитать с помощью стандартных формул. Радиус окружности будет определен в зависимости от типа треугольника.
Произвольный треугольник
Определить радиус окружности, которая вписана в какой-либо треугольник, можно, как удвоенную площадь треугольника, поделенную на его периметр.
В данном случае, a, b, c являются сторонами геометрической фигуры с тремя углами, S – ее площадь.
Прямоугольный треугольник
Радиус окружности, которую вписали в треугольник с прямым углом, представляет собой дробь с числителем в виде суммы катетов за минусом гипотезы и знаменателем, равным числу 2.
В формуле a и b являются катетами, c – гипотенузой треугольника.
Равнобедренный треугольник
Радиус окружности, которая вписана в равнобедренный треугольник, определяют по формуле:
В этом случае a – боковые стороны, b – основание треугольника.
Равносторонний треугольник
Расчет радиуса окружности, которая вписана в правильный или равносторонний треугольник, выполняют по формуле:
где a – сторона геометрической фигуры с тремя углами.
Как найти через высоту или стороны, примеры решения
Задача 1
Имеется геометрическая фигура с тремя углами, стороны которой составляют 5, 7 и 10 см. Требуется определить радиус окружности, которая вписана в этот треугольник.
Решение
В первую очередь необходимо определить, какова площадь треугольника. Для этого можно воспользоваться формулой Герона:
Затем применим формулу для расчета радиуса круга:
Ответ: радиус окружности составляет примерно 1,48 см.
Задача 2
Необходимо рассчитать радиус окружности, которая вписана в равнобедренный треугольник. Боковые стороны геометрической фигуры составляют 16 см, а основание равно 7 см.
Решение
Следует использовать подходящую формулу для расчета радиуса, подставив в нее известные величины:
Ответ: радиус окружности примерно равен 2,8 см.
Радиус окружности, вписанной в равнобедренный треугольник, можно найти по стандартной формуле.
Свойства равнобедренного треугольника дают возможность получить дополнительные формулы. Рассмотрим некоторые из них.
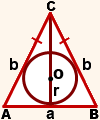
то
Так как формула площади равнобедренного треугольника по формуле Герона равна
то
Эту формулу можно упростить
Таким образом, радиус окружности, вписанной в равнобедренный треугольник, равен
Если найти площадь по боковой стороне b и высоте, проведенной к основанию ha:
то получим еще одну формулу для нахождения радиуса вписанной в равнобедренный треугольник окружности:

то
Из прямоугольного треугольника AOF
Если известна боковая сторона и угол при основании, из прямоугольного треугольника ACF найдем AF
а затем из треугольника AOF — OF:
Эти формулы могут помочь ускорить вычисления. Запоминать их необязательно, достаточно повторить рассуждения.

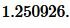
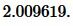
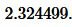
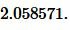
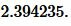
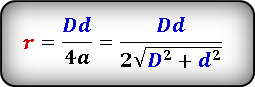
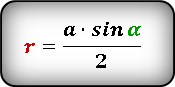
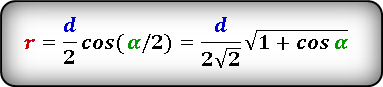
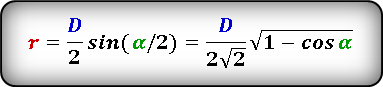
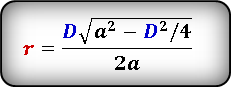
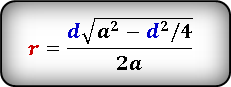
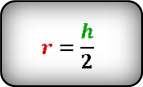
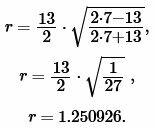
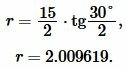
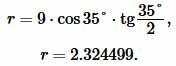
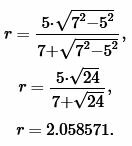
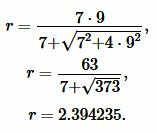
![Rendered by QuickLaTeX.com [r = frac{{2 cdot frac{a}{2}sqrt {{b^2} - frac{{{a^2}}}{4}} }}{{a + 2b}} = frac{{asqrt {{b^2} - frac{{{a^2}}}{4}} }}{{a + 2b}}.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-0a2c558a4cbf6011d9c11d2b0fca702c_l3.png)