Pv nrt как найти t

Как найти т из уравнения менделеева клапейрона

Уравнение Менделеева-Клапейрона — уравнение состояния для идеального газа, отнесенное к 1 молю газа. В 1874 г. Д. И. Менделеев на основе уравнения Клапейрона объединив его с законом Авогадро, используя молярный объем V_m и отнеся его к 1 молю, вывел уравнение состояния для 1 моля идеального газа:

pV = RT , где R — универсальная газовая постоянная,

R = 8,31 Дж/(моль . К)

Уравнение Клапейрона-Менделеева показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа. Для произвольной массы газа М, молярная масса которого m: pV = (М/m) . RT. или pV = N_АkT,

где N_А — число Авогадро, k — постоянная Больцмана.

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из параметров — давление, объем или температура — остается постоянным, а изменяются только остальные два и получить теоретически газовые законы для этих условий изменения состояния газа.

Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.

Изотермический процесс — процесс изменения состояния системы при постоянной температуре. Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон Бойля — Мариотта.

Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой — термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P₁V₁=P₂V₂=const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.

Изобарный процесс — процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака. Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const. Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.

Изохорный процесс — процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля. Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const. Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов.

Итак, из закона pV = (М/m) . RT выводятся следующие законы:

p = const => V/T = const — закон Гей — Люссака .

V= const => p/T = const — закон Шарля

Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. Парциальное давление — это такое давление, которое производил бы газ, если бы он один занимал весь объем, равный объему смеси.

Некоторых, возможно, интересует вопрос, каким образом удалось определить постоянную Авогадро N_A = 6,02·10 23 ? Значение числа Авогадро было экспериментально установлено только в конце XIX – начале XX века. Опишем один из таких экспериментов.

В откачанный до глубокого вакуума сосуд объемом V = 30 мл поместили навеску элемента радия массой 0,5 г и выдержали там в течение одного года. Было известно, что за секунду 1 г радия испускает 3,7·10 10 альфа-частиц. Эти частицы представляют собой ядра гелия, которые тут же принимают электроны из стенок сосуда и превращаются в атомы гелия. За год давление в сосуде выросло до 7,95·10 -4 атм (при температуре 27 о С). Изменением массы радия за год можно пренебречь. Итак, чему равна N_A?

Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:

N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.

Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/N_A. Отсюда:

N_A = NRT = 5,83 . 10 17 . 0,0821 . 300 = 6,02 . 10 23

PV 7,95 . 10 -4 . 3 . 10 -2

В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.

Уравнение Клапейрона-Менделеева

Что такое уравнение Клапейрона-Менделеева

Идеальный газ — это газ, в котором пренебрегают взаимодействием молекул газа между собой.

Идеальными считают разреженные газы. Особенно близкими к идеальным считают гелий и водород.

Идеальный газ — это упрощенная математическая модель, которая широко применяется для описания свойств и поведения реальных газов при атмосферном давлении и комнатной температуре.

Давление, объем и температура — это основные параметры состояния системы, и они связаны друг с другом. Соотношение, при котором определяется данная связь, называется уравнением состояния данного газа.

Существует эквивалентная макроскопическая формулировка идеального газа — это такой газ, который одновременно будет подчиняться закону Бойля-Мариотта и Гей-Люссака, то есть:

p V = c o n s t * T

В представленном выше уравнении состоянии газа под const подразумевается количество молей.

Свойства классического и квазиклассического идеального газа описываются уравнением состояния идеального газа, которое называется уравнением Менделеева-Клапейрона, ниже представлена формула Менделеева-Клапейрона.

p V = m M R T = n R T , где m — масса газа, M — молярная масса газа, R = 8 , 314 Д ж / ( м о л ь * К ) — универсальная газовая постоянная, T — температура (К), n — количество молей газа.

Таким образом давление и объем прямо пропорциональны количеству молей и температуре.

Также уравнение Клапейрона-Менделеева можно записать в ином виде:

p V = N k T , где N — это количество молекул газа массой m , k = 1 , 38 * 10 — 23 Д ж / К — постоянная Больцмана, которая определяет «долю» газовой постоянной, приходящуюся на одну молекулу и определяется по формуле:

N = m N A M , где

N A = 6 . 02 * 10 23 м о л ь — 1 ; — это постоянная Авогадро.

Какое значение имеет универсальная газовая постоянная

Универсальная газовая постоянная (R) — это величина, которая является константой, численно равная работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 K.

Значение данной константы находится как произведение постоянной Больцмана ( k = 1 , 38 * 10 — 23 Д ж / К ) на число Авогадро ( N A = 6 . 02 * 10 23 м о л ь — 1 ) . Таким образом универсальная газовая постоянная принимает следующее значение: R = 8 , 314 Д ж / ( м о л ь * К ) .

Постоянную Больцмана используют в формулах, описывающих изучаемое явление или поведение рассматриваемого объекта с микроскопической точки зрения, тогда как универсальная газовая постоянная более удобна при расчетах, касающихся макроскопических систем, когда число частиц задано в молях.

Связь с другими законами состояния идеального газа

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один трех макропараметров (давление, температура или объем) — остаются неизменными.

Количественные зависимости между двумя параметрами газа при фиксированном третьем параметре называют газовыми законами, которые связывают эти параметры.

Изопроцессы — это термодинамические процессы, во время протекания которых количество вещества и один из макропараметров состояния: давление, объем, температура или энтропия — остается неизменным.

В зависимости от того, какой параметр остается неизменным различают разные процессы, которые выражаются законами, являющимися следствием уравнения состояния газа:

• изотермический процесс (T=const);
• изохорный процесс (V=const);
• изобарный процесс (p=const).

Изотермический процесс (T=const)

Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.

Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой — термостатом. Им может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.

Согласно уравнению Клапейрона-Менделеева, в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же, то есть постоянно:

Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Именно поэтому он называется закон Бойля-Мариотта.

Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха).

Зависимость давления газа от объема при постоянной температуре изображается графической кривой — изотермой. Изотерма для различных температур представлена в координатах pV на рис.1. и представляет собой гиперболу.

Рис.1. Изотерма в pV — координатах.

Изохорный процесс (V=const)

Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.

Из уравнения состояния следует, что отношение давлений газа данной массы при постоянно объеме равно отношению его абсолютных температур:

p 1 p 2 = T 1 T 2

Газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.

Так, если в качестве одного из состояний газа выбрать состояние газа при нормальных условиях, тогда

p = p 0 T T 0 = p 0 γ T

Коэффициент γ называют температурным коэффициентом давления газа. Он одинаков для всех газов.

Зависимость давления газа от температуры при постоянном объеме изображается графически прямой, которая называется изохорой (Рис.2).

Рис.2 Изображение изохоры в pT-координатах.

Изобарный процесс (p=const)

Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным.

Из уравнения Клапейрона-Менделеева вытекает, что отношение объемов газа данной массы при постоянном давлении равно отношению его абсолютных температур.

V 1 V 2 = T 1 T 2

Если в качестве второго состояния газа выбрать состояние при нормальных условиях (нормальном атмосферном давлении, температуре таяния льда) следует:

V = V 0 T T 0 = V 0 α T

Этот газовый закон был установлен экспериментально в 1802 г французским ученым Гей-Люссаком.

Закон Гей-Люссака: объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре.

Коэффициент α называют температурным коэффициентом объемного расширения газов.

Зависимость объема газа от температуры при постоянном давлении изображается графической прямой, которая называется изобарой (Рис.3).

Рис. 3. Изобара в VT-координатах.

Использование универсального уравнения для решения задачи

В реальности проводятся различные физико-химические процессы. Рассмотрим каким образом уравнение состояния идеального газа и законы, связанные с ним находят применение для решения физических и химических задач.

Определить давление кислорода в баллоне объемом 1 м 3 при температуре t = 27 C o . Масса кислорода 1 кг.

Так как в уравнении даны объем и температура — два из трех макроскопических параметров, а третий (давление) нужно определить, то мы можем использовать уравнение Клапейрона-Менделеева:

p V = n R T = m M R T

Не забываем перевести температуру в Кельвины:

T = t + 273 = 27 + 273 = 300 K

Молярная масса кислорода известна из таблицы Менделеева:

M ( O 2 ) = 2 * 16 = 32 г / м о л ь = 32 * 10 — 3 к г / м о л ь

Выразим из уравнения состояния давления и поставим все имеющиеся данные:

p = n R T V = m R T M V = 1 * 8 . 31 * 300 32 * 10 — 3 * 1 = 77 . 906 П а = 78 к П а

Ответ: p = 78 кПа.

Каким может быть наименьший объем баллона, содержащего кислород массой 6,4 кг, если его стенки при t = 20 C o выдерживают p = 1568 Н / с м 2 ?

Используем уравнение Менделеева-Клапейрона, из которого выражаем объем кислорода, который нужно найти:

p = n R T V = m R T M V

Молярная масса кислорода предполагается равной:

M ( O 2 ) = 2 * 16 = 32 г / м 3

Не забываем перевести температуру в Кельвины:

T = t + 273 = 20 + 273 = 293 K

Переводим давление: p = 15680000 Па

Выражаем из уравнения Клапейрона-Менделеева объем и подставляем значения, данные в условиях задачи:

V = n R T p = m R T M p = 6 . 4 * 8 . 31 * 293 15680000 * 32 * 10 — 3 = 3 . 1 * 10 — 2 м 3 = 31 л .

Используя уравнение состояния идеального газа, доказать, что плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .

Согласно уравнению Менделеева-Клапейрона:

p = n R T V = m R T M V

Плотность — это величина, характеризующая массу некоторого объема и находится по формуле:

ρ = m V и л и V = m ρ

Тогда p m ρ = n R T = m R T M

Откуда выражаем плотность газа:

Для водорода эта формула запишется следующим образом:

ρ H 2 = p M H 2 R T

По условию задачи водород и любой другой газ находятся при одинаковых условиях, откуда следует, что:

ρ H 2 M H 2 = p R T

Поставим последнее выражение в выражение для плотности любого газа:

ρ = M * ρ H 2 M H 2

Молярная масса водорода, исходя из таблицы Менделеева равна 2 г/моль и тогда. Молекулярная масса численно равная молярной и представляет собой массу молекулы в атомных единицах, поэтому в дальнейшем мы совершили переход к молекулярной массе.

ρ = M r * ρ H 2 2

Вывод: плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .

Рассмотрим несколько задач на законы, связанные с уравнение Клапейрона-Менделеева, то есть на изотермические, изохорные, изобарные процессы.

При уменьшении давления газа в 2,5 раза его объем увеличился на 12 л. Какой объем занимал газ в начальном состоянии, если температура на протяжении всего процесса оставалась постоянной?

По условию задачи температура в ходе всего процесса оставалась постоянной, откуда следует, что у нас изотермический процесс, и мы можем воспользоваться для решения законом Бойля-Мариотта.

p 1 V 1 = p 2 V 2 , г д е p 1 – давление газа в начальном состоянии (до расширения), V 1 — объем газа в начальном состоянии, p 2 = p 1 2 . 5 — давление газа в конечном состоянии (после расширения), V 2 = V 1 + ∆ V — объем газа в конечном состоянии.

Откуда можем найти начальный объем:

p 1 V 1 = p 1 2 . 5 ( V 1 + ∆ V ) = p 1 2 . 5 V 1 + p 1 2 . 5 ∆ V

V 1 ( p 1 — p 1 2 . 5 ) = p 1 2 . 5 ∆ V

p 1 2 . 5 V 1 ( 2 . 5 — 1 ) = p 1 2 . 5 ∆ V

V 1 = ∆ V 1 , 5 = 8 л

Ответ: первоначальный объем газа был равен 8 л.

Газ находится в баллоне при температуре 400 К. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 1,5 раза?

Так как нагревание газа по условиям данной задачи происходит при постоянном объеме, значит перед нами изохорный процесс.

При изохорном процессе:

p 1 T 1 = p 2 T 2

T 2 = p 2 T 1 p 1

p 2 p 1 = 1 . 5 T 2 = 1 . 5 * T 1 = 1 . 5 * 400 = 600 K

При 27°C объем газа равен 600 мл. Какой объем займет газ при 57°C, если давление будет оставаться постоянным?

Так как давление по условию остается постоянным, то можем использовать закон Гей-Люссака.

V 1 V 2 = T 1 T 2

V_2 – искомый объем

Для правильного расчета необходимо перевести температуры из Цельсий в Кельвины:

T 1 = 273 + 27 = 300 K

T 2 = 273 + 57 = 330 K

T 2 V 1 T 1 = V 2

V 2 = ( 600 * 330 ) / 300 = 660 м л

Газ в трубе плавильной печи охлаждается от температуры t 1 = 1150 ° С д о t 2 = 200 ° С . Во сколько раз увеличивается плотность газа при этом? Давление газа не меняется.

Так как по условию задания давления газа не изменяется, значит перед нами изобарный процесс. Для решения воспользуемся законом Гей-Люссака:

V 1 V 2 = T 1 T 2

Перейдем к абсолютной температуре:

T 1 = 1150 + 273 = 1423 K

T 2 = 200 + 273 = 473 K

Масса газа: m = ρ 1 V 1 = ρ 2 V 2

Использование этих формул приводит к следующему:

Уравнение Клапейрона-Менделеева (уравнение состояния идеального газа).

Уравнение Клапейрона-Менделеева (1834 г) устанавливает связь между объемом V, давлением P и абсолютной температурой Т для газа:

n – число молей газа ;

P – давление газа, Па;

V – объем газа, м 3 ;

T – абсолютная температура газа, К;

R – универсальная газовая постоянная 8,314 Дж/моль×K.

Если объём газа выражен в литрах, то уравнение Клапейрона-Менделеева записывается в виде:

Из уравнения Клапейрона-Менделеева следует три закона:

Термодинамический
процесс
(тепловой процесс) – изменение
макроскопического состояния
термодинамической системы. Если разница
между начальным и конечным состояниями
системы бесконечно мала, то такой процесс
называют элементарным (инфинитезимальным).

Система,
в которой идёт тепловой процесс,
называется рабочим телом.

Тепловые
процессы можно разделить на равновесные
и неравновесные. Равновесным называется
процесс, при котором все состояния,
через которые проходит система, являются
равновесными состояниями. Такой процесс
приближённо реализуется в тех случаях,
когда изменения происходят достаточно
медленно, т. е. процесс является
квазистатическим.

Тепловые
процессы можно разделить на обратимые
и необратимые. Обратимым называется
процесс, который можно провести в
противоположном направлении через все
те же самые промежуточные состояния.

Виды
тепловых процессов:

Адиабатный
процесс — без теплообмена с окр. средой;

Изохорный
процесс — происходящий при постоянном
объёме;

Изобарный
процесс — происходящий при постоянном
давлении;

Изотермический
процесс — происходящий при постоянной
температуре;

Изоэнтропийный
процесс — происходящий при постоянной
энтропии;

Изоэнтальпийный
процесс — происходящий при постоянной
энтальпии;

Политропный
процесс — происходящий при постоянной
теплоёмкости.

Уравнение
Менделеева-Клайперона (уравнение
состояния идеального газа):

PV
= nRT,
где n
– число молей газа, P
– давление газа, V
– объем газа, T
– температура газа, R
– универсальная газовая постоянная

Изопроцессы
идеального газа. Их изображение в P—V
диаграммах.

1)
Изобарный процесс p
= const,
V/T
= const

2)
Изохорный процесс V
= const,
p/T
= const

3)
Изотермический процесс T
= const,
pV
= const

Термодинамические
процессы. Уравнение Менделеева-Клапейрона.
Изопроцессы идеального газа. Их
изображение на Р-V
диаграммах.

Термодинамические
процессы. Совокупность изменяющихся
состояний рабочего тела называется
термодинамическим процессом.

Идеальный
газ — изучаемый в термодинамике
воображаемый газ, у которого отсутствуют
силы межмолекулярного притяжения н
отталкивания, а сами молекулы представляют
собой материальные точки, не имеющие
объема. Многие реальные газы по своим
физическим свойствам весьма близки к
идеальному газу.

Основными
процессами в термодинамике являются:

• изохорный,
  протекающий при постоянном объеме;

• изобарный,
  протекающий при постоянном давлении;

• изотермический,
  происходящий при постоянной температуре;

• адиабатный,
  при котором теплообмен с окружающей
  средой отсутствует;

Изохорный
процесс

При
изохорном процессе выполняется условие
v= const.

Из
уравнения состояния идеального газа
(pv=RT) следует:

 p/T=R/v= const,

т.
е. давление газа прямо пропорционально
его абсолютной температуре:

 p₂/p₁=T₂/T₁.

Работа
расширения в изохорном процессе равна
нулю (l= 0), так как объем рабочего
тела не меняется (Δv= const).

Количество
теплоты, подведенной к рабочему телу в
процессе 1-2 при c_v= const
определяется по формуле:

q=c_v(T₂
—  T₁). 

Т.
к.l= 0, то на основании первого закона
термодинамики Δu=q, а значит
изменение внутренней энергии можно
определить по формуле:

Δu=c_v(T₂
— T₁).

Изменение
энтропии в изохорном процессе определяется
по формуле:

s₂
– s₁=
Δs =
c_vln(p₂/p₁)
= c_vln(T₂/T₁).

Изобарный
процесс

Изобарным
называется процесс, протекающий при
постоянном давлении p= const. Из
уравнения состояния идеального газа
слуедует:

v/T=R/p=const

или

 v₂/v₁=T₂/T₁,

т.
е. в изобарном процессе объем газа
пропорционален его абсолютной температуре.

Работа
будет равна:

l=p(v₂ – v₁).

Т.
к. pv₁=RT₁иpv₂=RT₂,
то

l=R(T₂ – T₁).

Количество
теплоты при c_p= const
определяется по формуле:

q=c_p(T₂
– T₁).

Изменение
энтропии будет равно: 

s₂
– s₁=
Δs =
c_pln(T₂/T₁).

Изотермический
процесс

При
изотермическом процессе температура
рабочего тела остается постоянной T= const, следовательно:

pv
= RT =
const

или

p₂/p₁=v₁/v₂,

т.
е. давление и объем обратно пропорциональны
друг другу, так что при изотермическом
сжатии давление газа возрастает, а при
расширении – снижается.

Работа
процесса будет равна:

l=RTln (v₂ – v₁)
=RTln (p₁ – p₂).

Так
как температура остается неизменной,
то и внутренняя энергия идеального газа
в изотермическом процессе остается
постоянной (Δu= 0) и вся подводимая
к рабочему телу теплота полностью
превращается в работу расширения:

q=l.

При
изотермическом сжатии от рабочего тела
отводится теплота в количестве, равном
затраченной на сжатие работе.

Изменение
энтропии равно:

s₂
– s₁= Δs=Rln(p₁/p₂)
=Rln(v₂/v₁).

Адиабатный
процесс

Адиабатным
называется процесс изменения состояния
газа, который происзодит без теплообмена
с окружающей средой. Так как dq= 0,
то уравнение первого закона термодинамики
для адиабатного процесса будет иметь
вид:

du+pdv= 0

или

Δu+l= 0,

следовательно

Δu=
—l. 

В
адиабатном процессе работа расширения
совершается только за счет расходования
внутренней энергии газа, а при сжатии,
происходящем за счет действия внешних
сил, вся совершаемая ими работа идет на
увеличение внутренней энергии газа.

Обозначим
теплоемкость в адиабатном процессе
через c_ад, и условие dq=
0 выразим следующим образом:

dq=c_адdT= 0.

Это
условие говорит о том, что теплоемкость
в адиабатном процессе равна нулю (c_ад= 0).

Известно,
что

с_p/c_v
=k

и
уравнение кривой адиабатного процесса
(адиабаты) в p, v-диаграмме имеет
вид:

pv^k= const.

В
этом выражении kносит названиепоказателя адиабаты(так же
ее называют коэффициентом Пуассона).

Значения
показателя адиабаты k для некоторых
газов:

k_{воздуха}= 1,4

k_{перегретого
пара}= 1,3

k_{выхлопных
газов ДВС}= 1,33

k_{насыщенного
влажного пара}= 1,135

Из
предыдущих формул следует:

l=
— Δu
= c_v(T₁
– T₂);

i₁
– i₂=
c_p(T₁
– T₂).

Техническая
работа адиабатного процесса (l_техн)
равна разности энтальпий начала и конца
процесса (i₁ – i₂).

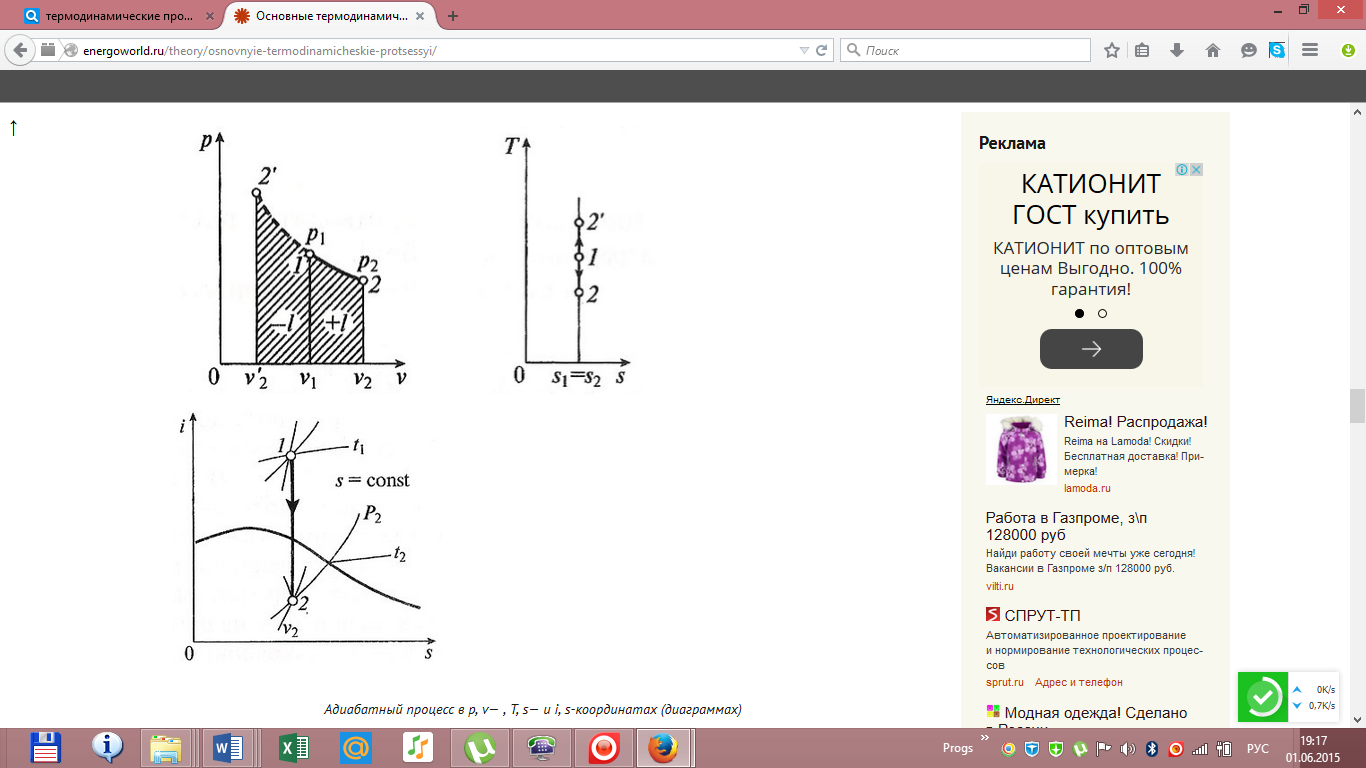
Адиабатный
процесс, происходящий без внутреннего 
трения в рабочем теле, называется
изоэнтропийным. ВT, s-диаграмме
он изображается вертикальной линией.

Обычно
реальные адиабатные процессы протекают
при наличии внутреннего трения в рабочем
теле, в результате чего всегда выделяется
теплота, которая сообщается самому
рабочему телу. В таком случае ds>
0, и процесс называетсяреальным
адиабатным процессом.

Уравнение
Менделеева-Клапейрона

Газы
нередко бывают реагентами и продуктами
в химических реакциях. Не всегда удается
заставить их реагировать между собой
при нормальных условиях. Поэтому нужно
научиться определять число молей газов
в условиях, отличных от нормальных.

Для
этого используют уравнение состояния
идеального газа(его также называют
уравнением Клапейрона-Менделеева):

PV
= nRT

где
n– число молей газа;

P
– давление газа (например, в атм;

V
– объем газа (в литрах);

T
– температура газа (в кельвинах);

R
– газовая постоянная (0,0821 л·атм/моль·K).

Например,
в колбе объемом 2,6 л находится кислород
при давлении 2,3 атм и температуре
26^оС. Вопрос: сколько молей O₂содержится в колбе?

Из
газового закона найдем искомое число
молей n:

Не
следует забывать преобразовывать
температуру из градусов Цельсия в
кельвины: (273 ^оС + 26^оС) = 299 K.
Вообще говоря, чтобы не ошибиться в
подобных вычислениях, нужно внимательно
следить за размерностью величин,
подставляемых в уравнение
Клапейрона-Менделеева. Если давление
дается в мм ртутного столба, то нужно
перевести его в атмосферы, исходя из
соотношения: 1атм = 760 мм рт. ст.
Давление, заданное в паскалях (Па), также
можно перевести в атмосферы, исходя из
того, что 101325 Па = 1атм.

Билет
16

Вывод
основного уравнения молекулярно-кинетической
теории. Число степеней свободы молекулы.
Закон распределения энергии по степеням
свободы.

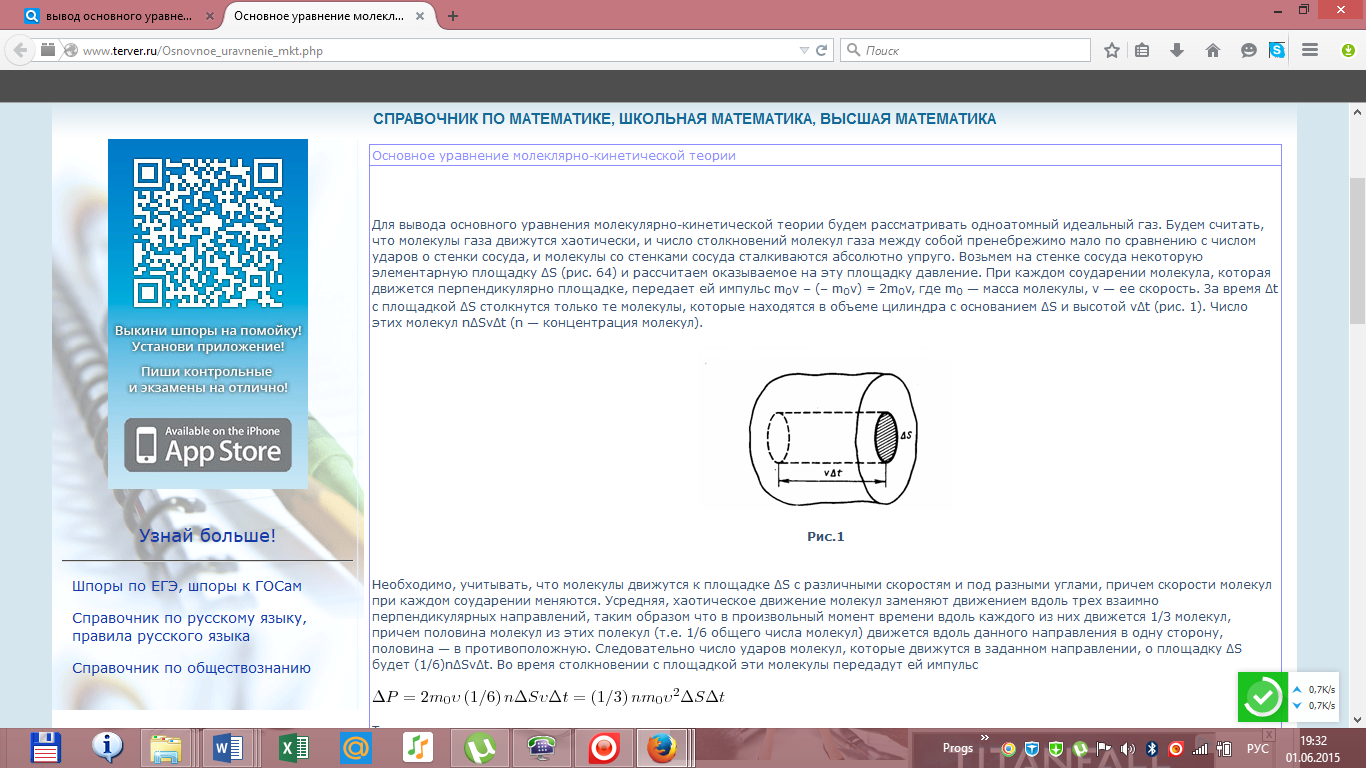
Вывод
основного уравнения МКТ.

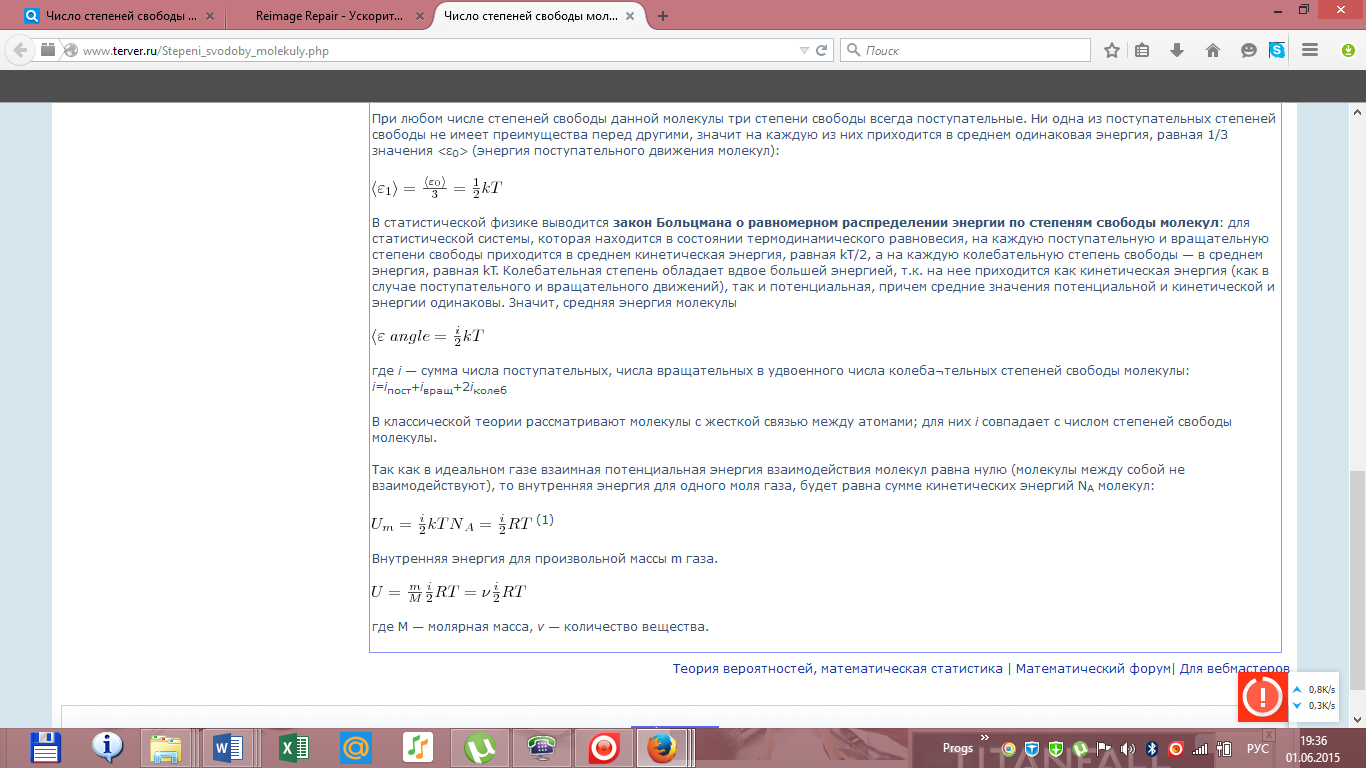
Число
степеней свободы молекулы. Закон
распределения энергии по степеням
свободы.

Билет
17.

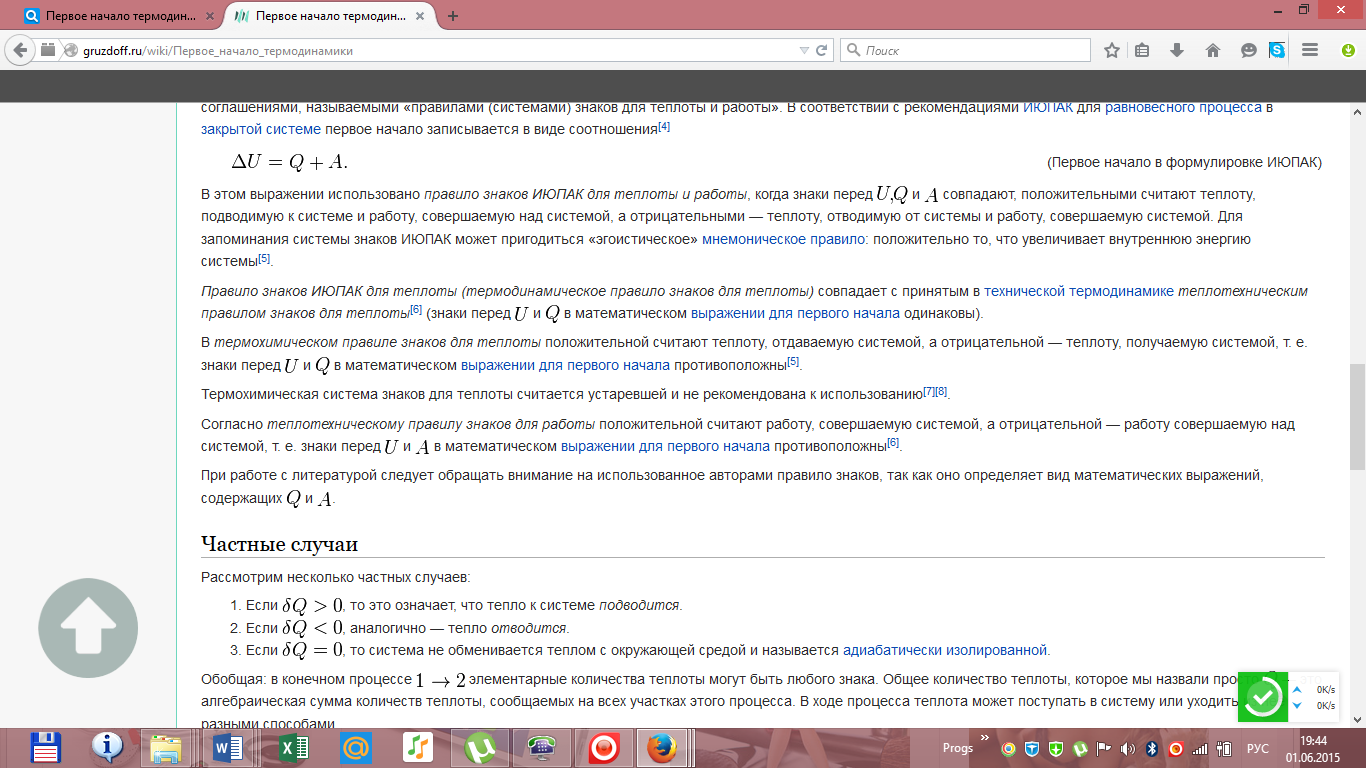
Первое
начало термодинамики. Работа газа при
изменении объема. Вычислить работу
изотермического расширения газа.

Количество
теплоты,
полученное системой, идёт на изменение
её внутренней энергии и совершение
работы против внешних сил

Изменение
внутренней энергии системы при переходе
её из одного состояния в другое равно
сумме работы внешних сил и количества
теплоты, переданного системе, то есть,
оно зависит только от начального и
конечного состояния системы и не зависит
от способа, которым осуществляется этот
переход. В циклическом процессе внутренняя
энергия не изменяется.

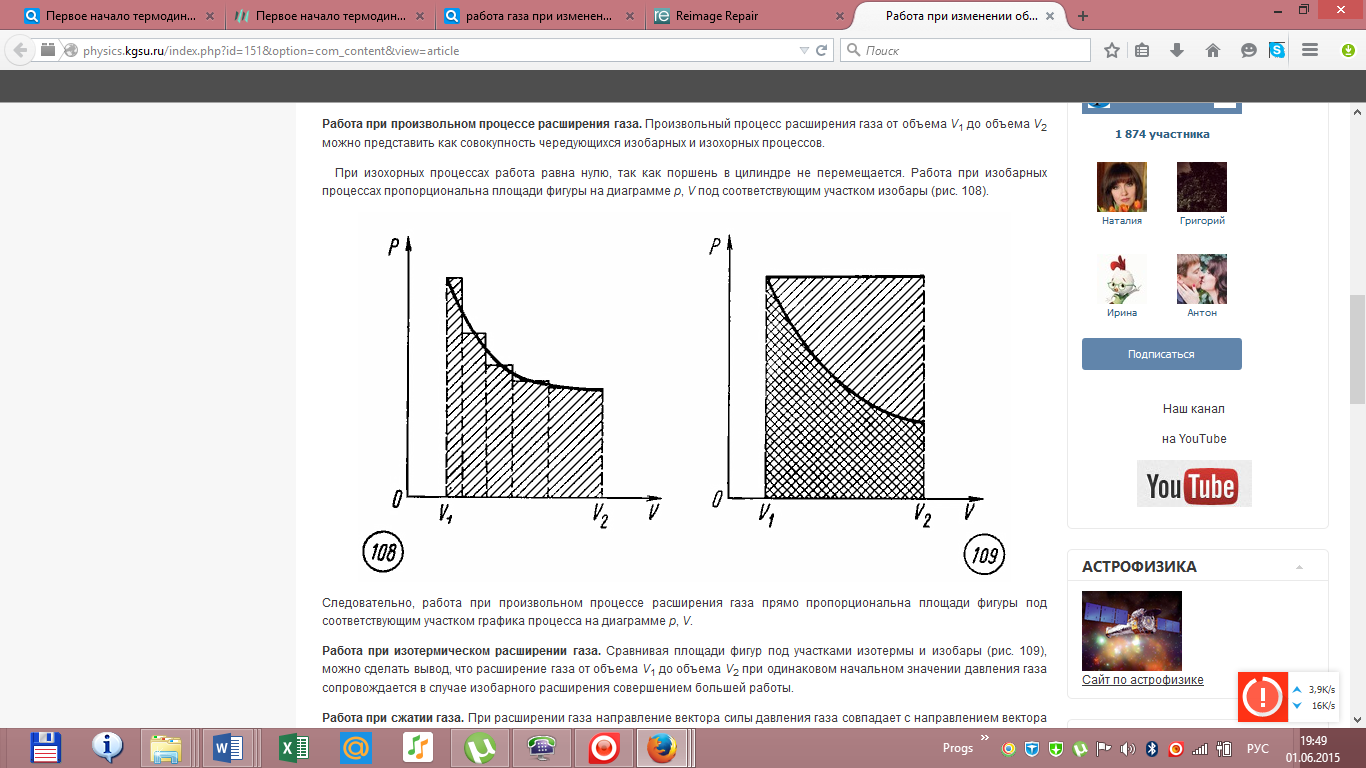
Работа
при изотермическом расширении газа
вычисляется как площадь фигуры под
графиком процесса.

Билет
18.

Теплоемкость
идеального газа.

Если
в результате теплообмена телу передается
некоторое количество теплоты, то
внутренняя энергия тела и его температура
изменяются. Количество теплоты Q,
необходимое для нагревания 1 кг
вещества на 1 К называют удельной
теплоемкостью вещества c. c = Q / (mΔT).

Во многих случаях удобно использовать
молярную теплоемкость C:

где
M – молярная масса вещества.

Определенная
таким образом теплоемкость не является
однозначной характеристикой вещества.
Согласно первому закону термодинамики
изменение внутренней энергии тела
зависит не только от полученного
количества теплоты, но и от работы,
совершенной телом. В зависимости от
условий, при которых осуществлялся
процесс теплопередачи, тело могло
совершать различную работу. Поэтому
одинаковое количество теплоты, переданное
телу, могло вызвать различные изменения
его внутренней энергии и, следовательно,
температуры.

Такая
неоднозначность определения теплоемкости
характерна только для газообразного
вещества. При нагревании жидких и твердых
тел их объем практически не изменяется,
и работа расширения оказывается равной
нулю. Поэтому все количество теплоты,
полученное телом, идет на изменение его
внутренней энергии. В отличие от жидкостей
и твердых тел, газ в процессе теплопередачи
может сильно изменять свой объем и
совершать работу. Поэтому теплоемкость
газообразного вещества зависит от
характера термодинамического процесса.
Обычно рассматриваются два значения
теплоемкости газов: C_V
– молярная теплоемкость в изохорном
процессе (V = const) и C_p
– молярная теплоемкость в изобарном
процессе (p = const).

В
процессе при постоянном объеме газ
работы не совершает: A = 0. Из первого
закона термодинамики для 1 моля газа
следует

C_VΔT = ΔU.

Изменение
ΔU внутренней энергии газа прямо
пропорционально изменению ΔT его
температуры.

Для
процесса при постоянном давлении первый
закон термодинамики дает:

p (V₂– V₁) = C_VΔT + pΔV,

где
ΔV – изменение объема 1 моля идеального
газа при изменении его температуры на
ΔT. Отсюда следует:

Отношение
ΔV / ΔT может быть найдено из уравнения
состояния идеального газа, записанного
для 1 моля:

где
R – универсальная газовая постоянная.
При p = const

Таким
образом, соотношение, выражающее связь
между молярными теплоемкостями C_p
и C_V,
имеет вид (формула Майера):

Молярная
теплоемкость C_p
газа в процессе с постоянным давлением
всегда больше молярной теплоемкости
C_V
в процессе с постоянным объемом

Отношение
теплоемкостей в процессах с постоянным
давлением и постоянным объемом играет
важную роль в термодинамике. Оно
обозначается греческой буквой γ.

Билет
19.

Цикл
Карно. Тепловая и холодильная машины.
КПД цикла Карно.

В
термодинамике цикл
Карно́ или процесс
Карно — это обратимый
круговой процесс, состоящий из двух
адиабатических и двух изотермических
процессов. В процессе Карно термодинамическая
система выполняет механическую работу
и обменивается теплотой с двумя тепловыми
резервуарами, имеющими постоянные, но
различающиеся температуры. Резервуар
с более высокой температурой называется
нагревателем, а с более низкой
температурой — холодильником.

Цикл
Карно назван в честь французского
учёного и инженера Сади Карно, который
впервые его описал в своём сочинении
«О движущей силе огня и о машинах,
способных развивать эту силу» в 1824 году.

Поскольку
обратимые процессы могут осуществляться
лишь с бесконечно малой скоростью,
мощность тепловой машины в цикле Карно
равна нулю. Мощность реальных тепловых
машин не может быть равна нулю, поэтому
реальные процессы могут приближаться
к идеальному обратимому процессу Карно
только с большей или меньшей степенью
точности. В цикле Карно тепловая машина
преобразует теплоту в работу с максимально
возможным коэффициентом полезного
действия из всех тепловых машин, у
которых максимальная и минимальная
температуры в рабочем цикле совпадают
соответственно с температурами
нагревателя и холодильника в цикле
Карно

.
Пусть тепловая машина
состоит из нагревателя
с температурой Тн, холодильника с
температурой Тх и рабочего
тела.

Цикл
Карно состоит из четырёх обратимых
стадий, две из которых осуществляются
при постоянной температуре (изотермически),
а две — при постоянной энтропии
(адиабатически). Поэтому цикл Карно
удобно представить в координатах T
(температура)
и S
(энтропия).

1.
Изотермическое
расширение
(на рис. 1 — процесс A→Б). В начале
процесса рабочее тело имеет температуру
Тн, то есть температуру нагревателя.
Затем тело приводится в контакт с
нагревателем, который изотермически
(при постоянной температуре) передаёт
ему количество
теплоты
Q.
При этом объём рабочего тела увеличивается,
оно совершает механическую работу, а
его энтропия возрастает.

2.
Адиабатическое
расширение
(на рис. 1 — процесс Б→В). Рабочее тело
отсоединяется от нагревателя и продолжает
расширяться без теплообмена с окружающей
средой. При этом температура тела
уменьшается до температуры холодильника
Тх, тело совершает механическую работу,
а энтропия остаётся постоянной.

3.
Изотермическое
сжатие
(на рис. 1 — процесс В→Г). Рабочее
тело, имеющее температуру Тн, приводится
в контакт с холодильником и начинает
изотермически сжиматься под действием
внешней силы, отдавая холодильнику
количество теплоты Q.
Над телом совершается работа, его
энтропия уменьшается.

4.
Адиабатическое
сжатие
(на рис. 1 — процесс Г→А). Рабочее тело
отсоединяется от холодильника и сжимается
под действием внешней силы без теплообмена
с окружающей средой. При этом его
температура увеличивается до температуры
нагревателя, над телом совершается
работа, его энтропия остаётся постоянной.

Обратный
цикл Карно

В
термодинамике
холодильных установок и тепловых насосов
рассматривают
обратный
цикл Карно,
состоящий из следующих стадии:
адиабатического сжатия за счёт совершения
работы (на рис. 1 — процесс В→Б);
изотермического сжатия с передачей
теплоты более нагретому тепловому
резервуару (на рис. 1 — процесс Б→А);
адиабатического расширения (на рис. 1 —
процесс
А→Г); изотермического расширения с
отводом теплоты от более холодного
теплового резервуара (на рис. 1 —
процесс Г→В).

Билет
20.

Второе
начало термодинамики. Энтропия. Третье
начало термодинамики.

Второе
начало термодинамики —
физический принцип, накладывающий
ограничение на направление процессов,
которые могут происходить в термодинамических
системах.

Второе
начало термодинамики запрещает так
называемые вечные
двигатели второго рода,
показывая, что коэффициент
полезного действия
не может равняться единице, поскольку
для кругового процесса температура
холодильника не может равняться
абсолютному нулю (невозможно построить
замкнутый цикл, проходящий через точку
с нулевой температурой).

Второе
начало термодинамики является постулатом,
не доказываемым в рамках классической
термодинамики.
Оно было создано на основе обобщения
опытных фактов и получило многочисленные
экспериментальные подтверждения.

Постулат
Клаузиуса:
«Невозможен
круговой процесс, единственным результатом
которого является передача теплоты от
менее нагретого тела к более нагретому»
(такой
процесс называется процессом
Клаузиуса).

Постулат
Томсона
(Кельвина):
«Невозможен
круговой процесс, единственным результатом
которого было бы производство работы
за счет охлаждения теплового резервуара»
(такой процесс называется процессом
Томсона).

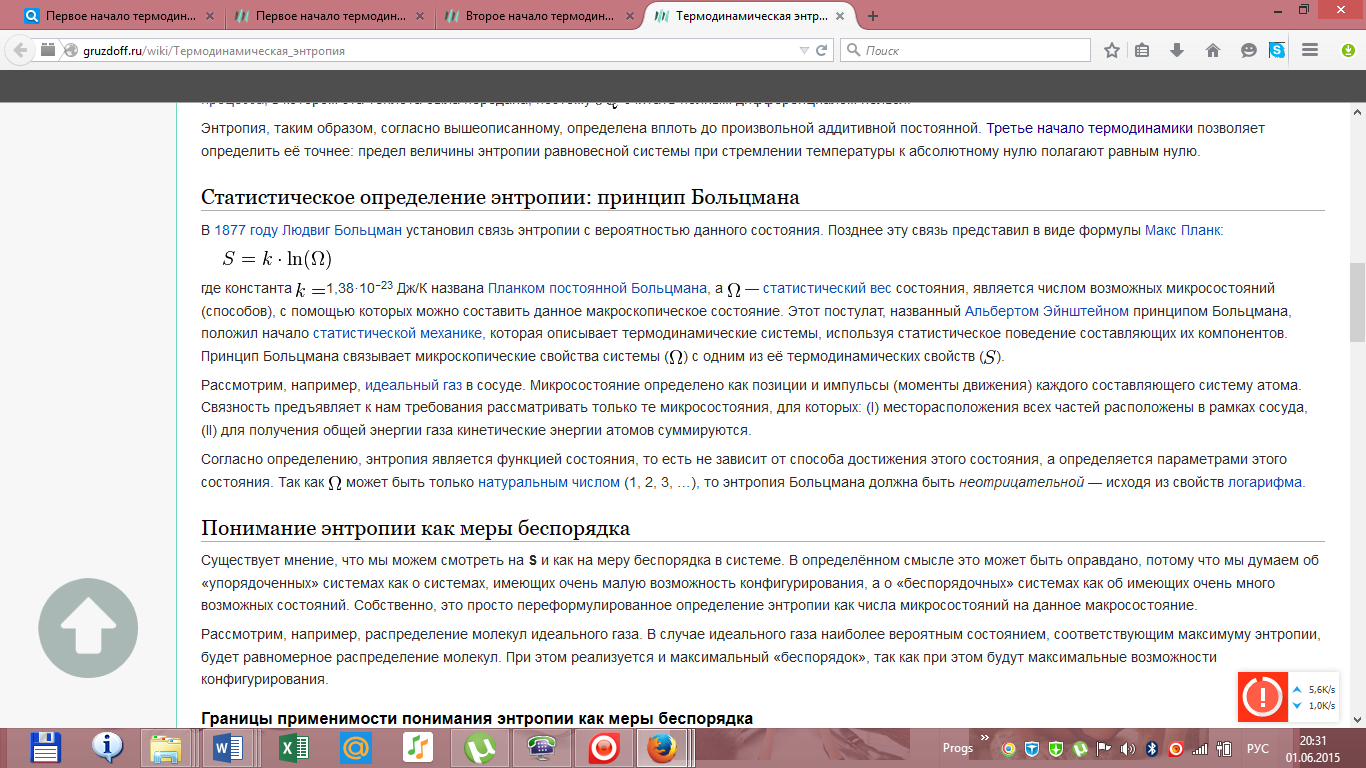
Энтропия
изолированной системы не может
уменьшаться» (закон
неубывания энтропии).

Такая
формулировка основывается на представлении
об энтропии как о функции
состояния
системы, что также должно быть
постулировано.

В
состоянии с максимальной энтропией
макроскопические необратимые процессы
(а процесс передачи тепла всегда является
необратимым из-за постулата Клаузиуса)
невозможны.

Третье
начало термодинамики
(теорема
Нернста) —
физический принцип, определяющий
поведение энтропии
при приближении температуры
к абсолютному
нулю.
Является одним из постулатов
термодинамики,
принимаемым на основе обобщения
значительного количества экспериментальных
данных.

Третье
начало термодинамики может быть
сформулировано так:

«Приращение
энтропии при абсолютном нуле температуры
стремится к конечному пределу, не
зависящему от того, в каком равновесном
состоянии находится система».

Третье
начало термодинамики относится только
к равновесным состояниям.

Поскольку
на основе второго начала термодинамики
энтропию можно определить только с
точностью до произвольной аддитивной
постоянной (то есть, определяется не
сама энтропия, а только её изменение).
Третье начало термодинамики может быть
использовано для точного определения
энтропии. При этом энтропию равновесной
системы при абсолютном нуле температуры
считают равной нулю.

Третье
начало термодинамики позволяет находить
абсолютное значение энтропии, что нельзя
сделать в рамках классической термодинамики
(на основе первого и второго начал
термодинамики).

Термодинамическая
энтропия
S,
часто просто именуемая энтропия,
— физическая
величина,
используемая для описания термодинамической
системы,
одна из основных термодинамических
величин.
Энтропия является функцией
состояния
и широко используется в термодинамике,
в том числе химической.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Идеальный газ является математической моделью газа. Эту модель мы часто можем встретить в задачках по термодинамике газов. Бок о бок вместе с этим понятием идет и Закон Идеального газа. Он определяет давление, температуру и объем идеального газа (соотношение всех этих элементов). Рассчитывается все это дело по следующей формуле: pV = nRT, где n – молекулы газа, R – газовая постоянная. В физике мы называем этот закон уравнением состояния вещества.
Конечно же, вы можете произвести все расчеты по уравнению Идеального газа самостоятельно. Этот процесс займет у вас некоторое количество времени. Если же вы хотите все ускорить и правильно рассчитать давление, объем или температуру газа, вы можете воспользоваться нашим легким и универсальным онлайн-калькулятором. Все необходимые расчеты будут произведены за вас!

Онлайн калькулятор рассчитывает Закон Идеального Газа:

Уравнение: PV = nRT

где,
Давление (P) = nRT / V,
Объем V = nRT / P,
Моль газа (n) = PV / RT,
Температура (T) = PV / nR,
R = 8,314 Дж К-1 моль-1, идеальный газ постоянно.

Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:

Примеры задач на уравнение Менделеева-Клапейрона

1. В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
   Вопрос: сколько молей кислорода содержится в колбе?

2. Некоторое количество гелия при 78 градусах Цельсия и давлении 45,6 атмосфер занимает объем 16,5 литров.
   Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)

В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.

Теперь немного формул.

Уравнение Клапейрона-Менделеева

где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль

Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также

где n — число молей газа

И как нетрудно заметить, соотношение

есть величина постоянная для одного и того же количества моль газа.

И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.

Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.

Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры

Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры

Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.

Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.