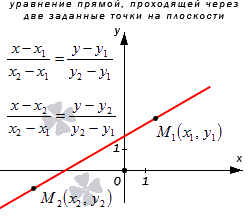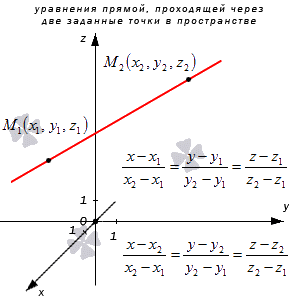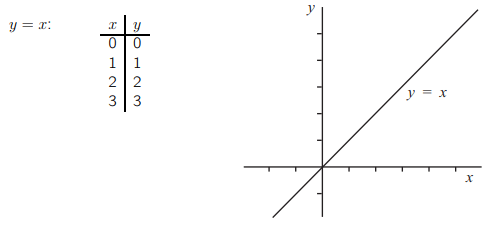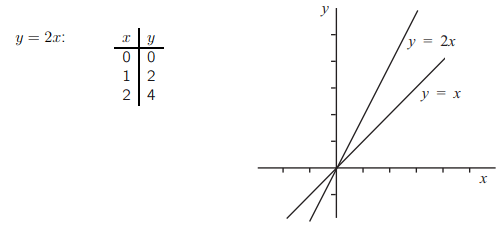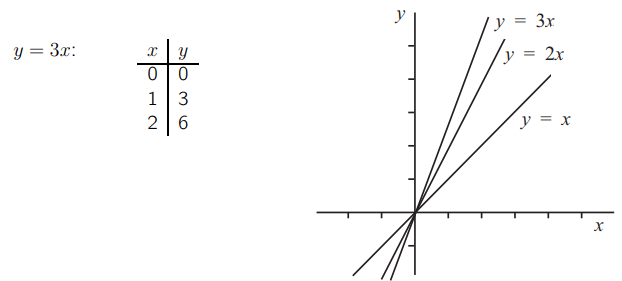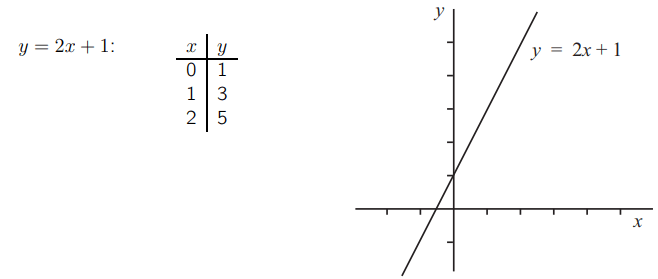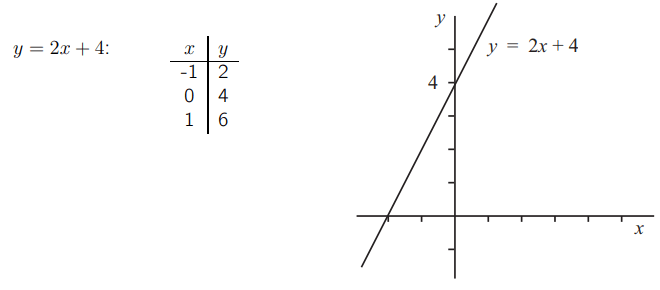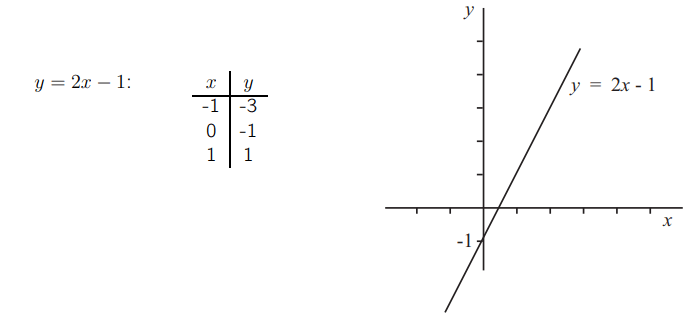Уравнение прямой, которая проходит через две заданные точки: примеры, решения
Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.
Уравнение прямой, проходящей через две заданные точки на плоскости
Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.
Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.
Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a , проходящей через две несовпадающие точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , находящиеся в декартовой системе координат.
В каноническом уравнении прямой на плоскости, имеющего вид x — x 1 a x = y — y 1 a y , задается прямоугольная система координат О х у с прямой, которая пересекается с ней в точке с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) .
Необходимо составить каноническое уравнение прямой a , которая пройдет через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) .
Прямая а имеет направляющий вектор M 1 M 2 → с координатами ( x 2 — x 1 , y 2 — y 1 ) , так как пересекает точки М 1 и М 2 . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 ) и координатами лежащих на них точках M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 .
Рассмотрим рисунок, приведенный ниже.
Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ .
Рассмотрим подробней на решении нескольких примеров.
Записать уравнение прямой, проходящей через 2 заданные точки с координатами M 1 — 5 , 2 3 , M 2 1 , — 1 6 .
Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x 1 , y 1 и x 2 , y 2 принимает вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . По условию задачи имеем, что x 1 = — 5 , y 1 = 2 3 , x 2 = 1 , y 2 = — 1 6 . Необходимо подставить числовые значения в уравнение x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . Отсюда получим, что каноническое уравнение примет вид x — ( — 5 ) 1 — ( — 5 ) = y — 2 3 — 1 6 — 2 3 ⇔ x + 5 6 = y — 2 3 — 5 6 .
Ответ: x + 5 6 = y — 2 3 — 5 6 .
При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.
Составить общее уравнение прямой, проходящей через точки с координатами M 1 ( 1 , 1 ) и M 2 ( 4 , 2 ) в системе координат О х у .
Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x — 1 4 — 1 = y — 1 2 — 1 ⇔ x — 1 3 = y — 1 1 .
Приведем каноническое уравнение к искомому виду, тогда получим:
x — 1 3 = y — 1 1 ⇔ 1 · x — 1 = 3 · y — 1 ⇔ x — 3 y + 2 = 0
Ответ: x — 3 y + 2 = 0 .
Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y = k x + b . Если необходимо найти значение углового коэффициента k и числа b , при которых уравнение y = k x + b определяет линию в системе О х у , которая проходит через точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , где x 1 ≠ x 2 . Когда x 1 = x 2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М 1 М 2 определена общим неполным уравнением вида x — x 1 = 0 .
Потому как точки М 1 и М 2 находятся на прямой, тогда их координаты удовлетворяют уравнению y 1 = k x 1 + b и y 2 = k x 2 + b . Следует решить систему уравнений y 1 = k x 1 + b y 2 = k x 2 + b относительно k и b .
Для этого найдем k = y 2 — y 1 x 2 — x 1 b = y 1 — y 2 — y 1 x 2 — x 1 · x 1 или k = y 2 — y 1 x 2 — x 1 b = y 2 — y 2 — y 1 x 2 — x 1 · x 2 .
С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 1 или y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 2 .
Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.
Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M 2 ( 2 , 1 ) и y = k x + b .
Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y = k x + b . Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M 1 ( — 7 , — 5 ) и M 2 ( 2 , 1 ) .
Точки М 1 и М 2 располагаются на прямой, тогда их координаты должны обращать уравнение y = k x + b верное равенство. Отсюда получаем, что — 5 = k · ( — 7 ) + b и 1 = k · 2 + b . Объединим уравнение в систему — 5 = k · — 7 + b 1 = k · 2 + b и решим.
При подстановке получаем, что
— 5 = k · — 7 + b 1 = k · 2 + b ⇔ b = — 5 + 7 k 2 k + b = 1 ⇔ b = — 5 + 7 k 2 k — 5 + 7 k = 1 ⇔ ⇔ b = — 5 + 7 k k = 2 3 ⇔ b = — 5 + 7 · 2 3 k = 2 3 ⇔ b = — 1 3 k = 2 3
Теперь значения k = 2 3 и b = — 1 3 подвергаются подстановке в уравнение y = k x + b . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y = 2 3 x — 1 3 .
Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.
Запишем каноническое уравнение прямой, проходящей через M 2 ( 2 , 1 ) и M 1 ( — 7 , — 5 ) , имеющее вид x — ( — 7 ) 2 — ( — 7 ) = y — ( — 5 ) 1 — ( — 5 ) ⇔ x + 7 9 = y + 5 6 .
Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x + 7 9 = y + 5 6 ⇔ 6 · ( x + 7 ) = 9 · ( y + 5 ) ⇔ y = 2 3 x — 1 3 .
Ответ: y = 2 3 x — 1 3 .
Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
Если в трехмерном пространстве имеется прямоугольная система координат О х у z с двумя заданными несовпадающими точками с координатами M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , проходящая через них прямая M 1 M 2 , необходимо получить уравнение этой прямой.
Имеем, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z и параметрические вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ способны задать линию в системе координат О х у z , проходящую через точки, имеющие координаты ( x 1 , y 1 , z 1 ) с направляющим вектором a → = ( a x , a y , a z ) .
Прямая M 1 M 2 имеет направляющий вектор вида M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) , где прямая проходит через точку M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , отсюда каноническое уравнение может быть вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , в свою очередь параметрические x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ z = z 1 + ( z 2 — z 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ z = z 2 + ( z 2 — z 1 ) · λ .
Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.
Написать уравнение прямой, определенной в прямоугольной системе координат О х у z трехмерного пространства, проходящей через заданные две точки с координатами M 1 ( 2 , — 3 , 0 ) и M 2 ( 1 , — 3 , — 5 ) .
Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 .
По условию имеем, что x 1 = 2 , y 1 = — 3 , z 1 = 0 , x 2 = 1 , y 2 = — 3 , z 2 = — 5 . Отсюда следует, что необходимые уравнения запишутся таким образом:
x — 2 1 — 2 = y — ( — 3 ) — 3 — ( — 3 ) = z — 0 — 5 — 0 ⇔ x — 2 — 1 = y + 3 0 = z — 5
Ответ: x — 2 — 1 = y + 3 0 = z — 5 .
Уравнение прямой, которая проходит через две заданные точки: примеры, решения
Время чтения: 26 минут
В этой статье мы рассмотрим концепцию уравнения прямой прямой. Мы попытаемся понять общее уравнение прямой, формулу прямой, способ нахождения уравнения прямой и откроем для себя другие интересные аспекты этого. Попробуйте свои силы в решении нескольких интересных примеров и вопросов для лучшего понимания концепции.
Уравнение прямой — может быть записано в различных формах. Прямая линия -это двумерная геометрическая фигура, которая простирается на обоих своих концах до бесконечности.
Для того чтобы освоить описанные приемы, необходимо много практиковаться, чтобы они стали привычными.
После прочтения информации по этой теме вы должны уметь:
- находить уравнение прямой прямой, учитывая ее наклон и пересечение с осью y;
- находить уравнение прямой, учитывая ее наклон и одну точку, лежащую на ней;
- найти уравнение прямой, учитывая две точки, лежащие на ней;
- дать уравнение прямой в любой из форм y = mx + c или ax + by + c = 0
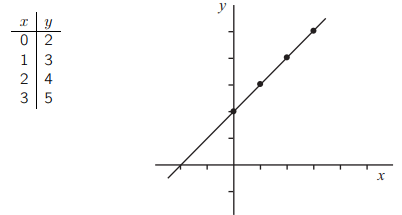
Уравнения прямых могут принимать различные формы в зависимости от фактов, которые мы знаем о прямых. Итак, для начала предположим, что у нас есть прямая линия содержащая точки из следующего списка.
На прямой есть еще много точек, но уже достаточно, чтобы увидеть закономерность. Если мы возьмем любое значение x и прибавим 2, мы получим соответствующее значение y: 0 + 2 = 2, 1 + 2 = 3, 2 + 2 = 4, и так далее. Между координатами x и y любой точки на прямой существует фиксированная зависимость, и уравнение y = x + 2 всегда верно для точек на прямой. Мы можем обозначить прямую, используя это уравнение.
Уравнение прямой, проходящей через начало координат с заданным коэффициентом
Предположим, что у нас есть прямая с уравнением y = x. Тогда для каждой точки на прямой координата y должна быть равна координате x. Таким образом, прямая будет содержать точки из следующего списка.
Мы можем найти коэффициент прямой, используя формулу для нахождения коэффициента:
Далее следует подставить первые два набора значений из таблицы. Получаем:
Таким образом, коэффициент этой прямой равен 1.
А как насчет уравнения y = 2x? Оно также представляет собой прямую линию, и для всех точек на y в два раза больше соответствующего значения x. Таким образом, линия будет содержать точки из следующем списке.
Если мы вычислим коэффициент прямой y = 2x, используя первые два набора значений в таблице, то получим:
Таким образом, коэффициент этой прямой равен 2.
Теперь возьмем уравнение y = 3x. Оно также представляет собой прямую линию, и для всех точек на прямой. Каждая точка y в три раза больше соответствующего значения x. Таким образом, линия будет содержать точки из следующего списка.
Если мы вычислим коэффициент прямой y = 3x, используя первые два набора значений в таблице, мы получим:
Следовательно, коэффициент этой прямой равен 3.
Мы можем начать видеть здесь закономерность. Все эти прямые имеют уравнения, где y равно некоторому числу, умноженному на x. И в каждом случае линия проходит через начало координат, а коэффициент прямой равен m.
Таким образом, если бы у нас была прямая с уравнением y = 13x, то мы бы указали, что коэффициент прямой будет равен 13. Аналогично, если бы у нас была прямая с уравнением y = -2x, то коэффициент будет равен -2. Таким образом, в общем случае уравнение y = mx представляет собой прямую линию, проходящую через начало координат с коэффициентом m.
Уравнение прямой с коэффициентом m, проходящей через начало координат, имеет вид:
Пересечение прямой y
Рассмотрим прямую линию с уравнением y = 2x + 1. Это уравнение имеет несколько иную форму в отличие от тех, которые мы видели ранее. Чтобы нарисовать график прямой, мы должны вычислить некоторые значения.
Обратите внимание, что при x = 0 значение y равно 1. Значит, эта прямая пересекает ось y в точке y = 1.
А как насчет прямой y = 2x + 4? Мы снова можем вычислить некоторые значения.
Эта линия пересекает ось y в точке y = 4.
А как насчет прямой y = 2x — 1? Мы снова можем вычислить некоторые значения.
Эта линия пересекает ось y в точке y = — 1.
Общее уравнение прямой — y = mx + c, где m — коэффициент, а y = c — значение на оси у, при через которое проходим прямая.
Это число c является пересечением с осью y.
Уравнение прямой с коэффициентом m и точкой пересечения c на оси y имеет вид:
Иногда нам задают уравнение прямой в другой форме. Предположим, у нас есть уравнение 3y — 2x = 6. Как показать, что оно представляет собой прямую линию, и найти ее коэффициент и значение точки пересечения с осью y?
Мы можем использовать алгебраическую перестановку, чтобы получить уравнение в виде y = mx + c:
Теперь уравнение находится в стандартной форме, и мы видим, что коэффициент равен [frac<2><3>], а значение точки пересечения с осью y равно 2.
Мы также можем работать в обратном направлении. Предположим, мы знаем, что прямая имеет коэффициент [frac<1><5>] и имеет вертикальное пересечение в точке y = 1. Каким будет ее уравнение?
Чтобы найти уравнение, достаточно подставить нужные значения в общую формулу y = mx + c.
Здесь m равно [frac<1><5>], а c — 1, поэтому уравнение равно y =[frac<1><5>]x + 1. Если мы хотим убрать дробь, мы можем также привести уравнение к виду 5y = x + 5, или 5y — x — 5 = 0.
Уравнение прямой прямой с заданным коэффициентом, проходящее через заданную точку на оси у
Предположим, что мы хотим найти уравнение прямой с коэффициентом [frac<1><3>], которое проходит через точку (1, 2). Здесь, хотя мы знаем коэффициент, мы не знаем значение точки пересечения с осью у, оно равно c.
Начнем с общего уравнения прямой y = mx + c.
Мы знаем, что коэффициент равен [frac<1><3>], именно поэтому мы можем сразу подставить это значение на место m. Это дает: [y=frac<1> <3>x+c]
Теперь мы используем тот факт, что прямая проходит через (1, 2). Это означает, что когда x = 1, y должно быть равна 2. Подставляя эти значения, находим:
Таким образом, уравнение прямой имеет вид:
Мы можем вывести общую формулу для задач такого типа, используя тот же метод. Мы возьмем общую прямую с коэффициентом m, проходящую через фиксированную точку [mathrmleft(x_<1>, y_<1>right)].
Начнем с общего уравнения прямой y = mx + c. Теперь мы используем тот факт, что прямая проходит через точку [mathrmleft(x_<1>, y_<1>right)]. Это означает, что при x = [x_<1>], y должно быть [y_<1>]. Подставляя эти значения, находим:
Таким образом, уравнение прямой имеет вид y = mx + [y_<1>-mathrm x_<1>].
Мы можем записать его в альтернативной форме
Тогда это прямая с уклоном m, проходящая через точку [left(x_<1>, y_<1>right)]. Таким образом, эта общая форма полезна, если вы знаете коэффициент и одну точку на прямой.
Уравнение прямой с коэффициентом m, проходящей через точку [left(x_<1>, y_<1>right)], имеет вид:.
Например, мы знаем, что прямая имеет коэффициент -2 и проходит через точку (-3, 2).
Мы можем воспользоваться формулой [y-y_<1>=mleft(x-x_<1>right)] и сразу подставить значения:
Упражнение 1
Найдите уравнение описанных ниже прямых (приведите уравнение в виде y = mx + c):
(1) коэффициент 3, проходящей через (1, 4);
(2) коэффициент -2, проходящей через (2, 0);
(3) коэффициент [frac<2><5>], проходящий через (5, -1);
(4) коэффициент 0, проходящий через (-1, 2);
(5) коэффициент -1, проходящий через (1, -1).
Глава 1. Уравнение прямой (стр. 1 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
Глава 1. Уравнение прямой
Геометрия развивается по многим направлениям. Возникновение компьютеров привело к появлению такой области математики как вычислительная геометрия. При создании современных приложений часто требуется разработка эффективных алгоритмов для определения взаиморасположения различных объектов на плоскости, вычисления расстояний между ними, вычисления площадей фигур и др.
В данной главе излагается материал, частично известный вам из курса математики. Мы рассмотрим методы решения геометрических задач, которые эффективно реализуются с помощью компьютера, что позволит вам по другому взглянуть на вопросы, изучаемые в рамках школьного курса геометрии. Для этого придется воспользоваться аналитическим представлением геометрических объектов.
1. 1. Формы записи уравнения прямой
В задачах часто приходится задавать на плоскости различные геометрические объекты. Простейшими геометрическими фигурами на плоскости являются точка и прямая. Точка задается указанием своих координат, например A(15; –5), B(x1; y1). Прямую можно задавать с помощью уравнения прямой. Существуют различные формы записи уравнения прямой. Выбор какой-то конкретной зависит от исходных данных, задающих прямую на плоскости. (Могут быть заданы координаты двух точек, через которые проводится прямая, или коэффициенты при неизвестных в линейном уравнении).
В декартовых координатах каждая прямая определяется уравнением первой степени. Уравнение вида
называется общим уравнением прямой.
Если в общем уравнении прямой коэффициент при y не равен нулю, то уравнение можно разрешить относительно y:
Обозначая k = 

получаем уравнение вида y = kx + b. Если же B = 0, то уравнение имеет вид
Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом; k – угловой коэффициент, b – величина отрезка, который отсекает прямая на оси Oy, считая от начала координат (рис. 1).
Уравнение y – y0 = k(x–x0) – это уравнение прямой с угловым коэффициентом k, которая проходит через точку с координатами (x0; y0).
Рассмотрим две точки с координатами (x1; y1) и (x2; y2), лежащие на прямой y = kx + b. Их координаты удовлетворяют уравнению прямой:
Вычитая из второго равенства первое, имеем y2 – y1 = k(x2 – x1), или
k =
Пусть точка с координатами (x; y) – произвольная точка на прямой, проходящей через точки с координатами (x1; y1) и (x2; y2) ( рис. 2 ). Тогда, с учетом того факта, что она имеет тот же коэффициент наклона, получаем
k =




является уравнением прямой, которая проходит через точки с координатами (x1; y1) и (x2; y2). Недостатком этой формулы является ее неопределенность при x1 = x2 и (или) y1 = y2. Поэтому ее лучше использовать в виде
Алгоритм для определения значений коэффициентов A, B, C общего уравнения прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим [1] :
C:= – x1*(y2 – y1)+y1*(x2 – x1)
Рассмотрим пример: x1 = 0, y1 = 0, x2 = 1, y2 = 2. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2) будет следующим:
C = –x1 * (y2 – y1) + y1 * (x2 – x1) = 0 * 2 + 0 * 1 = 0. ЌСледовательно, уравнение прямой будет иметь вид 2х – у = 0.
1. 2. Положение точек относительно прямой
Множество точек прямой, проходящей через две точки с координатами (x1; y1) и (x2; y2), удовлетворяет уравнению
Это значит, что если имеется точка с координатами (x0; y0) и (x0 – x1) * (y2 – y1) – (y0 – y1) * (x2 – x1) = 0, то эта точка лежит на прямой. B дальнейшем, вместо выражения (x – x1) * (y2 – y1) – (y – y1) * (x2 – x1) мы иногда будем использовать для краткости обозначение Ax + By + C или f(x1, y1, x2, y2, x, y).
Прямая Ax + By + C = 0, проходящая через две заданные точки с координатами (x1; y1) и (x2; y2), разбивает плоскость на две полуплоскости. Рассмотрим возможные значения выражения Ax + By + C.
1) Ax + By + C = 0 – определяет геометрическое место точек, лежащих на прямой.
Запишем алгоритм для определения, лежит ли точка с координатами (x3; y3) на прямой, проходящей через точки (x1; y1) и (x2; y2). Переменная P – переменная логического типа, которая имеет значение «истина», если точка лежит на прямой и «ложь» в противном случае.
если (x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)=0
2) Ax + By + C > 0 – определяет геометрическое место точек, лежащих по одну сторону от прямой.
3) Ax + By + C рис. 3 точки (x3; y3) и (x4; y4) лежат по одну сторону от прямой, точки (x3; y3) и (x5; y5) по разные стороны от прямой, а точка (x6; y6) лежит на прямой.
Рассмотрим пример: x1 = 1, y1 = 2, x2 = 5, y2 = 6. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим:
Следовательно, уравнение прямой будет иметь вид 4х – 4у + 4 = 0 или x – y + 1 = 0. Подставим координаты точек (3; 4), (1; 1), (2; 0), (0; 2) в уравнение прямой. Получим:
1 * 3 – 1 * 4 + 1 = 0, 1 * 2 – 1 * 0 + 1 > 0,
1 * 1 – 1 * 1 + 1 > 0, 1 * 0 – 1 * 2 + 1 L:=»по одну»
Z1:=(x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)
Z2:=(x4 – x1)*(y2 – y1) – (y4 – y1)*(x2 – x1)
½ то L:=»по разные» (1. 3)
1.3. Взаимное расположение двух отрезков
Пусть нам необходимо определить взаимное расположение двух отрезков. Отрезки на плоскости заданы координатами своих концевых точек. Предположим, что концевые точки одного из отрезков имеют координаты (x1; y1) и (x2; y2), а концевые точки другого – (x3; y3) и (x4; y4). Пусть общее уравнение первой прямой, проходящей через точки (x1;y1) и (x2;y2), имеет вид A1x + B1y + C1 = 0, а второй прямой, проходящей через точки (x3;y3) и (x4;y4), A2x + B2y + C2 = 0.
Определим расположение точек (x3; y3) и (x4; y4) относительно первой прямой. Если они расположены по одну сторону от прямой, то отрезки не могут пересекаться. Аналогично можно определить положение точек (x1; y1) и (x2; y2) относительно другой прямой.
Таким образом, если значения пары выражений Z1 = A1x3 + B1y3 + C1 и Z2 = A1x4 + B1y4 + C1 имеют разные знаки или Z1*Z2 = 0, а также пары Z3 = A2x1 + B2y1 + C2 и Z4 = A2x2 + B2y2 + C2 имеют разные знаки или Z3*Z4 = 0, то отрезки пересекаются. Если же значения пар выражений Z1 и Z2, или Z3 и Z4, имеют одинаковые знаки, то отрезки не пересекаются.
Различные случаи расположения отрезков показаны на рис. 4 .
На этом рисунке отрезки с концами в точках (x1; y1), (x2; y2) и (x4; y4), (x5; y5) пересекаются, отрезки с концами в точках (x1; y1), (x2; y2) и (x3; y3), (x4; y4) не пересекаются, а отрезки с концами в точках (x3; y3), (x4; y4) и (x4; y4) и (x5; y5) имеют общую вершину, что можно считать частным случаем пересечения.
Алгоритм для определения, пересекаются ли два отрезка с концами в точках (x1; y1), (x2; y2) и (x3; y3), (x4; y4) будет следующим:
Z1:=(x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)
Z2:=(x4 – x1)*(y2 – y1) – (y4 – y1)*(x2 – x1)
Z3:=(x1 – x3)*(y4 – y3) – (y1 – y3)*(x4 – x3)
Z4:=(x2 – x3)*(y4 – y3) – (y2 – y3)*(x4 – x3)
Приведенный фрагмент алгоритма не учитывает крайней ситуации, когда два отрезка лежат на одной прямой. В этом случае (x3 – x1) * (y2 – y1) – (y3 – y1) * (x2 – x1) = 0 и (x4 – x1) * (y2 – y1) – (y4 – y1) * (x2 – x1) = 0.
На рис. 5 отрезки, лежащие на одной прямой не пересекаются, а на рис. 6 – отрезки пересекаются.
Для того, чтобы определить взаимное расположение таких отрезков, поступим следующим образом. Обозначим
Здесь k1 является левой, а k2 – правой точкой проекции первого отрезка (отрезка, заданного координатами (x1; y1), (x2; y2)) на ось Ox. Аналогично k3 является левой, а k4 – правой точкой проекции второго отрезка (отрезка, заданного координатами (x3; y3), (x4; y4)) на ось Ox. Аналогично ищем преокции на ось OY.
Отрезки, лежащие на одной прямой будут пересекаться тогда, когда их проекции на каждую ось пересекаются. (Следует заметить, что если проекции двух произвольных отрезков пересекаются, то это не значит, что и сами отрезки пересекаются, что видно на рис. 7 ).
Для определения взаимного расположения проекций на ось OX воспользуемся следующим фактом (см. рис. 5 и рис. 6 ): координата левой точки пересечения проекций Lx равна max(k1; k3), т. е. максимальной из координат левых точек проекций. Рассуждая аналогично для правых точек проекций, получим, что координата правой точки Rx пересечения равна min(k2; k4). Для того, чтобы отрезки пересекались, необходимо, чтобы левая координата пересечения проекций была не больше правой координаты пересечения отрезков (такой случай имеет место на рис. 5 , когда Lx = х3, а Rx = х2). Поэтому условием пересечения проекций является выполнение неравенства Lx £ Rx. Аналогично можно вычислить величины Lу и Rу, беря соответствующие проекции на ось Оу.
Следует отметить, что длина пересечения проекций в этом случае равна величине Lx– Rx (если Lx– Rx = 0, то проекции имеют только общую точку).
1.4. Точка пересечения отрезков
Для определения места пересечения отрезков (если известно, что они пересекаются), достаточно определить точку пересечения прямых, на которых эти отрезки лежат.
Пусть A1x + B1y + C1 = 0 является уравнением прямой, проходящей через концевые точки первого отрезка, а A2x + B2y + C2 = 0 является уравнением прямой, проходящей через концевые точки второго отрезка.
Тогда для определения точки пересечения отрезков достаточно решить систему уравнений
Домножив первое уравнение на A2, а второе уравнение на A1, получим
Вычитая из первого уравнения второе, можно найти значение y:
y =
Аналогично можно вычислить значение x:
x =
Это справедливо в случае, если выражение A2 * B1 – A1 * B2 ¹ 0. Но мы уже знаем, что отрезки пересекаются и не лежат на одной прямой. А это невозможно, если A2 * B1 – A1 * B2 = 0.
2.1 Расстояния между точками. Расстояние от точки до прямой
Расстояние между точками M1(x1; y1) и M2(x2; y2) на плоскости ( рис. 8 ) определяется по формуле
D = 
Расстояние от точки до прямой на плоскости определяется как длина отрезка перпендикуляра, опущенного из точки на прямую. Уравнение вида

где T = 
Запишем алгоритм для определения расстояния от точки (x3; y3) до прямой, проходящей через точки (x1; y1) и (x2; y2).
C:= – x1*(y2 – y1)+y1*(x2 – x1) (1. 5)
Рассмотрим пример: x1 = 0, y1 = 0, x2 = 3, y2 = 4 x3 = –1, y3 = 7. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим:
Т = 


D = 

2.2. Расстояние между точкой и отрезком
Для определения расстояния между точкой и отрезком необходимо выяснить, пересекает ли перпендикуляр, опущенный из данной точки на прямую, проходящую через концы отрезка, сам отрезок. Если перпендикуляр пересекает отрезок, то расстояние между точкой и отрезком равно расстоянию между точкой и прямой, проходящей через отрезок. (Эту задачу вы уже умеете решать.)
Если перпендикуляр не пересекает отрезок, то расстояние между точкой и отрезком равно минимальному из расстояний между точкой и одним из концов отрезка.
Для определения взаимного расположения отрезка и перпендикуляра поступим следующим образом.
Рассмотрим треугольник, образованный тремя точками, две из которых (x1; y1) и (x2; y2) являются концами данного отрезка, а третья – данная точка с координатами (x3; y3) (см. рис. 10 , б, в). Конечно, может оказаться, что все точки лежат на одной прямой и такого треугольника не существует. В этом случае, однако, мы будем полагать, что треугольник существует, правда он вырожденный (особый). В вырожденном треугольнике длины сторон могут быть равными 0 (см. рис. 10 , а).
Более того, мы будем полагать, что данный отрезок является основанием рассматриваемого треугольника (см. рис. 10 , б, в).
При таких предположениях для решения исходной задачи нам достаточно определить, является ли один из углов при основании тупым или нет. Действительно, если один из углов при основании является тупым, то перпендикуляр, опущенный из вершины, соответствующей исходной точке, не попадает на основание (отрезок). Иначе перпендикуляр, опущенный из вершины, соответствующей исходной точке, попадает на основание (отрезок).
Для решения последней задачи воспользуемся следующим свойством. Пусть a, b, c – длины сторон треугольника, причем с – длина основания. Тогда треугольник является тупоугольным при основании, если
Поэтому, вычислив значения квадратов длин сторон, нетрудно определить, пересекает ли перпендикуляр, опущенный из точки (x3; y3) на прямую, отрезок с концами в точках (x1; y1) и (x2; y2). И если не пересекает, то расстояние от точки до отрезка равно минимуму из величин a, b. Если же пересекает, то необходимо воспользоваться свойством нормального уравнения прямой .
§ 3. Многоугольники
3.1. Виды многоугольников
Ломаной называется фигура, которая состоит из точек A1, A2, . An и соединяющих их отрезков A1A2, A2A3, . An – 1An ( рис. 11 , а). Точки называются вершинами ломаной, а отрезки – звеньями. Наиболее распространенным способом задания ломаной является использование таблицы, элементы которой соответствуют координатам вершин ломаной в порядке ее обхода из одного конца в другой. Длиной ломаной называется сумма длин ее звеньев.
Многоугольником называется замкнутая ломаная линия без самопересечений (рис. 11, б).
Плоским многоугольником называется конечная часть плоскости, ограниченная многоугольником (рис. 11, в).
Обход плоского многоугольника называется положительным, если при обходе область расположена по левую руку, и отрицательным, если область остается по правую руку.
Расстояние между фигурами на плоскости определяется как длина минимального отрезка, один конец которого принадлежит одной фигуре, а второй конец – другой фигуре.
3.2. Выпуклость многоугольников
Многоугольник является выпуклым, если для каждой прямой, проходящей через любую его сторону, все остальные вершины лежат в одной полуплоскости относительно прямой. Проверим для каждой прямой, проходящей через вершины (x1; y1) и (x2; y2), (x2; y2) и (x3; y3), . (xn – 1; yn – 1) и (xn; yn), (xn; yn) и (x1; y1) взаимное расположение вершин многоугольника. Если они каждый раз расположены в одной полуплоскости относительно проведенной прямой, то многоугольник выпуклый. Если же найдется прямая, проходящая через одну из сторон, и пара вершин многоугольника, лежащих по разные стороны относительно проведенной прямой, то многоугольник не является выпуклым. Случаи выпуклого и невыпуклого многоугольников изображены на рис. 12.
Можно заметить, что для каждой прямой, проходящей через вершины (x1; y1) и (x2; y2), (x2; y2) и (x3; y3), . (xn – 1; yn – 1) и (xn; yn), (xn; yn) и (x1; y1) достаточно ограничится определением взаимного расположения вершин многоугольника (xn; yn) и (x3; y3), (x1; y1) и (x4; y4), . (xn – 2; yn – 2) и (x1; y1), (xn – 1; yn – 1) и (x2; y2), соответственно. Если они каждый раз расположены в одной полуплоскости относительно проведенной прямой, то многоугольник выпуклый. Если же найдется прямая и пара вершин многоугольника, лежащих по разные стороны относительно проведенной прямой, то многоугольник не является выпуклым. Поэтому для определения, является ли многоугольник выпуклым, достаточно воспользоваться алгоритмом
нц для i от 1 до n
½ j:= mod( i, n +1 ) : номер вершины после вершины i
½ k:= mod (j, n +1) : номер вершины после вершины j
½½ то m:=n : номер вершины перед вершиной i
http://www.napishem.ru/spravochnik/matematika/uravnenie-pryamoj-kotoraya-prohodit-cherez-dve-zadannye-tochki-primery-resheniya.html
http://pandia.ru/text/79/489/58441.php
В игре «Horizon: Запретный Запад» всегда есть чем заняться, несмотря на огромный и безумно красивый постапокалиптический мир.
Кроме обилия побочных заданий, котлов, руин и охоты на различные виды машин, в игре есть и небольшие головоломки, в число которых входят «Обзорные точки».
«Обзорные точки» — это непродолжительное задание, которое в очередной раз приоткрывает завесу прошлого и позволяет взглянуть в эпоху до наступления конца света. Задача Элой достаточно проста – это сканирование вышки и поиск места сопоставления голографического изображения с реальной местностью.
Кроме того, изучение всех «Обзорных точек» — это обязательный этап для получения платины, если вы конечно же стремитесь к этому.
Примечание: Гайд обновляется по мере прохождения игры – всего доступно 9 «Обзорных точек».
Обзорная точка: Преграды
Найти первую вышку в игре труда не составит, так как Элой проходит мимо неё в задании «На грани», когда после разговора с Эрендом, мы отправляемся к месту откуда исходят звуки взрывов и борьбы.
Также цель «Обзорной точки» — это ничто иное как одни из «Руин с реликвиями».
Если стоять к месту сканирования вышки лицом, то для сопоставления голографического изображения развернитесь назад и найдите остатки разрушенного моста, через уже почти засохший ручей.
Останется только подойти к краю и направить голограмму на руины дома.
Обзорная точка: Роща Памяти
Натолкнуться на эту «Обзорную точку» можно по пути к «Скальному Кряжу», в ходе выполнения основного сюжетного задания «Сломанные небеса».
После сканирования, осмотритесь и далеко в стороне на скале есть старая ржавая спутниковая тарелка, которая как раз и напоминаем нужную голограмму.
Останется только забраться по точкам зацепа и подняться немногим выше тарелки.
4 238 просмотров — 20.02.2022
0
0
Представьте, что вы начинающий трейдер и дебютируете в биржевой игре с горящими глазами и в надежде получить первую прибыль. Но с чего начать? Как определить удачные точки входа в трейдинг? Как определить, когда лучше покупать торговую пару и какой самый подходящий момент для ее продажи? Иными словам, необходимо правильно установить точки входа и выхода в рынок, чтобы не упустить доход при снижении стоимости активов. Найти точки входа в биржевой рынок — значит найти самые удачные места, где нужно открывать сделку. Причем это могут быть как параметры цены, так и времени.
Однако, всегда нужно сохранять хладнокровие и дисциплину, ведь: лучше не спеша получить прибыль, чем очень быстро уйти в ноль. С этой задачей каждый раз справляются опытные трейдеры. Ведь от определения успешного момента для выгодной покупки или продажи актива, напрямую зависит получение прибыли и укрепление позиций на рынке.
Чтобы быть полностью уверенным в том, что позиция выбрана правильно, некоторым хватает всего лишь бегло проанализировать графики, а другие собирают и обрабатывают огромное количество информации и используют технический анализ. Например, чтобы точно определить удачный вход на рынок форекс, опытные трейдеры опираются на поток финансовых новостей и сопоставляют его с техническим анализом движения валютных пар.
В любом случае для выбора наиболее выгодной стратегии торговли, необходимы знания о линиях сопротивления и поддержки. Их понимание и действие по определенным правилам позволят определить сильную точку входа и выйти с максимальной прибылью.
Итак, как правильно определить точку входа в рынок? Какие точки входа в рынок криптовалют? Как сделать точный вход в рынок форекс? В этой статье мы будем говорить именно об этом.
ТЕОРИЯ
Для начала немного теории. Для того чтобы выбрать наиболее удачную точку входа в трейдинг, трейдер должен проанализировать рынок. В классическом анализе используются три основных индикатора (уровня), по которым игрок ориентируется и принимает решение о входе или выходе из рынка.
Три основных уровня:
- уровень поддержки — ценовой уровень, при достижении которого, график движения вниз разворачивается в обратную сторону. Данный уровень, будто поддерживает цену, не давая спуститься ей ниже;
- уровень сопротивления — ценовой уровень, при достижении которого, график движения вверх разворачивается в обратную сторону. В данном случае, уровень оказывает сопротивление цене, не давая ей вырасти выше;
- зеркальный уровень — этот уровень содержит максимальное количество информации. У него плавающая структура и момент его преобразования происходит, когда уровень сопротивления переходит в уровень поддержки или наоборот. В реальности это означает, что один из игроков рынка (быки или медведи) побеждает другого.
Другие уровни достаточно условны и могут использоваться трейдерами там, где они считают нужным их провести, например, чтобы определить индикатор входа в рынок форекс. Опытные игроки видят и выбирают точку опоры для будущих шагов достаточно легко. Однако, Александр Герчик советует новичкам чертить уровни около сильных точек — длинных проторговок или изломов тренда, дабы избежать лишнего риска.
ПРАКТИКА: ТОЧКИ ВХОДА В РЫНОК
Теперь от теории к практике. Как правильно определить точку входа в рынок? Как осуществить поиск точек входа в рынок? Как без помощи специальных индикаторов войти в рынок и начать торговать? Вашему вниманию 7 наиболее простых и эффективных точек входа на рынок.
7 ТОЧЕК ВХОДА НА РЫНОК
ТОЧКА 1. Уровень поддержки восходящего тренда.
Первая и одна из самых простых точек входа — третье касание цены при восходящем тренде. Когда отслеживается рост цен (восходящий тренд), появляется возможность провести наклонную линию вверх на графике. Это необходимо делать по двум основаниям ценовых барьеров, которые последовательно повышаются и имеют абсолютное дно по отношению к двум предыдущим и двум следующим основаниям. Именно третье касание линии графиком свидетельствует о том, что это наиболее удачная точка входа в трейдинг.
При использовании данной точки входа в рынок, необходимо выяснить заранее ценовые уровни. Лучше всего это делается на основании дневного графика, где свой ценовой уровень определяется для каждого дня.
Важно понимать, что возможны ложные пробои через линию тренда. Определить точно, истинный пробой или ложный, можно только тогда, когда бар, прорвавший тренд будет закрыт, и начнется новый. Поэтому, необходимо сохранять хладнокровие, дисциплину и не поддаваться ложным эмоциям.
ТОЧКА 2. Уровень сопротивления нисходящего тренда.
Данная точка входа в трейдинг, является прямой противоположностью предыдущей. Чтобы определить точку входу, необходимо также провести наклонную линию на графике, только в этот раз, линию проводить по ценовым вершинам. Ценовые вершины должны быть последовательно снижающимися иметь абсолютный пик цены по отношению к двум предыдущим и последующим барам.
Ориентироваться, как и в предыдущей точке, лучше на основании дневного графика, но для более точной информации не помешает использовать получасовые и часовые графики.
Данный метод торгов крайне надежен и прост. Но, как и любой другой инструментарий имеет множество нюансов, о которых более подробно рассказывает Александр Герчик в своем курсе по трейдингу.
ТОЧКА 3. Открытие позиции при прорыве уровня сопротивления.
В момент сомнения как правильно определить точку входа в рынок, часто приходится наблюдать, как цены движутся вверх, причем это движение развивается зигзагообразно. Обычно, в первой трети роста цены актива, когда тренд уже обозначился и покупатели (быки) активно взяли инициативу в свои руки, продавцы (медведи) еще не утратили своих амбиций и им удается за каждым ценовым пиком сбить цены до уровня предпоследнего максимума. При уверенном тренде, глубина коррекции редко пересекает порог в 23% и совсем редко в 38% от последнего движения вниз, которое завершено. Вот именно в этом промежутке — между точкой 38% и последней вершиной и следует покупать активы.
ТОЧКА 4. Открытие позиции при прорыве уровня поддержки.
Когда рынок собирается падать, прорывы идентифицируются преодолением уровней предыдущих минимумов цен. Когда рынок восстанавливается, он может поднять цены на актив на уровень поддержки, даже с вероятными проколами выше. Особенно часто, это происходит на ранних стадиях формирования тренда вниз. Именно здесь лучшая стратегия — продажа торговых пар выше этого уровня при минимальном проколе.
ТОЧКА 5. Вход при прохождении контр-тренда снизу вверх.
Когда график цены проходит сквозь линию тренда снизу вверх и фиксирует закрытие выше тренда в выбранном таймфрейме — индикатор удачной точки для входа в рынок. Обычно происходит так: наблюдается прохождение цен сквозь линию тренда, цены закрепляются выше, но когда происходит коррекция — стоимость актива снижается к тренду сверху. Возникает поддержка на линии тренда, который раньше играл роль уровня сопротивления. Как раз этот момент и является еще одной точкой для входа в рынок.
ТОЧКА 6. Продажа от контр-тренда.
Данный метод крайне эффективен и является одним из наиболее действенных способов, позволяющих занять медвежью позицию. Его суть в том, что необходимо продавать от контр-тренда, который до этого был восходящим и был в роли поддержки, но после пробития уровня цены — превратился в сопротивление.
Иными словами, покупка и продажа на контр-тренде — удачная стратегия, если за линией самого тренда фиксируется восходящая альтернатива, и линия сопротивления переходит в линию поддержки. Если значения цены на графике находятся в касательстве с ней — это четкий сигнал покупать активы. Если же ситуация противоположная и уровень поддержки пробит контр-трендом, а затем трансформируется в линию сопротивления, то здесь необходимо зафиксировать прибыль. Особую удачу принесут находящиеся рядом отчетливые зоны коррекции.
ТОЧКА 7. Торговля во флете.
Бывает так, что на графиках отсутствуют отчетливо выраженные нисходящие и восходящие тренды. В этот момент, есть возможность зарабатывать в коридорах условной стабильности. Те, кто интересуется среднесрочным и краткосрочным трейдингом — найдут себя в этом периоде рынка. При торговле во флете необходимо придерживаться всего двух правил:
- в момент, когда рынок поднимается выше среднего уровня (50% коррекции) последнего из завершенных рыночных движений — нужно покупать;
- в момент, когда рынок падает ниже среднего уровня (50% коррекции) последнего из завершенных движений — нужно продавать.
Анализ при данном способе торговли необходимо совершать основываясь на дневных и недельных графиках, несмотря на то, что торговать во флете лучше в рамках дня. Эта методика основывается на том, что рынок циклично падает и растет при пересечении разделительной границы в зоне флеттенда. Здесь активнее торгуют опытные трейдеры, освоившие работу с данным инструментом. Он обеспечивает определенные преимущества и положительно сказывается на результате. Чтобы чувствовать себя уверенно при торговле во флете, вам поможет обучающий курс Александра Герчика, где он подробно рассказывает об этом.
Вышеперечисленные 7 точек входа на рынок не привязаны к какому-то конкретному рынку. Они универсальны. Вы можете использовать их как для входа на рынок форекс, крипто-рынок, фондовую или товарную биржу. Однако, это инструменты. Как определить наиболее оптимальную точку входа? Как их найти? Об этом далее.
Часто задаваемые вопросы
-
1
Что такое Твх в трейдинге?
ТВХ это точка входа в сделку. Точкой входа считают стоимость, по которой трейдер открывает позицию на рынке.
-
2
Какие существуют индикаторы для входа и выхода из рынка?
Главными индикаторами для точек входа и выхода есть уровень поддержки, уровень сопротивления и зеркальный уровень.
-
3
Какие существуют точки входа на рынок торговли?
Существует 7 основных точек входа на рынок: уровень поддержки восходящего тренда, уровень сопротивления нисходящего тренда, открытие позиции при прорыве уровня сопротивления, открытие позиции при прорыве уровня поддержки, вход при прохождении контр-тренда снизу вверх, продажа от контр-тренда и торговля во флэте.
Результаты в трейдинге индивидуальны и зависят от опыта и личной дисциплины. Улучшить свои навыки и дисциплину можно на нашем Курсе: «Трейдинг Основы»
Полная версия материала доступна зарегистрированным пользователям
Зарегистрируйтесь и смотрите в свое удовольствие
Нажимая на кнопку я подтверждаю, что я
прочел(-ла) и принимаю Условия оказания услуг
и Политику конфиденциальности
Полная версия материала доступна зарегистрированным пользователям
Зарегистрируйтесь и смотрите в свое удовольствие
Полная версия материала доступна зарегистрированным пользователям
Восстановление пароля
Введите email, который вы
указывали при регистрации
Коэффициенты предоставлены

CCT Online Finals #1
21:30. Завершен
Bad News Eagles
2–1
Movistar Riders
12:30. Не начался
BIG
–
Endpoint
15:30. Не начался
Bad News Eagles
–
9ine
18:30. Не начался
Forze
–
Into The Breach
Прохождение игры Horizon Forbidden West включает целых девять обзорных точек, которые предстоит собрать персонажу! Точки хаотично разбросаны по карте, поэтому перед тем, как начать миссию по сбору точек, тебе нужно тщательно просканировать карту своим фокусом. Как только точка попадает в фокус, вокруг нее образуется фиолетовое свечение. Это подсказка, она расскажет, к чему относится найденная тобой точка. Чтобы выполнить задание обзорной точки, потребуется совместить контур с окружением, находящимся рядом с телефонным столбом. Как это сделать? Смотри подробный гайд по поиску и активации всех девяти обзорных точек Хорайзон Форбидден Вест. Желаем успехов!
Преграда – The Daunt
Самая первая и самая простая обзорная точка в игре. Чтобы преодолеть преграду нужно всего лишь взобраться на небольшой разрушенный мост и осмотреть руины, расположенные на противоположном берегу реки.
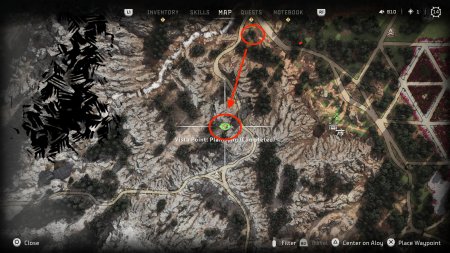
Песня долины – Plainsong
Эта точка располагается на большом расстоянии от первой обзорной точки – преграды. Чтобы добраться до песни долины, поднимайся по скалистой местности в южном направлении. Ориентир – старая, полуразрушенная смотровая площадка. Она находится рядом с руинами ветряной турбины. Взгляни направо – перед тобой желанная обзорная точка!
Обжигающее копье – Scalding Spear
Здесь действует принцип: просто и понятно. Ищи старую смотровую площадку рядом с телеграфным столбом. Тебе нужно забраться на эту площадку – используй бревно (пройдись по нему, как по мосту). Потребуется лишь немного бдительности: площадку охраняют крылья Солнца.
Стоячие пески – The Stillsands
Взгляни на ту часть карты, где находится пустыня. Обзорная точка стоячих песков будет прямо перед тобой! Телефонный столб в данном случае будет составляющей обзорной точки, а руины разрушенного Лас-Вегаса дополняют оставшуюся часть обзорной точки.
Дюнхоллоу – Dunehollow
Одна из самых сложных и труднодоступных обзорных точек игры Horizon Forbidden West. Она расположена под землей в самом сердце руин Лас-Вегаса. Добраться до точки можно с помощью подъемников, находящихся в поселении Хидден Эмбер. Несмотря на то, что начальная точка располагается к югу от Дюнхоллоу, решение найдется на полуразрушенном мосту в северном направлении от Дюнхоллоу. Найди самую восточную точку моста: на ней не будет перил и будет небольшой выступ, напоминающий треугольник. Займи позицию в середине этого участка и нажимай кнопку для активации точки. Важное уточнение: чтобы появилось фиолетовое свечение, Элой потребуется немного пошевелиться, что несколько затруднит добавление обзорной точки в твой арсенал.
Роща памяти – The Memorial Grove
Эту обзорную точку нужно искать рядом с заброшенным аэродромом. Нужно подняться в горы в восточном направлении и найти там место одной из уже знакомых тебе точек обзора. Займи эту локацию и выровняй антенну радара – точка активирована!
Длинный берег – The Long Coast
Эта обзорная точка довольно непростая для активации. Для ее открытия необходимо будет встать на самый край скалы. Нужно следовать прямо вниз по пляжной линии от столба для сбора мусора. Найди странное здание в форме квадрата и посмотри на него. Ура, в твоем арсенале еще одна точка Хорайзон Форбидден Вест!
Окутанные высоты – Shrouded Heights
Для активации этой точки тебе очень пригодится навык летать, который можно было получить при выполнении миссии в рамках основного сюжета: речь идет о квесте «Крылья десяти». Для активации обзорной точки потребуется взлететь на самый верх металлической башни из скелетов. Теоретически подняться на вершину башни можно и без способности летать (чередуй прыжки с опоры на опору и скалолазание), но это может быть смертельно опасным для Элой! Маленькая желтая подпорка, торчащая из угловой спицы на самой вершине руинов небоскреба – вот то, что тебе нужно для активации еще одной обзорной точки игры.
Остров Шпилей – Isle of Spires
Последняя обзорная точка игры Хорайзон Форбидден Вест располагается под водой. Для ее активации тебе понадобится навык длительного нахождения под водой и дайвинга с маской. Маску нужно будет предварительно получить (а точнее, изготовить самостоятельно с помощью верстака) в миссии «Посейдон» в рамках основного сюжета игры. Подробнее об этом написано в нашей статье «Как нырять в Horizon Forbidden West». Погрузившись на глубину, ищи желтую опору для рук на самом дне (в ней ты узнаешь уже известную ранее подводную точку). Проплыви рядом, не нажимая на треугольник для ускорения – Элой обхватит его и тем самым активирует последнюю обзорную точку игры.
Как получить платину в Horizon Forbidden West
Карта Horizon Forbidden West со всеми точками интереса
0
Horizon Forbidden West — это масштабная игра с открытым миром, в которой игроки могут выполнять множество действий, чтобы заработать дополнительные очки опыта, очки навыков, а иногда даже новое оружие. Одно из побочных действий, с которым игроки столкнутся в своем путешествии на запад, — это Обзорные точки. Это полувысокие башни, и поначалу игроки могут подумать, что им нужно попытаться взобраться на них или что-то в этом роде, но дело не только в этом.
Как только игроки подходят к Башня Виста в Плейнсонге , им нужно будет использовать способность Элой фокусироваться, нажав правую ручку управления. Сканируем базу Башня Виста Пойнт , и это даст Элой нечеткое изображение, которое нужно будет сопоставить с локацией в открытом мире. К счастью, игроки могут использовать это руководство для найдите изображение Vista Point и завершите башню Vista в Plainsong .
На карте будет показан желтый кружок, где можно найти изображение, но не будет указано точное местоположение. В то время как Элой даст игрокам несколько подсказок, найти, где изображение выстраивается в линию, все еще может быть непросто.
Vista Point: Plainsong в Horizon Forbidden West
Найдите место, где было снято изображение Vista
После сканирования файла Башня Vista Point в Plainsong , игроки захотят искать прямо на юг/юго-запад, чтобы найти точку изображения Vista. Следуйте по тропинке в гору, а затем взберитесь на несколько стен, чтобы добраться до захудалой области, которая выглядит как разрушенная смотровая площадка. Если игроки смотрят в сторону открытого поля, слева от них должна быть гигантская ветряная мельница и что-то похожее на гигантские сломанные антенны или спутниковые тарелки среди обломков.
Горизонт Запретный Запад игроков можете использовать изображение выше, чтобы увидеть точное местоположение изображения Vista Tower. Чуть ближе к уровню земли на горе есть еще один подобный выступ, но игрокам нужно пропустить его и продолжать двигаться дальше к тому, который показан на изображении ниже. Элой также будет бормотать что-то себе под нос о том, что находится в нужном месте, как только игроки доберутся до нужной смотровой площадки.
Нажмите на правый джойстик на контроллере и попытайтесь сопоставить изображение с реальным (в игре) миром, чтобы завершить побочную миссию Vista Tower. По завершении задания Элой получит XP, который, если будет заработано достаточно, повысит уровень Элой и даст ей больше очков навыков, чтобы разблокировать новые способности в меню.
Горизонт Запретный Запад уже доступна для PS4 и PS5.