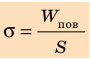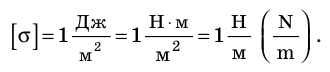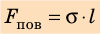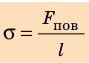Загрузить PDF
Загрузить PDF
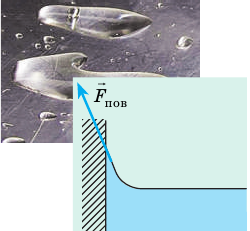
Поверхностное натяжение описывает способность жидкости противостоять силе тяжести. Например, вода на поверхности стола образует капли, поскольку молекулы воды притягиваются друг к другу, что противодействует силе тяжести.[1]
Именно благодаря поверхностному натяжению более тяжелые предметы, например насекомые, могут удерживаться на поверхности воды. Поверхностное натяжение измеряется в силе (Н), поделенной на единицу длины (м), или в количестве энергии на единицу площади.[2]
Сила, с которой взаимодействуют молекулы воды (когезионная сила), вызывает натяжение, в результате чего образуются капли воды (или других жидкостей). Поверхностное натяжение можно измерить с помощью нескольких простых предметов, которые есть практически в каждом доме, и калькулятора.
-
1
Запишите уравнение для поверхностного натяжения. В данном эксперименте уравнение для определения поверхностного натяжения выглядит следующим образом: F = 2Sd, где F — сила в ньютонах (Н), S — поверхностное натяжение в ньютонах на метр (Н/м), d — длина используемой в эксперименте иглы. Выразим из этого уравнения поверхностное натяжение: S = F/2d.
- Сила будет рассчитана в конце эксперимента.
- Прежде чем приступить к эксперименту, с помощью линейки измерьте длину иглы в метрах.
-
2
Сконструируйте небольшое коромысло.[3]
В данном эксперименте для определения поверхностного натяжения используются коромысло и небольшая игла, которая плавает на поверхности воды. Необходимо внимательно отнестись к сооружению коромысла, так как от этого зависит точность результата. Можно использовать различные материалы, главное, сделать горизонтальную перекладину из чего-то жесткого: дерева, пластмассы или плотного картона.- Определите центр стержня (например, соломинки или пластмассовой линейки), который вы собираетесь использовать в качестве перекладины, и просверлите или проткните в этом месте отверстие; это будет точка опоры перекладины, на которой та будет свободно вращаться. Если вы используете пластмассовую соломинку, просто проткните ее булавкой или гвоздем.
- Просверлите или проткните отверстия на концах перекладины так, чтобы они располагались на одинаковом расстоянии от центра. Проденьте через отверстия нитки, на которых вы подвесите чашку для груза и иглу.
- При необходимости подоприте коромысло книгами или другими достаточно твердыми предметами, чтобы перекладина оставалась в горизонтальном положении. Необходимо, чтобы перекладина свободно вращалась вокруг воткнутого в ее середину гвоздя или стержня.
-
3
Возьмите кусок алюминиевой фольги и сверните ее в форме коробочки или блюдца. Совсем не обязательно, чтобы это блюдце имело правильную квадратную или круглую форму. Вы заполните его водой или другим грузом, так что позаботьтесь о том, чтобы оно выдержало вес.
- Подвесьте коробочку или блюдце из фольги к одному концу перекладины. Проделайте по краям блюдца небольшие отверстия и проденьте через них нитку, так чтобы блюдце висело на перекладине.
-
4
Подвесьте к другому концу перекладины иглу или скрепку, так чтобы она располагалась горизонтально. Привяжите горизонтально иглу или скрепку к нити, которая свисает с другого конца перекладины. Чтобы эксперимент удался, необходимо расположить иглу или скрепку именно горизонтально.
-
5
Разместите на перекладине что-нибудь, например пластилин, чтобы уравновесить емкость из алюминиевой фольги. Прежде чем приступить к эксперименту, необходимо добиться, чтобы перекладина располагалась горизонтально. Блюдце из фольги тяжелее иглы, поэтому на его стороне перекладина опустится вниз. Прикрепите к противоположной стороне перекладины достаточное количество пластилина, чтобы она располагалась горизонтально.
- Это называется балансировкой.
-
6
Поместите свисающую на нитке иглу или скрепку в емкость с водой. На этом шаге потребуются дополнительные усилия, чтобы расположить иглу на поверхности воды. Проследите, чтобы игла не погрузилась в воду. Наполните емкость водой (или другой жидкостью с неизвестным поверхностным натяжением) и поставьте ее под висящей иглой, так чтобы игла расположилась прямо на поверхности жидкости.
- Проследите при этом, чтобы удерживающая иглу веревка оставалась на месте и была достаточно натянута.
-
7
Взвесьте на небольших весах несколько булавок или небольшое количество отмеренных капель воды. Вы будете добавлять в алюминиевое блюдце на коромысле по одной булавке или капле воды. При этом необходимо знать точный вес, при котором игла оторвется от поверхности воды.
- Посчитайте количество булавок или капель воды и взвесьте их.
- Определите вес одной булавки или капли воды. Для этого поделите общий вес на количество булавок или капель.
- Предположим, 30 булавок весят 15 граммов, тогда 15/30 = 0,5, то есть одна булавка весит 0,5 грамма.
-
8
Добавляйте булавки или капли воды по одной в блюдце из алюминиевой фольги до тех пор, пока игла не оторвется от поверхности воды. Постепенно добавляйте по одной булавке или капле воды. Внимательно наблюдайте за иглой, чтобы не пропустить момент, когда после очередного увеличения груза она оторвется от воды. Как только игла оторвется от поверхности жидкости, перестаньте добавлять булавки или капли воды.
- Посчитайте количество булавок или капель воды, при котором игла на противоположном конце перекладины оторвалась от поверхности воды.
- Запишите результат.
- Повторите опыт несколько (5 или 6) раз, чтобы получить более точные результаты.
- Посчитайте среднее значение полученных результатов. Для этого сложите число булавок или капель во всех экспериментах и поделите сумму на количество экспериментов.
-
9
Переведите число булавок в силу. Для этого следует умножить количество граммов на 0,00981 Н/г. Чтобы рассчитать поверхностное натяжение, необходимо знать силу, которая понадобилась для отрыва иглы от поверхности воды. Поскольку вы сосчитали вес булавок на предыдущем шаге, чтобы определить силу, достаточно умножить этот вес на 0,00981 Н/г.[4]
- Умножьте число помещенных в блюдце булавок на вес одной булавки. Например, если вы положили 5 булавок весом по 0,5 грамма, их общий вес составит 0,5 г/булавка = 5 x 0,5 = 2,5 грамма.
- Умножьте количество граммов на множитель 0,00981 Н/г: 2,5 x 0,00981 = 0,025 Н.
-
10
Подставьте полученные значения в уравнение и найдите искомую величину. С помощью полученных в ходе эксперимента результатов можно определить поверхностное натяжение. Просто подставьте найденные величины и вычислите результат.
- Допустим, что в приведенном выше примере длина иглы составляет 0,025 метра. Подставляем значения в уравнение и получаем: S = F/2d = 0,025 Н/(2 x 0,025) = 0,05 Н/м. Таким образом, поверхностное натяжение жидкости равно 0,05 Н/м.
Реклама
-
1
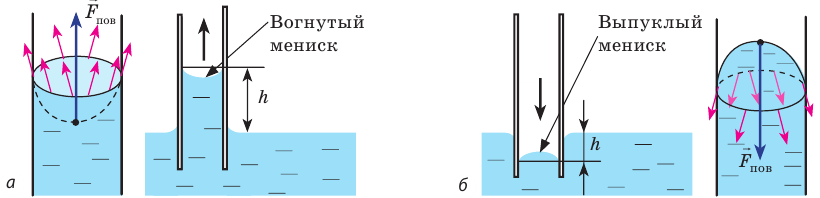
Узнайте о капиллярном эффекте. Чтобы понять капиллярные явления, сначала следует ознакомиться с силами адгезии и когезии. Адгезия вызывает прилипание жидкости к твердой поверхности, например стеклу. Благодаря силе когезии молекулы жидкости притягиваются друг к другу.[5]
. Совместное действие сил адгезии и когезии вызывает поднятие жидкости в тонких трубках.- По высоте поднятия жидкости в трубке можно рассчитать поверхностное натяжение этой жидкости.
- Силы когезии приводят к образованию пузырей и капель на поверхности. При контакте жидкости с воздухом молекулы жидкости притягиваются друг к другу, в результате чего образуется пузырь.
- Адгезия приводит к образованию мениска, который заметен в местах контакта жидкости со стенками стакана. Вогнутая форма мениска видна невооруженным глазом.[6]
- Примером капиллярного эффекта служит поднятие жидкости в соломинке, опущенной в стакан с водой.
-
2
Запишите уравнение для определения поверхностного натяжения. Поверхностное натяжение вычисляется следующим образом: S = (ρhga/2), где S — поверхностное натяжение, ρ — плотность исследуемой жидкости, h — высота подъема жидкости в трубке, g — ускорение свободного падения благодаря действующей на жидкость силе тяжести (9,8 м/с2), a — радиус капиллярной трубки.[7]
- При подстановке данных в это уравнение проследите, чтобы они были выражены в метрических единицах измерения: плотность в кг/м3, высота и радиус в метрах, ускорение свободного падения в м/с2.
- Если плотность жидкости не дана заранее, ее можно найти в справочнике или рассчитать по формуле плотность = масса/объем.
- Поверхностное натяжение измеряется в ньютонах на метр (Н/м). Ньютон равен 1 кг*м/с2.[8]
Чтобы самостоятельно определить единицы измерения, просто подставьте в уравнение только их, без численных значений: S = кг/м3 * м * м/с2 * м. Если сократить два метра в числителе и знаменателе, получаем 1 кг*м/с2/м, то есть 1 Н/м.
-
3
Налейте в емкость жидкость с неизвестным поверхностным натяжением. Возьмите неглубокую тарелку или миску и налейте в нее жидкость, так чтобы она покрывала дно на 2-3 сантиметра. Количество жидкости не играет роли, главное, чтобы было отчетливо видно, насколько она поднимется в капиллярной трубке.
- Если вы собираетесь экспериментировать с разными жидкостями, тщательно очистите и высушите тарелку, прежде чем наливать в нее другую жидкость, либо каждый раз используйте другую емкость.
-
4
Опустите в жидкость чистую тонкую трубку. По высоте подъема жидкости в этой трубке вы определите поверхностное натяжение. Трубка должна быть чистой, чтобы вы ясно видели, как высоко поднимется жидкость над своим уровнем в тарелке. Кроме того, трубка должна иметь постоянный радиус.
- Чтобы измерить радиус, просто приложите линейку к верхнему краю трубки и определите диаметр. Затем поделите диаметр на 2, и вы найдете радиус.
-
5
Измерьте высоту, на которую поднялась жидкость над своим уровнем в тарелке. Подведите край линейки к поверхности жидкости в тарелке и определите, на какую высоту поднялась жидкость в трубке. Вода в трубке поднимается из-за того, что подъемная сила поверхностного натяжения превышает тянущую вниз силу тяжести.[9]
-
6
Подставьте полученные значения в уравнение и проделайте вычисления. После того как вы определите все необходимые величины, подставьте их в уравнение и найдите поверхностное натяжение. Не забудьте перевести все значения в метрические единицы измерения, чтобы получить правильный результат.
- Предположим, мы измеряем поверхностное натяжение воды. Плотность воды составляет около 1 кг/м3 (в данном примере мы используем приблизительные значения).[10]
Ускорение свободного падения равно 9,8 м/с2. Пусть радиус трубки равен 0,029 м, а вода поднялась на высоту 0,5 м. Чему равно поверхностное натяжение воды? - Подставим полученные величины в уравнение и получим: S = (ρhga/2) = (1 x 9,8 x 0,029 x 0,5)/2 = 0,1421/2 = 0,071 Дж/м2.
Реклама
- Предположим, мы измеряем поверхностное натяжение воды. Плотность воды составляет около 1 кг/м3 (в данном примере мы используем приблизительные значения).[10]
-
1
Соберите все необходимое. Для данного эксперимента вам понадобятся пипетка, сухая монетка, вода, небольшая миска, средство для мытья посуды, растительное масло и полотенце. Все это можно найти дома или приобрести в ближайшем магазине. Можно обойтись без средства для мытья посуды и растительного масла, однако для сравнения вам понадобится несколько разных жидкостей.
- Прежде чем приступать к эксперименту, проследите, чтобы монетка была чистой и сухой. Если вы используете мокрую монетку, то получите неточные результаты.
- Данный эксперимент не позволяет рассчитать поверхностное натяжение, с его помощью можно лишь сравнить поверхностное натяжение разных жидкостей.
-
2
Капайте на поверхность монетки по одной капле жидкости за раз. Положите монетку на полотенце или другую поверхность, которую не страшно намочить. Наберите в пипетку первую жидкость, после чего не спеша наносите на монетку по одной капле. При этом считайте капли. Продолжайте до тех пор, пока жидкость не прольется за пределы монетки.
- Запишите, сколько капель потребовалось для того, чтобы жидкость пролилась за пределы монетки.
-
3
Повторите эту процедуру с разными жидкостями. Каждый раз при смене жидкости очищайте и сушите монетку. Сушите также поверхность, на которую вы кладете монетку. Используйте разные пипетки или очищайте пипетку перед новым экспериментом.
- Попробуйте добавить в воду немного средства для мытья посуды, затем покапайте водой на монетку и посмотрите, изменилось ли поверхностное натяжение.
-
4
Сравните число капель, которое требуется для разных жидкостей, чтобы заполнить монетку. Попробуйте повторить эксперимент с одной жидкостью несколько раз, чтобы оценить точность полученных результатов. Усредните результаты: сложите количество капель в разных экспериментах и поделите сумму на число экспериментов. Запишите, сколько капель понадобилось для различных жидкостей для того, чтобы заполнить монетку.
- Чем больше капель той или иной жидкости требуется для заполнения монетки, тем выше поверхностное натяжение данной жидкости.
- Средство для мытья посуды понижает поверхностное натяжение воды; добавив его, для заполнения монетки потребуется меньше капель.
Реклама
Что вам понадобится
- Соломинка, пластмассовая линейка или другой жесткий стержень
- Нитка
- Алюминиевая фольга
- Пластилин или что-нибудь подобное
- Длинная игла или гвоздь для удержания перекладины
- Скрепки или игла для погружения в воду
- Книги или другие массивные предметы, чтобы поддерживать коромысло
- Калькулятор
- Небольшая емкость
- Вода
- Пипетка или булавки
- Небольшие весы
- Неглубокая тарелка
Об этой статье
Эту страницу просматривали 9701 раз.
Была ли эта статья полезной?
Содержание:
Поверхностное натяжение жидкости:
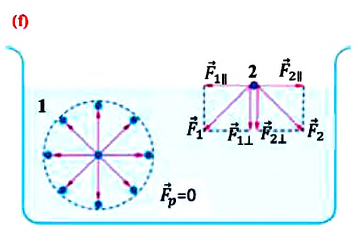
В отличие от газов жидкости имеют свободную поверхность. Молекулы, расположенные на поверхности жидкости, и молекулы внутри жидкости находятся в разных условиях:
a) молекулы внутри жидкости окружены другими молекулами жидкости со всех сторон. Молекула 1 внутри жидкости испытывает действие соседних молекул со всех сторон, поэтому равнодействующая сил притяжения, действующих на нее, равна нулю (f; молекула 1);
b) молекулы на поверхности жидкости испытывают действие со стороны соседних молекул жидкости только сбоку и снизу. Притяжение со стороны молекул газа (пара жидкости или воздуха) над жидкостью во много раз слабее, чем со стороны молекул жидкости, поэтому не принимаются во внимание (f; молекула 2). В результате каждая из равнодействующих сил
Сила поверхностного натяжения
Сила поверхностного натяжения — это сила, направленная по касательной к поверхности жидкости, перпендикулярно к линии, ограничивающей поверхность жидкости, и стремящаяся сократить площадь поверхности жидкости. Сила поверхностного натяжения прямо пропорциональна длине границы соприкосновения свободной поверхности жидкости с твердым телом:
Здесь 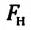
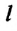
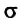
Коэффициент поверхностного натяжения
Коэффициент поверхностного натяжения — численно равен силе поверхностного натяжения, приходящейся на единицу длины линии, ограничивающей поверхность жидкости:
Значение коэффициента поверхностного натяжения зависит от вида жидкости и ее температуры, то есть с увеличением температуры жидкости коэффициент его поверхностного натяжения уменьшается и при критической температуре равен нулю. Единица коэффициента поверхностного натяжения в СИ:
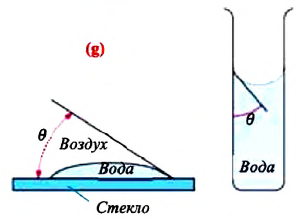
Смачивающая и несмачивающая жидкость. При внимательном рассмотрении можно увидеть искривление поверхности жидкости на границе между жидкостью и твердым телом.
Мениск — это искривление свободной поверхности жидкости в месте ее соприкосновении с поверхностью твердого тела (или другой жидкости). Угол между поверхностью мениска и поверхностью твердого тела называется краевым углом.
Значение краевого угла 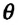
Смачивающая жидкость —это жидкость, у которой краевой угол острый. Сила взаимного притяжения между молекулами смачивающей жидкости и твердого тела больше, чем силы взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде становится вогнутой, например, вода в стеклянном сосуде — смачивающая жидкость (g).
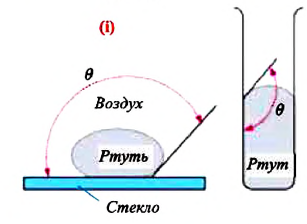
Несмачивающая жидкость — это жидкость, у которой краевой угол тупой. Сила взаимного притяжения между молекулами несмачивающей жидкости и твердого тела меньше, чем сила взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде бывает выпуклой, например, ртуть в стеклянном сосуде — несмачивающая жидкость (i).
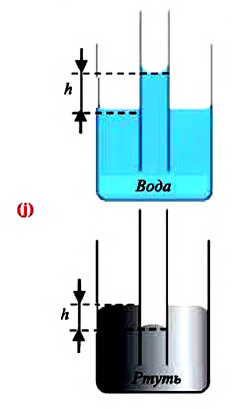
Капиллярные явления
В повседневной жизни встречаются и используются тела, с легкостью впитывающие в себя воду, например, полотенце, промокательная бумага, сахар, кирпич, растения и др. Это свойство в телах объясняется существованием в них большого количества очень узких трубочек — капилляров.
Капилляр — это узкая трубка (канал) диаметром меньше 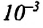
Капиллярными явлениями называют явления подъема смачивающей и опускания несмачивающей жидкости по капилляру относительно общего уровня жидкости под действием сил поверхностного натяжения (j).
В таблице 6.4 дана зависимость между величинами, характеризующими жидкость, поднимающуюся в капилляре.
Таблица 6.4
|
Характеристики жидкости, поднимающейся в капилляре |
Формула |
| Вес жидкости, поднимающейся в капилляре |
Где |
| Масса жидкости, поднимающейся в капилляре | 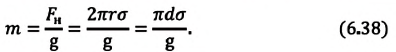 |
| Высота жидкости, поднимающейся в капилляре |
Если жидкость полностью смачиваемая, то получаем в Где |
| Давление жидкости, поднимающейся в капилляре | 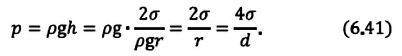 |
Поверхностное натяжение жидкости
Некоторые виды пауков могут передвигаться по поверхности воды не проваливаясь, как будто эта поверхность покрыта невидимой тонкой пленкой. такое же впечатление создается, если наблюдать за вытеканием воды из маленького отверстия — вода течет не тоненькой струйкой, а образует капли. Бумажная салфетка впитывает воду, едва коснувшись ее поверхности. какая сила является причиной всех этих явлений?
Каковы особенности поверхностного слоя жидкости
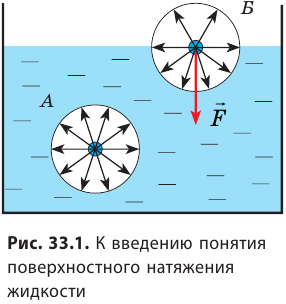
На свободной поверхности жидкости молекулы находятся в особых условиях, отличающихся от условий, в которых находятся молекулы внутри жидкости. Рассмотрим две молекулы — А и Б (рис. 33.1): молекула А находится внутри жидкости, а молекула Б — на ее поверхности. Молекула А окружена другими молекулами жидкости равномерно, поэтому силы, действующие на молекулу А со стороны молекул, попадающих в сферу межмолекулярного взаимодействия, скомпенсированы, то есть их равнодействующая равна нулю.
Молекула Б с одной стороны окружена молекулами жидкости, а с другой — молекулами газа. Со стороны жидкости на нее действует гораздо больше молекул, чем со стороны газа, поэтому равнодействующая F межмолекулярных сил направлена в глубь жидкости. Чтобы молекула из глубины попала в поверхностный слой, нужно совершить работу против межмолекулярных сил. Это означает, что молекулы поверхностного слоя жидкости (по сравнению с молекулами внутри жидкости) обладают избыточной потенциальной энергией. Эта избыточная энергия является частью внутренней энергии жидкости и называется поверхностной энергией (Wпов). Очевидно, что чем больше площадь S поверхности жидкости, тем больше поверхностная энергия: W S пов = σ , где σ (сигма) — коэффициент пропорциональности, который называют поверхностным натяжением жидкости.
Поверхностное натяжение жидкости — физическая величина, которая характеризует данную жидкость и равна отношению поверхностной энергии к площади поверхности жидкости:
Единица поверхностного натяжения в СИ — ньютон на метр:
Поверхностное натяжение жидкости определяется силами межмолекулярного взаимодействия, поэтому оно зависит:
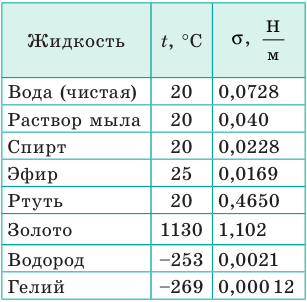
- от природы жидкости: у летучих жидкостей (эфир, спирт, бензин) поверхностное натяжение меньше, чем у нелетучих (ртуть, жидкие металлы);
- температуры жидкости: чем выше температура жидкости, тем меньше поверхностное натяжение;
- присутствия в составе жидкости поверхностно активных веществ — их наличие уменьшает поверхностное натяжение;
- свойств газа, с которым жидкость граничит. В таблицах обычно приводят значение поверхностного натяжения на границе жидкости и воздуха при определенной температуре (табл. 1).
Таблица 1
Поверхностное натяжение σ некоторых жидкостей
Что такое сила поверхностного натяжения
Поскольку поверхностный слой жидкости обладает избыточной потенциальной энергией (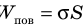
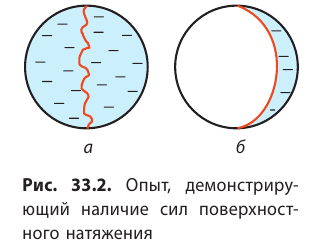
Наличие сил поверхностного натяжения делает поверхность жидкости похожей на натянутую резиновую пленку, однако упругие силы в резиновой пленке зависят от площади ее поверхности (от того, насколько пленка деформирована), а поверхность жидкости всегда «натянута» одинаково, то есть силы поверхностного натяжения не зависят от площади поверхности жидкости. Наличие сил поверхностного натяжения можно доказать с помощью такого опыта. Если проволочный каркас с закрепленной на нем нитью опустить в мыльный раствор, каркас затянется мыльной пленкой, а нить приобретет произвольную форму (рис. 33.2, а).
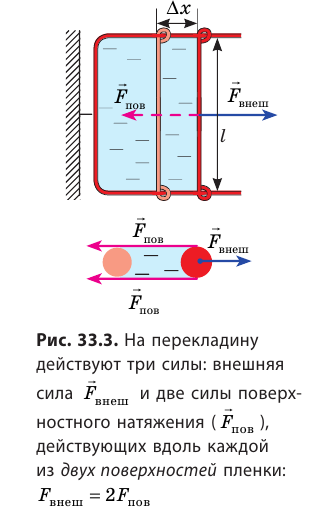
Если осторожно проткнуть иглой мыльную пленку по одну сторону от нити, сила поверхностного натяжения мыльного раствора, действующая с другой стороны, натянет нить (рис. 33.2, б). Опустим в мыльный раствор проволочную рамку, одна из сторон которой подвижна. На рамке образуется мыльная пленка (рис. 33.3). Будем растягивать эту пленку, действуя на перекладину (подвижную сторону рамки) с некоторой силой 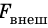
Если под действием этой силы перекладина переместится на ∆x , то внешние силы совершат работу: 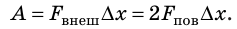
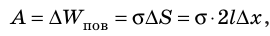
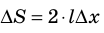
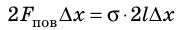
Таким образом, поверхностное натяжение σ численно равно силе поверхностного натяжения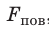
С одним из методов определения поверхностного натяжения жидкости вы ознакомитесь, выполняя лабораторную работу № 7.
- Заказать решение задач по физике
Где проявляется поверхностное натяжение
В жизни вы постоянно сталкиваетесь с проявлениями сил поверхностного натяжения. Так, благодаря ему на поверхности воды удерживаются легкие предметы (рис. 33.4) и некоторые насекомые.
Рис. 33.4. Монетка удерживается на поверхности воды благодаря силе поверхностного натяжения. (Чтобы провести такой опыт, монетку нужно потереть между пальцев и осторожно опустить на поверхность воды.)
Когда вы ныряете, ваши волосы расходятся во все стороны, но как только вы окажетесь над водой, волосы слипнутся, так как в этом случае площадь свободной поверхности воды намного меньше, чем при раздельном расположении прядей в воде. По этой же причине можно лепить фигуры из влажного песка: вода, обволакивая песчинки, прижимает их друг к другу.
Рис. 33.5. Капля удерживается около небольшого отверстия до тех пор, пока сила поверхностного натяжения уравновешивает силу тяжести
Стремлением жидкости уменьшить площадь поверхности объясняется и тот факт, что в условиях невесомости вода принимает форму шара, — при заданном объеме шарообразной форме соответствует наименьшая площадь поверхности. Форму шара приобретают тонкие мыльные пленки (мыльные пузыри). Поверхностным натяжением объясняется образование пены: пузырек газа, достигнув поверхности жидкости, имеет над собой тонкий слой жидкости; если пузырек мал, то архимедовой силы недостаточно, чтобы разорвать двойной поверхностный слой, и пузырек «застревает» вблизи поверхности. Благодаря поверхностному натяжению жидкость не выливается из маленького отверстия тоненькой струйкой, а капает (рис. 33.5), дождь не проливается через ткань зонта или палатки и т. д.
Почему одни жидкости собираются в капли, а другие растекаются
Наличие сил поверхностного натяжения проявляется в сферической форме мелких капелек росы, в каплях воды, разбегающихся по раскаленной плите, в капельках ртути на поверхности стекла. Однако при соприкосновении с твердым телом сферическая форма капли, как правило, не сохраняется. Форма свободной поверхности жидкости зависит также от сил взаимодействия молекул жидкости с молекулами твердого тела.
Если силы взаимодействия между молекулами жидкости больше, чем силы взаимодействия между молекулами жидкости и твердого тела, жидкость не смачивает поверхность твердого тела (рис. 33.6). Например, ртуть не смачивает стекло, а вода не смачивает покрытую сажей поверхность.
Рис. 33.6. Капля несмачивающей жидкости принимает форму, близкую к сферической, а поверхность жидкости вблизи стенки сосуда является выпуклой
Если же капельку ртути поместить на цинковую пластину, то капелька будет стремиться растечься по поверхности пластины; так же ведет себя и капелька воды на стекле (рис. 33.7). Если силы взаимодействия между молекулами жидкости меньше сил взаимодействия между молекулами жидкости и твердого тела, жидкость смачивает поверхность твердого тела.
Рис. 33.7. Капля смачивающей жидкости стремится растечься по поверхности твердого тела, а вблизи стенки сосуда поверхность жидкости принимает вогнутую форму
Почему жидкость поднимается в капиллярах
В природе часто встречаются тела, пронизанные многочисленными мелкими капиллярами (от лат. capillaris — волосяной) — узкими каналами произвольной формы. Такую структуру имеют бумага, дерево, почва, многие ткани и строительные материалы. В цилиндрических капиллярах искривленная поверхность жидкости представляет собой часть сферы, которую называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 33.8, а), а у несмачивающей — выпуклый (рис. 33.8, б).
Рис. 33.8. капиллярные явления: а — смачивающая жидкость поднимается по капилляру; б — несмачивающая жидкость опускается в капилляре
Поверхность жидкости стремится к минимуму потенциальной энергии, а искривленная поверхность обладает большей площадью по сравнению с площадью сечения капилляра, поэтому поверхность жидкости стремится выровняться и под ней возникает избыточное (отрицательное или положительное) давление — лапласово давление (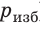
Под вогнутой поверхностью (жидкость смачивает капилляр) лапласово давление отрицательное и жидкость втягивается в капилляр. Так поднимаются влага и питательные вещества в стеблях растений, керосин по фитилю, влага в почве. Вследствие лапласового давления салфетки или ткань впитывают воду, брюки в дождливую погоду сильно намокают снизу и т. д. Под выпуклой поверхностью (жидкость не смачивает капилляр) лапласово давление положительное и жидкость в капилляре опускается. Чем меньше радиус капилляра, тем больше высота подъема (или опускания) жидкости (см. задачу ниже).
Пример решения задачи
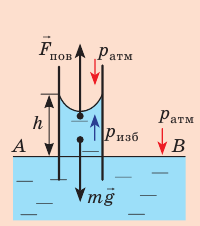
Капиллярную трубку радиусом r одним концом опустили в жидкость, смачивающую внутреннюю поверхность капилляра. На какую высоту поднимется жидкость в капилляре, если плотность жидкости ρ, а ее поверхностное натяжение σ ? Чему равно лапласово давление под вогнутой поверхностью капилляра? Смачивание считайте полным.
Решение:
На жидкость в капилляре действуют сила тяжести и сила поверхностного натяжения (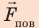
Поиск математической модели, решение
Поскольку m V = ρ , а объем воды в цилиндрическом капилляре 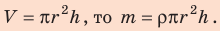
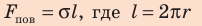
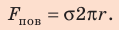
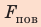

где R — радиус кривизны мениска (при полном смачивании r=R).
Ответ: (Данные выводы следует запомнить!)
Выводы:
- Свойства паров в физике
- Кипение жидкостей в физике
- Электромагнитные явления в физике
- Электромагнитные волны и их свойства
- Расчет количества теплоты при нагревании и охлаждении
- Удельная теплота сгорания топлива
- Плавление и кристаллизация в физике
- Испарение жидкостей в физике
Что такое поверхностное натяжение жидкости
Поверхностное натяжение — характеристика поверхности раздела двух фаз, которые находятся в равновесии. Характеристика определяется работой образования единицы площади этой поверхности раздела.
Выражается произведением:
(mathcal F=sigmamathcal l), Н
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(sigma) — коэффициент поверхностного натяжения, Н/м
(mathcal l) — длина, м
Направление силы: по касательной к поверхности.
Коэффициент поверхностного натяжения
Коэффициент поверхностного натяжения ((sigma)) — сила, которая действует на единицу длины линии, ограничивающей поверхность жидкости (Н/м).
Коэффициент поверхностного натяжения – коэффициент, равный работе, которую необходимо совершить для образования поверхности жидкости площадью (S) при постоянной температуре.
(sigma=frac{{mathcal F}_{пов}}{mathcal l} )
(sigma=frac{{mathcal F}_{пов}}{mathcal S})
(mathcal S) — площадь поверхности жидкости
Зависит от:
- Рода жидкости и ее свойств.
- Температуры (чем больше температура, тем меньше натяжение).
- Наличия ПАВ (поверхностно-активных веществ. Например, мыло).
- Присутствия каких-либо примесей.
- Свойств газа, контактирующего с жидкостью.
Чем вызвано поверхностное натяжение
Причина возникновения явления поверхностного напряжения: молекулы, которые составляют верхний слой жидкости. Они создают взаимодействие между собой, возникает натяжение.
Жидкости стремятся принять форму, которая требует минимальной площади поверхности.
Силы поверхностного натяжения
Силы поверхностного натяжения работают вдоль поверхности жидкости перпендикулярно контуру. Сокращают ее площадь. Это похоже на пленку, которая стягивает объем. На сам объем силы не оказывают влияние.
Примеры в окружающей среде
- движение водомерки по воде (ее лапки покрыты воскообразным веществом);
- капля росы, дождя, из пипетки;
- цилиндрическая форма струи воды;
- мыльный пузырь.
Расчет поверхностного натяжения в задачах
Задача 1
Дано
Имеется пипетка с диаметром отверстия (d=2) мм. В ходе опыта выяснилось, что (40) капель имеют массу равную (1,9) г. Вычислите коэффициент поверхностного натяжения.
Решение
Найдем массу одной капли и длину окружности.
(mathcal m=frac{{mathcal m}_{общ}}{mathcal n}\)
(mathcal l=mathrmpimathcal d\)
Напишем условие равновесия капли из пипетки.
({mathcal m}_0mathcal g=mathcal F\)
Подставим формулы.
(frac{mathcal m}{mathcal n}mathcal g=sigmamathrmpimathcal d\)
Выразим коэффициент поверхностного натяжения.
(sigma=frac{mathcal{mg}}{mathcal nmathrmpimathcal d}=frac{1,9ast10^{-3}ast10}{40ast3,14ast2ast10^{-3}}=75,6ast10^{-3};Н/м\)
Ответ: (75,6ast10^{-3};Н/м\)
Задача 2
Дано
Сосуд со ртутью имеет отверстие диаметром 70 мкм. Возможно ли без измерения определить максимальную высоту слоя ртути, при которой она не будет вытекать через отверстие?
Решение
Ртуть начнет вытекать тогда, когда произойдет увеличение силы ее давления относительно силы поверхностного натяжения.
(mathcal{pS}=mathcal F\rhomathcal{ghS}=sigmamathcal l\)
Выразим высоту.
(mathcal k=frac{sigmamathcal l}{rhomathcal{gS}}=frac{sigmamathrmpimathcal d}{rhomathcal g{displaystylefrac{mathrmpimathcal d^2}4}}=frac{4sigma}{rhomathcal{gd}}=frac{4ast472ast10^{-3}}{13600ast9,8ast70ast10^{-6}}=0,2;м\\)
Ответ: (0,2) м
Задача 3
Дано
Есть игла длиной (3,5) см и массой (0,3) г. Сможем ли мы произвести следующее действие: положить иголку на поверхность воды. Или же она утонет? Какие силы действуют на иголку?
Решение
На иглу действует сила тяжести. Если мы найдем ее и сравним с силой поверхностного натяжения, то узнаем ответ.
({mathcal F}_{тяж}=mathcal{mg}=0,3ast10^{-3}ast9,8=2,9ast10^{-3};Н\\\\)
({mathcal F}_{пн}=sigmamathcal l=73ast10^{-3}ast3,5ast10^{-2}=2,5ast10^{-3};Н\\\\\\\\)
Сравниваем силы и видим, что значение силы тяжести больше величины поверхностного натяжения.
Ответ: Игла утонет.
Задача 4
Почему возникают сложности с тем, чтобы снять мокрые перчатки с рук?
Ответ: Молекулы воды взаимодействуют с молекулами перчатки. По этой причине мы чувствуем сопротивление при стягивании перчаток с рук.
Задача 5
Дано
Есть капиллярная трубка ((R=0,5) мм). В ней столб жидкости высотой 11 мм. Определите плотность жидкости, если (sigma=22;мН/м.\\\\)
Решение
Воспользуемся формулой для капилляра.
(rho=frac{2sigmacosleft(alpharight)}{mathcal{hrg}}\\\\)
(alpha-угол;смачивания;жидкостью;стенки;капилляра.;Возьмем;за;90^circ\\\\)
(rho=frac{2,22ast10^{-3}ast1}{11ast10^{-3}ast0,5ast10^{-3}ast10}=800;кг/м^3\\\\)
Ответ: (800 кг/м^3\\\\)
Задача 6
Дано
Алюминиевое кольцо массой 7 г и радиусом 7,8 см соприкасается с мыльным раствором. Какую силу нужно приложить, чтобы оторвать кольцо от жидкости? Раствор имеет комнатную температуру.
Решение
Помимо натяжения на кольцо действует внешняя сила и сила тяжести.
Важно то, что кольцо соприкасается жидкости двумя сторонами. Умножаем на 2.
({mathcal F}_{пн}=2sigmamathcal l\mathcal l=2mathrm{πR}\{mathcal F}_{mathrm{пн}}=4mathrm{πσR}\\\\)
(mathcal F=mg+4mathrm{πσR}\mathcal F=7ast10^{-3}ast9,8+4mathrmpiast4ast10^{-2}ast7,8ast10^{-2}=0,11;mathrm Н\\\)
Ответ: 11 Н
Download Article
Download Article
Surface tension refers to the ability of a liquid to resist the force of gravity. For example, water forms droplets on a table because the water molecules at the surface group together against the force of gravity.[1]
Surface tension is what allows a denser object, such as an insect, to be able to float on the water’s surface. Surface tension is measured by the amount of force (N) exerted on a unit such as length (m) or the amount of energy of a measured area. These are measured as Newton per meter (or N/meter).[2]
The forces that water molecules exert on each other, or cohesive forces, cause the tension and are responsible for the shape of water (or other liquid) drops. You can measure surface tension with a few household items and a calculator.
-
1
Define the equation to solve for surface tension. In this experiment, the equation for surface tension will be determined by the equation F = 2sd. F is the force in newtons (N), s is the surface tension in (N/m), and d is the length of the needle used in the experiment. Rearranging the equation to solve for surface tension yields s = F/2d.[3]
- The force will be calculated at the end of the experiment.
- Measure the length of the needle in meters using a ruler before starting the experiment.
-
2
Construct a small balance beam.[4]
In this experiment, you will use a balance beam and a small needle floating on the surface of water to measure surface tension. The balance beam needs to be well constructed so that you can get an accurate result. You can use many different types of materials for this, just make sure the center beam is something sturdy like wood, plastic, or dense cardboard.- Mark the center of the material to be used for your beam (straw, plastic ruler) and drill or poke a hole through it; this will be the fulcrum point (the point that allows the beam to rotate freely). If you are using a plastic straw you can just poke a pin or nail right through it.
- Drill or poke a hole at each end of the beam ensuring that they are the same distance from the middle. Thread a string through each hole to serve as holders for the balance dishes. Make sure that there is 1 string for each hole at either end.
- Rest the nail horizontally between two stacks of books so that the center beam can rotate freely.
Advertisement
-
3
Fold a piece of aluminum foil to form a box or dish. The dish does not have to be exactly square or round. The dish will be filled with water or another weight, so make sure it is sturdy enough to support this.
- Hang the box or dish from one end of the beam. Poke small holes in the sides of the dish and thread the string through to hold up the dish.
-
4
Hang a needle or paper clip horizontally from the other end of the beam with thread. On the opposite side of the beam, tie a paper clip or needle to the end of the string so that it lays flat. For the experiment to work, it is important that the paper clip or needle is horizontal.
-
5
Place a piece of material such as clay or play-doh on the beam to counterbalance the aluminum container. Before beginning the experiment, you want to make sure that the beam is lying flat. The dish will be heavier than the needle, causing the beam to lower in the direction of the dish. Add enough clay to the opposite side of the beam so that the beam is level.
- This is called counterbalancing. The clay does not affect the calculations because it is balancing out the beam.
-
6
Place the needle or paper clip hanging from the beam into a container of water. This step may require some extra effort to ensure the needle is resting just on the top of the water’s surface. You do not want the needle submerged in the water. Fill a container with water (or other liquid of unknown surface tension) and place it underneath the needle at a height that allows the needle to rest directly on top the surface.
- Make sure the string holding the needle in place remains taut once the needle is on top of the water.
-
7
Weigh a batch of pins or several measured drops of water on a small postal scale. You will be adding pins or drops of water one at a time to the aluminum dish you constructed earlier. For the calculation, it is important to know exactly how much weight is required to lift the needle out of the water.
- Count out a number of pins or drops of water and weigh them.
- Determine the individual weight of each drop or pin by dividing the total weight by the number of pins or water drops.
- For example, let’s say 30 pins weigh 15 grams: 15/30 = 0.5. Each pin weighs 0.5 grams.
-
8
Add the pins or drops of water one at a time to your aluminum foil container until the needle is freed from the water’s surface. Slowly add a pin or a drop of water to the aluminum dish one pin/drop at a time. Watch the needle closely to see if it comes out of the water with each new addition. Stop adding pins/drops once the needle is no longer in contact with the surface of the water.
- Count the number of pins or drops of water needed to remove the counterweight from the water’s surface.
- Record each reading.
- Repeat the exercise several times (5 or 6) for more accurate readings.
- Calculate an average of the results by adding the total number of pins needed in each trial and dividing that by the total number of trials.
-
9
Convert the measurement of pins into force by multiplying the number of grams by 0.00981 N/g. To calculate the surface tension, you need to know the total amount of force required to remove the needle from the surface of the liquid. Because you weighed the pins in the previous step, you can easily do this calculation using the conversion factor 0.00981 N/g.[5]
- Multiply the number of pins added to the dish by the weight of each pin. For example, 5 pins at 0.5 g/pin = 5 x 0.5 = 2.5 g.
- Multiply the amount of grams by the conversion factor 0.00981 N/g: 2.5 x 0.00981 = 0.025 N.
-
10
Plug the variables into the equation and solve. Using the measurements you gathered throughout the experiment, you can now solve for force. Simply plug the numbers into the correct variable and solve using the proper order of operations.
- Continuing our example, let’s say the needle was 0.025 m long. Plugging the variables into the equation yields: S = F/2d = 0.025 N/(2 x 0.025) = 0.05 N/m. The surface tension of the liquid is 0.05 N/m.
Advertisement
-
1
Understand capillary action. In order to understand capillary action, you first need to understand adhesion and cohesive forces. Adhesion is the force that causes a liquid to stick to a solid surface, such as the edge of a glass. Cohesive forces are those that pull liquid molecules toward each other.[6]
The combination of adhesion and cohesive forces causes a liquid to rise up the center of a thin tube.- The height the liquid rises can be used to calculate the surface tension of that liquid.
- Cohesion causes water to form bubbles or droplets on a surface. When a liquid is in contact with air, the molecules feel attractive forces towards each other and make a bubble on the surface.
- Adhesion causes the meniscus that is seen in liquids when they cling to the sides of a glass. It is the concave shape at the top of the liquid seen at eye level.[7]
- An example of capillary action is watching water rise in a straw placed in a cup of water.
-
2
Define the equation to solve for surface tension. Surface tension is given by the equation S = (ρhga/2) where S is the surface tension, ρ (or rho) is the density of the liquid you are measuring, h is the height the liquid rises in the tube, g is the acceleration due to gravity acting on the liquid (9.8 m/s2) and a is the radius of the capillary tube.[8]
- When working through this equation, make sure all of your units are in the proper metric form: density in kg/m3, height and radius in meters, and gravity in m/s2.
- If the density of the liquid is not given, you can look it up in a reference book or calculate it using the equation density = mass/volume.
- The unit for surface tension is one newton per meter (N/m). A Newton is equal to 1 kg-m/s2. To work out the units on your own, simply solve the equation with just units. S = kg/m3 * m * m/s2 * m. Two of the meter units cancel out two of the per meter units and you are left with 1 kg-m/s2/m or 1 N/m.
-
3
Fill a container with the liquid of unknown surface tension. Using a shallow dish or bowl, fill it with about an inch of the liquid in question. The amount of liquid added does not matter as long as you can clearly see the rise in liquid within the capillary tube.[9]
- If you repeat this with different liquids, make sure the dish is thoroughly cleaned and dried before adding the next liquid. Alternatively, just use separate dishes for each liquid.
-
4
Place a clear, thin tube into the liquid. This is the tube that you will take your measurements from to calculate the surface tension. The tube must be clear so that you can see how far the liquid rises above the level in the dish. The tube must also have the same radius throughout.[10]
- To measure the radius, simply place a ruler across the top of the tube and determine the diameter. Divide the diameter by 2 and you have the radius.
- You can buy these tubes online or from a hardware store.
- It can be difficult to accurately measure small changes in the height the liquid will rise in a straw or wide tube. As the height to which the water will rise is inversely proportional to the diameter of the tube (narrower tube = higher rise) this experiment is much easier to do with a narrow transparent capillary tube. These can be purchased at low cost online, but confirm the inside diameter is provided (typically around 1mm-1.2mm) and both ends are open. As these are fragile and made of glass, ensure care when handling them.
-
5
Measure the height the liquid rises above the liquid in the container. Place the bottom of a ruler directly above the liquid in the dish and measure how high the liquid has risen into the tube. The water rises due to the upward force of surface tension being greater than the downward force of gravity.[11]
-
6
Plug the measured values into the equation and solve. Once you have determined all of the necessary variables, you can plug them into the formula and solve for surface tension. Remember to convert all of your values to metric so the problem can be solved properly.
- For example, let’s say we are measuring the surface tension of water. Water has a density around 1000 kg/m3 (we will use approximate values in this example).[12]
The variable g is always 9.8 m/s2. The radius of the tube is .029 m and the water rises 0.0005 m. What is the surface tension of the water? - Plugging the variables into the equation yields: S = (ρhga/2) = (1000 x 9.8 x 0.029 x 0.0005)/2 = 0.1421/2 = 0.071 J/m2.
- For example, let’s say we are measuring the surface tension of water. Water has a density around 1000 kg/m3 (we will use approximate values in this example).[12]
Advertisement
-
1
Gather your materials. For this experiment you will need an eye dropper, a dry penny, water, a small bowl, dish soap, oil, and a towel. Most of these items can be found around the house or purchased at the grocery store. You don’t have to use dish soap and oil, but you will want different liquids to compare their surface tensions.[13]
- Make sure the penny is completely clean and dry before beginning the experiment. If there are other liquids on the penny, the experiment will not be accurate.
- This experiment does not allow you to calculate surface tension, but just determine surface tensions of different liquids relative to each other.
-
2
Drip one drop of liquid at a time onto the penny. Place the penny on top of a towel or a surface that you don’t mind getting wet. Fill the eyedropper with the first liquid. Slowly, drip the liquid onto the penny, taking care to only drop one drop at a time. Count the number of drops it takes to fill the penny until the liquid runs over.[14]
- Write down how many drops it takes for the liquid to flow over the side of the penny.
-
3
Repeat the experiment with a different liquid. Clean and dry the penny in between each test of liquid. Dry the surface that you placed the penny on before repeating the experiment. Use multiple eyedroppers or clean it in between uses.[15]
- Try mixing a little bit of dish soap to the water and dropping again to see if the surface tension changes.
-
4
Compare the number of drops it takes to fill the penny for each liquid. Try repeating the experiment with the same liquid multiple times to see if you are getting an accurate count. Average the trials together by adding them together and dividing by the number of trials performed. Write down which substances required the most drops and which required the fewest to fill the penny.[16]
- Substances with a higher surface tension will have more drops on the penny than substances with a lower surface tension.
- The dish soap lowers the surface tension of the water, using fewer drops to fill the penny.
Advertisement
Add New Question
-
Question
Can I use pennies instead of water droplets or pins?
No. Pennies have a very dense and heavy surface rather than water droplets or pins.
-
Question
I have a homemade, non-bulb pipette, 66 cm long. When shut, fluid does not escape. Is there a universal formula for this effect? Surface tension, adhesion, gravity, air pressure?
If the fluid in the pipette’s exit flowed out, it would create a near vacuum, sucking the liquid back in. No gas can replace the liquid, so the only gas available attempts to fill the space. This creates the sucking force (like the principle of the vacuum cleaner) that keeps the liquid in place.
-
Question
What do I do if method 2 is not working? I’m submerging the tube in water, but there is no liquid above where the liquid in the dish ends.
Use a capillary tube that has a small inner radius. Moreover, use a travelling microscope for better readings and therefore better results.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Things You’ll Need
- Straw, plastic ruler or other stiff rod
- String
- Aluminum foil
- Modeling clay or other similar material
- Long needle or nail for fulcrum
- Paper clip or needle to submerge into water
- Books or other material of equal weight to support the balance beam
- Calculator
- Small container
- Water
- Eye dropper, pipette or pins
- Postal scale or other small weighing device
- Shallow dish
References
About This Article
Article SummaryX
To measure surface tension using the capillary method, fill a shallow dish with 1 inch of water. Measure the radius of a clear tube, then place the tube in the water and measure how high the water in the tube rises above the water in the container. Plug the measured value into your equation to calculate the surface tension. For more information on measuring surface tension from our Environmental Science reviewer, including how to calculate relative tension with a penny, keep reading.
Did this summary help you?
Thanks to all authors for creating a page that has been read 141,809 times.
Reader Success Stories
-
«I had this science fair project, and I didn’t know how to measure surface tension. I searched on wikiHow…» more
Did this article help you?
Поверхностное натяжение
Поверхностное натяжение
Опишем механизм возникновения поверхностного натяжения в жидкостях. Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости. Рассмотрим две молекулы A и B. Молекула A находится внутри жидкости, молекула B – на ее поверхности (рис. 1). Молекула A окружена другими молекулами жидкости равномерно, поэтому силы, действующие на молекулу A со стороны молекул, попадающих в сферу межмолекулярного взаимодействия, скомпенсированы, или, другими словами, их равнодействующая равна нулю. Молекула B с одной стороны окружена молекулами жидкости, а с другой стороны – молекулами газа, концентрация которых значительно ниже, чем концентрация молекул жидкости. Так как со стороны жидкости на молекулу B действует гораздо больше молекул, чем со стороны газа, равнодействующая всех межмолекулярных сил уже не будет равна нулю и будет направлена внутрь объема жидкости. Таким образом, для того чтобы молекула из глубины жидкости попала в поверхностный слой, нужно совершить работу против не скомпенсированных межмолекулярных сил. А это означает, что молекулы приповерхностного слоя, по сравнению с молекулами внутри жидкости, обладают избыточной потенциальной энергией, которая называется поверхностной энергией.
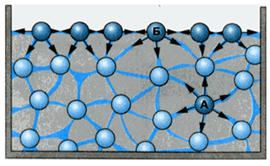
Очевидно, чем больше площадь поверхности жидкости, тем больше таких молекул, которые обладают избыточной потенциальной энергией, а значит тем больше поверхностная энергия. Этот факт можно записать в виде следующего соотношения:
где поверхностная энергия жидкости,
площадь свободной поверхности жидкости и
коэффициент пропорциональности, который называется коэффициентом поверхностного натяжения.
Коэффициент поверхностного натяжения
Единицей измерения коэффициента поверхностного натяжения в системе СИ является .
Коэффициент поверхностного натяжения жидкости зависит: 1) от природы жидкости (у «летучих жидкостей таких, как эфир, спирт, бензин, коэффициент поверхностного натяжения меньше, чем у «нелетучих – воды, ртути); 2) от температуры жидкости (чем выше температура, тем меньше поверхностное натяжение); 3) от свойств газа, который граничит с данной жидкостью; 4) от наличия поверхностно-активных веществ таких, как мыло или стиральный порошок, которые уменьшают поверхностное натяжение. Также следует отметить, что коэффициент поверхностного натяжения не зависит от площади свободной поверхности жидкости.
Из механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии. Вследствие поверхностного натяжения жидкость всегда принимает форму с минимальной поверхностью. Если на жидкость не действуют другие силы или их действие мало, жидкость будет стремиться принимать форму сферы, как, например, капля воды, мыльный пузырь. Также будет вести себя вода в невесомости. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы называютсясилами поверхностного натяжения.
Поэтому коэффициент поверхностного натяжения можно также определить как модуль силы поверхностного натяжения, действующей на единицу длины контура, ограничивающего свободную поверхность жидкости:
Наличие сил поверхностного натяжения делает поверхность жидкости похожей на упругую растянутую пленку, с той только разницей, что упругие силы в пленке зависят от площади ее поверхности (т.е. от того, как пленка деформирована), а силы поверхностного натяженияне зависятот площади поверхности жидкости. Если положить швейную иглу на поверхность воды, поверхность прогнется и не даст ей утонуть. Действием сил поверхностного натяжения можно объяснить скольжение легких насекомых таких, например, как водомерки, по поверхности водоемов (рис.2). Лапка водомерки деформирует водную поверхность, увеличивая тем самым ее площадь. Вследствие этого возникает сила поверхностного натяжения, которая стремится уменьшить подобное изменение площади. Равнодействующая сил поверхностного натяжения будет направлена вверх, компенсируя при этом силу тяжести.

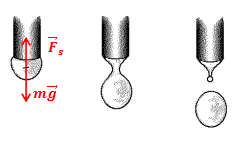
На действии сил поверхностного натяжения основан принцип действия пипетки (рис.3). Капелька, на которую действует сила тяжести, вытягивается вниз, тем самым увеличивая площадь своей поверхности. Естественно, возникают силы поверхностного натяжения, равнодействующая которых противоположна направлению силы тяжести, и которые не дают капельке растягиваться. При нажатии на резиновый колпачок пипетки, создается дополнительное давление, которое помогает силе тяжести, в результате чего капля падает вниз.























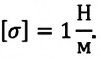
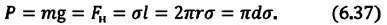
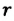 — радиус капилляра,
— радиус капилляра, 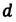 — диаметр капилляра.
— диаметр капилляра.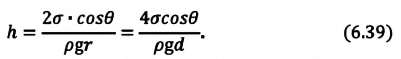
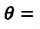
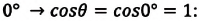

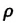 — плотность жидкости, поднимающейся в капилляре. Высота подъема жидкости в капилляре зависит от рода жидкости и обратно пропорциональна радиусу капилляра.
— плотность жидкости, поднимающейся в капилляре. Высота подъема жидкости в капилляре зависит от рода жидкости и обратно пропорциональна радиусу капилляра.