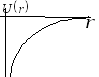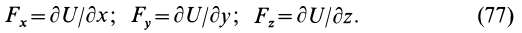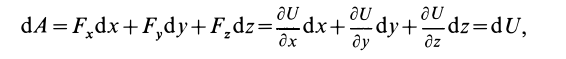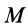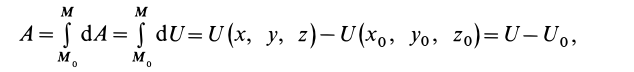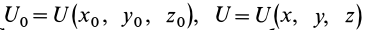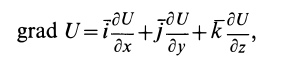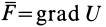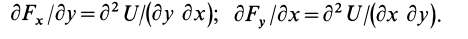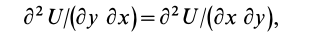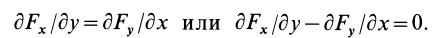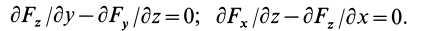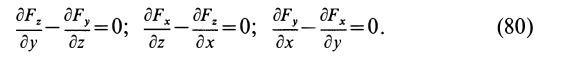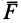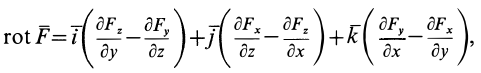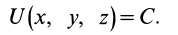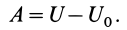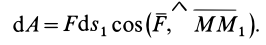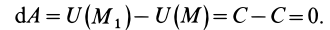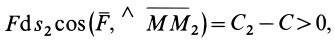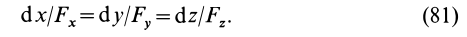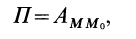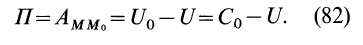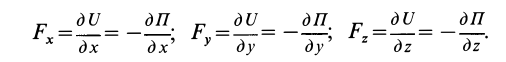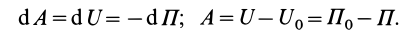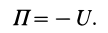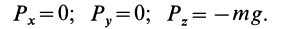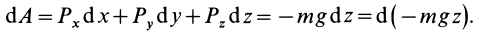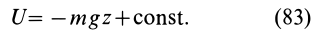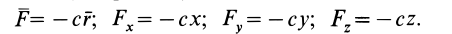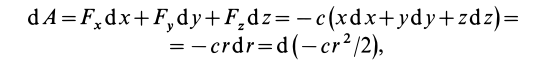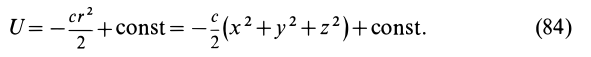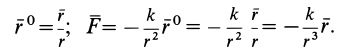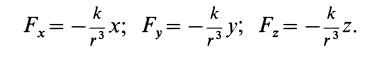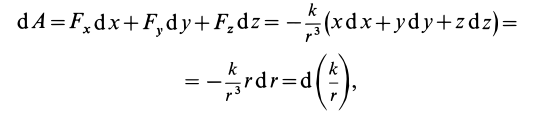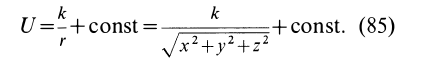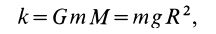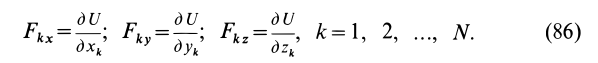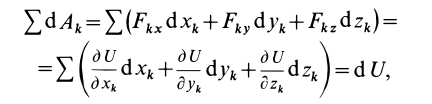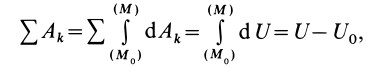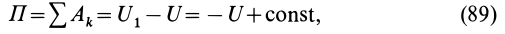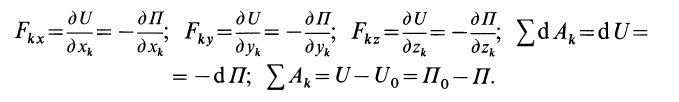Потенциальная энергия как найти перемещение

1. Понятие
   потенциальной энергии.

Определение:
стационарное силовое поле, в котором
работа силы поля на пути между любыми
двумя точками не
зависит от
выбора пути, а зависит только от положения
этих точек, называется потенциальным
полем (силы
— консервативными).

Можно иначе: если
работа сил на замкнутом пути равна нулю,
то поле потенциально.

Для потенциального
поля можно ввести понятие потенциальной
энергии,
исходя из следующих обстоятельств:

1. в системе, где
   действуют только консервативные силы,
   всякая работа связана лишь с изменением
   конфигурации системы (взаимного
   расположения тел);

2. работа сил равна
   нулю, если система возвращается к
   исходной конфигурации.

Определение:
запас работы, определяемый начальной
конфигурацией тел системы, называется
потенциальной
энергией системы.

Пример:
тело в поле силы тяжести и растянутая
пружина обладают определенным запасом
работы, которую они могут совершить.

Заметим, что
запас работы можно отсчитывать от разных
конфигураций.

Пример

: для
тела, поднятого на высоту

от поверхности земли и на высоту

от дна колодца, запас работы различен
в зависимости от точки отсчета.

Т.о., телу всегда
можно приписать любое наперед выбранное
значение потенциальной энергии. Это
соответствует тому обстоятельству, что
путем измерения совершаемой работы
может быть определена лишь разность
потенциальных энергий различных
конфигураций системы.

Выбор новой
отсчетной конфигурации, просто заменяет
одно нулевое положение другим, в свою
очередь, изменяя потенциальную энергию
любой
конфигурации системы на одну и ту же
постоянную величину.
Следовательно, работа, определяемая
как разность потенциальных энергий
системы в двух различных конфигурациях,
сохранит свое значение.

Покажем это,
определив работу при переходе системы
из положения

в положение

через потенциальные энергии соответствующих
конфигураций.

Пусть точка

характеризует положение системы, от
которого производится отсчет потенциальной
энергии
.

По
определению, потенциальная энергия
равна

в точке
:

,
в точке
:
.

Тогда
для консервативных сил можно записать

.
(9.1)

Работа,
совершаемая консервативными силами
при переходе системы из

положения

в положение
,
равна убыли потенциальной энергии
системы.

Работа
сил в потенциальном поле при переходе
из точки

в точку

не

зависит
от выбора точки отсчета потенциальной
энергии.

Т.о., потенциальная
энергия системы определена с точностью
до произвольной постоянной, зависящей
от выбора, так называемой, нулевой
конфигурацией системы, и в этом смысле
всегда существует неоднозначность в
её абсолютном значении.

Однако если
ход физических явлений зависит лишь от
разности значений потенциальной энергии
системы в различных состояниях, то
произвол в выборе начальной конфигурации
(произвольной постоянной) не может
отразиться на величине совершенной
системой работы.

В отличие от
кинетической энергии, которая существенно
положительна, потенциальная энергия
может быть меньше нуля. Так, например,
потенциальная энергия взаимодействия
двух одноименно заряженных частиц
больше нуля (если на бесконечно большом
удалении их друг от друга она положена
равной нулю), а разноименно заряженных
частиц – меньше нуля.

Отметим еще
одно важное обстоятельство. Потенциальную
энергию следует относить не к частице,
а к системе, которая состоит из частицы
и взаимодействующих с ней тел, создающих
силовое поле. При заданном характере
взаимодействия потенциальная энергия
взаимодействия частицы с данными телами
зависит только от положения частицы
относительно этих тел.

9.2. Примеры
потенциальных полей.

1. Однородное поле
   тяжести.

Потенциальная
энергия тела массой

в однородном поле тяжести равна

,

тогда

.

Константу

можно условно положить равной 0
(отсчитывать, скажем, от уровня моря),

1. Поле упругих сил.

Потенциальная
энергия растянутой (сжатой) пружины.

.

Элементарная
работа растяжения:

,

где
сила,
возникающая при деформации пружины.

Знак «минус»
появился из-за того, что перемещение и
сила направлены в

разные стороны.

Полная работа
при возвращении пружины в недеформированное
состояние равна

.

Эта работа
равна убыли потенциальной энергии
пружины:

.

Если энергию
недеформированной пружины положить

равной нулю
(в точке
),
то потенциальная энергия упруго

деформированной
пружины:

,
(9.2)

или иначе —
потенциальная
энергия осциллятора.

Осциллятор
(от лат. оscillo
– качаюсь) – физическая система,
совершающая колебания.

1. Гравитационное
   поле.

Сила притяжения
двух материальных точек массами

и
:

— сила центральная, консервативная. Для
простоты считаем, что масса

покоится, а масса

притягивается к ней и перемещается.
Сосчитаем работу по перемещению точки

из бесконечности в точку
:

Будем отсчитывать
потенциальную энергию, считая, что на
бесконечности
:

.
(9.3)

Из (9.3) следует, что
запас гравитационной энергии (работы)
максимален при бесконечном расстоянии
между телами.

Отметим, что такие
же соотношения (с точностью до знака)
справедливы для кулоновского
взаимодействия.

1. Связь между
   силой и потенциальной энергией
   (градиент).

Взаимодействие
частицы с окружающими телами можно
описать двумя способами: рассматривая
силы взаимодействия или рассматривая
потенциальную энергию взаимодействия.

Вообще говоря,
первый способ описания обладает большей
общностью, т.к. применим к таким силам,
поле которых не является потенциальным
(например, сила трения). Однако зачастую
«энергетический» подход к решению
поставленной задачи является гораздо
более эффективным, значительно упрощая
её решение.

Установим связь
между потенциальной энергией и силой
поля. Сформулируем задачу следующим
образом: пусть имеется силовое поле,
характеризуемое потенциальной энергией

как функцией положения частицы в поле;
требуется найти силу

по заданной потенциальной энергии.
Работа консервативной силы на конечном
пути определяется соотношением (9.1). По
аналогии выразим и элементарную работу
силы поля как убыль потенциальной
энергии и, одновременно, как скалярное
произведение силы на перемещение:

,

или

.
(9.4)

Запишем работу
силы при малом перемещении вдоль оси
:

,

предполагая, что
значения координат

и

не изменяются;

проекция вектора

на ось
.
Тогда (переходя к пределу при

и полагая

и

постоянными) выражаем
компоненту
силы

через частную производную от функции
:

.
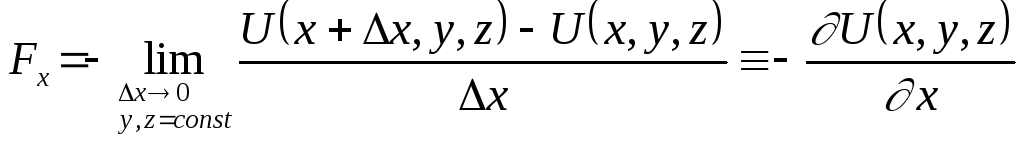
(9.5)

Замечание.
Символ частной производной

означает, что функция

при дифференцировании должна
рассматриваться как функция одного
аргумента
,
остальные же аргументы (в данном случае
и
)
должны при этом оставаться постоянными.

Аналогичные
соотношения получаем для двух других
переменных.

Итак, проекции
силы

на координатные оси:

.

Т.о., вектор силы

равен

.

Величину, стоящую
в скобках, называют градиентом
скалярной функции
.

Символически
полученное выражение можно записать
следующим образом:

.
(9.6)

Мы ввели оператор
градиента:

.
(9.7)

Формально
операцию

можно рассматривать как произведение
вектора

на скаляр
,
имея в виду, что скалярная функция

должна стоять справа от векторного
оператора
.

Итак, мы
установили связь между силой поля и
потенциальной энергией как функцией
координат. Теперь, зная потенциальную
энергию частицы в поле, можно определить
силу, действующую на частицу в каждой
точке рассматриваемого пространства:

,

(9.8)

т.е.
сила поля равна со знаком минус градиенту
потенциальной энергии
частицы в данной точке поля.

Примечание:
в выражении (9.4) стоит полный дифференциал
потенциальной энергии:

.

Смысл оператора
«градиент» (градиента).
Эквипотенциальные
поверхности.

Если ввести
понятие эквипотенциальной поверхности
– поверхности, во всех точках которой
потенциальная энергия имеет одинаковое
значение, то можно наглядно интерпретировать
смысл термина (операции) «градиент».

На рисунке изображены
эквипотенциальные кривые, причем
,
и показано направление векторов

и

в точке
.

Из формулы
(9.6) следует

1.
проекция вектора

на любое направление, касательное к

эквипотенциальной
поверхности в данной точке, равна нулю.

Следовательно,
вектор

нормален эквипотенциальной

поверхности в
данной точке.

2. вектор

направлен в сторону уменьшения

и

противоположен
по направлению вектору
.

Т.о., получаем,
что градиент

это вектор, направленный

по нормали к
эквипотенциальной поверхности в сторону

возрастания
потенциальной энергии
.

9.4. Поле
и потенциал поля.

Опыт показывает,
что для гравитационных и электростатических
взаимодействий сила
,
действующая на частицу со стороны
окружающих тел, может быть представлена
в виде произведения двух величин:

,

(9.9)

где

скалярная величина, которую следует
понимать как массу или заряд частицы,
соответственно,
векторная
величина, зависящая как от положения
частицы, так и от свойств окружающих
тел.

Такой подход
позволяет связать физическую интерпретацию
взаимодействия с понятием поля.
Говорят, что система окружающих частицу
тел создает в пространстве поле,
характеризуемое вектором
.
Частица, помещенная в это поле, испытывает
на себе действие силы, определяемой
выражением (9.9). При этом считают, что
поле, задаваемое вектором
,
существует безотносительно к тому,
находится в нем интересующая нас частица
или нет. Вектор

называют напряженностью
поля.

Принцип
суперпозиции полей.

Одно
из важнейших свойств поля заключается
в том, что поле, образованное несколькими
источниками, равно сумме полей, созданных
каждым из них, т.е.

.

Потенциал
поля.

Используя
введенные понятия и обозначения, можем
записать

,

поделив
обе части уравнения на

и обозначив
,
получаем

,
или
.

Функцию

называют потенциалом
поля. Потенциал поля,
как и потенциальная энергия, определяется
с точностью до прибавления произвольной
постоянной, которая является несущественной
и поэтому обычно опускается.

Потенциалы
гравитационного поля точечной массы

и кулоновского поля точечного заряда

определяются формулами

.

Итак,
поле можно описывать как векторным
,
так и скалярным

способом. Оба способа адекватны.
Практически скалярный способ описания
поля в большинстве случаев значительно
удобнее.

Связь напряженности
и потенциала поля.

Зная функцию

,
легко восстановить
вектор поля
:

,

что непосредственно
следует из (9.8).

Пример:
кулоновское поле.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #

  02.05.2015219.65 Кб62.doc

• #
• #
• #
• #
• #
• #

Содержание:

Потенциальное силовое поле:

Для вычисления работы силы на каком-либо перемещении в общем случае необходимо знать закон движения точки на этом перемещении. Есть класс сил, для которых работа не зависит от характера движения точки на рассматриваемом перемещении. Эти силы называют потенциальными, и они имеют важное значение в различных областях механики и физики.

Потенциальное силовое поле и силовая функция

Силовым полем называют часть пространства, в каждой точке которого на материальную точку действует определенная сила, зависящая от координат точки и времени. Силовое поле считают стационарным, если действующие силы не зависят от времени. Если же силы зависят от времени, то силовое поле является нестационарным.

Силовое поле называют потенциальным, если имеется силовая функция

Функцию 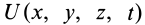называют силовой функцией.

Рис. 72

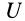
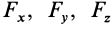
Рассмотрим основные свойства силовой функции стационарного силового поля. Из (77) следует, что силовая функция определяется с точностью до постоянной, так как для проекций силы на координатные оси требуются только частные производные по координатам от этой функции и добавление постоянной к функции не влияет на значения . Элементарная работа

т. e.

Таким образом, элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции. Иногда это свойство силовой функции принимают за ее определение; тогда (77) получают из (78).

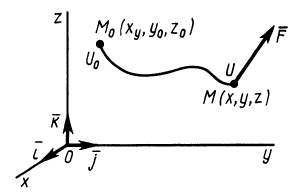
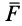
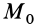
Полная работа силы на участке от точки до точки 

т.е.

где

Следовательно, полная работа силы на каком-либо перемещении точки равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории, по которой оно совершается, если силовая функция является однозначной.

Из (79) следует, что работа силы в потенциальном силовом поле по любому замкнутому пути равна нулю, так как значение силовой функции в начальной и конечной точках перемещения одинаково, если силовая функция не принимает других значений после возвращения в первоначальную точку.

Силовая функция может принимать другие значения после возвращения в первоначальную точку в зависимости от количества обходов, если область, ограниченная замкнутым путем обхода, содержит в себе специальные особые точки силовой функции.

Если применить понятие вектор-градиента от скалярной функции 

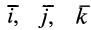
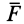
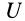
где — единичные векторы, направленные по осям координат, то силу можно выразить как градиент силовой функции :

Определим условия, которые позволяют по силам силового поля устанавливать, будет ли силовое поле потенциальным.

Если силовая функция 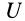существует, то

Так как

то

Аналогично,

Таким образом, полученные условия имеют вид

В векторном исчислении доказывается, что условия (80) не только необходимы, но и достаточны для существования силовой функции. Если использовать вектор вихря 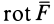 от вектора силы

то условия (80) можно выразить более кратко:

Таким образом, для того чтобы силовое поле было потенциальным, необходимо и достаточно, чтобы оно было безвихревым.

Непотенциальными силами являются силы сопротивления, зависящие от скорости, и силы трения. Силы сухого трения не будут потенциальными, так как хотя сила трения постоянна и не зависит от скорости, но направление силы трения от скорости зависит.

• Заказать решение задач по теоретической механике

Поверхности уровня и силовые линии

Если рассматривать точки потенциального силового поля, в которых силовая функция имеет одно и то же значение, например 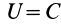, то все эти точки располагаются на поверхности, которую называют поверхностью равного уровня или поверхностью уровня.

Уравнение поверхности уровня имеет вид

Отметим некоторые свойства поверхностей уровня.

1.    Работа силы равна нулю, если начальная и конечная точки перемещения лежат на одной поверхности уровня. Действительно,

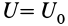
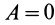
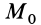
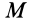
Если начальная и конечная точки лежат на одной поверхности уровня, то  и, следовательно, . Работа силы на перемещении между точками и не зависит от положения этих точек на своих поверхностях уровня. На любом перемещении между двумя точками рассматриваемых поверхностей уровня она одинакова (рис. 73).

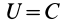
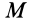
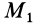
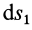
2.    Сила в потенциальном силовом поле всегда перпендикулярна поверхности уровня или, точнее, касательной плоскости поверхности уровня. Действительно, пусть имеем поверхность уровня . Возьмем на ней две бесконечно близкие точки и и вычислим элементарную работу на перемещении между этими точками:

С другой стороны,

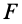
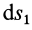
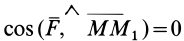
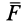
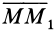
Так как и не равны нулю, то и, следовательно, угол между силой и перемещением  , лежащим в касательной плоскости к поверхности уровня, является прямым.

3.    Сила в потенциальном силовом поле всегда направлена в сторону возрастающих значений силовой функции. Для

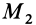
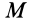
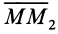
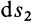
доказательства этого свойства силы возьмем точку на перпендикуляре к поверхности уровня, восставленном в точку в направлении возрастающих значений силовой функции. Тогда элементарная работа на элементарном перемещении , равном , вычисляется по формуле

так как .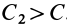

Рис. 73    

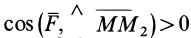
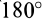
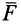
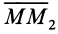
Следовательно,;  поэтому угол, равный , исключается и получается, что сила  направлена по  в сторону возрастающих значений силовой функции.

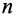
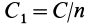
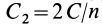
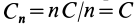
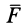
4. Если все силовое поле разбить поверхностями уровня на равных значений так, что для первой поверхности уровня , для второй и последней , то там, где соседние поверхности уровня ближе друг к другу, модуль силы больше, чем в местах, где поверхности уровня дальше отстоят друг от друга. Это свойство можно проверить, если заметить, что работа между точками любых двух соседних поверхностей в этом случае одна и та же. Следовательно, там, где расстояние между поверхностями меньше, сила по числовому значению больше, и наоборот.

Рис. 74

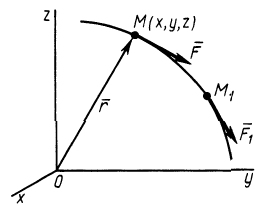
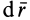
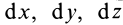
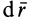
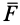
Наряду с поверхностями уровня в силовом поле вводят понятие силовой линии, т. е. такой линии, в каждой точке которой сила направлена по касательной к этой линии (рис. 74). Так как вектор с проекциями на оси всегда направлен по касательной к кривой, то из условия параллельности и следует, что

Эти дифференциальные уравнения относительно координат 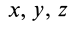являются дифференциальными уравнениями силовой линии.

Потенциальная энергия

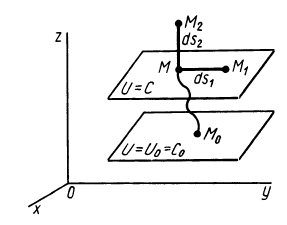
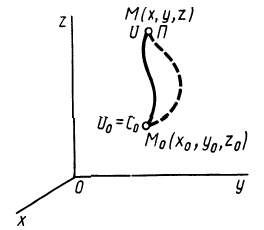
В случае потенциального силового поля наряду с силовой функцией можно ввести другую функцию, характеризующую запас энергии в данной точке поля,— потенциальную энергию в этой точке (рис. 75), или потенциальную энергию материальной точки в рассматриваемой точке силового поля.

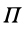
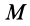
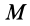
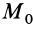
Потенциальной энергией материальной точки в рассматриваемой точке силового поля называют работу, которую совершают силы поля, действующие на материальную точку при перемещении ее из точки в начальную точку , т. е.

или

Рис. 75

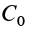
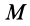
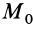
Постоянная  одна и та же для всех точек поля, зависящая от того, какая точка поля выбрана за начальную. Очевидно, что потенциальную энергию можно ввести только для потенциального силового поля, в котором работа не зависит от формы перемещения между точками и . Непотенциальное силовое поле не имеет потенциальной энергии, для него не существует и силовой функции.

На основании (77) и (82) имеем:

Из (78), (79) и (82) соответственно получаем

Из приведенных формул следует, что 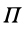 определяется с точностью до произвольной постоянной, которая зависит от выбора начальной точки, но эта произвольная постоянная не влияет на вычисляемые через потенциальную энергию силы и работу этих сил. Учитывая это, формулу (82) можно выразить так:

или

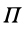
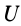
Потенциальную энергию в какой-либо точке поля с точностью до произвольной постоянной можно определить как значение силовой функции в этой же точке, взятое со знаком минус. По существу, достаточно одной из функций или .

Понятие потенциальной энергии было введено раньше, чем силовая функция. Силовая функция более удобна, так как некоторые формулы, содеражащие эту функцию, не имеют знака минус.

Примеры вычисления силовых функций

Если вычислить силовую функцию, то на основании (82′) будет известна и потенциальная энергия. Вычислим силовые функции однородного поля силы тяжести, силового поля линейной силы упругости и силового поля силы притяжения, действующей по закону Ньютона.

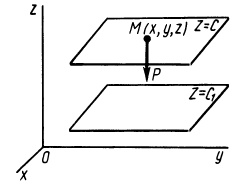
Силовая функция однородного поля силы тяжести. Если ось 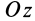(рис. 76) направить вертикально вверх, то проекции силы тяжести на координатные оси будут равны

Вычисляя элементарную работу силы 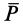, получаем

Так как элементарная работа является полным дифференциалом, то силовое поле силы тяжести является потенциальным и силовая функция этого поля определяется по формуле

По формуле (83) определяют силовую функцию однородного поля силы тяжести, т. е. поля, в котором сила тяжести постоянна по модулю и направлению. Уравнение поверхности уровня 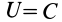или , т.е. поверхностями уровня являются горизонтальные плоскости.

Рис. 76

Силовая функция линейной силы упругости

Для линейной силы упругости (см. рис. 62) имеем:

Следовательно

так как .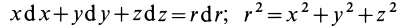

Силовую функцию линейной силы упругости определяют по формуле

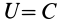
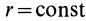
Поверхностями уровня  являются сферы .

Силовая функция силы притяжения по закону Ньютона

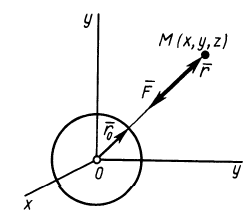
Вычислим силовую функцию поля земного притяжения. Если выбрать начало координат в центре Земли (рис. 77), то сила притяжения точки земным шаром .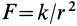

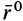
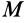
Сила F направлена к центру Земли; следовательно, вводя единичный вектор по радиусу-вектору от этого центра в рассматриваемую точку , имеем

Проецируя силу 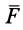на координатные оси, получаем:

Тогда

так как .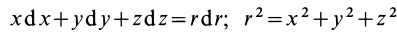

Рис. 77

Таким образом, силовая функция силы притяжения, по закону Ньютона,

Постоянную 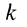 для, случая Земли можно выразить так:

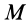
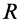
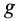
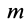
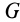
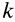
где —масса Земли; — радиус Земли; —ускорение силы тяжести на поверхности Земли; — масса точки; — постоянная тяготения. Если вместо Земли рассматривается другое небесное тело, изменяется только постоянная .

Силовая функция и потенциальная энергия системы

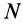
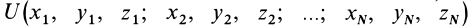
Для механической системы в потенциальном силовом поле можно ввести силовую функцию как функцию, зависящую от координат всех точек системы, т. е. от положения системы в силовом поле. Если система состоит из точек, то силовая функция зависит в общем случае от координат всех точек. Проекции силы, действующей на каждую точку системы,

Сумма элементарных работ всех сил, действующих на точки системы, определяется по формуле

или

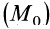
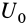
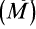
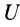
Таким образом, сумма элементарных работ сил поля, действующих на механическую систему, равна полному дифференциалу от силовой функции. Если вычислить сумму работ, которую совершат силы поля, действующие на механическую систему при перемещении системы из положения , в котором имеется силовая функция , в положение , в котором есть силовая функция , то

или

Следовательно, сумма работ сил поля, действующих на систему при перемещении системы из одного начального положения в другое, равна разности значений силовой функции в конечном и начальном положениях системы.

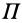
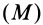
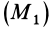
Потенциальной энергией системы в рассматриваемом положении  потенциального силового поля называют сумму работ сил поля, действующих на систему, которую эти силы совершают при перемещении системы из рассматриваемого положения в начальное положение , т. е.

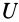
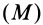
где —значение силовой функции для системы сил в положении ; —значение силовой функции в начальном положении.

Из (86) — (89) следует:

Однородным электрическим полем называют такое электрическое поле, вектор напряжённости которого не зависит от точки пространства ((vec{r(t)} =const)), где (vec{r(t)}) — радиус-вектор исследуемой точки.

Все силы можно разделить на потенциальные и непотенциальные.

Энергия.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа силы, мощность, кинетическая энергия, потенциальная энергия, закон сохранения механической энергии.

Мы приступаем к изучению энергии — фундаментального физического понятия. Но предварительно нужно разобраться с другой физической величиной — работой силы.

к оглавлению ▴

Работа.

Пусть на тело действует постоянная сила и тело, двигаясь прямолинейно по горизонтальной поерхности, совершило перемещение . Сила не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).

Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны)

Рис. 1.A=Fs

В этом простейшем случае работа определяется как произведение модуля силы на модуль перемещения:

. (1)

Единицей измерения работы служит джоуль (Дж): Дж=Н м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.

Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.

Пусть теперь вектор силы образует с вектором перемещения острый угол (рис. 2).

Разложим силу на две составляющие: (параллельную перемещению) и (перпендикулярную перемещению). Работу совершает только . Поэтому для работы силы получаем:

. Итак,

. (2)

Если вектор силы образует с вектором перемещения тупой угол , то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.

Например, работа силы трения скольжения, действующей на тело в рассмотренных ситуациях, будет отрицательной, так как сила трения направлена противоположно перемещению. В этом случае имеем:

, и для работы силы трения получаем:

,

где — масса тела, — коэффициент трения между телом и опорой.

Соотношение (2) означает, что работа является скалярным произведением векторов силы и перемещения:

.

Это позволяет вычислять работу через координаты данных векторов:

.

Пусть на тело действуют несколько сил и — равнодействующая этих сил. Для работы силы имеем:

,

или

,

где — работы сил . Итак, работа равнодействующей приложенных к телу сил равна сумме работ каждой силы в отдельности.

к оглавлению ▴

Мощность.

Часто имеет значение быстрота, с которой совершается работа. Скажем, на практике важно знать, какую работу сможет выполнить данное устройство за фиксированное время.

Мощность — это величина, характеризующая скорость совершения работы. Мощность есть отношение работы ко времени , за которое эта работа совершена:

.

Мощность измеряется в ваттах (Вт). 1 Вт = 1 Дж/с, то есть 1 Вт — это такая мощность, при которой работа в 1 Дж совершается за 1 с.

Предположим, что силы, действующие на тело, уравновешены, и тело движется равномерно и прямолинейно со скоростью . В этом случае существует полезная формула для мощности, развиваемой одной из действующих сил .

За время тело совершит перемещение . Работа силы будет равна:

.

Отсюда получаем мощность:

,

или

,

где -угол между векторами силы и скорости.

Наиболее часто эта формула используется в ситуации, когда — сила «тяги» двигателя автомобиля (которая на самом деле есть сила трения ведущих колёс о дорогу). В этом случае , и мы получаем просто:

.

к оглавлению ▴

Механическая энергия.

Энергия является мерой движения и взаимодействия любых объектов в природе. Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .

Опыт показывает, что энергия не появляется ниоткуда и не исчезает бесследно, она лишь переходит из одной формы в другую. Это самая общая формулировка закона сохранения энергии.

Каждый вид энергии представляет собой некоторое математическое выражение. Закон сохранения энергии означает, что в каждом явлении природы определённая сумма таких выражений остаётся постоянной с течением времени.

Измеряется энергия в джоулях, как и работа.

Механическая энергия является мерой движения и взаимодействия механических объектов (материальных точек, твёрдых тел).

Мерой движения тела является кинетическая энергия. Она зависит от скорости тела. Мерой взаимодействия тел является потенциальная энергия. Она зависит от взаимного расположения тел.

Механическая энергия системы тел равна сумме кинетической энергии тел и потенциальной энергии их взаимодействия друг с другом.

к оглавлению ▴

Кинетическая энергия.

Кинетической энергией тела (принимаемого за материальную точку) называется величина

,

где — масса тела, — его скорость.

Кинетической энергией системы из тел называется сумма кинетических энергий каждого тела:

.

Если тело движется под действием силы , то кинетическая энергия тела, вообще говоря, меняется со временем. Оказывается, именение кинетической энергии тела за некоторый промежуток времени равно работе силы . Покажем это для случая прямолинейного равноускоренного движения.

Пусть — начальная скорость, — конечная скорость тела. Выберем ось вдоль траектории тела (и, соответственно, вдоль вектора силы ). Для работы силы получаем:

.

(мы воспользовались формулой для , выведенной в статье «Равноускоренное движение»). Заметим теперь, что в данном случае проекция скорости отличается от модуля скорости разве что знаком; поэтому и . В результате имеем:

,

что и требовалось.

На самом деле соотношение справедливо и в самом общем случае криволинейного движения под действием переменной силы.

Теорема о кинетической энергии. Изменение кинетической энергии тела равно работе, совершённой приложенными к телу внешними силами за рассматриваемый промежуток времени.

Если работа внешних сил положительна, то кинетическая энергия увеличивается (, тело разгоняется).

Если работа внешних сил отрицательна, то кинетическая энергия уменьшается (, тело замедляет движение). Пример — торможение под действием силы трения, работа которой отрицательна.

Если же работа внешних сил равна нулю, то кинетическая энергия тела за это время не меняется. Нетривиальный пример — равномерное движение по окружности, совершаемое грузом на нити в горизонтальной плоскости. Сила тяжести, сила реакции опоры и сила натяжения нити всегда перпендикулярны скорости, и работа каждой из этих сил равна нулю в течение любого промежутка времени. Соответственно, кинетическая энергия груза (а значит, и его скорость) остаётся постоянной в процессе движения.

Задача. Автомобиль едет по горизонтальной дороге со скоростью и начинает резко тормозить. Найти путь , пройденный автомобилем до полной остановки, если коэффициент трения шин о дорогу равен .

Решение. Начальная кинетическая энергия автомобиля , конечная кинетическая энергия . Изменение кинетической энергии .

На автомобиль действуют сила тяжести , реакция опоры и сила трения . Сила тяжести и реакция опоры, будучи перпендикулярны перемещению автомобиля, работы не совершают. Работа силы трения:

.

Из теоремы о кинетической энергии теперь получаем:

.

к оглавлению ▴

Потенциальная энергия тела вблизи поверхности Земли.

Рассмотрим тело массы , находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем.

Если тело находится на высоте , то потенциальная энергия тела по определению равна:

где — ускорение свободного падения вблизи поверхности Земли.

Высоту не обязательно отсчитывать от поверхности Земли. Как мы увидим ниже (формулы (3), (4)), физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.

Найдём работу, совершаемую силой тяжести при перемещении тела. Предположим, что тело перемещается по прямой из точки , находящейся на высоте , в точку , находящуюся на высоте (рис. 3).

Рис. 3.A=mg(h1-h2)[/math]

Угол между силой тяжести и перемещением тела обозначим . Для работы силы тяжести получим:

.

Но, как видно из рис. 3, . Поэтому

,

или

. (3)

Учитывая, что , имеем также:

. (4)

Можно доказать, что формулы (3) и (4) справедливы для любой траектории, по которой тело перемещается из точки в точку , а не только для прямолинейного отрезка.

Работа силы тяжести не зависит от формы траектории, по которой перемещается тело, и равна разности значений потенциальной энергии в начальной и конечной точках траектории. Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.

Сила называется консервативной, если при перемещении тела работа этой силы не зависит от формы траектории, а определяется только начальным и конечным положением тела. Сила тяжести, таким образом, является консервативной. Работа консервативной силы по любому замкнутому пути равна нулю. Только в случае консервативной силы возможно ввести такую величину, как потенциальная энергия.

к оглавлению ▴

Потенциальна яэнергия деформированной пружины.

Рассмотрим пружину жёсткости . Начальная деформация пружины равна . Предположим,
что пружина деформируется до некоторой конечной величины деформации . Чему равна при этом работа силы упругости пружины?

В данном случае силу на перемещение не умножишь, так как сила упругости меняется в процессе деформации пружины. Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат.

Оказывается, сила упругости пружины также является консервативной. Её работа зависит лишь от величин и и определяется формулой:

.

Величина

называется потенциальной энергией деформированной пружины (x — величина деформации).

Следовательно,

,

что полностью аналогично формулам (3) и (4).

к оглавлению ▴

Закон сохранения механической энергии.

Консервативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел.

Механическая энергия тела равна сумме его кинетической и потенциальной энергий:

.

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом.

Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны и , в конечном положении — и . Работу внешних сил при перемещении тела из начального положения в конечное обозначим .

По теореме о кинетической энергии

.

Но работа консервативных сил равна разности потенциальных энергий:

.

Отсюда получаем:

,

или

.

Левая и правая части данного равенства представляют собой механическую энергию тела в начальном и конечном положении:

.

Следовательно, при движении тела в поле силы тяжести и/или на пружине механическая энергия тела остаётся неизменной при отсутствии трения. Справедливо и более общее утверждение.

Закон сохранения механической энергии. Если в замкнутой системе действуют только консервативные силы, то механическая энергия системы сохраняется.

При этих условиях могут происходить лишь превращения энергии: из кинетической в потенциальную и наоборот. Общий запас механической энергии системы остаётся постоянным.

к оглавлению ▴

Закон изменения механической энергии.

Если между телами замкнутой системы имеются силы сопротивления (сухое или вязкое трение), то механическая энергия системы будет уменьшаться. Так, автомобиль останавливается в результате торможения, колебания маятника постепенно затухают и т. д. Силы трения неконсервативны: работа силы трения очевидным образом зависит от пути, по которому перемещается тело между данными точками. В частности, работа силы трения по замкнутому пути не равна нулю.

Снова рассмотрим движение тела в поле силы тяжести и/или на пружине. Вдобавок на тело действует сила трения, которая за рассматриваемый промежуток времени совершает отрицательную работу . Работу консервативных сил (тяжести и упругости) по-прежнему обозначаем .

Изменение кинетической энергии тела равно работе всех внешних сил:

.

Но , следовательно

.

Отсюда

,

или

.

В левой части стоит величина — изменение механической энергии тела:

.

Итак,при движении тела в поле силы тяжести и/или на пружине изменение механической энергии тела равно работе силы трения. Так как работа силы трения отрицательна,изменение механической энергии также отрицательно: механическая энергия убывает.
Справедливо и более общее утверждение.

Закон изменения механической энергии. Изменение механической энергии замкнутой системы равно работе сил трения, действующих внутри системы.

Ясно, что закон сохранения механической энергии является частным случаем данного утверждения.

Конечно, убыль механической энергии не противоречит общефизическому закону сохранения энергии. В данном случае механическая энергия превращается в энергию теплового движения частиц вещества и их потенциальную энергию взаимодействия друг с другом, т. е. переходит во внутреннюю энергию тел системы.