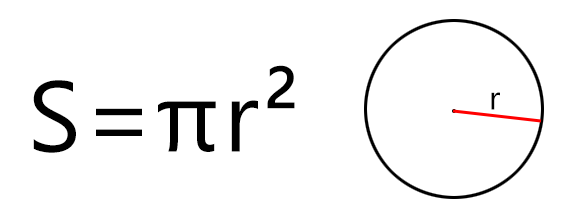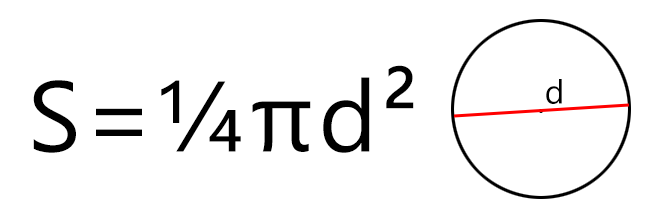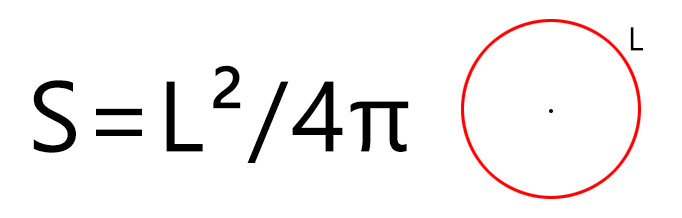Перейти к содержанию
Калькуляторы объёма и площади круга, цилиндра, куба, шара (сферы), конуса
На чтение 1 мин Просмотров 30.2к.
Обновлено 10.01.2022
Содержание
- Калькулятор площади и периметра (длины окружности) круга
- Калькулятор расчета площади и объёма шара (сферы)
- Калькулятор расчета объёма цилиндра
- Калькулятор расчета объёма параллелепипеда
- Калькулятор куба-объём, площадь поверхности

Калькулятор площади и периметра (длины окружности) круга
Калькулятор расчета площади и объёма шара (сферы)
Калькулятор расчета объёма цилиндра
Калькулятор расчета объёма параллелепипеда

Калькулятор куба-объём, площадь поверхности
Расчет объема круга
Круг — это геометрическое место точек на плоскости, расстояние от которых до его центра, не превышает заданного числа, называемого радиусом этого круга.
Формула расчета объема круга:
V — объем круга;
S — площадь круга;
h — толщина круга.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета объема круга. С помощью этого онлайн калькулятора расчета объема круга вы сможете вычислить объем круга по площади и толщине.
Все формулы объемов геометрических тел
1. Расчет объема куба
a — сторона куба
Формула объема куба, (V):
2. Найти по формуле, объем прямоугольного параллелепипеда
a , b , c — стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
3. Формула для вычисления объема шара, сферы
R — радиус шара
По формуле, если дан радиус, можно найти объема шара, (V):
4. Как вычислить объем цилиндра ?
h — высота цилиндра
r — радиус основания
По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V):
5. Как найти объем конуса ?
R — радиус основания
H — высота конуса
Формула объема конуса, если известны радиус и высота (V):
7. Формула объема усеченного конуса
r — радиус верхнего основания
R — радиус нижнего основания
h — высота конуса
Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса (V ):
8. Объем правильного тетраэдра
Правильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.
а — ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
a — сторона основания
h — высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
a — сторона основания
h — высота пирамиды
Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V):
11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h — высота пирамиды
a — сторона основания пирамиды
n — количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
Как рассчитать периметр круга или длину окружности
На данной странице калькулятор поможет рассчитать периметр круга или длину окружности онлайн. Для расчета задайте радиус или диаметр.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
http://www-formula.ru/2011-09-24-00-37-25
http://www.mozgan.ru/Geometry/PerimeterCircle
Formula.co.id — В этой статье мы узнаем, как рассчитать объем круга. Раньше мы уже знали, что такое круг, потому что с начальной школы мы выучили то, что называется кругом, потому что поэтому без необходимости задерживаться Опять же, давайте вместе обсудим формулу объема круга, и позже она будет сопровождаться примерами вопросов об объеме круга в качестве учебного материала для студентов. читатель.
Оглавление :
Определение Круга
Само определение круга — это набор всех точек на плоскости, которые равноудалены от фиксированной точки на плоскости. Тогда неподвижная точка называется центром круга, а расстояние от точки на окружности до его центра называется радиусом окружности.
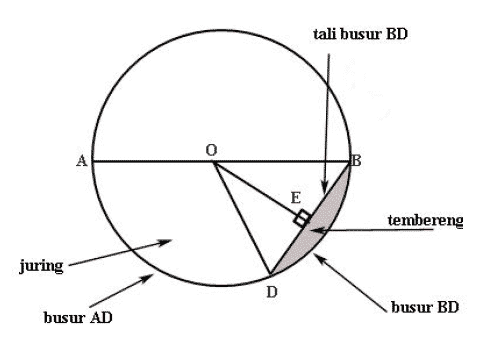
Чтобы было понятнее значение самого круга, здесь мы подробно объясним элементы круга, обратите внимание на изображение круга ниже:
Элементы круга
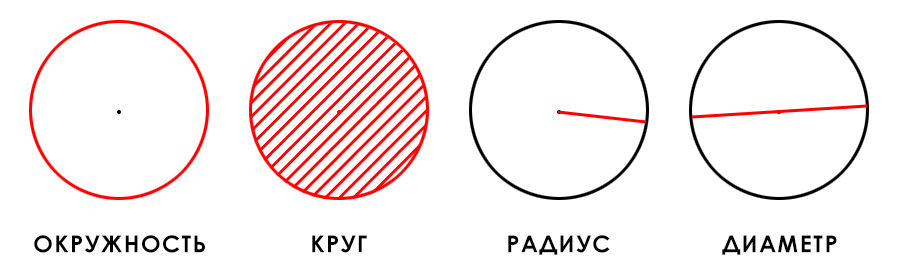
- Центр круга — это точка, расположенная в середине круга.
- радиус круга ( р ) — это линия от центра окружности до кривизны окружности.
- Диаметр ( d ) представляет собой прямую, соединяющую 2 точки на кривизне окружности, проходящей через центральную точку.
- Дуга окружности — это изогнутая линия, лежащая на кривой окружности, соединяющей любые 2 точки на кривой.
- Круговая хорда — это прямая линия в окружности, соединяющая 2 точки кривизны окружности.
- Уклон — это область в окружности, ограниченная дугой и хордой.
- Радиус — это область в круге, ограниченная двумя радиусами круга, и дугой, примыкающей к двум радиусам круга.
- Апофема — это линия, соединяющая центр круга с хордой круга. Линия перпендикулярна хорде окружности.
Продолжайте обсуждать свойства кругов.
Характеристики кругов
- У круга только одна сторона.
- Круг обладает бесконечной симметрией вращения.
- У круга бесконечная симметрия и оси.
- Но у круга нет вершин.
Формула объема круга
Для получения более подробной информации на сайте formula.co.id будут обсуждаться все формулы для круга, будь то формула площади, окружности и объема самого круга. Для получения более подробной информации о формуле, рассмотрите объяснение формулы ниже:
Формула объема круга:
V = х г2
Формула окружности круга:
К = 2 х х г
Формула площади круга:
L = х г2
Информация :
- = 22/7 или 3,14
- r = радиус (см)
Вам необходимо знать, что приведенная выше формула для площади и объема одинакова, но для определения объема число должно быть в одной и той же единице, а именно в кубических единицах или (см).3 ). Переходя к последнему обсуждению, formula.co.id предоставит вам пример вопроса с кругом, чтобы вы все лучше поняли формулу круга.
Пример круга
- Если круг имеет диаметр 80 см, какова площадь полукруга?
Отвечать:
Известен = d = 80 см
r = 80 см: 2 = 40 см
Спрошено = площадь полукруга?
Площадь полукруга = x r2
= 3,14 х 40 см х 40 см: 2
= 3,14 х 40 см х 40 см: 2
= 2512 см2
Итак, площадь полукруга составляет 2512 см.2
- Круг имеет радиус 14 см, какова длина окружности круга?
Отвечать:
Известен = r = 14 см
Спрошено = окружность круга?
Периметр = K = 2. π. р
= 2 х 22/7 х 14 см
= 88 см
Итак, окружность круга 88 см.
Таким образом, полный математический материал о круге, будь то понимание, элементы, свойства, примеры задач и формула для объема круга сфер, которые могут быть переданы, могут быть полезны …
Другие формулы:
- Формула объема блока
- Формула объема цилиндра
Как рассчитать площадь круга
На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Через радиус
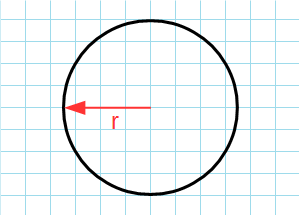
Формула для нахождения площади круга через радиус:
π — константа равная (3.14); r — радиус круга.
Через диаметр
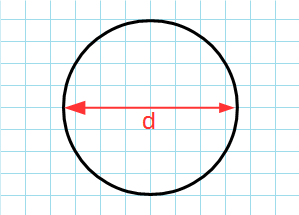
Формула для нахождения площади круга через диаметр:
π — константа равная (3.14); d — диаметр.
Через длину окружности

Формула для нахождения площади круга через длину окружности:
π — константа равная (3.14); l — длина окружности.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d — диаметр, а π – константа, равная 3,1415…):
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L — длина окружности, а π – константа, равная 3,1415…):
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:
Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
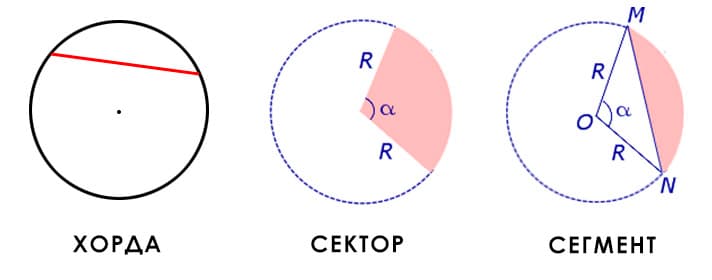
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии