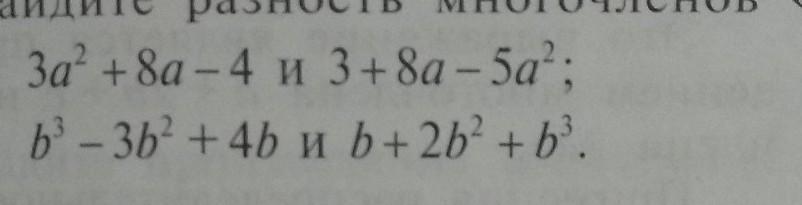Найти столбиком разность многочленов это как

ответы

ваш ответ

похожие темы

похожие вопросы 3

Алгоритмы сложения и вычитания многочленов

Сумма и разность произвольных многочленов – также многочлены.

О правилах раскрытия скобок – см. §4 данного справочника.

Примеры

Пример 1. Найдите сумму и разность многочленов:

а) $ 9x^3-7x^2+8 и 5x^2+x-2$

Сумма:

$ 9x^3-7x^2+8+5x^2+x-2 = 9x^3+(-7+5) x^2+x+(8-2)=9x^3-2x^2+x+6 $

Разность:

$ 9x^3-7x^2+8-(5x^2+x-2) = 9x^3-7x^2+8-5x^2-x+2 = $

$ = 9x^3+(-7-5) x^2-x+(8+2) = 9x^3-12x^2-x+10 $

б) $-frac{3}{5} xy+xy^2-frac{1}{6} и 1 frac{2}{3} xy-xy^2+1 $

Сумма:

$-frac{3}{5} xy+xy^2-frac{1}{6}+ 1 frac{2}{3} xy-xy^2+1 = (-frac{3}{5}+1 frac{2}{3})xy+0 cdot xy^2+(- frac{1}{6}+1)=$

$ =(1+frac{10-9}{15})xy+frac{5}{6} = 1 frac{1}{15} xy+ frac{5}{6} $

Разность:

$ -frac{3}{5} xy+xy^2-frac{1}{6}- (1 frac{2}{3} xy-xy^2+1) = -frac{3}{5} xy+xy^2-frac{1}{6}- 1frac{2}{3} xy+xy^2-1 = $

$ = (-frac{3}{5}-1 frac{2}{3})xy+(1+1)xy^2+(-frac{1}{6} -1) = (-1-frac{9+10}{15})xy+2xy^2-1 frac{1}{6} = $

$ =-2 frac{4}{15} xy+2xy^2-1 frac{1}{6} $

Пример 2. Вычислите значение выражения, если x = -5

а) $ 16x^4-x^3-(15x^4-x^3+1) = 16x^4-x^3-15x^4+x^3-1 = x^4-1 $

Подставляем: $ (-5)^4-1 = 625-1 = 624 $

б) $ 3x^3-2x^2+x-8-(x^3-2x^2+x) = 3x^3-2x^2+x-8-x^3+2x^2-x = 2x^3-8 $

Подставляем: $ 2 cdot (-5)^3-8 = 2 cdot (-125)-8 = -258 $

Пример 3. При каком значении x значение трёхчлена $ 2x^2+5x-3$ больше значения двучлена $2x^2+1$ на 4?

По условию: $ (2x^2+5x-3 )-(2x^2+1) = 4 $

$ 2x^2+5x-3-2x^2-1 = 4 $

5x-4 = 4

5x = 8

$ x = frac{8}{5} = 1,6 $

Ответ: 1,6

Пример 4. Какой многочлен нужно сложить с многочленом $ 2x^2+x-16 $, чтобы получить $x^3-x^2+2$?

Обозначим неизвестный многочлен P(x). По условию:

$ 2x^2+x-16+P(x) = x^3-x^2+2 $

$ P(x) = x^3-x^2+2-(2x^2+x-16) = x^3-x^2+2-2x^2-x+16 = x^3-3x^2-x+18 $

Ответ: $ x^3-3x^2-x+18 $

Алгебра

7 класс

Урок № 20

Сумма и разность многочленов

Перечень рассматриваемых вопросов:

• Алгебраические выражения.
• Многочлен.
• Сумма и разность многочленов.
• Стандартный вид многочлена.
• Правила раскрытия скобок (заключения в скобки).

Тезаурус.

Числовое выражение – выражение, состоящее из чисел, знаков математических действий и скобок.

Значение числового выражения – результат выполненных арифметических действий в числовом выражении.

Одночлен – алгебраическое выражение, являющееся произведением букв и чисел

Множители одночлена – буквы и числа, входящие в состав одночлена.

Нулевой одночлен – одночлен, среди множителей которого есть число ноль.

Стандартным видом одночлена называют такой его вид, в котором он представлен произведением числового множителя и натуральных степеней разных переменных.

Числовой множитель одночлена, записанного в стандартном виде, называется коэффициентом одночлена.

Подобные одночлены – одночлены, которые состоят из произведения одних и тех же степеней, но с разными или одинаковыми коэффициентами (числовыми множителями).

Многочлен – сумма одночленов.

Каждый одночлен, являющийся слагаемым многочлена, называют членом многочлена.

Многочлен стандартного вида – это многочлен, все члены которого являются одночленами стандартного вида, среди которых нет подобных членов.

Разность двух многочленов равна многочлену, членами которого являются: все члены уменьшаемого и, взятые с противоположными знаками, все члены вычитаемого. Сумма многочленов равна многочлену, членами которого являются все члены данных многочленов.

Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Перед нами следующее выражение 123+5 и 45-89. Можем ли между ними поставить знаки «+» или «–» и, соответственно, найти значение полученного выражения?

Конечно, да.

123 + 5 и 45 – 89

(123 + 5) + (45 – 89) = 84

(123 + 5) – (45 – 89) = 172

Оказывается, аналогичные арифметические операции можно выполнять и с многочленами, т.е. найти сумму и разность многочленов.

Посмотрим, как можно выполнить данные действия с многочленами.

Найдём многочлен равный сумме многочленов. Как это сделать?

Оказывается, сумма многочленов равна многочлену, членами которого являются все члены данных многочленов.

Например, сумма многочленов (а + с) и (k + х) равна многочлену (а + с) + (k + х) или а + с + k + х. Последний переход от левой части к правой называют раскрытием скобок.

Найдём многочлен равный разности многочленов. Как это сделать?

Оказывается, разность двух многочленов равна многочлену, членами которого являются все члены уменьшаемого и, взятые с противоположными знаками, все члены вычитаемого.

Например, разность двух многочленов а + с и k + х равна многочлену (а + с) – (k + х) или а + с – k – х. Последний переход от левой части к правой, так же как и при нахождении суммы, называют раскрытием скобок.

Рассмотрим правила раскрытия скобок.

Если перед скобками стоит знак плюс, то скобки можно опустить, не меняя знаки слагаемых, заключённых в скобки.

Например:

(а + с) + (х – у) = а + с + х – у

Если перед скобками стоит знак минус, то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки, на противоположный.

Например:

(а + с) + (х – у) = а + с – х + у

Стоит обратить внимание, что если перед скобками нет никакого знака, то подразумевается, что стоит знак плюс.

Например,

(d + k) – (m + n) = d + k – m –n

Обратный переход от правой части к левой в похожих выражениях называют заключением в скобки.

Рассмотрим правило заключения в скобки:

Чтобы заключить многочлен в скобки со знаком плюс перед ними, надо записать в скобки все его члены с теми же знаками.

Например:

а – с – k – х = (а – с) + (-k – х)

А чтобы заключить многочлен в скобки со знаком минус перед ними, надо записать в скобки все его члены с противоположными знаками.

Например:

а – с – k – х = (а – с) – (k + х)

Рассмотрим, как использовать эти правила для преобразования многочлена в стандартный вид. Пример:

Преобразуем разность многочленов в многочлен стандартного вида

( 5а– 4х + 15) – (10а + 13х – 14) = 5а- 4х + 15 – 10а – 13х + 14 = -5а – 17х + 29

Для выполнения задания, сначала будем использовать правило раскрытия скобок при нахождении разности многочленов. А затем приведём полученный многочлен к стандартному виду.

Итак, сегодня мы получили представление о том, как найти сумму и разность многочленов и, используя правило раскрытия скобок, приводить многочлен к стандартному виду.

Задание на сумму и разность многочленов.

Выполним следующее задание по теме: «Сумма и разность многочленов».

Запишите такой многочлен, чтобы его сумма с многочленом 3х + 1 была равна 9х – 4.

Решение:

Данное задание можно выполнить следующим образом.

Назовем неизвестный многочлен у, тогда можно составить следующее выражение, исходя из условия.

у + (3х + 1) = 9х -4

Найдём отсюда у

у = (9х – 4) – (3х + 1)

Раскроем скобки по правилу раскрытия скобок.

у = 9х – 4 – 3х + 1

Приведём многочлен к стандартному виду.

у = 6х – 3

Это и есть тот многочлен, который удовлетворяет условию задания.

Разбор заданий тренировочного модуля.

1. Приведите многочлен к стандартному виду (аt² – 5t²) – (10хt – 4t²) + (5хt + 11аtt).

Решение: Для решения задания, вспомним правила раскрытия скобок, перед которыми стоит знак «+» или «–». Если знак «+», то скобки можно опустить, не меняя знак, а если перед скобкой знак «–», то скобки можно опустить, меняя знак каждого слагаемого в скобках. Далее приведём к стандартному виду полученный многочлен, выделив в нём подобные члены.

(аt² – 5t²) – (10хt – 4t²) + (5хt + 11аtt) = аt² – 5t² – 10хt + 4t² + 5хt +11аt² = 12аt² – t² – 5хt.

Ответ: 12аt² – t² – 5хt

2. Представьте выражение каким-либо способом в виде разности двучлена и трехчлена:

3x⁴ – 12x³ – 3x² + 5x – 14

Варианты ответов:

1. (3x⁴ – 12x³ – 3x²) + (5x – 14)
2. (3x⁴ – 12x³) – (3x² + 5x – 14)
3. (3x⁴ – 12x³) – (3x² – 5x + 14)

Решение:

При выполнении задания можно сначала проанализировать ответы. По условию выражение должно быть составлено в виде разности двучлена и трехчлена. Поэтому первый ответ не подходит, т. к. в нём представлена сумма.

Ответы два и три очень похожи. Для нахождения верного ответа, заключим в скобки исходное выражение, как в ответах 2 и 3. Т. к. мы найдем разность, то по правилу заключения в скобки со знаком минус перед ними, надо записать в скобки все его члены с противоположными знаками. Поэтому правильный ответ №3.

3x⁴ – 12x³ – 3x² + 5x – 14 = (3x⁴ – 12x³) – (3x² – 5x + 14)

Ответ: (3x⁴ – 12x³) – (3x² – 5x + 14).