Найдите корни уравнений принадлежащие данному промежутку как - Avtoru.top

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

24 мая

Обновлённая панель инструментов

22 мая

Беседы Решу ЕГЭ по подготовке к ЕГЭ

11 мая

Решение досрочных ЕГЭ по всем предметам

5 мая

Обновленный поиск заданий по ключевым словам

1 мая

Новый сервис: можно исправить ошибки!

29 апреля

Разместили актуальные шкалы ЕГЭ  — 2023

24 апреля

Учителю: обновленный классный журнал

7 апреля

Новый сервис: ссылка, чтобы записаться к учителю

30 марта

Решения досрочных ЕГЭ по математике

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Тригонометрические уравнения

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 12 № 507595

а)  Решите уравнение

б)  Найдите корни этого уравнения, принадлежащие промежутку

Аналоги к заданию № 507595: 500917 501709 Все

Решение

Критерии

Видеокурс

Помощь

Тип 12 № 510018

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие промежутку

Источники:

Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень;

Демонстрационная версия ЕГЭ—2013 по математике;

Демонстрационная версия ЕГЭ—2015 по математике. Профильный уровень;

Демонстрационная версия ЕГЭ—2017 по математике. Профильный уровень.

Решение

Критерии

1 комментарий

Видеокурс

Помощь

Тип 12 № 504543

а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Аналоги к заданию № 504543: 504564 507292 510671 Все

Решение

Критерии

2 комментария

Видеокурс

Помощь

Тип 12 № 500366

а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Аналоги к заданию № 500366: 500587 501482 514505 Все

Решение

Критерии

4 комментария

Видеокурс

Помощь

Тип 12 № 509579

а)  Решите уравнение

б)  Найдите все корни уравнения, принадлежащие отрезку

Аналоги к заданию № 509579: 509926 509947 509968 Все

Решение

Критерии

Видеокурс

Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник

Отбор корней в тригонометрическом уравнение

В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.

а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]

Решим пункт а.

Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)

sqrt(2)cos^2x — cosx = 0

cosx(sqrt(2)cosx — 1) = 0

x1 = Pi/2 + Pin, n ∈ Z

sqrt(2)cosx — 1 = 0

x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z

x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z

Решим пункт б.

1) Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.

-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi

Сразу делим все на Pi

-7/2 меньше или равно 1/2 + n меньше или равно -2

-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2

-4 меньше или равно n меньше или равно -5/2

Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2

Аналогично делаем еще два неравенства

-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8

Целых n в этом промежутке нет

-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8

Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.

Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4

2) Отбор корней с помощью тригонометрической окружности

Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.

Обойдем раз против часовой стрелки

Обойдем 2 раза против часовой стрелки

Обойдем 1 раз по часовой стрелки (значения будут отрицательные)

Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]

Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.

Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.

Сравнение двух методов.

Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.

Решение тригонометрических уравнений на промежутке

Разделы: Математика

Цель урока:

а) закрепить умения решать простейшие тригонометрические уравнения;

б) научить выбирать корни тригонометрических уравнений из заданного промежутка

Ход урока.

1. Актуализация знаний.

а)Проверка домашнего задания: классу дано опережающее домашнее задание – решить уравнение и найти способ выбора корней из данного промежутка.

1)cos x = -0,5, где хI [- ]. Ответ: .

2) sin x = , где хI [0;2?]. Ответ: ; .

3)cos 2x = —, где хI [0;]. Ответ:

Ученики записывают решение на доске кто-то с помощью графика, кто-то методом подбора.

В это время класс работает устно.

Найдите значение выражения:

а) tg – sin + cos + sin . Ответ: 1.

б) 2arccos 0 + 3 arccos 1. Ответ: ?

в) arcsin + arcsin . Ответ: .

г) 5 arctg (-) – arccos (-). Ответ:– .

– Проверим домашнее задание, откройте свои тетради с домашними работами.

Некоторые из вас нашли решение методом подбора, а некоторые с помощью графика.

2. Вывод о способах решения данных заданий и постановка проблемы, т. е. сообщение темы и цели урока.

– а) С помощью подбора решать сложно, если задан большой промежуток.

– б) Графический способ не даёт точных результатов, требует проверку, и занимает много времени.

– Поэтому должен быть ещё как минимум один способ, наиболее универсальный -попробуем его найти. Итак, чем мы будем заниматься сегодня на уроке? (Учиться выбирать корни тригонометрического уравнения на заданном промежутке.)

– Пример 1. (Ученик выходит к доске)

cos x = -0,5, где хI [- ].

Вопрос: Отчего зависит ответ на данное задание? (От общего решения уравнения. Запишем решение в общем виде). Решение записывается на доске

х = + 2?k, где k R.

– Запишем это решение в виде совокупности:

– Как вы считаете, при какой записи решения удобно выбирать корни на промежутке? (из второй записи). Но это ведь опять способ подбора. Что нам необходимо знать, чтобы получить верный ответ? (Надо знать значения k).

(Составим математическую модель для нахождения k).

1 уровень: № 295 (а,б), № 317 (а,б)

2 уровень: № 307 (в), № 308 (б), № 326(б), № 327(б).

Как решать задание 13

О чем задача?

Задачи на решение тригонометрических уравнений, более сложных, чем в задании 5. В большинстве задач требуется не только решить уравнение, но и отобрать корни, принадлежащие определенному отрезку.

Как решать?

Шаг 1. Найдите область определения

Шаг 2. Приведите уравнение к виду простейших тригонометрических уравнений

Для того чтобы привести уравнение к виду простейших тригонометрических уравнений, применяйте следующие стандартные приемы:

Мы свели исходное уравнение к совокупности простейших тригонометрических уравнений [ cos x = − 1 , cos x = − 1 2 . left[begin cos x = -1 <,>\cos x = -frac<1> <2><.>endright. [ cos x = − 1 , cos x = − 2 1 .

Шаг 3. Решите простейшие тригонометрические уравнения

О решении простейших тригонометрических уравнений читайте в отдельной статье .

Убедитесь, что найденные вами корни принадлежат области определения уравнения.

Остается решить уравнение cos x = − 1 2 cos x =-frac<1> <2>cos x = − 2 1 .

Шаг 4. Выберите корни, принадлежащие отрезку, данному в условии

Корни, принадлежащие данному в условии отрезку, можно найти либо методом перебора, либо путем решения неравенства относительно k k k .

Найдем подходящие корни методом перебора. Для этого рассмотрим две серии корней по отдельности.

источники:

http://urok.1sept.ru/articles/419940

http://lampa.io/p/%D0%BA%D0%B0%D0%BA-%D1%80%D0%B5%D1%88%D0%B0%D1%82%D1%8C-%D0%B7%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5-13-000000009d385cbc7312b1ad6da2a9ec

Источник

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi}{3}+2pi n$ , где — целое, а найти надо корни на отрезке $left [frac{5 pi}{2};frac{9 pi}{2} right ].$ На указанном промежутке лежит точка 4 pi . От нее и будем отсчитывать. Получим: $x=4 pi +frac{pi}{3}=frac{13 pi}{3}.$

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение $2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

б) Найдите все корни этого уравнения, принадлежащие промежутку $left[-3pi right.;left.-frac{3pi }{2}right]$

$2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

Упростим левую часть по формуле приведения.

$2{{cos}^2 x+sqrt{3}{cos x}=0}$

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-3pi right.;left.-frac{3pi }{2}right].$

Видим, что указанному отрезку принадлежат решения $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Ответ: $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi }{3}+2pi n$ , где — целое, а найти надо корни на отрезке $[frac{5pi }{2};frac{9pi }{2}].$ На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: $x=4pi +frac{pi }{3}=frac{13pi }{3}.$

2. а) Решите уравнение ${({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) $3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}$

Степени равны, их основания равны. Значит, равны и показатели.

$3{cos x{sin x}}=frac{3{cos x}}{2}$

${cos x({sin x-frac{1}{2})=0}}$

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Отметим на тригонометрическом круге отрезок $left[-pi ;frac{pi }{2}right]$ и найденные серии решений.

Видим, что указанному отрезку принадлежат точки $x=-frac{pi }{2}$ и $x=frac{pi }{2}$ из серии $x=frac{pi }{2}+pi n,nin z.$

Точки серии $x=frac{5pi }{6}+2pi n,nin z$ не входят в указанный отрезок.

А из серии $x=frac{pi }{6}+2pi n,nin z$ в указанный отрезок входит точка $x=frac{pi }{6}.$

Ответ в пункте (б): $-frac{pi }{2},frac{pi }{6} , frac{pi }{2}.$

3. а) Решите уравнение ${cos 2x}+{{sin}^2 x=0,5}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{7pi }{2}right.;left.-2pi right].$

а)
${cos 2x}+{{sin}^2 x=0,5}$

Применим формулу косинуса двойного угла: $boldsymbol{cos2alpha =1-{2sin}^2alpha }$

$1-2{{sin}^2 x}+{{sin}^2 x}=0,5$

${{-sin}^2 x=-0,5}$

${{sin}^2 x=0,5}$

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке $left[-frac{7pi }{2}right.;left.-2pi right]$ с помощью двойного неравенства.

Сначала серия $x=frac{pi }{4}+pi n,nin Z.$

$-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le frac{1}{4}+nle -2$

$n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}$

Теперь серия $x=-frac{pi }{4}+pi n,nin Z$

$-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le -frac{1}{4}+nle -2$

$n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}$

$n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}$

Ответ: $-frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4}$ .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии $x=-frac{pi }{4}+2pi n,nin Z$ на отрезке $left[-frac{pi }{2}right.;left.20pi right].$ Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение $left({tg}^2x-3right)sqrt{11{cos x}}=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{5pi }{2};-pi right].$

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть ${tg x=frac{{sin x}}{{cos x}}}.$

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .

Ответ в пункте а) $x=pm frac{pi }{3}+2pi n, nin z$

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-frac{5pi }{2};-pi right].$

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

$x=frac{pi }{3}-2pi =-frac{5pi }{3}$ и $x=-frac{pi }{3}-2pi =-frac{7pi }{3}.$

5. а) Решите уравнение $sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}$

б) Найдите корни, принадлежащие отрезку

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых ${cos x}=frac{sqrt{2}}{2}$ или ${cos x}=-frac{sqrt{2}}{2}$ . Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии $x=-frac{3pi }{4}+2pi n$ не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке нам подходит корень $x =-frac{pi }{4}$ .

На отрезке нам подходят корни $x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}$ .

На отрезке — корни $x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Ответ в пункте б): $-frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Лучшие онлайн-курсы для подготовки к ЕГЭ

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Тригонометрические уравнения»

Открытый банк заданий по теме тригонометрические уравнения. Задания C1 из ЕГЭ по математике (профильный уровень)

Стереометрия. Расстояния и углы в пространстве

Задание №1179

Условие

а) Решите уравнение 2(sin x-cos x)=tgx-1.

б) Укажите корни этого уравнения, принадлежащие промежутку left[ frac{3pi }2;,3pi right].

Показать решение

Решение

а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 sin x-2 cos x-tg x=0. Учитывая, что cos x neq 0, слагаемое 2 sin x можно заменить на 2 tg x cos x, получим уравнение 1+2 tg x cos x-2 cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 cos x)=0.

1) 1-tg x=0, tg x=1, x=fracpi 4+pi n, n in mathbb Z;

2) 1-2 cos x=0, cos x=frac12, x=pm fracpi 3+2pi n, n in mathbb Z.

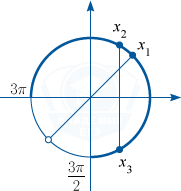
б) С помощью числовой окружности отберём корни, принадлежащие промежутку left[ frac{3pi }2;, 3pi right].

x_1=fracpi 4+2pi =frac{9pi }4,

x_2=fracpi 3+2pi =frac{7pi }3,

x_3=-fracpi 3+2pi =frac{5pi }3.

Ответ

а) fracpi 4+pi n, pmfracpi 3+2pi n, n in mathbb Z;

б) frac{5pi }3, frac{7pi }3, frac{9pi }4.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1178

Условие

а) Решите уравнение (2sin ^24x-3cos 4x)cdot sqrt {tgx}=0.

б) Укажите корни этого уравнения, принадлежащие промежутку left( 0;,frac{3pi }2right] ;

Показать решение

Решение

а) ОДЗ: begin{cases} tgxgeqslant 0\xneq fracpi 2+pi k,k in mathbb Z. end{cases}

Исходное уравнение на ОДЗ равносильно совокупности уравнений

left[!!begin{array}{l} 2 sin ^2 4x-3 cos 4x=0,\tg x=0. end{array}right.

Решим первое уравнение. Для этого сделаем замену cos 4x=t, t in [-1; 1]. Тогда sin^24x=1-t^2. Получим:

2(1-t^2)-3t=0,

2t^2+3t-2=0,

t_1=frac12, t_2=-2, t_2notin [-1; 1].

cos 4x=frac12,

4x=pm fracpi 3+2pi n,

x=pm fracpi {12}+frac{pi n}2, n in mathbb Z.

Решим второе уравнение.

tg x=0,, x=pi k, k in mathbb Z.

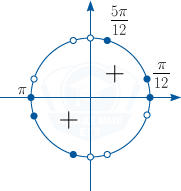
При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.

Знаком «+» отмечены 1-я и 3-я четверти, в которых tg x>0.

Получим: x=pi k, k in mathbb Z; x=fracpi {12}+pi n, n in mathbb Z; x=frac{5pi }{12}+pi m, m in mathbb Z.

б) Найдём корни, принадлежащие промежутку left( 0;,frac{3pi }2right].

x=fracpi {12}, x=frac{5pi }{12}; x=pi ; x=frac{13pi }{12}; x=frac{17pi }{12}.

Ответ

а) pi k, k in mathbb Z; fracpi {12}+pi n, n in mathbb Z; frac{5pi }{12}+pi m, m in mathbb Z.

б) pi; fracpi {12}; frac{5pi }{12}; frac{13pi }{12}; frac{17pi }{12}.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1177

Условие

а) Решите уравнение: cos ^2x+cos ^2fracpi 6=cos ^22x+sin ^2fracpi 3;

б) Укажите все корни, принадлежащие промежутку left( frac{7pi }2;,frac{9pi }2right].

Показать решение

Решение

а) Так как sin fracpi 3=cos fracpi 6, то sin ^2fracpi 3=cos ^2fracpi 6, значит, заданное уравнение равносильно уравнению cos^2x=cos ^22x, которое, в свою очередь, равносильно уравнению cos^2x-cos ^2 2x=0.

Но cos ^2x-cos ^22x= (cos x-cos 2x)cdot (cos x+cos 2x) и

cos 2x=2 cos ^2 x-1, поэтому уравнение примет вид

(cos x-(2 cos ^2 x-1)),cdot (cos x+(2 cos ^2 x-1))=0,

(2 cos ^2 x-cos x-1),cdot (2 cos ^2 x+cos x-1)=0.

Тогда либо 2 cos ^2 x-cos x-1=0, либо 2 cos ^2 x+cos x-1=0.

Решая первое уравнение как квадратное уравнение относительно cos x, получаем:

(cos x)_{1,2}=frac{1pmsqrt 9}4=frac{1pm3}4. Поэтому либо cos x=1, либо cos x=-frac12. Если cos x=1, то x=2kpi , k in mathbb Z. Если cos x=-frac12, то x=pm frac{2pi }3+2spi , s in mathbb Z.

Аналогично, решая второе уравнение, получаем либо cos x=-1, либо cos x=frac12.Если cos x=-1, то корни x=pi +2mpi , m in mathbb Z. Если cos x=frac12, то x=pm fracpi 3+2npi , n in mathbb Z.

Объединим полученные решения:

x=mpi , m in mathbb Z; x=pm fracpi 3 +spi , s in mathbb Z.

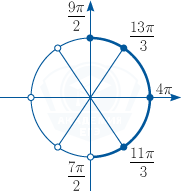
б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.

Получим: x_1 =frac{11pi }3, x_2=4pi , x_3 =frac{13pi }3.

Ответ

а) mpi, m in mathbb Z; pm fracpi 3 +spi , s in mathbb Z;

б) frac{11pi }3, 4pi , frac{13pi }3.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1176

Условие

а) Решите уравнение 10cos ^2frac x2=frac{11+5ctgleft( dfrac{3pi }2-xright) }{1+tgx}.

б) Укажите корни этого уравнения, принадлежащие интервалу left( -2pi ; -frac{3pi }2right).

Показать решение

Решение

а) 1. Согласно формуле приведения, ctgleft( frac{3pi }2-xright) =tgx. Областью определения уравнения будут такие значения x, что cos x neq 0 и tg x neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 cos ^2 frac x2=1+cos x. Получим уравнение: 5(1+cos x) =frac{11+5tgx}{1+tgx}.

Заметим, что frac{11+5tgx}{1+tgx}= frac{5(1+tgx)+6}{1+tgx}= 5+frac{6}{1+tgx}, поэтому уравнение принимает вид: 5+5 cos x=5 +frac{6}{1+tgx}. Отсюда cos x =frac{dfrac65}{1+tgx}, cos x+sin x =frac65.

2. Преобразуем sin x+cos x по формуле приведения и формуле суммы косинусов: sin x=cos left(fracpi 2-xright), cos x+sin x= cos x+cos left(fracpi 2-xright)= 2cos fracpi 4cos left(x-fracpi 4right)= sqrt 2cos left( x-fracpi 4right) = frac65.

Отсюда cos left(x-fracpi 4right) =frac{3sqrt 2}5. Значит, x-fracpi 4= arccos frac{3sqrt 2}5+2pi k, k in mathbb Z,

или x-fracpi 4= -arccos frac{3sqrt 2}5+2pi t, t in mathbb Z.

Поэтому x=fracpi 4+arccos frac{3sqrt 2}5+2pi k,k in mathbb Z,

или x =fracpi 4-arccos frac{3sqrt 2}5+2pi t,t in mathbb Z.

Найденные значения x принадлежат области определения.

б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=fracpi 4+arccos frac{3sqrt 2}5 и b=fracpi 4-arccos frac{3sqrt 2}5.

1. Докажем вспомогательное неравенство:

frac{sqrt 2}{2}<frac{3sqrt 2}2<1.

Действительно, frac{sqrt 2}{2}=frac{5sqrt 2}{10}<frac{6sqrt2}{10}=frac{3sqrt2}{5}.

Заметим также, что left( frac{3sqrt 2}5right) ^2=frac{18}{25}<1^2=1, значит frac{3sqrt 2}5<1.

2. Из неравенств (1) по свойству арккосинуса получаем:

arccos 1<arccos frac{3sqrt 2}5<arccos frac{sqrt 2}2,

0<arccosfrac{3sqrt2}{5}<frac{pi}{4}.

Отсюда fracpi 4+0<fracpi 4+arccos frac{3sqrt 2}5<fracpi 4+fracpi 4,

0<fracpi 4+arccos frac{3sqrt 2}5<fracpi 2,

0<a<fracpi 2.

Аналогично, -fracpi 4<arccosfrac{3sqrt2}{5}<0,

0=fracpi 4-fracpi 4<fracpi 4-arccos frac{3sqrt 2}5< fracpi 4<fracpi 2,

0<b<fracpi 2.

При k=-1 и t=-1 получаем корни уравнения a-2pi и b-2pi.

Bigg( a-2pi =-frac74pi +arccos frac{3sqrt 2}5,, b-2pi =-frac74pi -arccos frac{3sqrt 2}5Bigg). При этом -2pi <a-2pi <-frac{3pi }2,

-2pi <b-2pi <-frac{3pi }2. Значит, эти корни принадлежат заданному промежутку left( -2pi , -frac{3pi }2right).

При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.

Действительно, если kgeqslant 1 и tgeqslant 1, то корни больше 2pi. Если kleqslant -2 и tleqslant -2, то корни меньше -frac{7pi }2.

Ответ

а) fracpi4pm arccosfrac{3sqrt2}5+2pi k, kinmathbb Z;

б) -frac{7pi}4pm arccosfrac{3sqrt2}5.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1175

Условие

а) Решите уравнение sin left( fracpi 2+xright) =sin (-2x).

б) Найдите все корни этого уравнения, принадлежащие промежутку [0; pi ];

Показать решение

Решение

а) Преобразуем уравнение:

cos x =-sin 2x,

cos x+2 sin x cos x=0,

cos x(1+2 sin x)=0,

cos x=0,

x =fracpi 2+pi n, n in mathbb Z;

1+2 sin x=0,

sin x=-frac12,

x=(-1)^{k+1}cdot fracpi 6+pi k, k in mathbb Z.

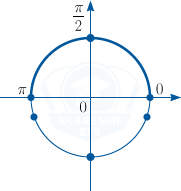
б) Корни, принадлежащие отрезку [0; pi ], найдём с помощью единичной окружности.

Указанному промежутку принадлежит единственное число fracpi 2.

Ответ

а) fracpi 2+pi n, n in mathbb Z; (-1)^{k+1}cdot fracpi 6+pi k, k in mathbb Z;

б) fracpi 2.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1174

Условие

а) Решите уравнение frac{sin x-1}{1+cos 2x}=frac{sin x-1}{1+cos (pi +x)}.

б) Найдите все корни этого уравнения, принадлежащие отрезку left[ -frac{3pi }{2}; -frac{pi }2 right].

Показать решение

Решение

а) Найдём ОДЗ уравнения: cos 2x neq -1, cos (pi +x) neq -1; Отсюда ОДЗ: x neq frac pi 2+pi k,

k in mathbb Z, x neq 2pi n, n in mathbb Z. Заметим, что при sin x=1, x=frac pi 2+2pi k, k in mathbb Z.

Полученное множество значений x не входит в ОДЗ.

Значит, sin x neq 1.

Разделим обе части уравнения на множитель (sin x-1), отличный от нуля. Получим уравнение frac 1{1+cos 2x}=frac 1{1+cos (pi +x)}, или уравнение 1+cos 2x=1+cos (pi +x). Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x. Это уравнение с помощью замены cos x=t, где -1 leqslant t leqslant 1 сводим к квадратному: 2t^2+t-1=0, корни которого t_1=-1 и t_2=frac12. Возвращаясь к переменной x, получим cos x = frac12 или cos x=-1, откуда x=frac pi 3+2pi m, m in mathbb Z, x=-frac pi 3+2pi n, n in mathbb Z, x=pi +2pi k, k in mathbb Z.

б) Решим неравенства

1) -frac{3pi }2 leqslant frac{pi }3+2pi m leqslant -frac pi 2 ,

2) -frac{3pi }2 leqslant -frac pi 3+2pi n leqslant -frac pi {2,}

3) -frac{3pi }2 leqslant pi+2pi k leqslant -frac pi 2 , m, n, k in mathbb Z.

Решение:

1) -frac{3pi }2 leqslant frac{pi }3+2pi m leqslant -frac pi 2 , -frac32 leqslant frac13+2m leqslant -frac12 -frac{11}6 leqslant 2m leqslant -frac56 , -frac{11}{12} leqslant m leqslant -frac5{12}.

Нет целых чисел, принадлежащих промежутку left [-frac{11}{12};-frac5{12}right].

2) -frac {3pi} 2 leqslant -frac{pi }3+2pi n leqslant -frac{pi }{2}, -frac32 leqslant -frac13 +2n leqslant -frac12 , -frac76 leqslant 2n leqslant -frac1{6}, -frac7{12} leqslant n leqslant -frac1{12}.

Нет целых чисел, принадлежащих промежутку left[ -frac7{12} ; -frac1{12} right].

3) -frac{3pi }2 leqslant pi +2pi kleqslant -frac{pi }2, -frac32 leqslant 1+2kleqslant -frac12, -frac52 leqslant 2k leqslant -frac32, -frac54 leqslant k leqslant -frac34.

Этому неравенству удовлетворяет k=-1, тогда x=-pi.

Ответ

а) frac pi 3+2pi m; -frac pi 3+2pi n; pi +2pi k, m, n, k in mathbb Z;

б) -pi .

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1173

Условие

а) Решите уравнение: sin ^2x+sin ^2fracpi 6=cos ^22x+cos ^2fracpi 3.

б) Укажите все корни, принадлежащие промежутку left[ frac{7pi }2;,frac{9pi }2right).

Показать решение

Решение

а) Так как sin fracpi 6=cos fracpi 3, то sin ^2fracpi 6=cos ^2fracpi 3, значит, заданное уравнение равносильно уравнению sin ^2 x=cos ^2 2x, которое, в свою очередь, равносильно уравнению sin ^2- cos ^2 2x=0.

Но sin ^ 2x-cos ^2 2x= (sin x-cos 2x)cdot (sin x+cos 2x) и

cos 2x=1-2 sin ^2 x, поэтому уравнение примет вид

(sin x-(1-2 sin ^2 x)),cdot (sin x+(1-2 sin ^2 x))=0,

(2 sin ^2 x+sin x-1),cdot (2 sin ^2 x-sin x-1)=0.

Тогда либо 2 sin ^2 x+sin x-1=0, либо 2 sin ^2 x-sin x-1=0.

Решим первое уравнение как квадратное относительно sin x,

(sin x)_{1,2}=frac{-1 pm sqrt 9}4=frac{-1 pm 3}4. Поэтому либо sin x=-1, либо sin x=frac12. Если sin x=-1, то x=frac{3pi }2+ 2kpi , k in mathbb Z. Если sin x=frac12, то либо x=fracpi 6 +2spi , s in mathbb Z, либо x=frac{5pi }6+2tpi , t in mathbb Z.

Аналогично, решая второе уравнение, получаем либо sin x=1, либо sin x=-frac12. Тогда x =fracpi 2+2mpi , m in mathbb Z, либо x=frac{-pi }6 +2npi , n in mathbb Z, либо x=frac{-5pi }6+2ppi , p in mathbb Z.

Объединим полученные решения:

x=fracpi 2+mpi,minmathbb Z; x=pmfracpi 6+spi,s in mathbb Z.

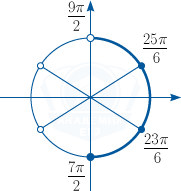
б) Выберем корни, которые попали в заданный промежуток с помощью числовой окружности.

Получим: x_1 =frac{7pi }2, x_2 =frac{23pi }6, x_3 =frac{25pi }6.

Ответ

а) fracpi 2+ mpi , m in mathbb Z; pm fracpi 6 +spi , s in mathbb Z;

б) frac{7pi }2;,,frac{23pi }6;,,frac{25pi }6.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1172

Условие

а) Решите уравнение log_2^2(2sin x+1)-17log_2(2sin x+1) +16=0.

б) Укажите корни этого уравнения, принадлежащие отрезку left[ fracpi 4;,2pi right].

Показать решение

Решение

а) После замены t=log_2(2 sin x+1) исходное уравнение примет вид t^2 -17t+16=0. Корни этого уравнения t=1, t=16. Возвращаясь к переменной x, получим:

left[!!begin{array}{l} log_2(2 sin x+1)=1,\ log_2(2 sin x+1)=16; end{array}right. left[!!begin{array}{l} 2sin x+1=2,\ 2sin x+1=2^{16}. end{array}right.

Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим:

sin x =frac12, x=(-1)^nfracpi 6+pi n,n in mathbb Z.

б) Запишем решение уравнения в виде x=fracpi 6 +2pi n,n in mathbb Z или x=frac{5pi }6+2pi k,kin mathbb Z и выясним, для каких целых значений n и k справедливы неравенства fracpi 4leqslant fracpi 6+2pi nleqslant 2pi и fracpi 4leqslant frac{5pi }6+2pi kleqslant 2pi.

Получим: frac1{24}leqslant nleqslant frac{11}{12} и -frac7{24}leqslant kleqslant frac7{12}, откуда следует, что нет целых значений n, удовлетворяющих неравенству frac1{24}leqslant nleqslant frac{11}{12};,,, k=0 — единственное целое k, удовлетворяющее неравенству -frac7{24}leqslant kleqslant frac7{12}.

При k=0, x=frac{5pi }6+2picdot 0=frac{5pi }6. Итак, frac{5pi }6 — корень уравнения, принадлежащий отрезку left[ fracpi 4;,2pi right].

Ответ

а) (-1)^nfracpi 6+pi n,n in mathbb Z.

б) frac{5pi }6.

Задание №1171

Условие

а) Решите уравнение 125^x-3cdot 25^x-5^{x+2}+75=0.

б) Укажите все корни этого уравнения, принадлежащие отрезку [log_54; log_511).

Показать решение

Решение

а) Преобразуем исходное уравнение и разложим на множители его левую часть.

5^{3x}-3cdot 5^{2x}-25cdot 5^x+25cdot 3=0,

5^{2x}(5^x-3)-25(5^x-3)=0,

(5^x-3)(5^{2x}-25)=0.

Получаем: 5^x-3=0 или 5^{2x}-25=0.

5^x-3=0, x=log_53 или 5^{2x}=25, x=1.

б) Нам нужно выбрать те корни уравнения, которые принадлежат отрезку [log_5 4; log_5 11]. Заметим, что log_5 3<log_5 4<1<log_5 11, значит, указанному отрезку принадлежит корень x=1.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1170

Условие

а) Решите уравнение 2cos xleft( cos x+cos frac{5pi }4right) + cos x+cos frac{3pi }4=0.

б) Найдите все корни этого уравнения, принадлежащие промежутку left[ pi ;,frac{5pi }2right).

Показать решение

Решение

а) Так как cos frac{5pi }4= cos left( pi +fracpi 4right) = -cos fracpi 4= -frac{sqrt 2}2 и cos frac{3pi }4= cos left( pi -fracpi 4right) = -cos fracpi 4= -frac{sqrt 2}2, то уравнение примет вид: 2cos xleft( cos x-frac{sqrt 2}2right) +cos x-frac{sqrt 2}2=0.Отсюда (2cos x+1)left( cos x-frac{sqrt 2}2right) =0.

Тогда cos x=-frac12; x=pmfrac{2pi }3+2pi n или cos x=frac{sqrt 2}2;, x=pmfracpi 4+2pi n, где n in mathbb Z.

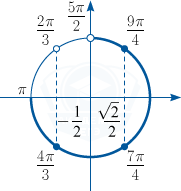
б) Корни, принадлежащие промежутку left[ pi ;,frac{5pi }2right), найдём с помощью числовой окружности: frac{4pi }3;,, frac{7pi }4;,, frac{9pi }4.

Ответ

а) pmfrac{2pi }3+2pi n;,, pmfracpi 4=2pi n, n in mathbb Z.

б) frac{4pi }3;, frac{7pi }4;, frac{9pi }4.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Лучшие репетиторы для сдачи ЕГЭ

Источник

Слайд 1

Методы отбора корней в тригонометрических уравнениях на заданном промежутке

Слайд 2

Баллы за задание №12 (С-1) 2015 2018 2020 2021 1 балл 90,7% 73, 7% 92,2% 100% 2 балла 69,4% 51,1% 83,5% 100%

Слайд 5

Обязательный минимум знаний sin x = a , -1  a  1 (  a   1) x = arcsin a + 2  n, n  Z x =  — arcsin a + 2  n, n  Z sin x = 1 x =  /2 + 2  k, k  Z sin x = — 1 x = —  /2 + 2  k, k  Z sin x = 0 x =  k, k  Z y x y x x y

Слайд 6

Обязательный минимум знаний cos x = a , -1  a  1 (  a   1) x =  arccos a + 2  n, n  Z arccos (- a) =  — arccos a cos x = 1 x = 2  k, k  Z cos x = — 1 x =  + 2  k, k  Z cos x = 0 x =  /2 +  k, k  Z y x y x y x

Слайд 7

Обязательный минимум знаний tg x = a , a  R x = arctg a +  n, n  Z arctg (- a) = — arctg a ctg x = a , a  R x = arcctg a +  n, n  Z arctg (- a) =  — arctg a

Слайд 8

Рекомендации по решению тригонометрических уравнений Свести уравнение к простейшему Некоторые методы решения тригонометрических уравнений Применение тригонометрических формул Использование формул сокращённого умножения Разложение на множители Сведение к квадратному уравнению относительно sin x, cos x, tg x Введением вспомогательного аргумента Делением обеих частей однородного уравнения первой степени ( asin x +bcosx = 0 ) на cos x Делением обеих частей однородного уравнения второй степени (a sin 2 x +bsin x cos x+ c cos 2 x =0) на cos 2 x

Слайд 9

Различные способы отбора корней cos 2x = ½, x  [-  /2; 3  /2] 2x = ± arccos ½ + 2  n, n  Z 2x = ±  /3 + 2  n, n  Z x = ±  /6 +  n, n  Z Отберём корни с помощью тригонометрической окружности Ответ : —  /6;  /6; 5  /6; 7  /6 Найти корни уравнения, принадлежащие данному промежутку (с помощью тригонометрической окружности)

Слайд 10

Различные способы отбора корней Найти корни уравнения, принадлежащие данному промежутку (арифметический, метод перебора) sin 3x = √3/2, x  [-  /2;  /2] 3x = ( – 1) k  /3 +  k, k  Z x = ( – 1) k  /9 +  k/3, k  Z Отберём корни с помощью перебора значений k: k = 0, x =  /9 – принадлежит промежутку k = 1, x = –  /9 +  /3 = 2  /9 – принадлежит промежутку k = 2, x =  /9 + 2  /3 = 7  /9 – не принадлежит промежутку k = – 1, x = –  /9 –  /3 = – 4  /9 – принадлежит промежутку k = – 2, x =  /9 – 2  /3 = – 5  /9 – не принадлежит промежутку Ответ: -4  /9;  /9; 2  /9

Слайд 11

Различные способы отбора корней tg 3x = – 1 , x  (-  /2;  ) 3x = –  /4 +  n, n  Z x = –  /12 +  n/3, n  Z Отберём корни с помощью неравенства: Ответ: – 5  /12; –  /12;  /4; 7  /12; 11  /12 –  /2 < –  /12 +  n/3 <  , – 1/2 < – 1/12 + n/3 < 1, – 1/2 + 1/12 < n/3 < 1+ 1/12, – 5/12 < n/3 < 13/12, – 5/4 < n < 13/4, n  Z, n = – 1; 0; 1; 2; 3 Найти корни уравнения, принадлежащие данному промежутку ( с помощью неравенства) n = – 1, x = –  /12 –  /3 = – 5  /12 n = 0, x = –  /12 n = 1, x = –  /12 +  /3 =  /4 n = 2, x = –  /12 + 2  /3 = 7  /12 n = 3, x = –  /12 +  = 11  /12

Слайд 12

Различные способы отбора корней Найти корни уравнения, принадлежащие данному промежутку ( с помощью графика) cos x = – √2/2, x  [ – 4; 5  /4] x =  arccos (– √2/2) + 2  n, n  Z x =  3  /4 + 2  n, n  Z Отберём корни с помощью графика: Ответ:  5  /4;  3  /4 x = –  /2 –  /4 = – 3  /4; x = –  –  /4 = – 5  /4

Слайд 13

1. Решить уравнение 7 2cosx = 49 sin2x и указать его корни на отрезке [  ; 5  /2] 7 2cosx = 49 sin2x, 7 2cosx = 7 2sin2x, 2cos x = 2sin 2x, cos x – 2 sinx cosx = 0, cos x (1 – 2sinx) = 0, cos x = 0 , x =  /2 +  k, k  Z или 1 – 2sinx = 0, sin x = ½, x =  /6 + 2  k, k  Z x = 5  /6 + 2  k, k  Z Решим уравнение: Проведём отбор корней с помощью тригонометрической окружности: Ответ: а)  /2 +  k, k  Z, x1 =  /6 + 2  k, k  Z; x2 = 5  /6 + 2  k, k  Z б) 3  /2; 5  /2; 13  /6 x = 2  +  /6 = 13  /6

Слайд 14

4cos 2 x + 8 cos (x – 3  /2) +1 = 0 4cos 2 x + 8 cos (3  /2 – x) +1 = 0, 4cos 2 x – 8 sin x +1 = 0, 4 – 4sin 2 x – 8 sin x +1 = 0, 4sin 2 x + 8sin x – 5 = 0, D/4 = 16 + 20 = 36, sin x = – 2,5  или sin x = ½ x1=  /6 + 2  k, k  Z x2 = 5  /6 + 2  k, k  Z 2. Решить уравнение 4cos 2 x + 8 cos (x – 3  /2) +1 = 0 Найти его корни на отрезке [3  ; 9  2]

Слайд 15

Проведем отбор корней на отрезке [3  ; 9  2] (с помощью графиков) x = 4  +  /6 = 25  /6 Ответ: а) x1 =  /6 + 2  k, k  Z x2 = 5  /6 + 2  k, k  Z б) 25  /6 sin x = ½ Построим графики функций y = sin x и y = ½

Слайд 16

3. Решить уравнение 4 – cos 2 2x = 3 sin 2 2x + 2 sin 4x Найти его корни на отрезке [0; 1] 4 – cos 2 2x = 3 sin 2 2x + 2 sin 4x 4 (sin 2 2x + cos 2 2x ) – cos 2 2x = 3 sin 2 2x + 4 sin 2x cos 2x, sin 2 2x + 3 cos 2 2x – 4 sin 2x cos 2x = 0 Если cos 2 2x = 0, то sin 2 2x = 0, что невозможно, поэтому cos 2 2x  0 и обе части уравнения можно разделить на cos 2 2x. tg 2 2x + 3 – 4 tg 2x = 0, tg 2 2x – 4 tg 2x + 3= 0, tg 2x = 1, 2x =  /4 +  n, n  Z x =  /8 +  n/2, n  Z или tg 2x = 3, 2x = arctg 3 +  k, k  Z x = ½ arctg 3 +  k/2, k  Z

Слайд 17

Проведём отбор корней на отрезке [0; 1] 4 – cos 2 2x = 3 sin 2 2x + 2 sin 4x x =  /8 +  n/2, n  Z или x = ½ arctg 3 +  k/2, k  Z Так как 0 < arctg 3<  /2, 0 < ½ arctg 3<  /4, то ½ arctg 3 является решением Так как 0 <  /8 <  /4 < 1,значит  /8 также является решением Другие решения не попадут в промежуток [0; 1], так как они получаются из чисел ½ arctg 3 и  /8 прибавлением чисел, кратных  /2. Ответ: а)  /8 +  n/2, n  Z ; ½ arctg 3 +  k/2, k  Z б)  /8; ½ arctg 3

Слайд 18

4. Решить уравнение log 5 (cos x – sin 2x + 25) = 2 Найти его корни на отрезке [2  ; 7  /2] log 5 (cos x – sin 2x + 25) = 2 cos x – sin 2x + 25 > 0, cos x – sin 2x + 25 = 25, 25 > 0, cos x – 2sin x cos x = 0, cos x (1 – 2sin x) = 0, cos x = 0, x =  /2 +  n, n  Z или 1 – 2sinx = 0, sin x = 1/2 x =  /6 + 2  k, k  Z x = 5  /6 + 2  k, k  Z Решим уравнение:

Слайд 19

1) x =  /2 +  n, n  Z 2    /2 +  n  7  /2, n  Z 2  1/2 + n  7/2, n  Z 2 – ½  n  7/2 – ½, n  Z 1,5  n  3, n  Z n = 2; 3 x =  /2 + 2  = 5  /2 x =  /2 + 3  = 7  /2 x = 2  +  /6 = 13  /6 x = 3  –  /6 = 17  /6 Проведём отбор корней на отрезке [2  ; 7  /2]: Проведём отбор корней на отрезке 2) sin x = 1/2 Ответ: а)  /2 +  n, n  Z; x1 =  /6 + 2  k, k  Z x2 = 5  /6 + 2  k, k  Z б) 13  /6 ; 5  /2; 7  /2; 17  /6

Слайд 20

5. Решить уравнение 1/sin 2 x + 1/sin x = 2 Найти его корни на отрезке [-5  /2; -3  /2] 1/sin 2 x + 1/sin x = 2 x   k Замена 1/sin x = t, t 2 + t = 2, t 2 + t – 2 = 0, t 1 = – 2, t 2 = 1 Решим уравнение: 1/sin x = – 2, sin x = – ½, x = –  /6 + 2  n, n  Z или x = – 5  /6 + 2  n, n  Z 1/sin x = 1, sin x = 1, x =  /2 + 2  n, n  Z

Слайд 21

1) x = —  /6 + 2  n, n  Z -5  /2  —  /6 + 2  n  -3  /2, n  Z -5/2  -1/6 + 2n  -3/2, n  Z -5/2 +1/6  2n  -3/2 + 1/6, n  Z – 7/3  2n  -4/3, n  Z -7/6  n  -2/3, n  Z n = -1 x = —  /6 — 2  = -13  /6 Рассмотрим остальные серии корней и проведём отбор корней на отрезке алгебраическим методом [-5  /2; -3  /2] Продолжим отбор корней на отрезке Ответ: а)  /2 + 2  n, n  Z ; x1 = —  /6 + 2  k, k  Z x2 = — 5  /6 + 2  k, k  Z б) -13  /6 ; -3  /2 2) x =  /2 + 2  n, n  Z -5  /2   /2 + 2  n  -3  /2, n  Z -5/2  1/2 + 2n  -3/2, n  Z -5/2 — 1/2  2n  -3/2 — 1/2, n  Z – 3  2n  -2, n  Z -1,5  n  -1, n  Z n = -1 x =  /2 — 2  = -3  /2

Слайд 22

6. Решить уравнение |sin x|/sin x + 2 = 2cos x Найти его корни на отрезке [-1; 8] Решим уравнение |sin x|/sin x + 2 = 2cos x 1)Если sin x >0, то |sin x| =sin x Уравнение примет вид: 2 cos x=3, cos x =1,5 – не имеет корней 2) Если sin x <0, то |sin x| =-sin x и уравнение примет вид 2cos x=1, cos x = 1/2, x = ±π/3 +2πk, k  Z Учитывая, что sin x < 0, то остаётся одна серия ответа x = — π/3 +2πk, k  Z Произведём отбор корней на отрезке [-1; 8] k=0, x= — π/3 , — π < -3, — π/3 < -1, -π/3 не принадлежит данному отрезку k=1, x = — π/3 +2π = 5 π/3<8, 5 π/3  [-1; 8] k=2, x= — π/3 + 4π = 11 π/3 > 8, 11 π/3 не принадлежит данному отрезку. Ответ: а) — π/3 +2πk, k  Z б) 5 π/3

Слайд 23

7. Решить уравнение 4sin 3 x=3cos(x- π/2) Найти его корни на промежутке [7  /2; 9  /2) Решим уравнение 4sin 3 x = 3cos(x- π/2) 4sin 3 x = 3cos(π/2-х), 4sin 3 x — 3cos(π/2-х) = 0, 4sin 3 x – 3sin x = 0, sin x (4sin 2 x – 3) = 0, sin x= 0 x=  n, n  Z или 4sin 2 x – 3=0, sin x=√3/2; sin x =-√3/2 sin x=√3/2, x1=  /3 + 2  k, k  Z, x2=4  /3 + 2  k, k  Z. sin x =-√3/2, x1=-  /3 + 2  k, k  Z, x2= -4  /3 + 2  k, k  Z.

Слайд 24

Объединим решения ( см. рисунок) Уравнение можно решить короче, зная формулу sin 3x = 3sinx – 4sin 3 x : 4sin 3 x – 3sin x =0, 3sin x – 4sin 3 x =0, s in 3x = 0, х =  m/3, m  Z или х =  m/3, m  Z

Слайд 25

Проведём отбор корней на промежутке [7  /2; 9  /2) х=  m/3, m  Z. 7  /2 ≤  m/3 < 9  /2, 21/2 ≤ m<27/2, m  Z, 10,5 ≤ m < 13,5, m  Z, m =10; 11; 12, x= 10  /3, x= 11  /3, x= 12  /3 Ответ : а)  m/3, m  Z; б) 10  /3; 11  /3; 12  /3

Слайд 26

8. Решить уравнение √1-sin 2 x= sin x Найти его корни на промежутке [5  /2; 4  ] Решим уравнение √1-sin 2 x= sin x. sin x ≥ 0, 1- sin 2 x = sin 2 x; sin x ≥ 0, sin x≥0, 2sin 2 x = 1; sin x =√2/2; sin x = — √2/2; sin x =√2/2 sin x =√2/2 x=(-1) k  /4 +  k, k  Z

Слайд 27

Проведём отбор корней на отрезке [5  /2; 4  ] x=(-1) k  /4 +  k, k  Z sin x =√2/2 у =sin x и у=√2/2 5  /2 +  /4 = 11  /4 Ответ: а) (-1) k  /4 +  k, k  Z ; б) 11  /4

Слайд 28

9. Решить уравнение (sin2x + 2 sin 2 x)/√-cos x =0 Найти его корни на промежутке [-5  ; -7  /2] Решим уравнение (sin2x + 2 sin 2 x)/√-cos x =0. 1) cos x <0 ,  /2 +2  n

Слайд 29

Отберём корни на заданном отрезке Отберём корни на заданном отрезке [-5  ; -7  /2] x=  +2  n, n  Z ; -5  ≤  +2  n ≤ -7  /2, -5-1 ≤ 2n ≤ -7/2-1, -3≤ n ≤ -9/4, n  Z n = -3, x=  -6  = -5  x= 3  /4 + 2  n, n  Z -5  ≤ 3  /4 + 2  n ≤ -7  /2 -23/8 ≤ n ≤ -17/8, нет такого целого n. Ответ: а)  +2  n, n  Z ; 3  /4 + 2  n, n  Z ; б) -5  .

Слайд 30

10. Решить уравнение 2sin2x =4cos x –sinx+1 Найти его корни на промежутке [  /2; 3  /2 ] Решим уравнение 2sin2x = 4cos x – sinx+1 2sin2x = 4cos x – sinx+1, 4 sinx∙cos x – 4cos x + sin x -1 = 0, 4cos x(sin x – 1) + (sin x – 1) = 0, (sin x – 1)(4cos x +1)=0, sin x – 1= 0, sin x = 1, x =  /2+2  n, n  Z или 4cos x +1= 0, cos x = -0,25 x = ± (  -arccos (0,25)) + 2  n, n  Z Запишем корни этого уравнения иначе x =  — arccos(0,25) + 2  n, x = -(  — arccos(0,25)) + 2  n, n  Z

Слайд 31

Отберём корни с помощью окружности x =  /2+2  n, n  Z, х =  /2; x =  -arccos(0,25)+2  n, х=-(  -arccos(0,25)) +2  n, n  Z, x =  — arccos(0,25), x =  + arccos(0,25) Ответ: а)  /2+2  n,  -arccos(0,25)+2  n, -(  -arccos(0,25)) +2  n, n  Z; б)  /2;  -arccos(0,25);  +arccos(0,25)

Источник

Отбор корней в тригонометрическом уравнение

Решение тригонометрических уравнений на промежутке

Ход урока.

1. Актуализация знаний.

Как решать задание 13

О чем задача?

Как решать?

Шаг 1. Найдите область определения

Шаг 2. Приведите уравнение к виду простейших тригонометрических уравнений

Шаг 3. Решите простейшие тригонометрические уравнения

Шаг 4. Выберите корни, принадлежащие отрезку, данному в условии

Лучшие онлайн-курсы для подготовки к ЕГЭ

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Тригонометрические уравнения»

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Не пропустите также: