Загрузить PDF
Загрузить PDF
Множество значений (область значений) функции — все значения, которые принимает функция в ее области определения. Другими словами, это те значения у, которые вы получаете при подстановке всех возможных значений х. Все возможные значения х и называются областью определения функции. Выполните следующие действия для нахождения множества значений функции.
-
1
Запишите функцию. Например: f(x) = 3x2 + 6x -2. Подставив x в уравнение, мы сможем найти значение y. Эта квадратичная функция, и ее график — парабола.
-
2
Найдите вершину параболы. Если вам дана линейная функция или любая другая с переменной в нечетной степени, например, f(x) = 6x3+2x + 7, пропустите этот шаг. Но если вам дана квадратичная функция или любая другая с переменной х в четной степени, нужно найти вершину графика этой функции. Для этого используйте формулу х=-b/2a. В функции 3x2 + 6x -2 a = 3, b = 6, c = -2. Вычисляем: х = -6/(2*3)= -1.
- Теперь подставьте х= -1 в функцию, чтобы найти у. f(-1) = 3*(-1)2 + 6*(-1) -2 = 3 — 6 -2 = -5.
- Координаты вершины параболы (-1,-5). Нанесите ее на координатную плоскость. Точка лежит в третьем квадранте координатной плоскости.
-
3
Найдите еще несколько точек на графике. Для этого подставьте в функцию несколько других значений х. Так как член x2 положительный, то парабола будет направлена вверх. Для подстраховки подставим в функцию несколько значений x, чтобы узнать, какие значения y они дают.
- f(-2) = 3(-2)2 + 6(-2) -2 = -2. первая точка на параболе (-2, -2)
- f(0) = 3(0)2 + 6(0) -2 = -2. Вторая точка на параболе (0,-2)
- f(1) = 3(1)2 + 6(1) -2 = 7. Третья точка на параболе (1, 7).
-
4
Найдите множество значений функции на графике. Найдите наименьшее значение у на графике. Эта вершина параболы, где у=-5. Так как парабола лежит выше вершины, то множество значений функции y ≥ -5.
Реклама
-
1
Найдите минимум функции. Вычислите наименьшее значение у. Допустим, минимум функции у=-3. Это значение может становиться все меньше и меньше, вплоть до бесконечности, так что минимум функции не имеет заданной минимальной точки.
-
2
Найдите максимум функции. Допустим, максимум функции у= 10. Как и в случае с минимумом, максимум функции не имеет заданной максимальной точки.
-
3
Запишите множество значений. Таким образом, множество значений функции лежит в диапазоне от -3 до +10. Запишите множество значений функции как: -3 ≤ f(x) ≤ 10
- Но, допустим, минимум функции у=-3, а ее максимум — бесконечность (график функции уходит бесконечно вверх). Тогда множество значений функции: f(x) ≥ -3.
- С другой стороны, если максимум функции у=10, а минимум — бесконечность (график функции уходит бесконечно вниз), то множество значений функции: f(x) ≤ 10.
Реклама
-
1
Запишите множество координат. Из множества координат можно определить его область значения и область определения. Допустим, дано множество координат: {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)}.[1]
-
2
Перечислите значения у. Чтобы найти область значений множества, просто запишите все значения у: {-3, 6, -1, 6, 3}.[2]
-
3
Удалите все повторяющиеся значения у. В нашем примере удалите «6»: {-3, -1, 6, 3}.[3]
-
4
Запишите область значений в порядке возрастания. Областью значений множества координат {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} будет {-3, -1, 3, 6}.[4]
-
5
Убедитесь, что множество координат дано для функции. Чтобы это было так, каждому одному значению х должно соответствовать одно значение у. Например, множество координат {(2, 3) (2, 4) (6, 9)} дано не для функции, потому что одному значению х=2 соответствуют два разных значения у: у=3 и у=4.[5]
Реклама
-
1
Прочитайте задачу. «Ольга продает билеты в театр по 500 рублей за билет. Общая вырученная сумма за проданные билеты является функцией от количества проданных билетов. Какова область значений этой функции?»
-
2
Запишите задачу как функцию. В этом случае М — общая вырученная сумма за проданные билеты, а t — количество проданных билетов. Так как один билет стоит 500 рублей, надо умножить количество проданных билетов на 500, чтобы найти вырученную сумму. Таким образом, функция может быть записана в виде M(t) = 500t.
- Например, если она продаст 2 билета, нужно умножить 2 на 500 — в итоге получим 1000 рублей, вырученных за проданные билеты.
-
3
Найдите область определения. Для нахождения области значений вы должны сначала найти область определения. Это все возможные значения t. В нашем примере Ольга может продать 0 или больше билетов, — она не может продать отрицательное число билетов. Поскольку мы не знаем количество мест в театре, можно предположить, что теоретически она может продать бесконечное число билетов. И она может продавать только целые билеты (она не может продать, например, 1/2 билета). Таким образом, область определения функции t = любое неотрицательное целое число.
-
4
Найдите область значений. Это возможное количество денег, которые Ольга выручит от продажи билетов. Если вы знаете, что область определения функции — любое неотрицательное целое число, а функция имеет вид: М(t) = 5t, то вы можете найти вырученную сумму, подставив в функцию любое неотрицательное целое число (вместо t). Например, если она продаст 5 билетов, то М(5) = 5*500 = 2500 рублей. Если она продаст 100 билетов, то М(100) = 500 х 100 = 50000 рублей. Таким образом, область значений функции — любые неотрицательные целые числа, кратные пятистам.
- Это означает, что любое неотрицательное целое число, которое делится на 500, является значением у (вырученная сумма) нашей функции.
Реклама
Советы
- В более сложных случаях лучше сначала чертить график, используя область определения, и только потом находить область значений.
- Посмотрите, можете ли вы найти обратную функцию. Область определения обратной функции равна области значений исходной функции.
- Проверьте, повторяется ли функция. Любая функция, которая повторяется вдоль оси x, будет иметь ту же область значений для всей функции. Например, область значений для f(x) = sin(x) будет составлять от -1 до 1.
Реклама
Об этой статье
Эту страницу просматривали 455 739 раз.
Была ли эта статья полезной?
subjects:mathematics:множество_значений_функции
Содержание
Математика ( Справочник )
-
-
Множество значений функции
-
Нахождение множества значений функции
Обозначения
-
D(f) — те значения, которые может принимать аргумент, т.е. область определения функции.
-
E(f) — те значения, которые может принимать функция, т.е. множество значений функции.
Способы нахождения областей значений функций.
-
последовательное нахождение значений сложных аргументов функции;
-
метод оценок/границ;
-
использование свойств непрерывности и монотонности функции;
-
использование производной;
-
использование наибольшего и наименьшего значений функции;
-
графический метод;
-
метод введения параметра;
-
метод обратной функции.
Рассмотрим некоторые из них.
Используя производную
Общий подход к нахождению множества значений непрерывной функции f(x) заключается в нахождении наибольшего и наименьшего значения функции f(x) в области ее определения (или в доказательстве того, что одно из них или оба не существуют).
В случае, если нужно найти множества значений функции на отрезке:
-
найти производную данной функции f ‘(x);
-
найти критические точки функции f(x) и выбрать те из них, которые принадлежат данному отрезку;
-
вычислить значения функции на концах отрезка и в выбранных критических точках;
-
среди найденных значений выбрать наименьшее и наибольшее значения;
-
Множество значений функции заключить между этими значениями.
Если областью определения функции является интервал, то используется та же схема, но вместо значений на концах используются пределы функции при стремлении аргумента к концам интервала. Значения пределов из не входят в множество значений.
Метод границ/оценок
Для нахождения множества значений функции сначала находят множество значений аргумента, а затем отыскивают соответствующие наименьше и наибольшее значения функции функции. Используя неравенства — определяют границы.
Суть состоит в оценке непрерывной функции снизу и сверху и в доказательстве достижения функцией нижней и верхней границы оценок. При этом совпадение множества значений функции с промежутком от нижней границы оценки до верхней обуславливается непрерывностью функции и отсутствием у неё других значений.
Свойства непрерывной функции
Другой вариант заключается в преобразовании функции в непрерывную монотонную, тогда используя свойства неравенств оценивают множество значений вновь полученной функции.
Последовательное нахождение значений сложных аргументов функции
Основан на последовательном отыскании множества значений промежуточных функций, из которых составлена функция
Области значений основных элементарных функций
| Функция | Множество значений |
|---|---|
| $y = kx+ b$ | E(y) = (-∞;+∞) |
| $y = x^{2n}$ | E(y) = [0;+∞) |
| $y = x^{2n +1}$ | E(y) = (-∞;+∞) |
| $y = k/x$ | E(y) = (-∞;0)u(0;+∞) |
| $y = x^{frac{1}{2n}}$ | E(y) = [0;+∞) |
| $y = x^{frac{1}{2n+1}}$ | E(y) = (-∞;+∞) |
| $y = a^{x}$ | E(y) = (0;+∞) |
| $y = log_{a}{x}$ | E(y) = (-∞;+∞) |
| $y = sin{x}$ | E(y) = [-1;1] |
| $y = cos{x}$ | E(y) = [-1;1] |
| $y = {rm tg}, x$ | E(y) = (-∞;+∞) |
| $y = {rm ctg}, x$ | E(y) = (-∞;+∞) |
| $y = arcsin{x}$ | E(y) = [-π/2; π/2] |
| $y = arccos{x}$ | E(y) = [0; π] |
| $y = {rm arctg}, x$ | E(y) = (-π/2; π/2) |
| $y = {rm arcctg}, x$ | E(y) = (0; π) |
Примеры
Найдите множество значений функции:
Используя производную
НЕ используя производную
Найдите наибольшее и наименьшее значения функции:
$f(x)=sin^{2}{x}+cos{x}-frac{1}{2}$
Используя метод границ/оценок
$y=5-4sin{x}$
$y=cos{7x}+5cos{x}$
$f(x)=1+2sin^{2}{x}$
$$
\ -1leqsin{x}leq 1
\ 0leqsin^{2}{x}leq 1
\ 0leq2sin^{2}{x}leq 2
\ 1leq1+2sin^{2}{x}leq 3
$$
Ответ: E(f) = [1; 3].
$f(x)=3-2^{3+{rm tg}^{2}, x}$
$$
\ -infty < {rm tg}, x < +infty
\ 0 leq {rm tg}^{2}, x < +infty
\ 3 leq 3+{rm tg}^{2}, x < +infty
\ 2^{3} leq 2^{3+{rm tg}^{2}, x} < +infty
\ -infty < -2^{3+{rm tg}^{2}, x} leq -8
\ -infty < 3-2^{3+{rm tg}^{2}, x} leq -5
$$
Ответ: E(f) = (–∞; -5].
$f(x)=2+sqrt{16-lg^{2}{x}}$
$$
\ -infty < lg{x} < +infty
\ 0 leq lg^{2}{x} < +infty
\ -infty < -lg^{2}{x} leq 0
\ -infty < 16-lg^{2}{x} leq 16
\ 0 leq sqrt{16-lg^{2}{x}} leq 4
\ 2 leq 2+sqrt{16-lg^{2}{x}} leq 6
$$
Ответ: E(f) = [2; 6].
$f(x)=sqrt{2-x}+sqrt{2+x}$
$y=sin{x}+cos{x}$
Используя непрерывную функцию
Иные
Использованная литература
Статьи:
-
Область значения функций в задачах ЕГЭ, Минюк Ирина Борисовна
-
Советы по нахождению множества значений функции, Беляева И., Федорова С.
-
Нахождение множества значений функции
-
Как решать задачи по математике на вступительных экзаменах, И.И.Мельников, И.Н.Сергеев
Рекомендуем
· Последние изменения: 2018/09/19 21:14 —
¶
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Функцией, заданной на множестве $X$ и принимающей значения из множества $Y$ называют некую закономерность, по которой каждому элементу из множества $X$ соответствует лишь один и только один элемент из множества $Y$.
Из этого определения следует, что множество (область) значений функции — это те значения функции $y(x)$, которые она может принимать соответственно области её определения. Теперь перейдём к следующему определению.
Определение 2
Область (множество) значений функции на некотором рассматриваемом отрезке — это интервал значений, которые функция принимает на этом рассматриваемом отрезке.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Чаще всего в учебной литературе встречается термин «множество значений функции». Кратко его обозначают $E(f)$.
Как определить область значения функции
Для определения множества значений функции пользуются графическим методом, методом поисков минимума и максимума, вычислением производной и другими.
Определение множества значений функции графическим методом
Графический метод подразумевает построение графика функции и изучение этого графика. Этот метод наиболее удобен, если не известна какая-либо закономерность изменения функции $f(x)$, а есть только набор произвольных точек или собственно сам график.
Пример 1
Рисунок 1. Определение множества значений функции графическим методом
На данном рисунке область значений функции $y=f(x)$ равна $E(y)=3$, так как на протяжении всего отрезка функция $y$ не меняет своего значения и всегда равна $3$, тогда как область определения функции $D(y)=[0;3.5]$.
Скобки в данном случае для области определения функции необходимо использовать квадратные, так как обе точки закрашены, то есть включены в отрезок. В случае если точки не закрашены, они не включаются в отрезок и тогда применяются круглые скобки.
«Множество значений функции» 👇
Метод нахождения области значения функции через производную
Метод нахождения области значения функции через производную состоит в том, чтобы сначала оценить область её определения (то есть определить те значения, которые может принимать аргумент $x$, а затем осуществить процедуру нахождения самой производной. После этого осуществляют поиск значений $x$, при которых производная функции равна нулю и при которых производная не существует.
Рассмотрим пример нахождения области значений функции через производную.
Пример 2
Дана функция $f(x)=sqrt{16-x^2}$. Найдите область её значений.
Сначала определяем, какие значения может принимать $x$ для существования функции.
При значении $x^2>16$ под корнем получается отрицательное число, а это значит, что область определения функции от $[-4;4]$ включительно.
Теперь найдём производную функции:
$(sqrt{16-x^2})’=-frac{x}{sqrt{16-x^2}}$
Если в знаменателе производной нуль, то производной не существует, в данном случае это условие выполняется при $x=±4$.
Приравниваем производную к нулю и находим значения $x$. Производная данной функции принимает нулевое значение при $x=0$. Теперь подставляем найденные значения производной в нашу функцию, и получаем, что наименьшее значение функции — это $f(4)$ и $f(-4)$, при этих значениях функция равна нулю, а наибольшее значение $f(x)$ — при $x=0$, в этой точке функция равна $16$.
Метод поиска минимума и максимума
Метод поиска минимума и максимума основан на том, чтобы найти максимальное и и минимальное значение, которые функция принимает на изучаемой области.
Пример 3
Определите область значений функции:
$y=6-4sinx$
Проанализируем данную функцию. Так как минимальное значение синуса равно минус единице, а а максимальное — единице, то подставив эти значения получаем, что $max(f(x))=10$ при $x=frac{3π}{2}$, а минимум $min(f(x))=2$ при $x=frac{π}{2}$. Следовательно, множество значений, которые может принимать данная функция — $E(x)=[2;10]$.
Разница между областью значения и областью определения функции
Стоит обратить внимание, что область значений функции — не одно и то же с термином «область определения функции».
Определение 3
Область определения функции $D(y)$ — это диапазон таких значений переменной $x$, при которых существует функция $y(x)$.
Например, рассмотрим функцию $y(x)=x^2$. В данном случае область определения этой функции будет множеством вещественных (действительных) чисел $mathbb{R}$, а сама функция будет принимать значения только положительных действительных чисел $mathbb{R}^+$, так как вещественное число, возведённое в квадрат, не может давать отрицательное значение. То есть, в этом примере множество значений функции — это множество положительных вещественных чисел $mathbb{R}^+$.
Также имеют место случаи, когда область определения функции совпадает с областью значений.
В качестве иллюстрации можно рассмотреть функцию $y(x)=2x$. За аргумент $x$ данная функция может принимать любое действительное число из множества $mathbb{R}$, а значения, которые будет принимать сама функция — это удвоенные числа из множества всех действительных чисел. То есть, в данном случае областью значений $E(y)$ будет также всё множество вещественных чисел $mathbb{R}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
3
6
Risolvere per ?
cos(x)=1/2
7
Risolvere per x
sin(x)=-1/2
8
Преобразовать из градусов в радианы
225
9
Risolvere per ?
cos(x)=( квадратный корень из 2)/2
10
Risolvere per x
cos(x)=( квадратный корень из 3)/2
11
Risolvere per x
sin(x)=( квадратный корень из 3)/2
12
График
g(x)=3/4* корень пятой степени из x
13
Найти центр и радиус
x^2+y^2=9
14
Преобразовать из градусов в радианы
120 град. 2+n-72)=1/(n+9)
Как найти домен и диапазон функции?
Домен и диапазон функции — это набор всех возможных входных и выходных данных функции соответственно. Здесь вы познакомитесь с областью определения и диапазоном функции, а также с тем, как ее вычислить.
Область определения и область значений любой функции можно найти алгебраически или графически.
Пошаговое руководство по поиску области и диапазона
Область и диапазон определены для отношения и представляют собой наборы всех (x)-координат и всех (y)-координат упорядоченных пар соответственно. Например, если соотношение (R = {(1, 2), (2, 2), (3, 3), (4, 3)}), то:
- Область (=) множество всех (x)-координат (= {1, 2, 3, 4})
- Диапазон (=) множество всех (y) )-координаты (= {2, 3})
Область определения и область значений функции
Область определения и область значений функции являются компонентами функции.
(color{blue}{Domain→ Function →Range})
Если существует функция (f: A →B) такая, что каждый элемент (A) отображается в элементы (B), то (A) — домен, а (B) — со-домен. Образ элемента (a) относительно отношения (R) задается выражением (b), где ((a,b) ∈ R). Областью действия функции является набор изображений. Область определения и область значений функции в общем случае обозначаются следующим образом: }).
Область определения и область значений этой функции (f(x) = 2x) задаются как область определения (D = {x ∈ N }) , область значений (R = {(y): y = 2x} ).
Домен функции
Домен функции относится ко «всем значениям», которые входят в функцию. Вот общие формулы, используемые для нахождения области определения различных типов функций. Здесь R — множество всех действительных чисел:
- Область определения любой полиномиальной (линейной, квадратичной, кубической и т.
д.) функции равна (color{blue}{R}).
- Областью определения квадратного корня функции (sqrt{x}) является (color{blue}{x≥0}).
- Областью определения экспоненциальной функции является (color{blue}{R}).
- Областью определения логарифмической функции является (color{blue}{x>0}).
- Чтобы найти область определения рациональной функции (y = f(x)), установите (color{blue}{знаменатель ≠ 0}).
Диапазон функции
Диапазон функции – это набор всех ее выходов. Пример. Рассмотрим функцию (f: A→ B), где (f(x) = 2x) и каждое из (A) и (B =) {множество натуральных чисел}. Здесь мы говорим, что (A) является доменом, а (B) является содоменом. Затем выход этой функции становится диапазоном. Диапазон (=) {множество четных натуральных чисел}. Элементы домена называются прообразами, а отображаемые элементы совместного домена называются изображениями.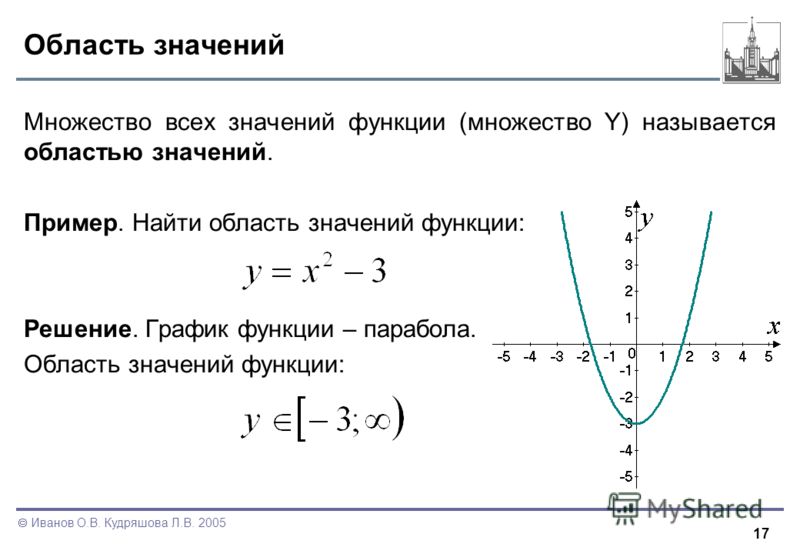
Область определения и диапазон тригонометрических функций
Посмотрите на график функции (sin) и (cos). Обратите внимание, что значение функций колеблется между (-1) и (1) и определено для всех действительных чисел.
Таким образом, для каждой из функций (sin) и (cos):
- Домен: Домен функций — это множество (color{blue}{R}).
- Диапазон: Диапазон функций: (color{blue}{[-1, 1]}).
Область определения и диапазон всех тригонометрических функций показаны ниже:
Область определения и диапазон функции абсолютного значения
Функция (y=|ax+b|) определена для всех действительных чисел. Итак, область определения функции абсолютного значения — это множество всех действительных чисел. Абсолютное значение числа всегда дает неотрицательное значение. Таким образом, областью значений функции абсолютного значения формы (y= |ax+b|) является (y ∈ R | y ≥ 0).
Область и диапазон функции абсолютного значения задаются следующим образом:
- Домен (color{blue}{= R})
- Диапазон (color{blue}{= [0, ∞)})
Домен и диапазон квадрата корневая функция
Функция (y=sqrt{left(ax+bright)}) определена только для (x ≥ -frac{b}{a}). Итак, область определения функции квадратного корня — это набор всех действительных чисел, больших или равных (frac{b}{a}).
Область определения и диапазон функции квадратного корня задаются следующим образом:
- Домен (color{blue}{= [-frac{b}{a},∞)})
- Диапазон (color{blue}{= [0,∞)})
Графики домена и диапазона
Другой способ определить домен и диапазон функций — использовать графики. Домен относится к набору возможных входных значений. Домен графика содержит все входные значения, показанные на оси (x). Диапазон представляет собой набор возможных выходных значений, показанных на оси (y). Самый простой способ найти диапазон функции — построить ее и найти (y)-значения, охватываемые графиком.
Чтобы найти диапазон квадратичной функции, достаточно посмотреть, имеет ли она максимальное или минимальное значение. Максимальное/минимальное значение квадратичной функции есть (y)-координата ее вершины.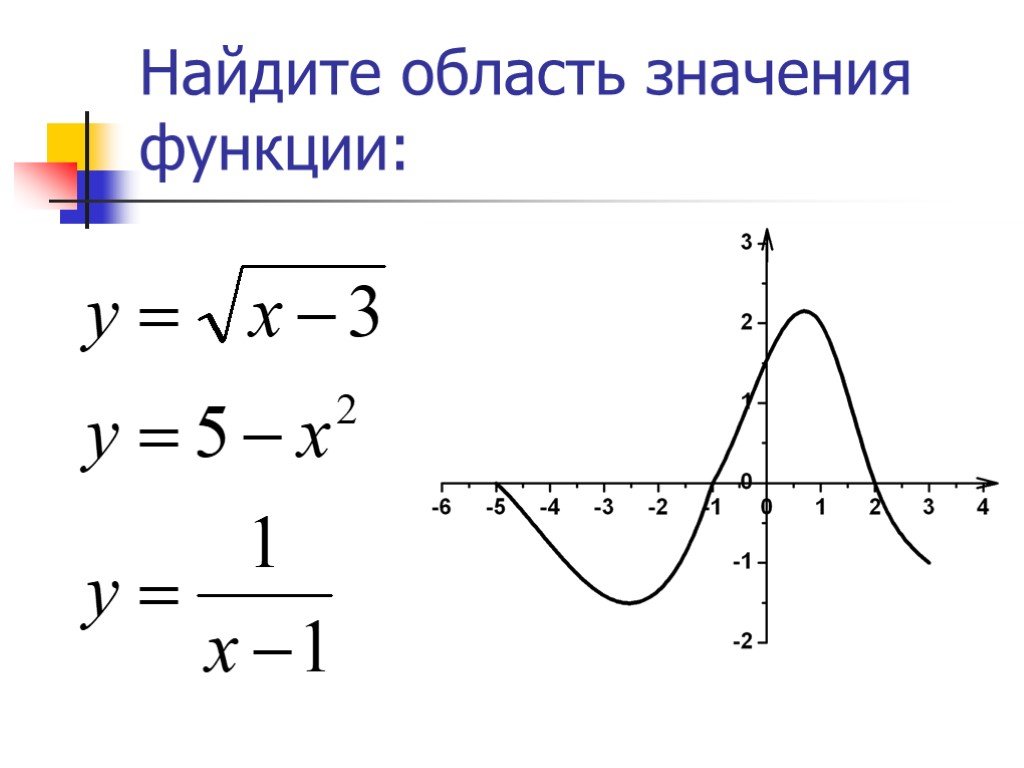
Домен обозначается всеми значениями слева направо по оси (x), а диапазон определяется размахом графика сверху вниз.
Поиск домена и диапазона — Пример 1:
Найдите область определения и область значений функции (y=2-sqrt{left(-3x+2right)}).
Решение:
Функция извлечения квадратного корня определяется только тогда, когда значение внутри нее является неотрицательным числом. Итак, для домена
(-3x+2≥0)
(-3x≥-2)
(x≤frac{2}{3})
Мы знаем, что функция квадратного корня всегда дает неотрицательное значение. Итак, для диапазона
(sqrt{left(-3x+2right)}ge 0)
(-sqrt{left(-3x+2right)}le :0) 92})
- (color{blue}{D= влево(-infty :,3вправо)чашка влево(3,infty :вправо), R=влево(-infty ,-1вправо)чашка :влево(-1 ,infty right)})
- (color{blue}{D=left(-infty ,infty right), R=left(4,infty right)})
- (color{blue}{D=left(-infty ,infty right), R=[0,infty)})
- (color{blue}{D=left( -infty ,infty right), R=(-infty,4]})
- (color{blue}{D=left(-infty :,0right)cup влево(0,infty :вправо), R=влево(-infty :,0вправо)чашка влево(0,infty :вправо)})
Как найти диапазон набора данных
Опубликован в
11 сентября 2020 г.
к
Прита Бхандари.
Отредактировано
11 ноября 2022 г.
В статистике диапазон — это разброс ваших данных от самого низкого до самого высокого значения в распределении. Это широко используемая мера изменчивости.
Наряду с мерами центральной тенденции меры изменчивости дают вам описательную статистику для обобщения вашего набора данных.
Диапазон вычисляется путем вычитания наименьшего значения из наибольшего. В то время как большой диапазон означает высокую изменчивость, малый диапазон означает низкую изменчивость в распределении.
Содержание
- Расчет диапазона
- Насколько полезен диапазон?
- Часто задаваемые вопросы об ассортименте
Рассчитать диапазон
Формула для расчета диапазона:
- R = диапазон
- H = наибольшее значение
- L = наименьшее значение
Диапазон — это самая простая для вычисления мера изменчивости.
- Упорядочить все значения в вашем наборе данных от меньшего к большему.
- Вычтите наименьшее значение из наибольшего.
Этот процесс одинаков независимо от того, являются ли ваши значения положительными или отрицательными, целыми числами или дробями.
Пример диапазонаВаш набор данных — возраст 8 участников.
| Участник | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Возраст | 37 | 19 | 31 | 29 | 21 | 26 | 33 | 36 |
Сначала расположите значения в порядке убывания, чтобы определить наименьшее значение ( L ) и наибольшее значение ( H ).
| Возраст | 19 | 21 | 26 | 29 | 31 | 33 | 36 | 37 |
|---|
Затем вычтите наименьшее значение из наибольшего.
П = В –
Л
Р = 37 – 19 = 18
Диапазон нашего набора данных равен 18 лет .
Насколько полезен диапазон?
Диапазон обычно дает вам хороший индикатор изменчивости, когда у вас есть распределение без экстремальных значений. В сочетании с мерами центральной тенденции диапазон может рассказать вам о размахе распределения.
Но диапазон может ввести в заблуждение, если в вашем наборе данных есть выбросы. Одно экстремальное значение в данных даст вам совершенно другой диапазон.
Пример диапазона со значением outlierOne в вашем наборе данных заменяется выбросом.
| Возраст | 19 | 21 | 26 | 29 | 31 | 33 | 36 | 61 |
|---|
Используя тот же расчет, на этот раз мы получаем совсем другой результат:
П = В
– Л
Ч = 61 – 19 = 42
С учетом выброса наш диапазон теперь равен 42 года .
В приведенном выше примере диапазон указывает на гораздо большую изменчивость данных, чем есть на самом деле. Хотя у нас большой диапазон, большинство значений на самом деле сгруппированы вокруг четкой середины.
Поскольку используются только два числа, на диапазон легко влияют выбросы. Он не может сам по себе сказать вам о форме частотного распределения значений.
Примечание. Чтобы получить четкое представление о изменчивости ваших данных, диапазон лучше всего использовать в сочетании с другими показателями изменчивости, такими как межквартильный размах и стандартное отклонение.
Что может сделать корректура для вашей статьи?
Редакторы Scribbr не только исправляют грамматические и орфографические ошибки, но и улучшают качество письма, следя за тем, чтобы в статье не было неясных выражений, избыточных слов и неудобных формулировок.
См. пример редактирования
Часто задаваемые вопросы об ассортименте
- Процитировать эту статью Scribbr
Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.
Бхандари, П.
(2022, 11 ноября). Как найти диапазон набора данных | Формула и примеры. Скриббр.
Проверено 19 декабря 2022 г.,
с https://www.scribbr.com/statistics/range/
Процитировать эту статью
Полезна ли эта статья?
Вы уже проголосовали. Спасибо 🙂
Ваш голос сохранен 🙂
Обработка вашего голоса.
Множество значений функции
Онлайн калькулятор поможет найти множество значений (область значений) функции — все значения, которые принимает функция в ее области определения. Другими словами, это те значения у, которые получаются при подстановке всех возможных значений х.
Теперь рассмотрим следующий вопрос: Как найти множество значений функции? Решение этой задачи с помощью онлайн калькулятора не составит труда, просто введите нужную функцию и получите ответ.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция «И» ∧: &&
дизъюнкция «ИЛИ» ∨: ||
отрицание «НЕ» ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»




















 д.) функции равна (color{blue}{R}).
д.) функции равна (color{blue}{R}). 

