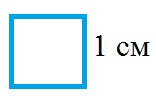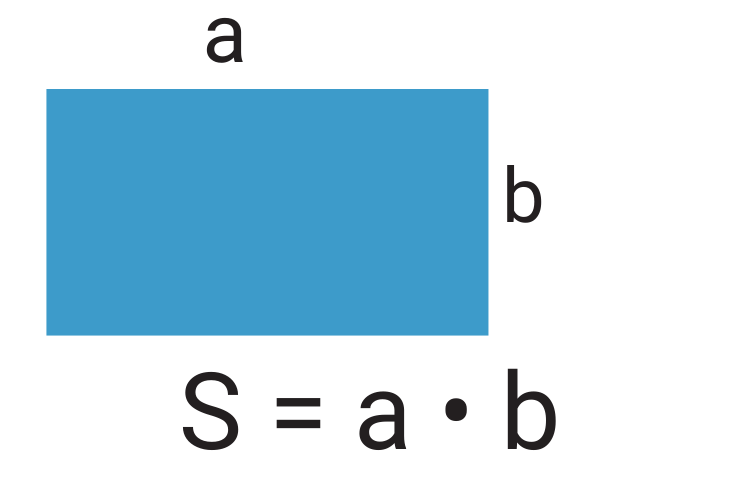Содержание:
- § 1 Формула нахождения площади прямоугольника
- § 2 Формула нахождения площади квадрата
§ 1 Формула нахождения площади прямоугольника
В этом уроке рассмотрим такие понятия как площадь фигуры и формулы нахождения площади прямоугольника и квадрата.
Давайте начертим квадрат со стороной 1 см.
Площадь одного такого квадратика называют квадратным сантиметром.
Пишут так:
один сантиметр в квадрате (1 см2).
Соответственно можем сделать вывод, что если какую – либо фигуру можно разбить на несколько таких квадратов, например, р квадратов, то ее площадь равна р см2.
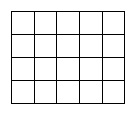
Перед вами рисунок, на котором изображен прямоугольник.
Он состоит из 4 полос, каждая из которых разбита на 5 квадратов со стороной 1 см.
Т.е. весь прямоугольник состоит из 20 квадратов (мы 4 умножили на 5, получили 20).
Значит площадь такого прямоугольника равна 20 см2.
Таким образом, получили правило:
Чтобы найти площадь прямоугольника, надо умножить его длину на ширину.
Это правило можно записать в виде формулы.
Для этого обозначим площадь прямоугольника буквой S, кстати площади всех фигур принято обозначать этой буквой, длину прямоугольника буквой a, ширину – буквой b.
Получаем формулу площади прямоугольника: S равно а умножить на b(S = аb).
§ 2 Формула нахождения площади квадрата
Теперь давайте рассмотрим следующую фигуру – квадрат, это тоже прямоугольник, но у него все стороны равны. Так как квадрат является прямоугольником, то воспользуемся формулой площади прямоугольника (S = аb). Но в случае квадрата b будет равно а, т.е. площадь равна а умножить на а, или принято записывать а в квадрате, значит: (S = а2). Получили еще одну формулу – формулу площади квадрата.
Начертим квадрат со стороной 5 см и найдем его площадь.
Площадь квадрата со стороной 5 см равна 5 в квадрате, т.е. 25 см2.
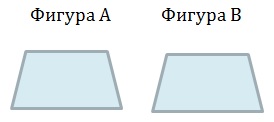
Давайте рассмотрим две фигуры:
Как узнать равны ли эти фигуры?
Это легко проверить, если выполнить наложение, т.е. одну фигуру наложить на другую. Если они полностью совместятся или совпадут, то они равные.
Таким образом, сформулируем правило:
Две фигуры называются равными, если они совпадут при наложении.
А как вы думаете, равны ли их площади и периметры? Конечно, да! Площади равных фигур равны. Периметры равных фигур равны. Но не всегда выполняется наоборот.
Например, прямоугольник со сторонами 16 и 4 см имеет площадь 64 см2 и квадрат со стороной 8 см тоже имеет площадь 64 см2, но эти фигуры не равны между собой.
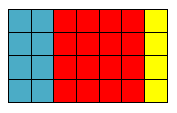
Давайте построим прямоугольник ABCD со сторонами 7 см и 4 см.
Разделим его на несколько частей.
Первая часть состоит из 8 см2, вторая часть – из 16 см2, третья часть – из 4 см2.
Если сложить все эти части, получим 8 + 16 + 4 = 28. Т.е. сумма площадей всех частей также равна 28 см2.
Итак, можно сделать вывод, что площадь всей фигуры равна сумме площадей ее частей.
Таким образом, на этом уроке мы рассмотрели такие понятия как площадь фигуры и формулы нахождения площади прямоугольника и квадрата.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013.
- Дидактические материалы по математике 5 класс. Автор — Попов М.А. – 2013.
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. – 2014.
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010.
- Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. – 2012.
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений/И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009.
Сегодня клоун Бим и дрессировщик Бом вместе с ребятами применяют на практике знания, как найти площадь для прямоугольника с разными сторонами.
Площадь фигуры — это размер куска плоскости внутри границ фигуры, измеренный в единицах измерения площади.
Единицы измерения площади — это площади квадратов, у которых стороны равны либо единице измерения длины, либо 10 м, либо 100 м: 1 кв.мм (квадрат со стороной 1 мм), 1 кв.см (квадрат со стороной 1 см), 1 кв.дм (квадрат со стороной 1 дм), 1 кв.м (квадрат со стороной 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м).
Определение. Площадь прямоугольника — это размер куска плоскости, лежащего внутри границ прямоугольника.
Правило. Для вычисления площади прямоугольника (с разными сторонами), если известны длины его сторон, достаточно перемножить длины двух прилежащих сторон. Результат записывается в единицах измерения площади. При необходимости результат укрупняют или раздробляют (см. Статью о переводе из одной единицы измерения площади в другую).
Площадь — это?
Площадь любого куска плоскости (фигуры)— это размер этого куска плоскости (куска плоскости внутри границ фигуры), измеренный в единицах измерения площади.
Бим и Бом пришли на работу в цирк пораньше. Бим зашел к Бому в гримерку.
— Привет, Бим!
— Привет, Бом!
— У нашей Буфетчицы сегодня день рождения. Я купил очень вкусных конфет, только вот упаковка видишь какая длинная. У тебя есть какая-нибудь красивая коробка, куда мы можем сложить конфеты и подарить Буфетчице?
— У меня много разных красивых коробочек. Но как мы узнаем, какая из них подходит, чтобы вместились все конфеты и было красиво?
Бом и Бим задумались.
— Ура!!! Придумал, — нашелся Бим. — У каждой коробки есть плоское донышко. Давай вычислим площади донышек у каждой коробки, то есть измерим площадь донышек в единицах измерения площади — квадратных сантиметрах.
— Тогда найдем, какая коробка подходит больше всего, — подхватил Бом. — Начнем с упаковки, где лежат конфеты. У упаковки донышко в виде прямоугольника. Значит, достаточно измерить длины короткой и длинной стороны.
— А чем будем измерять? — задумался Бим.
— Сейчас поищу, — ответил Бом. — Вот у меня есть сантиметр, линейка и листочек в клеточку.
— Дай, пожалуйста, мне листочек в клеточку, — попросил Бом. — Я проверю, что донышко упаковки — прямоугольник.
Как найти площадь прямоугольника с разными сторонами. Площадь прямоугольника — это?
Определение. Площадь прямоугольника — это размер куска плоскости, лежащего внутри границ прямоугольника.
Правило. Для вычисления площади прямоугольника, если известны длины его сторон, достаточно перемножить длины двух прилежащих сторон. Результат записывается в единицах измерения площади. При необходимости результат можно укрупнить или раздробить (см. Статью о переводе из одной единицы измерения площади в другую).
Бим приложил листочек к углам донышка упаковки.
— Проверил: у упаковки четыре угла, и все они — прямые. Тогда донышко упаковки — прямоугольник.
Бом начал читать свои записи:
“Площадь прямоугольника — это размер куска плоскости, лежащего внутри границ прямоугольника. Как найти площадь прямоугольника (с разными сторонами), если известны длины его сторон? Достаточно перемножить длины двух прилежащих сторон. Результат записывается в единицах измерения площади”.
— Теперь надо измерить длины двух сторон. Упаковка — длинная, тогда лучше взять сантиметр.
Бим измерил упаковку.
— Короткая сторона 8 см, длинная — 72 см. Вспоминаем, что для вычисления площади прямоугольника надо длину одной стороны умножить на длину прилежащей стороны. Умножаем:
72 х 8 =576 кв.см (см2).
— Сейчас принесу из подсобки коробки, которые у меня есть, — побежал Бом.
И — надо же! — по дороге Бом встретил Олю, Колю и Васю, которые пришли пораньше на представление.
— Ребята, как хорошо, что вы здесь! Идемте, поможете нам с Бимом подобрать Буфетчице на день рождения коробку.
Бом достал из подсобки коробки, и они все вместе вернулись к Биму.
— Ребята, мы с Бимом измерили площадь упаковки конфет, которые мы хотим переложить в более красивую коробку. Красиво сложим и подарим Буфетчице на день рождения, — объяснил Бим.
— Давайте вычислим площадь донышка каждой коробки, — предложил Вася. — В коробку, у которой площадь донышка равна площади донышка упаковки, мы переложим конфеты.
— Как здорово, что Бом принес все коробки, донышки у которых имеют вид прямоугольника! — обрадовался Коля. — Как найти площадь прямоугольника с разными сторонами? Надо измерить длины двух прилежащих сторон в одинаковых единицах измерения длины и их перемножить, — получим площадь прямоугольника в единицах измерения площади. Для коробок удобнее всего измерять длины сторон в сантиметрах, а площадь самих прямоугольников уже будет в квадратных сантиметрах. Оля, давай проверим, что донышки коробок — прямоугольники.
Коля и Оля взяли листочек в клеточку и с помощью него проверили, что у донышек все углы прямые.
Затем Коля, Вася и Оля вооружились листочком в клеточку, линейкой и сантиметровой лентой и измерили в сантиметрах длины прилежащих сторон донышек коробок.
Первым управился Коля:
— У меня большая сторона 36 сантиметров и короткая 16 сантиметров. Получаем площадь моей коробки
36 х 16 = 576 (кв.см).
Следующим был Вася:
— У меня длина коробки 30 см, а ширина — 20 см. Для вычисления площади коробки надо длину умножить на ширину прямоугольника. Получаем:
30 х 20 = 600 (кв.см)
Оля измеряла тщательнее всех, ведь у нее коробка была похожа на квадрат. Но надо было убедиться, точно ли у этой коробки равны обе стороны. Так и оказалось:
— У меня прилежащие стороны одинаковые по длине, обе равны 24 см. Перемножаем длины двух прилежащих сторон, получаем: 24 х 24 = 576 (кв.см).
— Тогда у нас выходят 3 коробки с одинаковыми площадями донышек — у упаковки, — подытожил Бом:
8 х 72 = 576 (кв.см), —
и еще у двух коробок
16 х 36 = 576 (кв.см),
24 х 24 = 576 (кв.см),
а также одна коробка площадью больше, чем у упаковки
30 х 20 = 600 (кв.см).
— Какую же коробку выбрать? — озадаченно спросил Бим.
— Давай возьмем в виде квадрата, посмотрите какая здесь красивая крышка! — решил Бом.
Ребята выложили конфеты из упаковки в коробку.
— Ага, — посмотрел Бом. — получились три ряда. Какая же площадь донышка одного ряда? Длина ряда 24 см, ширина — 8 см. Значит площадь донышка одного ряда равна:
24 х 8 = 192 (кв.см).
Всего три одинаковых ряда
192 х 3 = 576 (кв.см).
Ура! Все совпадает!
Бим, все же, спросил:
— Сейчас мы измеряли площадь в квадратных сантиметрах. А какие еще есть единицы измерения площади?
Единицы измерения площади
Единицы измерения площади — это площадь квадратов, у которых стороны равны либо единице измерения длины, либо 10 м, либо 100 м: 1 кв.мм (квадрат со стороной 1 мм), 1 кв.см (квадрат со стороной 1 см), 1 кв.дм (квадрат со стороной 1 дм), 1 кв.м (квадрат со стороной 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м). (<См. статью “Единицы измерения площади”>)
В каких единицах измерения площади мы можем записать площадь донышка одного ряда? — продолжил вопрос Бим.
Оля ответила сразу:
— Если мы будем укрупнять, то в дециметрах и сантиметрах.
576 кв.см = 5 кв.дм 76 кв.см
— А если мы будем раздроблять — в миллиметрах, — добавил Коля. —
576 кв.см =576 х 100 (кв.мм).
А еще единицы измерения площади 1 кв.м (квадрат со стороною 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м).
— Теперь я подпишу открытку. У меня красивый артистический почерк, — вызвался Бом.
— Хорошо, Бом. А мы с ребятами составим вопросы и ответы на них, — согласился Бим.
— Первый вопрос: Что называется площадью? — начал Вася.
— Второй вопрос: Дайте определение прямоугольника. — продолжил Коля. —
И третий вопрос: Что такое площадь прямоугольника?
— Четвертый вопрос: Как найти площадь прямоугольника (с разными сторонами)? — закончила Оля.
— И еще один, пятый, вопрос: Какие вы знаете единицы измерения площади? — добавил Бим.
Теперь я запишу ответы для проверки, — продолжил клоун:
1. Площадь — это размер куска плоскости внутри фигуры.
2. Прямоугольник — это фигура с 4-мя прямыми углами и с замкнутой границей из четырех отрезков.
3. Площадь прямоугольника — это площадь куска плоскости внутри границ прямоугольника.
4. Как найти площадь прямоугольника? Для нахождения площади прямоугольника перемножаются длины двух прилежащих сторон. Результат записывается в единицах измерения площади.
5. Единицы измерения площади — это площади квадратов, у которых стороны равны либо единице измерения длины, либо 10 м, либо 100 м: 1 кв.мм (квадрат со стороной 1 мм), 1 кв.см (квадрат со стороной 1 см), 1 кв.дм (квадрат со стороной 1 дм), 1 кв.м (квадрат со стороной 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м).
Итог подвел Бом:
— Мы сегодня узнали :
- что такое площадь
- что такое площадь прямоугольника
- как найти площадь прямоугольника
- единицы измерения площади.
Всем спасибо за помощь.
Заключение
Итак, теперь мы знаем ответ на вопрос: Как найти площадь прямоугольника с разными сторонами. А вам приходилось дарить конфеты в коробочках? Как видим, можно, в случае чего, упаковать подарок более изящно, а заодно — и математику повторить.
Идея необычной подачи материала принадлежит замечательному преподавателю математики Стуловой Лилии Валериевне.
Не забудьте оценить наши старания. По желанию подписывайтесь на нас в Яндекс.Дзен и в других социальных сетях!!!)))
Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.
Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.
Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.
S = a ∙ b
S – площадь
a – длина
b – ширина
Задания тренировочного модуля:
1. Заполните пропуски в таблице.
|
а |
5 |
6 |
3 |
|
|
b |
8 |
9 |
||
|
S |
15 |
56 |
24 |
Правильный ответ:
|
а |
5 |
7 |
6 |
3 |
|
b |
3 |
8 |
9 |
8 |
|
S |
15 |
56 |
54 |
24 |
2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.
12 см; 32 см; 24 см2; 32 см2; 24; 12 см2.
Правильный ответ: 32см2.
Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым