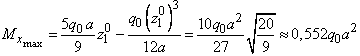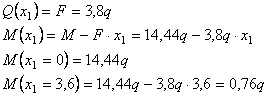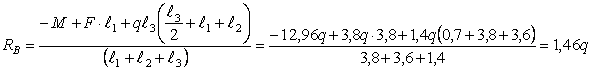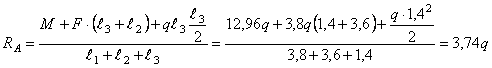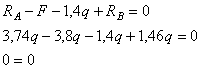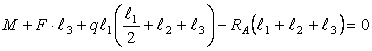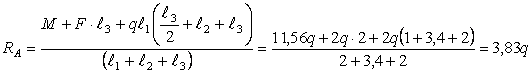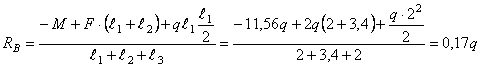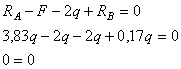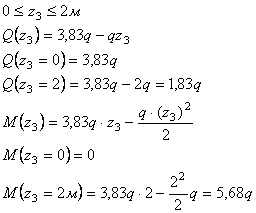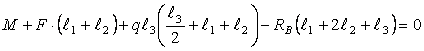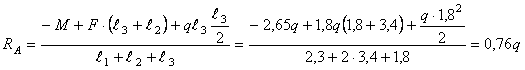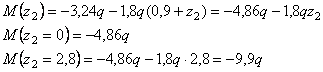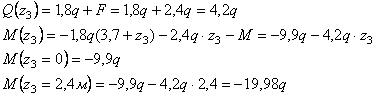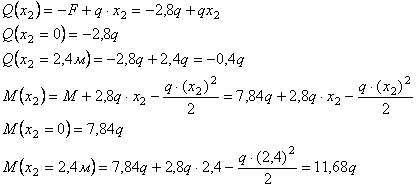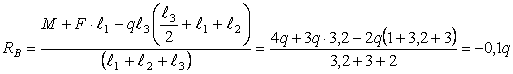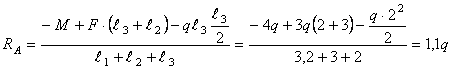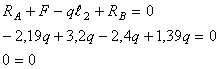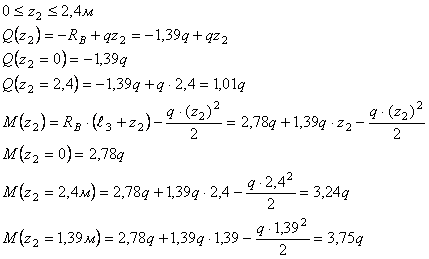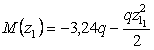Момент экстремума как найти

В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.

В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.

Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.

Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.

Поперечные силы и изгибающие моменты

При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (M_изг).

Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.

Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.

Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!

Обозначения поперечных сил и изгибающих моментов

Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.

Например, если выбрать следующие обозначения для координатных осей:

То, поперечная сила, будет обозначаться, как Q_y (параллельна оси y), а изгибающий момент, как M_x (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Q_y, M_z или Q_z, M_x. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – M_изг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.

Расчётная схема балки

Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:

А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.

К примеру, балка может иметь прямоугольное поперечное сечение:

Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.

Правила знаков для поперечных сил и изгибающих моментов

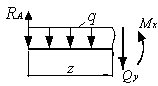
В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).

Расчётная схема

Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и М_изг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).

Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.

Правило знаков для поперечных сил

Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.

А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;

• ПРОТИВ часовой стрелки — учитываем её с «минусом».

Таким образом, для нашего случая, поперечная сила в сечении A будет равна:

Правило знаков для изгибающих моментов

Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.

Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.

Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.

В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.

На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»; 

• нижние волокна, то нужно учесть его с «плюсом».

Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.

Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:

Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:

Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:

Как построить эпюры поперечных сил и изгибающих моментов ?

В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.

Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉

Построение эпюр для консольной балки

В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

Будем рассчитывать балку справа налево.

Рассмотрим первый участок

Обозначим некоторое сечение 1-1 на расстоянии x₁, от свободного торца балки, при этом x₁ будет находиться в диапазоне: 0 ≤ x₁ ≤ 4м.

Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.

Поперечные силы на первом участке

Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:

Как видишь, поперечная сила будет постоянна на первом участке:

Уже можем отразить это на эпюре поперечных сил:

Изгибающие моменты на первом участке

Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:

Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

Откладываем полученные значения:

Расчёт второго участка

Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x₂ от начала участка (0 ≤ x₂ ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

Поперечные силы на втором участке

Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:

Теперь можем показать окончательную эпюру поперечных сил:

Изгибающие моменты на втором участке

Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:

Вычисляем значения на границах второго участка:

Показываем окончательную эпюру изгибащих моментов:

Проверка построенных эпюр

Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.

Определение реакций в жёсткой заделке

Первым делом, нам потребуется определить реакции в заделке:

Расчёт эпюр поперечных сил и изгибающих моментов

Рассчитываем все участки теперь слева направо:

Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.

Эпюра моментов со стороны растянутых или сжатых волокон

По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.

Причем сама эпюра была построенна со стороны растянутых волокон:

Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.

Учёт распределённой нагрузки

Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.

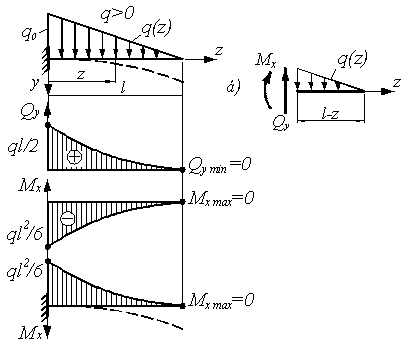
Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:

Определение поперечной силы и изгибающего момента в сечении A

Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.

После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:

Тогда поперечная сила Q_A будет равна:

Изгибающий момент M_{изг, A} будет равен:

Расчёт эпюр поперечных сил и изгибающих моментов

Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:

Уравнение для поперечных сил будет следующее:

Рассчитаем значения на эпюре поперечных сил:

Уравнение для изгибающих моментов будет следующее:

Тогда значения на эпюре будут такими:

На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.

Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:

Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:

Построение эпюр для двухопорной балки

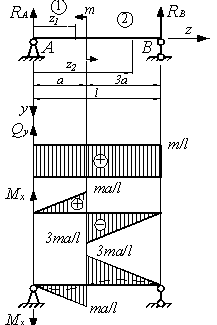
А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:

Определим реакции опор:

Рассчитываем первый участок:

Строим эпюры на первом участке:

Определение экстремума на эпюре моментов

Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.

Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:

Отсюда найти значение координаты:

Затем подставить это значение в уравнение для изгибающих моментов:

Теперь можем указать экстремум на эпюре:

Расчет эпюр на остальных участках

Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:

Определение экстремума:

Оценка правильности построенных эпюр поперечных сил и изгибающих моментов

И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.

Вот несколько признаков, правильно построенных эпюр:

• На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
• На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
• Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
• Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.

Построение
эпюр поперечной силы и изгибающего
момента для балок

Пример
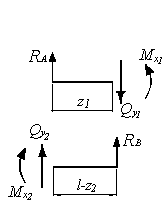
1.

Построить
эпюры внутренних усилий Q_y,
M_x
для балки (см. рис.).

а)
б)

Решение.

1.
Определение опорных реакций

Из
уравнений равновесия

находим

.

2.
Определение Q_y,
M_x
методом сечений (рис. б) и построение
эпюр

Из
уравнений равновесия отсеченных частей
балки находим

По
полученным значениям строим эпюры (рис.
а). Отметим, что сосредоточенный момент
не повлиял на характер эпюры Q_y.
На эпюре моментов сосредоточенный
момент вызвал скачок на величину этого
момента. Наклон прямых на эпюре моментов
одинаков, что соответствует правилу
Журавского.

Пример
2.

Построить
эпюры Q_y,
M_x
для балки (см. рис. а).

а)
б)

Решение.

1.
Определение опорных реакций

Из
уравнений равновесия

находим

.

2.
Определение Q_y,
M_x
методом сечения и построение эпюр

Из
уравнения равновесия отсеченной части
балки (рис. б) находим

.

Как
видно, график-эпюра

–
прямая линия, а

– квадратичная парабола. Полагая


и

,
находим значения усилий в этих точках.

При

значения внутренних усилий


а при

:



Отметим, что в шарнирах моменты всегда
равны нулю. На эпюре

при


перерезывающая сила

.
Это признак экстремума на эпюре моментов.
Вычислим при


максимум изгибающего момента

Откладываем
полученное значение на графике-эпюре
и проводим через три точки параболу. По
правилу зонтика и дождика выпуклость
параболы обращена к верху, а на перевернутой
эпюре моментов – к низу.
Эпюра моментов напоминает изогнутую
ось балки, изображенную на рис. а
пунктиром.

Пример
3.

Построить
эпюры Q_y,
M_x
для балки (см. рис. а).

а)
б)

Решение.

Методом
сечений (рис. б)
находим

Поскольку

то эпюра

–
квадратичная парабола, а

–
кубическая.

При

,


.
При

имеем

.
Эпюра

испытывает экстремум при

,
когда

Выпуклость эпюры

определяется знаком ее второй производной:

Так как
вторая производная возрастает, то
выпуклость направлена вниз.

Экстремум
эпюры моментов

имеет место в сечении, где

,
т.е. на конце консоли при

.
В этом сечении

.
Выпуклость кривой

определяется по знаку второй производной,
то есть по правилу зонтика:

В нашем
случае выпуклость направлена вверх.

Пример
4.

Построить
эпюры перерезывающих сил и изгибающих
моментов Q_y,
M_x
для балки (см. рис. а), если

,
интенсивность нагрузки

.

а)
б)

Решение.

1.
Определение опорных реакций из уравнений
равновесия

Составим
два независимых уравнения равновесия
моментов относительно опор A,
B:

Находим
опорные реакции

.

Для
статической проверки составляем третье
зависимое уравнение равновесия в
проекции на вертикальную ось:

.

Подставляем в это уравнение значения
найденных реактивных сил и получаем

Следовательно,
опорные реакции определены правильно.

2.
Определение Q_y,
M_x
методом сечения и построение их эпюр

Балка
имеет два участка


и


с различными аналитическими выражениями
внутренних силовых факторов.

На
первом участке (рис. б) методом
сечений с учетом


находим

Эпюра

−
квадратичная парабола, а

− кубическая.

При


имеем

,
а при


имеем

.
Согласно дифференциальным зависимостям
Журавского экстремум эпюры

имеет место в сечении

,
где

,
экстремум эпюры

в сечении, где

,
что дает

,

.

На
втором участке (рис. б) методом
сечений получаем

При




.
Эпюра

− постоянна, а

− наклонная прямая. Максимальный момент
определяется по формуле

.

3.
Расчет на прочность

Условие
прочности записываем в виде

Пример
6.

Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М.

Дано:
l₁=3,8 м; l₂=3,6
м; l₃=1,4 м, F=3,8q;
M=14,44q

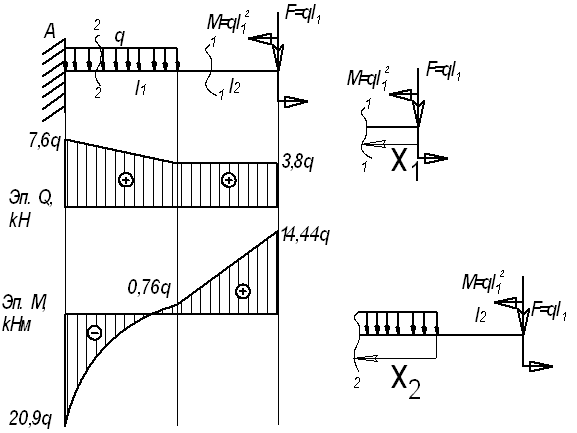
Решение.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Пример
7.

Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М.

Дано:
l₁=3,8 м; l₂=3,6
м; l₃=1,4 м, F=3,8q;
M=12,96q

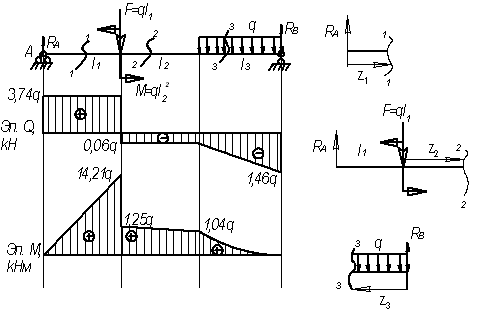
Решение.

Находим
реакции опор

Проверка

Реакции
опор найдены правильно.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим сечение 3-3:

Пример
8.

Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М.

Дано:
l₁=2 м; l₂=3,4
м; l₃=2 м, F=3,4q;
M=4q

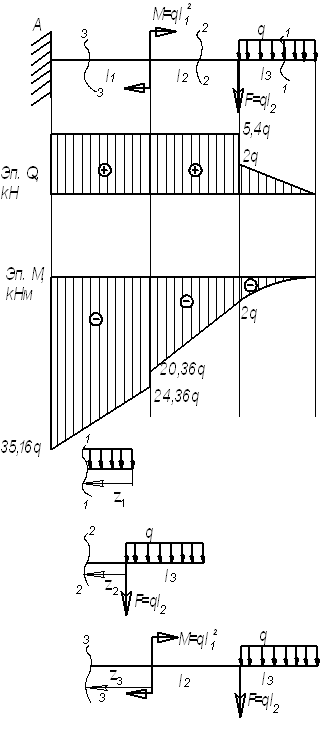
Решение.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
9.

Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М

Дано:
l₁=2 м; l₂=3,4
м; l₃=2 м, F=2q;
M=11,56q

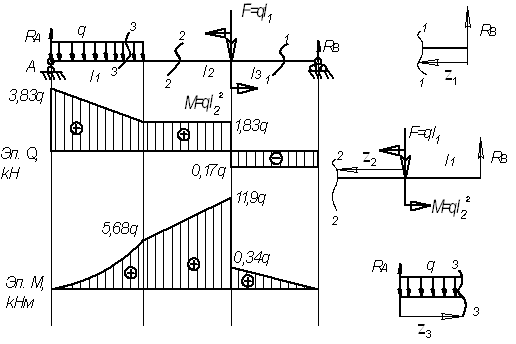
Решение.

Находим
реакции опор

Проверка

Реакции
опор найдены правильно.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим сечение 3-3:

Пример
10.

Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М

Дано:
l₁=2,3 м; l₂=3,4
м; l₃=1,8 м, F=3,4q;
M=2,65q

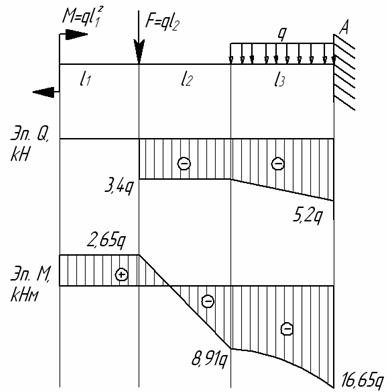
Решение.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример 11.

Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М

Дано:
l₁=2,3 м; l₂=3,4
м; l₃=1,8 м, F=1,8q;
M=2,65q

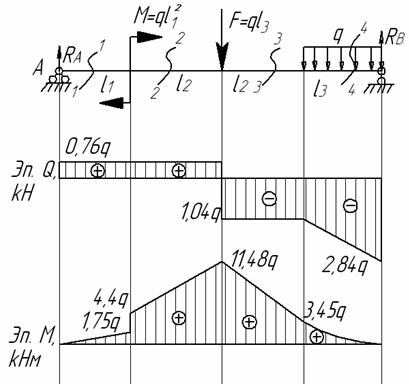
Решение.

Находим
реакции опор

Проверка

0=0

Реакции
опор найдены правильно.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Рассмотрим
сечение 4-4:

Пример
12.

Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М

Дано:
l₁=2,4 м; l₂=2,8
м; l₃=1,8 м, F=2,4q;
M=3,24q

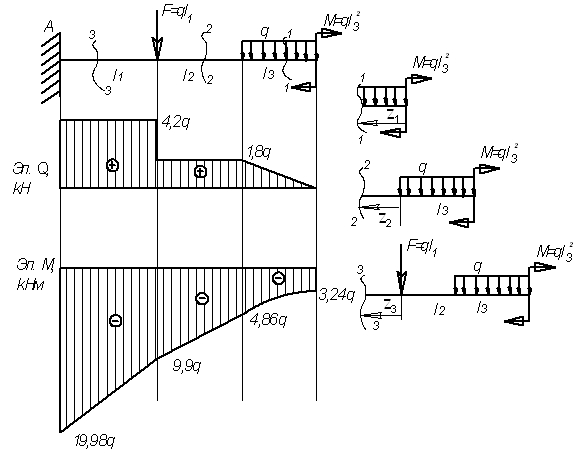
Решение.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
13.

Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М

Дано:
l₁=2,4 м; l₂=2,8
м; l₃=2 м, F=2,8q;
M=7,84q

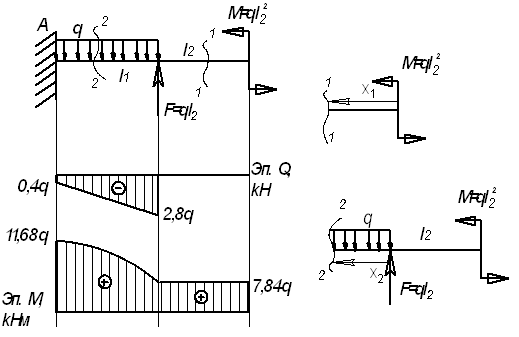
Решение.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Пример
14.

Для
заданной балки (см.рис.) построить эпюры
от силы Q и от
момента М

Дано:
l₁=3,2 м; l₂=3
м; l₃=2 м, F=3,2q;
M=10,24q

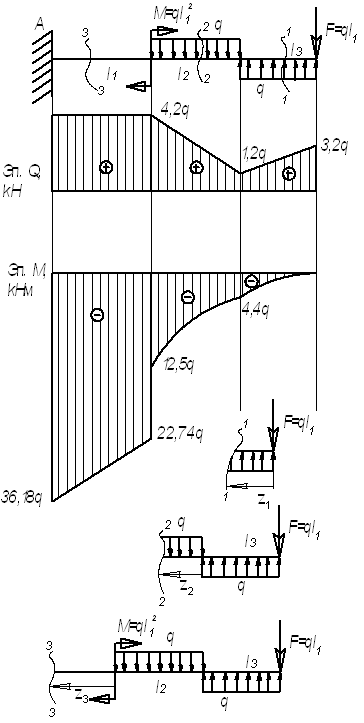
Решение.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
15.

Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М

Дано:
l₁=3,2 м; l₂=3
м; l₃=2 м, F=3q;
M=10,24q

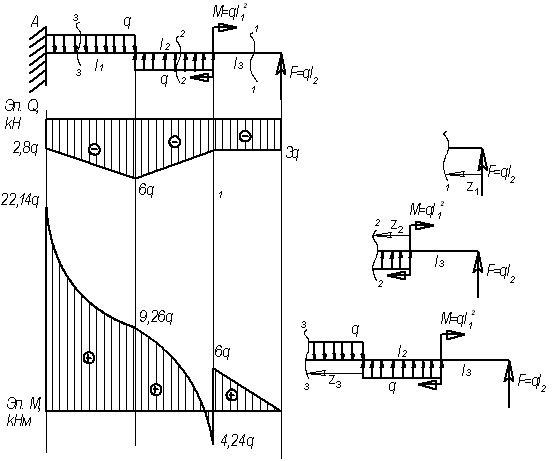
Решение.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
16.

Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М

Дано:
l₁=3,2 м; l₂=3
м; l₃=2 м, F=3q;
M=4q

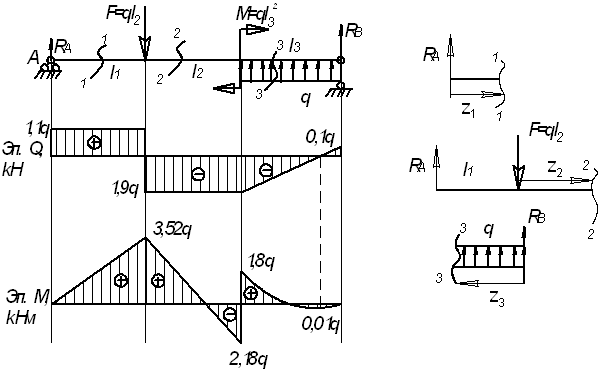
Решение.

Находим
реакции опор

Проверка

0=0

Реакции
опор найдены правильно.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
17.

Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М

Дано:
l₁=3,2 м; l₂=2,4
м; l₃=2 м, F=3,2q;
M=10,24q

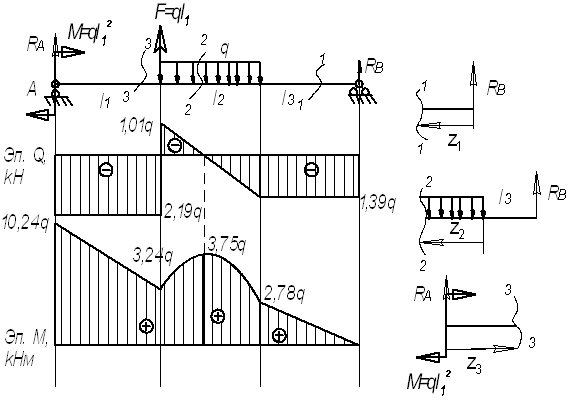
Решение.

Находим
реакции опор

Проверка

Реакции
опор найдены правильно.

Рассмотрим
сечение 1-1:

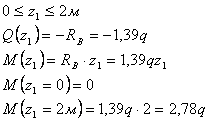
Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
18.

Для
заданной балки (см.рис.) построить эпюры
от силы Q и от момента
М

Дано:
l₁=3,6 м; l₂=2,6
м; F=3,6q;
M=3,24q

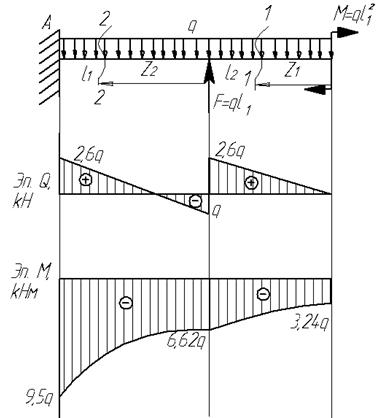
Решение.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Пример
19.

Для
заданной балки (см.рис.) построить эпюры
от силы Q и от
момента М

Дано:
l₁=3,6 м; l₂=3,2
м; l₃=1,8 м, F=3,6q;
M=12,96q

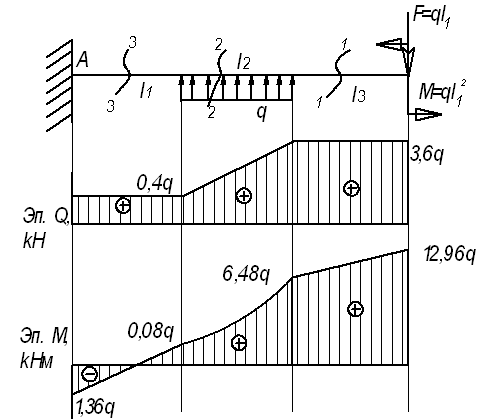
Решение.

Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
20.

Построить
эпюры Q_y
и М_х для балки с консолью.

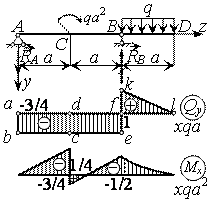
Решение.

1.
Определение опорных реакций. Составляем
уравнения равновесия:

,
R_A
a
—
qa²
—
qa
/2
= 0,

откуда


,

,
R_В
a
— qa²—
qa
a/2
= 0,

откуда


.

Проверка:


,
R_A
— R_B
+ qa
= 3qa/4 —
7qa/4 + qa
º
0.

2.
Построение эпюр поперечной силы и
изгибающего момента.

Э п ю
р а Q_y.
В сечении А происходит скачок вниз
на величину реакции R_A
и Q_A
= —R_A.
На всем протяжении участков АС и СВ
распределенная нагрузка отсутствует
(q = 0), поэтому эпюра
Q_y
представляется отрезком прямой,
параллельной оси абсцисс. Наличие пары
сил на эпюре Q_y
не отражается. В сечении В происходит
скачок вверх, равный по величине
приложенной реакции R_B,
и правее этого сечения имеем Q_BD
= Q_BC
+R_B=
-3qa/4 + 7qa/4
= qa. На участке BD
поперечная сила изменяется по линейному
закону (Q_y
= Q_o—qz)
от Q_o
= Q_BD
= qa до Q_D
= Q_BD
— qa = 0. По условию
загружения балки в сечении D
нет сосредоточенной силы, поэтому Q_D=0.
Совпадение значений Q_D,
полученных независимо друг от друга,
служит проверкой правильности построения
эпюры Q_y.

Э п ю
р а М_х. Она строится по
формуле М_х = М_о +


.
На опоре А нет пары сил, поэтому М_А
=0. На участке АС момент изменяется
по линейному закону. Находим момент в
сечении, бесконечно близком слева от
точки С: М_СА = М_о
+

=
-3 qa
/4
= -3qa²/4. По двум
точкам (А и С) строим наклонную
прямую. Пара сил, приложенная в сечении
С, вызывает растяжение нижних волокон
балки при движении слева направо, поэтому
на эпюре М_х скачок вниз и
в бесконечно близком сечении справа
от точки С изгибающий момент
равен: M_CB
= M_CA
+ qa² = qa²/4.
Находим момент в сечении В: M_B
= M_CB
+

=
qa²/4 — 3qa²/4
= —qa²/2 и по двум
точкам строим наклонную прямую. На
участке BD момент
изменяется по квадратичному закону,
достигая в сечении D
значения, равного M_D
= M_B
+

=
—qa²/2 + (1/2)qa
=
0. С другой стороны, по условию загружения
балки на свободном конце M_D
= 0. Совпадение результатов служит
проверкой правильности построения
эпюры М_х. По двум точкам
(В и D) приближенно
строим параболу, обращенную выпуклостью
вниз (в направлении нагрузки q).
Вершина параболы совпадает с точкой D,
так как Q_D
= 0.

Пример
21.

Построить
эпюры Q_y
и М_х для простой консоли,
изображенной на рисунке.

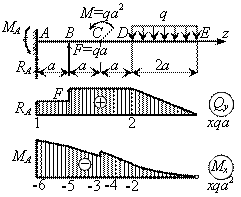
Решение.

1.
Определение опорных реакций. Составляем
уравнения равновесия:

,
M_A
+ F

+ M —
q
a
a
= 0,

откуда
M_A
= 6qa²;

,
R_A
= q
a
— F = qa.

2.
Построение эпюр поперечной силы и
изгибающего момента.

Э п ю
р а Q_y.
В сечении А имеем Q_A
= R_A
(скачок на величину и в направлении
реакции R_A
= qa). На участке АВ
погонной нагрузки нет, поэтому поперечная
сила постоянна. В сечении В поперечная
сила меняется скачком от Q_BA
= Q_A
= qa до Q_BC
= Q_BA
+ F = 2qa
(скачок на величину и в направлении силы
F = qa).
На участках ВС и CD
поперечная сила опять сохраняет
постоянное значение, т.е. Q_BC
= Q_CD
= 2qa. На участке DE
поперечная сила изменяется по линейному
закону от Q_D
= 2qa до Q_E
= Q_D
— q
a
= 0.

Э п ю
р а М_х. В сечении А
приложен момент М_А,
вызывающий растяжение верхних волокон,
поэтому на эпюре изгибающего момента
происходит скачок вверх на величину
момента M_A
= 6qa².

На
участке АВ М_х изменяется
по линейному закону. Вычисляем момент
в сечении В M_B
= M_A
+

= -6qa² + qa×a
= -5qa² и проводим
наклонную прямую. Аналогично на участках
ВС и СD. В
бесконечно близком сечении слева от
точки С момент равен M_СB
= M_B
+

=
-5qa² + 2qa

= -3qa².

В сечении
С на эпюре М_х скачок
вверх, равный приложенной паре сил M
= qa², и правее
этого сечения имеем M_CD
= M_CB
— qa² = -3qa²
— qa² = -4qa².

Момент
в сечении D M_D
= M_CD
+

= -4qa² + 2qa

= -2qa².

На
участке DE изгибающий
момент изменяется по закону квадратной
параболы, обращенной выпуклостью вниз
(в сторону погонной нагрузки q).
В сечении Е по условию загружения
балки М_Е = 0. По двум точкам
D и Е приближенно
строим параболу.

Пример
22.

Построить
эпюры Q_y
и М_х для балки.

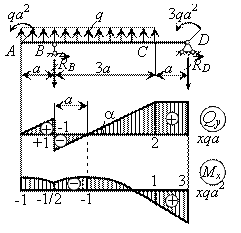
Решение.

1.
Определение опорных реакций. Составляем
уравнения равновесия:

,
q
a

+ qa²
+ 3qa²—R_D
a
= 0,

откуда
R_D
= 2qa;

,
R_B
a
+ qa²
+3qa²—q
a
a
= 0,

откуда
R_B
= 2qa.

П р о в е р к а

,
q×4a
— R_B
— R_D
= 4qa —
2qa — 2qa
= 0.

2.
Построение эпюр поперечной силы и
изгибающего момента.

Э п ю
р а Q_y. Строится по формуле
Q_y = Q_o ±
qz. В данном случае перед вторым
слагаемым следует взять знак “плюс”,
так как погонная нагрузка положительна
(см. правила построения эпюр). На участках
АВ и ВС эпюра Q_y
изображается прямой, наклоненной вверх
(в направлении погонной нагрузки q),
а на участке CD поперечная сила
постоянна (q = 0). В сечениях В и D
на балку действуют сосредоточенные
силы R_A и R_D,
поэтому на эпюре Q_y возникают
скачки. Вычисляем значения поперечной
силы в характерных точках Q_A
= 0,

Q_BA
= Q_A
+ q×a
= qa,

Q_BC
= Q_BA
— R_B
= qa — 2qa
= —qa,

Q_C
= Q_BC
+ q
a
= —qa + 3qa
= 2qa и строим эпюру
Q_y.

Э п ю
р а М_х. Она строится по
формуле М_х = М_о +

.
На участках с погонной нагрузкой (АВ
и ВС) изгибающий момент изменяется
по закону квадратной параболы M_x
= M_o + Q_oz +
0,5qz², обращенной выпуклостью
вверх (в сторону погонной нагрузки q).
В сечениях А и D,
где приложены сосредоточенные пары, на
эпюре М_х наблюдаются
скачки, причем момент qa²
вызывает растяжение сверху (при обходе
слева направо), поэтому в сечении А
скачок направлен вверх, а момент 3qa²
вызывает растяжение снизу (при обходе
справа налево), поэтому в сечении D
скачок происходит вниз. На участке АВ
парабола строится по двум точкам А
и В, а на участке ВС – по трем
точкам (к крайним точкам В и С
добавляется точка экстремума). Положение
точки экстремума определяется из условия
z_o
= Q_BC
/
.
Согласно дифференциальной зависимости

=
dQ/dz
= q, поэтому z_o
= qa/q
= 0. Вычисляем значения момента в
характерных точках:

M_A
= —qa², M_B
= M_A
+

= —qa² + (1/2)
a

= —qa²/2,

M_max
= M_B
+

= —qa²/2
— (1/2)

a

= —qa²,

M_C
= M_max
+

= —qa²
+ (1/2)
qa
a
= qa²

и строим эпюру М_х.

Пример
23.

По
заданной эпюре поперечной силы Q_y
установить нагрузку, действующую на
двухопорную балку, и ее опорные реакции.
Построить также эпюру изгибающего
момента, учитывая, что на правой опоре
С приложена пара сил.

Решение.

Скачки
на эпюре Q_y
свидетельствуют о приложенных в этих
сечениях сосредоточенных силах. Приняв
направление обхода слева направо,
получим: реакция в точке А равна R_A
= qa и направлена вверх;
в сечении В приложена сосредоточенная
сила F = 5qa,
направленная вверх; наконец, реакция
R_B
= 2qa и направлена вниз.
На участке АВ поперечная сила
изменяется по линейному закону, что
связано с наличием погонной нагрузки,
интенсивность которой определяется
как тангенс угла наклона прямой q_y
= dQ/dz = (-3qa — qa)/4a = —q.
Знак “минус” означает, что нагрузка
направлена вниз. Для определения
неизвестной пары сил М, приложенной
в сечении С, составим уравнение
моментов относительно этой точки:

,
—R_A
a
— F
a
+ q
a
a
+ M_C
= 0,

откуда M_C
= 2qa² и направлен
против часовой стрелки.

Эпюру
М_х строим по формуле М_х
= М_о +

.
На участке АВ изгибающий момент
изменяется по квадратичному закону. На
концевой шарнирной опоре А нет пары
сил, поэтому М_А = 0. В
сечении, где Q_y
= 0, изгибающий момент принимает
экстремальное значение:

M_max
= M_A
+

=
(1/2)qa

= qa²/2.

Находим
момент в сечении В: M_B
= M_max
+

=
qa²/2- (1/2)3qa
a
= -4qa² и по трем
точкам приближенно строим параболу,
обращенную выпуклостью вниз. На участке
ВС изгибающий момент изменяется
по линейному закону от M_B
= -4qa² до M_C
= M_B
+

=
-4qa² + 2qa
a
= 2qa². По условию
загружения балки также имеем M_C
=2qa². Совпадение
значений М_С, найденных
независимо друг от друга, свидетельствует
о правильности построения эпюры М_х.

Пример
24.

По
заданной эпюре изгибающего момента
построить эпюру поперечной силы и
определить нагрузку, действующую на
балку. Криволинейный участок эпюры М_х
очерчен по квадратной параболе, а кружком
отмечена ее вершина.

Решение.

На
участке АВ изгибающий момент
изменяется по квадратичному закону:
M_x
= M_o
+ Q_oz
— 0,5qz². Так как
вершина параболы совпадает с точкой
А, то М_о =М_А
=0 и Q_o
= 0. Следовательно, М_х =
-0,5qz². Момент в
бесконечно близком сечении слева от
опоры В, судя по приведенной
эпюре, равен М_ВА = -40 кНм.
С другой стороны, М_ВА =
-0,5q(2)².
Следовательно, q = 20
кН/м. Парабола обращена выпуклостью
вниз, поэтому и погонная нагрузка
направлена вниз.

В
сечении В изгибающий момент
изменяется скачком от М_ВА
= -40 кНм до М_ВС = -10 кНм, что
свидетельствует о наличии пары сил М₁
= 30 кНм, вызывающей растяжение нижних
волокон (при обходе слева направо), т.е.
направленной по часовой стрелке. На
опоре С приложена пара сил с моментом
М₂ = 20 кНм, вызывающая растяжение
снизу (при обходе справа налево), т.е.
направленная против часовой стрелки.

На
участке ВС поперечная сила постоянна
и равна тангенсу угла наклона прямой,
т.е. Q_BC = dM/dz =

=
(20 + 10)/3 = 10 кН. На участке АВ поперечная
сила изменяется по линейному закону
(Q_y = Q_o — qz)
от Q_o
= Q_A
= 0 до Q_BA
= —q

= -40 кН. По скачкам на эпюре Q_y
находим величины и направления реакций:
R_B
= 50 кН (направлена вверх) R_C
= 10 кН (направлена вниз).

Пример
25.

Построить
эпюры поперечных сил Q_Y
и изгибающего момента M_X
(см. рис.1).

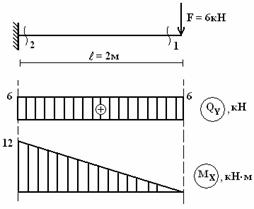
Рис.1

Решение.

1)
Проведем две оси, параллельные оси балки
(одну для эпюры Q_Y,
вторую для эпюры M_X).

2) Балка
имеет один участок загружения.

3) Строим
эпюру Q_Y.
Сделаем сечение (1), отбросим жесткую
заделку. Учитывая правило знаков, получим

.
В сечении (2) получим

.
Силы

,
так как сила F
поворачивает оставшуюся часть балки
вокруг сечения по часовой стрелке
(рис.2,а).

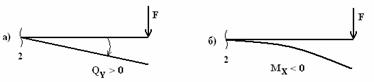
Рис. 2

Положительные
значения поперечной силы откладывают
всегда выше оси.

Соединим
их прямой линией, поставим знак, эпюру
заштрихуем, обозначим.

4) Строим
эпюру М_Х. Сделав сечение и отбросив
часть с жесткой заделкой, сосчитаем
момент от силы F относительно
сделанного сечения. Получим

.
Для эпюры изгибающих моментов принимается
следующее правило: значения моментов
откладываются от оси в сторону растянутого
волокна. Из рис.2,б, следует, что сила F
растягивает верхние волокна, поэтому
полученное значение М_Х откладываем
выше оси. Соединяем отложенные значения
прямой линией. Знак на эпюре изгибающих
моментов можно не ставить. Эпюру штрихуем
и обозначаем (рис.1).

5)
Проверка эпюр. К балке не приложена
распределенная нагрузка, следовательно,
на графиках Q_Y
и М_Х имеем прямые линии, причем
на эпюре Q_Y
это прямая, параллельная оси. На свободном
конце балки приложена сосредоточенная
сила F = 6кН


в этом сечении на эпюре Q_Y
образовался скачок, равный 6.

Пример
26.

Построить
эпюры поперечных сил Q_Y
и изгибающего момента M_X
(см. рис.).

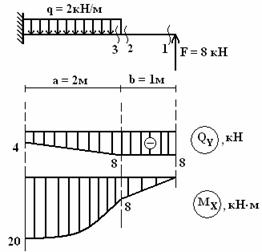
Решение.

1)
Проводим оси для построения эпюр.

2) Делим
балку на два участка загружения.

3) Строим
эпюру Q_Y.

1-й
участок:

;

.

Откладываем
значения ниже оси, соединяем прямой
линией.

2-й
участок:

;

.

Значение

откладываем ниже оси, соединяем прямой
линией.

Ставим
знаки, эпюру штрихуем и обозначаем.

4) Строим
эпюру М_Х.

1-й
участок:

;

.

Откладываем
значения

ниже оси, так как сила F
растягивает нижние волокна, соединяем
прямой линией.

2-й
участок:

;

.

Значения

откладываем ниже оси и соединяем
параболой. При этом выпуклость параболы
должна быть обращена в сторону действия
распределенной нагрузки. Это правило
называют «правилом паруса». Роль паруса
здесь играет эпюра, а роль ветра –
нагрузка.

5)
Проверка эпюр. На участке балки с
распределенной нагрузкой получаем на
эпюре Q_Y
наклонную прямую, на эпюре M_X
– параболу. В сечении с приложенной
сосредоточенной силой F
= 8 кН на эпюре Q_Y
образовался скачек равный 8.

Пример
27.

Построить
эпюры поперечных сил Q_Y
и изгибающего момента M_X
(см. рис.).

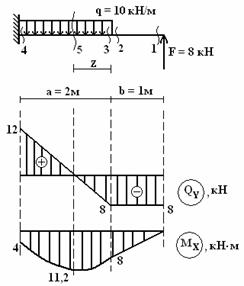
Решение.

1)
Проводим оси для построения эпюр.

2) Делим
балку на два участка загружения.

3) Строим
эпюру Q_Y.

1-й
участок.

;

.

Откладываем
значения ниже оси, соединяем прямой
линией.

2-й
участок.

;

.

Откладываем

ниже оси, а

— выше оси, соединяем прямой линией (см.
рис.).

4) Строим
эпюру М_Х.

1-й
участок:

;

.

Откладываем

ниже оси, соединяем с нулем прямой
линией.

2-й
участок:

Из
рисунка следует, что эпюра поперечных
сил Q_Y
на этом участке пересекает ось, то есть
в некотором сечении (5) сила

.
Отсюда следует, что в сечении (5) изгибающий
момент М_Х достигает экстремального
значения (максимума или минимума). Таким
образом, на этом участке следует
просчитать момент в трех точках.

.

.

Определим
экстремальное значение момента. Выясним
сначала, на каком расстоянии Z от
правой границы участка находится сечение
(5), в котором поперечная сила равна нулю.

.

Найдем
значение момента.

.

Откладываем
значения

ниже оси и соединяем параболой по правилу
«паруса», то есть выпуклостью вниз (см.
рис.).

5)
Проверка эпюр. Все линии на эпюрах
соответствуют приложенным нагрузкам,
силе F = 8 кН соответствует
скачок, равный 8 на эпюре Q_Y.

Пример
28.

Построить
эпюры поперечных сил Q_Y
и изгибающего момента M_X
(см. рис. 1).

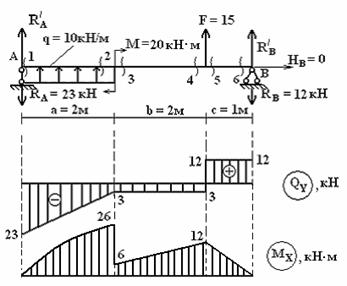
Рис.1

Решение.

1) Расчет
балки с шарнирным закреплением следует
начинать с определения реакций связей.
Расставим эти реакции. В шарнирно
–подвижной опоре А возникает одна
вертикальная реакция R¢_A.
В шарнирно-неподвижной опоре В, вообще
говоря, возникает две реакции –
вертикальная R¢_B
и горизонтальная Н_В, однако,
поскольку в случае вертикального
плоского изгиба все силы действуют
перпендикулярно оси балки, горизонтальная
реакция Н_В всегда будет равна
нулю, поэтому в дальнейшем показывать
ее на схеме балки не будем. Вертикальные
реакции найдем из уравнений статики.

;

.

;

.

При
записи уравнений использовалось
следующее правило знаков: если сила
поворачивает балку вокруг т.А (т.В) по
часовой стрелке, то момент от этой силы
берется со знаком «+».

Для
проверки найденных реакций используем
уравнение статики:

(сумма всех вертикальных сил должна
быть равна нулю). При этом силы, изображенные
на схеме балки направленными вверх,
берем со знаком «+».

.

Подставим
сюда найденные значения реакций со
своими знаками.

— 23 + 10
× 2 + 15 – 12 = 0; 35 – 25
=0; 0 = 0.

Поскольку
направления вертикальных реакций
поначалу были взяты произвольно, то
полученные в результате знаки «-» у
реакций R_A,
R_B
показывают, что мы не угадали направление
реакций, в действительности они направлены
вниз. Удобно изменить направление этих
реакций на обратное и в дальнейшем
считать эти реакции положительными
(см. рис.1).

2)
Проводим оси для построения эпюр.

3) Делим
балку на три участка загружения.

4) Так
как все реакции в закреплениях балки
найдены, то, сделав сечение, можно
отбрасывать любую (обычно более
загруженную) часть балки .

5) Строим
эпюру Q_Y.

1-й
участок.

(отбросили правую часть балки),

(отбросили левую часть балки).

Пару
сил М = 20 кНм при вычислении Q_Y,
естественно, не учитываем.

Откладываем
значения от оси, соединяем прямой линией.

2-й
участок.

;

.

3-й
участок.

;

.

6) Строим
эпюру М_Х.

1-й
участок:

;

.

Чтобы
не ошибиться в знаке изгибающего момента,
сечение, в котором он определяется,
следует представлять защемленным, а
опоры – отброшенными (рис.2):

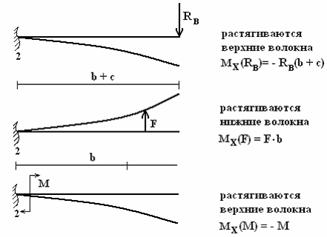
Рис.2

Откладываем
значения от оси и соединяем параболой
по правилу «паруса», то есть направленной
выпуклостью вверх.

2-й
участок:

.

Откладываем
значения выше оси, соединяем прямой
линией.

3-й
участок:

.

Отложенные
от оси значения соединяем прямой линией
(рис.1).

6)
Проверка эпюр. Все линии на эпюрах
соответствуют действующим нагрузкам.
К балке приложены три сосредоточенные
силы – R_A,
F, R_B.
На эпюре Q_Y
получили три скачка

на опоре А – равный R_A
= 23, на границе 2-го и 3-го участков –
равный F = 3 + 12 = 15, на опоре
В – равный R_B
= 12. К балке приложена пара сил М = 20. На
эпюре М_Х на границе 1-го и 2-го
участков имеем скачок, равный М = (26 — 6)
= 20.

Пример
29.

Построить
эпюры поперечных сил Q_Y
и изгибающего момента M_X
(см. рис.).

Решение.

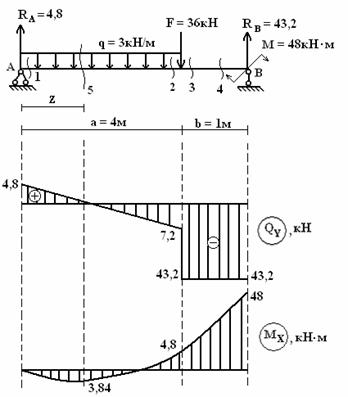
1) Найдем
реакции опор R_A,
R_B.

;

;

.

Проверка:

.

Обе
реакции получились положительными, то
есть мы угадали их направление, они
действительно направлены вверх.

2) Балка
имеет два участка загружения.

3) Строим
эпюру Q_Y.

1-й
участок.

;

.

Откладываем
значения от оси и соединяем прямой
линией.

2-й
участок.

;

.

Откладываем
значения от оси и соединяем прямой (см.
рис.).

4) Строим
эпюру М_Х.

1-й
участок:

Из эпюры
сил следует, что на этом участке будет
возникать экстремальный момент, поэтому
будем определять М_Х в трех сечениях.

(отбрасываем правую часть балки);

(отбрасываем левую часть балки).

Находим
координату Z сечения (5):

.

Находим
экстремальный момент.

.

Откладываем
значения от оси и соединяем параболой
по правилу «паруса», то есть выпуклостью
вниз.

2-й
участок.

;

.

Отложенные
от оси значения соединяем прямой (см.
рис.).

5)
Проверка эпюр.

Линии
эпюры соответствуют приложенным
нагрузкам. К балке приложены три
сосредоточенные силы – R_A,
F, R_B

на эпюре Q_Y
в соответствующих сечениях имеем скачки.

К балке
на опоре В приложена пара сил М: на эпюре
М_Х имеем на правом конце скачок,
равный М = 48.

Пример
30.

Дана
балка с действующими на нее нагрузками
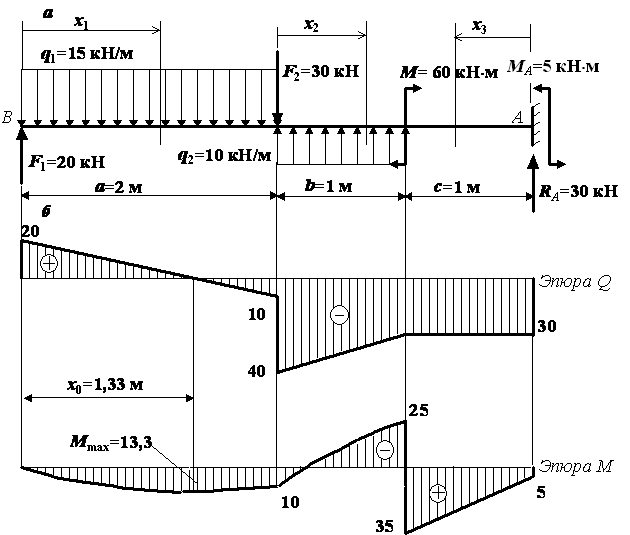
(рис. а). Требуется определить
внутренние усилия – поперечную силу Q
и изгибающий момент М в балке,
построить графики их изменения вдоль
оси стержня (эпюры Q и М).

Решение.

Прежде
всего найдем опорные реакции. Балка
имеет жесткое защемление на правом
конце (В балке с заделкой можно строить
эпюры Q и М без определения
опорных реакций, рассматривая все силы
с одной стороны от сечения – со свободного
конца. Но студенту, только начинающему
осваивать построение эпюр, рекомендуем
все же реакции находить. Это дополнительная
проверка правильности решения задачи)
и в этом закреплении при заданной
вертикальной нагрузке возникают две
опорные реакции: вертикальная реакция
R_A и реактивный момент M_A.
Горизонтальная реакция при действии
вертикальной нагрузки равна нулю. Это
следует из уравнения равновесия «сумма
проекций всех сил на горизонтальную
ось равна нулю». Определим R_A
и M_A, используя два других
уравнения статики. Желательно составлять
такие уравнения, в каждое из которых
входит только одна неизвестная. В данном
случае такими уравнениями являются
«сумма проекций всех сил на вертикальную
ось (ось z) равна нулю» и «сумма
моментов всех сил относительно точки
А равна нулю»:

;

;

;

Из
первого уравнения найдем R_A
= 30 кН, из второго – М_А
=5 кНм. Полученные положительные знаки
опорных реакций подтверждают выбранные
нами направления опорных реакций: R_A
– вверх, а М_А – против
часовой стрелки. Для проверки рекомендуем
использовать любое другое уравнение
равновесия, например

:

– 30×2
– 15×2×1
– 60 + 10×1×2,5
+ 30×4+5 = – 150 + 150 = 0.

Теперь
определяем внутренние усилия: поперечную
силу Q и изгибающий момент М. В
соответствии с методом сечений рассекаем
балку на каждом участке (в данной задаче
их три) произвольным сечением и
рассматриваем все силы, расположенные
с одной стороны от сечения: слева или
справа. Удобно рассматривать все силы
с той стороны от сечения, где сил меньше.
Начало отсчета координаты x на каждом
участке можно выбирать произвольным
образом. Например, на рис. а начало
отсчета x на каждом участке – свое
и находится в начале участка. Запишем
выражения для Q и М на каждом
участке.

Участок
1:

.

Рассмотрим
силы, расположенные слева от сечения.
По определению поперечной силы и с
учетом правила знаков для Q :

.

Здесь

– равнодействующая равномерно
распределенной нагрузки, действующей
слева от сечения.

По
определению изгибающего момента и с
учетом правила знаков для М :

,

где во
втором слагаемом

– плечо равнодействующей равномерно
распределенной нагрузки (
),
взятой слева от сечения (равнодействующая
приложена по середине длины отсеченной
части балки x₁).

Для
построения эпюр найдем значения Q
и М на границах участка:

в начале
участка (х₁ = 0)

,
а

;

в конце
участка (
)

;

.

Участок
2:

.

Снова
рассмотрим все силы, расположенные
слева от сечения.

;

.

Граничные
значения Q и М:

в начале
участка (
)

;

,

в конце
участка (
)

;

.

Участок
3:

.

Теперь
рациональнее рассмотреть все силы
справа от сечения. Тогда

;

.

Из этих
выражений следует, что поперечная сила
на третьем участке – постоянная величина,
а изгибающий момент меняется по линейному
закону и на границах участка имеет
следующие значения:

в начале
участка (
)

,

в конце
участка (
)

.

Запишем
результаты определения внутренних
усилий в таблицу, сосчитав численные
значения Q и М на границах участков
(табл. 1).

Таблица 1

Из
таблицы видно, что поперечная сила на
первом участке меняет свой знак, т. е.
график Q пересекает нулевую линию.
Это значит, что изгибающий момент на
этом участке имеет экстремум. Найдем
максимальное значение М на этом
участке. Сначала определим то значение
координаты х₁, при котором
поперечная сила равна нулю. Обозначим
это значение координаты х₀
(см. рис. ).

х₀ = 1,33 м.

Чтобы
найти максимальное значение изгибающего
момента, подставим х₀ в выражение
для М на первом участке:

кНм.

По
результатам вычислений в таблице строим
эпюры Q и М на каждом участке
(см. рис. б). Не забываем после
построения эпюр проанализировать
результаты по тем правилам проверки
правильности построения эпюр, которые
перечислены ранее.