Мода в физике как найти - Avtoru.top - решение различных проблем

Нормальные колебания (моды). Связанные колебательные системы

Под
нормальными
колебаниями
(нормальными
модами)
понимают собственные (свободные)
незатухающие гармонические колебания
в замкнутых
линейных
колебательных
системах (в
них отсутствуют как потери энергии, так
и приток извне колебательной энергии).

Каждое
нормальное колебание характеризуется
определенным значением частоты. Эти
частоты называются собственными
частотами
системы.

Вводится
понятие степеней свободы системы. Под
степенями
свободы
системы
понимают число независимых параметров,
описывающих возможные изменения
состояния системы. Линейные колебательные
системы (они представляют собой
гармонические осцилляторы, такие как
колебательный контур, пружинный маятник,
математический маятник) являются
системами с одной степенью свободы.
Действительно, для описания их движения
необходимо задать только один параметр.
Например, для механической системы этим
параметром является координата
,
описывающая движение материальной
точки относительно положения равновесия
(другие координатыу
и z
в этом случае не нужны). Для колебательного
контура таким параметром будет заряд
q
на обкладках конденсатора (другие
величины, такие как сила тока, напряжения
на конденсаторе и на катушке, определяются
из зависимости заряда
q
от времени
t).
Для линейных систем с одной степенью
свободы существует только одно нормальное
колебание, нормальная мода.

Связанные
колебательные системы
представляют собой системы с двумя и
более степенями свободы, рассматриваемые
как совокупность систем с одной степенью
свободы, взаимодействующих между собой.
Колебания, возникающие в связанных
системах, называют связанными
колебаниями.

В
дискретных
связанных системах,
состоящих
из
связанных гармонических осцилляторов
(например, механических маятников,
колебательных контуров), число нормальных
колебаний равно.

Примером
связанных систем могут служить два
колебательных контура, связанных между
собой индуктивной связью (рис. 5.27,а).
Колебания в одном контуре из-за наличия
связи вызывают колебания в другом, т.е.
происходит переход энергии из одного
контура в другой. Число нормальных
колебаний для таких контуров равно
двум.

Рис.
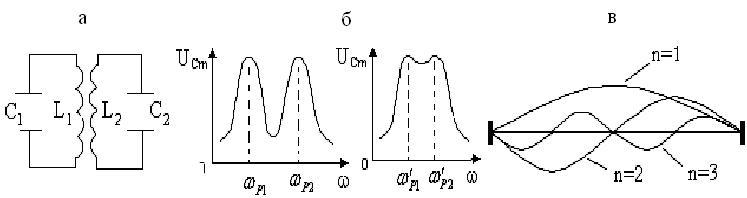
5.27

В
линейных
распределенных
системах
(струна,
мембрана, резонатор) существует
бесконечное, но счетное множество
нормальных колебаний.

Произвольное
свободное колебание системы может быть
представлено в виде суперпозиции
нормальных колебаний. При этом полная
энергия движения распадается на сумму
энергий отдельных нормальных колебаний.

Примером
такой системы являются колебания струны,
закрепленной на концах. Возбуждение в
ней поперечных колебаний приводит к
образованию стоячей волны, узлы которой
приходятся на закрепленные концы (рис.
5.27,в). На длине струны
укладывается целое число полуволн

,

,
n=1,2,3,…
. (5.92)

Все
частоты
представляют собой частоты нормальных
колебаний струны, частота,
соответствующаяn=1,
называется основной
частотой.
Основную частоту можно изменить, уменьшая
или увеличивая натяжение струны

,
(5.93)

где
F
– сила натяжения струны; ρ,
S
– плотность
материала струны и площадь ее поперечного
сечения соответственно.

Любое
колебание струны можно представить в
виде суммы ее нормальных колебаний.
Таким образом, линейная распределенная
система ведет себя как набор независимых
гармонических осцилляторов.

Полученная
формула (5.92) используется, в частности,
для определения спектра частот нормальных
колебаний кристаллической решетки,
связанных с тепловыми колебаниями
атомов.

Резонанс
в системах с несколькими степенями
свободы. При
внешнем возбуждении системы нормальные
колебания в значительной мере определяют
ее резонансные свойства. Резонанс может
возникнуть лишь в том случае, когда
частота гармонического внешнего
воздействия близка к одной из собственных
частот системы, либо к их линейной
комбинации, если внешнее воздействие
меняет параметры системы (параметрический
резонанс).

В
линейном приближении собственные
колебания этих систем представляют
собой набор нормальных колебаний (мод).
Если отклик системы представляет собой
суммарный отклик всех степеней свободы,
то тогда резонансная кривая будет
наложением резонансных кривых отдельных
нормальных колебаний и может иметь
сложный характер.

Так,
в системе с двумя степенями свободы,
ввиду того, что собственные колебания
могут происходить с двумя различными
частотами, резонанс наступает при
совпадении частоты гармонического
внешнего воздействия как с одной, так
и с другой нормальной частотой системы.
Подбором параметров нормальных колебаний
можно создать резонансную кривую любой
формы, что широко используется, например,
в радиотехнике для создания фильтрации
частот (рис. 5.27,б).

Наличие
связи изменяет характер резонансных
явлений в связанных системах по сравнению
с одиночным контуром. В связанных
системах резонанс наступает всякий
раз, когда частота внешнего воздействия
совпадает с одной из частот собственных
колебаний всей системы, отличающихся
от собственных частот отдельных контуров.
Например, в связанных системах, состоящих
из двух контуров, резонанс наступает
на двух резонансных частотах. При этом
для двух слабо взаимодействующих систем
с близкими собственными частотами
колебаний может происходить резонансная
перекачка энергии из одной подсистемы
в другую.

Соседние файлы в папке 1 семестр зачет

Источник

Различные нормальные моды в 1D решётке.

Нормальные колебания или нормальные моды — набор характерных для колебательной системы типов гармонических колебаний. Каждое из нормальных колебаний физической системы, например, колебаний атомов в молекулах, характеризуется своей частотой. Набор частот нормальных колебаний составляет колебательный спектр. Произвольное колебание физической системы можно представить в виде суперпозиции нормальных колебаний. Вынужденные колебания физической системы имеют резонанс на частотах, которые совпадают с частотами нормальных колебаний.

Содержание

1 Нормальные колебания в молекулах
- 1.1 Общая теория
- 1.2 Дипольный момент
2 Источники
3 Примечания

Нормальные колебания в молекулах

Общая теория

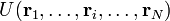
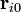
Потенциальная энергия взаимодействия атомов в молекулах является определённой функцией их координат $U(mathbf{r}_1, ldots, mathbf{r}_i, ldots, mathbf{r}_N)$ . Эта функция в целом рассчитывается из квантовой механики в адиабатическом приближении или задаётся определёнными модельными потенциалами. Равновесные положение атомов в молекулах $mathbf{r}_{i0}$ задаются условием минимума этой функции

$frac{partial U}{partialmathbf{r}_i} = 0$ .

Если вывести молекулу из равновесия так, что каждый атом сместится на некую величину 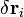$delta mathbf{r}_i$ , то в молекуле возникнут силы, которые постараются вернуть атомы в положение равновесия, а потенциальна энергия возрастёт и станет равной

$U(mathbf{r}_1,ldots, mathbf{r}_i, ldots, mathbf{r}_N) = U_0 + frac{1}{2} sum_{i,j=1}^N sum_{alpha,beta =1}^3 a_{ij}^{alphabeta} delta r_i^{alpha}delta r_j^{beta}$

где і и j — индексы атомов, α и β — индексы осей координат, U₀ — потенциальная энергия молекуулы в положении равновесия, а коэффициенты 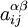$a_{ij}^{alphabeta}$ определяются разложением потенциальной энергии в ряд Тейлора в окрестности положения равновесия.

$a_{ij}^{alphabeta} = frac {partial^2 U}{partial r_i^alpha partial r_j^beta} left|_{mathbf{r}_i = mathbf{r}_{i0}} right. + frac {partial^2 U}{partial r_i^alpha partial r_i^beta} left|_{mathbf{r}_j = mathbf{r}_{i0}} right.$

Уравнения движения для смещённых из положения равновесия атомов имеют следующий вид:

$m_i frac{d^2}{dt^2} delta r_i^alpha = - sum_{j=1}^N sum_{beta = 1}^3 a_{ij}^{alphabeta} delta r_j^{beta}$

где m_i — масса i-того атома.

Если искать решения системы дифференциальных уравнений в виде

$delta r_i^alpha = b_i^alpha e^{iomega t }$ ,

то получим систему линейных уравнений

$m_i omega^2 b_i^alpha - sum_{j=1}^N sum_{beta = 1}^3 a_{ij}^{alphabeta} b_j^{beta} = 0. qquad (text{A})$

Всего таких уравнений 3N-6, где N — число атомов. 3 другие уравнения описывают движение центра массы молекулы, а ещё три — вращения молекулы, как целого^[1] . Система однородная, а следовательно имеет нетривиальное решение лишь при определённых частотах, которые находятся, если приравнять нулю детерминант этой системы

$left| m_i omega^2 delta_{ij} delta_{alphabeta} - a_{ij}^{alphabeta} right| =0$

где δ_ij — символ Кронекера.

Данный детерминант является уравнением (3N-6)-ей степени относительно ω², которое называется вековым или секулярным уравнением. Его корни определяют спектр собственных частот колебаний молекулы.

Собственные векторы 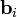$mathbf{b}_i$ уравнения (A) определяют 3N-6 нормальных мод колебаний молекулы.

Нормальные моды взаимно линейно независимы и взаимно ортогональны:

$sum_{i=1}^N mathbf{b}_i^m cdot mathbf{b}_i^n = 0$ ,

если m ne n , где m и n — индексы, которыми обозначены различные собственные векторы. Именно этой особенности нормальные моды обязаны своим названием.

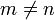
Дипольный момент

Если известны нормальные моды, которые задаются векторами 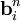$mathbf{b}_i^n$ , где индекс n — номер моды, а также частичные заряды атомов в молекулах, то можно образовать векторы:

$mathbf{d}^n = sum_i q_i mathbf{b}_i^n$ ,

которые называются дипольными моментами нормальных мод.

Во внешнем электрическом поле, например, в поле электромагнитной волны, энергия диполя определяется формулой 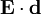. Поэтому те нормальные моды, которые имеют значительный дипольный момент сильно взаимодействуют с электромагнитными волнами (обычно инфракрасного диапазона). Те нормальные моды, для которых дипольного момента нет, или он очень мал, не поглощают и не излучают инфракрасные волны.

Например, симметричная молекула O₂ не имеет частичного заряда на своих атомах, поэтому кислород в атмосфере не становится препятствием для распространения инфракрасных волн. В молекуле CO₂ атомы кислорода несколько подтягивают электроны к себе от центрального атома углерода, поэтому все три атомы имеют небольшой частичный заряд. В молекуле углекислого газа (она линейная) есть три нормальные моды. Одна из них — это симметричные колебания атомов кислорода вдоль оси молекулы. Эта мода не имеет дипольного момента. Другая мода колебаний — асимметричные колебания атомов кислорода вдоль оси молекулы имает дипольный момент, как и третья мода, в которой молекула сгибается.

Источники

Федорченко А.М. . — Киев: Висшая школа, 1975., 516 с.

Примечания

↑ Для двухатомных молекул число уравнений равно 1, потому что вращение происходит только вокруг двух осей.

Wikimedia Foundation.
2010.

Источник

Мода (физика)

Режим (английский язык. Режим ), а также режим вибрации , в котором акустический даже пространственный режим , в механике также собственной моде , режим собственных колебаний или частичные колебания находится в физике , описание некоторых время стационарного свойств вала . Волна описывается как сумма различных мод.

Режимы различаются пространственным распределением интенсивности . Форма мод определяется граничными условиями, при которых распространяется волна. В отличие от тематически связанных нормальных колебаний, анализ по видам колебаний может применяться как к стоячим, так и к непрерывным волнам.

В акустике

Комнатная мода

Режимы помещения можно использовать для характеристики акустики помещения концертного зала .

Режимы комнаты обесцвечивают звук в комнате, потому что некоторые тона особенно заметны и имеют неравномерное распределение энергии в комнате. Если возникают дискретные резонансные частоты , они более заметны, чем если бы многие резонансные частоты равномерно распределены в спектре ( реверберация ).

Стоячая волна. Как вы можете видеть здесь, на каждом конце (разграничение комнаты) давление живота проявляется как максимум.

Определенное распределение резонансных частот — это физическое свойство помещения, которое зависит от его размеров. Возбуждаются только определенные частоты . И повышенный уровень, и продолжительность звука играют роль в этих резонансных эффектах .

Модная комната между двумя твердыми стенами. На стены всегда должно быть максимальное звуковое давление , которое там видно по выступам давления.

Выше примерно 300 Гц ( частота Шредера ) акустические моды комнаты в жилых комнатах не вызывают каких-либо слышимых искажений воспроизведения, поскольку моды сливаются друг с другом в виде плотных отражений и реверберации . С другой стороны, ниже 300 Гц они могут вызвать заметное изменение цвета звука. Поскольку они влияют на особенно низкие ноты, это воспринимается как гудение , гул или однотонный бас . Амплитуда акустической моды зависит от его положения в пространстве. Следовательно, степень обесцвечивания различается от места к месту.

В акустике типичной ( прямоугольной ) комнаты для прослушивания есть три типа стоячих режимов:

аксиальные (продольные) моды, явно доминирующие
тангенциальный и
диагональные режимы (также называемые обязательными или наклонными режимами).

Их частоты можно рассчитать следующим образом:

$f _ {{ mathrm {n_ {x} / n_ {y} / n_ {z}}}} = { frac {c_ {S}} {2}} { sqrt { left ({ frac {n_ {x}} {L}} right) ^ {2} + left ({ frac {n_ {y}} {B}} right) ^ {2} + left ({ frac {n_ {z }} {H}} right) ^ {2}}} ,$

Где:

Больше акустической моды

Осциллятор изгиба зажат с одной стороны — показана амплитуда отклонения второй моды

В акустике, режимы определения относительной прочности обертонов и , таким образом звук на инструменте , например Б. Органная труба или колокольчик .

Изгибающийся осциллятор

Прутки, зажатые с одной стороны , называются изгибающими колебаниями . Они могут вибрировать в нескольких режимах.

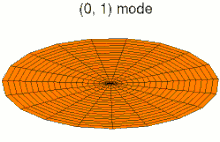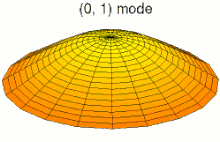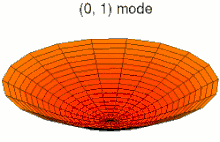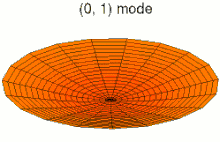
Колебания мембраны

Режим (1 с) $u _ {{01}}$

Мода (5д) $u _ {{23}}$

Форма колебаний зажатой прямоугольной пластины

Зажатая тонкая поверхность ( мембрана ), такая как барабан, может демонстрировать множество различных режимов вибрации. Эти частичные колебания приводят к неравномерности частотной характеристики громкоговорителей .

Полости

Объемные акустические резонаторы — это, например, Б. резонатор Гельмгольца или лампа Кундта , но они также играют важную роль в корпусах громкоговорителей ( фазоинвертор ), духовых инструментах и органных трубах .

Твердый

В твердых телах возникают различные режимы акустической вибрации , например, в кристаллах кварца , колокольчиках , гонгах , колокольчиках , треугольниках и т. Д. Помимо основной резонансной частоты, все эти тела могут также возбуждаться в более высоких режимах колебаний или, в связи с разным составом их режимов колебаний, иметь определенный звуковой характер. В твердых телах из-за существующего модуля сдвига также могут возникать поперечные волны и моды колебаний.

Форма корпусов и деталей машин определяет, какие режимы вибрации особенно возбуждаются во время работы. При подходящей, довольно неправильной форме можно избежать формирования мод колебаний на основе симметрии формы ; Таким образом можно уменьшить звуковое излучение и утомляемость из-за вибрации.

Электромагнитные волны

Для электромагнитных волн, таких как световые , лазерные и радиоволны , различают следующие типы режимов:

ПЭЙ или т ransversal- е LEKTRO м agnetic режим: Оба электрических и компонента магнитного поля всегда перпендикулярны к направлению распространения. Эта мода может распространяться только в том случае, если
- доступны два изолированных друг от друга проводника ( эквипотенциальные поверхности ), например, в коаксиальном кабеле , или
- отсутствует электрический проводник, например, в газовых лазерах или оптических волноводах .
Режимы TE или H: только составляющая электрического поля перпендикулярна направлению распространения, в то время как составляющая магнитного поля указывает направление распространения.
Режимы TM или E: только составляющая магнитного поля перпендикулярна направлению распространения, тогда как составляющая электрического поля указывает направление распространения.

Последние два режима особенно важны в волноводах .

Частота ТЕМ-волн не ограничена, что означает, что они могут распространяться по всему частотному спектру. С другой стороны, TM- и TE-волны могут распространяться только выше определенной частоты ( частоты среза ), которая зависит от геометрии проводника . Следовательно, на фиксированной частоте одновременно могут распространяться несколько мод. Однако это состояние нежелательно при передаче данных , поскольку целостность сигнала, то есть работа волноводов с низкой дисперсией , может быть гарантирована только при чистоте мод. Следовательно, волноводы (например, кабели или волноводы ) можно разумно использовать только для передачи сигнала до частоты среза первой более высокой моды.

В лазерной технологии режимы являются важным инструментом для определения характеристик лазерного луча. В частности, здесь представляют интерес поперечные моды , которые отличаются распределением интенсивности перпендикулярно направлению распространения. См. Также режим громкости .

В электротехнике необходимо, чтобы некоторые устройства работали оптимально, чтобы волна в основном содержала определенную моду. Примеры этого — магнетрон микроволновой печи или кристалл колеблющегося кварца .

В случае антенн, с другой стороны, часто желательно, чтобы никакой режим не был сильно предпочтительным.

Смотри тоже

Собственная частота
Модальный анализ

веб ссылки

Расчет комнатных режимов звука в кубовидных комнатах
Различие между режимами распределения звукового давления в помещениях и режимами колебаний струны.

Источник

Мода (в физике) — вид колебаний, возбуждающихся в сложных колебательных системах. Мода характеризуется пространственной конфигурацией колеблющейся системы, определяемой положением её узловых точек (линий или поверхностей), а также собственной частотой. Обычно каждой моде соответствует определённая собственная частота (см. Собственные колебания). Если собственные частоты двух или большего числа мод совпадают, то такие моды называются вырожденными.

См. также

Объёмный резонатор
Открытый резонатор
Радиоволновод
Колебания кристаллической решётки

Эта статья или раздел использует текст Большой советской энциклопедии.

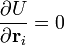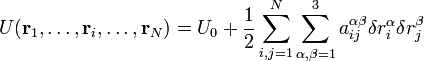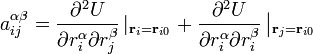
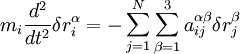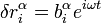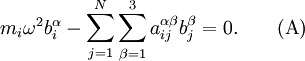
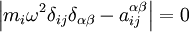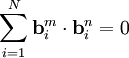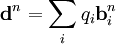Источник

Нормальные колебания (моды). Связанные колебательные системы

Содержание

Нормальные колебания в молекулах

Общая теория

Дипольный момент

Источники

Примечания

Мода (физика)

В акустике

Комнатная мода

Больше акустической моды

Изгибающийся осциллятор

Колебания мембраны

Полости

Твердый

Электромагнитные волны

Смотри тоже

веб ссылки

См. также

Не пропустите также: