6.1.1 Энтропия максимальна и равна:
Для
доказательства этого воспользуемся
методом неопределенных множителей
Лагранжа. С учетом условия нормировки,
когда
и, полагая
,
найдем экстремум функционала следующего
вида:
(7)
Дифференцируя
по
,
и приравнивая производные нулю, получаем
(8)
Отсюда
следует, что
и не зависит от номера
,
что может быть только при равенстве
всех
,
а значит
.
Подставляя
эту величину, вычислим:
(9)
Утверждение
6.1.1 доказано!
6.1.2 Энтропия есть величина вещественная и неотрицательная, а так же ограниченная.
Первые
два утверждения следуют из определения
энтропии и очевидного неравенства:
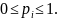
Для
доказательства третьего рассмотрим
слагаемое
.
При
результат очевиден. При
имеем
.
Раскроем неопределенность по правилу
Лопиталя, положив
:
(10)
Утверждение
6.1.2 доказано!
6.1.3
Энтропия максимальна и равна: Hmax
= logb
N
Для
доказательства этого воспользуемся
методом неопределенных множителей
Лагранжа.
С
учетом условия нормировки, когда
,
и, полагая b
=
e,
найдем экстремум функционала следующего
вида:
(11)
Фактически,
мы должны найти значение лямбда, при
котором определенный функционал будет
иметь точку экстремума.
Дифференцируя
по pi,
и приравнивая производные к нулю,
получаем:
(12)
Отсюда
следует, что
и
не зависит от номера i,
что может быть только при равенстве
всех pi,
а значит pi
= 1/N.
Подставляя
эту величину, вычислим:
(13)
Энтропия
как среднее значение количества
информации будет равна данному выражению.
Мы
доказали, что энтропия максимальна в
том случае, когда все события равновероятны
и при этом энтропия равна логарифму от
числа всех возможных сообщений.
6.1.4 Энтропия есть величина вещественная и неотрицательная, а так же ограниченная.
Первые
два утверждения следуют из определения
энтропии как среднего значения и
очевидного неравенства: 0 ≤ pi
≤ 1.
Для
доказательства третьего рассмотрим
слагаемое – pi
∙ logb
pi
При
pi
= 1 результат очевиден и равен 0.
При
pi
→ 0 имеем: – 0 ∙ logb
0=0 ∙ logb
∞
Получаем
неопределенность и запишем с изменением
знака данное выражение.
Раскроем
неопределенность по правилу Лопиталя,
положив b
= e:
(14)
Согласно
правилу Лопиталя, для нахождения предела
переходим к рассмотрению отношения
предела первых производных. После
преобразований убеждаемся, что и в этом
случае значение энтропии равно нулю.
Таким
образом, имеем важные характеристики
для энтропии, а именно, энтропия
вещественна, неотрицательна, ограничена.
Исследуя
свойства энтропии, интересно рассмотреть,
как ведут себя элементы, входящие в
состав суммы, определяющей энтропию. А
именно как ведет себя выражение
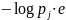
6.1.5
Докажем, что величина
(– pj
∙ log
pj)
принимает максимальное значение при
pj
= e
– 1
Доказательство
простое — возьмем производную от этого
выражения и приравняем к нулю.
(15)
Вывод:
и, следовательно, pj
= e
– 1
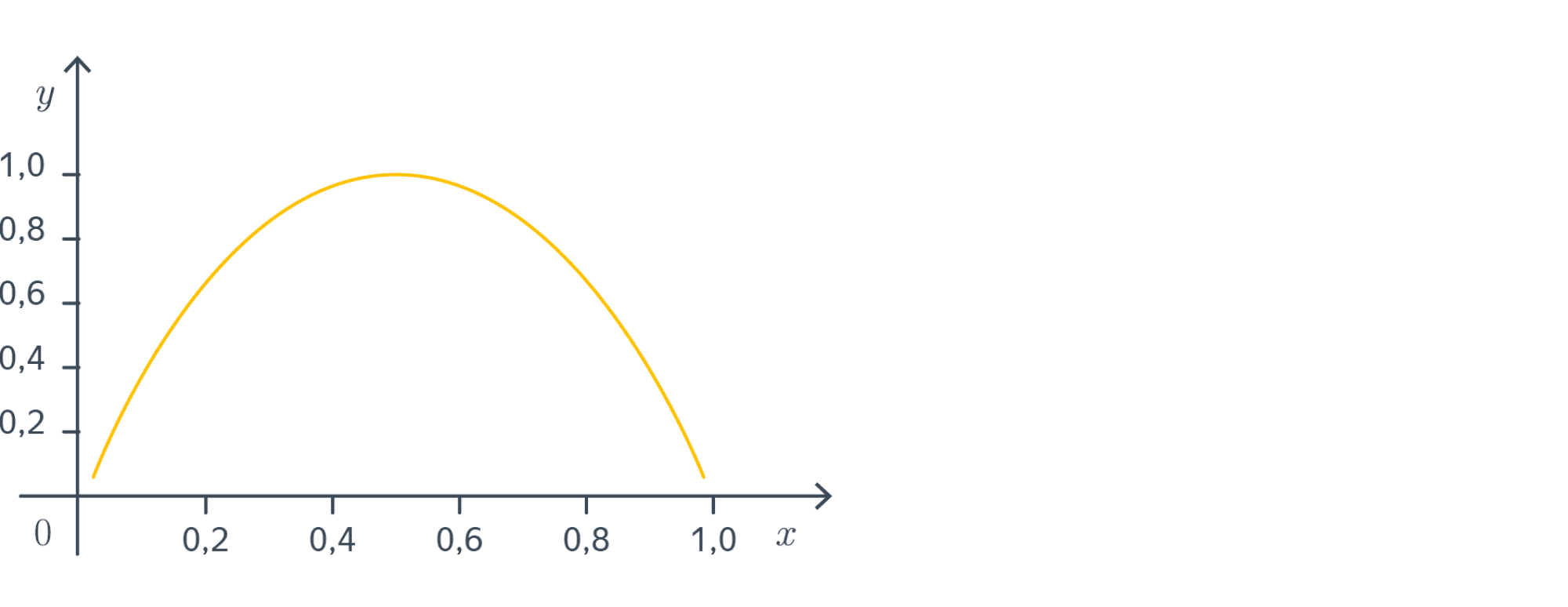
Для
наглядности построим график зависимости
этого произведения(–
pj
∙ log
pj)
от
.
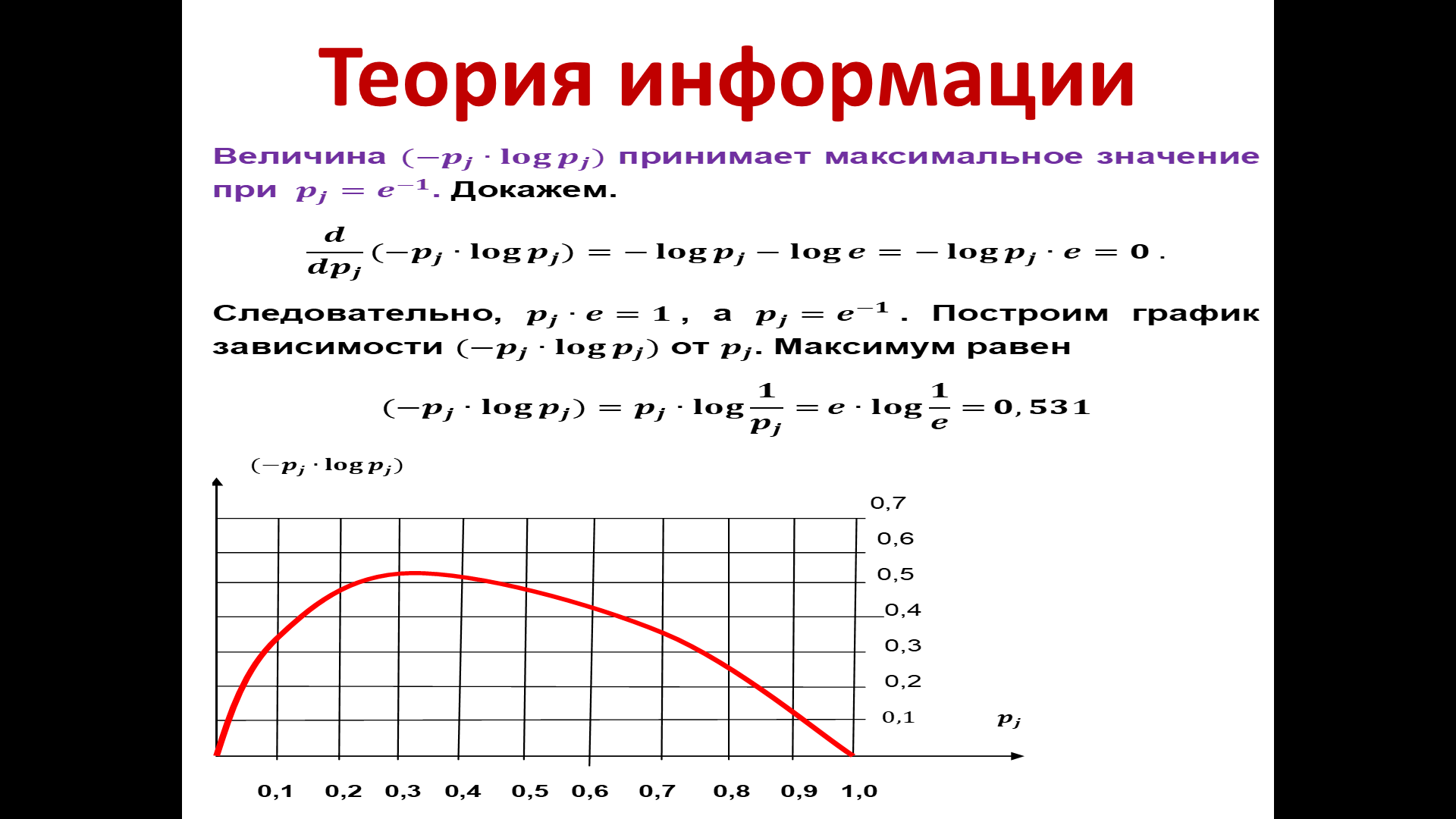
Рисунок
14 — График
зависимости произведения (–
pj
∙ log
pj)
от
.
Свой
максимум выражение достигает при pj
=
e
– 1
Максимум
равен:
Данные
исследования интересны тем, что изучая
источники сообщений, мы понимаем, при
каких условиях получаем определенные
значения энтропии и при каких условиях
она максимальна.
Соседние файлы в папке 3 курс (заочка)
- #
- #
15.02.20213.1 Mб46(Презентация) ТИ.pptx
- #
15.02.20218.19 Кб61(Решалка) 4 задание.xls
- #
- #
In statistics and information theory, a maximum entropy probability distribution has entropy that is at least as great as that of all other members of a specified class of probability distributions. According to the principle of maximum entropy, if nothing is known about a distribution except that it belongs to a certain class (usually defined in terms of specified properties or measures), then the distribution with the largest entropy should be chosen as the least-informative default. The motivation is twofold: first, maximizing entropy minimizes the amount of prior information built into the distribution; second, many physical systems tend to move towards maximal entropy configurations over time.
Definition of entropy and differential entropy[edit]
If 
then the entropy of 
If 


The quantity 

This is a special case of more general forms described in the articles Entropy (information theory), Principle of maximum entropy, and differential entropy. In connection with maximum entropy distributions, this is the only one needed, because maximizing 
The base of the logarithm is not important as long as the same one is used consistently: change of base merely results in a rescaling of the entropy. Information theorists may prefer to use base 2 in order to express the entropy in bits; mathematicians and physicists will often prefer the natural logarithm, resulting in a unit of nats for the entropy.
The choice of the measure 
Distributions with measured constants[edit]
Many statistical distributions of applicable interest are those for which the moments or other measurable quantities are constrained to be constants. The following theorem by Ludwig Boltzmann gives the form of the probability density under these constraints.
Continuous case[edit]
Suppose 






(i.e. whose density function is zero outside of 
the 
If there is a member in 



where we assume that 





[4]
Using the Karush–Kuhn–Tucker conditions, it can be shown that the optimization problem has a unique solution because the objective function in the optimization is concave in 
Note that if the moment conditions are equalities (instead of inequalities), that is,
then the constraint condition 
Discrete case[edit]
Suppose 

If there exists a member of C which assigns positive probability to all members of S and if there exists a maximum entropy distribution for C, then this distribution has the following shape:
where we assume that 


Again, if the moment conditions are equalities (instead of inequalities), then the constraint condition 
Proof in the case of equality constraints[edit]
In the case of equality constraints, this theorem is proved with the calculus of variations and Lagrange multipliers. The constraints can be written as
We consider the functional
where 


It is an exercise for the reader[citation needed] that this extremum is indeed a maximum. Therefore, the maximum entropy probability distribution in this case must be of the form (
The proof of the discrete version is essentially the same.
Uniqueness of the maximum[edit]
Suppose 








It follows that a distribution satisfying the expectation-constraints and maximising entropy must necessarily have full support — i. e. the distribution is almost everywhere positive. It follows that the maximising distribution must be an internal point in the space of distributions satisfying the expectation-constraints, that is, it must be a local extreme. Thus it suffices to show that the local extreme is unique, in order to show both that the entropy-maximising distribution is unique (and this also shows that the local extreme is the global maximum).
Suppose 




![{displaystyle Dlog(C(cdot ))vert _{vec {lambda }}=left.{frac {DC(cdot )}{C(cdot )}}right|_{vec {lambda }}=mathbb {E} _{p}[{vec {f}}(X)]={vec {a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/563dc18d4ef0029196432f4ed338f179aa85436e)


where 

where 





Caveats[edit]
Note that not all classes of distributions contain a maximum entropy distribution. It is possible that a class contain distributions of arbitrarily large entropy (e.g. the class of all continuous distributions on R with mean 0 but arbitrary standard deviation), or that the entropies are bounded above but there is no distribution which attains the maximal entropy.[a] It is also possible that the expected value restrictions for the class C force the probability distribution to be zero in certain subsets of S. In that case our theorem doesn’t apply, but one can work around this by shrinking the set S.
Examples[edit]
Every probability distribution is trivially a maximum entropy probability distribution under the constraint that the distribution has its own entropy. To see this, rewrite the density as 

to be the constant, 
.
Nontrivial examples are distributions that are subject to multiple constraints that are different from the assignment of the entropy. These are often found by starting with the same procedure 

A table of examples of maximum entropy distributions is given in Lisman (1972)[6] and Park & Bera (2009).[7]
Uniform and piecewise uniform distributions[edit]
The uniform distribution on the interval [a,b] is the maximum entropy distribution among all continuous distributions which are supported in the interval [a, b], and thus the probability density is 0 outside of the interval. This uniform density can be related to Laplace’s principle of indifference, sometimes called the principle of insufficient reason. More generally, if we are given a subdivision a=a0 < a1 < … < ak = b of the interval [a,b] and probabilities p1,…,pk that add up to one, then we can consider the class of all continuous distributions such that
The density of the maximum entropy distribution for this class is constant on each of the intervals [aj-1,aj). The uniform distribution on the finite set {x1,…,xn} (which assigns a probability of 1/n to each of these values) is the maximum entropy distribution among all discrete distributions supported on this set.
Positive and specified mean: the exponential distribution[edit]
The exponential distribution, for which the density function is
is the maximum entropy distribution among all continuous distributions supported in [0,∞) that have a specified mean of 1/λ.
In the case of distributions supported on [0,∞), the maximum entropy distribution depends on relationships between the first and second moments. In specific cases, it may be the exponential distribution, or may be another distribution, or may be undefinable.[8]
Specified mean and variance: the normal distribution[edit]
The normal distribution N(μ,σ2), for which the density function is
has maximum entropy among all real-valued distributions supported on (−∞,∞) with a specified variance σ2 (a particular moment). The same is true when the mean μ and the variance σ2 is specified (the first two moments), since entropy is translation invariant on (−∞,∞). Therefore, the assumption of normality imposes the minimal prior structural constraint beyond these moments. (See the differential entropy article for a derivation.)
Discrete distributions with specified mean[edit]
Among all the discrete distributions supported on the set {x1,…,xn} with a specified mean μ, the maximum entropy distribution has the following shape:
where the positive constants C and r can be determined by the requirements that the sum of all the probabilities must be 1 and the expected value must be μ.
For example, if a large number N of dice are thrown, and you are told that the sum of all the shown numbers is S. Based on this information alone, what would be a reasonable assumption for the number of dice showing 1, 2, …, 6? This is an instance of the situation considered above, with {x1,…,x6} = {1,…,6} and μ = S/N.
Finally, among all the discrete distributions supported on the infinite set 
where again the constants C and r were determined by the requirements that the sum of all the probabilities must be 1 and the expected value must be μ. For example, in the case that xk = k, this gives
such that respective maximum entropy distribution is the geometric distribution.
Circular random variables[edit]
For a continuous random variable 
When the mean and variance of the angles 

Maximizer for specified mean, variance and skew[edit]
There exists an upper bound on the entropy of continuous random variables on 


However, the maximum entropy is ε-achievable: a distribution’s entropy can be arbitrarily close to the upper bound. Start with a normal distribution of the specified mean and variance. To introduce a positive skew, perturb the normal distribution upward by a small amount at a value many σ larger than the mean. The skewness, being proportional to the third moment, will be affected more than the lower order moments.
This is a special case of the general case in which the exponential of any odd-order polynomial in x will be unbounded on 


Maximizer for specified mean and deviation risk measure[edit]
Every distribution with log-concave density is a maximal entropy distribution with specified mean μ and Deviation risk measure D.[10]
In particular, the maximal entropy distribution with specified mean 

Other examples[edit]
In the table below, each listed distribution maximizes the entropy for a particular set of functional constraints listed in the third column, and the constraint that x be included in the support of the probability density, which is listed in the fourth column.[6][7] Several examples (Bernoulli, geometric, exponential, Laplace, Pareto) listed are trivially true because their associated constraints are equivalent to the assignment of their entropy. They are included anyway because their constraint is related to a common or easily measured quantity. For reference, 


| Distribution Name | Probability density/mass function | Maximum Entropy Constraint | Support |
|---|---|---|---|
| Uniform (discrete) |  |
None | 
|
| Uniform (continuous) |  |
None | ![[a,b],](https://wikimedia.org/api/rest_v1/media/math/render/svg/23cb97ebba2cd3175f9a77446963c1849fc353ee)
|
| Bernoulli |  |
 |

|
| Geometric |  |
 |

|
| Exponential |  |
 |

|
| Laplace |  |
 |

|
| Asymmetric Laplace |  |
 |

|
| Pareto |  |
 |

|
| Normal |  |
 |

|
| Truncated normal | (see article) |  |
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
|
| von Mises |  |
 |

|
| Rayleigh |  |
 |

|
| Beta |  for for  |
  |
![[0,1],](https://wikimedia.org/api/rest_v1/media/math/render/svg/43e2b417e116123c724ee6f69cf309f6ad17a2d0)
|
| Cauchy |  |
 |

|
| Chi |  |
![{displaystyle operatorname {E} (x^{2})=k,,operatorname {E} (ln(x))={frac {1}{2}}left[psi left({frac {k}{2}}right)!+!ln(2)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63679f8512597d2338b1863ec3f86080b676c049) |

|
| Chi-squared |  |
 |

|
| Erlang |  |
 |

|
| Gamma |  |
 |

|
| Lognormal |  |
 |

|
| Maxwell–Boltzmann |  |
 |

|
| Weibull |  |
 |

|
| Multivariate normal |   |
 |

|
| Binomial |  |
 [11] [11] |

|
| Poisson |  |
 [11] [11] |

|
| Logistic |  |
 |

|
The maximum entropy principle can be used to upper bound the entropy of statistical mixtures.[12]
See also[edit]
- Exponential family
- Gibbs measure
- Partition function (mathematics)
- Maximal entropy random walk — maximizing entropy rate for a graph
Notes[edit]
- ^ For example, the class of all continuous distributions X on R with E(X) = 0 and E(X2) = E(X3) = 1 (see Cover, Ch 12).
Citations[edit]
- ^ Williams, D. (2001), Weighing the Odds, Cambridge University Press, ISBN 0-521-00618-X (pages 197-199).
- ^ Bernardo, J. M., Smith, A. F. M. (2000), Bayesian Theory, Wiley. ISBN 0-471-49464-X (pages 209, 366)
- ^ O’Hagan, A. (1994), Kendall’s Advanced Theory of Statistics, Vol 2B, Bayesian Inference, Edward Arnold. ISBN 0-340-52922-9 (Section 5.40)
- ^ Botev, Z. I.; Kroese, D. P. (2011). «The Generalized Cross Entropy Method, with Applications to Probability Density Estimation» (PDF). Methodology and Computing in Applied Probability. 13 (1): 1–27. doi:10.1007/s11009-009-9133-7. S2CID 18155189.
- ^ Botev, Z. I.; Kroese, D. P. (2008). «Non-asymptotic Bandwidth Selection for Density Estimation of Discrete Data». Methodology and Computing in Applied Probability. 10 (3): 435. doi:10.1007/s11009-007-9057-z. S2CID 122047337.
- ^ a b c Lisman, J. H. C.; van Zuylen, M. C. A. (1972). «Note on the generation of most probable frequency distributions». Statistica Neerlandica. 26 (1): 19–23. doi:10.1111/j.1467-9574.1972.tb00152.x.
- ^ a b Park, Sung Y.; Bera, Anil K. (2009). «Maximum entropy autoregressive conditional heteroskedasticity model» (PDF). Journal of Econometrics. 150 (2): 219–230. CiteSeerX 10.1.1.511.9750. doi:10.1016/j.jeconom.2008.12.014. Archived from the original (PDF) on 2016-03-07. Retrieved 2011-06-02.
- ^ Dowson, D.; Wragg, A. (September 1973). «Maximum-entropy distributions having prescribed first and second moments». IEEE Transactions on Information Theory (correspondance). 19 (5): 689–693. doi:10.1109/tit.1973.1055060. ISSN 0018-9448.
- ^ a b Jammalamadaka, S. Rao; SenGupta, A. (2001). Topics in circular statistics. New Jersey: World Scientific. ISBN 978-981-02-3778-3. Retrieved 2011-05-15.
- ^ a b Grechuk, B., Molyboha, A., Zabarankin, M. (2009) Maximum Entropy Principle with General Deviation Measures,
Mathematics of Operations Research 34(2), 445—467, 2009. - ^ a b Harremös, Peter (2001), «Binomial and Poisson distributions as maximum entropy distributions», IEEE Transactions on Information Theory, 47 (5): 2039–2041, doi:10.1109/18.930936.
- ^ Frank Nielsen; Richard Nock (2017). «MaxEnt upper bounds for the differential entropy of univariate continuous distributions». IEEE Signal Processing Letters. IEEE. 24 (4): 402-406. Bibcode:2017ISPL…24..402N. doi:10.1109/LSP.2017.2666792. S2CID 14092514.
References[edit]
- Cover, T. M.; Thomas, J. A. (2006). «Chapter 12, Maximum Entropy» (PDF). Elements of Information Theory (2 ed.). Wiley. ISBN 978-0471241959.
- F. Nielsen, R. Nock (2017), MaxEnt upper bounds for the differential entropy of univariate continuous distributions, IEEE Signal Processing Letters, 24(4), 402-406
- I. J. Taneja (2001), Generalized Information Measures and Their Applications. Chapter 1
- Nader Ebrahimi, Ehsan S. Soofi, Refik Soyer (2008), «Multivariate maximum entropy identification, transformation, and dependence», Journal of Multivariate Analysis 99: 1217–1231, doi:10.1016/j.jmva.2007.08.004
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Понятие энтропии ввел Р. Клаузиус в 1865 г.
Энтропия – функция состояния
Для того чтобы выяснить в чем состоит физический смысл энтропии, рассмотрим изотермический процесс и приведенное количество теплоты в этом процессе на очень малом участке этого процесса -$frac{delta Q}{T}$, где $delta Q$ – количество теплоты, которое получает тело, $T$ – температура тела.
Приведенное количество теплоты, которое сообщается телу в любом обратимом круговом процессе:
$oint {frac{delta Q}{T}=0left( 1 right).}$
Равенство нулю левой части выражения (1), который берут по замкнутому контуру, означает, что отношение δQ/T – это полный дифференциал некоторой функции состояния системы, которая не зависит от формы пути перехода системы из начального состояния в конечное.
Введем следующее обозначение:
$frac{delta Q}{T}=dSleft( 2 right)$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 1
Энтропией ($S$) называют функцию состояния, дифференциал которой равен приведенному количеству тепла на малом участке термодинамического процесса, которое передано системе в этом процессе.
Для обратимых процессов изменение энтропии равно нулю:
$Delta S=0left( 3 right)$.
Если выполняется необратимый процесс, то энтропия системы увеличивается:
$Delta S$>$0, left( 4 right)$.
Все реальные процессы являются необратимыми, поэтому в реальности энтропия изолированной системы способна только расти. Она становится максимальной в состоянии термодинамического равновесия.
Замечание 1
Формулы (3) и (4) выполняются только в том случае, если система замкнута. В том случае, если термодинамическая система может обмениваться теплом с внешней средой, то поведение энтропии может быть любым.
«Энтропия простыми словами с формулами» 👇
Неравенство Клаузиуса
Выражения (3) и (4) объединяются в неравенство, которое называется неравенством Клаузиуса:
$Delta Sge left( 5 right)$.
Неравенство Клаузиуса означает, что для замкнутой системы энтропия способна увеличиваться (если процесс необратим), или не изменяется (процесс обратим).
Неравенство Клаузиуса является математической записью второго начала термодинамики.
Знак изменения энтропии указывает направление течения процесса в обратимом процессе.
Во всех ординарных термодинамических системах при стремлении температуры к бесконечности, внутренняя энергия системы безгранично растет. Абсолютная температура при равновесных процессах может только большей нуля, следовательно, если система подвергается нагреву, то:
$dS$>$0.$
При уменьшении температуры системы имеем:
$dS$
Изменение энтропии в равновесном процессе
Допустим, что термодинамическая система совершает равновесный переход из состояния 1 в состояние 2, тогда изменение энтропии найдем как:
$Delta S=S_{2}-S_{1}=intlimits_1^2 {frac{delta Q}{T}=intlimits_1^2{frac{dU+delta A}{T}left( 6 right),} }$
где $dU$ – изменение внутренней энергии в рассматриваемом процессе; $delta A$ – работа, выполняемая в этом процессе.
Выражение (6) способно определить энтропию с точностью до аддитивной константы. Это означает то, что физическим смыслом обладает не энтропия, а ее разность.
$S=intlimits_{обр} {frac{delta Q}{T}+const, left( 7 right).}$
Свойства энтропии
Замечание 2
Энтропия – аддитивная величина. Это означает, что энтропию системы можно найти как сумму энтропий тел, которые эту систему образуют.
Свойство аддитивности имеют:
- масса;
- внутренняя энергия;
- количество теплоты.
Аддитивными не являются:
- объем,
- температура,
- давление.
Определение 2
Термодинамический процесс, в котором энтропия остается постоянной, называется изоэнтропийным процессом.
Так, при обратимом адиабатном процессе мы имеем:
$delta Q=0to S=const.$
Энтропия однородной термодинамической системы – это функция пары независимых параметров, характеризующих ее состояние, например, $ p,V$ или $ T,V$ при $ m=const$.
В этой связи можно записать, что:
$left( V,T right)=intlimits_0^T {C_{V}frac{dT}{T}+S_{01, }left( 8right).}$
или
$Sleft( p,T right)=intlimits_0^T {C_{p}frac{dT}{T}+S_{02, }left( 9right),}$
где $intlimits_0^T {C_{V}frac{dT}{T},}$ – находят для обратимого изобарного процесса; $intlimits_0^T {C_{p}frac{dT}{T}}$ – вычисляют для обратимого изохорного процесса, при изменении температуры от 0К до $T$; $C_V$ – теплоемкость изохорного процесса; $C_p$ – теплоемкость при изобарном процессе; $S_{01 }=S(V,0)$ ; $S_{02 }=S(p,0).$
Статистический смысл энтропии
Допустим, что энтропия в обратимом процессе претерпевает изменения под воздействием внешних условий, которые оказывают влияние на систему. Механизм действия этих условий на энтропию можно сформулировать так:
- Внешние условия определяют микросостояния, которые доступны системе, а также их количество.
- В рамках доступных для системы микросостояний, она приходит в состояние равновесия.
- Энтропия получает соответствующее значение. Получается, что величина энтропии идет за изменением внешних условий, принимая наибольшую величину, совместимую с внешними условиями.
Глубокий смысл энтропии раскрывается в статистической физике. Энтропия связана с термодинамической вероятностью состояния системы.
Определение 3
Термодинамическая вероятность ($W$) – количество способов, реализации данного состояния термодинамической системы. Или иначе, это число микросостояний, реализующих данное макросостояние.
Термодинамическая вероятность всегда больше или равна единице.
Энтропия системы и термодинамическая вероятность связаны между собой формулой Больцмана:
$S=k ln(W) (10),$
где $k$ – постоянная Больцмана.
- Формула (10) означает, что энтропия определена натуральным логарифмом количества микросостояний, которые реализуют рассматриваемое макросостояние.
- Согласно формуле Больцмана, энтропия – это мера вероятности состояния термодинамической системы.
- Говорят, что энтропия – мера беспорядка системы. Это статистическая интерпретация энтропии. Большее количество микросостояний, которое осуществляет макросостояние, соответствует большей энтропии.
- Если система находится в состоянии термодинамического равновесия, что соответствует наиболее вероятному состоянию системы, количество микросостояний наибольшее, энтропия в этом случае максимальна.
- Поскольку при необратимых процессах энтропия увеличивается, при статистическом толковании это значит, процессы в замкнутой системе проходят в направлении роста количества микросостояний. Это означает, что процессы идут от менее вероятных к более вероятным, до достижения вероятностью максимальной величины.
Замечание 3
Все статистические законы справедливы для систем, которые составлены из огромного количества частиц. Но эти законы могут нарушаться с небольшим числом частиц. Для систем с малым количеством частиц возможны флуктуации, это значит, что энтропия и термодинамическая вероятность состояний замкнутой системы на некотором временном отрезке могут убывать, а не расти или не изменяться.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Дулесов А.С.
1
Семенова М.Ю.
1
Хрусталев В.И.
1
1 ГОУ ВПО «Хакасский государственный университет им.Н.Ф. Катанова», Абакан
Рассмотрены свойства присущие энтропии необходимые при определении неопределенности состояний элементов, влияющих на изменение структуры технической системы. Основываясь на теории информации, выделены классические выражения определения энтропии, когда состояния элементов рассматриваются как независимые, совместные и возникающие при определенных условиях. Математические выкладки и представленные поясняющие примеры свидетельствуют о возможностях их применения для определения энтропии технических систем. Выделено свойство энтропии, которое указывает на необходимость рассмотрения только совместных состояний элементов, так как они связаны между собой не только через структурные, но и функциональные связи системы.
энтропия; мера неопределенности: техническая система; надежность
1. Дулесов А.С., Ускова Е.А. Применение формулы Хартли для оценки структурных связей элементов в задаче обеспечения надежного функционирования технических систем // Вопросы современной науки и практики. Университет им. В.И. Вернадского. – 2009. – №6(20). – С. 37–41.
2. Дулесов А.С., Ускова Е.А. Применение подходов Хартли и Шеннона к задачам определения количества информации технических систем // Вопросы современной науки и практики. Университет им. В.И. Вернадского. – 2009. –№2(16). – С. 46–50.
3. Леус В.А. О геометрическом обобщении энтропии // Проблемы передачи информации. – 2003. – Т. 39, Вып. 2. – С. 15–22.
4. Дулесов А.С., Швец С.В., Хрусталев В.И. Применение формулы Шеннона и геометрического обобщения для определения энтропии // Перспективы науки. Science prospects. – 2010. – № 3[05]. – С. 15–18.
Для технических систем предъявляются требования к сохранению высокого уровня надежности. Эволюция таких систем определила вопросы надежности в качестве главного направления в развитии науки о системной надежности.
Всякая система обладает определенной детерминированной или вероятностной природой функционирования. Поиск оптимальных путей решения проблем надежности наталкивается на вопрос о взаимосвязи структуры и функции. Имея структуру, можно сделать вывод о выполняемой ею функции. В основе надежного функционирования технических систем лежат принципы единства и избыточности структуры и функции.
Соблюдение принципа избыточности требует согласованных решений, вырабатываемых на основе экономических критериев, поскольку его нарушение приводит к недопустимому увеличению размеров, стоимости и других показателей. Поэтому в процессе проектирования и эксплуатации технических систем ключевое место для решения проблем надежности занимают процессы обработки данных и принятия решений. При этом параметры системы и приложенные к ней воздействия интерпретируют в виде детерминированных или статистических моделей. Последние имеют значение при исследовании сложных систем с большим количеством связей и факторов воздействия. Рассматривая состояния системы, из их многообразия выделяют подмножество состояний, различающихся между собой с точки зрения показателей надежности. Их отслеживание в динамике позволяет судить об эволюции системы, возможностях выбора вариантов решений, направленных на сохранение или повышение уровня надежности.
Случайное поведение технической системы, обусловленное влиянием незапланированных факторов, связано с неопределенностью, степень которой в различные моменты времени будет разной. На практике важно уметь численно оценивать степень неопределенности разнообразных состояний (структурных изменений) системы, чтобы иметь возможность сравнить их между собой. Важным показателем неопределенности является энтропия, определение величины которой может служить мерой структурного состояния системы. Рост энтропии отражает тенденцию к развитию хаотических процессов в системе, что свидетельствует о старении элементов системы, отсутствии должного управления и организационного поведения. Поэтому аналитику важно знать, оправдывает ли система возложенные на неё функции.
Энтропия как мера степени неопределенности. Каждый элемент технической системы несет информацию в орган контроля и управления о своем состоянии, природа поведения которого вероятностна. С точки зрения теории структурной надежности элемент может находиться в одном из двух состояний: работоспособное или отказ. Здесь мы имеем k = 2 равновероятных исхода опыта, то есть процесса эксплуатации элемента. Искомая численная характеристика степени неопределенности, а в нашем случае надежности эксплуатации элемента должна зависеть от k исходов и описываться функцией f(k). При k = 1 она должна обращаться в нуль, свидетельствуя о наличии полной определенности опыта.
Поскольку в системе имеется множество элементов, то данная функция должна учитывать неопределенность состояний всех рассматриваемых элементов. Пусть имеется два элемента α и β, которые работают независимо друг от друга (например, трансформаторы, кабели, линии и т.д., резервирующие друг друга с целью повышения надежности передачи энергии). Тогда с позиции надежности передачи каждый из этих элементов может находиться в k = 2 состояниях (работа и отказ). Если рассматривать сложный опыт αβ (параллельная независимая работа элементов), то степень его неопределенности будет характеризоваться функцией: для двух элементов f(kΣ) = f(k1) + f(k2); для многих — f(kΣ) = Σif(ki). Тогда мера неопределенности опыта, имеющего k = 2 равновероятных исходов, определится как logkΣ = Σilogki. Основание логарифма для k = 2 принимается равным 2, а неопределенность будет измеряться в битах.
Элемент α системы может находиться в двух состояниях с вероятностями: р — вероятность работоспособного состояния; q = 1 — р — вероятность отказа. Тогда в результате опыта оба исхода с вероятностями р и q дадут энтропию (например для элемента α):
, (1)
при условии p + q = 1.
Далее выделим свойства, свидетельствующие о том, что энтропия:
1) является величиной вещественной и неотрицательной, так как всегда 0 ≤ р ≤ 1, то log p ≤ 0 и, следовательно, — рlog p ≥ 0;
2) ограниченна из-за наличия условия: p + q = 1;
3) будет равна нулю, когда заранее известен исход опыта (p = 1 и q = 0, и наоборот: p = 0, q = 1);
4) максимальна, если оба состояния элемента равновероятны, то есть когда p = q = 0,5;
5) для бинарных (двоичных) сообщений может изменяться от нуля до единицы (см. п.1);
6) достигает максимума, равного единице, при p = q = 0,5.
Значения вероятностей могут быть получены расчетным путем исходя из опытной эксплуатации систем. Исходными величинами могут служить интенсивности отказов и восстановлений, время наработки на отказ и время восстановления и др. Соответственно вероятности отказа и работоспособности (безотказной работы) являются обобщенными показателями надежности и позволяют по выражению (1) определить обобщенное значение энтропии.
Исторически введение меры энтропии закрепилось за инженером Хартли, предложившим характеризовать степень неопределенности опыта с k исходами числом logk. Его мера базируется на предположении равновероятности исходов (для нашего случая: p = q = 0,5). Например, в работе [1] имеются пояснения, касающиеся определения степени неопределенности по Хартли. Однако данная мера малопригодна для нашего случая, в котором исходы не равновероятны.
Впоследствии К. Шеннон предложил принять в качестве меры неопределенности опыта α с исходами (состояниями) k = 1, 2, …, m величину
,
при условии . (2)
Из выражения (2) видно, что при состояниях m = 2 имеем выражение (1). Возможности применения (2) для определения энтропии структуры технической системы из двух элементов представлены в работе [2].
Следует иметь в виду, что меры Хартли и Шеннона не могут претендовать на полный учет всех факторов, определяющих неопределенность поведения системы в полном смысле, какая может встретиться в жизни. Например, следует определить энтропию для двух ансамблей случайных величин. В первом ансамбле имеется три величины (0,9; 1,1 и 1,0) с вероятностями соответственно (0,25; 0,5; 0,25), во втором — величины (100; 1; 1000) с вероятностями (0,5; 0,25; 0,25). Применив условие (2), видно, энтропии равнозначны и зависят только от вероятностей исходов опытов, но не зависят от того, каковы сами исходы: насколько они «близки» или «далеки» друг от друга в смысле величин. Тем не менее в работе [3] представлены выражения для определения такого рода соотношений между исходами, а в [4] даны пояснения о возможности применения их на практике.
Отмечая свойства и особенности применения энтропии, следует заметить, что при анализе работы технической системы основную роль играют статистические закономерности, поскольку в ней присутствуют потоки энергии, обеспечивающие её жизнедеятельность. Поэтому энтропия должна быть приспособлена для определения степени неопределенности сложных структур («составных опытов»), в которых «составные опыты» представляют собой серии следующих друг за другом испытаний.
Далее предложим выражения определения различного рода энтропий, пояснив их полезность при определении меры неопределенности структурированных систем.
Энтропия элементов, функционирующих независимо. Пусть система или подсистема состоит из двух независимо функционирующих элементов α и β. Отметим, что условие о независимости функционирования элементов формально, так как в технической системе большинство из них связано между собой как структурно, так и функционально. Рассматривая работу элементов как некоторые опыты α и β, для каждого из них будем иметь по два исхода (состояния) k = 2 с вероятностями р и q: для первого элемента состояния обозначим как Ap и Aq с вероятностями p(A) и q(A), для второго — Bp и Bq с вероятностями p(B) и q(B).
Рассмотрим сложный опыт α + β, состоящий в том, что рассматриваются два одновременно работающих элемента. Их эксплуатация показывает, что налицо имеем 2·2 = 4 исхода: оба работают — ApBp; 1-й работает, 2-й в ремонте — ApBq; 1-й в ремонте, 2-й работает — AqBp; оба в ремонте — AqBq.
Покажем далее, что для такого опыта выполняется правило сложения энтропий:
H(α + β) = H(α) + H(β).
Согласно вышепредставленным выражениям и опустив двойку в основании логарифма, запишем:
H(α + β) = -p(ApBp) log p(ApBp) — p(ApBq) log p(ApBq) —
— p(AqBp) log p(AqBp) — p(AqBq) log p(AqBq).
Так как элементы функционируют независимо друг от друга, например, отказ одного не влияет на отказ другого, то p(ApBp) = p(Ap)p(Bq), p(ApBq) = p(Ap)p(Bq) и т.д. Тогда последнее выражение можно переписать в виде
H(α + β) = -p(Ap)p(Bp)(log p(Ap) + logp(Bp)) — p(Ap)p(Bq)(log p(Ap) + logp(Bq)) —
— p(Aq)p(Bp)(logp(Aq) + logp(Bp)) — p(Aq)p(Bq)(log p(Aq) + logp(Bq)) =
= -p(Ap)(p(Bp) + p(Bq))logp(Ap) — p(Ap)[p(Bp)logp(Bp) + p(Bq)logp(Bq)] — p(Aq)(p(Bp) + + p(Bq))logp(Aq) — p(Aq)[p(Bp)logp(Bp) + p(Bq)log p(Bq)].
В данной формуле выражение в квадратных скобках дает нам для второго элемента энтропию со знаком «минус» (- H(β)), так же p(Bp) + p(Bq) = 1. Тогда последнее выражение перепишем в следующем виде:
H(α + β) = — p(Ap) log p(Ap) + p(Ap) H(β) — p(Aq) log p(Aq) + p(Aq) H(β).
После незначительных преобразований (с учетом, что p(Ap) + p(Aq) = 1) получим окончательно
H(α + β) = H(α) + H(β).
Если перейти к символам следующего содержания: i — порядковый номер элемента в системе; р и q — вероятности, тогда энтропия для двух независимо функционирующих элементов запишется следующим образом:

при условии pi+qi = 1.
Для n независимо функционирующих элементов будем иметь:
(3)
Выражение (3) применимо, когда состояние элемента не зависит от состояния других элементов. По сути, такой элемент рассматривается как отдельная подсистема без учета влияния внешних факторов.
Совместная энтропия. Известно, что практически все элементы в технической системе взаимосвязаны. Например, связь может быть обусловлена функцией передачи энергии от источника к потребителю. Поэтому события взаимосвязанных элементов могут совмещаться. Требуется определить энтропию совместного появления статистически зависимых опытов. Рассмотрим меру неопределенности для двух элементов, для каждого из них будем иметь по два исхода k = 2 с вероятностями р и q, с общим количеством исходов, равным 4, то есть N = 2n, где n — количество элементов в системе.
Учитывая обозначения состояний, представленных выше, запишем:
H(αβ) = — p(ApBp) log p(ApBp) — p(ApBq) log p(ApBq) — p(AqBp) log p(AqBp) —
— p(AqBq) log p(AqBq) = — p(Ap)p(Bp) log p(Ap)p(Bp) — p(Ap)p(Bq) log p(Ap)p(Bq) —
— p(Aq)p(Bp) log p(Aq)p(Bp) — p(Aq)p(Bq) log p(Aq)p(Bq).
В данном выражении соблюдается условие:
p(Ap)p(Bp) + p(Ap)p(Bq) + p(Aq)p(Bp) + p(Aq)p(Bq) = 1,
или p1p2 + p1q2 + q1p2 + q1q2 = 1, где подстрочные символы 1 и 2 указывают на номер элемента.
В общем виде совместная энтропия двух элементов
,
при , (4)
при условии, что сумма вероятностей 4-х состояний равна 1, а при равновероятных исходах H(αβ) = 2. Символы i и j означают соответственно порядковые номера состояний элементов. Условие (4) свидетельствует о том, что совместные события рассматриваются как независимые. Для трех и более взаимосвязанных элементов количество совместных состояний N = 2n.
Совместная энтропия, как было отмечено выше, является мерой неопределенности или мерой разнообразия состояний системы. С ростом числа её элементов и, следовательно, совместных состояний, энтропия увеличивается, достигая своего максимума при условии, что вероятности всех совместных состояний одинаковы.
Таким образом, совместная энтропия служит мерой свободы системы: чем больше энтропия, тем больше состояний доступно системе, тем больше у нее степеней свободы.
Дополнительно заметим, что выражения для определения совместной энтропии можно применить тогда, когда техническая система рассматривается с позиции неопределенности её разнообразных состояний (структурных изменений) с тем, чтобы иметь возможность сравнивать их между собой.
Однако совместная энтропия не позволяет определять степень неопределенности для системы, в которой решающую роль играет её структурное содержание при передаче материи или энергии от источника к потребителю. Например, по условию надежности передачи энергии выражение (4) не позволяет сопоставить между собой меры неопределенностей поставки энергии по цепочкам из двух последовательно и параллельно соединенных элементов. Здесь требуется выработать и использовать иные выражения, способные учитывать неопределенность в объемах поставки ресурсов (энергии) от источника к потребителю.
Условная энтропия. Пусть в системе два элемента α и β функционируют независимо. Например, в цепях из последовательно соединенных элементов отказ (предшествующее событие) одного из них приводит к отказу (последующему событию) другого элемента. Здесь результат второго опыта полностью определяется результатом первого. В этом случае энтропия не может быть определена как сумма энтропий H(α) и H(β), поскольку после появления события α событие β уже не будет содержать никакой неопределенности. Следовательно, можно предположить, что энтропия сложного опыта из α и β будет равна энтропии первого опыта α, а не сумме энтропий опытов α и β.
Покажем далее, чему равна энтропия сложного опыта из α и β в общем случае, то есть условная энтропия H(β/α). Воспользуемся ранее записанным выражением для определения H(αβ), выразив условную энтропию в виде:
В данном выражении нельзя использовать произведения, заменив, например, p(ApBp) на p(Ap)p(Bp) и далее по формуле. Поэтому введем взамен p(ApBp) и далее выражение p(Ap)p(Bp/Ap), в котором p(Bp/Ap) — условная вероятность события Bp при условии появления события Ap. Тогда последнее выражение перепишем в виде:

Известно, что p(Bp/Ap) + p(Bq/Ap) = 1 и p(Bp/Aq) + p(Bq/Aq) = 1. Кроме этого, если события Bp и Bq в опыте β являются достоверными, то условные вероятности p(Bp + Bq) /Ap = 1 и p(Bp + Bq) / Aq = 1.
Выделим из последнего выражения слагающие:
— p(Ap) log p(Bp/Ap) — p(Ap) log p(Bq/Ap)
и
— p(Aq) log p(Bp/Aq) — p(Aq) log p(Bq/Aq),
каждая из которых представляет собой энтропию опыта β при условии, что имели место события Ap и Aq. Эти два выражения — условные энтропии опыта β при условиях Ap и Aq, обозначаемые как H(B/Ap) и H(B/Aq).
Таким образом, выражение для H(β/α) может быть переписано в виде:
H(β/α) = -p(Ap)log p(Ap)- p(Aq)log p(Aq) +
+ p(Ap)H(B/Ap) + p(Aq) H(B/Aq).
В данном выражении первый и второй члены представляют собой энтропию опыта α, то есть H(α). Два последних члена представляют собой случайной величины, принимающие с вероятностями p(Ap) и p(Aq) значения H(B/Ap) и H(B/Aq), то есть значения, равные условной энтропии опыта β при условии, что опыт α имеет исходы Ap и Aq. В общей совокупности оба значения получили название — средняя условная энтропия опыта β при условии достоверного выполнения опыта α. Её можно записать в виде
H(B/α) = p(Ap) H(B/Ap) + p(Aq) H(B/Aq).
Тогда окончательно запишем:
H(β/α) = H(α) + H(B/α). (5)
Выражение (5) является правилом сложения энтропий.
Добавим к вышеизложенному следующее: средняя условная энтропия H(β/α) играет существенную роль в решении задач о потерях в технических системах; если знаем заранее, какой именно исход Ap или Aq опыта α имел место, то при определении условных энтропий H(B/Ap) и H(B/Aq) опыта β можно игнорировать условные вероятности p(Bp/Ap), p(Bq/Ap), p(Bp/Aq) и p(Bq/Aq).
С другой стороны, средняя условная энтропия H(β/α), выполнение которой не предполагает заранее известным исход α, глубоко отражает взаимосвязь между элементами α и β.
Отметим некоторые свойства H(B/α). Если вероятности p(Ap) и p(Аp) отличны от нуля (то есть элемент α может находиться в двух состояниях), то H(B/α) = 0 в случае, если H(B/Ap) = H(B/Aq) = 0. Это означает следующее: при любом состоянии элемента α результат состояния элемента β становится полностью определенным. Например, для двух последовательно соединенных элементов α и β, состояния с вероятностями p(Ap) и p(Аp) первого по пути движения энергии элемента α полностью определяют состояния и вероятности второго элемента β. В данном случае будем иметь: H(β/α) = H(α). Если элементы α и β рассматривать как независимо функционирующие, то
H(B/Ap) = H(B/Aq) = H(β) и H(B/α) = H(β).
Рассматривая возможные состояния элементов α и β, из теории информации известно, что 0 ≤ H(B/α) ≤ H(β). Это означает следующее: когда исход опыта β полностью определяется исходом α и когда оба опыта независимы, то они являются крайними.
Пример расчета. Пусть имеется структура системы, состоящая из трех элементов n = 3. Для каждого из элементов известны вероятности работы: р1 = 0,9; р2 = 0,8; р3 = 0,7. Соответственно вероятности отказа: q1 = (1- р1) = 0,1; q2 = 0,2; q3 = 0,3.
Если предположить, что все элементы функционируют независимо друг от друга, то будем иметь сложный опыт α +β + γ с наличием N = 23 = 8 состояний. Согласно выражению (3) энтропия независимых элементов
H(α + β + γ) = — p1log p1 — q1log q1 — p2log p2 — q2log q2 — p3log p3 — q3log q3 =
= — 0,9 log 0,9 — 0,1 log 0,1 — 0,8 log 0,8 — 0,2 log 0,2 — 0,7 log 0,7 —
— 0,3 log 0,3 = 2,072 бит.
Максимальная энтропия достигается при равенстве q = р = 0,5:
Hmax(α + β + γ) = — 5·(0,5 log 0,5) = 3 бит.
Максимальная энтропия означает следующее: каждый элемент системы находится в максимальной степени неопределенности, равной 1, а система в степени 3 (равной числу её элементов).
В технической системе элементы рассматриваются как выполняющие единую задачу, поэтому теория структурной надежности рассматривает появление различных состояний как совместные события. Их количество равно 8 и они рассматриваются как независимые. Запишем выражение и определим совместную энтропию трех элементов:

Максимальная энтропия достигается при равенстве q = р = 0,5:
Hmax(αβγ) = — 8·(0,53 log 0,53) = 3 бит.
Как видно из примера,
H(α + β + γ) = H(αβγ).
Это означает, что опыты в первом случае рассматривались как независимые в нарушении второго свойства энтропии.
Выводы
1. Дано теоретическое обоснование возможностей определения энтропии для технических систем, элементы которых несут информацию о вероятностях состояний (работоспособности и отказа).
2. Выделены свойства, присущие энтропии, когда элементы функционируют независимо и не независимо друг от друга, а также, когда их состояния совместны.
3. Свойства и выражения определения энтропии справедливы для технических систем в независимости от способа соединения их элементов.
Рецензенты:
Булакина Е.Н., д.т.н., доцент, профессор кафедры автомобилей и автомобильного хозяйства Хакасского технического института — филиала ФГАОУ ВПО «Сибирский федеральный университет», г. Абакан;
Кочетков В.П., д.т.н., профессор, профессор кафедры электроэнергетики Хакасского технического института — филиала ФГАОУ ВПО «Сибирский федеральный университет», г. Абакан.
Работа поступила в редакцию 22.02.2011.
Библиографическая ссылка
Дулесов А.С., Семенова М.Ю., Хрусталев В.И. СВОЙСТВА ЭНТРОПИИ ТЕХНИЧЕСКОЙ СИСТЕМЫ // Фундаментальные исследования. – 2011. – № 8-3.
– С. 631-636;
URL: https://fundamental-research.ru/ru/article/view?id=28596 (дата обращения: 27.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Мотивация: метод моментов
Метод моментов – это ещё один способ, наряду с методом максимального правдоподобия, оценки параметров распределения по данным $x_1,ldots,x_N$. Суть его в том, что мы выражаем через параметры распределения теоретические значения моментов $mu_k = mathbb{E}x^k$ нашей случайной величины, затем считаем их выборочные оценки $widehat{mu}_k = frac1Nsum_ix_i^k$, приравниваем их все друг к другу и, решая полученную систему, находим оценки параметров. Можно доказать, что полученные оценки являются состоятельными, хотя могут быть смещены.
Пример 1. Оценим параметры нормального распределения $mathcal{N}(mu, sigma^2)$ с помощью метода моментов.
Попробуйте сделать сами, прежде чем смотреть решение.
Теоретические моменты равны
$$mu_1 = mu,quadmu_2 = sigma^2 + mu^2$$
Запишем систему:
$$begin{cases}
widehat{mu} = frac1Nsum_i x_i,
widehat{sigma}^2 + widehat{mu}^2 = frac1Nsum_ix_i^2
end{cases}$$
Из неё очевидным образом находим
$$widehat{mu} = frac1Nsum_ix_i $$
$$widehat{sigma}^2 = frac1Nsum_ix_i^2 — left(frac1Nsum_i x_iright)^2=$$
$$=frac1Nsum_ileft(x_i — widehat{mu}right)^2$$
Легко видеть, что полученные оценки совпадают с оценками максимального правдоподобия
Пример 2. Оценим параметр $mu$ логнормального распределения
$$p(x) = frac1{xsqrt{2pisigma^2}}expleft(-frac{(log{x} — mu)^2}{2sigma^2}right)$$
при известном $sigma^2$. Будет ли оценка совпадать с оценкой, полученной с помощью метода максимального правдоподобия?
Попробуйте сделать сами, прежде чем смотреть решение.
Теоретическое математическое ожидание равно $expleft(mu + frac{sigma^2}2right)$, откуда мы сразу находим оценку $widehat{mu} = logleft(sum_ix_iright) — frac{sigma^2}2$.
Теперь запишем логарифм правдоподобия:
$$l(X) = -sum_ilog{x_i} — sum_ifrac{(log{x_i} — mu)^2}{2sigma^2} + const$$
Дифференцируя по $mu$ и приравнивая производную к нулю, получаем
$$widehat{mu}_{MLE} = frac1Nsum_ilog{x_i}$$
что вовсе не совпадает с оценкой выше.
Несколько приукрасив ситуацию, можно сделать вывод, что первые два выборочных момента позволяют если не править миром, то уверенно восстанавливать параметры распределений. А теперь давайте представим, что мы посчитали $frac1Nsum_ix_i$ и $frac1Nsum_ix_i^2$, а семейство распределений пока не выбрали. Как же совершить этот судьбоносный выбор? Давайте посмотрим на следующие три семейства и подумаем, в каком из них мы бы стали искать распределение, зная его истинные матожидание и дисперсию?
Почему-то хочется сказать, что в первом. Почему? Второе не симметрично – но что нас может заставить подозревать, что интересующее нас распределение не симметрично? С третьим проблема в том, что, выбирая его, мы добавляем дополнительную информацию как минимум о том, что у распределения конечный носитель. А с чего бы? У нас такой инфомации вроде бы нет.
Общая идея такова: мы будем искать распределение, которое удовлетворяет только явно заданным нами ограничениям и не отражает никакого дополнительного знания о нём. Но чтобы эти нестрогие рассуждения превратить в формулы, придётся немного обогатить наш математический аппарат и научиться измерять количество информации.
Энтропия и дивергенция Кульбака-Лейблера
Измерять «знание» можно с помощью энтропии Шэннона. Она определяется как
$$color{#348FEA}{H(P) = -sum_xP(x)log{P(x)}}$$
для дискретного распределения и
$$color{#348FEA}{H(p) = -int p(x)log{p(x)}dx}$$
для непрерывного. В классическом определении логарифм двоичный, хотя, конечно, варианты с разным основанием отличаются лишь умножением на константу.
Неформально можно представлять, что энтропия показывает, насколько сложно предсказать значение случайной величины. Чуть более строго – сколько в среднем бит нужно потратить, чтобы передать информацию о её значении.
Пример 1. Рассмотрим схему Бернулли с вероятностью успеха $p$. Энтропия её результата равна
$$-(1 — p)cdotlog_2(1 — p) — pcdotlog_2{p}$$
Давайте посмотрим на график этой функции:
Минимальное значение (нулевое) энтропия принимает при $pin{0,1}$. В самом деле, для такого эксперимента мы всегда можем наверняка сказать, каков будет его исход; обращаясь к другой интерпретации – чтобы сообщить кому-то о результате эксперимента, достаточно $0$ бит (ведь получатель сообщения и так понимает, что вышло).
Максимальное значение принимается в точке $frac12$, что вполне соответствует тому, что при $p=frac12$ предсказать исход эксперимента сложнее всего.
Дополнение для ценителей математики.
Попробуем для этого простого примера объяснить, почему среднее число бит, необходимых для передачи информации об исходе эксперимента, выражается формулой с логарифмами.
Теперь пусть $p$ произвольно. Рассмотрим $N»1$ независимых испытаний $x_1,ldots, x_N$; среди них будет $n_0approx (1-p)N$ неудачных и $n_1approx pN$ удачных. Посчитаем, сколько бит потребуется, чтобы закодировать последовательность $x_i$ для известных $n_0$ и $n_1$. Общее число таких последовательностей равно $C_N^{n_1} = frac{N!}{n_0!n_1!}$, а чтобы закодировать каждую достаточно будет $log_2left(frac{N!}{n_0!n_1!}right)$ бит – это количество информации, содержащееся во всей последовательности. Таким образом, в среднем, чтобы закодировать результат одного испытания необходимо
$$frac1Nlog_2left(frac{N!}{n_0!n_1!}right)$$
бит информации. Перепишем это выражение, использовав формулу Стирлинга $log{N!}approx Nlog{N} — N$:
$$frac1Nleft(log_2{N!} — log_2{n_0!} — log_2{n_1!}right) approx $$
$$approx constcdotfrac1Nleft(Nlog_2{N} — N — n_0log_2{n_0} + n_0 — n_1log_2{n_1} + n_1right) =$$
$$=constcdotfrac1Nleft(Nlog_2{N} — (1-p)Nlog_2{(1-p)N} — pNlog_2{pN}right) =$$
$$=constcdotleft(-(1-p)cdotlog_2(1-p) — plog_2{p}right)$$
Вот мы и вывели формулу энтропии!
Пример 2. Энтропия нормального распределения $mathcal{N}(mu, sigma^2)$ равна $frac12log(2pisigma^2) + frac12$, и чем меньше дисперсия, тем меньше энтропия, что и логично: ведь когда дисперсия мала, значения сосредоточены возле матожидания, и они становятся менее «разнообразными».
Энтропия тесно связана с другим важным понятием из теории информации – дивергенцией Кульбака-Лейблера. Она определяется для плотностей $p(x)$ и $q(x)$ как
$$color{#348FEA}{KL(p,vertvert, q) = int p(x)log{frac{p(x)}{q(x)}}dx}$$
в непрерывном случае и точно так же, но только с суммой вместо интеграла в дискретном.
Теоретико-информационный смысл дивергенции Кульбака-Лейблера.
Дивергенцию можно представить в виде разности:
$$KL(p,vertvert, q) = (-int p(x)log{q(x)}dx) — (-int p(x)log{p(x)}dx)$$
Вычитаемое – это энтропия, которая, как мы уже поняли, показывает, сколько в среднем бит требуется, чтобы закодировать значение случайной величины. Уменьшаемое похоже по виду, и можно показать, что оно говорит о том, сколько в среднем бит потребуется на кодирование случайной величины с плотностью $p$ алгоритмом, оптимизированным для кодирования случайной величины $q$. Иными словами, дивергенция Кульбака-Лейблера говорит о том, насколько увеличится средняя длина кодов для значений $p$, если при настройке алгоритма кодирования вместо $p$ использовать $q$. Более подробно вы можете почитать, например, в этом посте.
Дивергенция Кульбака-Лейблера в некотором роде играет роль расстояния между распределениями. В частности, $KL(p,vertvert, q)geqslant0$, причём дивергенция равна нулю, только если распределения совпадают почти всюду. Но при этом она не является симметричной: вообще говоря, $KL(p,vertvert, q)ne KL(q,vertvert, p)$.
Вопрос на подумать. Пусть $p(x)$ – распределение, заданное на отрезке $[a, b]$. Выразите его энтропию через дивергенцию Кульбака-Лейблера $p(x)$ с равномерным на отрезке распределением $q_U(x)=frac1{b-a}mathbb{I}_{[a,b]}(x)$.
Попробуйте вывести сами, прежде чем смотреть решение.
Распишем дивергенцию:
$$KL(p,vertvert, q_U) = -left(-int_a^b p(x)log{p(x)}dxright) — int_a^b p(x)log{underbrace{q(x)}_{=frac1{b-a}text{ на }[a,b]}}dx=$$
$$=log(b-a) — H(p)$$
Аналогичное соотношение можно выписать и для распределения, заданного на конечном множестве.
Принцип максимальной энтропии
Теперь наконец мы готовы сформулировать, какие распределения мы хотим искать.
Принцип максимальной энтропии. Среди всех распределений на заданном носителе $mathbb{X}$, удовлетворяющих условиям $mathbb{E}u_1(x) = mu_1$, …, $mathbb{E}u_k(x) = mu_k$, где $u_i$ – некоторые функции, мы хотим иметь дело с тем, которое имеет наибольшую энтропию.
В самом деле, энтропия выражает нашу меру незнания о том, как ведёт себя распределение, и чем она больше – тем более «произвольное распределение», по крайней мере, в теории.
Давайте рассмотрим несколько примеров, которые помогут ещё лучше понять, почему некоторые распределения так популярны:
Пример 1. На конечном множестве $1,ldots,n$ наибольшую энтропию имеет равномерное распределение (носитель – конечное множество из $n$ элементов, других ограничений нет).
Доказательство.
Пусть $p_i$, $i=1,ldots,n$ – некоторое распределение, $q_i=frac1n$ – равномерное. Запишем их дивергенцию Кульбака-Лейблера:
$$KL(pvertvert q) = sum_i p_ilog{p_i} — sum_i p_ilog{q_i} =$$
$$= -H(p) + log{n}underbrace{sum_ip_i}_{=1}$$
Так как дивергенция Кульбака-Лейблера всегда неотрицательна, получаем, что $H(p)leqslantlog{n}$. При этом равенство возможно, только если распределения совпадают.
Пример 2. Среди распределений, заданных на всей вещественной прямой и имеющих заданные матожидание $mu$ и дисперсию $sigma^2$ наибольшую энтропию имеет нормальное распределение $mathcal{N}(mu,sigma^2)$.
Доказательство.
Пусть $p(x)$ – некоторое распределение, $q(x)simmathcal{N}(mu, sigma^2)$. Запишем их дивергенцию Кульбака-Лейблера:
$$KL(pvertvert q) = int p(x)log{p(x)}dx — int p(x)log{q(x)}dx =$$
$$= -H(p) — int p(x)left(-frac12log(2pisigma^2) — frac1{2sigma^2}(x — mu)^2right)dx =$$
$$= — H(p) +frac12log(2pisigma^2)cdotunderbrace{int p(x)dx}_{=1} + frac1{2sigma^2}underbrace{int(x — mu)^2p(x)dx}_{=mathbb{V}p=sigma^2} =$$
$$= — H(p) + underbrace{frac12log(2pisigma^2) + frac12}_{=H(q)}$$
Так как дивергенция Кульбака-Лейблера всегда неотрицательна, получаем, что $H(p)leqslant H(q)$. При этом равенство возможно, только если распределения $p$ и $q$ совпадают почти всюду, а с точки зрения теории вероятностей такие распределения различать не имеет смысла.
Пример 3. Среди распределений, заданных на множестве положительных вещественных чисел и имеющих заданное матожидание $lambda$ наибольшую энтропию имеет показательное распределение с параметром $frac1{lambda}$ (его плотность равна $p(x) = frac1{lambda}expleft(-frac1{lambda}xright)mathbb{I}_{(0;+infty)}(x)$).
Все хорошо знакомые нам распределения, не правда ли? Проблема в том, что они свалились на нас чудесным образом. Возникает вопрос, можно ли их было не угадать, а вывести как-нибудь? И как быть, если даны не эти конкретные, а какие-то другие ограничения? Оказывается, что при некоторых не очень обременительных ограничениях ответ можно записать с помощью распределений экспоненциального класса. Давайте же познакомимся с ними поближе.
Экспоненциальное семейство распределений
Говорят, что семейство распределений относится к экспоненциальному классу, если оно может быть представлено в следующем виде:
$$color{#348FEA}{p(xverttheta) = frac1{h(theta)}g(x)cdotexpleft(theta^Tu(x)right)}$$
где $theta$ – вектор вещественнозначных параметров (различные значения которых дают те или иные распределения из семейства), $h, g > 0$, $u$ – некоторая вектор-функция, и, разумеется, сумма или интеграл по $x$ равняется единице. Последнее, в частности, означает, что
$$h(theta) = int g(x)expleft(theta^Tu(x)right)dx$$
(или сумма в дискретном случае).
Пример 1. Покажем, что нормальное распределение принадлежит экспоненциальному классу. Для этого мы должны представить привычную нам функцию плотности
$$p(x vert mu, sigma^2) = frac{1}{sqrt{2pi}sigma}expleft(-frac{(x-mu)^2}{2sigma^2}right)$$
в виде
$$p(xverttheta) = frac{g(x)cdotexpleft(sum_itext{(параметр)}_icdottext{(функция от x)}_iright)}{text{что-то, не зависящее от $x$}}$$
Распишем
$$frac{1}{sqrt{2pi}sigma}expleft(-frac{(x-mu)^2}{2sigma^2}right) =
frac{1}{sqrt{2pi}sigma}expleft(-frac1{2sigma^2}x^2 + frac{mu}{sigma^2}x — frac{mu^2}{2sigma^2}right)=$$ $$
frac{expleft(-frac1{2sigma^2}x^2 + frac{mu}{sigma^2}xright)}{sqrt{2pi}sigmaexpleft(frac{mu^2}{2sigma^2}right)}=$$
Определим
$$u_1(x) = x,qquad u_2(x) = x^2$$
$$theta_1 = frac{mu}{sigma^2},quad theta_2 = -frac1{2sigma^2}$$
$$h(theta) = sqrt{2pi}sigmaexpleft(frac{mu^2}{2sigma^2}right)$$
Если теперь всё-таки честно выразить $h$ через $theta$ (это мы оставляем в качестве лёгкого упражнения), то получится
$$p(x vert mu, sigma^2) = frac1{h(theta)}expleft(theta^Tu(x)right)$$
В данном случае функция $g(x)$ просто равна единице.
Пример 2. Покажем, что распределение Бернулли принадлежит экспоненциальному классу. Для этого попробуем преобразовать функцию вероятности (ниже $x$ принимает значения $0$ или $1$):
$$P(x vert p) = p^x(1 — p)^{1 — x} = expleft(xlog{p} + (1 — x)log(1 — p)right)$$
Теперь мы можем положить $u(x) = left(x, 1 — xright)$, $theta = left(log{p}, log(1 – p)right)$, и всё получится. Единственное, что смущает, – это то, что компоненты вектора $u(x)$ линейно зависимы. Хотя это не является формальной проблемой, но всё же хочется с этим что-то сделать. Исправить это можно, если переписать
$$p^x(1 — p)^{1 -x} = (1 — p)expleft(xlog{p} + (-x)log(1 — p)right) =$$
$$=(1 — p)expleft(xlog{frac{p}{1 — p}}right)$$
и определить уже минимальное представление с $u(x) = x$, $theta = log{frac{p}{1 — p}}$ (мы ведь уже сталкивались с этим выражением, когда изучали логистическую регрессию, не так ли?).
Вопрос на подумать. Принадлежит ли к экспоненциальному классу семейство равномерных распределений на отрезках $U[a, b]$? Казалось бы, да: так как:
$$p(x) = frac{1}{b — a}mathbb{I}_{[a,b]}(x)exp(0)$$
В чём может быть подвох?
Попробуйте определить сами, прежде чем смотреть ответ.
Нет, не принадлежит. Давайте вспомним, как звучало определение экспоненциального семейства. Возможно, вас удивило, что там было написано не «распределение относится», а «семейство распределений относится». Это важно: ведь семейство определяется именно различными значениями $theta$. В случае с равномерными распределениями у нас возникнет проблема с индикатором. Он не может попасть в $g(x)$, так как эта функция зависит только от $x$ и не зависит от параметров $a$ и $b$, Но в то же время индикатор не может попасть в $frac1{h(x)}$ или в экспоненту, потому что эти функции не могут быть равны нулю.
, и если нас интересует семейство равномерных распределений на отрезках, определяемое параметрами $a$ и $b$, то они не могут быть в функции $g(x)$, они должны быть под экспонентой, а экспонента ни от чего не может быть равна индикатору.
При этом странное и не очень полезное семейство с нулём параметров, состоящее из одинокого распределения $U[0,1]$ можно считать относящимся к экспоненциальному классу: ведь для него формула
$$p(x) = mathbb{I}_{[0,1]}(x)exp(0)$$
будет работать.
Как мы увидели, к экспоненциальным семействам относятся как непрерывные, так и дискретные распределения. Вообще, к ним относится большая часть распределений, которыми Вам на практике может захотеться описать $Y vert X$. В том числе
- нормальное
- распределение Пуассона
- экспоненциальное
- биномиальное, мультиномиальное (с фиксированным числом испытаний)
- геометрическое
- $chi^2$-распределение
- бета-распределение
- гамма-распределение
- распределение Дирихле
К экспоненциальным семействам не относятся, к примеру: семейство равномерных распределений на отрезке, семейство $t$-распределений Стьюдента, семейство распределений Коши, смеси нормальных распределений.
MLE для семейства из экспоненциального класса
Возможно, вас удивил странный и на первый взгляд не очень естественный вид $p(xverttheta)$. Но всё не просто так: оказывается, что оценка максимального правдоподобия параметров распределений из экспоненциального класса устроена очень интригующе.
Запишем функцию правдоподобия выборки $X = (x_1,ldots,x_N)$:
$$p(Xverttheta) = h(theta)^{-N}cdotleft(prod_{i=1}^Ng(x_i)right)cdotexpleft(theta^Tleft[sum_{i=1}^Nu(x_i)right]right)$$
Её логарифм равен
$$l(Xverttheta) = -Nlog{h(theta)} + sum_{i=1}^Nlog{g(x_i)} + theta^Tleft[sum_{i=1}^Nu(x_i)right]$$
Дифференцируя по $theta$, получаем
$$nabla_{theta}l(Xverttheta) = -Nnabla_{theta}log{h(theta)} + left[sum_{i=1}^Nu(x_i)right]$$
Тут нам потребуется следующая
Лемма. $nabla_{theta}log{h(theta)} = mathbb{E}u(x)$
Доказательство.
Как мы уже отмечали в прошлом пункте:
$$h(theta) = int g(x)expleft(theta^Tu(x)right)dx$$
Следовательно,
$$nabla_{theta}log{h(theta)} = frac{nabla_{theta}int g(x)expleft(theta^Tu(x)right)dx}{int g(x)expleft(theta^Tu(x)right)dx} =$$
$$= frac{int u(x)g(x)expleft(theta^Tu(x)right)dx}{h(theta)} =$$
$$=int u(x)cdotfrac1{h(theta)}g(x)expleft(theta^Tu(x)right)dx = mathbb{E}u(x)$$
Кстати, можно ещё доказать, что
$$frac{partial^2}{partial theta_ipartialtheta_j}log{h(theta)} = text{Cov}(u_i(x), u_j(x))$$
Приравнивая $nabla_{theta}l(Xverttheta)$ к нулю и применяя лемму, мы получаем, что
$$color{#348FEA}{mathbb{E}u(x) = frac1Nleft[sum_{i=1}^Nu(x_i)right]}$$
Таким образом, теоретические матожидания всех компонент $u_i(x)$ должны совпадать с их эмпирическими оценками, а метод максимального правдоподобия совпадает с методом моментов для $mathbb{E}u_i(x)$ в качестве моментов. И в следующем пункте выяснится, что распределения из семейств, относящихся к экспоненциальному классу, это те самые распределения, которые имеют максимальную энтропию из тех, что имеют заданные моменты $mathbb{E}u_i(x)$.
Пример.
Рассмотрим вновь логнормальное распределение:
$$p(x) = frac1{xsqrt{2pisigma^2}}expleft(-frac{(log{x} — mu)^2}{2sigma^2}right) =$$
$$=frac1{xsqrt{2pisigma^2}}expleft(-frac1{2sigma^2}log^2{x} + frac{mu}{sigma^2}log{x} — frac{mu^2}{2sigma^2}right) =$$
$$=frac1{xsqrt{2pisigma^2}expleft(frac{mu^2}{2sigma^2}right)}expleft(underbrace{frac{mu}{sigma^2}}_{=theta_1}underbrace{log{x}}_{=u_1(x)} -underbrace{frac1{2sigma^2}}_{=theta_2}underbrace{log^2{x}}_{=u_2(x)} right) =$$
$$frac{1}{sqrt{-pitheta_2^{-1}}cdotexp{-frac{theta_1^2}{4theta_2}}}cdotfrac1xexpleft(theta_1u_1(x) + theta_2u_2(x)right)$$
Как видим, логнормальное распределение тоже из экспоненциального класса. Вас может это удивить: ведь выше мы обсуждали, что для него метод моментов и метод максимального правдоподобия дают разные оценки. Но никакого подвоха тут нет: мы просто брали не те моменты. В данном случае $u_1(x) = log{x}$, $u_2(x) = log^2{x}$, их матожидания и надо брать; тогда для параметров, получаемых из MLE, должно выполняться
$$mathbb{E}log{x} = frac1Nsum_ilog{x_i},quad mathbb{E}log^2{x} = frac1Nsum_ilog^2{x_i}$$
Матожидания в левых частях мы должны выразить через параметры – и нам для этого совершенно не обязательно что-то интегрировать! В самом деле:
$$mathbb{E}log{x} = frac{partial}{partialtheta_1}log{h(theta)} =$$
$$=frac{partial}{partialtheta_1}left(-frac12log{pi} + frac12log{theta_2} — frac{theta_1^2}{4theta_2^2}right) = -frac{theta_1}{2theta_2^2}$$
$$mathbb{E}log^2{x} = frac{partial}{partialtheta_2}log{h(theta)} = frac1{2theta_2} + frac{theta_1^2}{2theta^3}$$
Теорема Купмана-Питмана-Дармуа
Теперь мы наконец готовы сформулировать одно из самых любопытных свойств семейств экспоненциального класса.
В следующей теореме мы опустим некоторые не очень обременительные условия регулярности. Просто считайте, что для хороших дискретных и абсолютно непрерывных распределений, с которыми вы в основном и будете сталкиваться, это так.
Теорема. Пусть $p(x) = frac1{h(theta)}expleft(theta^Tu(x)right)$ – распределение, причём $theta$ – вектор длины $n$ и $mathbb{E}u_i(x) = alpha_i$ для некоторых фиксированных $alpha_i$, $i=1,ldots,n$. Тогда распределение $p(x)$ обладает наибольшей энтропией среди распределений с тем же носителем, для которых $mathbb{E}u_i(x) = alpha_i$, $i=1,ldots,n$. При этом оно является единственным с таким свойством (в том смысле, что любое другое распределение, обладающее этим свойством, совпадает с ним почти всюду).
Идея обоснования через оптимизацию.
Мы приведём рассуждение для дискретного случая; в абсолютно непрерывном рассуждения будут по сути теми же, только там придётся дифференцировать не по переменных, а по функциям, и мы решили не ввергать читателя в мир вариационного исчисления.
В дискретном случае у нас есть счётное семейство точек $x_1, x_2,ldots$, и распределение определяется счётным набором вероятностей $p_i$ принимать значение $x_i$. Мы будем решать задачу
$$begin{cases}
-sum_j p_jlog{p_j}longrightarrowmax,
sum_jp_ju_i(x_j) = alpha_i, i = 1,ldots,n,
sum_jp_j = 1,
p_jgeqslant0
end{cases}$$
Запишем лагранжиан:
$$mathcal{L} = sum_j p_jlog{p_j} + sum_itheta_ileft(alpha_i — sum_jp_ju_i(x_j)right)+$$
$$+theta_0left(sum_jp_j — 1right) — sum_jlambda_jp_j$$
Продифференцируем его по $p_j$:
$$frac{partialmathcal{L}}{partial p_j} = log{p_j} + 1 — sum_itheta_iu_i(x_j) + theta_0 — lambda_j$$
Приравнивая это к нулю, получаем
$$p_j = frac{expleft(langle theta, u(x_j)rangleright)}{expleft(lambda_j — theta_0 — 1right)}$$
Числитель уже ровно такой, как и должен быть у распределения из экспоненциального класса; разберёмся со знаменателем. Во-первых, легко видеть, что условие $p_jgeqslant0$ заведомо выполнено (ведь тут сплошные экспоненты), так что его можно было выкинуть из постановки задачи оптимизации или, что то же самое, положить $lambda_j = 0$. Параметр $theta_0$ находится из условия $sum_jp_j = 1$, а точнее, выражается через остальные $theta_i$, что позволяет записать знаменатель в виде $h(theta)$.
Идея доказательства «в лоб».
Как и следовало ожидать, оно ничем не отличается от того, как мы доказывали максимальность энтропии у равномерного или нормального распределения. Пусть $q(x)$ – ещё одно распределение, для которого
$$int u_i(x)q(x)dx = int u_i(x)p(x)dx$$
для всех $i = 1,ldots,n$. Тогда
$$0leqslant KL(qvertvert p) = int q(x)logleft(frac{q(x)}{p(x)}right)dx = $$
$$=underbrace{int q(x)log{q(x)}dx}_{-H(q)} — int q(x)log{p(x)}dx=$$
$$=-H(q) — int q(x)left(-log{h(theta)} + sum_itheta_iu_i(x)right)dx =$$
$$=-H(q) — log{h(theta)}underbrace{int q(x)dx}_{=1=int p(x)dx} — sum_itheta_iunderbrace{int q(x)u_i(x)dx}_{=int p(x)u_i(x)dx} =$$
$$=-H(q) — int p(x)left(-log{h(theta)} + sum_itheta_iu_i(x)right)dx =$$
$$=-H(q) + int p(x)log{p(x)}dx = -H(q) + H(p)$$
Таким образом, $H(p)geqslant H(q)$, причём по уже не раз использованному нами свойству дивергенции Кульбака-Лейблера из $H(p) = H(q)$ будет следовать то, что $p$ и $q$ совпадают почти всюду.
Рассмотрим несколько примеров:
Пример 1. Среди распределений на множестве ${1,2,3,ldots}$ неотрицательных целых чисел с заданным математическим ожиданием $mu$ найдём распределение с максимальной энтропией.
В данном случае у нас лишь одна функция $u_1(x) = x$, которая соответствует фиксации матожидания $mathbb{E}x$. Плотность будет вычисляться только в точках $x=k$, $k=1,2,ldots$ и будет иметь вид
$$p_k = p(k) = frac1{h(theta)}expleft(theta kright)$$
В этой формуле уже безошибочно угадывается геометрическое распределение с $p = 1 — e^{theta}$. Параметр $p$ можно подобрать из соображений того, что математическое ожидание равно $mu$. Матожидание геометрического распределения равно $frac1p$, так что $p = frac1{mu}$. Окончательно,
$$p_k = frac1{mu}left(1 — frac1{mu}right)^{k-1}$$
Пример 2. Среди распределений на всей вещественной прямой с заданным математическим ожиданием $mu$ найдём распределение с максимальной энтропией.
А сможете ли вы его найти? Решение под катом.
Теория говорит нам, что его плотность должна иметь вид
$$p(x) = frac1{h(theta)}expleft(theta xright)$$
но интеграла экспоненты не существует, то есть применение «в лоб» теоремы провалилось. И неспроста: если даже рассмотреть все нормально распределённые случайные величины со средним $mu$, их энтропии, равные $frac12 + frac12log(2pisigma^2)$ не ограничены сверху, то есть величины с наибольшей энтропией не существует.

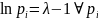
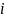
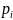
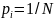
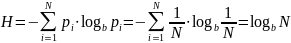
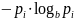
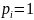
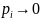
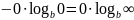

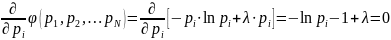
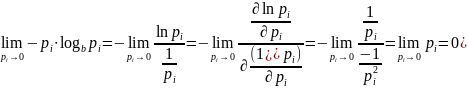
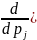
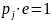




![{displaystyle mathbb {E} [f_{j}(X)]geq a_{j}quad {mbox{ for }}j=1,ldots ,n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84066edcbb6dcf42aa80ca868215f7ee7d47918e)


![{displaystyle mathbb {E} [f_{j}(X)]=a_{j}quad {mbox{ for }}j=1,ldots ,n,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9d72340c2f0e971cdfa528e3d631546e5a3191f)








![{displaystyle {begin{array}{rcl}0&=&D_{u}^{2}log(C(cdot ))vert _{vec {gamma }}\&=&left.D_{u}left({frac {D_{u}C(cdot )}{C(cdot )}}right)right|_{vec {gamma }}\&=&left.{frac {D_{u}^{2}C(cdot )}{C(cdot )}}right|_{vec {gamma }}-left.{frac {(D_{u}C(cdot ))^{2}}{C(cdot )^{2}}}right|_{vec {gamma }}\&=&mathbb {E} _{q}[(langle u,{vec {f}}(X)rangle )^{2}]-left(mathbb {E} _{q}[langle u,{vec {f}}(X)rangle ]right)^{2}=mathrm {Var} _{q}(langle u,{vec {f}}(X)rangle )\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c0fd3cff6d6faede7fa21f6d97bb70ef4feee29)