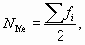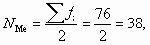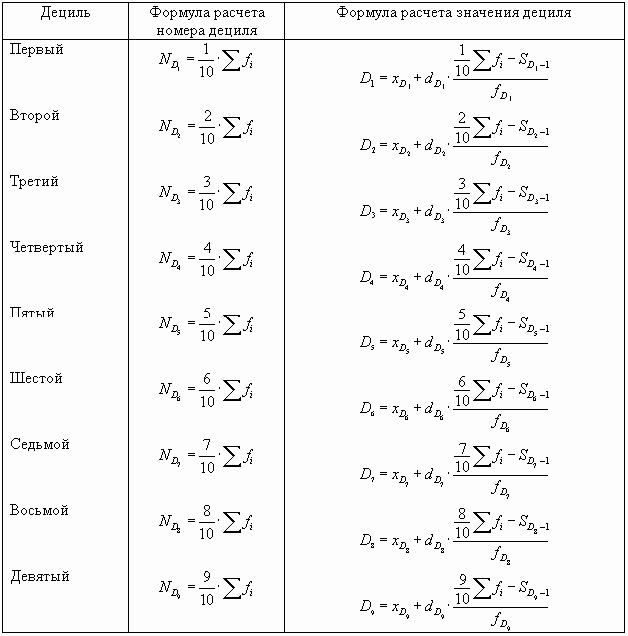-
Коэффициенты, характеризующие концентрацию изучаемого признака в определенных группах Коэффициент Герфиндаля
Обобщенная
оценка степени структуризации явления
в целом обычно выполняется по формуле
уровня концентрации(иликоэффициент
Герфиндаля), который более чувствителен
к изменению долей групп с наибольшим
удельным весом в итоге, определяемый
по формуле:
где

общем итоге изучаемого значения признака;m– количество выделенных
в совокупности групп.
Максимальное
значение коэффициента – 10 000 (если
доли в процентах) или 1(если доли в
числах). Чем ближе значение коэффициента
к максимальному, тем более высокая
концентрация изучаемого признака в
одной или нескольких группах. Минимальное
значение коэффициента – 100 (если доля
в процентах) или 0,01 (если доли в числах).
Эффективное число групп
Обратная
индексу Герфиндаля величина – это
эффективное число группв структуре,
которое показывает количество групп
без учета групп, имеющих ничтожно малые
доли, определяется по формуле:
E = 1/H.
|
Выработка |
кол-во |
среднее |
выработка |
dxj |
dxj2 |
|
10-16 |
5 |
13 |
65 |
0,0035 |
0,00001225 |
|
16-22 |
110 |
19 |
2090 |
0,1127 |
0,01270129 |
|
22-28 |
182 |
25 |
4550 |
0,2454 |
0,06022116 |
|
28-34 |
120 |
31 |
3720 |
0,2006 |
0,04024036 |
|
34-40 |
90 |
37 |
3330 |
0,1796 |
0,03225616 |
|
40-46 |
60 |
43 |
2580 |
0,1392 |
0,01937664 |
|
46-52 |
45 |
49 |
2205 |
0,119 |
0,014161 |
|
612 |
18540 |
1 |
0,17896886 |
Коэффициент
Герфиндаля
что говорит о незначительной концентрации
изучаемого признака (выработки) в одной
или нескольких группах.
Количество эффективных групп E = 1/H =
1/0.179 = 5.6. Этот показатель показывает,
что изучаемый признак сконцентрирован
в 6 группах из 7 имеющихся. Что опять же
подтверждает относительно равномерное
распределение выработки среди групп
рабочих.
-
Коэффициенты, характеризующие дифференциацию изучаемого признака в совокупности
На
основе квантилей рассчитываются
различные коэффициенты дифференциации
изучаемого признака: децильный
(квартильный, перцентильный) коэффициент,
коэффициент фондов, коэффициент Джинни.
Эти коэффициенты характеризуют
неравномерность распределения признака
в изучаемой совокупности. Например,
неравенство в распределении доходов
(как сильно доходы наиболее обеспеченной
группы отличаются от доходов наименее
обеспеченной группы).
Децильный
коэффициент дифференциации
где
Этот
коэффициент показывает во сколько раз
самое маленькое значение признака среди
10% единиц наблюдения с самыми большими
значениями признака (самый маленький
доход 10% самых обеспеченных) больше чем
самое большое значение признака среди
10% единиц наблюдения с самыми маленькими
значениями признака (самый большой
доход 10% самых малообеспеченных).
Квартильный
коэффициент дифференциации
где
Этот
коэффициент показывает во сколько раз
самое маленькое значение признака среди
25% единиц наблюдения с самыми большими
значениями признака (самый маленький
доход 25% самых обеспеченных) больше чем
самое большое значение признака среди
25% единиц наблюдения с самыми маленькими
значениями признака (самый большой
доход 25% самых малообеспеченных).
Коэффициент
фондов– соотношение
среднего значения изучаемого признака
в десятой децильной группе к среднему
значению изучаемого признака в первой
децильной группе
Этот
коэффициент показывает во сколько раз
среднее значение признака среди 10%
единиц наблюдения с самыми большими
значениями признака (средний доход 10%
самых обеспеченных) больше чем среднее
значение признака среди 10% единиц
наблюдения с самыми маленькими значениями
признака (средний доход 10% самых
малообеспеченных).
Первая
децильная группа – это интервал значений
от минимального до первого дециля.
Десятая децильная группа – это интервал
значений от девятого дециля до
максимального значения. Среднее для
интервала значений – это середина
интервала.
Следовательно,


Чем
большее значение принимают эти
коэффициенты, тем большее неравенство
в распределении благ (обязанностей)
между десятой децильной группой и первой
децильной группой.
Рассмотрим эти коэффициенты на примере.
Сведения о выработке рабочих за октябрь
|
Выработка |
кол-во |
накопленная |
||
|
10-16 |
5 |
5 |
||
|
16-22 |
110 |
115 |
||
|
22-28 |
182 |
297 |
||
|
28-34 |
120 |
417 |
||
|
34-40 |
90 |
507 |
||
|
40-46 |
60 |
567 |
||
|
46-52 |
45 |
612 |
||
|
612 |
||||
|
номер |
значение |
|||
|
1 |
1×(612+1):10= |
61,3 |
16+(22-16)×((612/10)-5)/110= |
19,07 |
|
9 |
9×(612+1):10= |
551,7 |
40+(46-40)×(9×(612/10)-567)/60= |
44,38 |
|
1 |
1×(612+1):4= |
153,25 |
22+(28-22)×((612/4)-115)/182= |
23,25 |
|
3 |
3×(612+1):4= |
459,75 |
34+(40-34)×(3×(612/4)-417)/90= |
36,8 |
|
Децильный |
44,38 |
2,3 |
|
Квартильный |
36,8 |
1,6 |
Значение
коэффициентов позволяют сделать
следующие выводы: самая маленькая
выработка 10% лучших рабочих превышает
лучшую выработку 10 % самых непроизводительных
рабочих в 2,3 раза.
Самая
низкая выработка 25% лучших рабочих
превышаю лучшую выработку 25% самых
непроизводительных рабочих в 1,6 раза.
Для
расчета коэффициента фондов нужно найти
средние значение 1-ой и 10-ой децильных
групп.


Этот коэффициент позволяет сделать
вывод, что средняя выработка лучших
рабочих в 3.3 раза превышает выработку
самых низкопроизводительных рабочих.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
What Is a Quartile?
A quartile is a statistical term that describes a division of observations into four defined intervals based on the values of the data and how they compare to the entire set of observations.
Key Takeaways
- The quartiles data into three points—a lower quartile, median, and upper quartile—to form four groups of the dataset.
- Along with the minimum and maximum values of the data set, the quartiles divide a set of observations into four sections, each representing 25% of the observations.
- Quartiles are used to calculate the interquartile range, which is a measure of variability around the median.
Understanding Quartiles
To understand the quartile, it is important to understand the median as a measure of central tendency. The median in statistics is the middle value of a set of numbers. It is the point at which exactly half of the data lies below and above the central value.
So, given a set of 13 numbers that are sorted (ascending or descending), the median would be the seventh number. The six numbers preceding this value are the lowest numbers in the data, and the six numbers after the median are the highest numbers in the dataset given. Because the median is not affected by extreme values or outliers in the distribution, it is sometimes preferred to the mean.
The median is a robust estimator of location but says nothing about how the data on either side of its value is spread or dispersed. That’s where the quartile steps in. The quartile measures the spread of values above and below the mean by dividing the distribution into four groups.
How Quartiles Work
Just like the median divides the data into half so that 50% of the measurement lies below the median and 50% lies above it, the quartile breaks down the data into quarters so that 25% of the measurements are less than the lower quartile, 50% are less than the median, and 75% are less than the upper quartile.
There are three quartile values—a lower quartile, median, and upper quartile—to divide the data set into four ranges, each containing 25% of the data points. The lower quartile, or first quartile, is denoted as Q1 and is the middle number that falls between the smallest value of the dataset and the median. The second quartile, Q2, is also the median. The upper or third quartile, denoted as Q3, is the central point that lies between the median and the highest number of the distribution.
Now, we can map out the four groups formed from the quartiles. The first group of values contains the smallest number up to Q1; the second group includes Q1 to the median; the third set is the median to Q3; the fourth category comprises Q3 to the highest data point of the entire set.
Each interval contains 25% of the total observations. Generally, the data is arranged from smallest to largest:
- First interval: The set of data points between the minimum value and the first quartile.
- Second interval: The set of data points between the lower quartile and the median.
- Third interval: The set of data between the median and the upper quartile.
- Fourth interval: The set of data points between the upper quartile and the maximum value of the data set.
Example of Quartile
Suppose the distribution of math scores in a class of 19 students in ascending order is:
- 59, 60, 65, 65, 68, 69, 70, 72, 75, 75, 76, 77, 81, 82, 84, 87, 90, 95, 98
First, mark down the median, Q2, which in this case is the 10th value: 75.
Q1 is the central point between the smallest score and the median. In this case, Q1 falls between the first and fifth score: 68. (Note that the median can also be included when calculating Q1 or Q3 for an odd set of values. If we were to include the median on either side of the middle point, then Q1 will be the middle value between the first and 10th score, which is the average of the fifth and sixth score—(fifth + sixth)/2 = (68 + 69)/2 = 68.5).
Q3 is the middle value between Q2 and the highest score: 84. (Or if you include the median, Q3 = (82 + 84)/2 = 83).
Now that we have our quartiles, let’s interpret their numbers. A score of 68 (Q1) represents the first quartile and is the 25th percentile. 68 is the median of the lower half of the score set in the available data—that is, the median of the scores from 59 to 75.
Q1 tells us that 25% of the scores are less than 68 and 75% of the class scores are greater. Q2 (the median) is the 50th percentile and shows that 50% of the scores are less than 75, and 50% of the scores are above 75. Finally, Q3, the 75th percentile, reveals that 25% of the scores are greater and 75% are less than 84.
Special Considerations
If the datapoint for Q1 is farther away from the median than Q3 is from the median, then we can say that there is a greater dispersion among the smaller values of the dataset than among the larger values. The same logic applies if Q3 is farther away from Q2 than Q1 is from the median.
Alternatively, if there is an even number of data points, the median will be the average of the middle two numbers. In our example above, if we had 20 students instead of 19, the median of their scores will be the arithmetic average of the 10th and 11th numbers.
Quartiles are used to calculate the interquartile range, which is a measure of variability around the median. The interquartile range is simply calculated as the difference between the first and third quartile: Q3–Q1. In effect, it is the range of the middle half of the data that shows how spread out the data is.
For large datasets, Microsoft Excel has a QUARTILE function to calculate quartiles.
How Do You Find the Lower Quartile of a Data Set?
The lower quartile of a data set is a point where about 25% of observations are below that point, and 75% of data points are above that point. In other words, it is the middle value between the lowest data point and the median of the data set.
How Do You Find the Upper Quartile of a Data Set?
The upper quartile is the point where about 75% of observations are below that point and 25% of observations are higher than that point. In other words, it is the middle value between the median of the data set and the maximum value.
What Is the Interquartile Range of a Data Set?
The interquartile range is the middle 50% of measurements in a data set—in other words, the range of data between the upper quartile and the lower quartile. This is more statistically meaningful than using the full range of data, because it omits possible outliers.
Формула для расчета квартиля в статистике
Формула квартилей — это статистический инструмент для расчета дисперсии заданных данных путем деления их на четыре определенных интервала, сравнения результатов со всем набором наблюдений и комментирования различий в наборах данных.
Он часто используется в статистике для измерения дисперсий, которые описывают разделение всех данных наблюдений на четыре определенных интервала на основе значений данных и того, где они находятся по сравнению со всем набором данных наблюдений.
Он делится на 3 точки: нижний квартиль, обозначаемый Q1, который находится между наименьшим значением и медианой данного набора данных. Медиана, обозначаемая Q2, является медианой, а верхний квартиль, обозначаемый Q3, представляет собой среднюю точку между медианой. Медианная формула в статистике используется для определения среднего числа в наборе данных, расположенном в порядке возрастания. Медиана = {(n+1)/2}поток больше и наибольшее число в заданном наборе данных распределения.
Формула квартиля в статистике представлена следующим образом:
Формула квартилей для Q1= ¼(n+1)-го члена Формула квартилей для Q3= ¾(n+1)-го члена Формула квартилей для Q2= Q3–Q1 (эквивалентно медиане)
Объяснение
Квартили будут делить измерения данного набора данных или выборки на четыре одинаковые или равные части. Например, 25% измерений данного набора данных (представленных Q1) не превышают нижний квартиль. 50% измерений не превышают медианы, т. е. Q2; наконец, 75% будет меньше, чем верхний квартиль, который обозначает Q3. Следовательно, 50% измерений данного набора данных находятся между Q1, нижним квартилем, и Q2, верхним квартилем.
Примеры
Давайте рассмотрим несколько простых и сложных примеров квартилей в excelQuartile. В функциях ExcelQuartile используются для поиска различных квартилей в наборе данных и они являются частью статистических функций Excel. Есть три квартили; первый квартиль (Q1) — это среднее число между наименьшим значением и медианным значением набора данных. Второй квартиль (Q2) является медианой данных. Третий квартиль (Q3) — это среднее значение между медианой набора данных и максимальным значением. Чтобы лучше понять его, прочитайте больше.
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%}
Вы можете скачать этот шаблон формулы квартиля Excel здесь — Формула квартиля Excel Шаблон
Пример №1
Рассмотрим набор данных из следующих чисел: 10, 2, 4, 7, 8, 5, 11, 3, 12. Вам необходимо вычислить все 3 квартили.
Решение:
Используйте следующие данные для расчета квартиля.
Расчет медианы или Q2 можно выполнить следующим образом:
Медиана или Q2 = Сумма (2+3+4+5+7+8+10+11+12)/9
Медиана или Q2 будет –
Медиана или Q2 «=» 7
Поскольку количество наблюдений нечетное, то есть 9, медиана будет лежать на 5-й позиции, то есть 7, и то же самое будет Q2 для этого примера.
Расчет Q1 можно выполнить следующим образом:
Q1= ¼ (9 + 1)
= ¼ (10)
Q1 будет –
Q1 «=» 2,5
Это означает, что Q1 является средним значением 2-й и 3-й позиций наблюдений, которые здесь равны 3 и 4, а среднее значение того же равно (3 + 4)/2 = 3,5.
Расчет Q3 можно выполнить следующим образом:
Q3 = ¾ (9 + 1)
= ¾ (10)
Q3 будет –
Q3 «=» 7.5 Срок
Это означает, что Q3 является средним значением 8-й и 9-й позиций наблюдений, которые здесь равны 10 и 11. То же самое среднее равно (10+11)/2 = 10,5.
Пример #2
Simple Ltd. — производитель одежды, работающий по схеме, чтобы порадовать своих сотрудников за их усилия. Руководство обсуждает запуск новой инициативы, в которой говорится, что они хотят разделить своих сотрудников следующим образом:
- Верхние 25%, лежащие выше Q3 — 25 долларов за ткань
- Больше, чем средний, но меньше, чем Q3 — 20 долларов за ткань.
- Больше, чем Q1, но меньше, чем Q2 — 18 долларов за ткань.
- Руководство собрало среднесуточные данные о производительности за последние 10 дней в расчете на одного (среднего) работника.
- 55, 69, 88, 50, 77, 45, 40, 90, 75, 56.
- Используйте формулу квартилей для построения структуры вознаграждения.
- Какое вознаграждение получит сотрудник, если он произведет 76 готовых вещей?
Решение:
Используйте следующие данные для расчета квартиля.

40, 45, 50, 55, 56, 69, 75, 77, 88, 90
Расчет квартиля Q1 может быть следующим:
Q1 = ¼ (n+1)-й член
= ¼ (10+1)
= ¼ (11)
Q1 будет –
Q1 «=» 2.75 Срок
Здесь необходимо взять среднее значение, состоящее из 2-го и 3-го членов, которые равны 45 и 50. Формула рассчитывается путем сложения всех значений заданного набора, обозначаемого суммированием X, и деления его на количество значений, заданных в наборе, обозначаемом N. Подробнее о том же: (45 + 50) / 2 = 47,50
Q1 составляет 47,50, что составляет 25% минимума.
Расчет квартиля Q3 можно выполнить следующим образом:
Q3 = ¾ (n+1)-й член
= ¾ (11)
Q3 будет –
Q3 «=» 8.25 Срок
Здесь необходимо взять среднее значение 8-го и 9-го членов, то есть 88 и 90. Среднее значение равно (88 + 90) / 2 = 89,00.
Q3 — 89, что составляет 25% лучших.
Расчет медианы или Q2 может быть следующим:
Среднее значение (Q2) = 8,25 – 2,75.
Медиана или Q2 будет –
Медиана или Q2«=» 5.5 Срок
Здесь необходимо взять среднее значение, которое составляет 5 и 6 56 и 69. Среднее значение равно (56 + 69) / 2 = 62,5.
Q2 или медиана составляет 62,5.
Что составляет 50% населения.
Диапазон вознаграждения будет следующим:
47.50 — 62.50 — 18 долларов за ткань.
> 62,50 — 89 получат 20 долларов за ткань
> 89,00 получите 25 долларов за ткань
Если работник производит 76, он будет лежать выше Q1. Следовательно, будет иметь право на бонус в размере 20 долларов.
Пример №3
Преподавание частных коуч-классов предполагает вознаграждение студентов из верхних 25% квартили советами межквартильным студентам, находящимся в этом диапазоне, и повторным сдачей занятий для студентов, находящихся ниже Q1. Используйте формулу квартиля, чтобы определить, с какими последствиями он столкнется, если он наберет в среднем 63 балла. .
Решение :
Используйте следующие данные для расчета квартиля.
Данные для 25 студентов.

Расчет квартиля Q1 может быть следующим:
Q1 = ¼ (n+1)-й член
= ¼ (25+1)
= ¼ (26)
Q1 будет –
Q1 «=» 6.5 Срок
Q1 составляет 56,00, что составляет нижние 25%
Расчет квартиля Q3 можно выполнить следующим образом:
Q3 = ¾ (n+1)-й член
= ¾ (26)
Q3 будет –
Q3 «=» 19.50 Срок
Здесь необходимо взять среднее значение 19-го и 20-го членов, то есть 77 и 77. Среднее значение равно (77+77)/2 = 77,00.
Q3 составляет 77, что составляет 25% лучших.
Медиана или Q2 будет –
Медиана или Q2=19,50 – 6,5
Медиана или Q2 будет –
Медиана или Q2 «=» 13 Срок
Q2 или медиана составляет 68,00.
Что составляет 50% населения.
ргнев будет:
56.00 – 68.00
>68.00 – 77.00
77.00
Актуальность и использование формулы квартилей
Квартили позволяют быстро разделить заданный набор данных или выборку на четыре основные группы, упрощая пользователю оценку того, к какой из четырех групп относится точка данных. В то время как медиана, которая измеряет центральную точку набора данных, является надежной оценкой местоположения. Он не говорит, насколько данные наблюдений лежат на той или иной стороне или рассеяны или разбросаны. Квартиль измеряет разброс или дисперсию. В статистике дисперсия (или разброс) — это средство описания степени распределения данных вокруг центрального значения или точки. Это помогает понять распределение данных. Подробнее о значениях выше и ниже среднего арифметического Среднее арифметическое Среднее арифметическое обозначает среднее значение всех наблюдений ряда данных. Это совокупность всех значений в наборе данных, деленная на общее количество наблюдений или среднее значение, разделяющее распределение на четыре основные группы, описанные выше.
Рекомендуемые статьи
Эта статья была руководством по формуле квартилей. Здесь мы узнаем, как рассчитать квартили в статистике, используя ее формулу, практические примеры и загружаемый шаблон Excel. Вы можете узнать больше о моделировании в Excel из следующих статей:
- Оценщики баллов
- Квартильное отклонениеКвартильное отклонениеКвартильное отклонение основано на разнице между первым квартилем и третьим квартилем в частотном распределении, и эта разница также известна как межквартильный размах, разница, деленная на два, известна как квартильное отклонение или полумежквартильный размах.Подробнее
- Формула коэффициента вариацииФормула коэффициента вариацииКоэффициент вариации – это систематизированная мера дисперсии вероятностного или частотного распределения. Он определяется как отношение стандартного отклонения к среднему. читать далее
- Вычислить коэффициент корреляцииВычислить коэффициент корреляцииКоэффициент корреляции, иногда называемый коэффициентом взаимной корреляции, представляет собой статистическую меру, используемую для оценки силы взаимосвязи между двумя переменными. Его значения варьируются от -1,0 (отрицательная корреляция) до +1,0 (положительная корреляция). читать далее
Содержание
Спрятать
- Что такое квартиль?
- Как работают квартили
- Какова цель квартилей?
- Как найти квартили в Excel
- №1. Сортируйте свои числа
- № 2. Выполнить задание
- Советы по использованию функции квартиля в Excel
- №1. Ценности следует пересмотреть.
- № 2. Определить различные кварты
- №3. Вручную проверьте точность.
- Что такое квартильный пример?
- #Шаг 1: подсчитайте количество наблюдений в наборе данных
- #Шаг 2: Отсортируйте наблюдения по возрастанию
- #Шаг 3: Найдите первый квартиль
- #Шаг 4: Найдите второй квартиль
- #Шаг 5: Найдите третий квартиль
- Как интерпретировать квартили
- №1. Сравнение наблюдений
- № 2. медиана
- №3. Межквартильный размах (IQR)
- Формулы квартилей
- №1. Для первого квартиля, сокращенно Q1.
- № 2. Для второго квартиля, сокращенно Q2.
- №3. Для третьего квартиля, сокращенно Q3.
- № 4. Для межквартильного диапазона.
- Как рассчитывается квартиль?
- №1. Пример Квартиль 1
- № 2. Пример 2 квартили
- Почему он называется квартилем?
- Как разделить данные на 4 квартили?
- Что такое 25-процентный квартиль?
- Что такое 5 квартилей?
- Каковы шаги, чтобы найти первый квартиль?
- Для чего используется формула квартилей?
- Как мы используем квартиль?
- Заключение
- Статьи по теме
- Рекомендации
Компании часто используют Excel для организации статистики, чтобы лучше понимать свои данные. Функция квартилей, которая делит данные на четыре категории в диапазоне, — это одна из функций, которую некоторые люди могут использовать в своих электронных таблицах. Понимание квартилей может помочь вам решить, может ли этот расчет дать новое понимание ваших числовых данных. В этой статье мы объясним, что такое квартиль, на упрощенном примере, как он рассчитывается и его цель среди других основных фактов, которые вам необходимо знать. Давайте продолжим!
Что такое квартиль?
Квартиль — это статистический термин, который относится к разделению наблюдений на четыре определенных интервала на основе значений данных и того, как они соотносятся со всем набором наблюдений.
Квартили — это значения Excel, которые делят числовые значения на четыре части. Люди предпочитают квартили процентилям, например 25% самых высокооплачиваемых клиентов. Четыре квартили следующие:
- Первый квартиль: Первый квартиль включает самые низкие 25% диапазона данных.
- Второй квартиль: Второй квартиль включает следующую низшую группу чисел. В эту группу входят числа через медиану набора данных.
- Третий квартиль: Третий квартиль — это вторая по величине группа чисел выше медианы.
- Четвертый квартиль: четвертый квартиль включает 25% самых высоких чисел в диапазоне данных.
Например, если данные колеблются от одного до восьми, каждый попадает в один из следующих квартилей:
- Первый квартиль: 1 и 2
- Второй квартиль: 3 и 4
- Третий квартиль: 5 и 6
- Четвертая квартиль: 7 и 8
Как работают квартили
Quartiles делит данные на четверти, так что 25% измерений меньше нижнего квартиля, 50% меньше медианы и 75% меньше верхнего квартиля, точно так же, как медиана делит данные пополам, так что 50% измерений ниже медианы и 50% выше ее.
Набор данных разделен на четыре диапазона, каждый из которых содержит 25% точек данных, с использованием трех квартильных значений: нижнего, медианного и верхнего. Нижний квартиль, или первый квартиль, обозначается как Q1 и представляет собой среднее число между наименьшим и медианным значениями набора данных. Медиана также находится во втором квартиле, Q2. Верхний или третий квартиль, обозначаемый как Q3, является центральной точкой распределения, лежащей между медианой и наибольшим числом.
Теперь мы можем наметить четыре группы, образованные квартилями. Первый набор значений включает наименьшее число до Q1; второй набор включает Q1 в медиану; третий набор включает медиану для Q3; и четвертая категория включает Q3 до самой высокой точки данных во всем наборе.
Какова цель квартилей?
Квартили удивительно полезны и могут служить цели в различных контекстах. Одна из хороших целей квартилей заключается в том, что они могут помочь вам понять основную тенденцию и изменчивость вашего набора данных и даже помочь вам найти выбросы. Отображение их в виде диаграммы может помочь вам понять распределение ваших данных.
Q2 — это медиана, и она делит набор данных пополам. Для асимметричных распределений это полезная мера центральной тенденции. Межквартильный размах (IQR) является мерой изменчивости. Интервал между первым и третьим квартилями.
IQR = Q3 – Q1
Большие IQR указывают на более широкий диапазон значений. Независимо от формы распределения половина наблюдений попадает в межквартильный диапазон.
Медиана и межквартильный размах являются более надежными показателями, чем более привычные среднее значение и стандартное отклонение. Выбросы мало влияют на любую статистику, потому что они не зависят от каждого значения. Кроме того, межквартильный диапазон идеально подходит для асимметричных распределений, таких как медиана.
Еще одно полезное назначение квартилей заключается в том, что они также могут помочь вам найти выбросы.
Как найти квартили в Excel
При поиске квартилей в Excel у вас есть несколько вариантов:
№1. Сортируйте свои числа
Вы можете получить свои квартили, упорядочив числа в диапазоне данных от самого низкого до самого высокого. В электронной таблице вы можете отсортировать их по столбцу. Например, ваши числа могут быть:
| A | B | |
| 1 | 9 | 1 |
| 2 | 1 | 3 |
| 3 | 3 | 3 |
| 4 | 5 | 5 |
| 5 | 7 | 6 |
| 6 | 6 | 7 |
| 7 | 2 | 9 |
Формула квартилей требует двух основных значений: квартили и массивы. Каждый квартиль представляет собой отдельный набор значений. Они пронумерованы от 0 до 4:
- 0: наименьшее значение в диапазоне чисел.
- 1: Это первый квартиль или 25-й процентиль.
- 2: Это второй или медианный квартиль или 50-й процентиль.
- 3: Это 75-й процентиль или третий квартиль.
- 4: это самое высокое значение в диапазоне.
№ 2. Выполнить задание
В Excel функция квартиля возвращает квартиль для любого набора данных. В Excel для расчета квартилей используется следующая формула:
= КВАРТИЛЬ (массив; кварта)
Где:
- Наблюдения и советы этой статьи мы подготовили на основании опыта команды массив представляет весь диапазон значений, для которых вы хотите найти квартили.
- кварта какой квартиль вы хотите найти.
Советы по использованию функции квартиля в Excel
Вот несколько советов по использованию функции квартилей Excel:
№1. Ценности следует пересмотреть.
Перед запуском функции квартиля дважды проверьте, чтобы ваши числа были в порядке возрастания в одном столбце и были правильными. Функция генерирует сообщение об ошибке, если какая-либо из ячеек пуста или содержит текст или специальные символы. Если значение кварты в вашей команде меньше нуля или больше четырех, вы можете получить сообщение об ошибке.
№ 2. Определить различные кварты
Каждая кварта может предоставить вам уникальные данные, которые вы можете использовать. Например, вам может быть интересно узнать, сколько покупатель тратит в самом низком процентиле покупок, а также в верхних квартилях. Это может помочь вам определить, как создавать конкретные бизнес-цели для определенных групп. Вычисление каждого квартиля для широкого диапазона данных может показать вам больше, чем среднее значение или медиану, поскольку оно показывает изменение в наборе данных.
№3. Вручную проверьте точность.
Чтобы проверить ваши данные, вы можете вручную рассчитать квартили, используя следующие формулы:
- Нижний квартиль = (N+1) x 1/4
- Средний квартиль = (N+1) x 2/4
- Верхний квартиль = (N+1) x 3/4
Число N обозначает количество целых чисел в вашем наборе данных. Результат указывает, какой квартиль представляет каждая позиция. Например, если формула нижнего квартиля дает результат шесть, шестое число в вашей последовательности является нижним квартилем. Формулы для расчета четвертого квартиля не существует, поскольку это максимальное значение в диапазоне.
Что такое квартильный пример?
Рассмотрите возможность проведения небольшого исследования развития речи у детей в возрасте 1–6 лет. Вы пишете статью об исследовании и хотите включить возрастные квартили детей.
| Age (years) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| частота | 2 | 3 | 4 | 1 | 2 | 2 |
#Шаг 1: Подсчитайте количество наблюдений в наборе данных.
n = 2 + 3 + 4 + 1 + 2 + 2 = 14
#Шаг 2: Сортировка наблюдений в порядке возрастания
1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 5, 5, 6, 6
#Шаг 3: найти первый квартиль
n * (1/4) = 14 * (1/4) = 3.5
3.5 не является целым числом, поэтому Q1 — это число в позиции 4.
1, 1, 2, 22, 3, 3, 3, 3, 4, 5, 5, 6, 6
Q1 = 2 года
#Шаг 4: найти второй квартиль
n * (2/4) = 14 * (2/4) = 7
7 — целое число, поэтому Q2 — это среднее чисел в позициях 7 и 8.
1, 1, 2, 2, 2, 3, 3, 33, 4, 5, 5, 6, 6
Q2 = (3 + 3) / 2
Q2 = 3 года
#Шаг 5: найти третий квартиль
n * (3/4) = 14 * (3/4) = 10.5
10.5 не является целым числом, поэтому Q3 — это число в позиции 11.
1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 55, 6, 6
Q3 = 5 года
Как интерпретировать квартили
Квартили могут предоставить полезную информацию о конкретном наблюдении или наборе данных.
№1. Сравнение наблюдений
Квартили могут помочь вам понять наблюдение по отношению к остальной части выборки или генеральной совокупности. Вы можете определить, находится ли наблюдение в нижних 25 %, средних 50 % или верхних 25 %, сравнив его с квартилями.
№ 2. медиана
Медиана, или второй квартиль, является мерой центральной тенденции. Это среднее число является хорошим индикатором среднего или наиболее центрального значения данных, особенно для асимметричных распределений или распределений с выбросами.
№3. Межквартильный размах (IQR)
Межквартильный размах (IQR) является мерой изменчивости. Это расстояние между первой и третьей квартилями. Он представляет собой распределение средних 50% данных.
IQR = Q3 — Q1
IQR является превосходной мерой изменчивости для асимметричных или заполненных выбросами распределений. Поскольку IQR включает только средние 50% данных, на него не влияют экстремальные значения, в отличие от диапазона.
- Асимметрия: Расстояние между квартилями может указывать на то, является ли распределение асимметричным или симметричным.
- Выявление выбросов: Выбросы можно определить с помощью межквартильного диапазона (IQR). Выбросы — это наблюдения, которые либо чрезвычайно высоки, либо чрезвычайно низки. Выброс определяется как любое наблюдение, которое более чем на 1.5 IQR отличается от первого или третьего квартиля.
Формулы квартилей
Существуют четыре основные формулы квартилей, используемые для определения первого, второго, третьего и интерквартилей.
№1. Для первого квартиля, сокращенно Q1.
Первый квартиль = Q1 = ((n + 1) / 4)-й член
№ 2. Для второго квартиля, сокращенно Q2.
Второй квартиль = Q2 = ((n + 1) / 2)-й член
№3. Для третьего квартиля, сокращенно Q3.
Третий квартиль = Q3 = (3(n + 1)/4)-й член
№ 4. Для межквартильного диапазона.
Межквартильный = Q3 – Q1 = (3(n + 1)/4) й член – ((n + 1)/4) й термин
Мы можем написать общую формулу для расчета квартиля, используя три приведенные выше формулы для первого, второго и третьего квартилей.
Как рассчитывается квартиль?
Квартили можно легко рассчитать с помощью формул.
№1. Пример Квартиль 1
Оценить все квартильные части данного набора данных, 2, 9, 7, 29, 34, 61, 25, 19, 16?
Решения
- Шаг 1: Начните с заданного набора чисел.
2, 9, 7, 29, 34, 61, 25, 19, 16
- Шаг 2: Отсортируйте заданный набор чисел в порядке возрастания.
2, 7, 9, 16, 19, 25, 29, 34, 61
- Шаг 3: Подсчитайте данный набор чисел и умножьте на n.
N = 9
- Шаг 4: Используя общую формулу квартилей, определите первый, второй и третий квартиль.
Qk = k (n + 1) / 4)-й член
- Шаг 5: Подставьте k = 1, 2, 3 вместо первого, второго и третьего квартилей.
Для к = 1
Q1 = 1 (9 + 1) / 4)-й член
Q1 = 1 (10) / 4)-й член
Q1 = (10) / 4)-й член
Q1 = (5) / 2)-й член
Q1 = 2.5-й срок
Для к = 2
Q2 = 2 (9 + 1) / 4)-й член
Q2 = 2 (10) / 4)-й член
Q2 = (10/2)-й член
Q2 = 5-й срок
Для к = 3
Q3 = 3 (9 + 1) / 4)-й член
Q3 = 3 (10) / 4)-й член
Q3 = (30/4)-й член
Q3 = (15/2)-й член
Q3 = 7.5-й срок
- Шаг 6: Возьмите рассчитанные значения из организованного набора данных квартилей.
Для Q1
Q1 = 2.5-й срок
Q1 = 2-й срок + 3-й срок / 2
Q1 = 7 + 9/2
Q1 = 16/2
Q1 = 8
Для Q2
Q2 = 5-й срок
Q2 = 19
Для Q3
Q3 = 7.5-й срок
Q3 = 7-й + 8-й / 2
Q3 = 29 + 34 / 2
Q3 = 63/2
Q3 = 31.5
- Шаг 7: Примените общую формулу для расчета межквартильного диапазона и введите значения.
межквартильный = Q3 – Q1
межквартильный = 31.5 — 8
межквартильный = 23.5
В результате квартили данного множества равны Q1 = 8. Q2 = 19, Q3 = 31.5 и интерквартиль = 23.5.
№ 2. Пример 2 квартили
Найдите интерквартиль следующего набора данных: 23, 19, 3, 12, 22, 18, 11?
Решения
- Шаг 1: Начните с заданного набора чисел.
23, 19, 3, 12, 22, 18, 11
- Шаг 2: Отсортируйте заданный набор чисел в порядке возрастания.
3, 11, 12, 18, 19, 22, 23
- Шаг 3: Подсчитайте данный набор чисел и умножьте на n.
N = 7
- Шаг 4: Теперь применим общую интерквартильную формулу.
Межквартильный диапазон = Q3 – Q1
- Шаг 5: Определите первый и третий квартили.
Для Q1
Q1 = (n + 1) / 4)-й член
Q1 = (7 + 1) / 4)-й член
Q1 = (8) / 4)-й член
Q1 = 2-й срок
Для Q3
Q3 = 3(n + 1) / 4)-й член
Q3 = 3(7 + 1) / 4)-й член
Q3 = 3(8) / 4)-й срок
Q3 = (24/4)-й член
Q3 = 6-й срок
- Шаг 6: введите результаты третьего и первого квартилей в формулу межквартили.
межквартильный = 6-й срок — 2-й срок
межквартильный = 22 — 11
межквартильный = 11
Почему он называется квартилем?
Квартиль — это тип квантиля в статистике, который делит количество точек данных на четыре части или четверти примерно одинакового размера. Для вычисления квартилей данные должны быть упорядочены от наименьшего к наибольшему; таким образом, квартили являются разновидностью порядковой статистики.
Как разделить данные на 4 квартили?
Щелкните пустую ячейку где-нибудь на листе в Excel. Например, выберите ячейку B1. Введите «= КВАРТИЛЬ (A1: A10,1)» после ввода.
Что такое 25-процентный квартиль?
25-й процентиль также называют первым или нижним квартилем. 25-й процентиль — это значение, при котором 25% ответов находятся ниже него, а 75% ответов — выше него.
Что такое 5 квартилей?
Сводка состоит из пяти значений: самых экстремальных значений набора данных (максимальное и минимальное значения), нижнего и верхнего квартилей и медианы. Эти значения представлены в следующем порядке: минимальное значение, нижний квартиль (Q1), медианное значение (Q2), верхний квартиль (Q3) и максимальное значение.
Каковы шаги, чтобы найти первый квартиль?
Мы используем следующие шаги для определения первого квартиля:
- Не забудьте расположить точки данных в порядке от наименьшей до наибольшей важности.
- Найдите медиану всего набора данных и разделите его на две равные части.
- Возьмите медиану нижней половины набора данных.
Для чего используется формула квартилей?
Набор наблюдений делится на четыре равные части по формуле квартилей. Первый квартиль расположен между первым членом и медианой. Медиана представляет второй квартиль. Третий квартиль — это значение, которое находится между медианой и последним членом.
Как мы используем квартиль?
Квартили часто используются в данных о продажах и опросах для классификации населения. Например, КВАРТИЛЬ можно использовать для определения 25% самых высоких доходов населения.
Заключение
Теперь вы можете понять все основные понятия, связанные с квартилем, просто прочитав эту статью. В этом руководстве подробно и последовательно объясняется цель и все, что вам нужно знать о квартиле, включая пример и способ его расчета. Пожалуйста, оставьте вопрос в разделе комментариев, если вам нужна дополнительная помощь.
Статьи по теме
- СРЕДНЯЯ СТОИМОСТЬ СТРАХОВАНИЯ ДОМА: лучшие практики и тарифы Великобритании на 2023 год (обновлено)
- Список компаний на триллион долларов 2019/2020
- 5 кредитных историй: почему они важны? (+ Подробное руководство для начинающих)
- YOY: годовой анализ, расчеты роста и инвестиций, формулы и примеры
- СКОЛЬКО СТОИТ ДОМ В США В 2023 ГОДУ.
- САМООЦЕНКА: Подробное объяснение и все, что вы должны знать
Рекомендации
- scribbr
- Финансовая
- р-блогеры
- В самом деле
8.2. Медиана, квартили, децили
Медиана — это значение признака, которое делит статистическую совокупность на две равные части: половина единиц совокупности имеет значения признака не меньше медианы, другая половина — значения признака не больше медианы.
Значения изучаемого признака всех единиц статистической совокупности можно расположить в порядке возрастания (или убывания). В этом случае мы получим ранжированный ряд. Если число единиц совокупности нечетное, то значение признака, находящееся в середине ранжированного ряда, будет являться медианой. Если число единиц совокупности четное, то медианой будет средняя величина из двух значений признака, находящихся в середине ряда.
Пример 8.5. Имеются следующие данные о результатах сдачи экзамена по статистике в студенческой группе:
| Номер студента | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Оценка по статистике | 3 | 4 | 2 | 3 | 4 | 4 | 4 | 3 | 4 | 5 | 5 |
Представим их в виде ранжированного ряда:
| Номер студента | 3 | 1 | 4 | 8 | 2 | 5 | 6 | 7 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Оценка по статистике | 2 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 5 | 5 |
Как видим, в ранжированном ряду оценки расположились следующим образом: сначала записана одна неудовлетворительная оценка (ее получил студент, имеющий в ведомости номер 3), затем три оценки «удовлетворительно», пять оценок «хорошо» и две оценки «отлично». В середине ранжированного ряда, имеющего нечетное число членов, стоит оценка «4», которую получил студент, записанный в ведомости под номером 5. Следовательно, оценка «4 (хорошо)» является медианой для данного ряда распределения. Пять студентов получили оценки 4 и ниже (2, 3, 3, 3, 4), другие пять студентов — 4 и выше (4, 4, 4, 5, 5).
Пример 8.6. Имеются данные о цене антоновских яблок в шести магазинах города. Представим их сразу в виде ранжированного ряда:
| Название магазина | «Огонек» | «Маяк» | «Заря» | «Татьяна» | «Ночной» | «Любимый» |
|---|---|---|---|---|---|---|
| Цена яблок, руб. за кг | 40 | 41 | 42 | 44 | 44 | 45 |
В середине ранжированного ряда находятся цены двух магазинов, причем они разные. Медиана определяется как средняя величина из этих значений признака. Она равна 43 руб. [(42 + 44) : 2 = 43].
Таким образом, в 50% магазинов города яблоки продаются по цене не выше 43 руб. за килограмм, а в других 50% магазинов — по цене не ниже 43 руб.
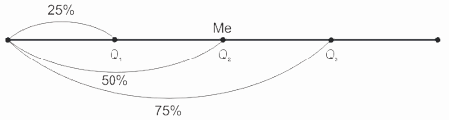
Квартили (Q) делят ранжированный ряд на четыре равные части: первый квартиль (Q1) включает значения признака, не превышающие 25% единиц совокупности, второй квартиль (Q2) — совпадает с медианой (Ме), третий квартиль (Q3) — значения признака, не превышающие 75% единиц совокупности (рис. 8.3).
Рис.
8.3.
Деление ранжированного ряда на четыре равные части
Децили (D) делят ранжированный ряд на десять равных частей: первым децилем (D1) является значение признака, которое не превышает 10% единиц совокупности, вторым (D2) — 20%, третьим (D3) — 30% и т.д. При этом пятый дециль (D5) совпадает с медианой и вторым квартилем (Q2) (рис. 8.4).
Рис.
8.4.
Деление ранжированного ряда на десять равных частей
Медиана, квартили и децили относятся к группе квантилей. Квантили — это показатели, которые делят вариационные ряды на определенное количество равных частей. Среди них, помимо названных, также имеются квантили, которые делят ряд на пять равных частей, перцентили — на сто и т.д.
Структурные показатели не зависят от того, имеются ли в статистической совокупности аномальные (резко выделяющиеся) наблюдения. И если средняя величина при их наличии теряет свою практическую значимость, то информативность медианы наоборот усиливается — она начинает выполнять функции средней, т.д. характеризовать центр совокупности.
Способы расчета рассматриваемых структурных показателей зависят от вида вариационного ряда. Рассмотрим их подробнее.
8.2.1. Определение структурных средних в дискретных вариационных рядах
Для определения медианы в дискретных вариационных рядах:
- находят ее порядковый номер по формуле
- строят ряд накопленных частот;
- находят накопленную частоту, которая равна порядковому номеру медианы или его превышает;
- варианта, соответствующая данной накопленной частоте, является медианой.
Пример 8.7. Определим медианный стаж сотрудников страховой компании на основе следующих данных:
| Время работы, лет, xi | Число сотрудников, чел., fi | Накопленная частота, Si |
|---|---|---|
| 1 | 5 | 5 |
| 2 | 7 | 12 |
| 3 | 4 | 16 |
| 4 | 9 | 25 |
| 5 | 13 | 38 |
| 6 | 10 | 48 |
| 7 | 16 | 64 |
| 8 | 13 | 77 |
| Итого | 77 | — |
Номер медианы равен
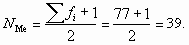
Для того чтобы найти значение варианты, стоящей на 39 месте, рассчитаем накопленные частоты. Для пятой группы накопленная частота равна 38. Это означает, что 38 работников имеют стаж работы 5 лет и меньше. Для шестой группы накопленная частота — 48 (она первая превышает порядковый номер медианы), следовательно, в эту группу входят сотрудники с порядковыми номерами от 39 до 48, в том числе и искомый 39-й сотрудник. Стаж работы сотрудников в шестой группе — 6 лет. Значит, Ме = 6. Итак, 50% сотрудников работают в данной страховой компании не более шести лет.
Квартили и децили определяют аналогично медиане: сначала находят их номер, затем среди накопленных частот ищут такую, которая первая равна или превышает порядковый номер показателя, ей соответствует варианта, которая является искомым показателем. Номера квартилей рассчитываются по формулам:
Порядковые номера децилей исчисляются следующим образом:
Определим квартили по данным примера 8.7. Их номера равны:
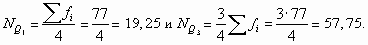
Первая накопленная частота, превышающая 19,25, равна 25. Ей соответствует варианта 4, являющаяся первым квартилем. Первая накопленная частота, которая превышает 57,75 — это 64; ей соответствует варианта, равная 7. Это третий квартиль. Итак, 25% сотрудников работают в данной компании не более четырех лет, а 75% — не более семи лет.
Аналогично определяются децили. Например, восьмой дециль вычисляется следующим образом:

Накопленная частота 64 — первая, превышающая ND8, ей соответствует значение признака — 7 лет, т.д. у 80% сотрудников стаж работы в данной компании не превышает семи лет.
8.2.2. Определение структурных средних в интервальном вариационном ряду
В интервальных рядах сначала определяют медианный интервал. Для этого так же, как и в дискретных рядах, рассчитывают порядковый номер медианы

Накопленной частоте, которая равна номеру медианы или первая его превышает, в интервальном вариационном ряду соответствует медианный интервал. Обозначим эту накопленную частоту SМе. Непосредственно расчет медианы проводят по формуле:

где хМе — нижняя граница медианного интервала;
dMe — величина медианного интервала;
SMe — 1 — накопленная частота интервала, предшествующего медианному;
fMe — частота медианного интервала.
Пример 8.8. По следующим данным определим медианное значение суммы выданных банками кредитов:
| Сумма выданных кредитов, млн ден. ед. | Количество банков, fi | Накопленная частота, Si. |
|---|---|---|
| 20-40 | 8 | 8 |
| 40-60 | 15 | 23 |
| 60-80 | 21 | 44 |
| 80-100 | 12 | 56 |
| 100-120 | 9 | 65 |
| 120-140 | 7 | 72 |
| 140-160 | 4 | 76 |
| Итого | 76 | — |
Проведем расчет:
- определим порядковый номер медианы
- определим накопленную частоту медианного интервала: SМе > NМе; SМе = 44;
- определим соответствующий ей медианный интервал «60-80»;
- рассчитаем значение медианы по формуле
т.е. у 50% банков сумма выданных кредитов не превышает 74,286 млн ден. ед.
Далее произведем расчет квартилей и децилей в интервальном вариационном ряду.
Для приведенного интервального ряда необходимо определить:
- номер первого (нижнего) квартиля:
тогда ей соответствует интервал «40-60», в котором находится первый квартиль;
- номер третьего (верхнего) квартиля:
тогда ей соответствует интервал «100-120», в котором находится третий квартиль;
- первый (нижний) квартиль рассчитаем по формуле:
т.е. у 25% банков сумма выданных кредитов не превышает 54,7 млн ден. ед.;
- третий (верхний) квартиль рассчитаем по формуле:
т.е. у 75% банков сумма выданных кредитов не превышает 102,2 млн ден. ед.
Аналогично квартилям определяем децили. Формулы, используемые в ходе расчетов, поместим в таблицу.
|
|
|
Здесь хD — нижняя граница децильного интервала; dD — величина децильного интервала; SD — 1 — сумма накопленных частот интервала, предшествующего децильному; fD — частота децильного интервала. |
Номер шестого дециля равен:

В статистике для характеристики степени неоднородности совокупности часто используют коэффициенты дифференциации (квартильные и децильные). Децильный коэффициент дифференциации представляет собой отношение девятого дециля к первому:

Данный коэффициент показывает, во сколько раз варианта, выше которой находятся 10% единиц совокупности, имеющих самые большие значения признака, больше варианты, ниже которой находятся 10% единиц совокупности с самыми маленькими значениями признака. Аналогично квартильный коэффициент дифференциации определяется как отношение третьего квартиля к первому.
В заключение отметим, что приблизительное равенство средней арифметической, моды и медианы, рассчитанных по отношению к одному и тому же ряду, говорит о том, что значения признака в изучаемой совокупности имеют нормальный закон распределения (или приближаются к нему).
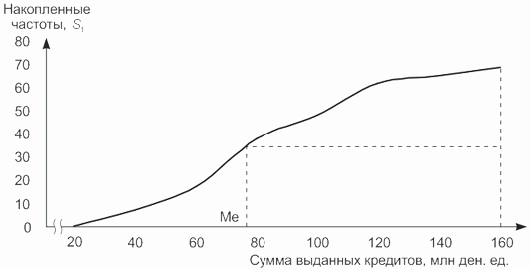
Медиана может быть определена графически по кумуляте. Для этих целей на оси ординат, где отмечаются накопленные частоты, находится точка, соответствующая полусумме всех частот (т.е. порядковому номеру медианы). Из нее проводится прямая параллельно оси абсцисс до пересечения с графиком (кумулятой распределения). Абсцисса точки пересечения соответствует медиане данного ряда распределения.
Рис.
8.5.
Определение медианы по кумуляте