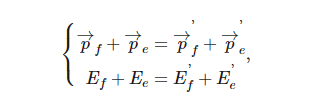Комптоновская длина волны электрона как найти

Современная физика описывает явления, которые, на первый взгляд, противоречат здравому смыслу. Знаете ли вы, что свет может взаимодействовать с электронами? В результате этих взаимодействий электрон может достичь определенной скорости, а свет… меняет свое направление и длину волны. Это явление называется эффектом Комптона. Проанализировав эту статью, вы увидите, что этот удивительный эффект имеет очень простое объяснение. Чтобы понять его, нам понадобятся лишь базовые знания механики и простые факты из современной физики.

Простое объяснение эффекта Комптона

Эффект Комптона — это явление, при котором свет взаимодействует с электронами. Давайте сначала уточним, что именно мы подразумеваем под словом «свет». Оказалось, что свет имеет двойственную природу — в одних экспериментах его природа волновая, в других — корпускулярная.

Рис. 1. Следует ли рассматривать свет как волны или как частицы?

Свет волновой природы — это электромагнитные волны (или электромагнитное излучение), с которыми мы знакомы. Подтверждение того, что свет может вести себя как волна, было получено в 1803 году английским физиком Томасом Янгом. Он провел серию гениальных экспериментов, в которых показал, что свет претерпевает дифракцию и интерференцию, то есть явления, характерные для волн. Эти эксперименты XIX века утвердили мнение о том, что свет является разновидностью волны.

Это мнение оставалось практически неизменным в течение 100 лет! Однако уже в то время были обнаружены явления и эффекты, которые нельзя было объяснить, исходя из того, что свет имеет только волновую природу. Фотоэлектрический эффект, заключающийся в выбросе электронов с поверхности металлов, оказался большой проблемой. Свойства этого явления противоречили волновой природе света.

В 1900 году немецким физиком Максом Планком была написана первая статья, постулирующая частичную природу света. В 1905 году на основе работы Планка световая квантовая гипотеза была представлена Альбертом Эйнштейном, также уроженцем Германской империи того времени. Эта гипотеза постулировала, что свет можно рассматривать как поток частиц. Наименьшая «порция» света (квант света) называется фотоном. Используя свою гипотезу, Эйнштейн смог объяснить фотоэлектрический эффект и его свойства. В 1921 году за это объяснение он получил Нобелевскую премию.

Давайте теперь вернемся к эффекту Комптона. Он получил свое название от имени американского физика Артура Холли Комптона. Комптон изучал рассеяние рентгеновских лучей. Полученные им результаты не соответствовали волновой природе света в то время. Для того чтобы правильно объяснить полученные результаты, Комптон, как и Эйнштейн, должен был предположить, что свет состоит из потока частиц. В 1923 году физик опубликовал работу, описывающую новый эффект, и очень скоро, в 1927 году, он получил Нобелевскую премию за свои исследования! Как видите, в то время новая, зарождающаяся отрасль физики (сейчас она называется современной физикой) была полем многих захватывающих и новаторских научных исследований.

Эффект Комптона делает известной как волновую, так и корпускулярную природу света. Этот эффект связан с взаимодействием рентгеновских и гамма-лучей с электронами. В результате этого взаимодействия электрон приобретает определенную скорость и выбрасывается, а излучение меняет направление и длину волны. Когда излучение, особенно свет, меняет направление, мы говорим, что оно рассеяно. Схема явления Комптона показана на рис. 2.

Рис. 2. Схема эффекта Комптона

В явлении Комптона излучение с длиной волны λ_fпадает на свободный или слабо связанный электрон. Что это значит? «Свободный» электрон не взаимодействует ни с какими другими объектами, в то время как «слабо связанным» электрон называется тогда, когда энергия связи электрона намного меньше энергии падающего фотона.

В результате освещения электрон приобретает определенную скорость под углом φ к первоначальному направлению распространения излучения. Излучение, в свою очередь, рассеивается под углом θ к первоначальному направлению, длина волны также изменяется, и ее новое значение составляет λ_f^‘.

Формулы для расчета энергии и импульса фотона

Чтобы понять и описать, что происходит во время эффекта Комптона, давайте рассматривать рентгеновские лучи (или гамма-лучи) как поток частиц. Если бы мы использовали только волновое описание, изменение длины волны излучения не могло бы быть объяснено. Такой эффект не возникает при классическом рассеянии. Если предположить, что мы рассматриваем излучение как поток фотонов, то мы имеем дело с упругим столкновением одной частицы (фотона) с другой частицей (электроном). Упругое столкновение можно рассматривать на основе известных законов механики — должны выполняться принципы сохранения импульса и энергии:

где буквы p и E обозначают импульс и энергию частицы, соответственно. Подстрочные индексы f и e означают фотон и электрон, соответственно. «Штрихованные» индексы относится к величинам после рассеяния, «нештрихованные» индексы — к величинам до рассеяния. Итак, нам удалось свести сложный вопрос современной физики к простой механике, как при столкновении бильярдных шаров!

Для справки. Упругое столкновение — столкновение, при котором импульс и энергия системы (в классической физике — кинетическая энергия) не изменяются.

Чтобы решить приведенную выше систему уравнений и определить неизвестные значения импульса и энергии после рассеяния, необходимо разложить вектор импульса на составляющие. В нашем двумерном случае мы получаем в общей сложности три уравнения: два, описывающие импульс (в горизонтальном и вертикальном направлениях), и одно, описывающее энергию:

Что такое импульс и энергия фотона? Для их определения мы должны обратиться к двойственной природе излучения. Значение импульса фотона (частицы) связано с длиной волны света λ следующим соотношением: p_f = h / λ .

где h = 6,63 * 10^-34 Дж*с — постоянная Планка. Энергия фотона составляет: E_f = p_f * c = h*c / λ

где c = 3 * 10⁸ м/с — скорость света в вакууме. Вы уже видите взаимосвязь природы волн и частиц? Чтобы объяснить явление Комптона, мы должны рассматривать излучение как поток частиц, которые, подобно пулям, сталкиваются с электронами и приводят их в движение. С другой стороны, мы не можем определить энергию и импульс фотонов, не обращаясь к их волновой природе.

Формулы для расчета импульса и энергии релятивистских частиц

А каковы будут импульс и энергия электрона? В явлении Комптона отражающийся электрон может достигать очень высоких скоростей, составляющих значительную долю скорости света. Это означает, что к электрону нужно относиться релятивистски. Нельзя записать импульс и энергию электрона классическим способом, потому что масса движущегося электрона отличается от его массы покоя (и зависит от скорости). Релятивистская связь между энергией E и импульсом p следующая:

E = m₀ * c⁴ + p² * c²

где m₀ — масса покоя. Для электрона это m₀ = 9,1*10^-31 кг. Далее мы будем обозначать массу покоя электрона через m_e. Конечно, если мы используем релятивистское выражение для движущегося электрона, то это же выражение должно быть использовано «с другой стороны уравнения» для покоящегося электрона. Когда электрон находится в состоянии покоя (до освещения), его импульс равен нулю, что означает, что мы можем выразить энергию (покоя) как: E_e = m_e * c² .

В релятивистской физике мы говорим, что энергия покоя связана только с тем, что тело наделено массой. В этом смысл знаменитой формулы Эйнштейна — энергия и масса эквивалентны. Увеличение энергии тела приводит к увеличению его массы.

Анализируя рис. 2, мы видим, что отдельные компоненты импульса могут быть определены простыми тригонометрическими соотношениями. Таким образом, в конечном итоге наша система уравнений принимает вид, показанный ниже. Первое уравнение относится к горизонтальной составляющей импульса, второе — к вертикальной, а третье выражает принцип сохранения энергии.

В типичном лабораторном эксперименте мы освещаем электроны излучением с фиксированной длиной волны λ и получаем, как правило, угол рассеяния фотона θ. Тогда неизвестные в приведенной выше системе уравнений имеют вид λ^‘, p^‘_e и φ. Для получения окончательного выражения, описывающего эффект Комптона, эта система обычно преобразуется к форме, показанной ниже. Мы рекомендуем вам провести эти расчеты самостоятельно. В Интернете вы найдете множество советов о том, как это сделать.

Δλ = λ^‘ — λ = ( h / m_e * c ) * ( 1 — cos θ )

Эта форма решения позволяет нам быстро определить разность длин волн между падающим и рассеянным фотоном. Зная длину волны падающего фотона и угол рассеяния фотона θ , мы можем быстро определить длину волны рассеянного фотона. Зная длины волн, мы можем вычислить энергии обоих фотонов, а затем, исходя из принципа сохранения энергии, энергию электрона после рассеяния.

Разница Δλ = λ^‘ — λ называется комптоновским сдвигом или комптоновским смещением. Выражение λ_c = h / m_e * c ≈ 2,43 * 10^-12 м называется комптоновской длиной волны.

Если выражаться образно, то можно сказать, что излучение после столкновения со свободными электронами меняет направление… и цвет — потому что меняется длина волны. Однако такое утверждение не совсем точно. Когда мы говорим о «цвете света», мы имеем в виду свет видимого диапазона, то есть с длиной волны от 400 до 700 нм. Комптоновское рассеяние, однако, не наблюдается для видимого излучения. Эффект возникает для рентгеновских и гамма-лучей, т.е. для излучения с на порядки большей энергией фотонов (или на много порядков меньшей длиной волны), чем видимый свет.

Два случая комптоновского рассеяния

Рассмотрим теперь два крайних случая комптоновского рассеяния. Первый возникает, когда угол рассеяния фотона θ = 0°. Это означает, что фотон не меняет своего направления после столкновения с электроном. Эта ситуация показана на рис. 3. Мы видим, что:

λ^‘ — λ = ( h / m_e * c ) * (1 — 1) = 0 → λ^‘ = λ

Длина волны фотона до и после столкновения одинакова. Это означает, что фотон не передает импульс или энергию электрону. Поэтому электрон остается в состоянии покоя, а фотон продолжает двигаться без рассеяния.

Рис. 3. Случай «отсутствия» рассеяния в явлении Комптона

Другой крайний случай — когда θ = 180°. Образно говоря, фотон «отскакивает» от электрона и начинает двигаться в прямо противоположном направлении. Такая ситуация называется обратным рассеянием фотона. Тогда у нас есть:

λ = ( h / m_e * c ) * (1 + 1) = 2h / m_e * c

При обратном рассеянии разность длин волн фотона принимает максимально возможное значение. Это означает, что фотон передает электрону максимально возможную энергию и импульс. Эта ситуация показана на рис. 4.

Рис. 4. Случай обратного рассеяния в явлении Комптона

Список использованной литературы

Комптон А. Рассеяние рентгеновских лучей как частиц // Эйнштейновский сборник 1986—1990. — М.: Наука, 1990. — С. 398—404. — 2600 экз.
Camphausen KA, Lawrence RC. «Principles of Radiation Therapy» in Pazdur R, Wagman LD, Camphausen KA, Hoskins WJ (Eds) Cancer Management: A Multidisciplinary Approach. 11 ed. 2008.
Филонович С. Р. Артур Комптон и его открытие // Эйнштейновский сборник 1986—1990. — М.: Наука, 1990. — С. 405—422. — 2600 экз.
Эффект Комптона. Учебно-методическое пособие / Р.Р. Гайнов, Е.Н. Дулов, М.М. Бикчантаев // Казань: Казанский (Приволжский) федеральный университет, 2013. – 24 с.: 7 илл.

Источник

From Wikipedia, the free encyclopedia

The Compton wavelength is a quantum mechanical property of a particle, defined as the wavelength of a photon whose energy is the same as the rest energy of that particle (see mass–energy equivalence). It was introduced by Arthur Compton in 1923 in his explanation of the scattering of photons by electrons (a process known as Compton scattering).

The standard Compton wavelength λ of a particle is given by

${displaystyle lambda ={frac {h}{mc}},}$

while its frequency f is given by

${displaystyle f={frac {mc^{2}}{h}},}$

where h is the Planck constant, m is the particle’s proper mass, and c is the speed of light. The significance of this formula is shown in the derivation of the Compton shift formula. It is equivalent to the de Broglie wavelength for a particle with velocity ${displaystyle v={frac {c}{sqrt {2}}}}$ .

The CODATA 2018 value for the Compton wavelength of the electron is 2.42631023867(73)×10⁻¹² m.^[1] Other particles have different Compton wavelengths.

Reduced Compton wavelength[edit]

The reduced Compton wavelength ƛ (barred lambda, denoted below by ) is defined as the Compton wavelength divided by 2π:

${displaystyle {bar {lambda }}={frac {lambda }{2pi }}={frac {hbar }{mc}},}$

where ħ is the reduced Planck constant.

Role in equations for massive particles[edit]

The inverse reduced Compton wavelength is a natural representation for mass on the quantum scale, and as such, it appears in many of the fundamental equations of quantum mechanics. The reduced Compton wavelength appears in the relativistic Klein–Gordon equation for a free particle:

${displaystyle mathbf {nabla } ^{2}psi -{frac {1}{c^{2}}}{frac {partial ^{2}}{partial t^{2}}}psi =left({frac {mc}{hbar }}right)^{2}psi .}$

It appears in the Dirac equation (the following is an explicitly covariant form employing the Einstein summation convention):

${displaystyle -igamma ^{mu }partial _{mu }psi +left({frac {mc}{hbar }}right)psi =0.}$

The reduced Compton wavelength is also present in Schrödinger’s equation, although this is not readily apparent in traditional representations of the equation. The following is the traditional representation of Schrödinger’s equation for an electron in a hydrogen-like atom:

${displaystyle ihbar {frac {partial }{partial t}}psi =-{frac {hbar ^{2}}{2m}}nabla ^{2}psi -{frac {1}{4pi epsilon _{0}}}{frac {Ze^{2}}{r}}psi .}$

Dividing through by hbar c and rewriting in terms of the fine-structure constant, one obtains:

${displaystyle {frac {i}{c}}{frac {partial }{partial t}}psi =-{frac {bar {lambda }}{2}}nabla ^{2}psi -{frac {alpha Z}{r}}psi .}$

Distinction between reduced and non-reduced[edit]

The reduced Compton wavelength is a natural representation of mass on the quantum scale and is used in equations that pertain to inertial mass, such as the Klein–Gordon and Schrödinger’s equations.^[2]^: 18–22

Equations that pertain to the wavelengths of photons interacting with mass use the non-reduced Compton wavelength. A particle of mass m has a rest energy of E = mc². The Compton wavelength for this particle is the wavelength of a photon of the same energy. For photons of frequency f, energy is given by

${displaystyle E=hf={frac {hc}{lambda }}=mc^{2},}$

which yields the Compton wavelength formula if solved for λ.

Limitation on measurement[edit]

The Compton wavelength expresses a fundamental limitation on measuring the position of a particle, taking into account quantum mechanics and special relativity.^[3]

This limitation depends on the mass m of the particle.
To see how, note that we can measure the position of a particle by bouncing light off it – but measuring the position accurately requires light of short wavelength. Light with a short wavelength consists of photons of high energy. If the energy of these photons exceeds mc², when one hits the particle whose position is being measured the collision may yield enough energy to create a new particle of the same type.^{[citation needed]} This renders moot the question of the original particle’s location.

This argument also shows that the reduced Compton wavelength is the cutoff below which quantum field theory – which can describe particle creation and annihilation – becomes important. The above argument can be made a bit more precise as follows. Suppose we wish to measure the position of a particle to within an accuracy Δx. Then the uncertainty relation for position and momentum says that

${displaystyle Delta x,Delta pgeq {frac {hbar }{2}},}$

so the uncertainty in the particle’s momentum satisfies

${displaystyle Delta pgeq {frac {hbar }{2Delta x}}.}$

Using the relativistic relation between momentum and energy E² = (pc)² + (mc²)², when Δp exceeds mc then the uncertainty in energy is greater than mc², which is enough energy to create another particle of the same type. But we must exclude this greater energy uncertainty. Physically, this is excluded by the creation of one or more additional particles to keep the momentum uncertainty of each particle at or below mc. In particular the minimum uncertainty is when the scattered photon has limit energy equal to the incident observing energy. It follows that there is a fundamental minimum for Δx:

${displaystyle Delta xgeq {frac {1}{2}}left({frac {hbar }{mc}}right).}$

Thus the uncertainty in position must be greater than half of the reduced Compton wavelength ħ/mc.

Relationship to other constants[edit]

Typical atomic lengths, wave numbers, and areas in physics can be related to the reduced Compton wavelength for the electron ( ${textstyle {bar {lambda }}_{text{e}}equiv {tfrac {lambda _{text{e}}}{2pi }}simeq 386~{textrm {fm}}}$ ) and the electromagnetic fine-structure constant ( ${textstyle alpha simeq {tfrac {1}{137}}}$ ).

The Bohr radius is related to the Compton wavelength by:

${displaystyle a_{0}={frac {1}{alpha }}left({frac {lambda _{text{e}}}{2pi }}right)={frac {{bar {lambda }}_{text{e}}}{alpha }}simeq 137times {bar {lambda }}_{text{e}}simeq 5.29times 10^{4}~{textrm {fm}}}$

The classical electron radius is about 3 times larger than the proton radius, and is written:

${displaystyle r_{text{e}}=alpha left({frac {lambda _{text{e}}}{2pi }}right)=alpha {bar {lambda }}_{text{e}}simeq {frac {{bar {lambda }}_{text{e}}}{137}}simeq 2.82~{textrm {fm}}}$

The Rydberg constant, having dimensions of linear wavenumber, is written:

${displaystyle {frac {1}{R_{infty }}}={frac {2lambda _{text{e}}}{alpha ^{2}}}simeq 91.1~{textrm {nm}}}$

${displaystyle {frac {1}{2pi R_{infty }}}={frac {2}{alpha ^{2}}}left({frac {lambda _{text{e}}}{2pi }}right)=2{frac {{bar {lambda }}_{text{e}}}{alpha ^{2}}}simeq 14.5~{textrm {nm}}}$

This yields the sequence:

${displaystyle r_{text{e}}=alpha {bar {lambda }}_{text{e}}=alpha ^{2}a_{0}=alpha ^{3}{frac {1}{4pi R_{infty }}}.}$

For fermions, the reduced Compton wavelength sets the cross-section of interactions. For example, the cross-section for Thomson scattering of a photon from an electron is equal to^{[clarification needed]}

${displaystyle sigma _{T}={frac {8pi }{3}}alpha ^{2}{bar {lambda }}_{text{e}}^{2}simeq 66.5~{textrm {fm}}^{2},}$

which is roughly the same as the cross-sectional area of an iron-56 nucleus. For gauge bosons, the Compton wavelength sets the effective range of the Yukawa interaction: since the photon has no mass, electromagnetism has infinite range.

The Planck mass is the order of mass for which the Compton wavelength and the Schwarzschild radius ${displaystyle r_{rm {S}}=2GM/c^{2}}$ are the same, when their value is close to the Planck length ( $l_{{{rm {P}}}}$ ). The Schwarzschild radius is proportional to the mass, whereas the Compton wavelength is proportional to the inverse of the mass. The Planck mass and length are defined by:

${displaystyle m_{rm {P}}={sqrt {hbar c/G}}}$

${displaystyle l_{rm {P}}={sqrt {hbar G/c^{3}}}.}$

Geometrical interpretation[edit]

A geometrical origin of the Compton wavelength has been demonstrated using semiclassical equations describing the motion of a wavepacket.^[4] In this case, the Compton wavelength is equal to the square root of the quantum metric, a metric describing the quantum space: ${displaystyle {sqrt {g_{kk}}}=lambda _{c}}$

References[edit]

^ CODATA 2018 value for Compton wavelength for the electron from NIST.
^ Greiner, W., Relativistic Quantum Mechanics: Wave Equations (Berlin/Heidelberg: Springer, 1990), pp. 18–22.
^ Garay, Luis J. (1995). «Quantum Gravity And Minimum Length». International Journal of Modern Physics A. 10 (2): 145–65. arXiv:gr-qc/9403008. Bibcode:1995IJMPA..10..145G. doi:10.1142/S0217751X95000085. S2CID 119520606.
^ Leblanc, C.; Malpuech, G.; Solnyshkov, D. D. (2021-10-26). «Universal semiclassical equations based on the quantum metric for a two-band system». Physical Review B. 104 (13): 134312. arXiv:2106.12383. Bibcode:2021PhRvB.104m4312L. doi:10.1103/PhysRevB.104.134312. ISSN 2469-9950. S2CID 235606464.

External links[edit]

Length Scales in Physics: the Compton Wavelength

Источник

~ 42 мин

Введение

Максимальная скорость перемещения, абсолютный нуль температуры, квант действия, гравитационная сингулярность… — физика прочно ассоциируется в общественном сознании с предельными явлениями. Эти явления трудны для изучения, их едва ли можно постичь воображением, но они остаются очень притягательными для философского размышления.

Элементарные частицы — одно из таких предельных явлений. Развитие субатомной физики в XX веке вновь породило широкий интерес к философской теме дискретности материи. Над осмыслением элементарности частиц трудились многие физики по всему миру, а сами частицы то получали статус элементарных, то теряли его вслед за новыми открытиями в физике. И если сам атом, его ядро, протон и нейтрон, когда-то считавшиеся элементарными, уже давно таковыми не считаются, то электрон сохранил этот статус по сей день.

Принято считать, что электрон является элементарной частицей, то есть таким объектом, который является частью, элементом других объектов, но сам существует только как целый и собственных частей, элементов не имеет¹ ² . Также часто предполагается, что он не имеет и размера, представляя собой «точечный заряд».

Идея бесструктурного и точечного электрона не может удовлетворить интереса и показывает лишь недостаток современных знаний о структуре элементарных частиц. Выражаясь языком эмпиризма, структура электрона ещё не обнаружена. Действительно, даже современная экспериментальная техника, несмотря на громкие успехи, вынуждена лишь указывать предел своих возможностей в обнаружении внутреннего устройства электрона³ .

В то же время вынужденная необходимость воздвигать эпистемологические перегородки противна живому материалистическому познанию. Исследуем ли мы материю «вглубь», переходя от меньшего к меньшему, или «вширь», переходя от большего к большему, — мы не хотим и не можем остановиться. Даже если мы наконец-то найдём самую мельчайшую частицу материи, мы устремимся искать частицу поменьше.

Наблюдая историю «неделимости» тех или иных объектов, мы приходим к выводу, что любая неделимость или элементарность должна быть условной. Распространению идеи о полной, окончательной, фундаментальной элементарности некоторых частиц служит не столько недостаток эмпирических данных, сколько недостаток популярной философии.

Рассмотрим проблему структуры электрона в развитии, принимая во внимание историческую ограниченность в понимании проблемы на разных этапах развития науки.

По традиции атомизма, которая получила новое дыхание в физике второй половины XIX века, электрон мыслился как неделимый объект, который несёт в себе элементарный, то есть тоже неделимый, электрический заряд.

Сомнение в элементарности учёные высказывали и в то время. Австрийский физик Эрнст Эренгафт на основании своих опытов пришёл к выводу, что существует субэлектрон, частица с зарядом, меньшим, чем заряд электрона. Эту идею оспаривал американец Милликен, который своими глубоко продуманными экспериментами установил значение элементарного заряда e⁻, близкое к современному. Дискуссия о субэлектроне продолжалась до конца 1920-х годов и затем заглохла. Электрон как атом электричества был утверждён эмпирически, и научная общественность это приняла⁴ .

Как искать структуру?

Для начала рассмотрим два определения понятия «структура»:

«Структура — это взаимообусловленная совокупность связей элементов в составе системы, определяющая собой её качественную специфику»⁵ .

«Структура (от лат. structura — строение, расположение, порядок) — совокупность устойчивых связей объекта, обеспечивающих его целостность и тождественность самому себе, то есть сохранение основных свойств при различных внешних и внутренних изменениях⁶ .

Выделим из этих понятий связанные категории. Структура как качество есть способ связи частей в целом. Обладать структурой, или, что то же самое, свойством структурированности — значит, в первую очередь, состоять из элементов. В первом плане элементы относятся к структуре как части к целому, но этим их взаимоопределение не исчерпывается. Сущность структуры заключается в общей связи элементов. Связь элементов структуры — это устойчивые взаимные отношения элементов друг к другу и к структуре в целом.

Из этого сделаем заключение, что те условия, при которых связи между элементами существуют, являются и условиями, при которых существует структура.

Исследуя электрон, сперва найдём связи, в которых заключается пространственная определённость целого объекта. Будем подходить к вопросу о структуре с этой «внешней» стороны пространственной определённости, и, в первую очередь, со стороны проблемы протяжённости электрона. Проще говоря, найдём его размер.

Шарик

Итак, встаёт вопрос о размере электрона, который в классической физике представлялся атомом-шариком. Характерным размером шара является радиус — его у электрона и принялись искать физики в начале XX века. В конце первого десятилетия был получен «классический радиус электрона». Классический радиус электрона понимается как радиус полой сферы, по площади которой равномерно распределён заряд, равный заряду электрона. Радиус прямо пропорционален квадрату заряда и обратно пропорционален массе покоя электрона:

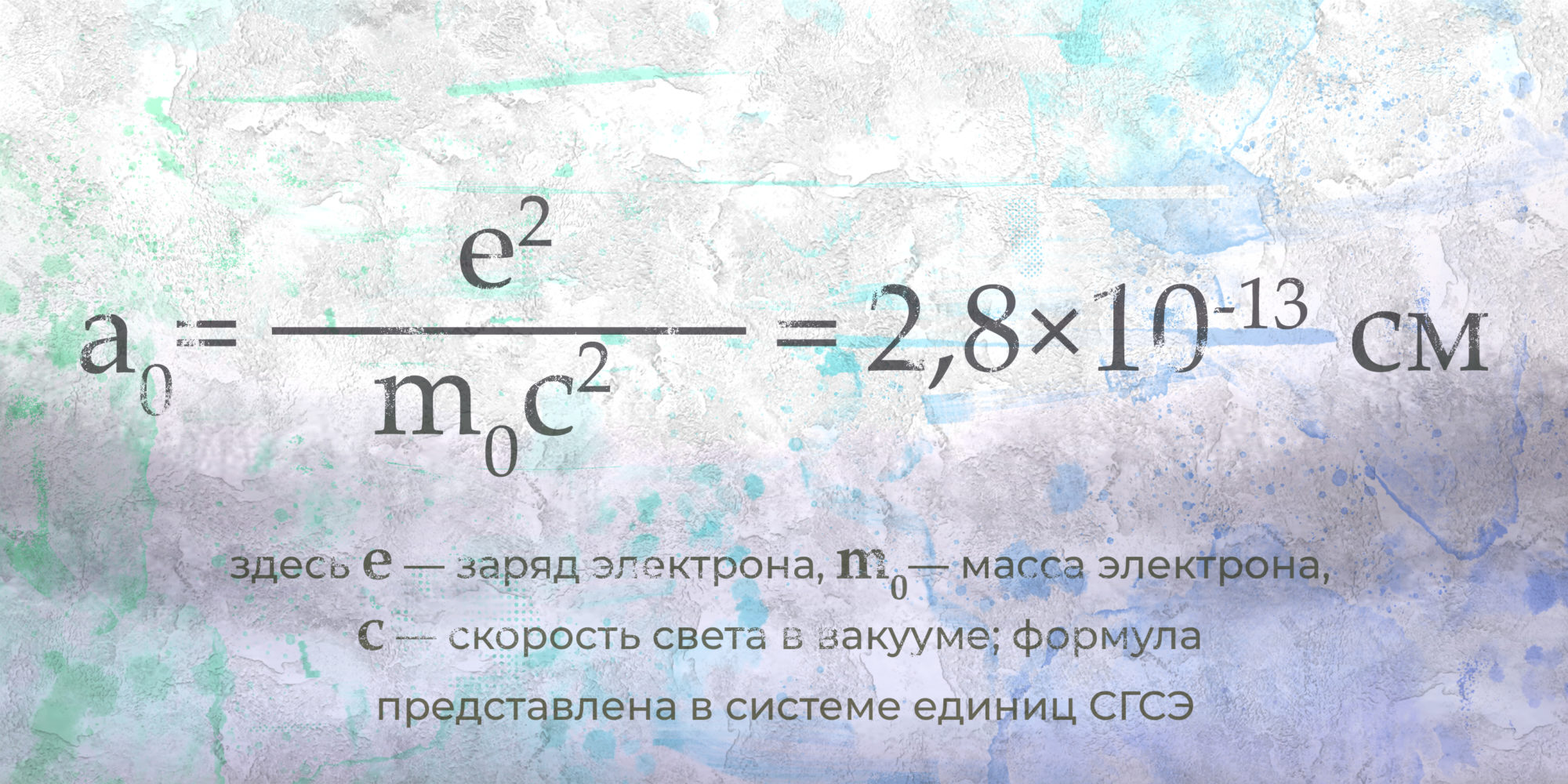
Однако специальная теория относительности поставила под сомнения физический смысл найденной величины. Понятие размера элементарной частицы противоречит релятивистской теории. В известном курсе теоретической физики Ландау и Лифшица это обстоятельство описано так:

«Очевидно, что если бы элементарная частица обладала конечными размерами, т. е. была бы протяжённой, то она не могла бы деформироваться, так как понятие деформации связано с возможностью независимого движения отдельных частей тела.
Но, как мы только что видели, теория относительности показывает невозможность существования абсолютно твёрдых тел. Таким образом, в классической (неквантовой) релятивистской механике частицам, которые мы рассматриваем как элементарные, нельзя приписывать конечных размеров. Другими словами, в пределах классической теории элементарные частицы должны рассматриваться как точечные»⁷ .

Советский физик Блохинцев пишет:

«Однако оказалось, что все попытки развить теорию этого электрона-шарика приводили к фундаментальному противоречию с теорией относительности. Теория относительности требовала, чтобы электрон был точечным. Требование же „точечности“ электрона в свою очередь приводит к противоречию, потому что энергия электрона, а вместе с тем его масса в этом случае оказывались бесконечными, что противоречило, конечно, и самой относительности. Электронная теория имела в то время очень большие успехи, но все успехи были связаны с явлениями, в которых электрон выступал как точка. К тому же нужно сказать, что никаких экспериментальных средств для исследования структуры электронов, т. е. для исследования масштабов порядка a = 2,8 · (10⁻¹³) см, в то время не было. Их и сейчас почти нет [Речь о 1959 г. — А. Б.]»⁸ .

С возникновением квантовой механики сильнее пошатнулась идея электрона как шарика с определённым радиусом. Так, в 20-х годах прошлого века квантовая механика дала новую величину для оценки размера электрона — комптоновскую длину. Это изменение длины волны фотона, кванта света, при рассеянии на электроне:

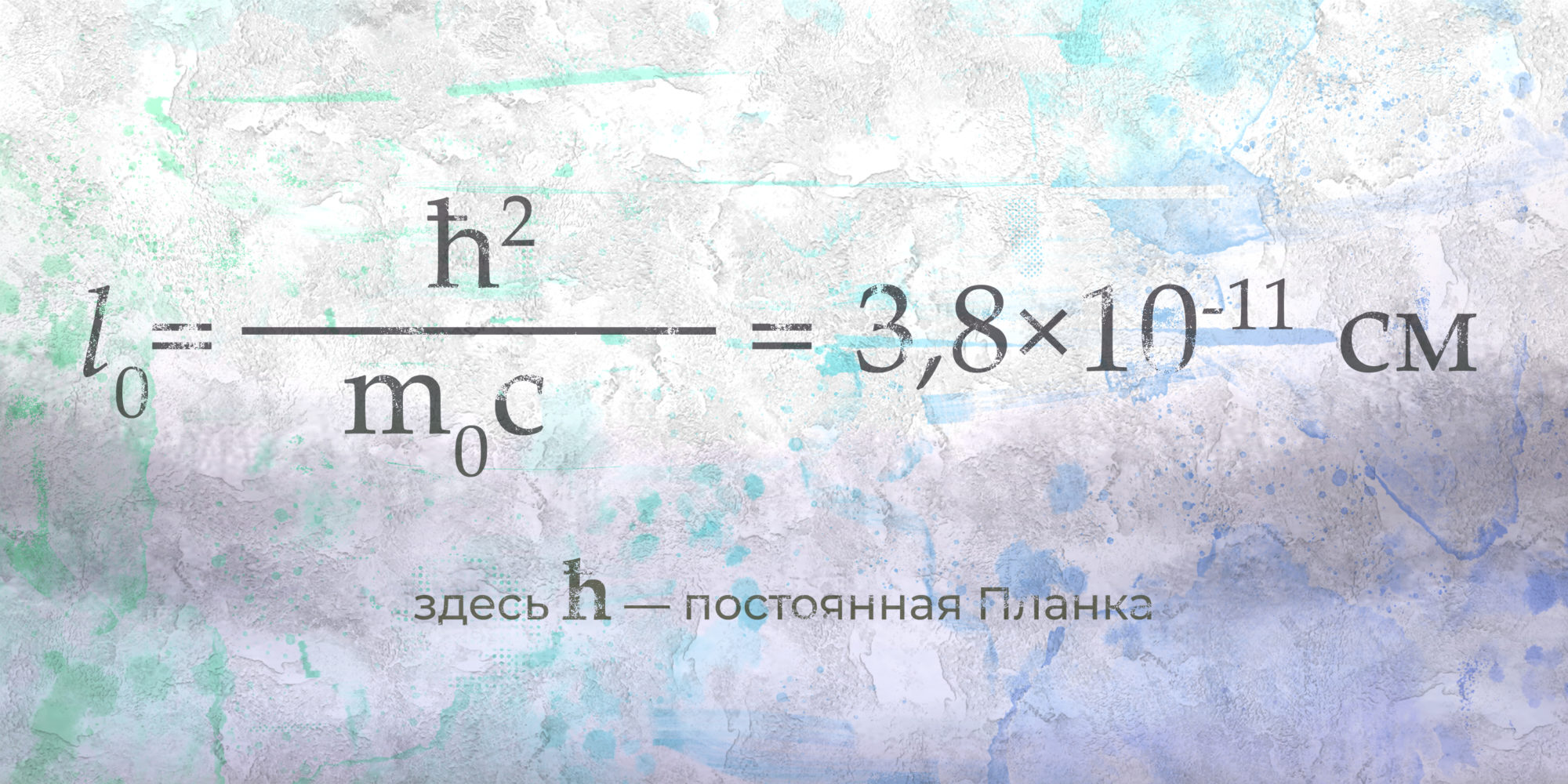
Комптоновская длина оказалась в 137 раз больше классического радиуса электрона, что может показаться странным: новая и более точная теория, казалось бы, должна была дать более точные результаты. Обе величины были подтверждены множеством экспериментов. Но обе же величины характеризуют два совершенно несопоставимых по размеру шарика. Возникает вопрос о физическом смысле рассмотренных величин: какой именно объект они характеризуют?

Это затруднение привело к выводу, что подходить к структуре и размеру электрона с «классических» позиций нельзя. Комптоновская длина волны задала тот масштаб, начиная с которого становятся непригодными обычные концепции размера для частицы.

Теперь мы шагнём из 1923 года, явившего нам комптоновский эффект, в 1924 год, когда физик Луи де Бройль высказал свою гипотезу об универсальном корпускулярно-волновом дуализме.

Волна

С развитием квантовой механики возникло представление о волновом поведении вещества. Эксперименты по дифракции электронов обнаружили волновое поведение, подтвердив теорию. Было установлено, что электрон как волна имеет волновую пространственную характеристику: длину волны. Длина волны электрона в атоме водорода получается порядка 10⁻⁸ см, что в 1000 раз больше комптоновской длины и в 100 000 раз больше классического радиуса. Это значит, что игнорировать волновые свойства электрона нельзя: волна имеет не меньше прав на форму электрона, чем шарик.

Подход к электрону как к волне поменял представления об искомой структуре. Можно разделить волну на элементы (гребни, впадины, волновая поверхность) и параметризовать их (амплитуда возмущений, длина волны, частота). Но остается ещё главный вопрос, к которому тяготеют все остальные. Если волна — это распространение возмущения в пространстве, тогда возмущением какой среды является электрон?

Об этом пишет советский физик Блохинцев:

«Вначале были попытки рассматривать сами частицы как образования из волн, распределённые в некоторой области пространства. Интенсивность волны де Бройля рассматривалась в этой концепции как величина, характеризующая плотность среды, из которой образована частица. Это понимание волн де Бройля имело совершенно классический характер. Основанием для него служило то обстоятельство, что в некоторых, весьма частных случаях, оказалось возможным (теоретически) построить волновые образования, движение которых совпадает с движением частицы, движущейся по законам классической механики»⁹ .

Основоположник квантовой механики, Эрвин Шрёдингер, дал одну из первых интерпретаций волновой природы, согласно которой электрон представляет собой волновой пакет. Собранные вместе волны лишь кажутся нам частицей, так как частоты этих волн довольно близки и распространяются они с близкой скоростью, что позволяет их обнаружить как нечто, плотно заполняющее небольшой объём пространства и сохраняющее свою обособленность.

Рисунок 1. Компьютерное моделирование интерференции двух волновых пакетов. Зелёная плоскость — плоскость X–Y, где встречаются два электрона. Вертикальное зелёное направление показывает вещественную часть волновой функции. На полупрозрачной белой плоскости наверху отображается плотность вероятности обнаружения частицы (квадрат модуля волновой функции) в виде синего пятна.

Если свободный электрон летит вдаль в виде сгустка волн, то в атоме электрон-волна замыкается на орбитали и образует стоячую волну. Таким образом, вместо шарика, вращающегося вокруг атома, как планета вокруг звезды, электрон представляет собой нечто, размазанное по орбите и при этом колеблющееся.

«…Э. Шрёдингер рассматривал электрон в атоме как отрицательно заряженное облако, плотность которого пропорциональна квадрату значения волновой функции в соответствующей точке атома»¹⁰ .

Компьютерное моделирование интерференции двух противоположно циркулирующих электронов в атоме водорода в электромагнитном поле¹¹ .

Понятие волнового пакета предполагает, что волны, из которых он состоит, имеют близкие, но не одинаковые скорости распространения. Разумеется, эта разница со временем приводит к удалению волн друг от друга — волновой пакет «расплывается» за довольно малое время, что противоречит наблюдаемой стабильности электрона.

Свободно летящая частица в виде волнового пакета. Со временем пакет «расплывается».

Собственно, электрон-волна-облако противоречит идеи об элементарности. Казалось бы, вот решение проблемы — отдельные волны из волнового пакета и образуют электрон, их соотношение определяет его структуру. Но модель волнового пакета не согласуется ни с теми опытными данными, где электрон проявляет себя как частица, ни с теми, где электрон проявляет себя как волна. Волновой пакет противоречит реальной стабильности и целостности электрона.

Надо признать, что Шрёдингер в своём толковании подменяет двойственность природы электрона первичностью волновой природы по отношению к корпускулярной, тем самым отрицая двойственность. Обратная точка зрения состоит в том, что электрон-волна-облако состоит из колебаний более мелких частиц, как это имеет место в воздушных и водяных. И это толкование также нужно отвергнуть:

«Равным образом нельзя допустить, что сами волны являются образованием частиц или, точнее говоря, возникают в среде, образованной частицами. Опыт показывает, что дифракционная картина, возникающая на фотопластинке, не зависит от интенсивности падающего пучка частиц, а следовательно, и от плотности частиц в единице объёма. Чтобы получить одну и ту же дифракционную картину, можно уменьшить интенсивность, но увеличивать экспозицию: важно лишь общее число прошедших частиц. Этот факт определённо показывает, что каждый из электронов дифрагирует независимо от других»¹² .

Квантовая механика не дала механистического ответа на вопрос о структуре электрона, в том смысле, что не заглянула внутрь шарика. Но она дала много новой информации о пространственных характеристиках электрона. Были определены и новые величины, характеризующие электрон. Например, электрон теперь имеет не только массу и заряд, но ещё и спин и магнитный момент.

Если квантовая механика так настойчиво доказывает, что к малому объекту в целом неприменимы «классические», по сути — механистические, представления, то эти представления неприменимы и к структуре этого объекта. Следует отойти и от механистического представления о волне, аналогичной волнам на поверхности воды, потому что распространение квантовой волны происходит не в привычном нам пространстве, а в фазовом «пространстве» состояний, которое представляет собой определённый род математического множества. Волновая функция характеризует некоторое состояние квантового объекта, но не внутреннюю структуру. Квантовые величины являются характеристиками состояний и представляют собой показатели, внешнюю определённость, которая должна выражать внутреннюю.

Вращение и направленность

Можно сделать вывод, что квантовая механика не дала ответа на вопрос о структуре, но, что не менее важно, уточнила постановку этого вопроса. Кроме того, квантовая механика не смогла решить проблему бесконечной массы электрона. Макс Борн и Леопольд Инфельд в 1934 г. предложили оригинальное решение проблемы бесконечной массы в обход квантовой механики. Они преобразовали классическую электромагнитную теорию в нелинейную теорию. Но с квантовой механикой эта теория оказалась несовместима, и от неё отказались.

Распространившаяся среди физиков и принятая впоследствии Шрёдингером статистическая интерпретация признаёт объективный характер как волновых свойств, так и корпускулярных. Но в различных интерпретациях, разработанных на основе статистической, прослеживается некоторое «тяготение смыслов» в сторону частиц, в сторону первичности корпускулярной природы.

Несмотря на то, что основу полноценной квантовой механики заложили волновая теория Шрёдингера и понятие корпускулярно-волнового дуализма, все микрообъекты и в наше время больше понимаются как частицы. Но специфические характеристики микрообъектов, например, спин частицы, трудно поддаются классическим механическим представлениям.

Как может спин характеризовать структуру электрона? Перед тем, как пытаться ответить на этот вопрос, проследим кратко историю открытия этого понятия. Для этого вернёмся в эпоху старой квантовой теории Бора и Зоммерфельда.

Гипотезу об электроне, вращающемся вокруг своей оси, впервые предложил А. Комптон в 1921 г. Но Комптон не воспользовался своей идеей для объяснения аномального эффекта Зеемана, и его работа не оказала влияния на дальнейший ход событий.

В 1922 году в опыте Штерна — Герлаха была подтверждена гипотеза Зоммерфельда о пространственном квантовании в магнитном поле. Под этим подразумевается дискретность возможных пространственных ориентаций момента импульса. Схема опыта была следующей. Небольшая печь выпускала через отверстие серебряный пар. Из пара выделялся пучок атомов серебра, который пропускался через неоднородное магнитное поле и осаждался на пластинке. В результате получалось, что в поле пучок всегда расщеплялся на два, вместо того чтобы равномерно распределиться по пластинке. Результат этого опыта показал, что атомы серебра обладают общим моментом импульса и магнитным моментом, который может принимать только две ориентации относительно направления магнитного поля.

В 1925 г. немецкий физик Вольфганг Паули, исследуя дублетный характер спектров щелочных металлов, а также аномальный эффект Зеемана, высказал предположение для объяснения этих явлений, согласно которому электрону можно приписать некоторую «двузначность». Смысл двузначности Паули не объяснил.

В том же 1925 г. Ральф Крониг, узнав об идеях Паули, высказал предположение, что эта двузначность является результатом того, что самому электрону нужно приписать момент импульса, равный ½ ħ, и соответственный магнитный момент. Если полный момент j отличается от орбитального момента l на ±½, то это означает, что каждый электрон в дополнение к моменту, связанному с орбитальным движением, имеет ещё собственный момент с проекцией, равной ±½ ħ, на любое выбранное направление. Чтобы интерпретировать этот момент динамически, Крониг предположил, что электрон вращается вокруг собственной оси¹³ . Соображения Кронига не встретили поддержки ни у Паули, ни у ряда других теоретиков. Против гипотезы о вращении электрона высказывалось много возражений¹⁴ .

В том же 1925 г. появилась заметка Уленбека и Гаудсмита, в которой эти авторы независимо выдвинули идею о внутреннем моменте импульса и связанном с ним магнитном моменте.

«На языке моделей, который до создания квантовой механики был единственной основой для обсуждения, этот собственный момент электрона можно наглядно изобразить только как вращение электрона вокруг своей оси. Правда, такое представление сопряжено с рядом серьёзных трудностей»¹⁵ .

В речи, произнесённой в Лейдене в 1955 г. по случаю занятия профессорской кафедры Лоренца, Уленбек рассказал об открытии и публикации гипотезы о вращающемся электроне:

«Гаудсмит и я пришли к этой идее, изучая статью Паули, в которой был сформулирован знаменитый принцип запрета и электрону впервые приписывались четыре квантовых числа. Вывод Паули был довольно формальным; он не связывал никакой конкретной картины со своим предложением. Для нас оно казалось загадкой. Мы свыклись с представлением, что каждому квантовому числу соответствует степень свободы, и, с другой стороны, с точечностью электрона, который, очевидно имел лишь три степени свободы, и не могли найти место для четвёртого квантового числа. Мы могли принять его только в том случае, если электрон является маленькой сферой, способной вращаться…
Несколько позже мы обнаружили из работы Абрагама, что множитель 2 в магнитном моменте вращающейся сферы с поверхностным зарядом можно понять классически. Это ободрило нас, но наш энтузиазм в значительной мере остыл, когда мы обнаружили, что скорость вращения на поверхности электрона должна во много раз превышать скорость света! …
Лоренц … очень заинтересовался нашей идеей, хотя, я думаю, в душе относился к ней несколько скептически. … через неделю он передал нам … рукопись, содержавшую длинные расчёты электромагнитных свойств вращающегося электрона. Мы не вполне поняли их, но было очевидно, что представление о вращающемся электроне, если его принимать всерьёз, связано с большими трудностями. Например, магнитная энергия электрона должна быть столь велика, что его масса по принципу эквивалентности должна превосходить массу протона, или, если принять известное значение массы, его размеры должны превосходить размеры атома! И то, и другое казалось бессмыслицей»¹⁶ .

Паули неохотно принимал гипотезу вращающегося электрона из-за её классического механического содержания. Действительно, трудно говорить о моменте импульса, не думая о вращении. Здесь снова обнаруживается ограниченность понятий механики и связанных с ними представлений.

Спин — характеристика, которая не имеет прямого аналога в классической механике. Она имманентна для частицы, выражает внутренне присущую подвижность. Это единственная квантовая характеристика, которая указывает на собственную пространственную ориентированность электрона безотносительно окружения. В этом смысле можно сказать, что спин выражает структуру частицы.

На данном этапе такое объяснение было бы чрезвычайно туманным. Мы также не выявили, какое свойство волны выражает спин, а упомянули только интерпретацию спина для классического представления о частице. Позже, когда мы выясним роль статистики в квантовых явлениях, значение спина откроется нам с другой стороны.

Неопределённость

В 1927 году Вернер Гейзенберг ввёл в свою теорию соотношение неопределённостей, которое стало принципом квантовой механики. Согласно этому соотношению, определённость (в субъективистской терминологии — точность измерения или точность знания) импульса и координаты взаимно ограничивают друг друга: увеличение одной определённости уменьшает другую. Это же соотношение справедливо для энергии и отрезка времени, в течение которого квантовый объект обладает этой энергией. Соотношение неопределённостей следовало из признания волновой природы частиц.

«Как следует из квантовой механики, одна из противоречивых тенденций, свойственных механическому движению, заключается в том, что всякая тенденция к пространственному ограничению движения неразрывно соединена с тенденцией к увеличению количества движения. Взаимосвязь между этими двумя противоречивыми тенденциями количественно выражается соотношением неопределённости…»¹⁷

В некоторых учебниках и научно-популярных материалах объяснение этого принципа строится на толковании определённости как точности измерения, наблюдения или знания. Такое объяснение неверно и превращает теоретическую физику из науки в игру субъективных эффектов. Соотношения неопределённостей выражают объективно реальную закономерность, а значит, расширяют, а не ограничивают наши познавательные способности, как бы ни противились этому самоназванные «материалисты», по невежеству отрицающие квантовую механику за агностицизм.

«Квантовая механика в своей основе отрицает представление о движении как сумме состояний покоя. Квантовая механика глубже раскрывает сущность движения, так как показывает, что всякое явление, ограничивающее положение частицы в пространстве в то же время изменяет её количество движения»¹⁸ .

Данная мысль философа Владимира Готта проясняет важное философское отличие новой механики от старой. Если в классической механике апория Зенона о летящей стреле устранялась введением в теорию математических понятий предельного перехода и отношения бесконечно малых величин, то в квантовой механике абстрактные представления о покое и жёсткой локализации исчезают по чисто физическим соображениям, потому что сами объекты исследования проявляют себя как не-покоящиеся и не-локализованные. Диалектический принцип, согласно которому материя всегда находится в движении, здесь обнаруживается в квантовой механике с необычайной ясностью. Попирая обывательскую метафизику, диалектика пробивает себе дорогу.

Имея в виду принцип неопределённостей, мы можем по-новому рассмотреть вопрос о структуре. В первую очередь становится понятным, что не получится даже умозрительно схватить электрон в какой-то точке, обездвижить, изолировать от внешних воздействий и затем препарировать. Сама «размытость» по пространству или энергии переходит в разряд структурных свойств, так как посредством этой «размытости» электрон может взаимодействовать с окружением. Структура не может быть только внутренней определённостью — это было бы абсолютизацией категории внутреннее. Следовательно, не нужно рассматривать строго локализованный объект, то есть замкнутый в ограниченной области пространства, пределы которого мы по механистической традиции назвали бы границами самого объекта. Всеобщее взаимодействие частиц материи оказывается существеннее и определённее, чем их собственное бытие (бытие-в-себе), изолированность которого всегда относительна. В квантовой механике эта диалектика вошла в саму физическую основу теории. Мы продолжим эти рассуждения далее при рассмотрении выводов квантовой теории поля.

Окружение

После опубликования уравнения Шрёдингера в 1926 году Оскар Клейн и Владимир Фок независимо друг от друга обобщили это уравнение на случай релятивистских частиц. Полноценную квантово-релятивистскую теорию взаимодействия электронов с электромагнитным полем разработал Поль Дирак в 1928 г. Все результаты теории Дирака оказываются в согласии с экспериментами и с результатами существовавших ранее теорий, основанных на гипотезе о вращающемся электроне.

«… в намерения Дирака не входило простое построение теории вращающегося электрона. Он подошёл к решению задачи по-другому, сформулировав вопрос, который сейчас кажется очень странным. В начале своей статьи, написанной в 1928 г., Дирак спрашивает:

„Почему Природа непременно должна предпочесть эту конкретную модель электрона, а не просто удовлетвориться существованием точечного заряда?“

С современной точки зрения, такой вопрос аналогичен вопросу „Почему бактерия имеет только одну оболочку?“ Наличие спина ħ/2 — это просто одно из свойств, определяющих электрон, а не какую-то иную частицу из множества частиц с различными спинами, известных на сегодняшний день. Тем не менее, в 1928 г. можно было верить, что всё вещество состоит из электронов и чего-то похожего, но обладающего положительным зарядом и являющегося составной частью атомных ядер»¹⁹ .

Из теории Дирака следовало существование состояний электрона с отрицательной энергией. Дирак интерпретировал эти состояния как бесконечный фон, заполненный электронами — электронный вакуум, который в силу своей однородности во Вселенной недоступен для наблюдения. Этот фон проявляется только тогда, когда электрон из фона перейдёт в «реальное» состояние с положительной энергией, а на месте электрона образуется «дырка» в фоне с положительным зарядом e⁺. В 1932 г. такие дырки были обнаружены экспериментально как реальные частицы с помощью камеры Вильсона в магнитном поле. Их назвали позитронами.

Для более глубокого исследования структуры электрона мы обратимся теперь к выводам квантовой теории поля, которая явилась развитием и обобщением квантовой механики, квантово-релятивистской теории Дирака и классической теории поля.

Понятие виртуальных частиц введено в квантовой теории поля для интерпретации математической модели взаимодействия частиц. Виртуальные частицы являют собой промежуточные состояния системы взаимодействующих частиц. Виртуальность в физическом смысле означает, что частица не существует дольше того времени, которое требуется для обладания определённой энергией.

Несмотря на популярность вопроса о характере реальности виртуальных частиц, который иногда поднимается в философской литературе, научпопе и интернете, некоторые физические явления позволяют нам с уверенностью рассматривать виртуальные частицы как объективно реальные вещи.

Электромагнитное поле, создаваемое электроном, распространяется виртуальными фотонами. Для любого, в том числе виртуального, фотона может быть реализована пороговая реакция превращения в пару электрон — позитрон под действием внешнего для виртуального фотона поля. Виртуальные электрон и позитрон, родившиеся из виртуального фотона вблизи «реального» электрона, испытывают на себе действие его поля. Вследствие электростатического отталкивания (по закону Кулона) виртуальные электроны несколько удаляются от «реального» электрона, а позитроны приближаются к нему, так что вокруг него возникнет область со скоплением положительных зарядов. Это явление, предсказанное теоретически, получило название поляризации вакуума. Экспериментально оно проявляется в виде отклонения в энергии между энергетическими уровнями атома водорода.

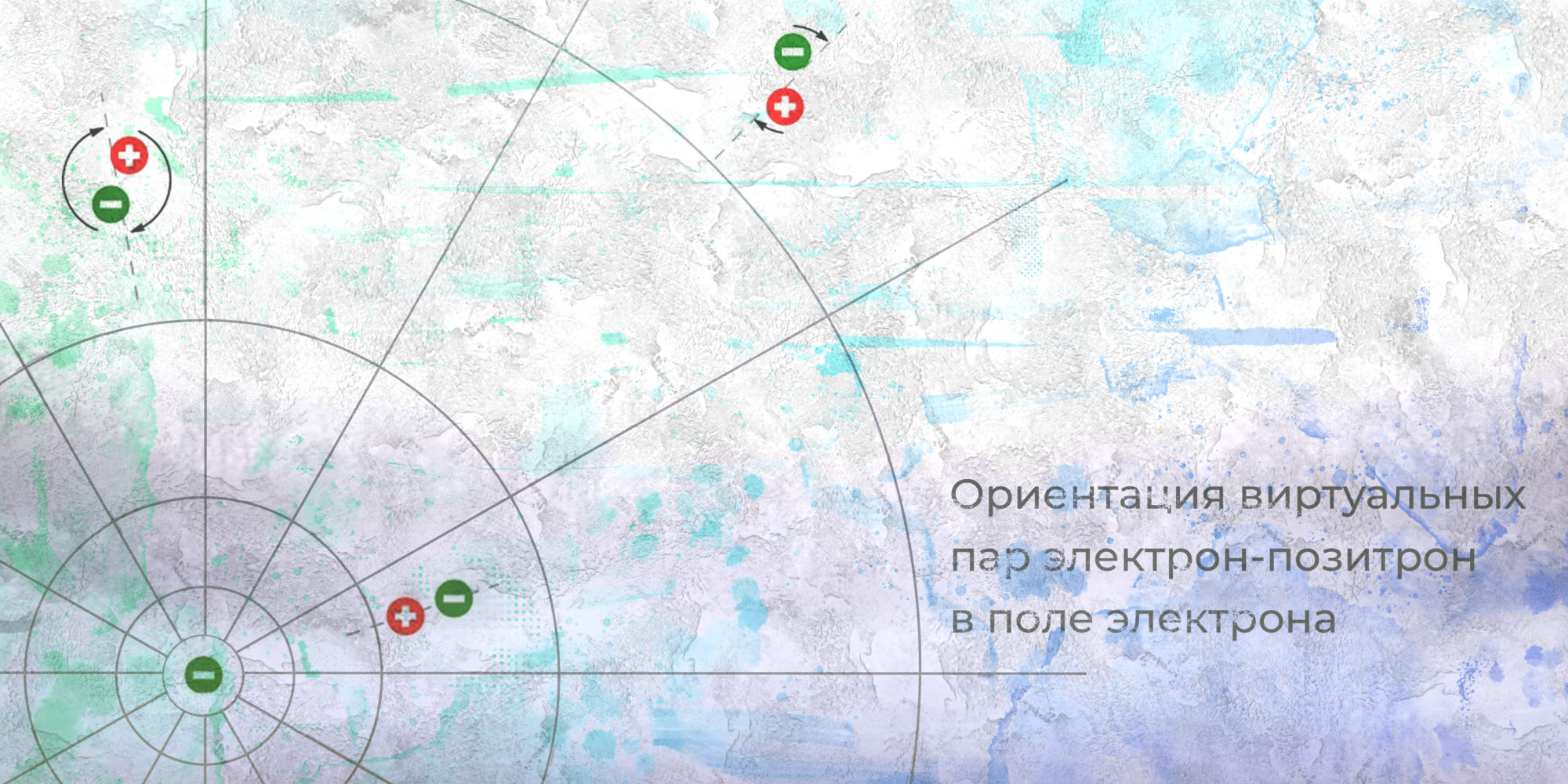
Помимо того, что в поисках структуры электрона вновь и вновь шатаются наши обыденные представления о частице, также пошатнуться должны и привычные представления о физическом поле. Выводы квантовой теории поля показали ограниченность метафизических представлений о вакууме как о пустоте, о поле как о «месте, где действует сила», о взаимодействии объектов в умозрительных условиях изоляции от внешнего мира.

Развитие квантовой теории поля утвердило среди физиков одну из основных диалектико-материалистических идей: объект или процесс должен рассматриваться во взаимной связи и взаимном действии с окружением. По сути, объекты и процессы — одно и то же. Каждая «вещь» — это процесс взаимодействия чего-то с чем-то, а каждый процесс взаимодействия объектов может проявлять себя как «отдельный» объект.

«Диалектический материализм указывает, что все предметы и явления в природе находятся во взаимной связи и обусловленности. Любое явление можно понять правильно только в связи с окружающим миром. Поэтому в изучении свойств микрообъектов важнейшую роль играет изучение внешних связей, т. е. взаимодействий данного микрообъекта с другими телами и полями. … Таким образом, если внутренние связи определяют структуру объекта, то во внешних связях его структура проявляется. … Во всяком взаимодействии с внешними телами оказываются как внутренние, так и внешние связи. Но в одних случаях определяющую роль играют внутренние связи, в других — внешние. Безусловно, пространственная конфигурация играет в этом определённую роль. Но нельзя придавать ей такой категорический характер. Например, в случае атома мы довольно точно можем произвести такое относительное подразделение связей на внутренние и на внешние. В случае же „элементарных“ частиц это в настоящее время сделать действительно затруднительно, так как они ещё очень слабо изучены»²⁰ .

Понимание структуры как внутренней определённости, проявляющейся во внешних связях, нужно применить к структуре квантовых объектов. Для таких объектов размывается грань между пространственно-внутренним и пространственно-внешним. Ещё вернее будет сказать, что в микромире явно обнаруживается условность этой грани и неправомерность её абсолютизации, к которой привык метафизический обыденный ум. Связи и взаимодействие объекта с его окружением нельзя рассматривать как только внешнее. Эти связи столько же определяют структуру микрообъектов, сколько и проявляют её.

Следовательно, электромагнитное поле электрона является его структурой, оно — явление структуры. Это поле взаимодействует само с собой: кванты поля, виртуальные фотоны, превращаются в электрон-позитронные пары; действие поля на эти пары приводит к перераспределению этих частиц, которое обратным образом влияет на поле. Производное от поля окружение из позитронов тоже составляет структуру электрона. Кроме того, виртуальные позитроны сами имеют вокруг себя «ещё более» виртуальное поле, которое также поляризуется. Чем выше степень этой виртуализации, тем более ничтожно явление, но для общей картины об этом нужно упомянуть.

Стоит отметить некоторые существенные затруднения, с которыми столкнулась квантовая теория поля и которые до сих пор не преодолены окончательно, хотя разработаны различные математические приёмы устранения этих затруднений в расчётах. Это не умаляет смысл предшествующих рассуждений о структуре электрона, но даёт идеи для дальнейшего поиска.

По предсказаниям теории поляризация вакуума должна приводить либо к бесконечной массе электрона, либо к нулевому заряду, так как число экранирующих позитронов вокруг электрона должно быть бесконечно большим.

Когда Виктор Вайскопф подсчитал собственную массу электрона с учётом поляризации вакуума, то он получил поразительно малый радиус электрона²¹ :

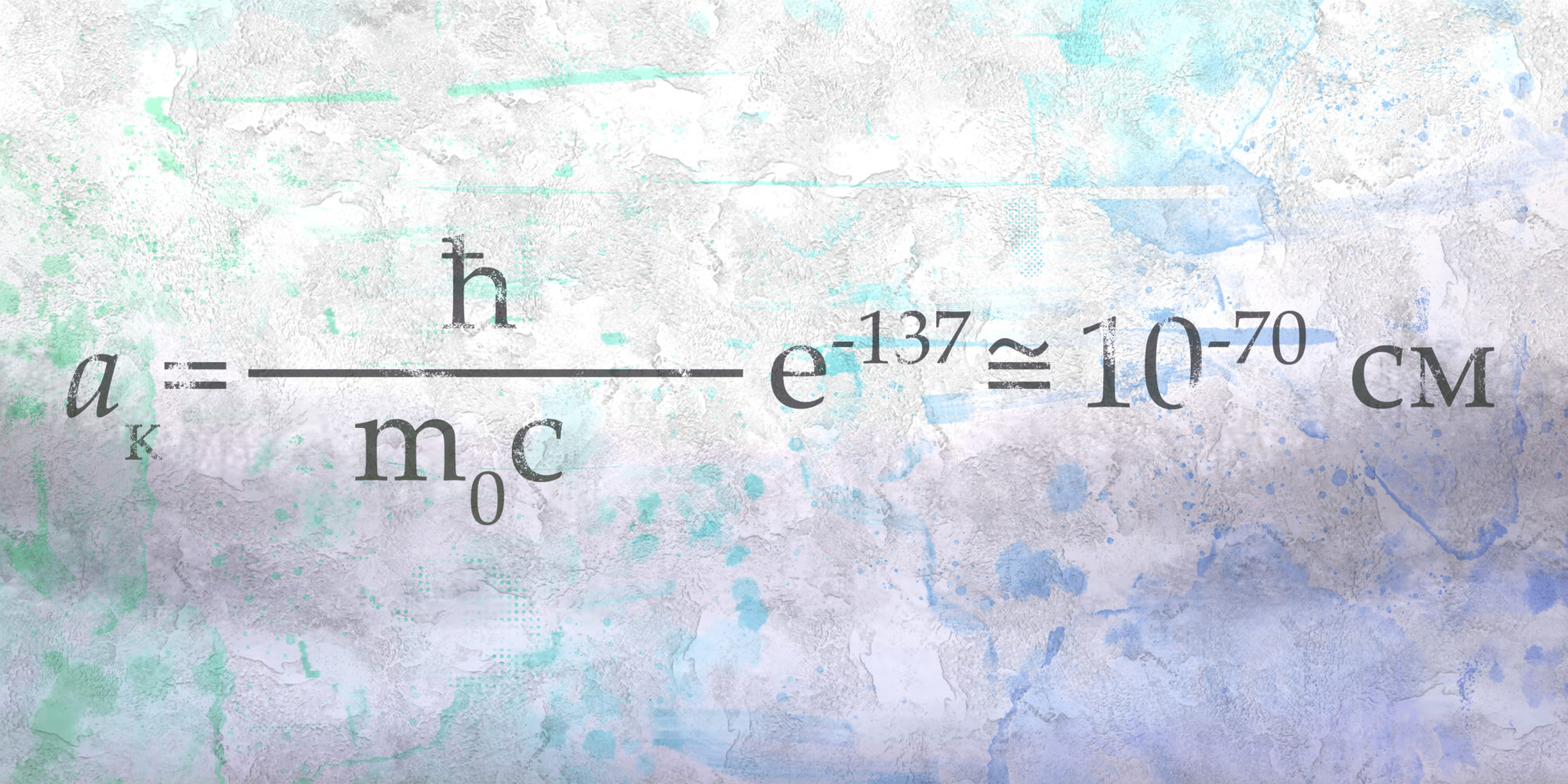
Эта величина оказалась слишком малой, и её физический смысл сомнителен. Даже гравитационный радиус электрона (~10⁻⁵⁵ см) больше этой величины. Для сравнения, гравитационный радиус Земли составляет всего 0,844 см. Это говорит о том, что в структуре электрона может существенную роль играть гравитация, которая, как известно, не учитывается в квантовой физике. Таким образом, можно сказать, что квантовая теория отодвинула проблему структуры электронов в область исключительно малых масштабов.

Мы приняли, что результат взаимодействия электрона с собственным полем, которое находится как бы «вне» электрона, в вакууме, является структурным элементом самого электрона. Есть ещё один интересный эффект взаимодействия электрона с вакуумом. Оказалось, что электроны в атомах движутся не ровно по тем «орбиталям», которые рассчитываются в квантовой механике. Из-за взаимодействия электрона с «флуктуациями вакуума» происходит что-то вроде неустранимого броуновского движения возле орбитали, «дрожание» электрона.

Эти явления, несмотря на их тонкость, указывают на совершенную неадекватность представлений о вакууме как о пустоте. Сейчас мало кто из учёных представляет себе вакуум буквально, если речь не идёт об упрощённых моделях. Кроме того, снова оказывается неверным и представление о пространственных границах, жёстко и устойчиво локализующих микрочастицу.

Так что же внутри?

К текущей строчке мы подошли с некоторым развитием нашего исходного представления. До этого мы обращались с электроном как с всё той же классической частицей-шариком, которому мы просто добавляли всякие необычные квантовые свойства. Вначале мы взяли электрон в общем классическом понимании частицы и в специальном понимании электрона как такой частицы, которая является атомом электричества, и попытались оценить его размер. Далее, мы посмотрели на электрон как на волну в интерпретации Шрёдингера (волновой пакет), затем учли спин и те особенности, которые вносит в понимание структуры соотношение неопределённостей.

Наконец, когда мы подобрались к квантово-полевым явлениям, мы подошли к структуре электрона с другой стороны: если до этого мы указывали на проявление структуры «извне» электрона, то теперь мы можем показать структуру «внутри», разделяя его «по слоям». Общий принцип определения структуры объекта должен оставаться одним и тем же для любых приближений и уточнений. Заключаться он должен в определении структуры его взаимодействий как «внешних», так и «внутренних».

При переходе к квантовой теории поля перед нами предстаёт совсем другая физическая картина существования и взаимодействия объектов, где различие между собственно частицей (дискретным) и полем (непрерывным) становится условной и относительной.

Имея в виду эти соображения, перейдём теперь к «послойному» описанию структуры, которое привёл в своих статьях Дмитрий Блохинцев²² ²³ . Размер различных слоёв соответствует характерным величинам различных видов взаимодействия, в которых участвует электрон. Блохинцев особо уделяет внимание «слабым» явлениям, таким, как описанные выше поляризация вакуума и броуновское движение. Кроме этого, он оценивает область слабого взаимодействия, в котором участвует электрон, через виртуальный процесс распада электрона на мюон, электронное антинейтрино и мюонное нейтрино. Радиус этого взаимодействия имеет порядок 10⁻¹⁶ см.

Блохинцев представляет схематичное изображение структуры электрона, разделённой на слои виртуальных частиц, соответствующих различным взаимодействиям.

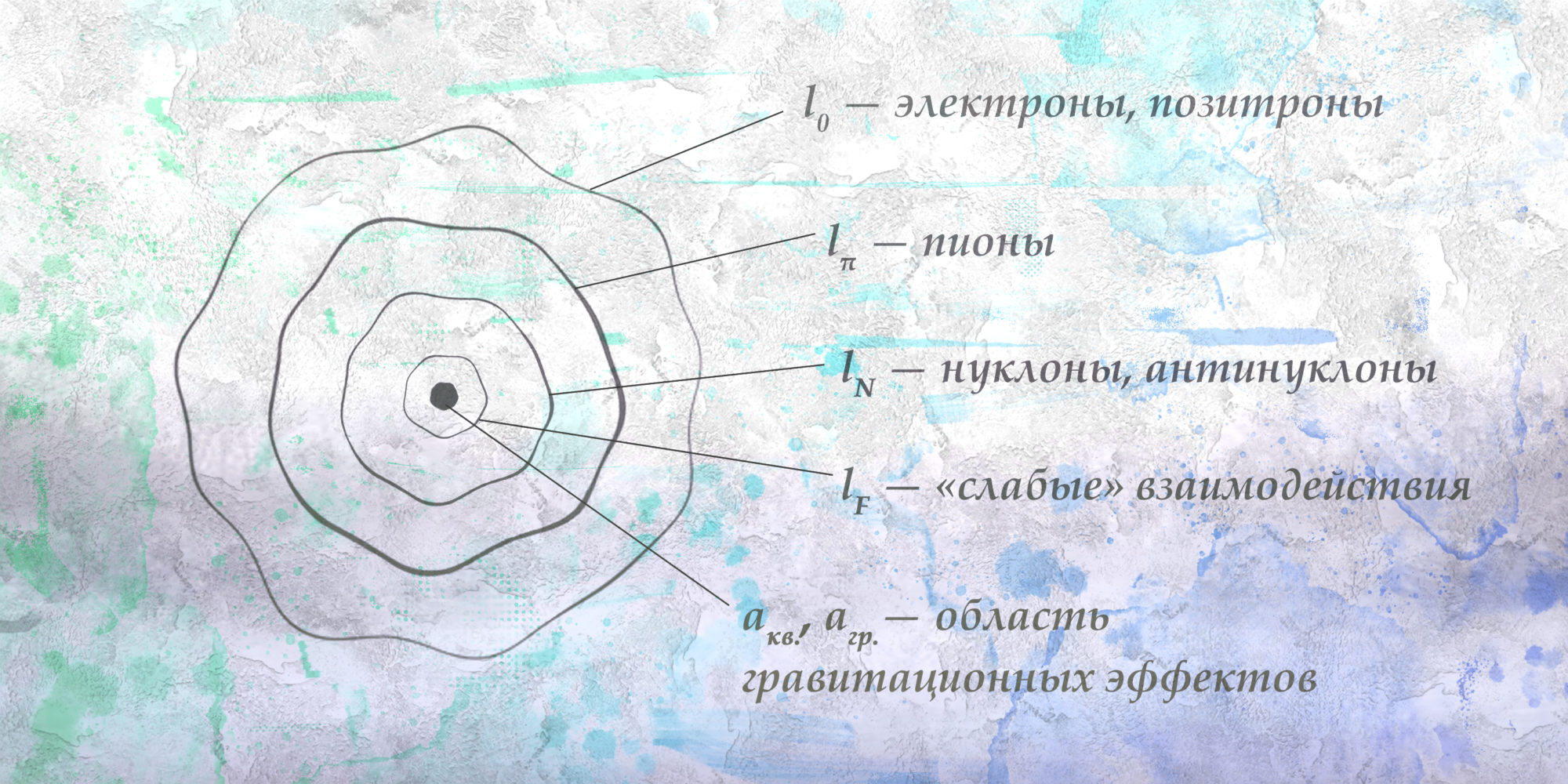
Данная схема основана на псевдоклассическом представлении об электроне, неподвижно закреплённом в какой-то точке пространства²⁴ .

Итак, электрон испускает и поглощает виртуальные фотоны, кванты своего электромагнитного поля. Эти фотоны поляризуют вакуум, так что первый внешний слой «атмосферы» электрона состоит из виртуальных пар электрон — позитрон. Эта атмосфера имеет размеры комптоновской длины электрона, то есть порядка 10⁻¹¹ см. Плотность этой атмосферы ничтожна из-за малости постоянной тонкой структуры, определяющей силу электромагнитных взаимодействий.

Процессы, продуцирующие следующие слои вглубь атмосферы, также протекают виртуально, чтобы не нарушался закон сохранения энергии. Кроме того, эти процессы могут быть производными от других виртуальных процессов, например, от поляризации вакуума. Ближе к центру электрона должна возникать атмосфера из пар других частиц — π-мезонов. Характерный размер составляет 1,4 ⋅ 10⁻¹³ см. Атмосфера π-мезонов, в свою очередь, продуцирует атмосферу виртуальных нуклонов и антинуклонов. Масштаб этого слоя составляет 2 ⋅ 10⁻¹⁴. Таким образом, вокруг центра электрона имеется система оболочек, образованных парами частиц и античастиц разного сорта. Все эти оболочки имеют очень малую плотность.

Ещё на меньших расстояниях (10⁻¹⁶ см) будут существенными слабые взаимодействия, которые только в этом масштабе будут заметными. И где-то совсем в глубине электрона будет существенна величина гравитационного взаимодействия ~10⁻⁵⁵ см и «квантовый» радиус электрона ~10⁻⁷⁰ см (см. выше оценку Вайскопфа для учёта поляризации вакуума).

Блохинцев приводит следующее пояснение к представленной схеме:

«…нужно отметить, что электрон — частица очень лёгкая, и поэтому при всех процессах [С рождением более тяжёлых виртуальных частиц. — А. Б.], которые мы рассмотрели, электрон получает сильную отдачу. В силу этого, в действительности структура электрона не такая наглядная, как мы изобразили выше.
Портрет электрона, который мы могли бы получить на опыте, должен походить на портрет лица, прыгающего со стула на стул перед своим фотографом»²⁵ .

Заключение

Мы рассмотрели, как обогащалось физическое понимание структуры электрона в ходе развития физической теории. Кроме того, мы увидели, что это развитие привело к развитию философского понимания структуры: от механистического понятия к диалектическому. Философ Владимир Свидерский показал в своей работе, что понятие структуры и структурных элементов в диалектическом материализме развивалось в связи с развитием физики элементарных частиц:

if«Прежде всего, если рассматривать „элементарные частицы“ в качестве элементов, образующих физические объекты, то бросаются в глаза следующие их особенности. … элементы естественно представлять в виде каких-либо пребывающих или изменяющихся процессов или устойчивых отношений, находящихся в некоторой структурной связи с другими процессами и отношениями. Подобные элементы, испытывая на себе влияние других элементов и всей системы как целого, в то же время сохраняли своё отличие, самостоятельность и определённую независимость от других элементов в рамках данного целого.
В случае же „элементарных“ частиц любой из элементов предполагает прямую или косвенную связь его с другими элементами, способность перехода его во все другие элементы и, наконец, возможность порождения при определённых условиях данным элементом всех других элементов. Таким образом, здесь каждый элемент несёт на себе печать других элементов в смысле потенций и возможностей перехода в них и черт того общего физического целого, которое реализуется совокупностью „элементарных“ частиц и полей в нашей части Вселенной»²⁶ .

«…структурные связи и соотношения [частицы] с другими частицами определяются её внутренней структурой. Таким образом, обнаруживается органическая связь внутренней структуры элементов со структурой возможной связи между элементами»²⁷ .

Заявления о бесструктурных частицах имеют под собой ложные основания и являются результатом путанных философских взглядов. К счастью, на практике наука не останавливается на подобных заявлениях.

Развитие физики снова и снова опровергает устаревшие идеалистические представления об элементарных частицах. Но современные учёные-физики часто оказываются идеалистами и поддерживают противные науке концепции. Причина этого лежит не в физике, а в условиях жизни учёных в современном обществе. Сформировавшись в эпоху глубокой реакции как узкие специалисты, подверженные всем заблуждениям буржуазной пропаганды в той же мере, что и таксисты, и доставщики еды и продавцы-консультанты, физики просто не могут противостоять потоку идеалистических помоев, льющемуся со всех сторон. Противостоять и бороться с невежеством может тот, кто в ходе самостоятельных поисков доходит до диалектического материализма.

Талантливый физик, понимающий диалектический материализм, способен на основе существующего массива экспериментальных данных и физических теорий находить ответы на основополагающие вопросы о природе. Пример — Дмитрий Иванович Блохинцев, на основе работ которого написана эта статья. Конечно, нельзя полагать, что он поставил точку в проблеме структуры электрона. Он прочертил линию к множеству новых вопросов, ответить на которые предстоит уже современным физикам. Так и развивается человеческое познание.

Нашли ошибку? Выделите фрагмент текста и нажмите Ctrl+Enter.

Источник

Комптоновская длина волны — параметр элементарной частицы: величина размерности длины, характерная для релятивистских квантовых процессов, идущих с участием этой частицы

$Large lambda_0=frac{2pi hbar }{mc}=frac{h}{mc}$

Формула комптоновской длины волны получается из формулы Де-Бройлевской длины волны путём замены скорости частицы v на скорость света c.

Де-Бройлевской длины волны : $large lambda=frac{h}{mupsilon }$

Название Комптоновская длина волны связано с тем, что величина определяет изменение длины волны электромагнитного излучения при комптоновском рассеянии.

Для электрона : $large lambda_0^e=frac{2pi hbar }{mc}=frac{h}{mc}=2.42*10^{-12}$

Для протона : $large lambda_0^p=frac{2pi hbar }{mc}=frac{h}{mc}=1.32*10^{-15}$

Чаще всего используется приведенная Комптоновская длина волны :

$large overline lambda_0=frac{hbar }{mc}$

Посчитаем приведенную Комптоновскую длину волны для электрона и протона

Для электрона : $large overline lambda_0^e=frac{hbar }{mc}=3.86*10^{-13}$

Для протона : $large overline lambda_0^p=frac{hbar }{mc}=2.1*10^{-16}$

Комптоновская длина волны определяет масштаб пространственных неоднородностей полей, при которых становятся существенными квантовые релятивистские процессы. Действительно, если рассматривается некоторое волновое поле, например электромагнитное, длина волны которого меньше Комптоновская длина волны электрона , то энергия квантов этого поля оказывается большей энергии покоя электрона и, следовательно, в этом поле становится возможным и происходит рождение электрон-позитронных пар. Такие процессы порождения частиц описываются релятивистской квантовой теорией.

Комптоновская длина волны определяет также расстояние, на которое может удалиться виртуальная частица с массой m от точки своего рождения. Поэтому радиус действия ядерных сил по порядку величины равен Комптоновская длина волны p-мезона $( lambda_0 sim 10^{-13})$ . Аналогично, поляризация вакуума за счёт рождения виртуальных электрон-позитронных пар проявляется на расстояниях порядка Комптоновская длина волны электрона.

В Формуле мы использовали :

— Комптоновская длина волны

— Приведенная Комптоновская длина волны

— Скорость света

$h=6.6260^{−34}$ — Постоянная Планка

$m_e=9,1093820^{−31}$ — Масса электрона

— Постоянная Дирака

Источник

Эффект Комптона

В 1923
году американский физик А. Комптон,
исследуя рассеяние монохроматических
рентгеновских лучей веществами с
легкими атомами (парафином, бором
и др.), обнаружил, что в составе рассеянного
излучения наряду с излучением
первоначальной длины волны наблюдается
также излучение более длинных волн.

Рис.
12. Спектры
рассеянного излучения.

Эффектом
Комптона
называется упругое рассеяние
коротковолнового электромагнитного
излучения (рентгеновского и излучения)
на свободных или слабо связанных
электронах вещества, сопровождающееся
увеличением длины волны.

Эффект
Комптона
не укладывается в рамки волновой теории,
согласно которой длина волны излучения
не должна изменяться при рассеянии.

Пусть
на покоящийся электрон с массой m
и энергией покоя m₀c²
падает рентгеновский фотон
с энергией h.
В результате упругого столкновения
электрон приобретает импульс,
равный
,
и его полная энергия становится
равнойmc².
Фотон, столкнувшись с электроном,
передает ему часть своей энергии
и импульса и изменяет направление
движения (рассеивается) на угол .

Рис.
13. Расчетная
схема

p_e=mv

p_ф=
h/c

p_ф=h/c



Закон сохранения энергии

(12)

Закон
сохранения импульса

(13)

(14)

(12)

(15)

(16)

формула
Комптона, (17)

комптоновская
длина волны электрона.

Эффект
Комптона наблюдается не только на
электронах, но и на других заряженных
частицах, например, протонах. Однако
ввиду большой массы протона его отдача
ощущается лишь при рассеянии фотонов
очень больших энергий.

6.
Двойственная корпускулярно-волновая
природа света

Волновые
свойства света

Длина
волны ,
частота 

Интерференция,
дифракция, поляризация

Корпускулярные
свойства света

Энергия
_ф
, масса m_ф,
импульс р_ф
фотона

Тепловое
излучение, давление света, фотоэффект,
эффект Комптона

Волновые
и корпускулярные свойства света не
исключают, а взаимно дополняют друг
друга. Эта взаимосвязь отражается и в
уравнениях:

Свет
представляет собой диалектическое
единство
этих двух свойств, в проявлении этих
противоположных свойств света имеется
определенная закономерность: с уменьшением
длины волны (увеличением частоты)
всё более отчетливо проявляются квантовые
свойства света, а с увеличением длины
волны (уменьшением частоты) основную
роль играют его волновые свойства. Таким
образом, если «перемещаться» по
шкале электромагнитных волн в сторону
более коротких (от радиоволн до
-лучей),
то волновые свойства электромагнитного
излучения будут постепенно уступать
место всё более отчетливо проявляющимся
квантовым свойствам.

Глава 5. Квантовая физика

5.3. Эффект Комптона *)

Концепция
фотонов, предложенная А. Эйнштейном
в 1905 г. для объяснения фотоэффекта,
получила экспериментальное подтверждение
в опытах американского физика А. Комптона
(1922 г.). Комптон исследовал упругое
рассеяние коротковолнового рентгеновского
излучения на свободных (или слабо
связанных с атомами) электронах вещества.
Открытый им эффект увеличения длины
волны рассеянного излучения, названный
впоследствии эффектом
Комптона,
не укладывается в рамки волновой теории,
согласно которой длина волны излучения
не должна изменяться при рассеянии.
Согласно волновой теории, электрон под
действием периодического поля световой
волны совершает вынужденные колебания
на частоте волны и поэтому излучает
рассеянные волны той же частоты.

Схема
Комптона представлена на рис. 5.2.1.
Монохроматическое рентгеновское
излучение с длиной волны λ₀,
исходящее из рентгеновской трубки R,
проходит через свинцовые диафрагмы и
в виде узкого пучка направляется на
рассеивающее вещество-мишень P
(графит, алюминий). Излучение, рассеянное
под некоторым углом θ, анализируется с
помощью спектрографа рентгеновских
лучей S,
в котором роль дифракционной решетки
играет кристалл K,
закрепленный на поворотном столике.
Опыт показал, что в рассеянном излучении
наблюдается увеличение длины волны Δλ,
зависящее от угла рассеяния θ:

Δλ = λ — λ₀ = 2Λ sin² θ / 2,

где
Λ = 2,43·10^–3 нм
– так называемая комптоновская
длина волны,
не зависящая от свойств рассеивающего
вещества. В рассеянном излучении наряду
со спектральной линией с длиной волны
λ наблюдается несмещенная линия с длиной
волны λ₀.
Соотношение интенсивностей смещенной
и несмещенной линий зависит от рода
рассеивающего вещества.

Рисунок
5.3.1.

Схема
эксперимента Комптона.

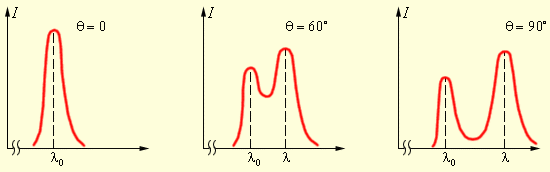
На
рис. 5.3.2 представлены кривые
распределения интенсивности в спектре
излучения, рассеянного под некоторыми
углами.

Рисунок
5.3.2.

Спектры
рассеянного излучения.

Объяснение
эффекта Комптона было дано в 1923 году
А. Комптоном
и П. Дебаем (независимо) на основе
квантовых представлений о природе
излучения. Если принять, что излучение
представляет собой поток фотонов, то
эффект Комптона есть результат упругого
столкновения рентгеновских фотонов со
свободными электронами вещества. У
легких атомов рассеивающих веществ
электроны слабо связаны с ядрами атомов,
поэтому их можно считать свободными. В
процессе столкновения фотон передает
электрону часть своей энергии и импульса
в соответствии с законами сохранения.

Рассмотрим
упругое столкновение двух частиц –
налетающего фотона, обладающего энергией
E₀ = hν₀
и импульсом p₀ = hν₀ / c,
с покоящимся электроном, энергия покоя
которого равна
Фотон,
столкнувшись с электроном, изменяет
направление движения (рассеивается).
Импульс фотона после рассеяния становится
равнымp = hν / c,
а его энергия E = hν < E₀.
Уменьшение энергии фотона означает
увеличение длины волны. Энергия электрона
после столкновения в соответствии с
релятивистской формулой (см. § 4.5)
становится равной
гдеp_e– приобретенный импульс электрона.
Закон сохранения записывается в виде

или

Закон сохранения
импульса

можно переписать в
скалярной форме, если воспользоваться
теоремой косинусов (см. диаграмму
импульсов, рис. 5.3.3):

Рисунок
5.3.3.

Диаграмма
импульсов при упругом рассеянии
фотона на покоящемся электроне.

Из
двух соотношений, выражающих законы
сохранения энергии и импульса, после
несложных преобразований и исключения
величины p_eможно получить

mc²(ν₀ – ν) = hν₀ν(1 – cos θ).

Переход
от частот к длинам волн
приводит
к выражению, которое совпадает с формулой
Комптона, полученной из эксперимента:

Таким
образом, теоретический расчет, выполненный
на основе квантовых представлений, дал
исчерпывающее объяснение эффекту
Комптона и позволил выразить комптоновскую
длину волны Λ через фундаментальные
константы h,
c
и m:

Как
показывает опыт, в рассеянном излучении
наряду со смещенной линией с длиной
волны λ наблюдается и несмещенная линия
с первоначальной длиной волны λ₀.
Это объясняется взаимодействием части
фотонов с электронами, сильно связанными
с атомами. В этом случае фотон обменивается
энергией и импульсом с атомом в целом.
Из-за большой массы атома по сравнению
с массой электрона атому передается
лишь ничтожная часть энергии фотона,
поэтому длина волны λ рассеянного
излучения практически не отличается
от длины волны λ₀
падающего излучения.

Источник

Простое объяснение эффекта Комптона

Формулы для расчета энергии и импульса фотона

Формулы для расчета импульса и энергии релятивистских частиц

Два случая комптоновского рассеяния

Список использованной литературы

Reduced Compton wavelength[edit]

Role in equations for massive particles[edit]

Distinction between reduced and non-reduced[edit]

Limitation on measurement[edit]

Relationship to other constants[edit]

Geometrical interpretation[edit]

See also[edit]

References[edit]

External links[edit]

Введение

Как искать структуру?

Шарик

Волна

Вращение и направленность

Неопределённость

Окружение

Так что же внутри?

Заключение

Эффект Комптона

Закон сохранения энергии

Глава 5. Квантовая физика

Не пропустите также: