Перейти к контенту
Математика
Время чтения 1 мин.Просмотры 20.1к.
Значение суммы чисел двух слагаемых складывается из суммы этих слагаемых. Для дошкольника или ученика 1 класса эта фраза просто набор букв, и если вы хотите, чтобы ваш малыш легко понял, что же такое слагаемое слагаемое сумма, то покажите ему картинки и таблицы из этой статьи. Эти изображение с подписями доходчиво расскажут юному ученику, что из себя представляет операция сложения.
Слагаемое плюс слагаемое равно сумма.
Вспомни!
Из чего состоит сумма.
Заполни окошки в таблице.
Повторяем изученное.
2+3=5.
Слагаемое плюс слагаемое равно сумма.
Простой пример.
Что такое сложение.
Слагаемое слагаемое сумма
Сумма и разность векторов
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
Сумма векторов
Сложение векторов выполняется по правилу треугольника.
Геометрическая интерпретация:
Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .
Для сложения векторов также используется правило параллелограмма.
Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
Элементы вектора c равняются попарной сумме соответствующих элементов a и b .
» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
| Для плоских задач | a + b = x + bx; ay + by> |
| Для трехмерных задач | a + b = x + bx; ay + by; az + bz> |
| Для n-мерных векторов | a + b = 1 + b1; a2 + b2; . an + bn> |
Свойства сложения векторов
1. Коммутативность: a + b = b + a
2. Ассоциативность: ( a + b ) + c = a + ( b + c )
3. Прибавление к нулю: a + 0 = a
4. Сумма противоположных векторов: a + (- a ) = 0
Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.
Разность векторов
Для вычитания векторов также применяется правило треугольника.
Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:
Формула вычитания векторов
Элементы вектора c равны попарной разности соответствующих элементов a и b .
» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
| Для плоских задач | a — b = x — bx; ay — by> |
| Для трехмерных задач | a — b = x — bx; ay — by; az — bz> |
| Для n-мерных векторов | a — b = 1 — b1; a2 — b2; . an — bn> |
Примеры задач
Задание 1
Вычислим сумму векторов и .
Задание 2
Найдем разность векторов и .
Сложение и вычитание векторов
Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .
Существование: Имеем два следующих случая:
Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора ( overrightarrow ) выполняется равенство
Для произвольных точек ( A, B и C ) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec <0>)
Длина нулевого вектора равна нулю:
( left| vec <0>right| = 0 )
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <- , — , — > right) )
Умножение вектора на число
Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .
Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:
Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;
Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )
Обозначение: ( overrightarrow=koverrightarrow ) .
Сложение и вычитание векторов
Формулы сложения и вычитания векторов
Формулы сложения и вычитания векторов для плоских задач
В случае плоской задачи сумму и разность векторов a = < ax ; ay > и b = < bx ; by > можно найти, воспользовавшись следующими формулами:
Формулы сложения и вычитания векторов для пространчтвенных задач
В случае пространственной задачи сумму и разность векторов a = < ax ; ay ; az > и b = < bx ; by ; bz > можно найти, воспользовавшись следующими формулами:
Формулы сложения и вычитания n -мерных векторов
В случае n -мерного пространства сумму и разность векторов a = < a 1 ; a 2 ; . ; an > и b = < b 1 ; b 2 ; . ; bn > можно найти, воспользовавшись следующими формулами:
Примеры задач на сложение и вычитание векторов
Примеры плоских задач на сложение и вычитание векторов
Примеры пространственных задач на сложение и вычитание векторов
Примеры задач на сложение и вычитание векторов с размерностью большей 3
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
http://calcsbox.com/post/slozenie-i-vycitanie-vektorov.html
http://ru.onlinemschool.com/math/library/vector/add_subtract/
Содержание
- Глава 2. Решение задач
- Сумма ряда
- Понятие суммы ряда
- Вычисление суммы ряда почленным дифференцированием
Глава 2. Решение задач
Рассчитайте, какую сумму необходимо положить на депозит, чтобы через пять лет она выросла до 500 000 руб., если ставка процента – 15% годовых и проценты начисляются ежеквартально. Ответ округлите до копеек. А если первоначально положить 250 000 руб., то какую сумму следует ожидать через пять лет? Ответ округлите до копеек.
Алгоритм решения задачи
При решении задачи аналитическим способом используем формулу:

ПС – текущая стоимость вклада
БС – будущая стоимость вклада
Кпер – общее число периодов начисления процентов
Ставка – процентная ставка за период
Данная формула не учитывает знак «минус» для денежных потоков от клиента. Подставив в формулу числовые данные, получим:
Для расчета суммы текущего вклада зададим исходные данные в виде таблицы.
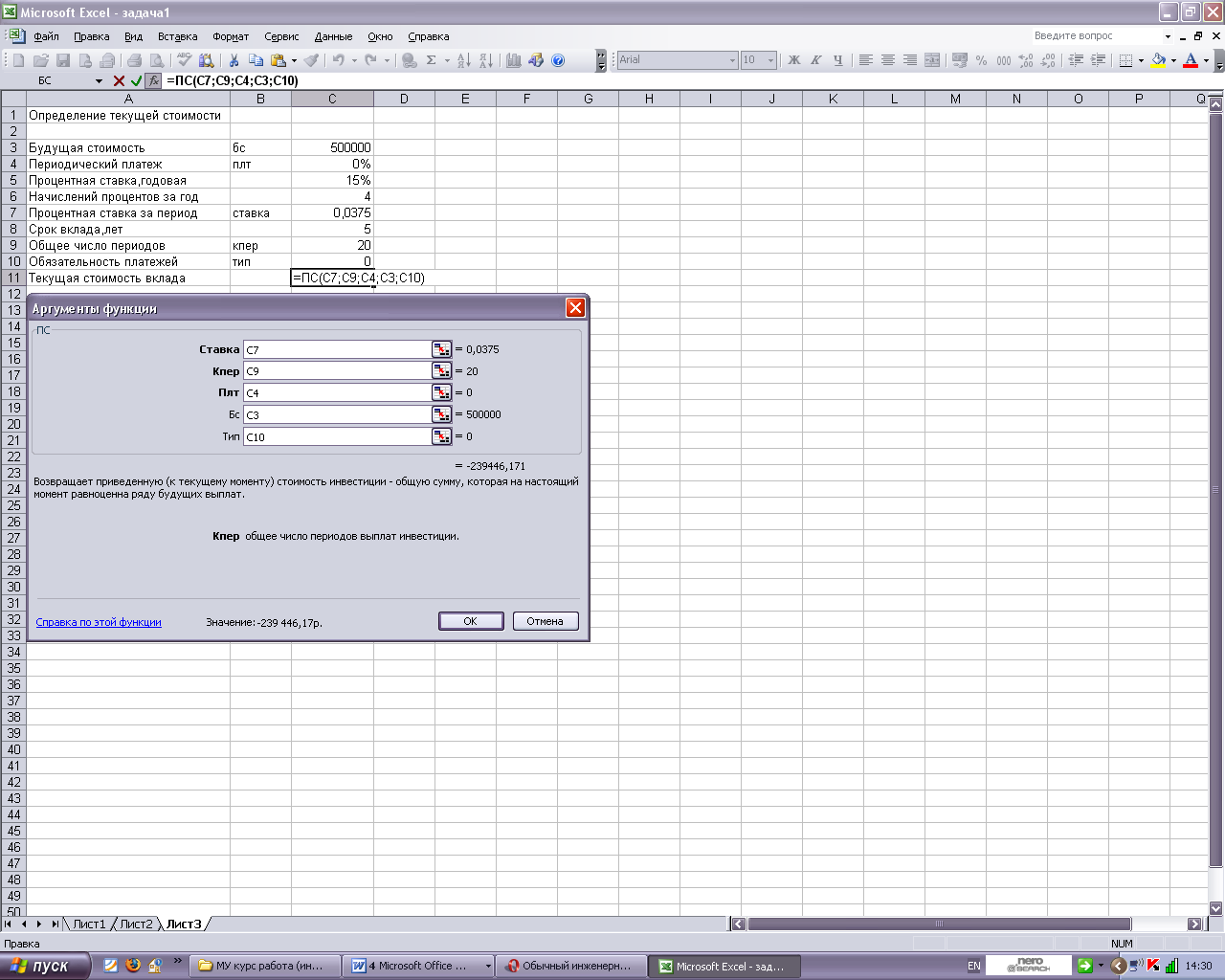
Поскольку необходимо рассчитать текущую сумму вклада на основе постоянной процентной ставки, то используем ПС(ставка ;кпер;плт;бс;тип). Опишем способы задания аргументов данной функции.
В связи с тем, что проценты начисляются каждый квартал, аргумент ставка равен 15%/4. общее число периодов начисления равно 5*4 (аргумент кпер). Аргумент плт отсутствует, так как вклад не пополняется. Аргумент тип равен 0, так как в подобных операциях проценты начисляются в конце каждого периода (задается по умолчанию). Если решать данную задачу с точки зрения вкладчика, то аргумент пс (начальная стоимость) збудет равен отрицательному числу, поскольку для вкладчика это отток его денежных средств (вложение средств). На рисунке 1 показан ввод заданных параметров.
Рисунок 1 — Фрагмент листа Excel с решением задачи об определении текущей стоимости
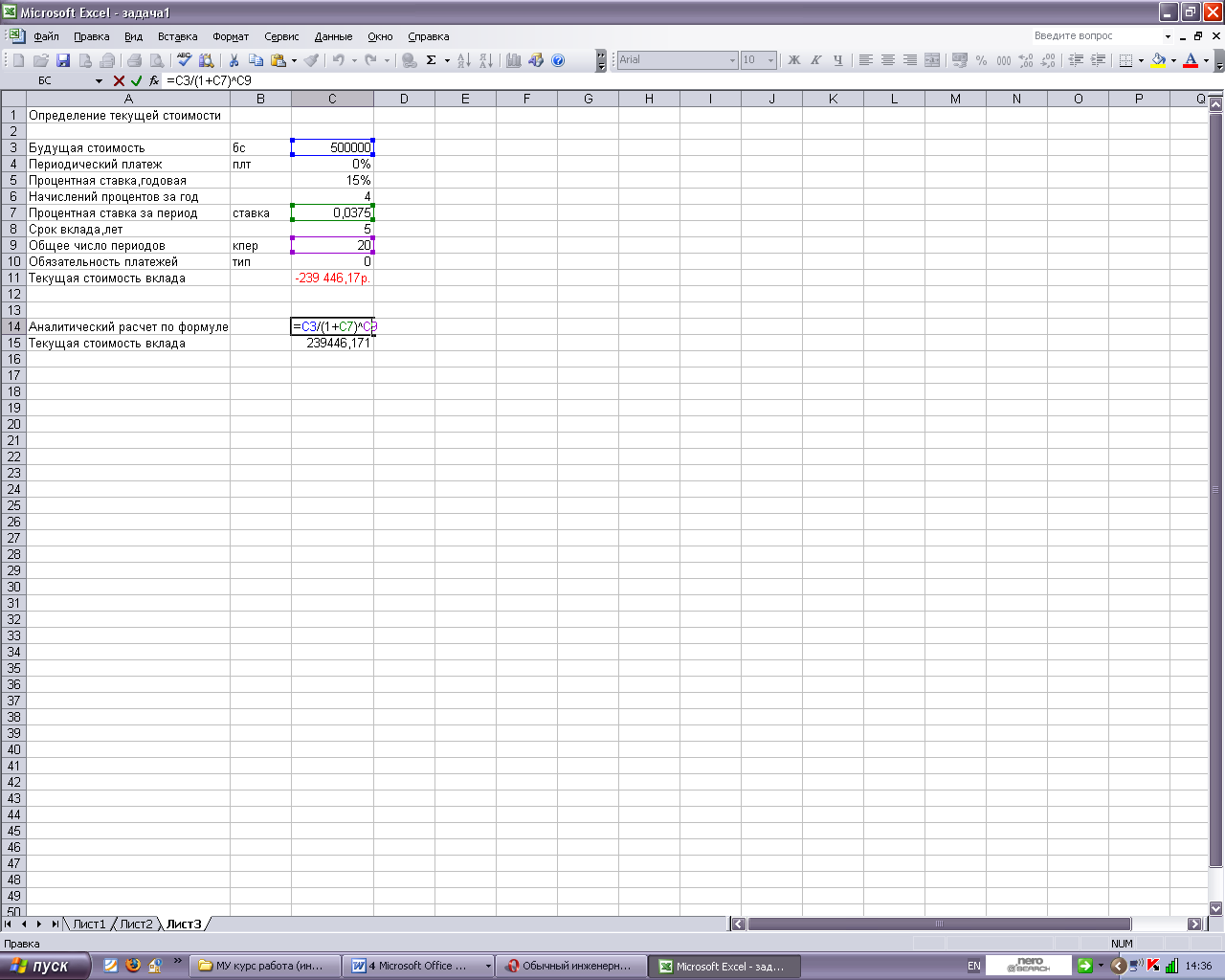
Проверка решения аналитическим методом представлена на рисунке 2.
Рисунок 2 — Фрагмент листа Excel с аналитическим решением задачи об определении текущей стоимости
Далее решаем вторую часть задачи.
Аналитический способ решения:
Подставив в формулу числовые значения, получаем:
БС = 250000 – (1+ 0,0375) 20 = 522037,999 руб.
Поскольку необходимо рассчитать единую сумму вклада на основе постоянной процентной ставки, то используем БС(ставка;кпер;плт;пс;тип).
Если решать данную задачу с точки зрения вкладчика, то аргумент пс (начальная стоимость вклада), равный 250 000 руб., задается в виде отрицательной величины (-250 000), поскольку для вкладчика это отток его денежных средств (вложение средств). На рисунке 3 показано решение второй части задачи.
Рисунок 3 — Фрагмент листа Excel с решением задачи об определении будущей стоимости
Проверка решения аналитическим методом представлена на рисунке 2.
Рисунок 4 — Фрагмент листа Excel с аналитическим решением задачи об определении будущей стоимости
Определите, через сколько лет обычные ежеквартальные платежи размером 3 150 руб. принесут доход в 450 000 руб. при ставке 14% годовых. Рассчитайте сумму ежеквартальных платежей, исходя из десятилетнего срока. Ответ округлите до копеек.
Алгоритм решения задачи
Решим первую часть задачи.
Аналитический способ решения задачи.
У нас есть формула:
Поскольку в данной задаче ПС = 0, выразим из данной формулы КПЕР:
Найдем количество лет, через которые данные платежи принесут заданный доход. Для этого 52/4 = 13 лет.
Решим задачу в MS Excel.
Для нахождения количества лет, через которые платежи размером 3150 рублей принесут доход в 450000 рублей, для начала найдемобщее количество периодов выплаты на основе периодических постоянных выплат и постоянной процентной ставки: КПЕР (ставка ;плт;пс;бс;тип), а затем общее число периодов выплат разделим на количество начислений процентов за год. Таким образом, мы ответим на вопрос задачи.
В данном случае ставка = 14%/4, тип = 0 (по умолчанию), пс отсутствует, плт по условию задачи = -3150 руб, т.к. данная сумма для вкладчика является оттоком средств.
На рисунке 5 мы видим нахождение общего количества периодов выплат с помощью MS Excel.
Рисунок 5. Фрагмент листа Excel с нахождение общего количества периодов выплат
На рисунке 6 изображено второе действие задачи (Мы поделили кпер на количество начислений процентов за год).
Рисунок 6. Фрагмент листа Excel с нахождение количества лет
Таким образом, при обычных ежеквартальных платежах размером 3 150 руб. и ставке 14% годовых потребуется 13 лет для получения дохода в 450000 рублей.
Теперь решим вторую часть задачи.
Решение аналитическим способом:
Выплаты, определяемы функцией ПЛТ, включают основные платежи и платежи по процентам. Расчет выполняется по формуле
Для определения ежемесячных выплат применяется функция ПЛТ с аргументами: Ставка = 14%/4 (ставка процента за квартал); Кпер = 10*4 = 40 (общее число кварталов начисления процентов); Бс = 450000 (будущая стоимость вклада); Тип = 0,так как в подобных операциях проценты начисляются в конце каждого периода (задается по умолчанию). Иллюстрация решения данной задачи в Excel приведена на рисунке 5.
Рисунок 5 — Иллюстрация применения функции ПЛТ
Результат со знаком «минус», так как 5322,28 руб. клиент ежеквартально вносит в банк.
Имеется следующая таблица.
Определить сумму налога на наследование при условии, что действует налоговая шкала, представленная в таблице.
В указанной таблице процент взимается со стоимости, превышающей нижнюю границу рассматриваемой ступени налоговой шкалы, а числа задают фиксированную сумму налога МРОТ.
Размер облагаемой налогом суммы МРОТ
Решение аналитическим способом.
Для решения этой задачи нам потребуется рассмотреть каждого наследника.
Первый из них – Лушников является наследником первой очереди и унаследованная им сумма составляет 1560 руб. Исходя из второй таблицы, он облагается налогом, равным 5% от суммы наследования (1560*0,05). Сумма налога = 78 руб.
Федоров – наследник второй очереди и его сумма наследования составляет 3500 руб., следовательно, его сумма налога составляет 3500*0,3+255 = 1275 руб.
Семенов является наследником первой очереди, его сумма наследования равна 2200 руб., а сумма налога, которую он должен выплатить составляет 2200*0,1+42,5 = 262,2 руб.
Бобров – наследник первой очереди, сумма наследования равна 760 руб., сумма налога равна 0 руб.
И наконец, Колесников – наследник второй очереди, он имеет сумму наследования 1800 руб., а сумма налога равна 1800*0,2+85 = 445 руб.
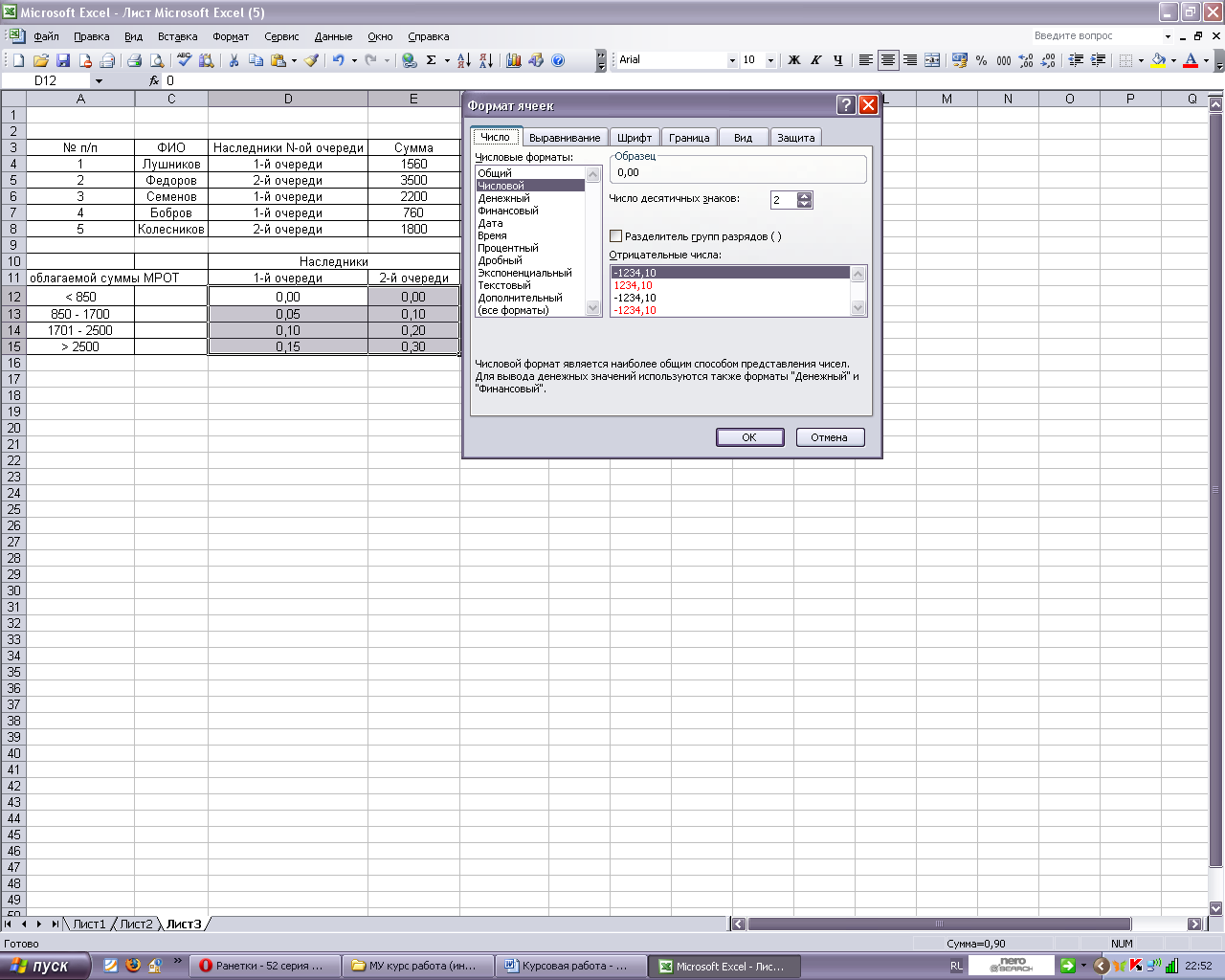
Теперь нам нужно решить эту задачу в MS Excel. Для этого создаем 2 данные таблички, как показано на рисунке 6. При этом во второй табличке изменим формат ячеек (Для этого выделяем 2 и 3 столбцы таблицы, нажимаем правой кнопкой мыши: формат ячеек – числовой, с количеством чисел после запятой = 2). Также при рассмотрении 2 таблицы мы не будем учитывать числа 42,2; 85,0; 127,5 и 225,0 из 2 и 3 столбца для более удобных расчетов. Данные числа мы приплюсуем в конце. Данные преобразования показаны на рисунке 7.
Рисунок 6. Фрагмент листа Excel с условиями задачи 3.
Рисунок 7. Фрагмент листа Excel с установлением формата ячеек.
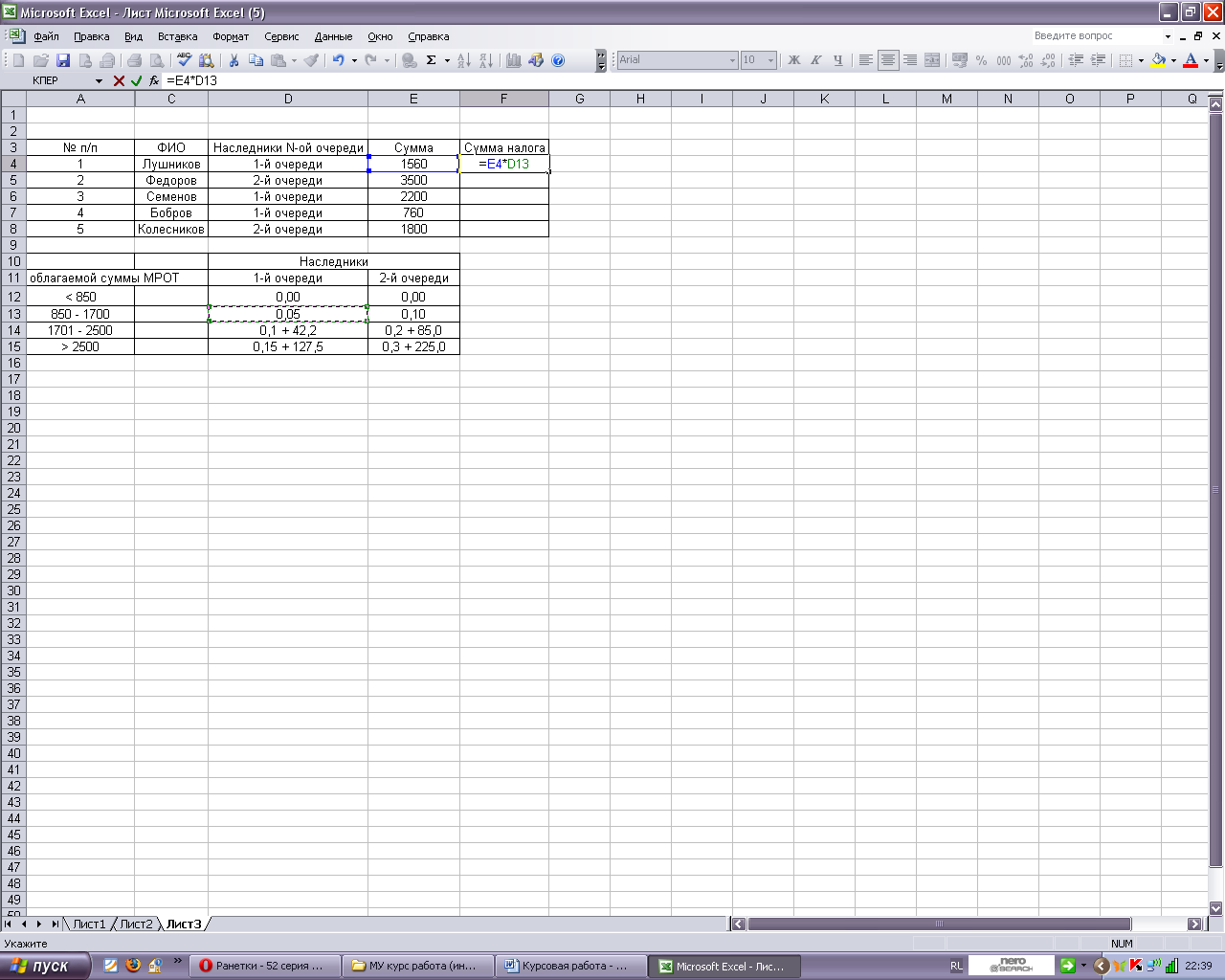
На рисунке 8 показано первое действие задачи.
Рисунок 8. Фрагмент листа Excel с началом решения задачи
Аналогичным способом находим остальные суммы налога. Результаты вычисления показаны на рисунке 9.
Рисунок 9. Фрагмент листа Excel с решением задачи
И в последнем действии мы находим окончательную сумму налога для каждого наследника. На рисунке 10 показано, как найти сумму налога в конечном счете. Ответы, полученные в результате вычисления, показаны на рисунке 11.
Рисунок 10. Фрагмент листа Excel с выполнением действий
Рисунок 11. Фрагмент листа Excel с результатом выполненных действий
Как мы видим, Excel – это не более изощренный текстовый редактор с сеткой, которая принуждает пользователя заносить информацию в небольшие отдельные ячейки, вместо того, чтобы предложить все пространство листа.
Огромная разница между ячейками рабочей таблицы и страницами текстового редактора состоит в том, что каждая ячейка позволяет не только редактировать и форматировать текст, но и выполнять вычисления. Эти вычисления основаны на формулах, которые пользователь создает в различных ячейках таблицы, зачастую пользуясь мастером функций, очень облегчающим работу.
Вычислительные возможности Excel и ее способности по редактированию и форматированию дают в итоге чудесную программу для создания любого документа, который может содержать текстовые и числовые данные и позволяет выполнять вычисления.
Поскольку таблицы содержат динамические формулы, их итоговые значения всегда будут актуальны. А это очень важно в современных условиях.
Список используемой литературы
1. Гобарева Я.Л. Технология экономических расчетов средствами MS EXCEL: учебное пособие / Я.Л.Гобарева, О.Ю.Городецкая, А.В.Золотарюк. – М.: КНОРУС, 2006. – 344 с.
2. Информатика и информационные технологии. Учебник для 10-11 классов / Угринович Н.Д. – М.: БИНОМ. – 511 с.
3. Комягин В.Б. Компьютер для студентов. Самоучитель. Быстрый старт. Учебное пособие // М.: Триумф, 2003. с. – 400.
Источник
Сумма ряда
Содержание:
Понятие суммы ряда
Постановка задачи. Найти сумму ряда
где 
План решения. Суммой ряда 


где
1. По условию задачи
Если корни знаменателя различаются на целое число, т.е. 




По этой ссылке вы найдёте полный курс лекций по высшей математике:
2. Разлагаем общий член ряда на элементарные дроби:
и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.
3. Находим 

сократив соответствующие слагаемые.
4. Вычисляем сумму ряда по формуле (1)
и записываем ответ.
Пример:
Найти сумму ряда
Решение:
1. Корни знаменателя 




2. Разлагаем общий член ряда на элементарные дроби
и выписываем несколько членов ряда:
3. Сокращая все слагаемые, какие возможно, находим 
4. Вычисляем сумму ряда по формуле (1):
Ответ:
Возможно вам будут полезны данные страницы:
Вычисление суммы ряда почленным интегрированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
с областью сходимости 
3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
Заметим, что так как ряд (1) сходится в граничной точке 
6. Вычисляем интеграл, делаем замену 

Замечание. Если ряд имеет вид
то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:
и вычисляем сумму каждого ряда почленным интегрированием.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
В граничных точках при 


Следовательно, данный ряд сходится при всех 
2. Сделаем замену 
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке 
Заметим, что так как ряд (1) сходится в граничной точке 

6. Заменяя 

Ответ.
Вычисление суммы ряда почленным дифференцированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов

3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем
6. Вычисляем производную и делаем замену 

Замечание. Если ряд имеет вид
то вычисляем сумму трех рядов, причем при вычислении суммы ряда
применяем теорему о почленном дифференцировании степенного ряда дважды.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством 



2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии:
Следовательно, 

4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (2), получаем
Заменяя 

Ответ.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Источник
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
- Взять все числа от 5 до 15 (снизу и сверху знака Σ).
- С каждым из этих чисел сделать то, что написано справа от Σ, — то есть умножить на два.
- Сложить результаты этих операций.
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Вёрстка:
Кирилл Климентьев
Компоненты
арифметических действий и их взаимосвязь.
1.
Компоненты
при сложении:
1 слагаемое, 2 слагаемое, сумма.
2.
Компоненты
при вычитании:
уменьшаемое, вычитаемое, разность.
3.
Компоненты
при умножении:
1 множитель, 2 множитель, произведение.
4.
Компоненты
при делении:
делимое, делитель , частное.
5.
Назвать
результаты всех действий:
при сложении — сумма
при вычитании — разность
при умножении — произведение
при делении – частное
6.
Как найти
неизвестное слагаемое?
Чтобы найти неизвестное слагаемое, нужно
из суммы вычесть известное слагаемое.
Х+4=12 или 4+х=12
Х=12-4 х=12-4
Х=8 х=8____
8+4=12 4+8=12
12=12 12=12
7.
Как найти
неизвестное уменьшаемое?
Чтобы найти неизвестное уменьшаемое, надо
к разности прибавить вычитаемое.
Х-7=3
Х=3+7
Х=10
10-7=3
3=3
8.
Как найти
неизвестное вычитаемое?
Чтобы найти неизвестное вычитаемое, надо
из уменьшаемого вычесть разность.
8-х =5
х=8-5
х=3
8-3=5
5=5
9. Как
найти неизвестный множитель?
Чтобы найти неизвестный множитель, надо
произведение разделить на известный множитель.
х·3=6 4·х=8
х=6:3 х=8:4
х=2 х=2
2·3=6 4·2=8
6=6 8=8
10. Как найти неизвестное делимое?
Чтобы найти неизвестное делимое, надо
частное умножить на делитель.
х:5=3
х=3·5
х=15
15:5=3
3=3
11.
Как найти
неизвестный делитель?
Чтобы найти неизвестный делитель, надо
делимое разделить на частное.
6:х=2
х =6:2
х=3
6:3=2
2=2
Геометрический материал.
Квадрат – это прямоугольник, у которого
все стороны равны.
13.
Что такое
прямоугольник?
Прямоугольник – это четырёхугольник, у
которого все углы прямые. Противоположные стороны прямоугольника равны.
14.
Что такое
треугольник?
Треугольник – многоугольник, у которого
три угла и три стороны.
15. Что такое четырёхугольник?
Четырёхугольник – геометрическая фигура,
у которой четыре угла и четыре стороны.
Периметр ( Ρ) – это сумма длин сторон
какой-нибудь геометрической фигуры.
Площадь (S) – это внутренняя часть
какой-нибудь геометрической фигуры
(прямоугольника, квадрата и т.д)
17.
Как найти
периметр квадрата?
У квадрата 4 стороны, равные между
собой. Чтобы найти периметр (Р) квадрата, нужно длину одной стороны (а) умножить на 4.
Р□ =
a · 4
18.
Как найти
периметр прямоугольника?
Чтобы найти периметр
прямоугольника, нужно сложить все 4 стороны прямоугольника
Или
сложить длину и ширину
прямоугольника и умножить на 2.
Ρ=a+b+a+b
или
Ρ=(a+b)·2
19.
Как найти
периметр треугольника?
Чтобы найти периметр
треугольника, нужно сложить все 3 стороны.
20.
Как найти
сторону квадрата, если известен периметр?
У квадрата 4 стороны, равные между
собой. Чтобы найти сторону квадрата, нужно Ρ разделить на 4.
a=Ρ:4
21.
Как найти сторону прямоугольника, если известен
периметр и другая сторона?
Чтобы найти сторону
прямоугольника, нужно
Ρ разделить на 2
и вычесть
другую сторону.
a=Ρ:2 – b
b=Ρ:2 – a
22. В каких единицах измеряется периметр?
Периметр
измеряется в мм, см, дм, метрах.
23.
Как найти площадь квадрата?
Площадь квадрата равна произведению двух
его сторон.
S□ = a · a
24. Как найти площадь прямоугольника?
Чтобы найти площадь прямоугольника, надо
длину прямоугольника умножить на его ширину.
S = a · b
25. Как найти сторону прямоугольника,
если известна площадь и другая его сторона?
Чтобы найти одну из сторон
прямоугольника, нужно площадь прямоугольника разделить на известную сторону.
a=S : b
b= S : a
26. В каких
единицах измеряется площадь?
Площадь измеряется в квадратных единицах: мм², см², дм², м².
27. Назвать единицы длины.
Единицы длины
— мм,
см,
дм, м, км.
28. Рассказать таблицу мер длины.
1см
= 10мм
1дм
= 10см
1дм
= 100мм
1м
= 10 дм
1м
= 100 см
1км = 1000м
29. Сколько
квадратных сантиметров
в
1квадратном метре?
1м²
= 10 000см²
30. Сколько
квадратных дециметров
в
1 квадратном метре?
1м²
= 100дм²
31. Рассказать таблицу мер площади.
1м²
= 100дм² = 10 000см²
1дм²
= 100см² = 10 000мм²
1см²
= 100мм²
Масса.
32. Назвать единицы массы.
Масса измеряется в граммах, килограммах,
центнерах, тоннах.
33. Рассказать таблицу мер массы.
1кг
= 1000г
1ц
= 100кг
1т
= 10ц
1т
= 1000кг
Время.
34. Назвать
единицы измерения времени.
Время
измеряется секундами, минутами, часами, сутками, неделями, месяцами,
годами, веками.
35. Рассказать таблицу мер времени.
1мин
= 60сек.
1час
= 60мин
1час
= 3600сек.
1сут.
= 24часа
1год
= 12мес. =
365сут. или 366сут.
1век
= 100лет
Взаимосвязь скорости, времени и расстояния.
36. Как
найти скорость?
Чтобы найти скорость ( v ), надо расстояние ( S ) разделить на время ( t ), затраченное в пути.
v = S : t
37. Как найти время?
Чтобы найти время ( t ), надо расстояние ( S ) разделить на скорость
( v ).
t = S : v
38. Как найти расстояние?
Чтобы найти расстояние ( S ), нужно скорость ( v ) умножить на время ( t ).
S = v · t
Взаимосвязь цены, количества, стоимости.
39. Что такое цена?
Цена – стоимость одного предмета,
единицы товара.
40. Как найти стоимость?
Чтобы найти стоимость, нужно цену
умножить на количество.
Ст = Ц · К
41. Как найти цену?
Чтобы найти цену, нужно стоимость
разделить на количество.
Ц
= Ст : К
42. Как найти
количество?
Чтобы найти количество, нужно стоимость
разделить на цену.
К = Ст : Ц
43. Задачи на дроби.
Дробь — ⅔
2
– числитель
3
– знаменатель
44. Как найти дробь числа?
Чтобы найти дробь числа, нужно число
разделить на знаменатель, а потом умножить на числитель.
45. Как найти число по дроби?
Чтобы
найти число по дроби, нужно число разделить на числитель и умножить на
знаменатель.
Взаимосвязь
работы, времени и производительности.
46. Что такое производительность?
Как найти производительность?
Производительностью
( v )
называют работу, выполненную за единицу времени.
Чтобы
найти производительность ( v ), надо всю
выполненную работу разделить на время.
v = A : t
47. Как найти выполненную работу?
Выполненная работа равна
производительности, умноженной на время работы.
A = v · t
48. Как найти время работы?
Чтобы узнать время работы, надо работу
разделить на производительность.
t = A : v
49. Как
найти среднее арифметическое?
Чтобы найти среднее арифметическое надо
сумму разделить на число слагаемых.














































 , целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем






































