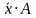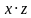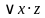Схемотехника. Минимизация логических функций
Время на прочтение
5 мин
Количество просмотров 368K
Минимизация логических функций является одной из типовых задач в процессе обучения схемотехнике. Посему считаю, что такая статья имеет место быть, надеюсь Вам понравится.

Зачем это нужно?
Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок.
К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся, например, метод Квайна, метод карт Карно, метод испытания импликант, метод импликантных матриц, метод Квайна-Мак-Класки и др. Эти методы наиболее пригодны для обычной практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В тех случаях, когда число аргументов больше шести, обычно используют метод Квайна-Мак-Класки.
В процессе минимизации той или иной логической функции, обычно учитывается, в каком базисе эффективнее будет реализовать ее минимальную форму при помощи электронных схем.
Минимизация логических функций при помощи карт Карно
Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
Возможность поглощения следует из очевидных равенств
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.
Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.
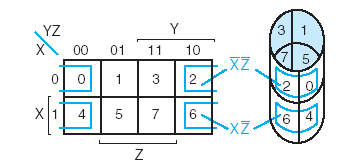
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.
Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:
В общем случае можно сказать, что 2K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.
Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.
Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им термы можно склеивать.
Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.
Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):
- Объединяем смежные клетки содержащие единицы в область, так чтобы одна область содержала 2n (n целое число = 0…
) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
- Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
- Не смежные области расположенные симметрично оси(ей) могут объединяться в одну;
- Область должна быть как можно больше, а кол-во областей как можно меньше;
- Области могут пересекаться;
- Возможно несколько вариантов накрытия.
Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например(для Карт на 2-ве переменные):
 |
 |
 |
 |
 |
 |
 |
 |
|||||||
 |
 |
 |
 |
 |
 |
 |
 |
|||||||
 |
 |
 |
 |
 |
 |
|||||||||
 |
 |
 |
 |
 |
 |
|||||||||
 |
 |
 |
 |
 |
 |
|||||||||
 |
 |
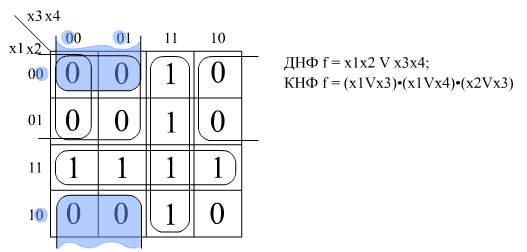
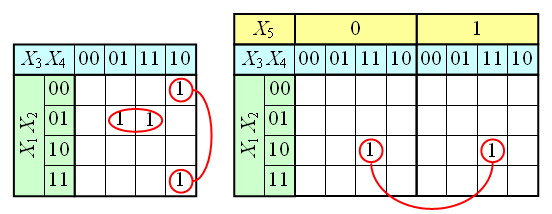
Для КНФ всё то же самое, только рассматриваем клетки с нулями, не меняющиеся переменные в пределах одной области объединяем в дизъюнкции (инверсии проставляем над единичными переменными), а дизъюнкции областей объединяем в конъюнкцию. На этом минимизация считается законченной. Так для Карты Карно на рис.1 выражение в формате ДНФ будет иметь вид:
В формате КНФ:
Правила минимизации с использованием карт Карно
1. В карте Карно группы единиц
(для получения ДНФ) и группы нулей (для
получения КНФ) необходимо обвести
четырехугольными контурами. Внутри
контура должны находится только
одноименные значения функции.
Этот процесс соответствует операции
склеивания.
2. Количество клеток внутри
контура должно быть целой степенью
двойки (1,2,4,8,16…).
3. При проведении контуров крайние строки
карты (верхние и нижние, левые и правые),
а также угловые клетки, считаются
соседними (для карт до 4-х переменных).
4. Каждый контур должен включать
максимально возможное количество
клеток.
5. Все единицы (нули) в карте (даже
одиночные) должны быть охвачены контурами.
Любая единица (нуль) может входить в
контуры произвольное количество раз.
6. Множество контуров, покрывающих все
1 (0) функции образуют тупиковую ДНФ
(КНФ).
7. В элементарной конъюнкции (дизъюнкции),
которая соответствует одному контуру,
остаются только те переменные, значение
которых не изменяется внутри обведенного
контура.
8. Переменные булевой функции
входят в элементарную коньюнкцию (для
значений функции 1) без инверсии, если
их значение на соответствующих координатах
равно 1 и с инверсией — если 0.
Для значений булевой функции,
равных 0, записываются элементарные
дизьюнкции, куда переменные входят без
инверсии, если их значение на соответствующих
координатах равно 0 и с инверсией — если
1. Тупиковая форма записи функции,
полученная при минимизации по карте
Карно, используется при проектировании
логических устройств так же, как и
полученная методом алгебраической
минимизации
-
Пример в карте Карно четырех
переменных можно выделить группу из
четырех клеток в первом столбце, группу
из четырех угловых клеток и группу из
двух соседних клеток в нижней строке
(табл.).
|
Таблица |
|||||
|
х |
00 |
01 |
11 |
10 |
|
|
х3х4 |
00 |
1 |
0 |
0 |
1 |
|
01 |
1 |
0 |
0 |
0 |
|
|
11 |
1 |
0 |
0 |
0 |
|
|
10 |
1 |
0 |
1 |
1 |
В результате минимизированная функция
представляет собой сумму трех произведений,
соответствующих отдельным группам:
Рассмотрим возможные варианты
расположения единиц в карте Карно.
1)Рядом стоящие элементарные
квадраты, в которых записаны «1»,
образуют прямоугольники 4×2. Рядом
стоящими считаем как непосредственно
рядом расположенные квадраты, так и
квадраты, находящиеся в строках 1 и 4 и
столбцах 1 и 4.
Каждому прямоугольнику 4×2
в минимальной форме будет соответствовать
произведение из одного сомножителя.
Пусть после заполнения получили таблицу:
|
x3x4 x1x2 |
00 |
01 |
11 |
10 |
||||
|
00 |
1 |
0 |
1 |
1 |
1 |
3 |
1 |
2 |
|
01 |
1 |
4 |
1 |
5 |
0 |
7 |
0 |
6 |
|
11 |
1 |
12 |
1 |
13 |
0 |
15 |
0 |
14 |
|
10 |
1 |
8 |
1 |
9 |
1 |
11 |
1 |
10 |
В данном случае можно
составить 2 прямоугольника 4X2,
целиком состоящих из «1». На первом
прямоугольнике x1,
принимает значение 0 и 1, x2=0,1
X4=0,1
X3=0
поэтому в минимальной форме будет
присутствовать произведение, состоящие
из
,
т.к. толькообращается
в 1 на всем наборе. Аналогично для второго
прямоугольника находим.
Окончательно:
Здесь ограничились поиском только двух
прямоугольников, т.к. они включили в
себя все «№» таблицы.
2)
Рядом стоящие
элементарные квадраты, в которых записаны
«1» образуют прямоугольники 2×1.
В этом случае в минимальной форме будут
присутствовать произведения из трех
сомножителей.
|
x3x4 x1x2 |
00 |
01 |
11 |
10 |
||||
|
00 |
1 |
0 |
0 |
1 |
0 |
3 |
1 |
2 |
|
01 |
0 |
4 |
1 |
5 |
0 |
7 |
0 |
6 |
|
11 |
0 |
12 |
1 |
13 |
0 |
15 |
0 |
14 |
|
10 |
0 |
8 |
0 |
9 |
0 |
11 |
1 |
10 |
Здесь можно выделить
3 прямоугольника: 0-2; 5-13; 2-10;
На первом
наборе: X1=0,
X2=0,
X3=0
и 1, X4=0.
Поэтому
имеем:
.
На втором
наборе: ,на
третьем:
Окончательно
получаем:
3)
Из элементарных
квадратов, в которых записаны “1”,
составить вышеописанные фигуры нельзя.
В этом случае квадратам, в которых
записаны “1” будут соответствовать
произведения из четырех сомножителей.
|
x3x4 x1x2 |
00 |
01 |
11 |
10 |
||||
|
00 |
1 |
0 |
0 |
1 |
0 |
3 |
0 |
2 |
|
01 |
0 |
4 |
0 |
5 |
1 |
7 |
0 |
6 |
|
11 |
0 |
12 |
0 |
13 |
0 |
15 |
0 |
14 |
|
10 |
0 |
8 |
1 |
9 |
0 |
11 |
0 |
10 |
Здесь имеем:
-
ПримерРассмотрим минимизацию
булевой функции трех переменных
f ( 1,3,5,6,7 ) = 1
Решение
Построим минимальную ДНФ
Функция 3-х переменных
функция f ( 1,3,5,6,7 ) = 1
1.шаг
2. шаг
Построим минимальную КНФ
1. шаг
2 шаг
-
Пример
Рассмотрим минимизацию булевой функции
четырех переменных
f ( 3,7,11,12,13,14,15 ) = 1.
Функция 4-х переменных
КНФ

2. шаг
-
шаг
-
шаг
Соседние файлы в папке ДМ ВВО
- #
- #
- #
- #
- #
- #
- #
Минимизация булевых функций
Ясно, что при разработке логических схем, немаловажной является задача минимизации количества используемых элементов (другими словами, логических операций).
В связи с этим, возникает задача минимизации логических функций в некотором классе формул. В частности, в классах ДНФ и КНФ.
- Минимальная ДНФ
- Такая ДНФ, которая содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей ДНФ.
- Минимальная КНФ
- Такая КНФ, которая содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей КНФ.
Процесс нахождения минимальных форм, собственно, и называется минимизацией. В простых случаях, для минимизации достаточно тождественных преобразований. В более сложных – используются специальные алгоритмы.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя членами, содержащими одинаковые переменные, вхождения которых (с отрицанием и без) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
[
;overline{x_1};x_2x_3x_4
vee
;overline{x_1};x_2;overline{x_3};x_4 =
;overline{x_1};x_2x_4 (x_3 vee;overline{x_3};) =
;overline{x_1};x_2x_4 mathbin{&}1 =
;overline{x_1};x_2x_4.
]
Аналогично для КНФ:
[
(;overline{x_1};vee x_2vee x_3vee x_4)
(;overline{x_1};vee x_2vee;overline{x_3};vee x_4) =
;overline{x_1};vee x_2vee x_4vee x_3;overline{x_3}; =
;overline{x_1};vee x_2vee x_4vee 0 =
;overline{x_1};vee x_2vee x_4.
]
Возможность поглощения следует из очевидных равенств
[
A vee;overline{A}; = 1
][
A;overline{A}; = 0.
]
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск членов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей.
Минимизирующие карты Карно
- Карта Карно
-
Графический способ минимизации булевых функций. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как построенная соответствующим образом таблица истинности функции.
Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.
Булевы функции (N) переменных, представленные в виде СДНФ или СКНФ, могут иметь в своём составе (2^N) различных элементарных членов.
Элементарные члены СДНФ или СКНФ образуют структуру, топологически эквивалентную (N)-мерному кубу. Действительно, если рассматривать набор значений функции (x_1,,ldots,,x_N) как (N)-мерный вектор ({x_1,,ldots,,x_N}), мы получим набор точек, лежащих на ортах (N)-мерной системы координат, и удаленных друг от друга на (1). Другими словами, мы получим (N)-мерный гиперкуб с ребром (1).
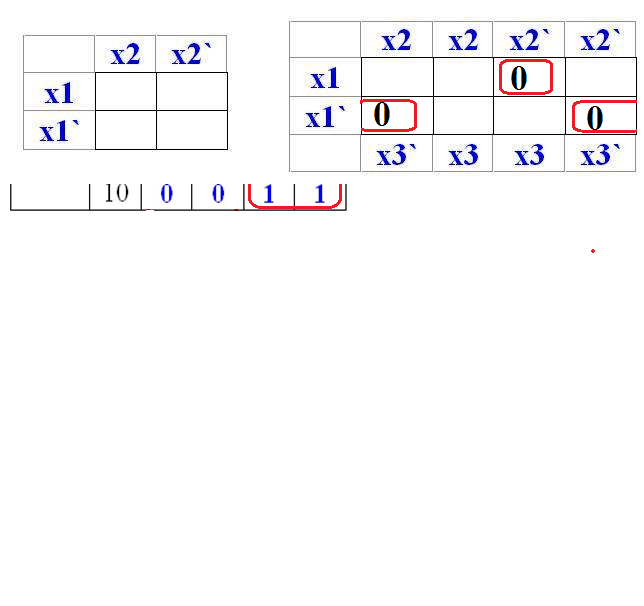
Например, для функции двух переменных, заданной таблицей истинности:
| (x_1) | (x_2) | (f(x_1,x_2)) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
можно построить эквивалентный ей квадрат:
0 01 1 11 0 00 1 10
Или, если обозначить вершины соответствующими элементарными конъюнкциями и выделить вершины, конъюнкции которых входят в СДНФ:
0 x̅₁x₂ 1 x₁x₂ 0 x̅₁x̅₂ 1 x₁x̅₂
Или СКНФ:
0 x₁∨x̅₂ 1 x̅₁∨x̅₂ 0 x₁∨x₂ 1 x̅₁∨x₂
Можно заметить, что члены, находящиеся на одной стороне квадрата, могут быть склеены. Соответственно, если составляется ДНФ, то операции производятся только над вершинами, в которых функция имеет значение (1) (по правилам построения СДНФ). Если же составляется КНФ, то над вершинами, в которых функция имеет значение (0) (по правилам построения СКНФ).
При этом, сохраняются переменные, значение которых на стороне постоянно.
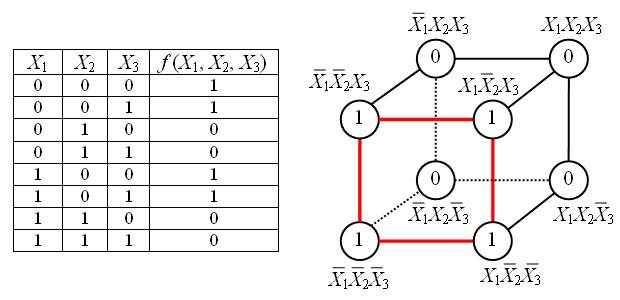
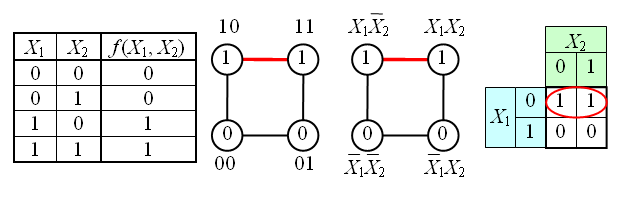
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.
Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации. Например, четыре члена, принадлежащие одной грани куба, объединяются в один с поглощением двух переменных:
[
;overline{x_1};;overline{x_2};;overline{x_3};
vee
x_1;overline{x_2};;overline{x_3};
vee
;overline{x_1};;overline{x_2};x_3
vee
x_1;overline{x_2};x_3
=]
[ =
;overline{x_2}; (;overline{x_1};;overline{x_3}; vee;overline{x_1};x_3 vee x_1;overline{x_3}; vee x_1x_3)
= ;overline{x_2}; (;overline{x_1}; vee x_1)(;overline{x_3}; vee x_3) = ;overline{x_2};
]
В общем случае можно сказать, что (2^K) членов, принадлежащие одной (K)–мерной грани гиперкуба, склеиваются в один член, при этом поглощаются (K) переменных.
Карта Карно представляет собой развертку гиперкуба на плоскость. Например, трехмерный куб из предыдущего примера можно развернуть следующим образом:
1 x̅₁x̅₂x̅₃ 1 x̅₁x̅₂x₃ 0 x̅₁x₂x̅₃ 0 x̅₁x₂x₃ 0 x₁x₂x₃ 0 x₁x₂x̅₃ 1 x₁x̅₂x₃ 1 x₁x̅₂x̅₃
Карта Карно является представлением такой двумерной развертки в виде таблицы.
| (_{x_3}backslash^{x_1x_2}) | (00) | (01) | (11) | (10) |
|---|---|---|---|---|
| (0) | (1) | (0) | (0) | (1) |
| (1) | (1) | (0) | (0) | (1) |
В этой карте самые левые ячейки смежны самым правым.
Ясно, что на одной (K)-мерной грани могут лежать (2^K) вершин. Следовательно, в карте Карно выбираются группы по (2^K) смежных ячеек, и в результирующую ДНФ или КНФ входят только те переменные, которые неизменны в рамках данной группы. Общее число членов соответствует числу групп в карте Карно, а число неизменных переменных обратным образом зависит от количества элементов в группе. Как следствие, группы необходимо выбирать как можно более большими. Следует отметить, что одна комбинация переменных может входить в несколько групп.
Для функций четырех переменных, требуется развертка 4-мерного гиперкуба. Карта Карно в таком случае имеет вид:
| (_{x_3x_4}backslash^{x_1x_2}) | (00) | (01) | (11) | (10) |
|---|---|---|---|---|
| (00) | (f(0,0,0,0)) | (f(0,1,0,0)) | (f(1,1,0,0)) | (f(1,0,0,0)) |
| (01) | (f(0,0,0,1)) | (f(0,1,0,1)) | (f(1,1,0,1)) | (f(1,0,0,1)) |
| (11) | (f(0,0,1,1)) | (f(0,1,1,1)) | (f(1,1,1,1)) | (f(1,0,1,1)) |
| (10) | (f(0,0,1,0)) | (f(0,1,1,0)) | (f(1,1,1,0)) | (f(1,0,1,0)) |
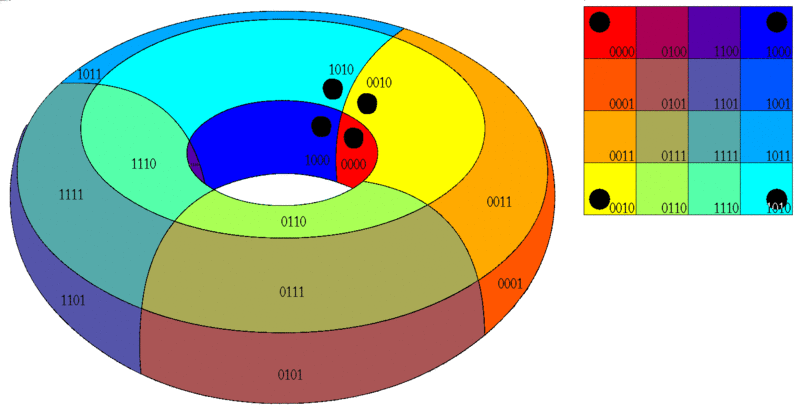
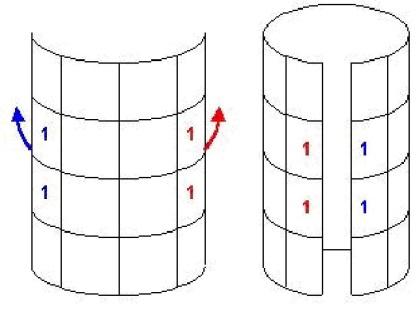
В данном случае, все крайние ячейки смежны друг другу. Это можно себе представить, натянув эту развертку на тор (“бублик”):
Возможно так же построение карт Карно для функций 5 и 6 переменных, однако работа с ними значительно затрудена. Для числа переменных, большего 6, использование карт Карно попросту непрактично.
Пример
Рассмотрим функцию, имеющую следующую таблицу истинности:
| (x_1) | (x_2) | (x_3) | (x_4) | (f(x_1, x_2, x_3, x_4)) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
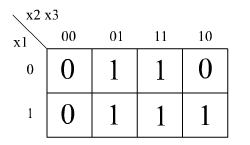
Перепишем эту таблицу в виде карты Карно:
| x₃x₄x₁x₂ | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 1 | 1 | 0 | 0 |
| 01 | 1 | 0 | 0 | 0 |
| 11 | 0 | 1 | 1 | 0 |
| 10 | 1 | 1 | 1 | 0 |
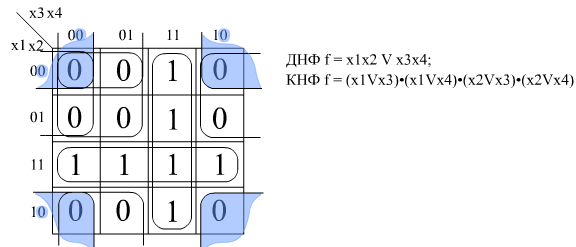
Легко выделяются три группы. Исходя из этого, записывается ДНФ:
(;overline{x_1};;overline{x_2};;overline{x_3};)(vee)(;overline{x_1};;overline{x_4};)(vee)({x_2}{x_3})
Метод Куайна-МакКласки
Метод Куайна-МакКласси строится на основе того же аппарата, что и карты Карно, однако оказывается более практичным для большего количества переменных.
Алгоритм заключается последовательной склейке, и затем редукции результата.
Склейка
Сначала элементарные члены совершенной формы записываются в двоичной форме в таблицу, где группируются по количеству единиц.
Затем, члены, которые отличаются одной переменной (одним битом), могут быть склеены. В таком случае единица заменяется на “-”. Очевидно, что склеены могут быть только члены из соседних групп
Члены, которые нельзя склеить, обозначаются звездочкой «*».
Полученные склеенные члены могут, в свою очередь, так же быть склеены. При этом “-” трактуется как “третье” значение.
Когда никакие члены больше не могут быть склеены, из членов, отмеченных “*”, составляется сокращенная форма, которая не обязательно минимальна. После этого производится редукция.
Редукция
Для редукции, составляется таблица, в строки которой включаются члены сокращенной формы, а в столбцы – члены совершенной.
В ячейках ставится отметка (например, крестик “×”), если соответствующий член сокращенной формы поглощает соответствующий член совершенной формы (т.е. если заголовок строки является частью заголовка столбца).
Выбираются столбцы, содержащие только один “×”. Соответсвтующие им члены сокращенной формы составляют ядро, и должны войти в минимальную форму.
Если ядро не перекрывает все столбцы, то в минимальную форму так же включаются несколько членов сокращенной формы, не входящих в ядро, таким образом, чтобы члены минимальной формы перекрывали все столбцы таблицы.
Пример
Найдем минимальную форму функции
| n | x₁ | x₂ | x₃ | x₄ | f |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 1 |
| 11 | 1 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | 1 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 1 |
Члены СДНФ в двоичной нотации:
- 0000 = 0
- 0001 = 1
- 0010 = 2
- 0011 = 3
- 0101 = 5
- 0111 = 7
- 1000 = 8
- 1010 = 10
- 1100 = 12
- 1101 = 13
- 1111 = 15
Группировка:
0
- 0000 = 0
1
- 0001 = 1
- 0010 = 2
- 1000 = 8
2
- 0011 = 3
- 0101 = 5
- 1010 = 10
- 1100 = 12
3
- 0111 = 7
- 1101 = 13
4
- 1111 = 15
Склейка 1:
- 0, 1 = 000-
- 0, 2 = 00-0
- 0, 8 = -000
- 1, 3 = 00-1
- 1, 5 = 0-01
- 2, 3 = 001-
- 2,10 = -010
- 8,10 = 10-0
- 8,12 = 1-00
- 3,7 = 0-11
- 5,7 = 01-1
- 5,13 = -101
- 12,13 = 110-
- 7,15 = -111
- 13,15 = 11-1
Группировка 2:
- 0, 1 = 000-
- 2, 3 = 001-
- *12,13 = 110-
- 0, 2 = 00-0
- 1, 3 = 00-1
- 8,10 = 10-0
- 5,7 = 01-1
- 13,15 = 11-1
- 1, 5 = 0-01
- *8,12 = 1-00
- 3,7 = 0-11
- 0, 8 = -000
- 2,10 = -010
- 5,13 = -101
- 7,15 = -111
Склейка 2:
- *0,1,2,3 = 00–
- *0,2,8,10 = -0-0
- *5,7,13,15 = -1-1
- *1,3,5,7 = 0–1
Итого, члены сокращенной формы:
- 12,13 = 110-
- 8,12 = 1-00
- 0,1,2,3 = 00–
- 0,2,8,10 = -0-0
- 5,7,13,15 = -1-1
- 1,3,5,7 = 0–1
Редукция:
| 0 | 1 | 2 | 3 | 5 | 7 | 8 | 10 | 12 | 13 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 12,13 | × | × | |||||||||
| 8,12 | × | × | |||||||||
| 0,1,2,3 | × | × | × | × | |||||||
| 0,2,8,10 | × | × | × | ⊗ | |||||||
| 5,7,13,15 | × | × | × | ⊗ | |||||||
| 1,3,5,7 | × | × | × | × |
Кружком обведены члены ядра.
Ядро, таким образом, включает члены -0-0 и -1-1. Для получения минимальной формы, нам нужно перекрыть дополнительно столбцы 1, 3, 12. Для этого можно взять, например, 0,1,2,3 = 00– и 12,13 = 110-:
[
f =
;overline{x_2};;overline{x_4}; vee
{x_2}{x_4} vee
;overline{x_1};;overline{x_2}; vee
{x_1}{x_2};overline{x_3};
]
Карта Карно:
| x₃x₄x₁x₂ | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 1 | 1 | 1 | |
| 01 | 1 | 1 | 1 | |
| 11 | 1 | 1 | 1 | |
| 10 | 1 | 1 |
Занятие 17. Тема «Минимизация функций с помощью карт Карно»
План лекции:
-
Понятие карты Карно
-
Виды карт Карно и метод их заполнение
-
Принципы склейки
-
Правило нахождения МДНФ и МКНФ
Понятие карты Карно
МДНФ – минимальная дизъюнктивная нормальная форма
МКНФ — минимальная конъюнктивная нормальная форма
Метод карт Карно позволяет быстро получить минимальные ДНФ и КНФ.
Карта Карно – это таблица, каждая клетка в ней соответствует набору переменных булевой функции в её таблице истинности. Строки и столбцы карты обозначаются таким образом, чтобы любые соседние клетки по строкам или по столбцам отличались бы между собой значением только одной переменной. Это сделано для того, чтобы было бы возможно применить закон склеивания.
Виды карт Карно и метод их заполнение
Карта Карно для 2-х переменных – квадратная таблица размером 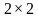
|
х1 х2 |
0 |
1 |
|
0 |
||
|
1 |
Ячейки заполняются 0 или 1, полученные в последнем столбце таблицы истинности, соответствующие наборам 00, 01, 10, 11.
Карта Карно для 3-х переменных – прямоугольная таблица размером 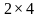
|
х2х3 х1 |
00 |
01 |
11 |
10 |
|
0 |
||||
|
1 |
Любые две рядом расположенные клетки являются соседними. Клетки, находящиеся на границах одной строки или столбца, так же считаются соседними, то есть, клетки, которые будут соседними при скручивании карты в вертикальный и горизонтальный цилиндры.
Карта Карно для 4-х переменных – квадратная таблица размером 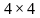
Карта Карно для 5-х переменных – прямоугольная таблица размером 

Минимизация функций с помощью карт Карно или нахождение МДНФ (МКНФ) – это процесс склеивания одинаковых значений, стоящих в соседних ячейках.
Принципы склейки
-
Склейку клеток карты Карно можно осуществлять по единицам (если необходимо получить МДНФ) или по нулям (если требуется МКНФ).
-
Склеивать можно только прямоугольные области с числом единиц (нулей) 2n, где n — целое число.
-
Область, которая подвергается склейке, должна содержать только единицы (нули).
-
Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой и могут объединяться в прямоугольники. Следствием этого правила является смежность всех четырёх угловых ячеек карты Карно для N=4. Если во всех четырёх угловых ячейках стоят единицы (нули), они могут быть объединены в квадрат.
-
Все единицы (нули) должны попасть в какую-либо область.
-
С точки зрения МДНФ (МКНФ), число областей должно быть как можно меньше (каждая область представляет собой терм), а число клеток в области должно быть как можно больше (чем больше клеток в области, тем меньше переменных содержит терм).
-
Области могут пересекаться.
-
Область должна располагаться симметрично оси (оси располагаются через каждые четыре клетки) Несмежные области, расположенные симметрично оси, могут объединяться в одну.
Правило нахождения МДНФ (МКНФ).
Берём первую полученную область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию для МДНФ (дизъюнкцию для МКНФ) этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию для МДНФ (для МКНФ не ставим инверсию). Если переменная единичная, то не ставим инверсию для МДНФ (ставим инверсию для МКНФ). Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией для МДНФ (дизъюнкции областей объединяем конъюнкцию для МКНФ).
Функции могут быть записаны не формулой, а аналитическим путем, то есть содержать номера наборов из таблицы истинности дизъюнктивно (
Пример. 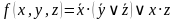
|
x |
y |
z |
|
|
|
|
|
|
B |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
Для нахождения МДНФ
— Составим карту для 3-х переменных и заполним ее 1 из последнего столбца таблицы истинности.
|
уz х |
00 |
01 |
11 |
10 |
|
0 |
1 |
1 |
1 |
|
|
1 |
1 |
1 |
— Выделим покрытия по принципам склейки
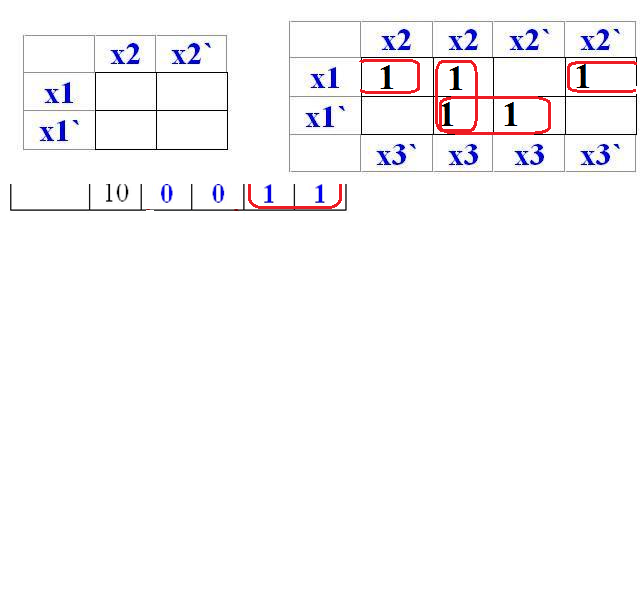


x y z x y z x y z
0 0 0 0 0 1 1 0 1
0 1 0 1 0 1 1 1 1
МДНФ: у=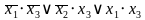
Для нахождения МКНФ
— Составим карту для 3-х переменных и заполним ее 0 из последнего столбца таблицы истинности.
|
уz х |
00 |
01 |
11 |
10 |
|
0 |
0 |
|||
|
1 |
0 |
0 |
— Выделим покрытия по принципам склейки
— Для каждого покрытия составляем элементарную дизъюнкцию, зачеркивая столбец с разными значениями и записывая оставшие переменные с инверсией, если все 1 и без инверсии, если все 0.
x y z x y z
1 0 0 0 1 1
1 1 0
МКНФ: у=
Задание для самостоятельного выполнения
-
составить карту Карно и найти МДНФ и МКНФ для следующих функций
а)
б)
-
Ответить на контрольные вопросы:
-
Что называется картой Карно?
-
Какие разновидности карт Карно есть?
-
Как заполняются карты Карно?
-
Для чего нужны принципы склейки?.
-
Чем отличается правило нахождения МДНФ от правила нахождения МКНФ?
-
Пользуясь этим и теоретическим материалом учебника М.С. Спирина «Дискретная математика» глава 4 п.4,6,3 стр.180, выполнить 1 задание.
Выполненное задание отправить на адрес электронной почты преподавателя. Имя файла – фамилия студента и номер занятия. (например Петров-17)
Users may refer the below rules & step by step procedure to learn how to find the minimum sum of products for the Boolean expression using 3 variables A, B & C. Users can use this KMap/Karnaugh’s map calculator for 3 variables to verify the results of K-map or to generate the work for any corresponding input values to learn how to solve Karnaugh’s map manually.
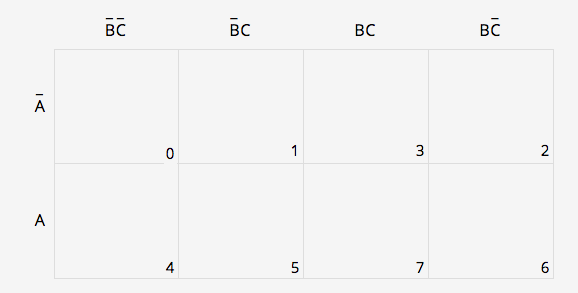
step 1 When using KMAP solver, generally users should be careful while placing the min-terms because, addressing the min-terms of KMAP table is bit different and is based on the Gray-code method. For, three variables the address of the rows are
In Binary Form
Row 1: 000, 001, 011, 010
Row 2: 100, 101, 111, 110
In Decimal Form
Row 1: 0, 1, 3, 2
Row 2: 4, 5, 7, 6
Row 1: ABC, ABC, ABC, ABC
Row 2: ABC, ABC, ABC, ABC
step 2 Write the Boolean expression in the SOP form. Place 1 for those positions and 0s for everything else.
step 3 Group the 1s. The counting of 1s in the group should be in the form of 23, 22 and 21. Therefore you can’t group single 1s, three 1s or five 1s or six 1s or seven 1s. The possible combinations of grouping are eight 1s, four 1s and two 1s together.
step 4 Check for eight 1s group and encircle the combination, if any.
step 5 Check for four 1s and encircle the combination of four 1s, if any. When combining 4 1s the last column and first column considered adjacent to each other. Similarly, the last row and first row considered adjacent to each other. The four corner cells of the KMAP table also considered as adjacent to each other.
step 6 Check for two 1s and encircle the combination, if any.
step 7 Find the appropriate product term for each combinations.
step 8 Add all the product terms brings the Minimum SOP of the given Boolean expression




 ) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;

 1х2
1х2