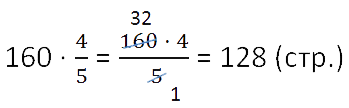В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
Download Article
Download Article
Finding the fraction of a number is the same as multiplying the number and the fraction. This simple method can be used for any kind of number (percent, fraction, mixed number, decimal), but is easiest with whole numbers. To solve the problem, you will need to know basic multiplication and division.
-
1
Write out the problem. If the problem you are working with is a word problem, first you need to write out all of the numbers involved in the calculation. If you were given the numbers written out already, you can skip this step.
- For example: What is one-third of seven?
- When you see “of” written between two numbers in a word problem, think of it as meaning multiply. Thus, one-third of seven actually means one-third multiplied by seven.
- Writing out the problem gives you (1/3) x 7.
-
2
Multiply the whole number by the numerator. When working with whole numbers, you will only multiply the number by the numerator (the top number) of the fraction. The denominator remains the same throughout the multiplication process.[1]
- For example: (1/3) x 7 = 7/3.
Advertisement
-
3
Divide by the denominator. Divide the product by the denominator (the bottom number) of the fraction. At this stage, the fraction might be an improper fraction, meaning that the numerator is larger than the denominator, or it will just need to be reduced.[2]
- For example: After multiplying, the fraction is 7/3. Three doesn’t divide evenly into seven so you will have a remainder. Three goes into seven twice with one leftover; therefore, the final answer is the mixed number 21/3.
Advertisement
-
1
Simplify the improper fraction. An improper fraction is one where the numerator is a larger number than the denominator. Always simplify an improper fraction before writing the final answer. To simplify, divide the numerator by the denominator and write the remainder as a fraction.[3]
- For example: 10/3
- Divide: 10/3 = 9 remainder 1
- Write the remainder as a fraction: 1/3
-
2
Write the mixed number. A mixed number contains both a whole number and a fraction. It is the simplest form of an improper fraction. To write the mixed number, simply write the whole number and the fraction that was created by the remainder.[4]
- For example: 10/3, 3 goes into 10 3 times with a remainder of 1. The mixed number is 31/3.
-
3
Reduce a fraction to its simplest form. Once you have multiplied through, you need to reduce the fraction. You can divide by a smaller number until the fraction is completely reduced.[5]
- For example: Simplify the fraction 4/8. Divide both numbers by four to simplify. The simplest form of 4/8 is 1/2.
Advertisement
Add New Question
-
Question
Jack has $48, he spends $18. What fraction of his money is left?
There is 30 left. 30 is 30/48 of 48. 30/48 = 5/8.
-
Question
If Susan works 10 hours a day, and her boss allows her to use (1/8) of the 10 hours for lunch. How long is her lunch break?
Find the answer with this equation: 10 x 1/8 = 10/8 = 1¼ = 1 hour and 15 minutes.
-
Question
What fraction represents 3 x 3/2?
Multiply the whole number by the numerator, and keep the denominator.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
To find a fraction of a whole number, multiply the whole number by the numerator of the fraction. Divide the product by the denominator of the fraction, then reduce the answer to a mixed number in its simplest form. If you want to learn how to reduce the fraction into its simplest form, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 151,035 times.
Did this article help you?
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Нахождение дроби от числа
Поддержать сайт
Дроби используют в математике, чтобы кратко обозначить часть
рассматриваемой величины.
Но если есть часть, то обязательно есть и целое (то, отчего
была взята эта часть).
Зная целое, можно найти его часть, указанную соответствующей дробью.
Запомните!
Чтобы найти дробь (часть) от числа, нужно это число
умножить на данную дробь.
Пример. Рассмотрим задачу.
В книге 160 страниц. Юра прочитал
книги. Сколько страниц
прочитал Юра?
Прежде всего найдём в задаче целое. Это — вся книга и в ней всего
160 страниц.
Посмотрим на дробь (часть) от целого:
.
Знаменатель равен 5, значит, целое разделили
на 5 частей и мы можем найти сколько страниц составляет
часть.
- 160 : 5 = 32 (стр.) — составляет часть страниц.
- Числитель дроби равен 4, значит взято 4 части.
- 32 · 4 = 128 (стр.) — составляют книги.
Оба действия можно записать кратко, в соответствии с правилом нахождения части от целого.
Ответ: Юра прочитал 128 страниц.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Загрузить PDF
Загрузить PDF
Нахождение дроби от числа равнозначно умножению числа на дробь. Описанный метод применим к любому числу (процентам, обыкновенным дробям, смешанным числам, десятичным дробям), но лучше пользоваться им при работе с целыми числами. Чтобы освоить описанный метод, нужно знать операции умножения и деления.
-
1
Запишите задачу. Если в задаче числа представлены словами, запишите их цифрами. Если же в задаче даются цифры, пропустите этот шаг.
- Например: найдите одну третью от семи?
- Если в задаче между двумя числами стоит предлог «от», нужно перемножить эти числа. Таким образом, в нашем примере одну третью нужно умножить на семь.
- Запишите это так: (1/3) x 7.
-
2
Целое число умножьте на числитель. Работая с целым числом, всегда умножайте его на числитель (верхнее число) дроби. Знаменатель не меняется на протяжении всего процесса умножения.[1]
- В нашем примере: (1/3) x 7 = 7/3.
-
3
Полученный результат разделите на знаменатель. Результат умножения разделите на знаменатель (нижнее число) дроби. На данном этапе дробь может быть неправильной, то есть числитель больше знаменателя, или дробь нужно просто сократить.[2]
- В нашем примере после перемножения числа и дроби получилась дробь 7/3. Семь на три не делится нацело, поэтому получится остаток: 7/3 = 2 с остатком 1. Таким образом, в результате получится смешанное число: 21/3
Реклама
-
1
Упростите неправильную дробь. Это дробь, у которой числитель больше знаменателя. Перед тем как написать окончательный ответ, обязательно упростите неправильную дробь, то есть преобразуйте ее в смешанное число. Для этого разделите числитель на знаменатель, а остаток запишите в числителе новой дроби.
- Например: 10/3
- Разделите: 10/3 = 9 с остатком 1.
- Остаток запишите в числителе новой дроби (знаменатель не меняется): 1/3
-
2
Запишите смешанное число. Смешанное число состоит из целой части и дробной части. Это упрощенная форма неправильной дроби. Чтобы записать смешанное число, рядом напишите целое число и дробь, которая получена из остатка.[3]
- Например: 10/3. Разделите 10 на 3: 10/3 = 3 с остатком 1. Смешанное число: 31/3.
-
3
Сократите дробь до наименьших значений числителя и знаменателя. Выполнив умножение, сократите дробь. Для этого разделите числитель и знаменатель на некоторый общий делитель.
- Например, сократите дробь 4/8. Разделите числитель и знаменатель на 4: 4/8 = 1/2.
Реклама
Об этой статье
Эту страницу просматривали 13 418 раз.
Была ли эта статья полезной?
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Умножение обыкновенных дробей
Правило умножения обыкновенных дробей:
При умножении двух дробей получается дробь, в числителе которой записывается произведение числителей данных дробей, а в знаменателе – произведение знаменателей:
$frac{a}{b}cdotfrac{c}{d}=frac{acdot c}{bcdot d}$
Замечание 1
Данное правило можно использовать для умножения правильных и неправильных дробей, дробей с одинаковыми и разными знаменателями.
Пример 1
Умножить обыкновенную дробь $frac{12}{23}$ на обыкновенную дробь $frac{4}{5}$.
Решение.
Произведение числителей данных дробей равно $12cdot 4=48$.
Произведение знаменателей равно $23cdot 5=115$.
Найдем произведение дробей $frac{12}{23}$ и $frac{4}{5}$:
$frac{12}{23}cdot frac{4}{5}=frac{12cdot 4}{23cdot 5}=frac{48}{115}$.
Ответ: $frac{48}{115}$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример 2
Выполнить умножение дробей $frac{5}{17}$ и $frac{43}{4}$.
Решение.
По правилу умножения обыкновенных дробей получим:
$frac{5}{17}cdot frac{43}{4}=frac{5cdot 43}{17cdot 4}=frac{215}{68}$
Получили неправильную дробь, из которой выделим целую часть:
$frac{215}{68}=frac{3 11}{68}$
Ответ: $frac{3 11}{68}$.
Замечание 3
Если хотя бы одна из умножаемых дробей сократима, можно выполнить ее сокращение до умножения. Для этого числители и знаменатели раскладывают на простые множители и сокращают одинаковые множители числителя и знаменателя.
«Умножение дробей, нахождение дроби от числа» 👇
Пример 3
Вычислить произведение дробей $frac{6}{42}cdot {49}{9}$.
Решение.
Используя правило умножения обыкновенных дробей, найдем:
$frac{6}{42}cdot frac{49}{9}=frac{6cdot 49}{42cdot 9}$.
Разложим числитель и знаменатель дроби на простые множители:
$frac{6cdot 49}{42cot 9}=frac{2cdot 3cdot 7cdot 7}{2cdot 3cdot 7cdot 3cdot 3}$.
Сократим одинаковые множители в числителе и знаменателе:
$frac{2cdot 3cdot 7cdot 7}{2cdot 3cdot 7cdot 3cdot 3}=frac{7}{9}$.
Ответ: $frac{7}{9}$.
При умножении дробей можно использовать переместительное свойство умножения:
Замечание 4
При изменении мест множителей их произведение не изменится:
$frac{a}{b}cdot {c}{d}=frac{c}{d}cdot {a}{b}=frac{acdot c}{bcdot d}$
Нахождение дроби от числа
Замечание 5
Чтобы найти дробь от числа, нужно умножить число на эту дробь.
Правило умножения обыкновенной дроби на натуральное число:
В результате умножения дроби на натуральное число получают дробь, у которой числитель равен произведению числителя дроби и натурального числа, а знаменатель остается неизменным:
$frac{a}{b}cdot n=frac{acdot n}{b}$
Если представить натуральное число $n$ в виде неправильной дроби $frac{n}{1}$ и применить правило умножения двух дробей, получим:
$frac{a}{b}cdot n=frac{a}{b}cdot frac{n}{1}=frac{acdot n}{bcdot 1}=frac{acdot n}{b}$
Пример 4
Выполнить умножение обыкновенной дроби $frac{7}{13}$ на натуральное число $8$.
Решение.
При умножении числителя дроби $7$ на натуральное число $8$ получим $56$. Воспользуемся правилом умножения дроби на число:
$frac{7}{13}cdot 8=frac{56}{13}$
Т.к. полученная дробь – неправильная, выделим целую часть:
$frac{56}{13}=4 frac{4}{13}$
Ответ: $frac{7}{13}cdot 8=4 frac{4}{13}$.
Замечание 6
Если в результате умножения дроби на число получают сократимую дробь или неправильную дробь, необходимо сократить дробь или выделить целую часть.
Пример 5
Умножить обыкновенную дробь $frac{4}{25}$ на натуральное число $5$.
Решение.
Используя правило умножения обыкновенной дроби на натуральное число, получим:
$frac{4}{25}cdot 5=frac{4cdot 5}{25}=frac{20}{25}$.
В результате умножения получили сократимую дробь $frac{20}{25}$ (признак делимости на $5$). Выполним ее сокращение:
$frac{20}{25}=frac{20div 5}{25div 5}=frac{4}{5}$.
Краткая запись решения:
$frac{4}{25}cdot 5=frac{4cdot 5}{25}=frac{20}{25}=frac{4}{5}$.
Ответ: $frac{4}{25}cdot 5=frac{4}{5}$.
Замечание 7
Если умножаемая дробь сократима или натуральное число и знаменатель дроби имеют общий делитель, можно выполнить сокращение дроби, разложив ее числитель и знаменатель на простые множители и сократив одинаковые множители числителя и знаменателя.
Пример 6
Вычислить произведение $frac{6}{42}cdot 49$.
Решение.
Используя правило умножения дроби на число, найдем:
$frac{6}{42}cdot 49=frac{6cdot 49}{42}$.
Разложим числитель и знаменатель дроби на простые множители:
$frac{6cdot 49}{42cdot 9}=frac{2cdot 3cdot 7cdot 7}{2cdot 3cdot 7}$.
Сократим одинаковые множители в числителе и знаменателе:
$frac{2cdot 3cdot 7cdot 7}{2cdot 3cdot 7}=frac{7}{1}=7$.
Ответ: $1$.
При умножении дроби на натуральное число можно использовать переместительное свойство:
Замечание 8
При изменении мест множителей их произведение не изменится:
$frac{a}{b}cdot n=ncdot frac{a}{b}=frac{acdot n}{b}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме