Задача 31272 Известна точка пересечения диагоналей.
Условие
Известна точка пересечения диагоналей квадрата К( 1,5; 2,5) и уравнение одной из его сторон х-4у = 0. Найти координаты вершин квадрата и составить уравнения его диагоналей.
Все решения
Уравнение стороны запишем в виде
y=(1/4)x
k=1/4
tg α =1/4
Уравнение диагонали в общем виде:
y=k_(1)x+b
(Диагонали квадрата являются биссектрисами прямых углов квадрата, значит угол между стороной и диагональю квадрата равен 45^(o))
Так как
tg( β — α )=(tg β -tg α )/(1+tg β *tg α )
и
y=(5/3)x+b — уравнение диагонали
Подставим координаты точки К
Диагонали взаимно перпендикулярны.
Значит уравнение второй диагонали
y=(-3/5)x+b
Подставим координаты точки К
2,5=(-3/5)*1,5+b
b=3,4
Координаты одной вершины получим как координаты точки пересечения стороны х-4у=0 и диагонали у=(5/3)х
<х-4у=0
<у=(5/3)х
Координаты второй вершины получим как координаты точки пересечения стороны х-4у+24=0 и диагонали у=(-3/5)х+3,4
<х-4у=0 ⇒ y=(1/4)x
<у=(-3/5)х+3,4
Координаты двух других точек можно найти из симметрии.
Уравнение квадрата в декартовой системе координат.
Проанализируем расположение квадрата на координатной плоскости.
В общем случае уравнение квадрата в декартовой (прямоугольной) системе координат принимает вид:
где точка О`(a;b) – точка пересечения диагоналей квадрата;
d – длина диагонали квадрата.
В частном случае, когда точка О(0;0) — начала координат, является одновременно и точкой пересечения диагоналей квадрата, уравнение квадрата принимает вид:
где d– длина диагонали квадрата.
Примеры решений по аналитической геометрии на плоскости
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости. Задачи касаются расположения прямых на плоскости (параллельны, перпендикулярны, перескаются), взаимного расположения точек и прямых, вычисления характерстик геометрических фигур (треугольников, ромбов, параллелограммов), нахождения расстояний, длин, уравнений.
Геометрия на плоскости: решения онлайн
Геометрические фигуры
Задача 1. Уравнение одной из сторон квадрата $x+3y-5=0$. Составить уравнения трех остальных сторон квадрата, если $(-1,0)$ – точка пересечения его диагоналей.
Задача 2. Дан параллелограмм $ABCD$, три вершины которого $A(-3,5,-4)$, $B(-5,6,2)$, $C(3,-5,-2)$. Найти четвертую вершину и острый угол параллелограмма.
Задача 3. Найти координаты вершин квадрата, если известны координаты одной вершины $(-8,12)$ и уравнение одной стороны $y=13/7 cdot x -30/7$.
Задача 4. Вычислить координаты вершин ромба, если известны уравнения двух его сторон $х + 2у = 4$ и $х + 2у = 10$ и уравнение одной из его диагоналей $у = х + 2$.
Задача 5. Две стороны параллелограмма заданы уравнениями $у = х — 2$ и $5у = х + 6$, диагонали его пересекаются в начале координат. Найти длины его высот.
Точки и прямые
Задача 6. Через начало координат провести прямую, равноудаленную от точек $А(2, 2)$ и $В(4, 0)$.
Задача 7. Написать уравнение биссектрис углов между прямыми $2х + 3у = 10$ и $3х + 2у = 10$.
Задача 8. Найти точку, симметричную точке $M(2,-1)$ относительно прямой $x-2y+3=0$.
Задача 9. Даны координаты точки $A$ и уравнение прямой $l$.
Требуется:
1) составить уравнение прямой $l_1$, проходящей через точку $A$ параллельно прямой $l$;
2) составить уравнение прямой $l_2$, проходящей через точку $A$ перпендикулярно прямой $l$;
3) Найти расстояние от точки $A$ до прямой $l$;
4) Изобразить на чертеже точку $A$ и прямые $l, l_1, l_2$.
Задача 10. Даны три точки $M_1(-1;5$), $M_2(2;1)$, $M_3(4;11)$.
2.1 Составить уравнения прямых
А) перпендикулярной; Б) параллельной прямой $M_1M_2$ и проходящей через точку $M_3$, используя:
1) уравнение прямой, проходящей через точку с заданным нормальным вектором;
2) уравнение прямой, проходящей через точку с заданным направляющим вектором;
3) уравнение прямой, проходящей через точку с заданным угловым коэффициентом.
2.2 На отрезке $M_1M_2$ найти координаты точки $M_4$, находящейся к точке $M_1$ в два раза ближе, чем к точке $M_2$.
Задача 11. Прямая задана уравнениями $$ left < beginx&=5-3lambda,\ y&=1+4lambda.\ end right. $$ Перейти к другой форме задания прямой:
А) по точке и нормальному вектору,
Б) ее общему уравнению.
Задача 12. Даны точки $A, B, C, D$. Запишите уравнения прямых $AB$ и $CD$. Найти расположение этих прямых относительно друг друга.
http://www.calc.ru/Uravneniye-Kvadrata-V-Dekartovoy-Sisteme-Koordinat.html
http://www.matburo.ru/ex_ag.php?p1=aggeom
Задача 65941 .Составить уравнения сторон квадрата,…
Условие
.Составить уравнения сторон квадрата, если
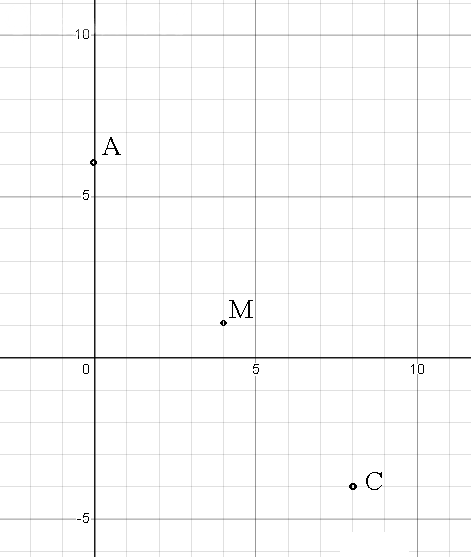
известны координаты вершины A(0, 6) и уравнения
диагоналей AC:
5x+4y-24=0 , BD:
4x-5y-11=0 .
математика ВУЗ
1029
Решение
★
AC: 5x+4y–24=0
BD:4x–5y–11=0 .
Диагонали квадрата пересекаются в точке М
Найдем координаты точки М, решаем систему уравнений:
[m]left{begin {matrix} 5x+4y–24=0\4x–5y–11=0 end {matrix}right.[/m] ⇒
Решаем систему способом сложения.
Умножаем первое уравнение на 5, второе на 4:
[m]left{begin {matrix} 25x+20y–120=0\16x–20y–44=0 end {matrix}right.[/m]
и складываем ( т.е заменяем одно из уравнений суммой этих уравнений):
[m]left{begin {matrix} 25x+20y–120=0\41x–164=0 end {matrix}right.[/m]
[m]left{begin {matrix} 25cdot 4+20y–120=0\x=4 end {matrix}right.[/m] ⇒
[m]left{begin {matrix} y=1\x=4 end {matrix}right.[/m]
M(4:1)
M — середина АС
Применяем формулы для нахождения координат середины отрезка
Координаты точки M как середины АС
[m]x_{M}=frac{x_{A}+x_{C}}{2}[/m] ⇒ [m]x_{C}=2x_{M}-x_{A}=2cdot 4-0=8[/m]
[m]y_{M}=frac{y_{A}+y_{C}}{2}[/m] ⇒ [m]y_{C}=2y_{M}-y_{A}=2cdot 1-6=-4[/m]
Применяем свойства диагоналей квадрата:
АМ=МС=ВМ=МD
АМ=sqrt((4-0)^2+(1-6)^2)=sqrt(16+25)=sqrt(41)
ВМ=sqrt((x_(B)-0)^2+(y_(B)-6)^2) ⇒
sqrt((x_(B)-0)^2+(y_(B)-6)^2) =sqrt(41)
Возводим в квадрат:
(x_(B)-0)^2+(y_(B)-6)^2=41
Так как точка B принадлежит прямой BD, то её координаты удовлетворяют уравнению этой прямой:
4x_(В)–5y_(В)–11=0 .
Решаем систему двух уравнений, находим координаты точки B
{(x_(B)-0)^2+(y_(B)-6)^2=41
{4x_(В)–5y_(В)–11=0 .
Аналогично находим координаты точки D
Чтобы составить уравнения сторон применяем формулу уравнения прямой, проходящей через две точки
Написать комментарий
Составить уравнение сторон квадрата
-
Dimon7869
- Сообщения: 5
- Зарегистрирован: 02 ноя 2015, 21:27
Составить уравнение сторон квадрата
Составить уравнение сторон квадрата,если известны координаты вершины А(-2;10) и уравнения диагоналей АС: 5х+4y-30=0,BD: 4x-5y+17=0.Заранее огромное спасибо!
-
Алексей
- Администратор
- Сообщения: 1680
- Зарегистрирован: 18 янв 2014, 03:13
Re: Составить уравнение сторон квадрата
Сообщение
Алексей » 06 ноя 2015, 12:26
Попробуйте по такой схеме:
- Найти координаты точки O — пересечения диагоналей AC и BD, для чего решить систему (left{begin{aligned}&5x+4y-30=0;\&4x-5y+17=0end{aligned}right.)
- Точка O — середина отрезка AC. Зная координаты точки O и точки A, найти координаты точки C.
- Прямые CB, CD и AB, AD пересекают диагональ BD под углом 45 градусов. Зная координаты точек А и С, а также уравнение диагонали BD, находим уравнения сторон. Пример решения такой задачи можно найти в первом томе решебника под редакцией Каплана на странице 45 (задача 4.18).
«Именно то, что наиболее естественно, менее всего подобает человеку.» Братья Стругацкие, «Хромая судьба»
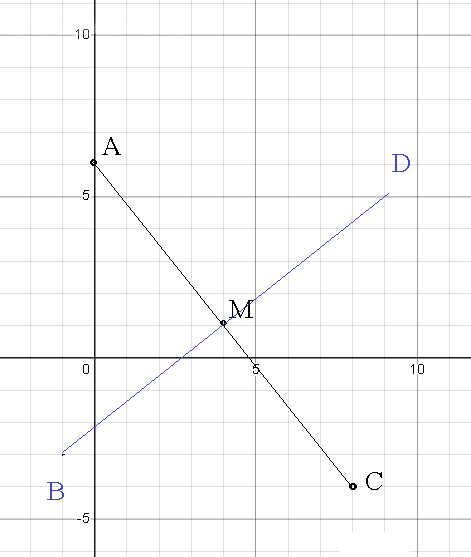
Дано:
А(1;4) — вершина квадрата.
D(5;1) — точка пересечения диагоналей.
Найти: Уравнения сторон квадрата.
Пошаговое объяснение:
Рисунок к задаче в приложении. Решение силой Разума — глазами.
Мысль 1 — диагонали квадрата перпендикулярны, а точка их пересечения делит их по середине.
Мысль 2. Расстояние от т. А до т. D даже не вычисляя (по теореме Пифагора — это будет 3:4:5) — используем катеты — 3 и 4.
Вычисляем координаты вершин используя точку D(5;1) и всего два числа: 3 и 4.
B(8;5), C(9;-2), E(2;-3) — арифметика для первого класса.
2. Уравнения прямых — сторон квадрата — по формуле y = k*x + b находим по координатам двух точек.
ДАНО: A(1;4), B(8;5)
1) k = (Ay-By)/(Ax-Bx)=(4-5)/(1-8)= 1/7 (0,14) — наклон прямой
2) b = Ay-k*Ax=4-(1/7)*1=3 6/7 сдвиг по оси ОУ
Уравнение Y(AB) = x/7+3 6/7 (3,86) — ответ
ДАНО: Е(2;-3), С(9;-2)
1) k = 1/7 — наклон прямой, как и у прямой АВ.
2) b = Еy-k*Еx=-3-(1/7)*2=-3 2/7- сдвиг по оси ОУ
Уравнение Y(ЕС) = x/7- 3 2/7 (3,28) — ответ
ДАНО: Е(2;-3), А(1;4)
1) k = (Еy-Аy)/(Еx-Аx)=(-3-4)/(2-1)=-7 — наклон прямой
2) b = Еy-k*Еx=-3-(-7)*2=11 — сдвиг по оси ОУ
Уравнение Y(ЕА) = -7*x+11 — ответ
ДАНО: В(8;5), С(9;-2)
1) k = -7 — наклон прямой, как и у прямой ЕА.
2) b = Вy-k*Вx=5-(-7)*8=61- сдвиг по оси ОУ
Уравнение Y(ВС) = -7*x+61 — ответ
Задача решена полностью.
Тема: уравнения сторон квадрата (Прочитано 7899 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Даны ур-ия 2х сторон квадрата. 4x-3y-17=0 и 4x-3y+3=0. Составить уравнения двух других его сторон, при условии, что точка А(2;-3) является вершиной этого квадрата.
мной решено:
1. т.к это квардат, его стороны перпендикулярны, значит произведение угловых коэффицентов перпен-ых сторон равно -1. значит К неизвестных сторон = -3/4.
2. уравнение одной стороны нашла как ур-ей по заданной точке А и найденного углового коэффицента. 3x+4y+6=0.
3. нашла координаты еще одной точки решив такую систему
4x-3y+3=0
3x+4y+6=0.
С(-6/5;-3/5)
а как теперь найти ур-ей еще одной стороны не могу сообразить.
Теперь вам осталось провести параллельную прямую по отношению к АС на расстоянии АС от нее.
Пожалуйста не пишите голое условие! Сначало мы выслушаем Ваши мысли или хотябы вопросы, но конкретные и лишь потом дадим необходимые советы!
Но можете всего этого и не делать, если Вас не интересует результат
Если не хотите разбираться сами закажите решение на сайте.
Хм, а я вот так вот сделал.
Обозначаем неизвестную точку принадл неизвестной прямой и прямой 4x-3y-17=0 как В(x1,y1)
так как точка А известна, то запишем ур-е 4х-3у-17=0 в виде прямой, проход через 2 точки
x-2 y+3
—- = ——
x1-2 y1+3 скомпоновывая, получаете x(y1+3)+y(2-x1)-3×1-2y1=0 при этом условие совпадения двух прямых A/A1=B/B1=C/C1 , решаем и получаем точку В, дальше очевидно, подставляете точку В в ур-е неизвестной прямой (вы не знаете только свободный член, его и находите).
депрессивный зануда и социофоб.
Выглядит правильно) Но это же легко проверить — провести(построить ) по полученным точкам построить еще одну сторону квадрата.
Пожалуйста не пишите голое условие! Сначало мы выслушаем Ваши мысли или хотябы вопросы, но конкретные и лишь потом дадим необходимые советы!
Но можете всего этого и не делать, если Вас не интересует результат
Если не хотите разбираться сами закажите решение на сайте.
спасибо за помощь!
Semen_K.
длина АС= 4, как мне теперь отсюда найти ур-ей стороны BD если у нас нет координат ни одной точки?
Nikgamer. Ваш способ пока не до конца разобрала, вернее разобрала, построила графически, но у меня квадрат не получился. сижу ищу ошибку в вычислениях))
Я уже не помню как выглядят уравнения параллельных прямых. Но можно и по другому: уравнение одной из сторон есть, точка на этой прямой есть, можно сотавить уравнение длины отрезка на уже известной прямой но с одной точкой и другой неизвестной точкой + совместно с этим уравнением рассмотреть уравнение этой прямой. Можно получить еще одну точку. И т.д.
Пожалуйста не пишите голое условие! Сначало мы выслушаем Ваши мысли или хотябы вопросы, но конкретные и лишь потом дадим необходимые советы!
Но можете всего этого и не делать, если Вас не интересует результат
Если не хотите разбираться сами закажите решение на сайте.
Спасибо!! ушла дорешивать)))