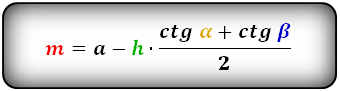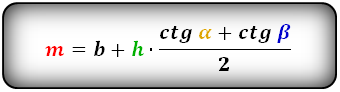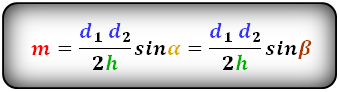Как составить уравнение средней линии трапеции - Avtoru.top

Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?

Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.

1 способ

Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.

Пример.

1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.

Решение:

М — середина отрезка AB, N — середина BC.

По формулам координат середины отрезка

$[x_M = frac{{x_A + x_B }}{2} = frac{{ - 2 + 1}}{2} = - frac{1}{2};]$

$[y_M = frac{{y_A + y_B }}{2} = frac{{ - 4 + 6}}{2} = 1;]$

$[x_N = frac{{x_B + x_C }}{2} = frac{{1 + 7}}{2} = 4;]$

$[y_N = frac{{y_B + y_C }}{2} = frac{{6 + 0}}{2} = 3.]$

Таким образом,

$[M( - frac{1}{2};1),N(4;3).]$

Составим уравнение прямой MN, например, в виде y=kx+b:

$[left{ begin{array}{l} 1 = k cdot ( - frac{1}{2}) + b; \ 3 = k cdot 4 + b; \ end{array} right.]$

Отсюда

$[k = frac{4}{9},b = frac{{11}}{9},]$

$[y = frac{4}{9}x + frac{{11}}{9},9y = 4x + 11,4x - 9y + 11 = 0.]$

2 способ

Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.

Решение:

$[M( - frac{1}{2};1)]$

— середина отрезка AB. Составим уравнение прямой AC:

$[left{ begin{array}{l} - 4 = k cdot ( - 2) + b; \ 0 = k cdot 7 + b; \ end{array} right.]$

$[k = frac{4}{9},b = - frac{{28}}{9}, Rightarrow y = frac{4}{9}x - frac{{28}}{9}.]$

Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.

Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:

$[k_{MN} = k_{AC} = frac{4}{9},]$

то есть уравнение прямой MN ищем в виде

$[y = frac{4}{9}x + b.]$

Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:

$[1 = frac{4}{9} cdot ( - frac{1}{2}) + b, Rightarrow b = 1 + frac{2}{9} = frac{{11}}{9}.]$

Таким образом, уравнение прямой MN

$[y = frac{4}{9}x + frac{{11}}{9}]$

или

Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.

Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).

Решение:

1 способ

Сначала следует определить основания данной трапеции.

Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.

A(-2;1), D(0;-3), отсюда

$[left{ begin{array}{l} 1 = k cdot ( - 2) + b; \ - 3 = k cdot 0 + b; \ end{array} right. Rightarrow k = - 2,b = - 3.]$

Значит, уравнение прямой AD: y= -2k-3.
B(1;5), C(4;-1),

$[left{ begin{array}{l} 5 = k cdot 1 + b; \ - 1 = k cdot 4 + b; \ end{array} right. Rightarrow k = - 2,b = 7.]$

Уравнение прямой BC: y= -2k+7.

Поскольку угловые коэффициенты прямых равны:

$[k_{AD} = k_{BC} = - 2,]$

то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины AB и CD соответственно.

$[x_M = frac{{x_A + x_B }}{2} = frac{{ - 2 + 1}}{2} = - frac{1}{2},]$

$[y_M = frac{{y_A + y_B }}{2} = frac{{1 + 5}}{2} = 3,]$

$[x_N = frac{{x_C + x_D }}{2} = frac{{4 + 0}}{2} = 2,]$

$[y_N = frac{{y_C + y_D }}{2} = frac{{ - 1 + ( - 3)}}{2} = - 2.]$

Составим уравнение прямой MN, M(-1/2;3), N(2;-2):

$[left{ begin{array}{l} 3 = k cdot ( - frac{1}{2}) + b; \ - 2 = k cdot 2 + b; \ end{array} right. Rightarrow k = - 2,b = 2,]$

то есть y=-2k+2.

2 способ

Уравнение AD — y= -2k-3, середина AB — M(-1/2;3). Составляем уравнение прямой MN, параллельной прямой AD.

$[k_{MN} = k_{AD} = - 2.]$

Значит уравнение MN ищем в виде y= -2x+b.

Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:

$[3 = - 2 cdot ( - frac{1}{2}) + b, Rightarrow b = 2.]$

Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.

Источник

Уравнение средней линии

Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.

Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.

М — середина отрезка AB, N — середина BC.

Составим уравнение прямой MN, например, в виде y=kx+b:

— середина отрезка AB. Составим уравнение прямой AC:

Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.

Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:

то есть уравнение прямой MN ищем в виде

Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:

Таким образом, уравнение прямой MN

Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.

Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).

Сначала следует определить основания данной трапеции.

Значит, уравнение прямой AD: y= -2k-3.
B(1;5), C(4;-1),

Уравнение прямой BC: y= -2k+7.

Поскольку угловые коэффициенты прямых равны:

Составим уравнение прямой MN, M(-1/2;3), N(2;-2):

Уравнение AD — y= -2k-3, середина AB — M(-1/2;3). Составляем уравнение прямой MN, параллельной прямой AD.

Значит уравнение MN ищем в виде y= -2x+b.

Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:

Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.

Все формулы средней линии трапеции

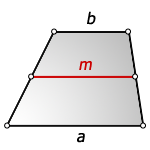
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции — отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.

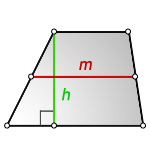
1. Формула средней линии трапеции через основания

b — верхнее основание

a — нижнее основание

m — средняя линия

Формула средней линии, ( m ):

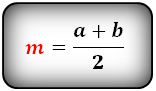
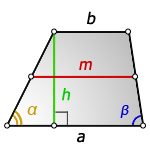
2. Формулы средней линии через основание, высоту и углы при нижнем основании

b — верхнее основание

a — нижнее основание

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции, ( m ):

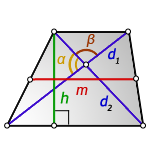
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

α , β — углы между диагоналями

d ₁ , d ₂ — диагонали трапеции

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции , ( m ):

4. Формула средней линии трапеции через площадь и высоту

S — площадь трапеции

h — высота трапеции

m — средняя линия

Трапеция. Формулы, признаки и свойства трапеции

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Основы трапеции — параллельные стороны
Боковые стороны — две другие стороны
Средняя линия — отрезок, соединяющий середины боковых сторон.

Равнобедренная трапеция — трапеция, у которой боковые стороны равны
Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам

Основные свойства трапеции

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

BC : AD = OC : AO = OB : DO

d ₁ 2 + d ₂ 2 = 2 a b + c 2 + d 2

Сторона трапеции

Формулы определения длин сторон трапеции:

a = b + h · ( ctg α + ctg β )

b = a — h · ( ctg α + ctg β )

a = b + c· cos α + d· cos β

b = a — c· cos α — d· cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

Средняя линия трапеции

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

2. Формула определения длины средней линии через площадь и высоту:

Высота трапеции

Формулы определения длины высоты трапеции:

h = c· sin α = d· sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d ₁ d ₂	=	sin δ ·	d ₁ d ₂
a + b	a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d ₁ d ₂	=	sin δ ·	d ₁ d ₂
2 m	2 m

4. Формула высоты трапеции через площадь и длины оснований:

5. Формула высоты трапеции через площадь и длину средней линии:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

d ₁ = √ a 2 + d 2 — 2 ad· cos β

d ₂ = √ a 2 + c 2 — 2 ac· cos β

2. Формулы диагоналей через четыре стороны:

d ₁ =	√	d 2 + ab —	a ( d 2 — c 2 )
a — b

d ₂ =	√	c 2 + ab —	a ( c 2 — d 2 )
a — b

d ₁ = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2

d ₂ = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2

d ₁ = √ c 2 + d 2 + 2 ab — d ₂ 2

d ₂ = √ c 2 + d 2 + 2 ab — d ₁ 2

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

3. Формула площади через диагонали и угол между ними:

S =	d ₁ d ₂	· sin γ	=	d ₁ d ₂	· sin δ
2	2

4. Формула площади через четыре стороны:

S =	a + b	√	c 2 —	(	( a — b ) 2 + c 2 — d 2	)	2
2	2( a — b )

5. Формула Герона для трапеции

S =	a + b	√ ( p — a )( p — b )( p — a — c )( p — a — d )
\| a — b \|

где

p =	a + b + c + d	— полупериметр трапеции.
2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d ₁
4√ p ( p — a )( p — c )( p — d ₁)

где

a — большее основание

Окружность вписанная в трапецию

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
2	2	a + b

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

источники:

http://www-formula.ru/average-line-trapeze

http://ru.onlinemschool.com/math/formula/trapezium/

Источник

1) Найдем, какая из пар сторон является основаниями (AB и CD или AD и BC)

$AB,;CD:\{2-1over1-4}=-{1over3}\{3-6over6-5}=-3\-3neq-{1over3}\\BC,;AD:\{1-3over4-6}=1\{2-6over1-5}=1\1=1$

Значит BC и AD параллельны. Значит средняя линия проходит через середины сторон AB и CD. Координаты середин сторон:

$M({2+1over2},{1+4over2})=M({3over2},{5over2})\N({3+6over2},{6+5over2})=N({9over2},{11over2})$

Составим уравнение прямой, проходящей через эти точки:

${x-{3over2}over {9over2}-{3over2}}={y-{5over2}over{11over2}-{5over2}}\\x-{3over2}=y-{5over2}\\y=x+1$

Источник

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,662
гуманитарные
33,654
юридические
17,917
школьный раздел
611,978
разное
16,905

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник

1) Найдем, какая из пар сторон является основаниями (AB и CD или AD и BC)

$AB,;CD:\{2-1over1-4}=-{1over3}\{3-6over6-5}=-3\-3neq-{1over3}\\BC,;AD:\{1-3over4-6}=1\{2-6over1-5}=1\1=1$

$M({2+1over2},{1+4over2})=M({3over2},{5over2})\N({3+6over2},{6+5over2})=N({9over2},{11over2})$

Составим уравнение прямой, проходящей через эти точки:

${x-{3over2}over {9over2}-{3over2}}={y-{5over2}over{11over2}-{5over2}}\\x-{3over2}=y-{5over2}\\y=x+1$

Источник

Уравнение средней линии

Все формулы средней линии трапеции

Трапеция. Формулы, признаки и свойства трапеции

Основные свойства трапеции

Сторона трапеции

Формулы определения длин сторон трапеции:

Средняя линия трапеции

Формулы определения длины средней линии трапеции:

Высота трапеции

Формулы определения длины высоты трапеции:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

Площадь трапеции

Формулы определения площади трапеции:

Периметр трапеции

Формула определения периметра трапеции:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

Окружность вписанная в трапецию

Формула определения радиуса вписанной в трапецию окружности

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

Не пропустите также: