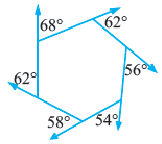
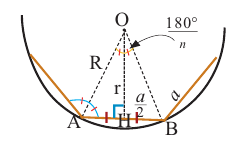
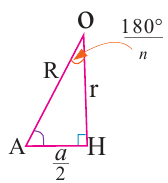
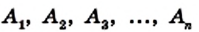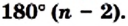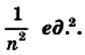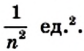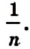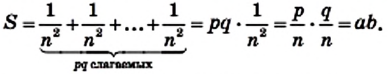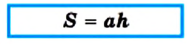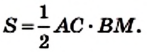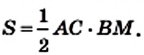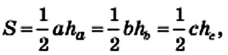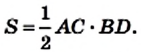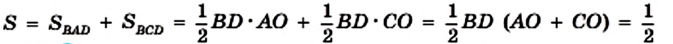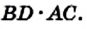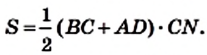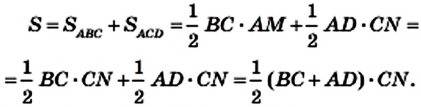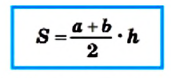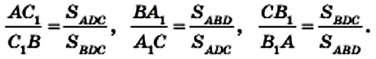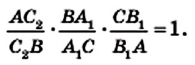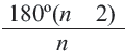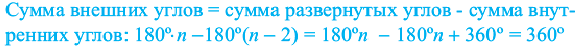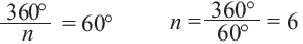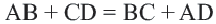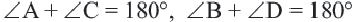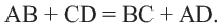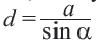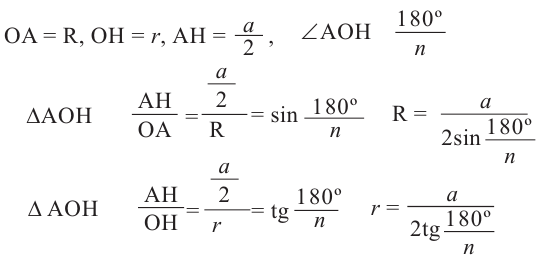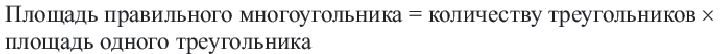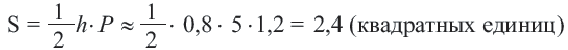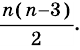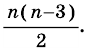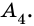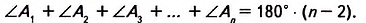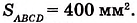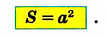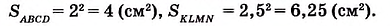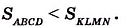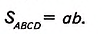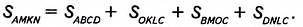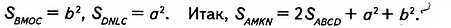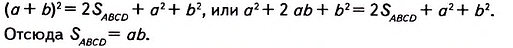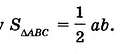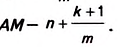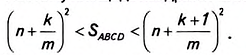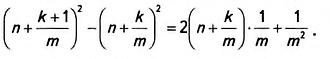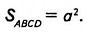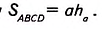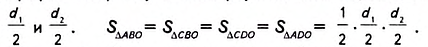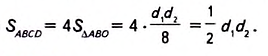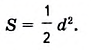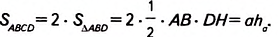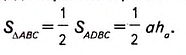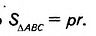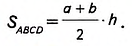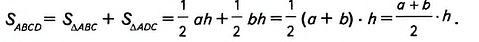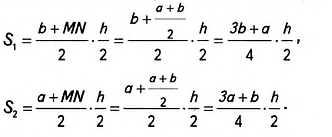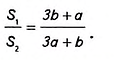Уравнения многоугольников
Автор работы: Шпакова Маргарита Андреевна, г.о. Тольятти, МБУ СОШ
№ 58, 8 класс
Научный руководитель: Владимирова Ольга Ивановна, учитель математики первой категории МБУ СОШ № 58.
В школьном курсе математики учащиеся часто встречаются с алгебраическими уравнениями, уравнениями прямых, уравнениями окружностей, квадратными уравнениями и т.д. Что собой представляют уравнения многоугольников, учащиеся не знают.
Как, например, выглядит уравнение треугольника? Можно ли по фигуре на плоскости составить уравнение? Можно ли рассчитать площадь фигуры по заданному уравнению? Можно ли по заданному уравнению определить, что за многоугольник? Решение этих вопросов меня и заинтересовало. В них есть проблема моей исследовательской работы.
Цель работы: изучить и исследовать на примерах методы, которые дают возможность получить уравнение с модулем любого выпуклого многоугольника на плоскости, координаты вершин которого известны. Найти взаимосвязь площади фигуры от ее уравнения.
Основные ЗАДАЧИ исследования:
- Познакомиться с некоторыми видами уравнений прямых на плоскости (уравнение прямой в отрезках, уравнение прямой, проходящей через две различные точки на плоскости);
- Научиться составлять уравнение прямой через заданную точку и параллельную другой прямой;
- Научиться составлять уравнение прямой, проходящей через две заданные точки;
- Научиться по уравнению строить многоугольник на плоскости и наоборот, по чертежу составлять уравнение многоугольника;
- Изучить метод областей при решении уравнений, содержащих знак модуля.
Как известно из курса геометрии, любая прямая на координатной плоскости может быть задана уравнением вида
ах+by+с = 0
Подобное уравнение называют линейным. Уравнение такого вида называют также общим уравнением прямой на плоскости.
Если ax+by+c = 0 — уравнение некоторой прямой m, то уравнение ax+by+c = p, где р ≠ 0, задает прямую m`, параллельную m. Это следует из того, что данные два уравнения не имеют общих решений, а значит, прямые не имеют общих точек.
У параллельных прямых
y=k1x+b
y=k2x+d
k1=k2
Пример1. Составим уравнение прямой, проходящей через точку М (1;-2) и параллельной прямой 3x-4y+5=0
Подставляя координаты точки М в левую часть уравнения, получаем значение 16. Значит, искомым уравнением прямой будет 3x+4y+5=16 или окончательно 3x+4y-11=0.
Пусть известны координаты двух точек М1 (x1;y2), М2 (x2;y2), лежащих на данной прямой. Составим уравнение прямой, проходящей через две заданные точки:
=
(x-x1)(y2-y1)-(y-y1)(x2-x1)=0
Пример 2. Составим уравнение прямой, проходящей через точку М1 (3;1) и М2 (2;2).
Получаем такое уравнение (x-3)(2-1)-(y-1)(2-3)=0
после преобразований выходит х+у-4=0.
Если известны координаты (а;0) и (0;b) точек пересечения прямой с осями Ох и Оу, то для этой прямой проще всего записать уравнение в отрезках +
= 1.
Рассмотрим на координатной плоскости ху треугольник с вершинами в точках А (х1;у1), В (х2;у2), С (х3;у3). Уравнение прямой, на которой лежит сторона АВ этого треугольника, можно записать в виде
(x-x1)(y2-y1)-(y-y1)(x2-x1)=0.
Подставим координаты третьей вершины С (х3;у3) в левую часть этого уравнения,
получим некоторое значение
q=(x3-x1)(y2-y1)-(y3-y1)(x2-x1)
Чтобы понять геометрический смысл числа q, заметим, что уравнение
(х-х1)(у2-у1)-(у-у1)(х2-х1)=q задает прямую, параллельную стороне АВ данного треугольника. Поэтому для каждой точки этой прямой результат подстановки ее координат в левую часть уравнения тот же, что и для точки C (х3;у3), и дает число q. Значит, то же значение получится и для точки С1 (х4;у1) пересечения упомянутой прямой с прямой у=у1, параллельной оси абсцисс и проходящей через вершину A треугольника. Но в этой точке
(х-х1)(у2-у1)-(у-у2)(х2-х1) = (х4-х1)(у2-у1). Геометрический смысл последнего выражения понять уже несложно: |(х4-х1)(у2-у1)| площадь параллелограмма со сторонами АВ и АС1. Длина стороны АС1 равна |х4-х1|, а длина высоты параллелограмма, опущенной из вершины B на эту сторону, есть |у2-у1|. Поэтому |q| есть площадь ΔАВС1, но она такая же, что и у ΔАВС. В результате приходим к следующей формуле для площади треугольника
S =|(x3-x1)(y2-y1)-(y3-y1)(x2-x1)|. (3, стр. 169).
Уравнение треугольника
Если треугольник задан в декартовой системе координат и имеет своими вершинами точки А (х1;у1), В (х2;у2), С (х3;у3), то можно составить уравнение треугольника:
|(x-x1)(y2-y1)-(y-y1)(x2-x1)| + |(x-x2)(y3-y2)-(y-y2)(x3-x2)| +
+ |(x-x3)(y1-y3)—(y-y3)(x1-x3)| = 2S, где
S =|(x3-x1)(y2-y1)-(y3-y1)(x2-x1)|.
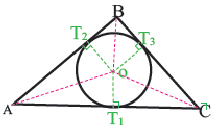
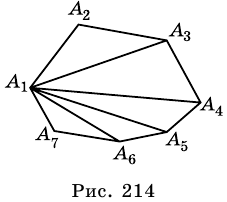
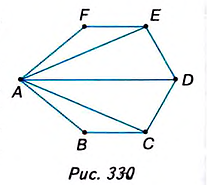
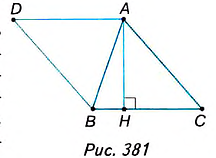
Пример 3. Составим уравнение треугольника, изображенного на рисунке. Для этого составим уравнения прямых, которые являются его сторонами, по формуле
(x-x1)(y2-y1)-(y-y1)(x2-x1)=0, задающей уравнение прямой по двум ее точкам. При этом допустимым считаем раскрытие скобок и приведение подобных слагаемых и недопустимым – умножение обеих частей уравнения на некоторое число (за исключением -1).
А(0;1), В(1;0), С(-1;0)
Уравнения сторон имеют вид: х-у+1=0, х+у-1=0, 2у=0. Сложив модули левых частей этих уравнений, и приравняв полученное выражение к удвоенной площади ΔАВС, равной в данном случае 1, приходим к искомому уравнению |x-y+1|+|x+y-1|+2|y|=2.
Описанный метод дает возможность получить уравнение любого выпуклого многоугольника на плоскости, координаты вершин которого известны.
Уравнение квадрата, ромба
Пример 4. Составить уравнение квадрата:
|x-1| + |y-1| + |x| + |y| = 1. Площадь равна 1.
Пример 5. Составить уравнение ромба:
Через точки с координатами (1;0), (0;1) уравнение прямой: x +y -1 = 0.
Через точки с координатами (-1;0), (0;1) уравнение прямой: x – y + 1 = 0.
Через точки с координатами (-1;0), (0;-1) уравнение прямой: x + y + 1 = 0.
Через точки с координатами (0;-1), (1;0) уравнение прямой: -x + y + 1 = 0.
Получили: | x + y — 1| + | x – y + 1| + | x + y + 1| + | -x + y + 1 | = 4.
Этот же ромб имеет другое уравнение: |х| + |у| = 1, которое лучше решать «методом областей». Площадь ромба равна 2.
Пример 6. Докажите, что уравнения: |x + y| + |x — y| = 2 и |x + 1| + |y + 1| + |x -1| +|y — 1| =4 относятся к одному квадрату.
Первое уравнение лучше решать «методом областей», где вся плоскость разбивается прямыми у =-х и у=х на четыре области, значит, искомая фигура четырехугольник, стороны которого параллельны осям координат. Из уравнений каждой области у=1, х=1и т.д. понимаем, что это квадрат, площадь которого равна 4.
Второе уравнение наглядно изображено, подтверждая первое.
Пример 7. Определить вид многоугольника по уравнениям:
|х| + 3|у| = 6; |х-3| + |у+3| = 3; |х-1| + 7|у| = 1.
Во всех случаях даны уравнения ромба .
Уравнение шестиугольника
Пример 8. Изобразить на плоскости многоугольник по данному уравнению: |x|+|y|+|x+y|=4.
Из данного уравнения следует, что х=0, у=0, х= -у –прямые, которые разбивают плоскость на несколько областей.
Найдем уравнение прямой, стороны многоугольника, в каждой из областей:
- (2;1)
х+у+х+у=4
2х+2у=4
х+у=2
х=2-у
- (-1;2)
-х+у+х+у=4
2у=4
у=2
- (-2;1)
-х+у-х-у=4
-2х=4
х=-2
- (-2;-1)
-х-у-х-у=4
-2х-2у=4
-х=2+у
х=-2-у
- (1;-2)
х-у-х-у=4
-2у=4
у=-2
- (2;-1)
х-у+х+у=4
2х=4
х=2
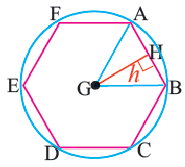
В каждой из полученных областей построили соответствующую прямую. Получили шестиугольник, площадь которого равна 12.
Пример 9. Определить вид многоугольника: 2|х| + |у| + |3х-4у| = 10.
По аналогии с предыдущим примером дано уравнение шестиугольника, так как прямые х=0, у=0, у=0,75х разбивают плоскость на 6 областей.
Вывод: чтобы определить вид многоугольника, нужно использовать или «метод областей» (по числу получившихся областей), или количество прямых, которые являются сторонами многоугольника. Чтобы составить уравнение многоугольника, можно так же использовать предыдущие два метода.
Литература
- Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые – М.: Наука, 1976.
- Виленкин Н.Я. Множества на координатной плоскости. Факультативный курс: Избранные вопросы математики 7 -8. – М.: Просвещение, 1978.
- Никольская И.Л. Факультативный курс по математике: учебное пособие для 7 -9 классов. – М.: Просвещение, 1991.
| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
УРАВНЕНИЯ
МНОГОУГОЛЬНИКОВ
И СПИРАЛЕЙ НА
ИХ ОСНОВЕ
А.М. Белов
Различные
геометрические
фигуры
обычно
описываются
либо
графически,
либо
словесными
формулировками.
Уравнения, не
требующие
при
применении
использования
дополнительных
словесных
формулировок,
существуют
только для
задания
прямой,
окружности,
эллипса и
фигур (линий),
получаемых
на их основе.
В число
геометрических
фигур для
описания,
которых
используются
уравнения не
входят
многоугольники.
Актуальность
получения
уравнений
многоугольников
определяется,
прежде всего,
их
практически
бесконечным
разнообразием
и
повсеместным
использованием
объектов,
имеющих
форму
различных
многоугольников.
При
этом конечно
нельзя
утверждать,
что при
описании
многоугольников
совсем не
используются
никакие
уравнения.
При описании
многоугольников
могут
использоваться
системы
линейных
уравнений,
задающих
прямые, но при
этом эти
системы
линейных
уравнений
обязательно
должны
сопровождаться
словесными
описаниями,
ограничивающими
область
применения
каждого из
входящего в
систему
уравнения
или
символами,
обозначающими
эти
словесные
описания. В
противном
случае
график такой
системы
уравнений
будет
представлять
собой не
многоугольник,
а несколько
пересекающихся
прямых линий.
Это связано с
тем, что
линейное
уравнение
без
соответствующих
словесных
пояснений не
в состоянии
определить
отдельный
отрезок или
отдельную
точку.
Таким
образом,
очевидно, что
для
составления
уравнений
многоугольников
необходимо
применять
уравнения
способные
определить
произвольный
отрезок без
использования
при этом
дополнительных
словесных
описаний.
Необходимыми
свойствами
обладает
специальное
уравнение ,
состоящее
из суммы
произведений:
[ x/xi
]*[ xi/x]*yi
. В этом
выражении: [ ] –
знак,
обозначающий
целую часть
числа и далее
по тексту
статьи
предполагает
выполнение
процедуры по
отбрасыванию
дробной
части числа ,
yi
— значение
функции при
значении
аргумента x
равном xi
.
В
работе [1] было
показано, что
на основе
использования
специального
уравнения
можно
получить
уравнения
обеспечивающие
определение
отдельных
отрезков или
линий,
состоящих из
нескольких
отрезков.
Далее
приведены
конкретные
примеры
уравнений
многоугольников
составленных
на основе
использования
специального
уравнения. В
качестве
примеров
были выбраны
треугольник
и
прямоугольник
ориентированные
по разному
относительно
координатных
осей. Не
имеющие
сторон
параллельных
координатным
осям и
имеющие
стороны
параллельные
координатным
осям. Все
уравнения
других
многоугольников
будут иметь
вид
аналогичный
виду
приведенных
ниже в
качестве
примеров
уравнений.
Сформировать
уравнения
для других
многоугольников
можно так же
по тем же
правилам, что
и для
уравнения
треугольника
или
прямоугольника.
При этом
различия
уравнений
для разных
многоугольников
будут
выражаться в
основном в их
объеме. Чем
больше
сторон имеет
многоугольник,
тем больше
объем его
уравнения.
Кроме этого
необходимо
отметить, что
многоугольники
ориентированные,
так, что хотя
бы одна их
сторона
оказывается
параллельной
оси y, могут
быть
представлены
только в виде
уравнения,
задающего
неявную
функцию.
Произвольный
треугольник,
не
содержащий
ни одной
стороны
параллельной
оси y,
однозначно
определяется
в виде
неявной
функции,
заданной
уравнением (1).
Решения
уравнения (1)
относительно
x
приведены в
виде системы
уравнений (2).
График
уравнения (1),
построенный
при
значениях
координат
вершин
треугольника
x1 = -175; x2=20;
x3=170;
y1=
-150; y2=140; y3=
-20 приведен на
рис. 1.
Произвольный
прямоугольник,
содержащий
стороны
параллельные
оси y,
определяется
в виде
неявной
функции,
заданной
уравнением (3)
для всех x и y>0.
График
уравнения (3),
построенный
при x1 = 25; x2=250;
y1= 30; y2=220
приведен на
рис. 2.
Уравнения
многоугольников
(1, 3)
обеспечивают
возможность
составления
уравнений
треугольной
и
прямоугольной
спиралей.
Треугольная
спираль
может быть
определена
системой
уравнений (4).
График
системы
уравнений (4)
приведен на
рис. 3.
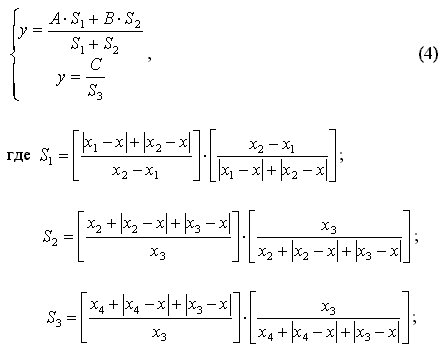
где
x01;
x02;
x03;
y01;
y02;
y03 –
координаты
вершин
начального
треугольника,
начиная с
которого
начинает
раскручиваться
спираль; D
– шаг спирали; N
– номер витка
спирали.
График
системы
уравнений (4)
на рис. 3 был
построен при x01=
-5; x02=
-1; x03=7;
y01=
-5; y02=7;
y03=
-2; D=7.
Необходимо
отметить, что
система
уравнений (4)
не является
универсальной.
Так она не
определяет
спираль, если
у начального
треугольника
одна из его
сторон будет
параллельна
оси y
и в ряде
других
случаев,
касающихся в
основном
положения
вершин
начального
треугольника
относительно
осей
координат.
Прямоугольная
спираль
может быть
определена
уравнением (5)
для всех x
и y>0.
График
системы
уравнений (5)
приведен на
рис. 4.
где
x01;
x02 и
y01;
y02
–
соответственно
координаты,
определяющие
ширину и
высоту
начального
прямоугольника,
начиная с
которого
начинает
раскручиваться
спираль; D
– шаг спирали; N
– номер витка
спирали.
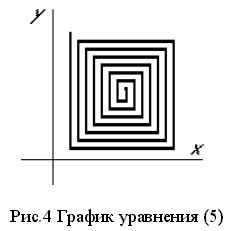
График
уравнения (5)
на рис. 4 был
построен при x01= 145; x02=
160; y01=
145; y02=170;
D=7.
Приведенные
примеры
показывают
принципиальную
возможность
задания
аналитическим
способом
уравнений
многоугольников
и спиралей на
их основе.
Необходимо
отметить, что
в уравнениях
(1), (3) и (5) нельзя
производить
дальнейшие
сокращения
точно так же,
как нельзя
заменять
выражение x/x
на 1, если
допускается,
что х может
быть равно
нулю.
Приведенные
уравнения
спиралей
можно
рассматривать
так же, как
уравнения,
задающие
фракталы, так
как каждый
виток
спирали по
форме
повторяет
предыдущие,
имея
различия
лишь в
размерах, т. е.
спирали
имеют все
основные
свойства
фракталов.
Литература
1. Белов А.М. К
вопросу
задания в
аналитическом
виде
ступенчатых
и импульсных
функций. http://www.laboratory.ru.
Читайте: Уравнение правильных многоугольников в полярных координатах
Читайте: Уравнение спиралей в виде многоугольников в полярных координатах
Выход на главную страницу
май 2003 год
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Как задать уравнением правильный многоугольник в дек-х к-х?
|
|
06/08/12 |
Здравствуйте!
|
|
|
|
|
ИСН |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
||
18/05/06 |
А какая принципиальная разница между уравнением и системой?
|
||
|
|
|||
|
Sender |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
|
14/01/11 |
|
|
|
|
|
vld |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
|
06/08/12 |
Спасибо, Sender. Но хотелось бы общую формулу получить.
|
|
|
|
|
Aritaborian |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
|
11/06/12 |
Sender , с квадратом всё ясно, но как строится формула шестиугольника? Что-то я никак не пойму…
|
|
|
|
|
Kitonum |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
|
15/03/13 |
В полярных координатах уравнение правильного n-угольника можно записать так: , где
|
|
|
|
|
ИСН |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
||
18/05/06 |
Не надо в полярных. И не надо целую часть. Можно же как сказал Sender .
|
||
|
|
|||
|
Aritaborian |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
|
11/06/12 |
Можно же как сказал Sender. Sender не раскрыл загадку.
|
|
|
|
|
ИСН |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
||
18/05/06 |
Да всё он раскрыл. Подумаешь, загадка. Вы видели когда-нибудь график функции — менее минуты назад — Забыл уточнить: трёхмерный график. (Это функция от x и y.)
|
||
|
|
|||
|
Kitonum |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
|
15/03/13 |
Не надо в полярных. И не надо целую часть. Можно же как сказал Sender . А чем не нравятся полярные координаты? Всё таки явное уравнение. На мой взгляд с ним работать удобнее, чем с неявным в декартовых. Например, построить график. Код: n:=7:
|
|
|
|
|
ИСН |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
||
18/05/06 |
Тем, что вопрос был про декартовы. А так-то к Вашему уравнению претензий нет.
|
||
|
|
|||
|
TOTAL |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
||
23/08/07 |
Так годится?
|
||
|
|
|||
|
ИСН |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
||
18/05/06 |
— менее минуты назад — Вместо третьего корня можно же сразу подставить константу.
|
||
|
|
|||
|
TOTAL |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
||
23/08/07 |
(Оффтоп) Вместо третьего корня можно же сразу подставить константу. Так мы же не стали мараться и задали произвольный многоугольник с известными координатами вершин.
|
||
|
|
|||
|
vld |
Re: Как задать уравнением правильный многоугольник в дек-х к-х?
|
|
06/08/12 |
TOTAL, да ты вообще красавчик!) Взял точку на стороне многоугольника, сложил расстояния от нее до ближайших вершин и отнял длину стороны, т.к. очевидно что нуль получается. И так получилось N похожих уравнений с правой частью равной нулю, и перемножил их! Все правильно сделал, претензий нет) — 07.02.2014, 21:47 — Да и тем более этим уравнением можно задать любой многоугольник в
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Уравнение многоугольника
Составление и решение уравнений многоугольников
Скачать:
| Вложение | Размер |
|---|---|
| составление и решение уравнений многоугольников | 124.82 КБ |
Предварительный просмотр:
Автор работы: Шпакова Маргарита Андреевна, г.о. Тольятти, МБУ СОШ
Научный руководитель: Владимирова Ольга Ивановна, учитель математики первой категории МБУ СОШ № 58.
В школьном курсе математики учащиеся часто встречаются с алгебраическими уравнениями, уравнениями прямых, уравнениями окружностей, квадратными уравнениями и т.д. Что собой представляют уравнения многоугольников, учащиеся не знают.
Как, например, выглядит уравнение треугольника? Можно ли по фигуре на плоскости составить уравнение? Можно ли рассчитать площадь фигуры по заданному уравнению? Можно ли по заданному уравнению определить, что за многоугольник? Решение этих вопросов меня и заинтересовало. В них есть проблема моей исследовательской работы.
Цель работы: изучить и исследовать на примерах методы, которые дают возможность получить уравнение с модулем любого выпуклого многоугольника на плоскости, координаты вершин которого известны. Найти взаимосвязь площади фигуры от ее уравнения.
Основные ЗАДАЧИ исследования:
- Познакомиться с некоторыми видами уравнений прямых на плоскости (уравнение прямой в отрезках, уравнение прямой, проходящей через две различные точки на плоскости);
- Научиться составлять уравнение прямой через заданную точку и параллельную другой прямой;
- Научиться составлять уравнение прямой, проходящей через две заданные точки;
- Научиться по уравнению строить многоугольник на плоскости и наоборот, по чертежу составлять уравнение многоугольника;
- Изучить метод областей при решении уравнений, содержащих знак модуля.
Как известно из курса геометрии, любая прямая на координатной плоскости может быть задана уравнением вида
Подобное уравнение называют линейным. Уравнение такого вида называют также общим уравнением прямой на плоскости.
Если ax+by+c = 0 — уравнение некоторой прямой m, то уравнение ax+by+c = p, где р ≠ 0, задает прямую m`, параллельную m. Это следует из того, что данные два уравнения не имеют общих решений, а значит, прямые не имеют общих точек.
У параллельных прямых
Пример1 . Составим уравнение прямой, проходящей через точку М (1;-2) и параллельной прямой 3x-4y+5=0
Подставляя координаты точки М в левую часть уравнения, получаем значение 16. Значит, искомым уравнением прямой будет 3x+4y+5=16 или окончательно 3x+4y-11=0.
Пусть известны координаты двух точек М 1 (x 1 ;y 2 ), М 2 (x 2 ;y 2 ), лежащих на данной прямой. Составим уравнение прямой, проходящей через две заданные точки:
(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0
Пример 2 . Составим уравнение прямой, проходящей через точку М 1 (3;1) и М 2 (2;2).
Получаем такое уравнение (x-3)(2-1)-(y-1)(2-3)=0
после преобразований выходит х+у-4=0.
Если известны координаты (а;0) и (0;b) точек пересечения прямой с осями Ох и Оу, то для этой прямой проще всего записать уравнение в отрезках + = 1.
Рассмотрим на координатной плоскости ху треугольник с вершинами в точках А (х 1 ;у 1 ), В (х 2 ;у 2 ), С (х 3 ;у 3 ). Уравнение прямой, на которой лежит сторона АВ этого треугольника, можно записать в виде
(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0.
Подставим координаты третьей вершины С (х 3 ;у 3 ) в левую часть этого уравнения,
получим некоторое значение
q=(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )
Чтобы понять геометрический смысл числа q, заметим, что уравнение
(х-х 1 )(у 2 -у 1 )-(у-у 1 )(х 2 -х 1 )=q задает прямую, параллельную стороне АВ данного треугольника. Поэтому для каждой точки этой прямой результат подстановки ее координат в левую часть уравнения тот же, что и для точки C (х 3 ;у 3 ), и дает число q. Значит, то же значение получится и для точки С 1 (х 4 ;у 1 ) пересечения упомянутой прямой с прямой у=у 1 , параллельной оси абсцисс и проходящей через вершину A треугольника. Но в этой точке
(х-х 1 )(у 2 -у 1 )-(у-у 2 )(х 2 -х 1 ) = (х 4 -х 1 )(у 2 -у 1 ). Геометрический смысл последнего выражения понять уже несложно: |(х 4 -х 1 )(у 2 -у 1 )| площадь параллелограмма со сторонами АВ и АС 1 . Длина стороны АС 1 равна |х 4 -х 1 |, а длина высоты параллелограмма, опущенной из вершины B на эту сторону, есть |у 2 -у 1 |. Поэтому |q| есть площадь ΔАВС 1 , но она такая же, что и у ΔАВС. В результате приходим к следующей формуле для площади треугольника
S = |(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )|. (3, стр. 169).
Если треугольник задан в декартовой системе координат и имеет своими вершинами точки А (х 1 ;у 1 ), В (х 2 ;у 2 ), С (х 3 ;у 3 ), то можно составить уравнение треугольника:
|(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )| + |(x-x 2 )(y 3 -y 2 )-(y-y 2 )(x 3 -x 2 )| +
+ |(x-x 3 )(y 1 -y 3 )—(y-y 3 )(x 1 -x 3 )| = 2S, где
S = |(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )|.
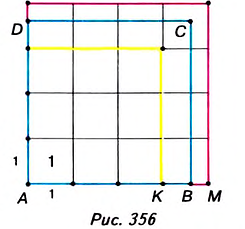
Пример 3 . Составим уравнение треугольника, изображенного на рисунке. Для этого составим уравнения прямых, которые являются его сторонами, по формуле
(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0, задающей уравнение прямой по двум ее точкам. При этом допустимым считаем раскрытие скобок и приведение подобных слагаемых и недопустимым – умножение обеих частей уравнения на некоторое число (за исключением -1) .
Уравнения сторон имеют вид: х-у+1=0, х+у-1=0, 2у=0. Сложив модули левых частей этих уравнений, и приравняв полученное выражение к удвоенной площади ΔАВС, равной в данном случае 1, приходим к искомому уравнению |x-y+1|+|x+y-1|+2|y|=2.
Описанный метод дает возможность получить уравнение любого выпуклого многоугольника на плоскости, координаты вершин которого известны.
Уравнение квадрата, ромба
Пример 4 . Составить уравнение квадрата:
|x-1| + |y-1| + |x| + |y| = 1. Площадь равна 1.
Пример 5 . Составить уравнение ромба:
Через точки с координатами (1;0), (0;1) уравнение прямой: x +y -1 = 0.
Через точки с координатами (-1;0), (0;1) уравнение прямой: x – y + 1 = 0.
Через точки с координатами (-1;0), (0;-1) уравнение прямой: x + y + 1 = 0.
Через точки с координатами (0;-1), (1;0) уравнение прямой: -x + y + 1 = 0.
Получили: | x + y — 1| + | x – y + 1| + | x + y + 1| + | -x + y + 1 | = 4.
Этот же ромб имеет другое уравнение: |х| + |у| = 1, которое лучше решать «методом областей». Площадь ромба равна 2.
Пример 6 . Докажите, что уравнения: |x + y| + |x — y| = 2 и |x + 1| + |y + 1| + |x -1| +|y — 1| =4 относятся к одному квадрату.
Первое уравнение лучше решать «методом областей», где вся плоскость разбивается прямыми у =-х и у=х на четыре области, значит, искомая фигура четырехугольник, стороны которого параллельны осям координат. Из уравнений каждой области у=1, х=1и т.д. понимаем, что это квадрат, площадь которого равна 4.
Второе уравнение наглядно изображено, подтверждая первое.
Пример 7. Определить вид многоугольника по уравнениям:
|х| + 3|у| = 6; |х-3| + |у+3| = 3; |х-1| + 7|у| = 1.
Во всех случаях даны уравнения ромба .
Пример 8 . Изобразить на плоскости многоугольник по данному уравнению: |x|+|y|+|x+y|=4.
Из данного уравнения следует, что х=0, у=0, х= -у –прямые, которые разбивают плоскость на несколько областей.
Найдем уравнение прямой, стороны многоугольника, в каждой из областей:
Уравнение квадрата в декартовой системе координат.
Проанализируем расположение квадрата на координатной плоскости.
В общем случае уравнение квадрата в декартовой (прямоугольной) системе координат принимает вид:
где точка О`(a;b) – точка пересечения диагоналей квадрата;
d – длина диагонали квадрата.
В частном случае, когда точка О(0;0) — начала координат, является одновременно и точкой пересечения диагоналей квадрата, уравнение квадрата принимает вид:
где d– длина диагонали квадрата.
Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 



Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию




Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://www.calc.ru/Uravneniye-Kvadrata-V-Dekartovoy-Sisteme-Koordinat.html
http://www.evkova.org/krivyie-vtorogo-poryadka
Содержание:
Изучив материал этой лекции, вы узнаете формулу, с помощью которой можно найти сумму углов выпуклого многоугольника.
- Вы расширите свои представления о такой знакомой вам величине, как площадь.
- Вы научитесь находить площадь параллелограмма, треугольника, трапеции.
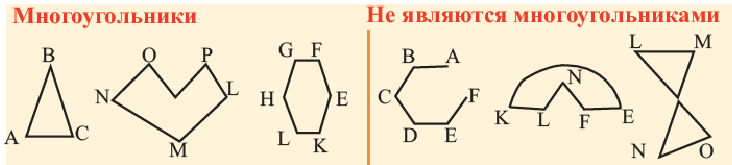
Определение многоугольников
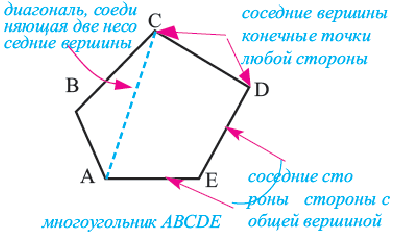
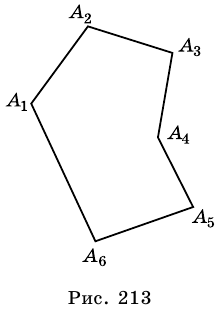
Рассмотрим фигуру, состоящую из точек
Фигура, образованная этими отрезками, ограничивает часть плоскости, выделенную на рисунке 195 зеленым цветом. Эту часть плоскости вместе с отрезками 
Стороны, являющиеся соседними отрезками, называют соседними сторонами многоугольника. Вершины, являющиеся концами одной стороны, называют соседними вершинами многоугольника.
Две соседние стороны многоугольника образуют угол многоугольника. Например, на рисунке 196 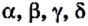
Многоугольник называют по количеству его углов: треугольник, четырехугольник, пятиугольник и т. п.
Многоугольник обозначают по его вершинам. Например, на рисунке 197 изображен пятиугольник ABCDE. В обозначении многоугольника буквы, стоящие рядом, соответствуют соседним вершинам. Например, пятиугольник, изображенный на рисунке 197, можно обозначить еще и так: CDEAB, EABCD, EDCBA и т. д.
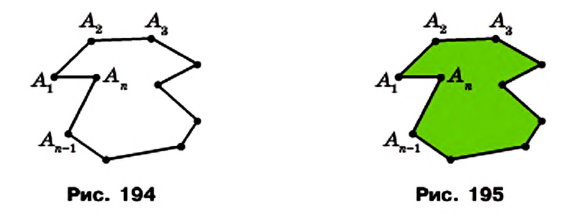
Периметром многоугольника называют сумму длин всех его сторон.
Отрезок, соединяющий несоседние вершины многоугольника, называют диагональю. Например, на рисунке 198 отрезок АЕ — диагональ шестиугольника ABCDEF.
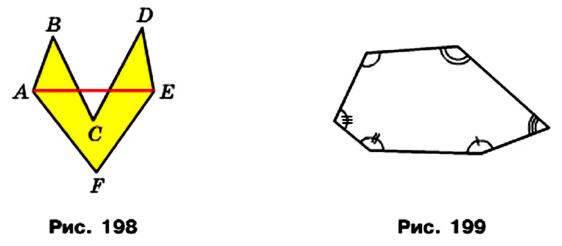
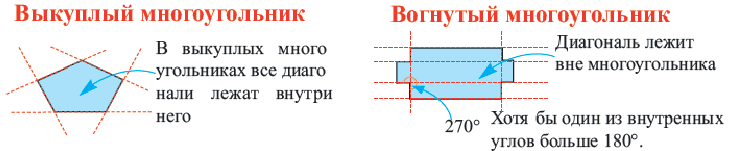
На рисунке 199 изображен многоугольник, все углы которого меньше развернутого. Такой многоугольник называют выпуклым. Из сказанного следует, что любой треугольник является выпуклым многоугольником. Заметим, что многоугольники, изображенные на рисунках 196-198, не являются выпуклыми.
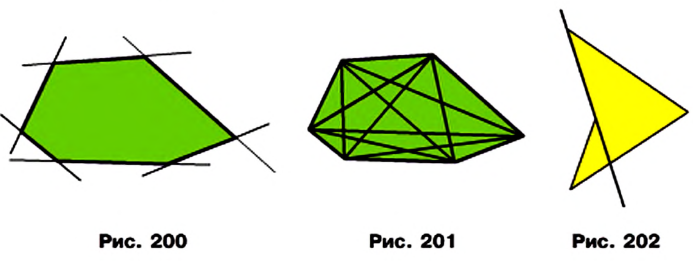
Выпуклый многоугольник обладает такими свойствами:
- выпуклый многоугольник расположен в одной полуплоскости относительно любой прямой, содержащей его сторону (рис. 200);
- выпуклый многоугольник, отличный от треугольника, содержит любую свою диагональ (рис. 201).
Если многоугольник не является выпуклым, то он такими свойствами не обладает (рис. 198, 202).
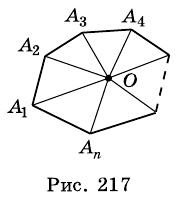
Теорема 19.1. Сумма углов выпуклого n-угольника равна
Доказательство. Для случая n = 3 теорема была доказана в 7 классе (теорема 16.1).
Пусть 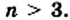
Докажем, что сумма всех его углов равна 180° (n-2).
Проведем все его диагонали, выходящие из вершины 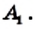
Отметим, что эта теорема справедлива и для любого многоугольника, не являющегося выпуклым.
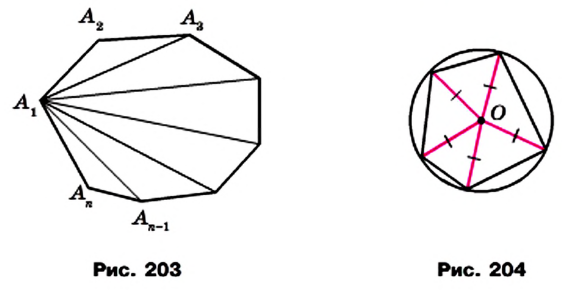
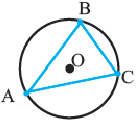
Определение. Окружность называют описанной около многоугольника, если она проходит через все его вершины.
На рисунке 204 изображена окружность, описанная около многоугольника. В этом случае также говорят, что многоугольник вписан в окружность.
Центр окружности, описанной около многоугольника, равноудален от всех его вершин. Следовательно, этот центр принадлежит серединным перпендикулярам всех сторон многоугольника, вписанного в окружность.
Около многоугольника можно описать окружность, если существует точка, равноудаленная от всех его вершин. Следовательно, если серединные перпендикуляры всех сторон многоугольника пересекаются в одной точке, то около такого многоугольника можно описать окружность.
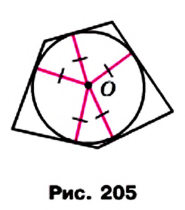
Определение. Окружность называют вписанной в многоугольник, если она касается всех его сторон.
На рисунке 205 изображена окружность, вписанная в многоугольник. В этом случае также говорят, что многоугольник описан около окружности.
Центр окружности, вписанной в многоугольник, равноудален от всех его сторон. Следовательно, этот центр принадлежит биссектрисам всех углов многоугольника, описанного около окружности.
Понятие площади многоугольника. Площадь прямоугольника
С такой величиной, как площадь, вы часто встречаетесь в повседневной жизни: площадь квартиры, площадь дачного участка, площадь поля и т. п.
Опыт подсказывает вам, что равные земельные участки имеют равные площади, что площадь квартиры равна сумме площадей всех ее помещений (комнат, кухни, коридора и т. д.).
Вы знаете, что площади земельных участков измеряют в сотках (арах) и гектарах; площади регионов и государств — в квадратных километрах; площадь квартиры — в квадратных метрах.
На этих практических знаниях о площади основывается определение площади многоугольника.
Определение. Площадью многоугольника называют положительную величину, которая обладает следующими свойствами:
- равные многоугольники имеют равные площади;
- если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
- за единицу измерения площади принимают единичный квадрат, то есть квадрат со стороной, равной единице измерения длины.
Измерить площадь многоугольника — это значит сравнить его площадь с площадью единичного квадрата. В результате получают числовое значение площади данного многоугольника. Это число показывает, во сколько раз площадь данного многоугольника отличается от площади единичного квадрата.
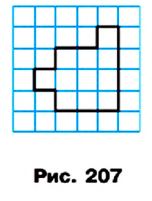
Например, если клетку вашей тетради принять за единичный квадрат, то площадь многоугольника, изображенного на рисунке 207, будет равна 11 квадратным единицам (кратко записывают: 11 ед.2).
Обычно для нахождения площади используют формулы, то есть вычисляют площадь многоугольника по определенным элементам (сторонам, диагоналям, высотам и т. д.). Некоторые из формул вы уже знаете. Например, вы неоднократно применяли формулу S = ab, где S — площадь прямоугольника, а и b — длины его соседних сторон.
Для доказательства этой формулы потребуется следующая лемма.
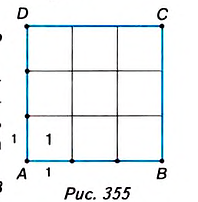
Лемма. Площадь квадрата со стороной 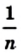
Доказательство. Рассмотрим единичный квадрат и разделим его на 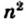
Из определения площади многоугольника (свойство 1) следует, что все эти квадраты имеют равные площади. По свойству 2 сумма площадей этих квадратов равна площади единичного квадрата, то есть 1 ед.2. Поэтому площадь каждого маленького квадрата равна
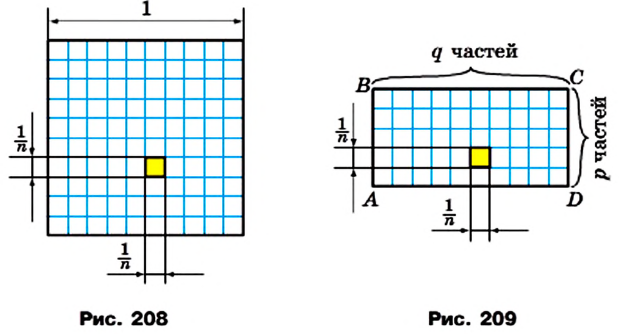
Теорема 20.1. Площадь прямоугольника равна произведению длин его соседних сторон.
Доказательство. На рисунке 209 изображен прямоугольник ABCD, длины соседних сторон которого равны a и b: АВ = а, ВС = b. Докажем для случая, когда а и b — рациональные числа, что площадь S прямоугольника вычисляют по формуле S = ab.
Числа а и b представим в виде обыкновенных дробей с одинаковыми знаменателями:
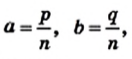
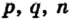
Разделим сторону АВ на р равных частей, а сторону ВС — на q равных частей. Через точки деления проведем прямые, параллельные сторонам прямоугольника. Тогда прямоугольник будет разделен на 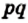
Согласно лемме площадь каждого квадрата равна 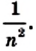
Рассмотрение случая, когда хотя бы одно из чисел а или b является иррациональным, выходит за рамки школьного курса геометрии.
Определение. Многоугольники, имеющие равные площади, называют равновеликими.
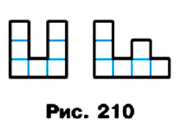
Из определения площади (свойство 1) следует, что все равные фигуры равновелики. Однако не все фигуры, имеющие равные площади, являются равными. Например, на рисунке 210 изображены два многоугольника, каждый из которых составлен из семи единичных квадратов. Эти многоугольники равновелики, но не равны.
Площадь параллелограмма
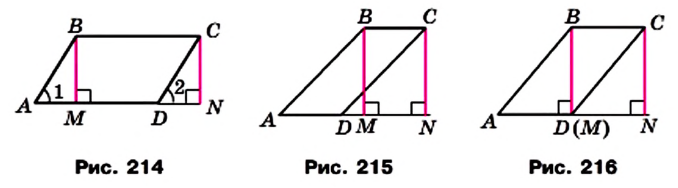
Теорема 21.1. Площадь параллелограмма равна произведению его стороны и высоты, проведенной к этой стороне.
Доказательство. На рисунке 214 изображены параллелограмм ABCD, площадь которого равна S, и его высота ВМ. Докажем, что S = ВС • ВМ.
Проведем высоту CN. Легко показать (сделайте это самостоятельно), что четырехугольник MBCN — прямоугольник. Покажем, что он равновелик данному параллелограмму.
Площадь параллелограмма равна сумме площадей треугольника АВМ и трапеции MBCD. Площадь прямоугольника равна сумме площадей указанной трапеции и треугольника DCN. Однако треугольники АВМ и DCN равны по гипотенузе и острому углу (отрезки АВ и CD равны как противолежащие стороны параллелограмма, углы 1 и 2 равны как соответственные при параллельных прямых АВ и DC и секущей AD). Значит, эти треугольники равновелики. Отсюда следует, что параллелограмм ABCD и прямоугольник MBCN равновелики.
По теореме 20.1 площадь прямоугольника MBCN равна произведению длин сторон ВС и ВМ. Тогда S = ВС • ВМ, где S — площадь параллелограмма ABCD.
Для завершения доказательства надо рассмотреть случаи, когда основание М высоты ВМ не будет принадлежать стороне AD (рис. 215) или совпадет с вершиной D (рис. 216). И в этом случае параллелограмм ABCD и прямоугольник MBCN будут равновеликими. Докажите этот факт самостоятельно.
Если обозначить длины стороны параллелограмма и проведенной к ней высоты соответственно буквами а и h, то площадь S параллелограмма вычисляют по формуле
Площадь треугольника
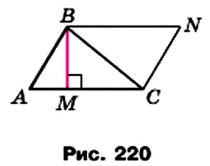
Теорема 22.1. Площадь треугольника равна половине произведения его стороны и проведенной к ней высоты.
Доказательство. На рисунке 220 изображены треугольник АВС, площадь которого равна S, и его высота ВМ. Докажем, что
Через вершины В и С треугольника проведем прямые, параллельные сторонам АС и АВ соответственно (рис. 220). Пусть эти прямые пересекаются в точке N. Четырехугольник ABNC — параллелограмм по определению. Треугольники АВС и NCB равны (докажите это самостоятельно). Следовательно, равны и их площади. Тогда площадь треугольника АВС равна половине площади параллелограмма ABNC. Высота ВМ треугольника АВС является также высотой параллелограмма
ABNC. Отсюда
Если воспользоваться обозначениями для высот и сторон треугольника АВС, то согласно доказанной теореме имеем:
где S — площадь треугольника.
Следствие. Площадь прямоугольного треугольника равна половине произведения его катетов.
Докажите эту теорему самостоятельно.
Пример №1
Докажите, что площадь ромба равна половине произведения его диагоналей.
Решение:
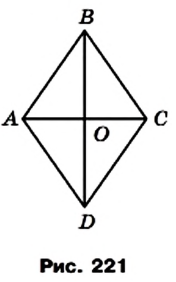
На рисунке 221 изображен ромб ABCD, площадь которого равна S. Его диагонали АС и BD пересекаются в точке О. Докажем, что
Поскольку диагонали ромба перпендикулярны, то отрезки АО и СО являются высотами треугольников BAD и BCD соответственно. Тогда можно записать:
Площадь трапеции
Теорема 23.1. Площадь трапеции равна произведению полусуммы ее оснований и высоты.
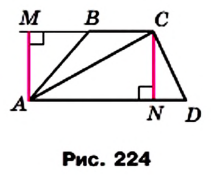
Доказательство. На рисунке 224 изображена трапеция ABCD (AD||BC), площадь которой равна S. Отрезок CN — высота этой трапеции. Докажем, что
Проведем диагональ АС и высоту AM трапеции. Отрезки AM и CN являются высотами треугольников АВС и ACD соответственно.
Имеем:
Если обозначить длины оснований трапеции и ее высоты соответственно буквами 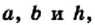
Следствие. Площадь трапеции равна произведению ее средней линии и высоты.
Равносоставленные и равновеликие многоугольники
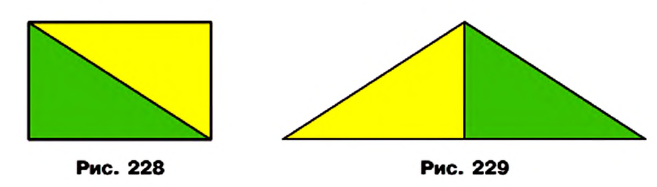
Если некоторый многоугольник можно разрезать на части и составить из них другой многоугольник, то такие два многоугольника называют равносоставленными.
Например, если прямоугольник разрезать вдоль его диагонали (рис. 228), то получим два равных прямоугольных треугольника, из которых можно составить равнобедренный треугольник (рис. 229). Фигуры на рисунках 228 и 229 — равно составленные.
Очевидно, что равносоставленные многоугольники являются равновеликими. Этот факт применяют при доказательстве теорем и решении задач. Например, доказывая теорему 21.1, мы фактически разрезали параллелограмм на треугольник АВМ и трапецию MBCD, из которых составили прямоугольник MBCN (см. рис. 215).
Если треугольник разрезать вдоль средней линии, то из полученных треугольника и трапеции можно составить параллелограмм (рис. 230).
Легко установить (сделайте это самостоятельно), что такое разрезание треугольника приводит к еще одному доказательству теоремы о площади треугольника (теорема 22.1). Этой же цели служит разрезание треугольника на части, из которых можно составить прямоугольник (рис. 231).
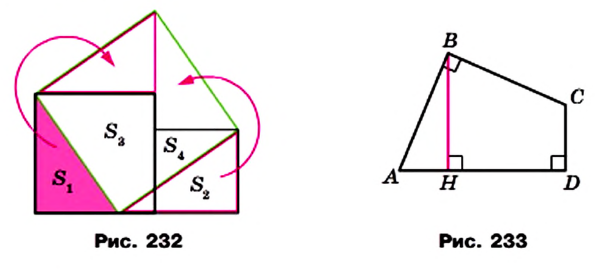
Евклид в своей знаменитой книге «Начала» формулирует теорему Пифагора так:
«Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах».
Если показать, что можно разрезать квадраты, построенные на катетах, на части и составить из этих частей квадрат со стороной, равной гипотенузе, то тем самым будет доказана теорема Пифагора.
На рисунке 232 показан один из возможных способов такого разрезания. Квадраты, построенные на катетах, разрезаны на части, площади которых равны 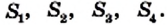
Из определения площади многоугольника следует, что равносоставленные многоугольники являются равновеликими. Но совсем неочевидной является такая теорема.
Теорема. Любые два равновеликих многоугольника являются равносоставленными.
Впервые этот факт доказал в 1832 г. венгерский математик Фаркаш Бойяи. Позднее немецкий математик Пауль Гервин нашел другое доказательство. Поэтому эту теорему называют теоремой Бойяи—Гервина.
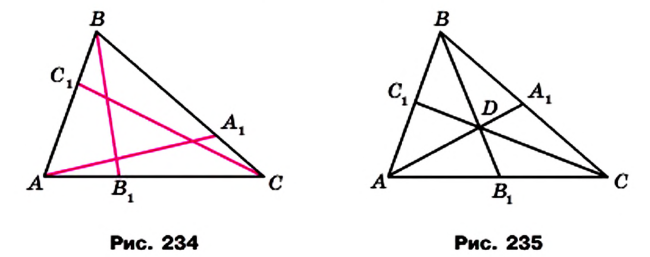
Теорема Чевы
На сторонах ВС, СА и АВ треугольника АВС отметим произвольные точки 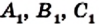
Если точки 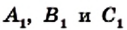
Если три прямые пересекаются в одной точке, то их называют конкурентными.
Теорема Чевы дает общий критерий конкурентности произвольных трех чевиан.
Теорема. Для того чтобы, чевианы 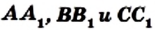
Доказательство. Докажем сначала необходимое условие конкурентности: если чевианы 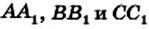
Воспользовавшись результатом ключевой задачи 757, можно записать (рис. 235):
Перемножив записанные равенства, получим равенство (*).
Докажем теперь достаточное условие конкурентности: если выполняется равенство (*), то чевианы 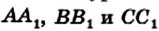
Пусть чевианы 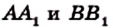
Сопоставляя это равенство с равенством (*), приходим к выводу, что 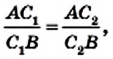
Напомню:
Сумма углов выпуклого n-угольника
Сумма углов выпуклого n-угольника равна 180° (n — 2).
Окружность, описанная около многоугольника
Окружность называют описанной около многоугольника, если она проходит через все его вершины.
Окружность, вписанная в многоугольник
Окружность называют вписанной в многоугольник, если она касается всех его сторон.
Площадь многоугольника
Площадью многоугольника называют положительную величину,
которая обладает следующими свойствами:
- равные многоугольники имеют равные площади;
- если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
- за единицу измерения площади принимают единичный квадрат, то есть квадрат со стороной, равной единице измерения длины.
Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон.
Равновеликие многоугольники
Многоугольники, имеющие равные площади, называют равновеликими.
Площадь параллелограмма
Площадь параллелограмма равна произведению его стороны и высоты, проведенной к этой стороне.
Площадь треугольника
Площадь треугольника равна половине произведения его стороны и проведенной к ней высоты.
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника равна половине произведения его катетов.
Площадь трапеции
- Площадь трапеции равна произведению полусуммы ее оснований и высоты.
- Площадь трапеции равна произведению ее средней линии и высоты.
Ломанная линия и многоугольники
Ломаная линия состоит из таких нескольких последовательно-соединенных отрезков: конец первого является началом второго, конец второго является началом третьего и т.д. Если конечная точка последнего отрезка совпадает с начальной точкой первого отрезка, то ломаная называется замкнутой. Многоугольник — это фигура, образованная замкнутой ломаной линией, в которой смежные отрезки не лежат на одной прямой, а несмежные — не пересекаются.
- Многоугольник — это плоская фигура.
- Стороны состоят из конечного числа отрезков.
- Многоугольник это замкнутая фигура, делящая плоскость на 2 части: внутреннюю замкнутую область и внешнюю бесконечную область.
- Многоугольник обозначают буквами, указывающими его вершины.
Многоугольники бывают выпуклые и вогнутые. Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой содержащей его сторону. Если не лежит в одной полуплоскости — вогнутым.
Многоугольник называется правильным, если у него все стороны все углы конгруэнтны.
В многоугольнике количество вершин, сторон и углов одинаковые. Многоугольник с 
Соответственно количеству сторон, многоугольники называются треугольными, четырехугольными, пятиугольными, шестиугольными т.д. Из любой вершины выпуклого 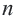
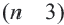
Внутренние и внешние углы многоугольника
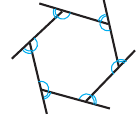
Угол, образованный двумя сторонами, исходящими из данной вершины называется внутренним углом при данной’ вершине выпуклого многоугольника. Угол, смежный с внутренним углом многоугольника называется внешним. Сумма внутренних и внешних углов (взятых по одному при каждой вершине) многоугольника при любой вершине равна 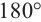
Теорема 1. Сумма внутренних углов выкуплого 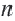
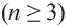
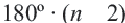
Следствие: Каждый внутренний угол правильного 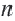
Теорема 2. Сумма внешних углов выкуплого многоугольника равен 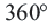
Следствие 2. Каждый внешний угол правильного 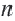
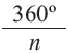
Пример №2
Один из внешних углов правильного многоугольника равен 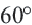
a) найдите градусную меру внутреннего угла многоугольника;
b) найдите число сторон многоугольника.
Решение: а) 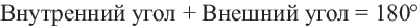
Внутренний угол:
b)
Многоугольники вписанные в окружность и описанные около окружности
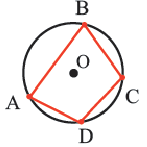
Определение 1. Многоугольник называется вписанным в окружность, если все его вершины лежат на окружности, а окружность называется описанной около многоугольника. На рисунке треугольник 
Определение 2. Многоугольник называется описанным около окружности, если все его стороны касаются окружности, а окружность называется вписанной в многоугольник. На рисунке четырехугольник 
Окружность, вписанная в треугольник и описанная около нее
Теорема 1. В любой треугольник можно вписать окружность. Центром этой окружности будет точка пересечения биссектрис углов треугольника.
Теорема 2. Около любого треугольника можно описать окружность. Центром этой окружности будет точка пересечения серединных перпендикуляров к сторонам треугольника.
Теорема 3. Если в окружность вписан прямоугольный треугольник, то гипотенуза является диаметром этой окружности.
Обратная теорема. Если сторона треугольника, вписанного в окружность, является диаметром, то этот треугольник — прямоугольный.
Доказательство 1-ой теоремы (текстовое). Проведем биссектрисы углов 



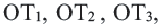
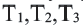
Доказательство 2-ой теоремы. Через середины сторон 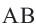
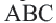

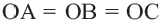
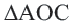

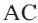

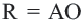
Замечание: Около данного треугольника можно описать только одну окружность. В данную окружность можно вписать бесконечное количество треугольников.
Свойства четырехугольников, вписанных в окружность и описанного около нее
В отличие от треугольников, не во всякий четырехугольник можно вписать или описать окружность.
Теорема 4. В любом описанном четырехугольнике суммы противоположных сторон равны.
Обратная теорема. Если суммы противоположных сторон четырехугольника равны, то в этот четырехугольник можно вписать окружность.
Теорема 5. Сумма двух противоположных углов четырехугольника, вписанного в окружность, равна
Обратная теорема. Если сумма противоположных углов четырехугольника равна 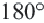
Доказательство теоремы 4: Пусть точки 
Если сложить почленно эти равенства, получим 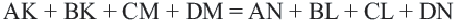
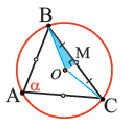
Отношение стороны треугольника, вписанного в окружность, к синусу противолежащего угла равно диаметру этой окружности:
Исследуйте данное доказательство для случая, когда центр окружности расположен внутри треугольника, обсудите и напишите в тетради.
В любой правильный многоугольник можно вписать и описать окружность. Центры этих окружностей совпадут. Биссектрисы углов правильного многоугольника пересекаются в точке 
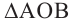
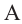
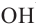
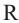
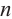
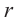
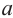
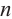
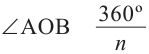
Задача на построение: Постройте правильный шестиугольник.
1. Нарисуйте отрезок 
2. Циркулем нарисуйте окружность, радиус которой равен длине этого отрезка.
3. Не меняя раствора циркуля, разбейте всю окружность на части одинаковой длины и отметьте их точками.
4. Соедините последовательно отмеченные точки. Получится правильный шестиугольник, вписанный в окружность.
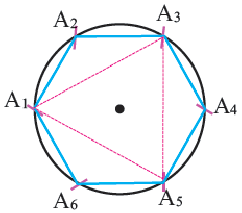
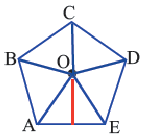
Если соединить попарно некоторые вершины правильного шестиугольника 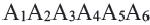
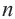
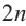
Площадь правильного многоугольника
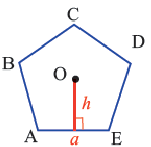
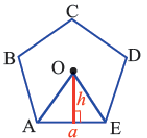
Центр правильного многоугольника. Центр окружности, описанного около правильного многоугольника или вписанного в него, является центром правильного многоугольника. Центр правильного многоугольника находится на одинаковом расстоянии от всех вершин и всех сторон многоугольника.
Апофема правильного многоугольника. Перпендикуляр, проведенный из центра многоугольника к его стороне, называется апофемой. Апофема правильного многоугольника равна радиусу вписанной окружности.
Выполните следующее упражнение по шагам и выведите формулу зависимости площади правильного многоугольника от апофемы.
1. Нарисуйте правильный пятиугольник 
2. Из центра 

3. Соедините точки 
4. Выразите площадь треугольника 
5. Соедините точки 
6. Обратите внимание на то, что площадь пятиугольника равна сумме площадей этих треугольников. Площадь пятиугольника:
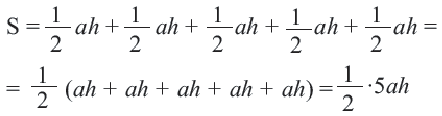
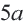
Площадь правильного многоугольника:
Соединив центр правильного 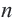
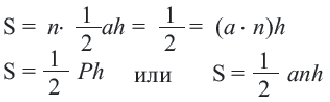
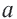

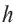
Пример №3
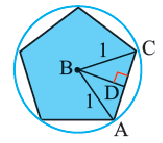
В окружность радиусом равным единице, вписан правильный пятиугольник. Найдите площадь пятиугольника. Решение:
Площадь многоугольника:
Нужно найти апофему 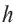
Центральный угол 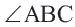
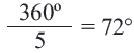
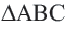
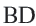
Тогда 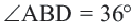

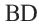
Сторона пятиугольника:

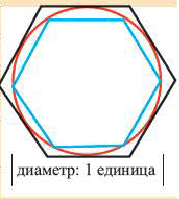
Историческое сведение. В 3-ем веке до н.э. Архимед — древнегреческий ученый, для того, чтобы определить численное значение 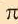
1. Принимая за единицу диаметр окружности, найдите периметр вписанного шестиугольника.
2. Покажите, что длина окружности с единичным диаметром равна 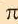
3. Нарисуйте радиус окружности. Найдите периметр описанного шестиугольника.
4. Напишите неравенство: 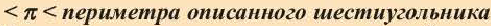
Увеличив число сторон многоугольника в 2 раза и продолжая вычисления для 12-ти, а затем для 96-ти угольного многоугольника Архимед, определил, что значения 
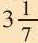
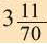
Паркетирование
Паркетированием называется покрытие площади фигурами до заполнения всей пустоты.
Если сумма углов при общей вершине многоугольника равна 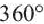
Справочный материал по многоугольникам
Многоугольник и его элементы.
Сумма углов выпуклого многоугольника. многоугольник, вписанный в окружность, и многоугольник, описанный около окружности.
Рассмотрим фигуру 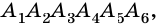
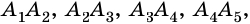
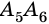
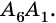
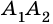
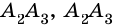

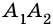
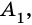

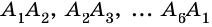
Очевидно, что количество вершин многоугольника равно количеству его сторон.
Сумму длин всех сторон многоугольника называют его периметром.
Наименьшее количество вершин (сторон) у многоугольника — три. В этом случае имеем треугольник. Еще одним отдельным видом многоугольника является четырехугольник.
Многоугольник, у которого 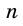
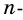
Две стороны многоугольника называют соседними, если они имеют общую вершину. Стороны многоугольника, не имеющие общей вершины, называют несоседними. Например, стороны 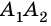
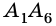
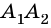
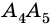
Две вершины многоугольника называют соседними, если они принадлежат одной стороне, а вершины многоугольника, не принадлежащие одной стороне, называют несоседними.
Например, вершины 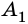
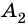
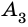
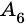
Отрезок, соединяющий две несоседние вершины многоугольника, называют диагональю многоугольника. На рисунке 214 изображены диагонали многоугольника 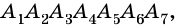
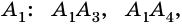
Пример №4
Сколько диагоналей имеет 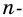
Решение:
Из каждой вершины 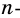

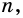
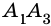
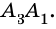
Ответ.
Углы, стороны которых содержат соседние стороны многоугольника, называют углами многоугольника. Пятиугольник 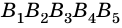
Если каждый из углов многоугольника меньше развернутого, то такой многоугольник называют выпуклым. Если хотя бы один угол многоугольника больше развернутого, то такой многоугольник называют невыпуклым.
Многоугольник 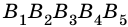
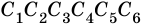
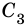
Теорема (о сумме углов выпуклого 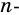
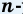
Доказательство:
Выберем во внутренней области многоугольника произвольную точку 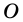
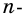
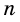
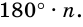
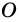
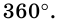
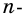
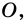
Углы выпуклого многоугольника называют еще его внутренними углами. Угол, смежный с внутренним углом многоугольника, называют внешним углом многоугольника. На рисунке 218 угол 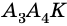
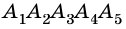
Очевидно, что каждый многоугольник имеет по два внешних угла при каждой вершине.
Пример №5
Докажите, что сумма внешних углов выпуклого 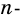
Решение:
Сумма внутреннего и внешнего углов при каждой вершине многоугольника равна 180°. Поэтому сумма всех внутренних и внешних углов 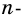
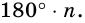
Многоугольник называют вписанным в окружность, если все его вершины лежат на окружности. Окружность при этом называют описанной около многоугольника (рис. 219).
Около многоугольника не всегда можно описать окружность. Если же это возможно, то центром такой окружности является точка пересечения серединных перпендикуляров к сторонам многоугольника (как и в случае треугольника).
Многоугольник называют описанным около окружности, если все его стороны касаются окружности. Окружность при этом называют вписанной в многоугольник (рис. 220).
Не в каждый многоугольник можно вписать окружность. Если же это возможно, то центром такой окружности является точка пересечения биссектрис внутренних углов многоугольника (как и в случае треугольника).
Многоугольник и его свойства
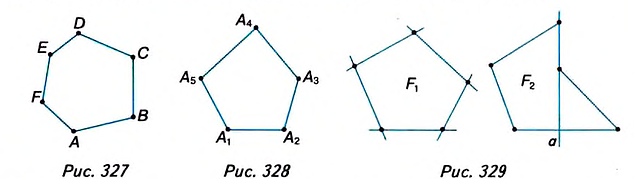
Вы уже знаете, что такое треугольник и четырёхугольник. Более общим является понятие многоугольника. На рисунке 327 вы видите многоугольник ABCDEF. Он состоит из отрезков АВ, ВС, CD, DE, EFy FA, размещённых таким образом, что смежные отрезки не лежат на одной прямой, а несмежные -не имеют общих точек. Отрезки, из которых состоит многоугольник, называются его сторонами, углы, образованные смежными сторонами, — углами, а вершины этих углов — вершинами многоугольника.
В зависимости от количества вершин (углов либо сторон) многоугольник называется треугольником, четырёхугольником, пятиугольником и т. д. Многоугольник с n вершинами называется n-угольником.
Многоугольник обозначают названиями его вершин, например шестиугольник ABCDEF (рис. 327), пятиугольник 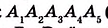
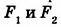
Ни одна из прямых, проходящих через стороны многоугольника 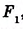
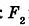
В дальнейшем мы будем рассматривать лишь выпуклые многоугольники.
Периметром многоугольника называется сумма длин всех его сторон. Его обозначают буквой Р.
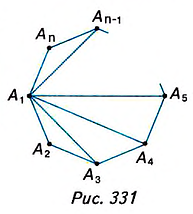
Посмотрите на рисунок 330. В шестиугольнике ABCDEF отрезки AC, AD, АЕ соединяют вершину А с несоседними вершинами. Это — диагонали шестиугольника.
Диагональю n-угольника называется отрезок, который соединяет две несоседние его вершины.
Теорема (о сумме углов n-угольника).
Сумма углов n-угольника равна 180° • (n — 2).
Дано: 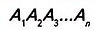
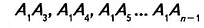
Доказательство. В заданном n-угольнике диагонали 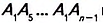
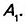
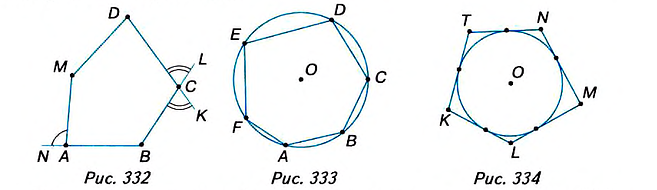
Угол, смежный с углом многоугольника (рис. 332), называется внешним углом многоугольника.
Многоугольники могут быть вписанными в окружность (рис. 333) или описанными около окружности (рис. 334). Попытайтесь дать определения и сравните их с указанными в учебнике.
Многоугольник все вершины которого лежат на окружности, называется вписанным, в эту окружность, а окружность — описанной около этого многоугольника.
Многоугольнику все стороны которого касаются окружности, называется описанным около этой окружности, а окружность — вписанной в этот многоугольник.
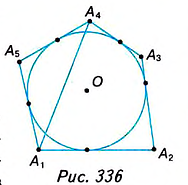
Стороны вписанного многоугольника и его диагонали — это хорды окружности. Каждый его угол является вписанным углом (рис. 335).
Стороны описанного многоугольника являются касательными к окружности, а его диагонали — секущими (рис. 336).
1. Геометрическая фигура называется простой, если её можно разбить на конечное количество треугольников. Многоугольник — это простая фигура (см. рис. 330 и 331), а окружность не является простой фигурой (рис. 337). Даже вписав в окружность многоугольник с очень большим количеством сторон, мы только приблизим его контур к окружности. Поэтому в геометрии длину окружности и площадь круга находят другими методами, чем периметр и площадь многоугольника.
2. У вас может возникнуть вопрос: Всегда ли из равенства сторон многоугольника следует равенство его углов и наоборот? Нет, это свойство лишь треугольника. Вы знаете пример четырёхугольника, в котором все стороны равны, а углы — не равны. Это ромб. В прямоугольнике все углы равны, а вот стороны — нет. Среди многоугольников с большим количеством вершин также можно выделить равносторонние многоугольники, в которых не все углы равны (рис. 338), и равноугольные многоугольники, в которых не все стороны равны
Понятие площади
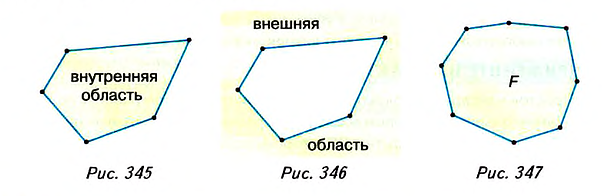
Многоугольник разбивает плоскость на две области — внутреннюю (рис. 345) и внешнюю (рис. 346).
Многоугольник вместе с его внутренней областью называется плоским многоугольником.
Каждый плоский многоугольник (например, многоугольник F на рис. 347) занимает часть плоскости. Если эту часть плоскости выразить некоторым числом, то получим площадь многоугольника. Далее будем говорить «площадь многоугольника», имея в виду, что многоугольник -плоский. Это относится и к другим плоским фигурам.
Площадь обозначают буквой S. Иногда указывают название фигуры, например 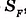
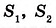
На рисунке 348 фигуры 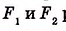
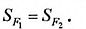
Единицы измерения площади кратко записываем так: 1 см2, а говорим: «один квадратный сантиметр». Говорить «сантиметр в квадрате» -неправильно!
Некоторые единицы измерения площади имеют специальные названия: ар (квадрат со стороной 10м), гектар (квадрат со стороной 100 м) и т. д.
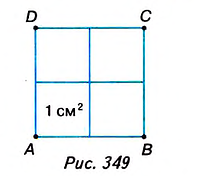
На рисунке 349 вы видите квадрат ABCD со стороной 2 см. Он состоит из четырёх квадратов площадью 1 см2, поэтому его площадь равна 4 см2.
Можем записать:
Ясно, что площадь любой фигуры выражается положительным числом. Изменится ли площадь квадрата ABCD, если за единицу измерения принять 1 мм2? Нет, площадь квадрата не изменится, но будет выражена иначе:
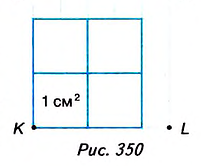
На рисунке 350 длина стороны квадрата KLMN равна 2,5 см. Он вмещает четыре квадрата площадью 1 см2 и ещё 9 маленьких квадратов площадью 0,25 см2. Поэтому 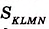
Ясно, что площадь любой фигуры равна сумме площадей частей, из которых она состоит.
Из предыдущих классов вы знаете, что площадь квадрата со стороной а можно вычислить иначе — по формуле площади квадрата:
Для квадратов ABCD и KLMN получим:
Поскольку 4 см2 < 6,25 см2, то можем записать:
Формулу площади квадрата будем считать основной, поэтому принимаем её без доказательства. Для других фигур формулы площади нужно выводить, исходя из основных свойств площади. Сформулируем их.
Основные свойства площади
- Площадь каждой фигуры больше нуля.
- Равные фигуры имеют равные площади.
- Площадь фигуры равна сумме площадей фигур, из которых она состоит.
- Единицей измерения площади является площадь квадрата со стороной, равной единице длины.
Основные свойства площади подсказывают способ выведения формул площади.
Для того чтобы вывести формулу площади многоугольника, нужно: либо разбить его на части, формулы площадей которых известны, либо дополнить его до такой фигуры, формула площади которой известна.
Теорема (о площади прямоугольника).
Площадь прямоугольника равна произведению его смежных сторон.
Дано: ABCD— прямоугольник (рис. 351),
AB=a,AD=b.
Доказать:
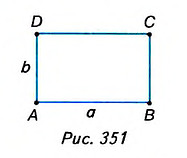
Доказательство. Достроим данный прямоугольник ABCD до квадрата AMKN со стороной о + b (рис. 352). Тогда S
С другой стороны, квадрат AMKNcociom из двух прямоугольников ABCD и OKLC и двух квадратов ВМОС и DNLC. Поэтому, по третьему свойству площади,
Прямоугольники ABCD и OKLC равны, поскольку равны смежные стороны а и b. Поэтому, по второму свойству площади, 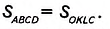
Далее получим:
Следствие. Площадь прямоугольного треугольника с катетами а и b равна половине произведения катетов.
Действительно, диагональ АС разбивает прямоугольник ABCD со сторонами а и b (рис. 353) на два равных прямоугольных треугольника ABC и ADC с катетами а и b. Поэтому
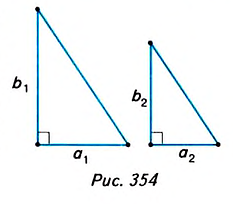
Пример №6
Докажите, что отношение площадей подобных прямоугольных треугольников равно квадрату их коэффициента подобия.
Решение:
Пусть один из заданных прямоугольных треугольников (рис. 354) имеет катеты 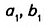
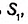
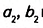
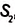
Докажем, что
Поскольку треугольники подобны, то 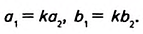
У вас может возникнуть вопрос: Как доказать, что площадь квадрата равна квадрату его стороны? Пусть сторона квадрата ABCD равна а. Возможны два случая: сторону АВ можно разбить на целое число п единичных отрезков (рис. 355); на стороне АВ можно разместить л единичных отрезков, но остаётся ещё отрезок, который короче единичного (рис. 356).
Рассмотрим первый случай (рис. 355). Разобьём сторону АВ на п единичных отрезков (на рисунке их три), тогда о — n • 1 — n. Аналогично разобьём сторону AD. Через точки деления проведём прямые, перпендикулярные АВ и AD. Эти прямые разбивают квадрат ABCD на 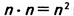
Поэтому 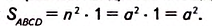
Рассмотрим второй случай (рис. 356). Пусть на отрезке АВ помещается n единичных отрезков и остаётся ещё отрезок длиной меньше 1. Это означает, что отрезок АК из п единичных отрезков меньше отрезка АВ, а отрезок AM из n + 1 единичных отрезков — больше этого отрезка. Получаем неравенство: n < а < n + 1.
Чтобы точнее оценить площадь заданного квадрата, разделим единичный отрезок на т равных частей. Тогда длина каждой части будет равна 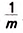
Пусть на отрезке АК их помещается 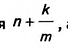
Число а будет лежать в пределах 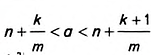
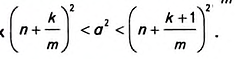
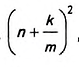
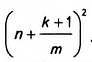
При увеличении количества точек деления число т станет как угодно большим. Площадь квадрата ABCD и квадрат числа а будут лежать в пределах, разность которых как угодно мала:
А это возможно лишь в случае, если
3. Символ S для обозначения площади фигуры происходит от латинского слова superficils, что означает «поверхность».
Параллелограмм и его площадь
Вы уже знаете формулы площадей трёх фигур -квадрата, прямоугольника и прямоугольного треугольника. Выведем формулу площади параллелограмма.
Теорема (о площади параллелограмма).
Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.
Дано: ABCD — параллелограмм (рис. 367), DH— высота, АВ= a, DH= 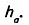
Доказать: 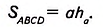
Доказательство. Проведём из вершины С высоту СМ= DH = 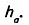

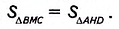
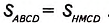
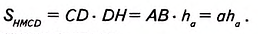
Пример №7
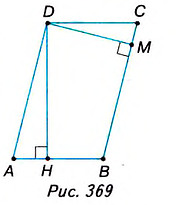
В параллелограмме стороны равны 8 см и 6,4 см, а высота, проведённая к большей стороне, — 6 см. Найдите высоту параллелограмма, проведённую к меньшей его стороне.
Решение:
Пусть ABCD— данный параллелограмм (рис. 369), в котором ab =6,4 см, ВС — 8 см, DM= 6 см.
Требуется найти высоту DH.
Площадь параллелограмма ABCD можно выразить двумя способами: либо как произведение стороны ВС на высоту DAf, либо как произведение стороны АВ на высоту DH.
Для того чтобы найти длину неизвестной стороны или высоту параллелограмма, выразите площадь двумя способами: через одну из двух смежных сторон параллелограмма и высоту, проведённую к ней, и через другую смежную сторону и соответствующую ей высоту. Составьте и решите уравнение относительно искомой величины.
Можно ли найти площадь ромба по стороне и высоте, проведённой к ней? Можно, поскольку ромб — частный вид параллелограмма.
Вы знаете, как находить площадь прямоугольного треугольника по его катетам. Воспользуемся этим, чтобы вывести ещё одну формулу площади ромба.
Теорема (о площади ромба по его диагоналям).
Площадь ромба равна половине произведения его диагоналей.
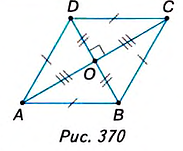
Дано: ABCD — ромб (рис. 370), АС и BD — диагонали,
Доказать:
Доказательство. В ромбе ABCD все стороны равны. Его диагонали АС и BD взаимно перпендикулярны и в точке пересечения делятся пополам. Поэтому они разбивают ромб на четыре равных прямоугольных треугольника ABO, СВО, CDO и ADO с катетами
Поскольку площадь ромба равна сумме площадей этих треугольников, то
Следствие. Площадь квадрата равна половине квадрата его диагонали.
Утверждение следует из того, что квадрат — это частный вид ромба и имеет равные диагонали, пусть d. Следовательно,
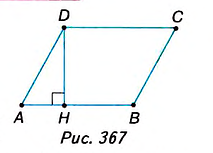
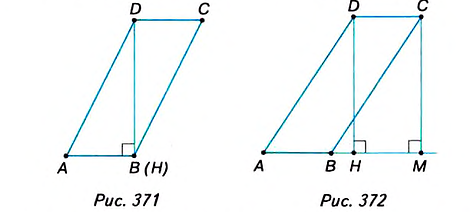
1. У вас может возникнуть вопрос: Зависит ли формула площади параллелограмма ABCD от расположения высоты DH (рис. 368)? Нет, не зависит. В расположении точки H возможны три случая. Один из них рассмотрен в учебнике. Ещё два случая: точка Н находится либо в вершине В параллелограмма (рис. 371), либо на продолжении его стороны АВ (рис. 372).
Во втором случае (рис. 371) параллелограмм ABCDсостоит из двух равных прямоугольных треугольников ABD u CDB, поэтому
В третьем случае (рис. 372) доказательство аналогично изложенному в учебнике. Проведите это самостоятельно.
2. Для фигур, имеющих равные площади, используют специальное название — равновеликие. Например, параллелограмм ABCD и прямоугольник HMCD на рисунке 372 являются равновеликими. Понятно, что два равных многоугольника всегда равновелики, но не любые два равновеликих многоугольника равны.
Два многоугольника называются равносоставленными, если их можно разбить на одинаковое количество попарно равных многоугольников, в частности треугольников. Таковы, например, параллелограмм ABCD и прямоугольник
HMCD на рисунке 368, поскольку каждый состоит из общей для них трапеции и равных прямоугольных треугольников ADH и ВСМ.
Между равновеликими и равносоставленными фигурами существует такая связь: равносоставленные многоугольники являются равновеликими (из определения о равносоставленных многоугольниках); равновеликие многоугольники являются равносоставленными. Последнее утверждение известно, как «теорема Больяи — Гервина», доказанная в XIX в. Интересно, что Фаркаш Больяи (1775 — 1856, Венгрия), доказавший теорему, был отцом Яноша Больяи (1802 — 1860) — одного из творцов неевклидовой геометрии. Янош Больяи.
Треугольник и его площадь
Вы уже знаете, как вычислить площадь прямоугольного треугольника по его катетам. Возникает вопрос: Как найти площадь любого треугольника по его стороне и высоте, проведённой к этой стороне?
Теорема (о площади треугольника).
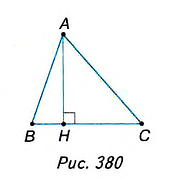
Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне.
Дано: 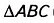
Доказать:
Доказательство. На стороне АВ заданного треугольника ABC построим равный ему треугольник BAD (рис. 381). Образованный четырёхугольник ADBC— параллелограмм, поскольку, по построению, AD = ВС, BD = АС. В нём сторона ВС= а, высота АН=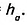
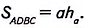
Следовательно:
Пример №8
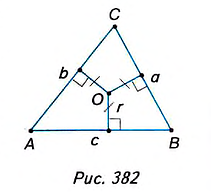
Докажите, что площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
Решение:
Пусть ABC — данный треугольник (рис. 382), в котором ВС= а, АС— b, АВ= с, 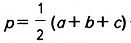
Докажем, что
Соединим отрезками вершины треугольника ABC с центром О вписанной в него окружности (рис. 383). Получаем три треугольника — ВОС, АОС и АОВ. В каждом из них радиус вписанной окружности r является высотой, проведённой к стороне, равной соответственно a, b или с.
Поэтому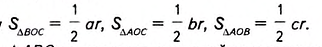
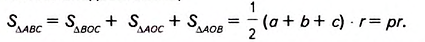
1. Способы вычисления площади треугольника (а также прямоугольника и трапеции) были известны ещё в Древнем Египте. Сведения об этом дошли до нас на папирусах. Среди них наиболее известные — папирус Ринда (около 1800 г. до н. э.), содержащий 84 задачи с решениями (страница из этого папируса на рис. 384), и так называемый московский папирус (около 1600 г. до н. э.), он содержит 25 задач с решениями. Чтобы найти площадь треугольника, древние египтяне основание треугольника делили пополам и умножали на высоту. А для определения площади равнобедренного треугольника использовали полупроизведение его боковых сторон.
2. Геометрические расчёты по точным формулам проводились и в древнем Вавилоне. Сведения сохранились на клинописных табличках (образец вы видите на рис. 385). Дошедшие до нас тексты свидетельствуют, что вавилоняне знали и использовали в практических задачах пропорциональность параллельных отрезков. Например, они умели вычислять длину отрезков AW, СМ и ВМ (рис. 386) в треугольнике ABC по его стороне АС= 30, разности S, — S2 = 42 площадей трапеции и треугольника, на которые разбивается данный треугольник параллельной прямой MN, и разности ВМ — СМ = 20. Сейчас для решения этой задачи нам пришлось бы составлять систему уравнений.
Трапеция и её площадь
Вы знаете, чтобы вывести формулы площадей прямоугольника, параллелограмма или треугольника, надо составить из этих фигур такие, площади которых умеете находить. Воспользуемся этим способом и выведем формулу площади трапеции.
Теорема (о площади трапеции).
Площадь трапеции равна произведению полусуммы её оснований на высоту.
Дано: ABCD— трапеция (рис. 397),
AB и CD — основания, СН— высота, АВ=о, CD=b, CH=h. а + b
Доказать:
Доказательство. Проведём в трапеции диагональ АС (рис. 398). Она разбивает трапецию на два треугольника ABC и ADC. Высота h трапеции является высотой треугольника ABC, проведённой к стороне АВ = а, и равна высоте треугольника ADC, проведённой к стороне CD = b. Площадь трапеции равна сумме площадей этих треугольников, поэтому
Пример №9
Диагонали АС и BD трапеции ABCD пересекаются в точке О (рис. 399). Докажите, что треугольники AOD и ВОС имеют равные площади.
Решение:
Рассмотрим треугольники ABD и ABC. В них сторона АВ— общая, а высоты, проведённые к этой стороне, равны высоте трапеции. Поэтому 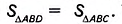
Следовательно, площади треугольников AOD и ВОС равны как разности равных площадей.
Для того чтобы установить, что неравные фигуры имеют равные площади, нужно доказать, что площади этих фигур равны либо сумме равных площадей, либо разности равных площадей.
1. У вас может возникнуть вопрос: Существует ли трапеция, средняя линия которой делит её площадь пополам?
Существование фигуры с заданными свойствами можно доказать, если привести пример такой фигуры. Однако не всегда этот путь — самый простой. История свидетельствует о том, что иногда на поиски примера, подтверждающего существование некоторого математического объекта, учёные затрачивали многие годы. Чтобы упростить поиск, проводят предварительные аналитические расчёты. Именно это мы и сделаем, чтобы ответить на поставленный вопрос. Пусть трапеция ABCD (рис. 400) имеет основания а и b и высоту h. Средняя линия MN разбивает её на две трапеции с равными высотами 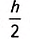
Найдём отношение площадей 
Равенство площадей 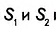
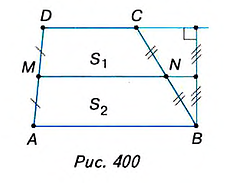
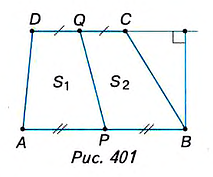
Интересно, что отрезок, соединяющий середины оснований трапеции (иногда его называют второй средней линией трапеции), делит площадь трапеции пополам. Докажите это самостоятельно, используя рисунок 401.
2. Изучая четырёхугольники, вы узнали о дельтоиде (рис. 402). Этот четырёхугольник, как и ромб, имеет взаимно перпендикулярные диагонали. Существуют трапеции со взаимно перпендикулярными диагоналями (рис. 403), а также произвольные четырёхугольники с аналогичным свойством (рис. 404). И ромб, и дельтоид, и указанная трапеция являются частными видами четырёхугольников со взаимно перпендикулярными диагоналями.
Докажите самостоятельно, что площадь четырехугольника со взаимно перпендикулярными диагоналями равна половине произведения этих диагоналей. Эта формула справедлива и для ромба, и для дельтоида, и для трапеции.
- Площадь многоугольника
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Площадь прямоугольника
- Площади фигур в геометрии
- Площади поверхностей геометрических тел
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии

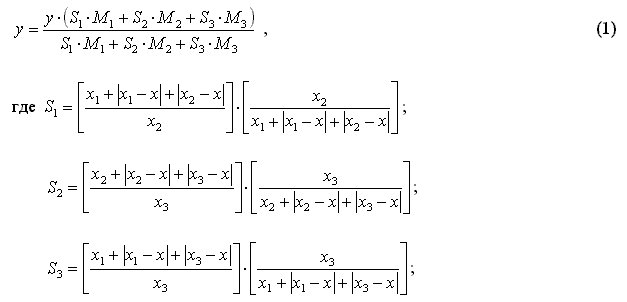

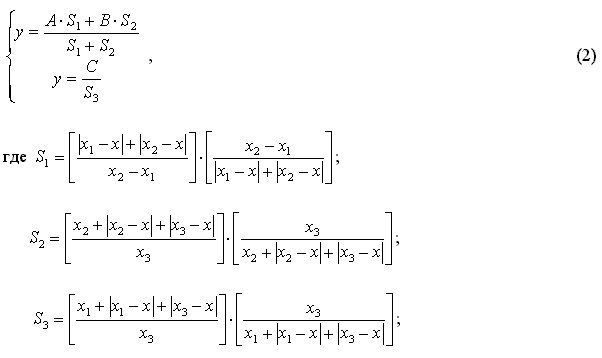
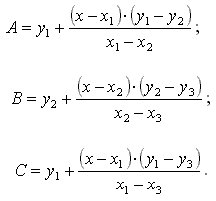
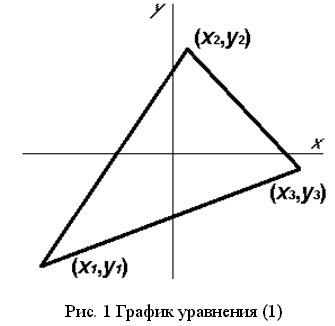
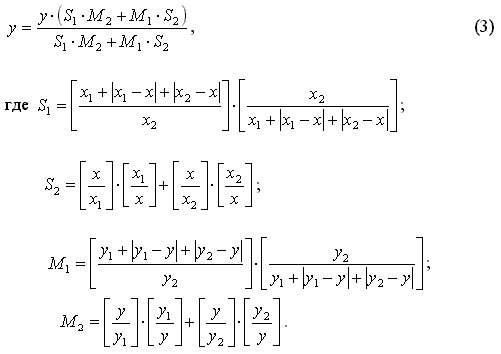
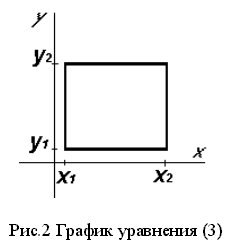
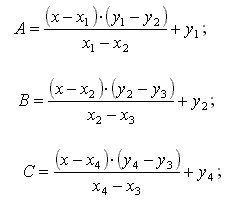
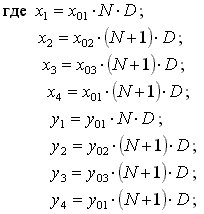
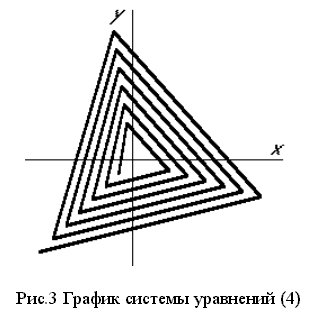
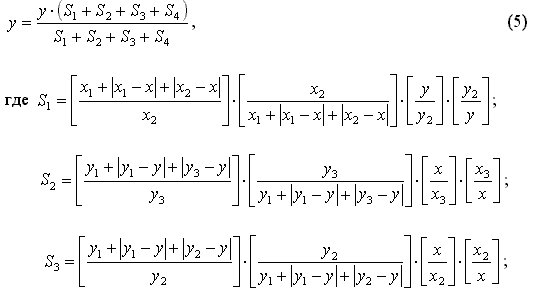
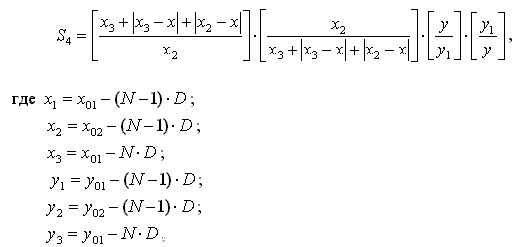
![$r=frac{Rcos(frac{pi}{n})}{cos(|(frac{{varphi}n}{2pi}-[frac{{varphi}n}{2pi}])cdotfrac{2pi}{n}-frac{pi}{n}|)}$ $r=frac{Rcos(frac{pi}{n})}{cos(|(frac{{varphi}n}{2pi}-[frac{{varphi}n}{2pi}])cdotfrac{2pi}{n}-frac{pi}{n}|)}$](https://dxdy-04.korotkov.co.uk/f/7/8/5/785f69a112838de35ee8bf144059bdf282.png)
 — полярный радиус,
— полярный радиус,  — полярный угол,
— полярный угол,  — радиус описанной окружности, квадратные скобки в знаменателе означают целую часть числа.
— радиус описанной окружности, квадратные скобки в знаменателе означают целую часть числа. ?
?


 , хоть правильный, хоть неправильный.
, хоть правильный, хоть неправильный.