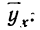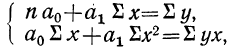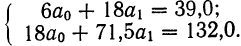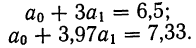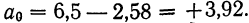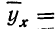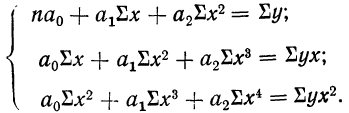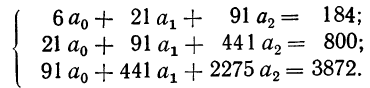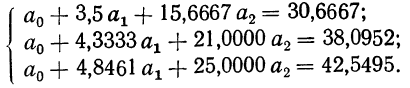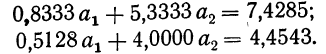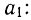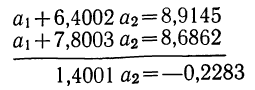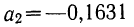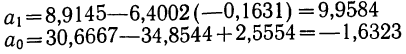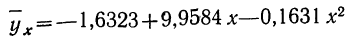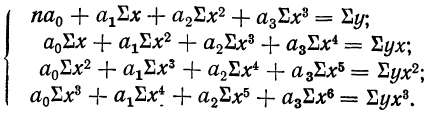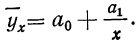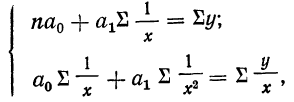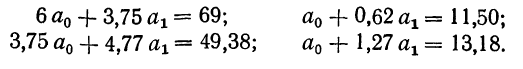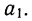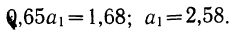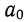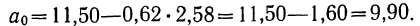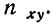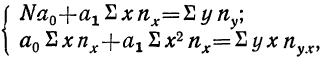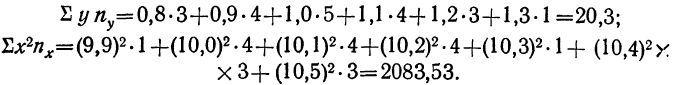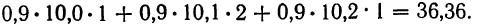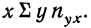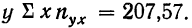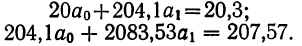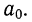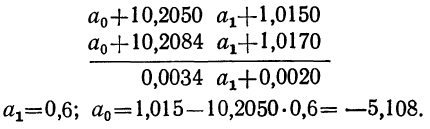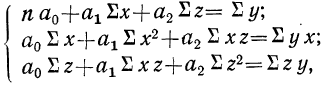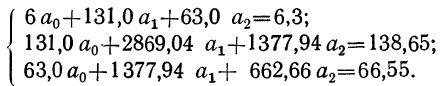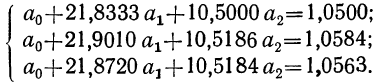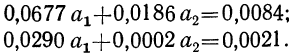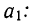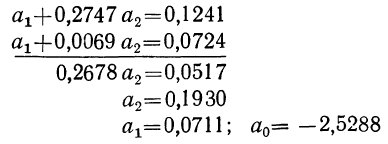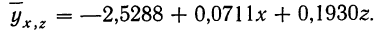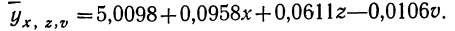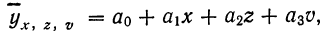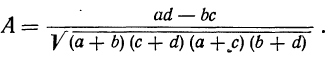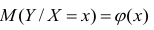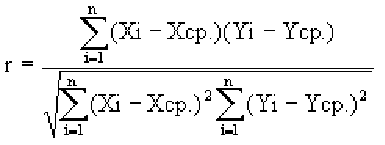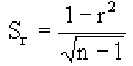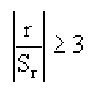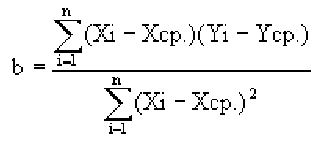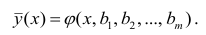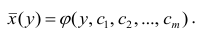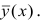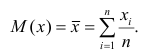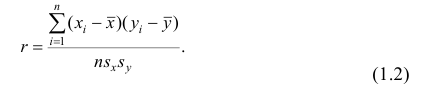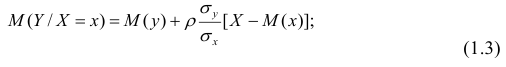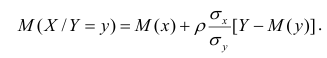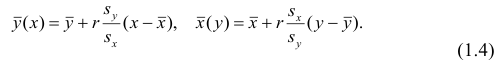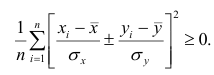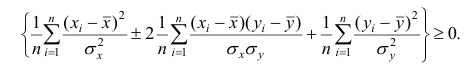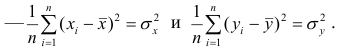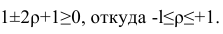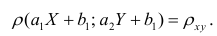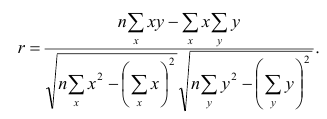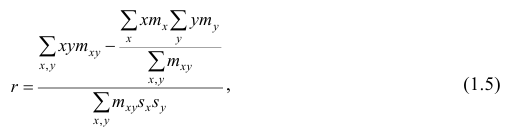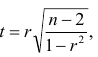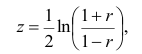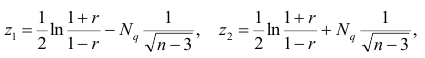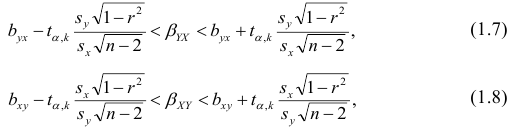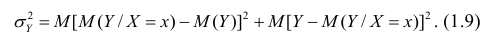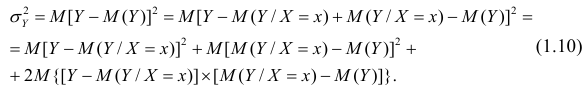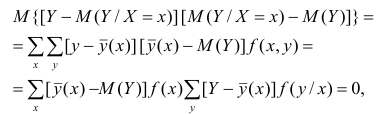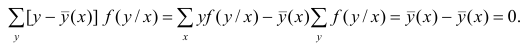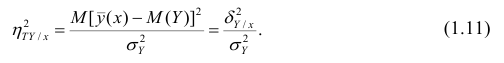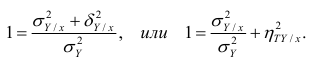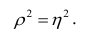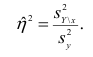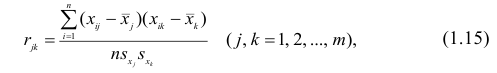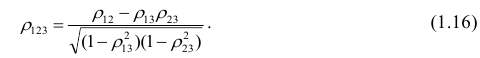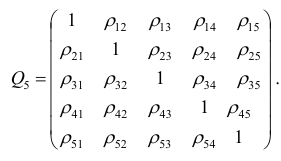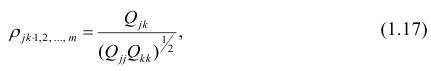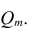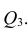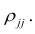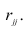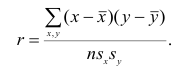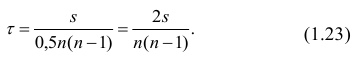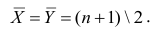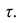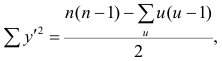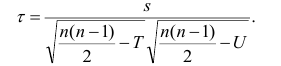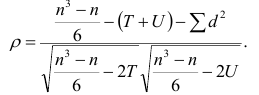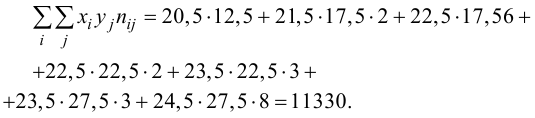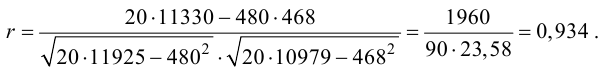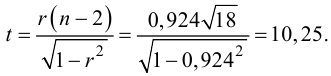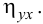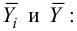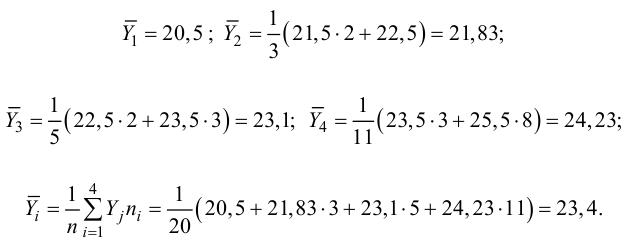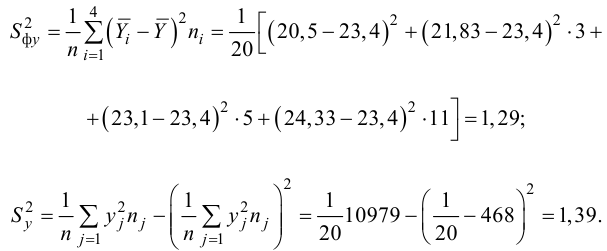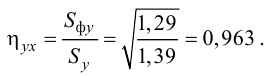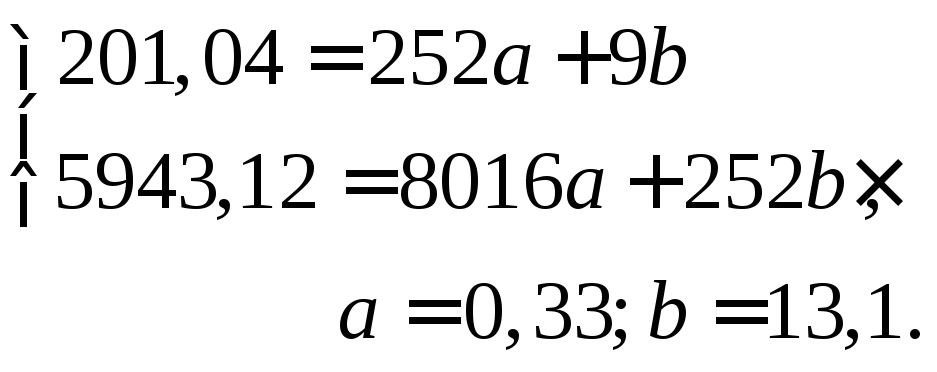Как составить уравнение корреляции

Корреляция — определение и вычисление с примерами решения

Содержание:

Понятие о корреляции:

Марксистская философия учит, что каждое явление природы и общества не возникает само по себе, отдельно от других, а находится в связи с другими явлениями, причем каждое из них представляет собой единство составляющих его частей и свойств. Для того чтобы познать какое-либо явление, необходимо изучить его не только во всех сложных взаимоотношениях с окружающими явлениями-факторами, но также во взаимосвязи всех его сторон.

Если всеобщая связь и взаимозависимость явлений составляют один из наиболее общих законов, то основной задачей науки является изучение этой взаимосвязи.

В математической статистике взаимосвязь явлений изучается методом корреляции. Термин корреляция происходит от английского слова correlation — соотношение, соответствие. Особенность изучения связи явлений методом корреляции состоит в том, что нельзя изолировать влияние посторонних факторов либо потому, что эти факторы неизвестны, либо потому, что их изоляция невозможна. Поэтому метод корреляции применяется для того, чтобы при сложном взаимодействии посторонних влияний выяснить, какова была бы зависимость между результатом фактором, если бы посторонние факторы не изменялись и своим изменением не искажали основную зависимость. При этом небольшое число наблюдений не дает возможности обнаружить закономерность связи.

Первая задача корреляции заключается в выявлении на основе наблюдения над большим количеством фактов того, как изменяется в среднем результативный признак в связи с изменением данного фактора. Это изменение предполагает условие неизменности ряда других факторов, хотя искажающее влияние этих других факторов на самом деле имеет место. Вторая задача заключается в определении степени влияния искажающих факторов.

Первая задача решается нахождением уравнения связи.

Вторая задача решается при помощи различных показателей тесноты связи.

Такими показателями являются меры тесноты связи, найденные разными исследователями, а также коэффициент корреляции и корреляционное отношение.

Результативный и факториальный признаки

При изучении влияния одних признаков явлений на другие из цепи признаков, характеризующих данное явление, выделяются два признака — факториальный и результативный. Необходимо установить, какой из признаков является факториальным и какой результативным. В этом помогает прежде всего логический анализ.

Пример. Себестоимость промышленной продукции отдельного предприятия зависит от многих факторов, в том числе от объема продукции на данном предприятии. Себестоимость продукции выступает в этом случае как результативный признак, а объем продукции — как факториальный.

Другой пример. Чтобы судить о преимуществах крупных предприятий перед мелкими, рассмотрим, как увеличивается производительность труда рабочих крупных предприятий, и выявим зависимость производительности труда от увеличения размеров предприятия.

Таблица!

Группировка магазинов Министерства торговли по числу рабочих мест на 1 января 1960 г.1

Группы магазинов по числу рабочих мест Число магазинов Товарооборот в расчете на одного работника за квартал (в тыс. руб.)

Всего 68 375 117

Из них

с числом рабочих мест:

• с 1 19 893 109
• с 2 18 030 108
• с 3—4 16 508 108
• с 5—7 8 321 111
• с 8—10 2 868 118
• с 11 — 15 1 559 122
• с 16 и более 1 196 139
• J

Группировка показывает прямую зависимость производительности труда торговых работников, выражающуюся в товарообороте, приходящегося на одного работника, от размера магазина. Признак группировки — число рабочих мест — является факториальным, товарооборот — результативным признаком.

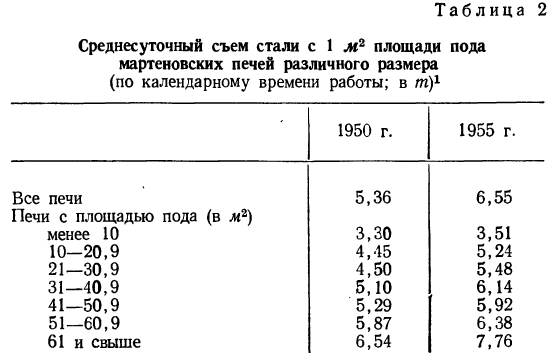
От размеров производства зависит также производительность оборудования, о чем свидетельствует следующая таблица:

Из таблицы ясно видна связь между размерами печей и их производительностью. Эта связь прямая: чем крупнее печь, тем она производительнее.

Однако зависимость результативного признака (суточного съема стали) от факториального носит не обязательный характер. Если в общей массе мы наблюдаем эту связь, то в отдельных группах бывают и отступления от общей закономерности. Такие отступления—характерная особенность статистической связи вообще, о которой будет рассказано ниже.

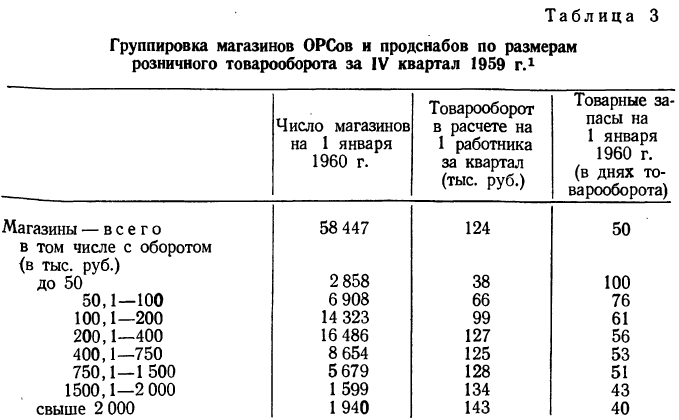
Группировки позволяют выявить и зависимость нескольких результативных признаков от одного факториального. Рассмотрим табл. 3.

В этой таблице мы видим зависимость двух результативных признаков: товарооборота на одного работника и товарных запасов—от размеров магазинов. Зависимость товарооборота от размеров магазина прямая, а зависимость товарных остатков от размеров магазина — обратная. В первом случае она растет с ростом размеров магазина, во втором уменьшается. Однако то и другое благоприятно.

Графическое изображение связи

Графическое изображение изучаемых явлений позволяет не только установить наличие или отсутствие связи между ними, но и изучить характер этой связи, иначе говоря изучить форму связи и ее тесноту.

Имея перед собой числовые характеристики факториального и результативного признаков одного и того же явления, можно каждую пару чисел изобразить в виде точки на плоскости. Для этого на плоскости берем две взаимно перпендикулярные линии и образуем систему координат. В этой системе по оси абсцисс откладываем значения факториального признака, а по оси ординат— значения результативного признака. Каждая пара чисел дает при этом точку на плоскости координатного поля.

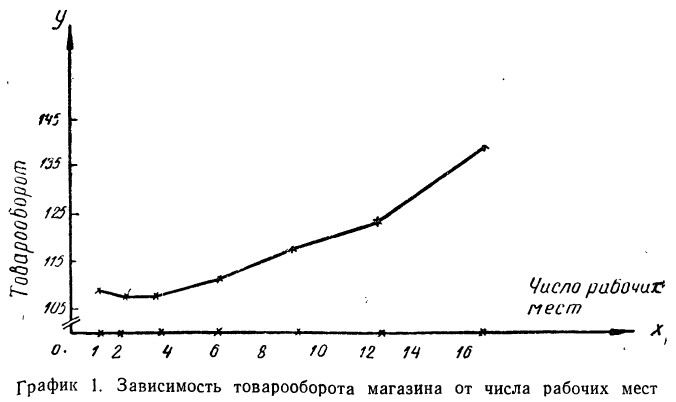
Возьмем, например, группировку магазинов по числу рабочих мест, данную на стр. 239, и будем откладывать число рабочих мест по горизонтальной оси (оси Ох), а товарооборот в расчете на одного работника — по вертикальной оси (оси Оу). Будем иметь ряд точек, соединив которые получим ломаную линию, которая называется ломаной регрессии (см. график 1).

Как видно из графика, с ростом числа рабочих мест в магазине растет и товарооборот, приходящийся на одного работника, что говорит о связи между этими признаками, причем связи прямой. График подчеркивает эту зависимость ходом ломаной линии из нижнего угла в верхний правый угол.

Такого же рода зависимость будем наблюдать на графике 2, изучая связь между величиной мартеновских печей по площади пода и среднесуточным съемом стали с 1 пода. Как и в предыдущем примере, факториальный признак — величину площади пода — будем откладывать на оси абсцисс, а результативный — среднесуточный съем стали с 1 пода — на оси ординат.

Здесь также ясно выраженная прямая зависимость между результативным и факториальным признаками.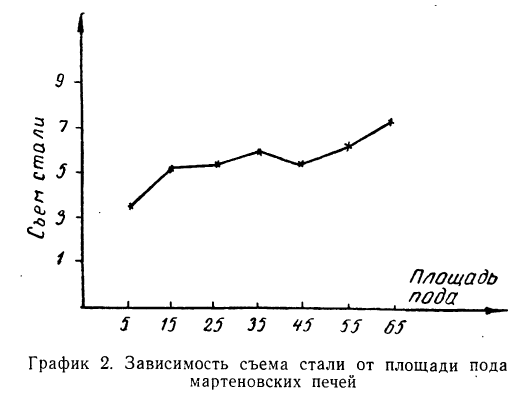

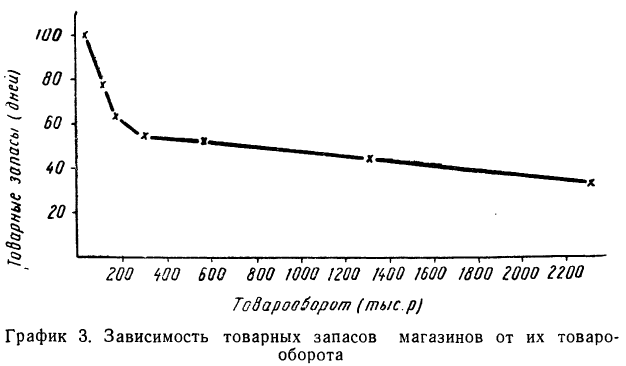
По-другому будет выглядеть график зависимости товарных запасов от размера товарооборота магазина.

Здесь мы наблюдаем ярко выраженную обратную связь между признаками: падение товарных запасов сопровождается ростом размера магазина по товарообороту.

Графический метод наглядно иллюстрирует зависимость, выявленную группировкой. Недостаток графического метода изучения связи заключается в том, что он позволяет выявить связь лишь между двумя признаками.

Функциональные и статистические связи

До сих пор говорилось о связях между явлениями и их признаками без объяснения формы и степени этих связей. В приведенных примерах связи носят логически обоснованный характер, но числовое выражение этих связей говорит о том, что они проявляются не всегда одинаково. В определенных случаях имеются отступления от наблюдаемых общих закономерностей. В приведенной на стр. 240 таблице о среднесуточном съеме стали с 1 пода печи наблюдается зависимость съема стали от размера печи по площади пода, но эта зависимость за 1955 г. искажена показателями 5-й группы, где съем стали значительно ниже, чем в 4-й группе. Если бы рассматривалась при этом каждая печь в отдельности, то это несоответствие установленному правилу зависимости проявлялось бы неоднократно. Но средние величины съема стали, вычисленные на основании данных довольно большого числа печей в группе, говорят о явно выраженной зависимости. Связи между явлениями, или их признаками. проявляющиеся в изменении в зависимости от одного признака характеристик распределения (из которых главная — средняя) другого признака, называются связями статистическими.

Статистические связи характеризуются тем, что в них результативный признак не полностью определяется влиянием признака факториального. Это влияние проявляется лишь в среднем, а в отдельных случаях получаются результаты, даже противоречащие установленной связи.

В отличие от статистических связей связи функциональные характеризуются тем, что при таких связях факториальный признак полностью определяет величину результативного признака.

Функциональные связи почти не встречаются в явлениях общественной жизни, отличающихся сложностью и многообразием существующих и проявляющихся взаимосвязей. Но во многих явлениях в основе статистических связей лежат функциональные связи. Связь функциональная может показывать зависимость между результативным признаком и несколькими аргументами. Так, площадь прямоугольника зависит от длины его двух сторон, путь, проходимый телом, зависит от скорости его движения и времени движения и т. д.

Уравнение связи

Наблюдая статистическую связь между двумя признаками, математическая статистика стремится придать этой связи форму функциональной, т. е. связи, выражаемой при помощи математической функции.

На помощь приходит ее графическое изображение при отыскании нужной функции связи. При этом необходимо стремиться найти такую функцию, которая давала бы наименьшее отклонение от полученных при наблюдении значений их признаков, которая выражала бы основную зависимость, проявляющуюся в эмпирическом материале. Уравнение этой функции будет уравнением связи между результативным и факториальным признаками.

Уравнение связи находится с помощью способа наименьших квадратов, который требует, чтобы сумма квадратов отклонений эмпирических значений от значений, получаемых на основании уравнения связи, была минимальной.

Применение способа наименьших квадратов позволяет находить параметры уравнения связи при помощи решения системы так называемых нормальных уравнений, различных для связи каждого вида.

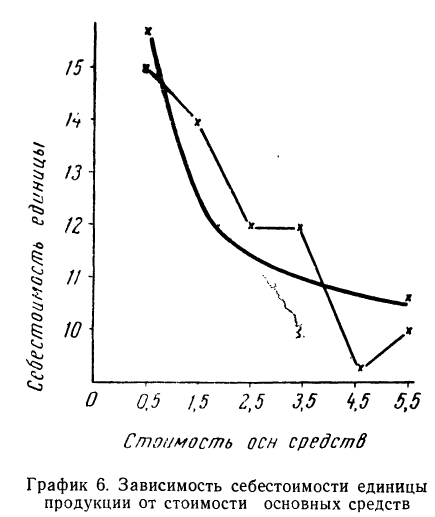
Чтобы отметить, что зависимость между двумя признаками выражается в среднем, значения результативного признака, найденные по уравнению связи, обозначаются

Зная уравнение связи, можно вычислить заранее среднее значение результативного признака, когда значение факториального признака известно. Таким образом, уравнение связи является методом обобщения наблюдаемых статистических связей, методом их изучения.

Применение той или иной функции в качестве уравнения связи разграничивает связи по их форме: линейную связь и криволинейную связь (параболическую, гиперболическую и др.).

Рассмотрим уравнения связи для зависимостей от одного признака при разных формах связи (линейной, криволинейной параболической, гиперболической) и для множественной связи.

Линейная зависимость

Уравнение связи как уравнение прямой 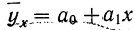применяется в случае равномерного нарастания результативного признака с увеличением признака факториального. Такая зависимость будет зависимостью линейной (прямолинейной).

Параметры уравнения прямой линии 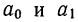находятся путем решения системы нормальных уравнений, получаемых по способу наименьших квадратов:

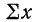
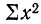
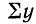
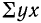
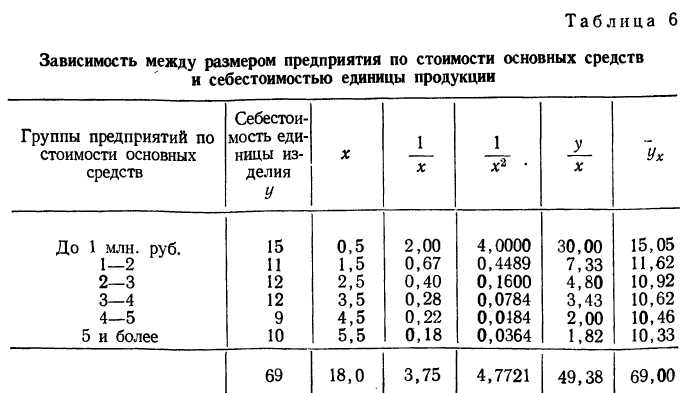
где n — число полученных при наблюдении пар взаимосвязанных величин; — сумма значений факториального признака;

— сумма квадратов значений факториального признака;

— сумма значений результативного признака; — сумма произведений значений факториального признака на значения результативного признака.

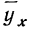
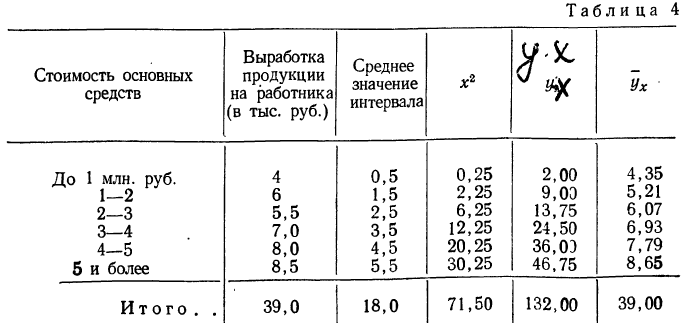
Примером расчета параметров уравнения и средних значений результативного признака может служить следующая таблица, являющаяся результатом группировки по факториальному признаку и подсчета средних по результативному признаку.

Группировка предприятий по стоимости основных средств и подсчет сумм необходимы для уравнения связи.

Из таблицы находим: 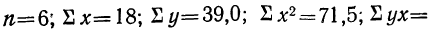132,0. Строим систему двух уравнений с двумя неизвестными:

Поделив каждый член в обоих уравнениях на коэффициенты при 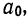получим:

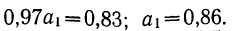
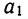
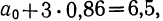
Вычтем из второго уравнения первое: Подставив значения в первое уравнение найдем

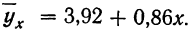
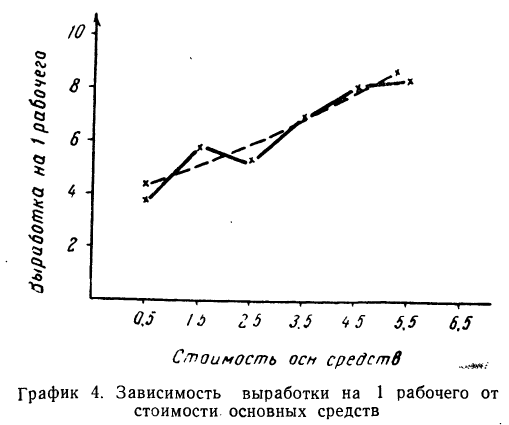
Уравнение связи примет вид: Подставив в это уравнение соответствующие х, получим значения результативного признака, отражающие среднюю зависимость у от х в виде корреляционной зависимости.

Заметим, что суммы, исчисленные по уравнению и фактические, равны между собой. Изображение фактических и вычисленных значений на графике 4 показывает, что уравнение связи отображает наблюденную зависимость в среднем.

Параболическая зависимость

Параболическая зависимость, выражаемая уравнением параболы 2-го порядка 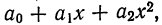имеет место при ускоренном возрастании или убывании результативного признака в сочетании с равномерным возрастанием факториального признака.

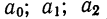
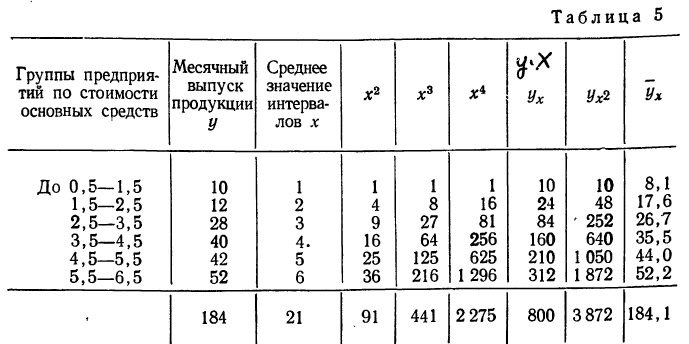
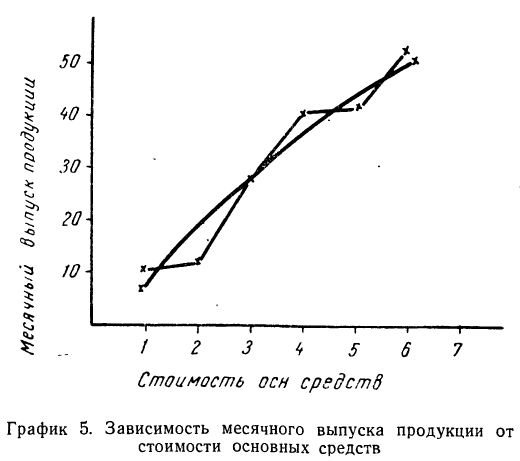
Параметры уравнения параболы вычисляются путем решения системы 3 нормальных уравнений:

Возьмем для примера зависимость месячного выпуска продукции (у) от величины стоимости основных средств (х). Оба показателя округлены до миллионов рублей. Расчеты необходимых сумм приведем в таблице 5.

По данным таблицы, составляем систему уравнений:

После деления всех уравнений на коэффициенты при 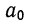получим:

Вычтя из второго уравнения первое и из третьего второе, получим два новых уравнения с двумя неизвестными:

Полученные уравнения снова разделим на коэффициенты при

Следовательно,

Запишем уравнение параболы, выражающей связь между х и у.

Графическое сопоставление опытных данных и данных расчета (см. график 5) показывает почти полное совпадение хода обеих линий, что говорит о хорошем воспроизведении опытных данных расчетными средними значениями результативного признака.

В практике изучения связи между признаками, кроме параболы 2-го порядка, применяются параболы и более высоких порядков. Чем выше порядок параболы, тем точнее он воспроизводит опытные данные.

Если уравнение связи представляет собой параболу 3-го порядка 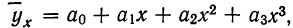то система нормальных уравнений примет вид:

Имея соответствующие хну, можем составить Дополнительную расчетную таблицу по следующей схеме:

которая используется для нахождения нужных сумм. Решив систему 4 уравнений, найдем параметры 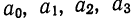и, следовательно, уравнение связи.

Уравнение гиперболы

Обратная связь указывает на убывание результативного признака при возрастании факториального. Такова линейная связь при отрицательном значении 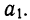В ряде других случаев обратная связь может быть выражена уравнением гиперболы

Параметры уравнения гиперболы 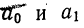находятся из системы нормальных уравнений:

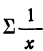
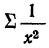
где — сумма величин, обратных значениям факториального признака, а — сумма их квадратов.

Примером расчета обратной связи по гиперболе может служить следующая таблица:

Составив по данным таблицы систему уравнений и разделив каждый член обоих уравнений на коэффициенты при а, получим:

Находим вычитанием из второго уравнения первого величину

Подставив вместо 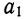его значение, получим

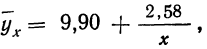
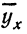
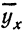
Запишем уравнение связи в общем виде затем, подставив каждое значение х в уравнение, находим по любой строке таблицы. Строим ломаную по парам х и у и кривую по х и . Ломаная и кривая очень близки друг к другу.

Корреляционная таблица

При большом объеме наблюдений, когда число взаимосвязанных пар велико, парные данные легко могут быть расположены в корреляционной таблице, являющейся наиболее удобной формой представления значительного количества пар чисел.

В корреляционной таблице один признак располагается в строках, а другой — в колонка таблицы. Число, расположенное в клетке на пересечении графы и колонки, показывает, как часто встречается данное значение результативного признака в сочетании с данным значением факториального признака.

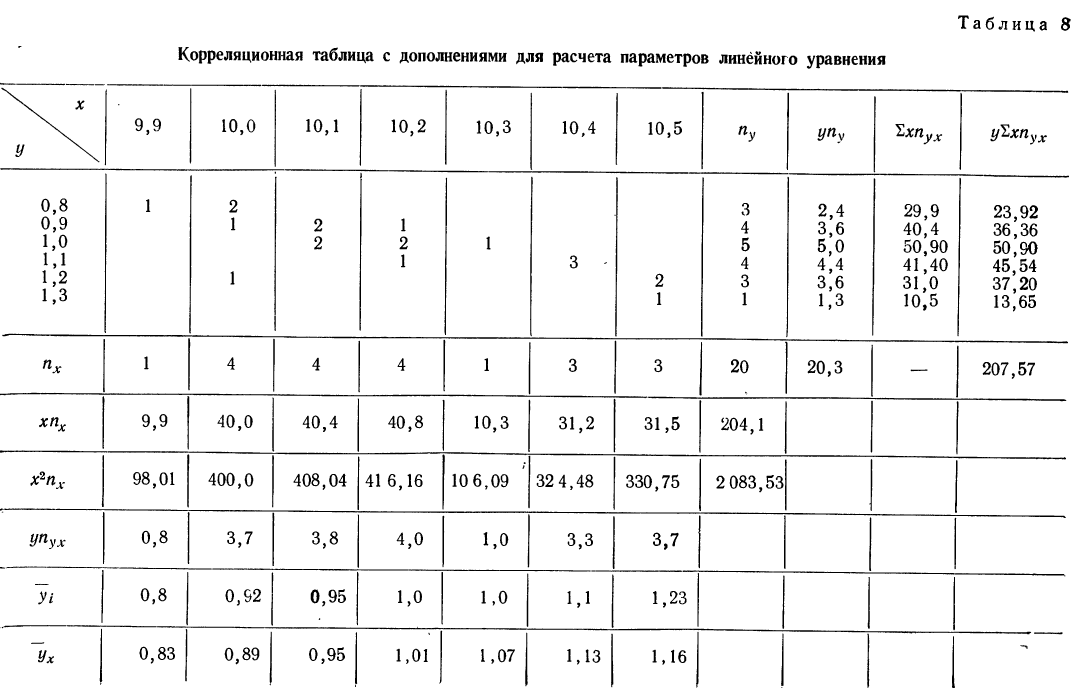
Для простоты расчета возьмем небольшое число наблюдений на 20 предприятиях за средней месячной выработкой продукции на одного рабочего (тыс. руб. — у) и за стоимостью основных производственных средств (млн. руб. — х).

В обычной парной таблице эти сведения располагаются так:

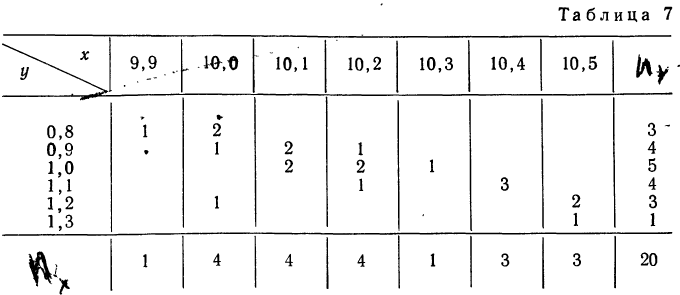
Сведем эти данные в корреляционную таблицу.

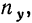
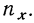
Итоги строк у показывают частоту признака итоги граф х — частоту признака Числа, стоящие в клетках корреляционной таблицы, являются частотами, относящимися к обоим признакам и обозначаются

Корреляционная таблица даже при поверхностном знакомстве дает общее представление о прямой и обратной связи. Если частоты расположены по диагонали вниз направо, то связь между признаками прямая (при увеличивающихся значениях признака в строках и графах). Если же частоты расположены по диагонали вверх направо, то связь обратная.

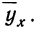
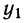
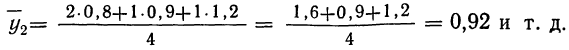
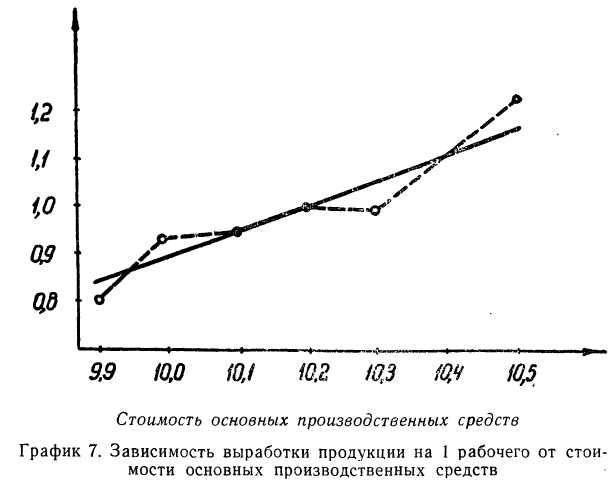
Для предварительного суждения о связи по корреляционной таблице можно для каждого столбца рассчитать средние значения Так, в первом столбце х = 9,9, а имеет лишь одно значение, равное 0,8. Найдем среднее значение для второго столбца. Оно будет равно:

Следовательно, при 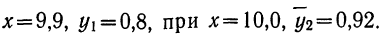Выпишем все значения х и соответствующие им

Зависимость, выраженная в таблице, более ярко и убедительно выступит в «ломаной регрессии», когда каждую пару чисел нанесем на график (см. график 7).

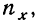
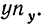
По корреляционной таблице можно вести расчеты параметров уравнения связи, как уравнения прямой, так и уравнений параболы и гиперболы. При этом необходимо учитывать, что сочетание каждой пары значений может встречаться не один, а несколько раз. Сами значения хну необходимо взвешивать, т. е. умножать на соответствующие частоты. Для самого признака х частота будет обозначаться для признака Частоту сочетаний обозначим

Ввиду сказанного мы можем систему нормальных уравнений написать так, чтобы были учтены веса. Тогда для линейной зависимости система нормальных уравнений примет вид:

где N — число произведенных наблюдений (число пар). В приведенной корреляционной таблице N = 20. 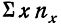будет суммой произведений соответствующих х на их частоты. В данной таблице эта сумма составит:

9,9 +10,0 • 4 +10,1 • 4 + 10,2 • 4 +10,3 • 1 +10,4 • 3 +10,5 • 3 = 204.

—сумма произведений у на соответствующие частоты. В нашем примере она равна:

включает сумму произведений всех х на у и на для тех клеток корреляционной таблицы, в которых записаны частоты. Рассчитаем суммы произведений для 1-й и 2-й строки

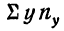
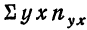
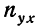
Нетрудно заметить, что в каждой строке у повторяется столько раз, сколько раз мы его суммируем, а, следовательно, у можно вынести за скобку.

• Для 1-й строки: 0,8 (9,9 • 1 +10,0 • 2) =23,92.
• Для 2-й строки:

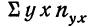
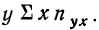
Следовательно, сумма произведений может быть записана при постоянном у, как Заметим, что сумма произведений может быть записана и рассчитана как произведение

Продолжим расчет для последующих строк.

Общая сумма по всем строкам

Система нормальных уравнений может быть записана по результатам подсчета в таком виде:

Для расчета параметров уравнения линейной связи делим каждое из уравнений на коэффициенты при

Уравнение связи 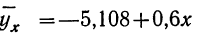определяет среднюю зависимость выработки рабочего от стоимости основных средств. Вычислительная работа облегчается, если в самой корреляционной таблице путем записи дополнительных граф и строк производить нужные подсчеты для решения системы уравнений.

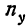
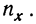
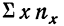
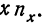
Число наблюдений N может быть подсчитано и по столбцу как его сумма. Она равна итогу по строке Для определения необходимо ввести новую строку Итог этой строки и дает искомую сумму.

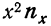
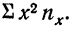
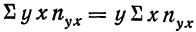
Следующая дополнительная строка представляет возможность определить Далее, и может быть определена на основе расчета двух дополнительных граф:

В корреляционной таблице (см. табл. в последних строках дается расчет для построения ломаной регрессии — для построения прямой (см. график 7).

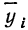
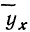
Корреляционная таблица позволяет вычислять уравнение связи для любой формы: прямой, параболы, гиперболы и др. Однако в подобной таблице видна зависимость результативного признака лишь от одного факториального.

Зависимость результативного признака от двух или более факториальных признаков носит название множественной связи.

Множественная связь

Исследование зависимости результативного признака от двух или нескольких факториальных признаков возможно при помощи уравнения множественной связи.

В простейшем уравнении множественной связи предполагается, что зависимость между признаками линейная. Сначала рассмотрим линейную зависимость результативного признака (у) от двух факториальных (х, z). Уравнение связи в этом случае выразится формулой 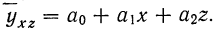Параметры этого уравнения находятся при решении системы нормальных уравнений, получаемых для способа наименьших квадратов

где п — число одновременных наблюдений по трем признакам;

—суммы соответствующих значений по этим признакам.

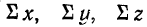
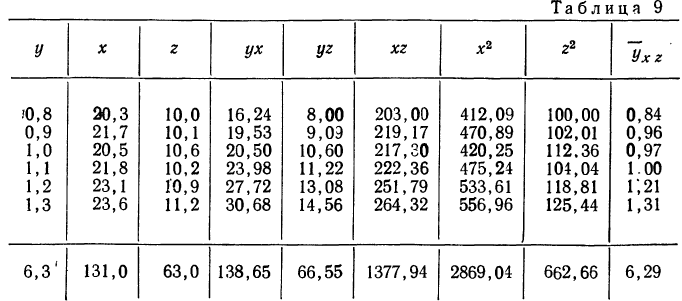
Все расчеты удобно сосредоточить в специальной таблице, как это делается в приводимом ниже примере.

Рассмотрим зависимость средней урожайности ячменя (у) на равных участках от количества внесенных минеральных удобрений (х) и количества выпавших в период цветения осадков (z).

Средняя урожайность исчислялась по участкам с равным количеством внесенных удобрений и с равным количеством выпавших осадков.

Пользуясь данными таблицы, составляем систему трех уравнений:

Поделив все члены уравнений на коэффициенты при 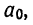получим:

Вычитая из второго уравнения сначала первое, а затем третье, получим 2 уравнения с двумя неизвестными:

Делим каждый член обоих уравнений на коэффициенты при

Уравнение связи, определяющее зависимость результативного признака (у) от двух факториальных

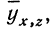
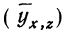
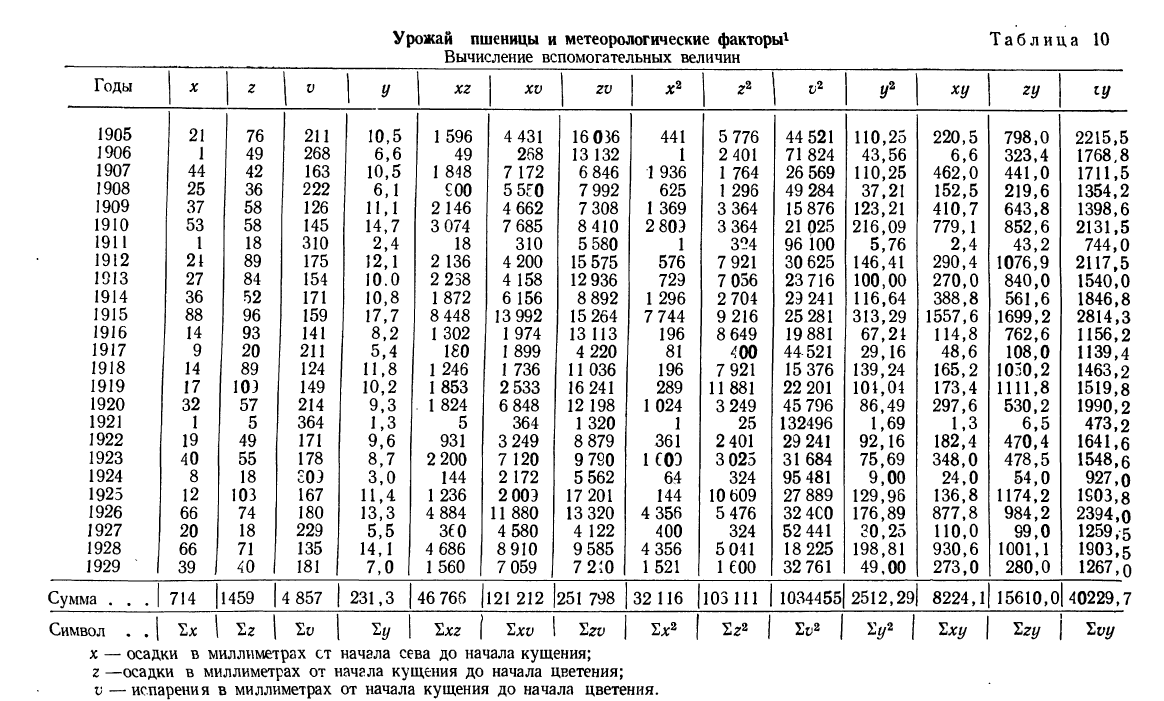
Вычислив по этому уравнению при соответствующих х и z величины замечаем, что суммы опытных данных (y) и расчетных данных совпадают, а отдельные значения их мало отличаются друг от друга.

Найдем уравнение связи между урожайностью пшеницы на Безенчукской опытной станции и тремя факторами (х, z, v).

Статистические данные, полученные в результате наблюдения, и расчеты представлены в табл. 10, откуда возьмем необходимые данные для составления системы нормальных уравнений:

Следовательно,, корреляционное уравнение будет:

Расширив число факториальных признаков, можно найти уравнение множественной связи для 4, 5, 6 и т. д. признаков. При этом необходимо брать только такие признаки, которые оказывают существенное влияние на величину результативного признака, ибо учет несущественных, второстепенных признаков лишь увеличивает расчетную работу при нахождении уравнения связи, а не приближает к более полному изучению связи.

Если число факториальных признаков возрастает, возрастает и число членов уравнения связи. Так, для трех факториальных признаков линейное уравнение связи будет записано формулой:

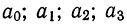
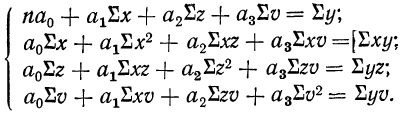
где параметры уравнения находятся путем решения системы четырех нормальных уравнений:

Построив соответствующую таблицу, получим в ней необходимые суммарные данные для приведенной системы уравнений (см. табл. 10).

Мерой существенности влияния того или иного факториального признака на результативный являются показатели тесноты связи.

В настоящем издании мы рассмотрим эмпирические меры тесноты связи, полученные разными исследователями, и меры тесноты связи, основанные на измерении вариации.

Эмпирические меры тесноты связи

Эмпирические меры тесноты связи позволяют оценить степень связи между явлениями или факторами, находящимися в зависимости один от другого. Эмпирические меры получены различными исследователями, занимавшимися статистической обработкой фактического материала. Они получены ранее, чем был открыт метод корреляции. Практическое пользование эмпирическими показателями довольно удобно.

К эмпирическим мерам тесноты относятся:

• а) коэффициент ассоциации:
• б) коэффициенты взаимной напряженности;
• в) коэффициент Фехнера;
• Г) коэффициент корреляции рангов;

Рассмотрим каждый из них.

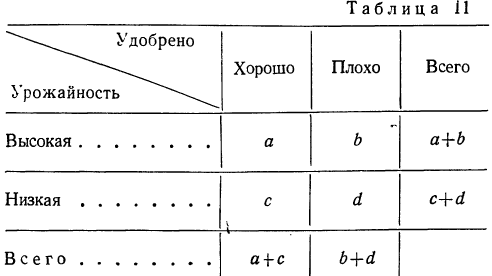
а) Коэффициент ассоциации. Коэффициент ассоциации как мера тесноты связи применяется для изучения связи двух качественных признаков, состоящих только из двух групп. Для его вычисления строится четырехклеточная таблица корреляции, которая выражает связь между двумя явлениями, каждое из которых, в свою очередь, должно быть альтернативным, т. е. состоящим только из двух видов, качественно отличных друг от друга. Например, при изучении зависимости урожая от количества внесенных в почву удобрений выделяем по урожайности и по количеству внесенных удобрений лишь по две группы. При этом условии можно построить следующую четырехклеточную таблицу.

Числа, стоящие на пересечении строк и граф — a,b,c,d, показывают, сколько участков встречается с тем и другим количеством удобрений, внесенным в почву, с той и другой урожайностью.

Мера тесноты связи — коэффициент ассоциации — исчисляется по формуле:

Заполнив клетки конкретными числовыми данными, получим следующую четырехклеточную таблицу, где числа, стоящие в клетках, — гектары посевов.

Коэффициент ассоциации равен: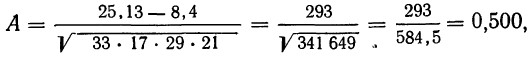
что говорит о достаточно тесной прямой связи между урожайностью и степенью удобрения почв.

Коэффициент ассоциации может иметь и отрицательные значения, когда ad

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Корреляционный анализ в Excel. Пример выполнения корреляционного анализа

Корреляционный анализ – это распространённый метод исследования, применяемый для определения уровня зависимости 1-й величины от 2-й. В табличном процессоре есть особый инструмент, который позволяет реализовать данный тип исследования.

Суть корреляционного анализа

Он необходим для определения зависимости между двумя разными величинами. Иными словами, происходит выявление того, в какую сторону (меньшую/большую) меняется величина в зависимости от изменений второй.

Назначение корреляционного анализа

Зависимость устанавливается тогда, когда начинается выявление коэффициента корреляции. Этот метод отличается от анализа регрессии, так как здесь только один показатель, рассчитываемый при помощи корреляции. Интервал изменяется от +1 до -1. Если она плюсовая, то повышение первой величины способствует повышению 2-й. Если минусовая, то повышение 1-й величины способствует понижению 2-й. Чем выше коэффициент, тем сильнее одна величина влияет на 2-ю.

Важно! При 0-м коэффициенте зависимости между величинами нет.

Расчет коэффициента корреляции

Разберем расчёт на нескольких образцах. К примеру, есть табличные данные, где по месяцам описаны в отдельных столбцах траты на рекламное продвижение и объём продаж. Исходя из таблицы, будем выяснять уровень зависимости объема продаж от денег, затраченных на рекламное продвижение.

Способ 1: определение корреляции через Мастер функций

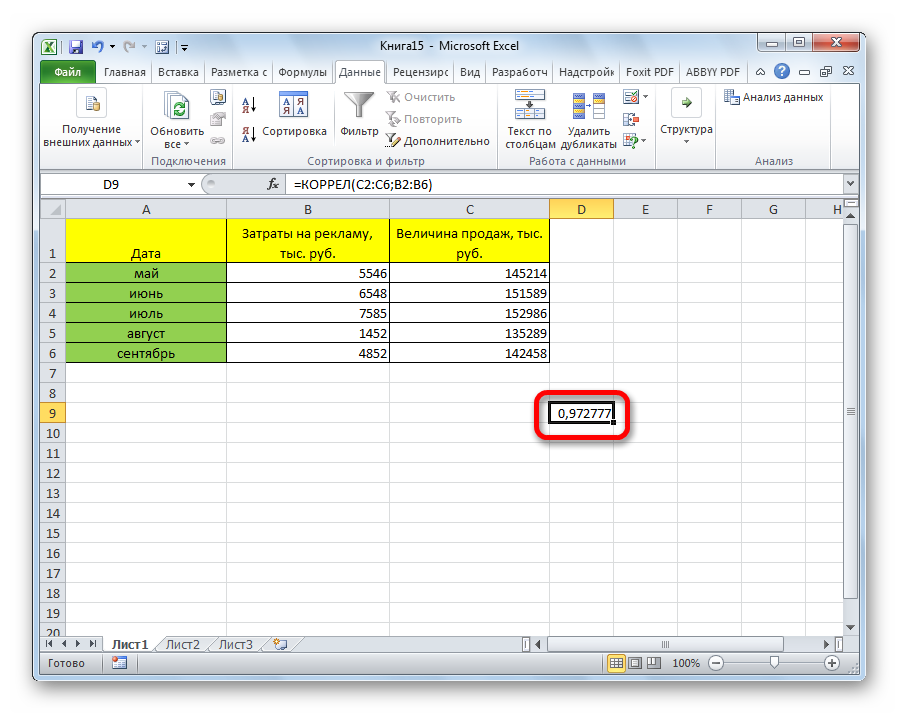
КОРРЕЛ – функция, позволяющая реализовать корреляционный анализ. Общий вид — КОРРЕЛ(массив1;массив2). Подробная инструкция:

1. Необходимо произвести выделение ячейки, в которой планируется выводить итог расчета. Нажать «Вставить функцию», находящуюся слева от текстового поля для ввода формулы.

1

1. Открывается «Мастер функций». Здесь необходимо найти КОРРЕЛ, кликнуть на нее, затем на «ОК».

2

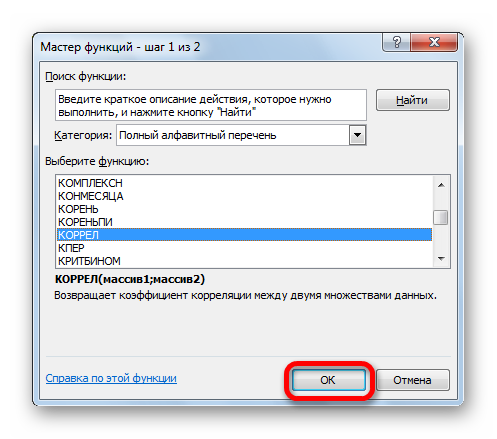
1. Открылось окошко аргументов. В строку «Массив1» необходимо ввести координаты интервалы 1-го из значений. В рассматриваемом примере — это столбец «Величина продаж». Нужно просто произвести выделение всех ячеек, которые находятся в этой колонке. В строку «Массив2» аналогично необходимо добавить координаты второй колонки. В рассматриваемом примере — это столбец «Затраты на рекламу».

3

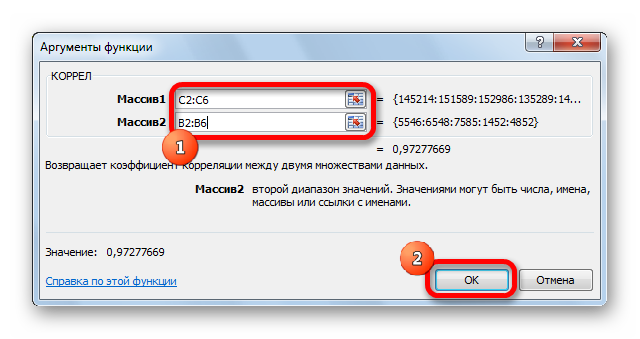
1. После введения всех диапазонов кликаем на кнопку «ОК».

Коэффициент отобразился в той ячейке, которая была указана в начале наших действий. Полученный результат 0,97. Этот показатель отображает высокую зависимость первой величины от второй.

4

Способ 2: вычисление корреляции с помощью Пакета анализа

Существует еще один метод определения корреляции. Здесь используется одна из функций, находящаяся в пакете анализа. Перед ее использованием нужно провести активацию инструмента. Подробная инструкция:

1. Переходим в раздел «Файл».

5

1. Открылось новое окошко, в котором нужно кликнуть на раздел «Параметры».
2. Жмём на «Надстройки».
3. Находим в нижней части элемент «Управление». Здесь необходимо выбрать из контекстного меню «Надстройки Excel» и кликнуть «ОК».

6

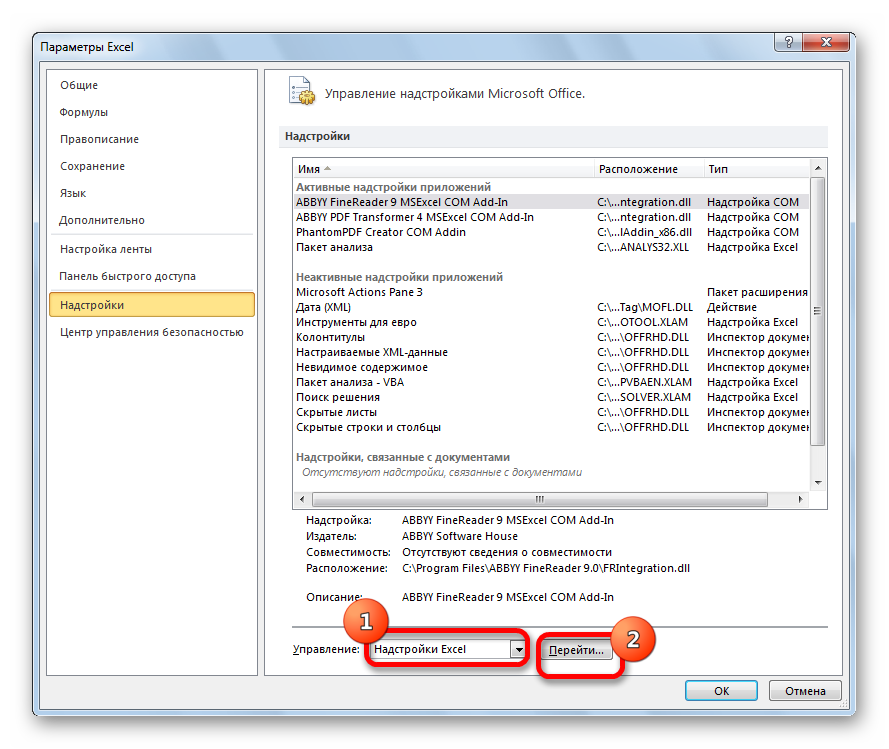
1. Открылось специальное окно надстроек. Ставим галочку рядом с элементом «Пакет анализа». Кликаем «ОК».
2. Активация прошла успешно. Теперь переходим в «Данные». Появился блок «Анализ», в котором необходимо кликнуть «Анализ данных».
3. В новом появившемся окошке выбираем элемент «Корреляция» и жмем на «ОК».

7

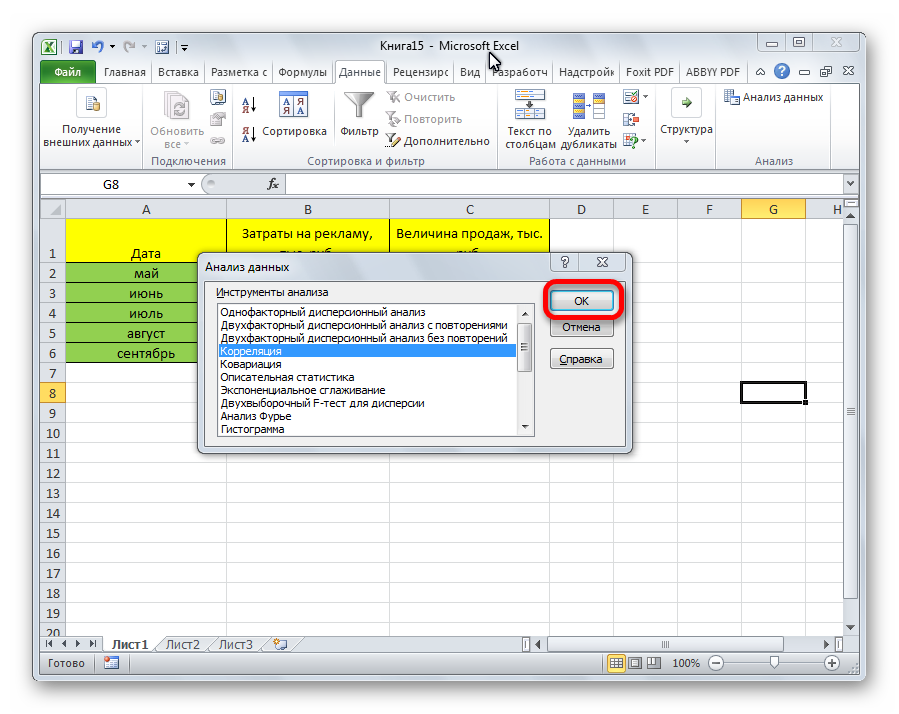
1. На экране появилось окошко настроек анализа. В строчку «Входной интервал» необходимо ввести диапазон абсолютно всех колонок, принимающих участие в анализе. В рассматриваемом примере — это столбики «Величина продаж» и «Затраты на рекламу». В настройках отображения вывода изначально выставлен параметр «Новый рабочий лист», что означает показ результатов на другом листе. По желанию можно поменять локацию вывода результата. После проведения всех настроек нажимаем на «ОК».

8

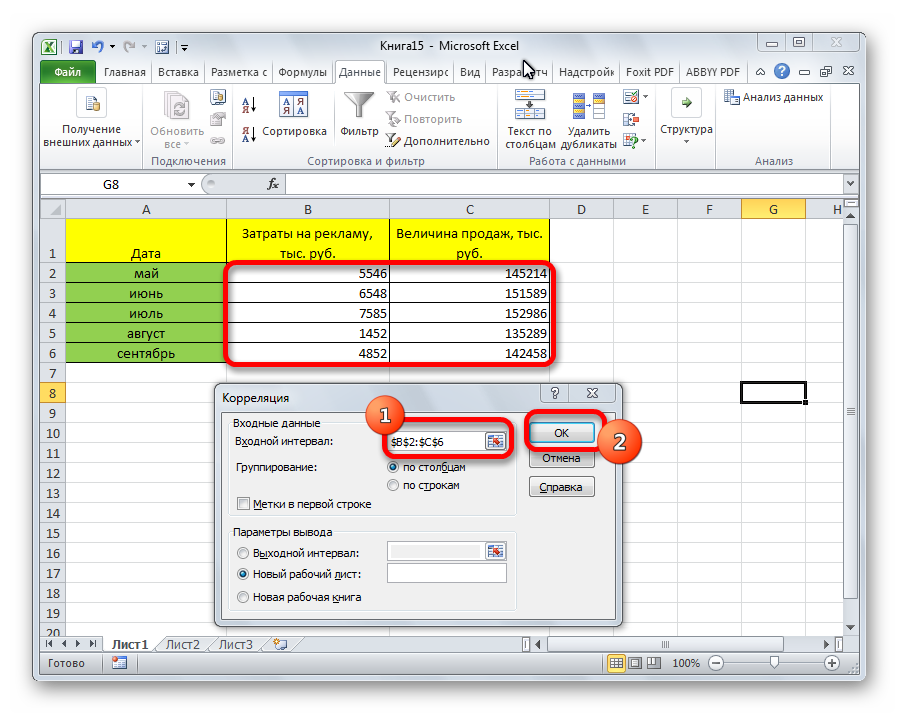
Вывелись итоговые показатели. Результат такой же, как и в первом методе – 0,97.

Определение и вычисление множественного коэффициента корреляции в MS Excel

Для выявления уровня зависимости нескольких величин применяются множественные коэффициенты. В дальнейшем итоги сводятся в отдельную табличку, именуемую корреляционной матрицей.

1. В разделе «Данные» находим уже известный блок «Анализ» и жмем «Анализ данных».

9

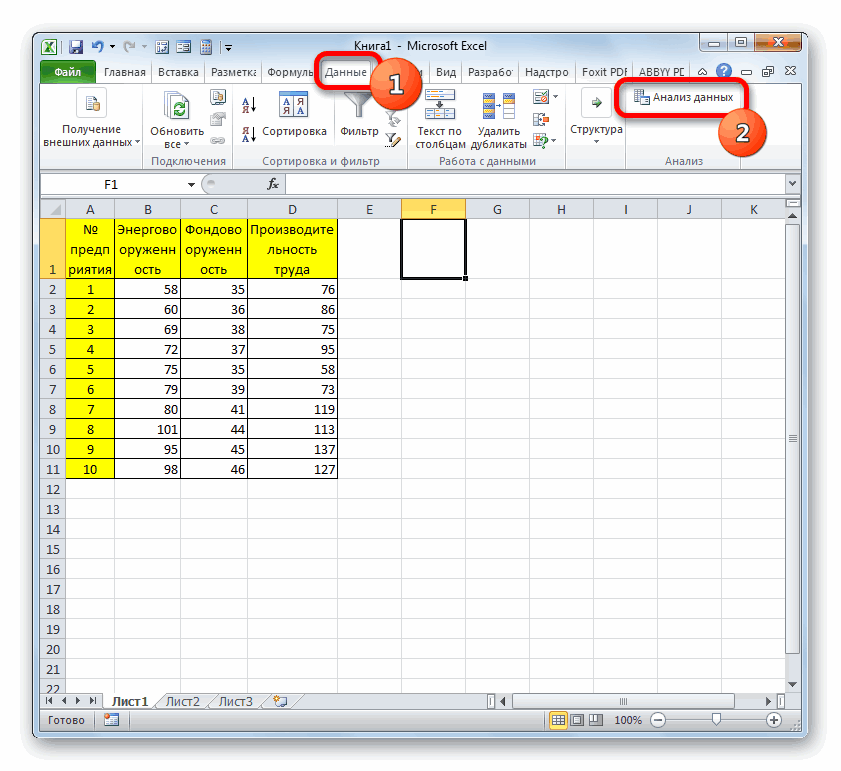
1. В отобразившемся окошке жмем на элемент «Корреляция» и кликаем на «ОК».
2. В строку «Входной интервал» вбиваем интервал по трём или более столбцам исходной таблицы. Диапазон можно ввести вручную или же просто выделить его ЛКМ, и он автоматически отобразится в нужной строчке. В «Группирование» выбираем подходящий способ группировки. В «Параметр вывода» указывает место, в которое будут выведены результаты корреляции. Кликаем «ОК».

10

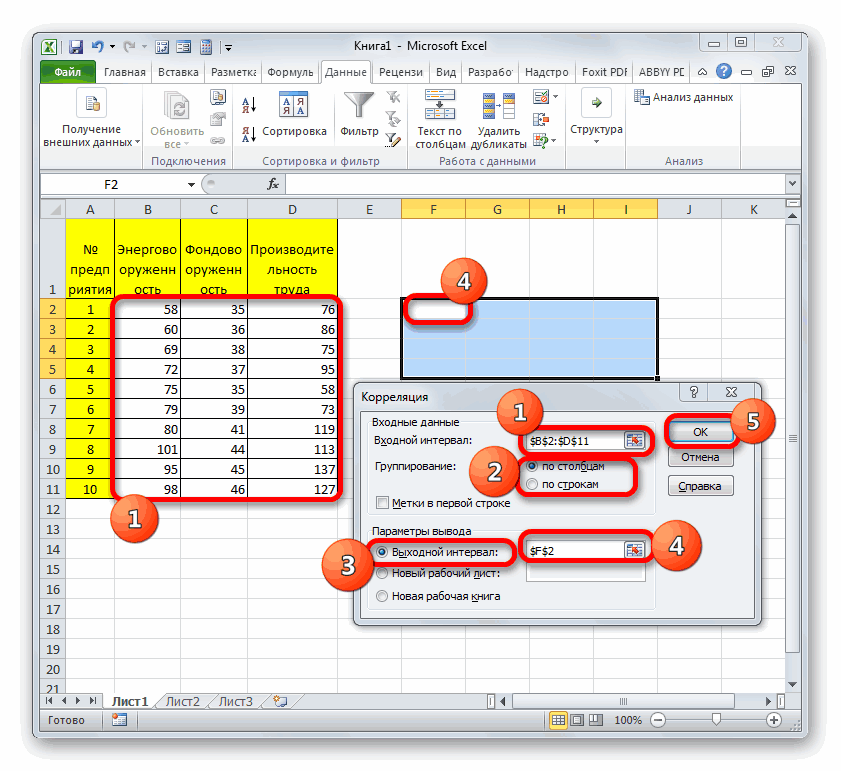
1. Готово! Построилась матрица корреляции.

11

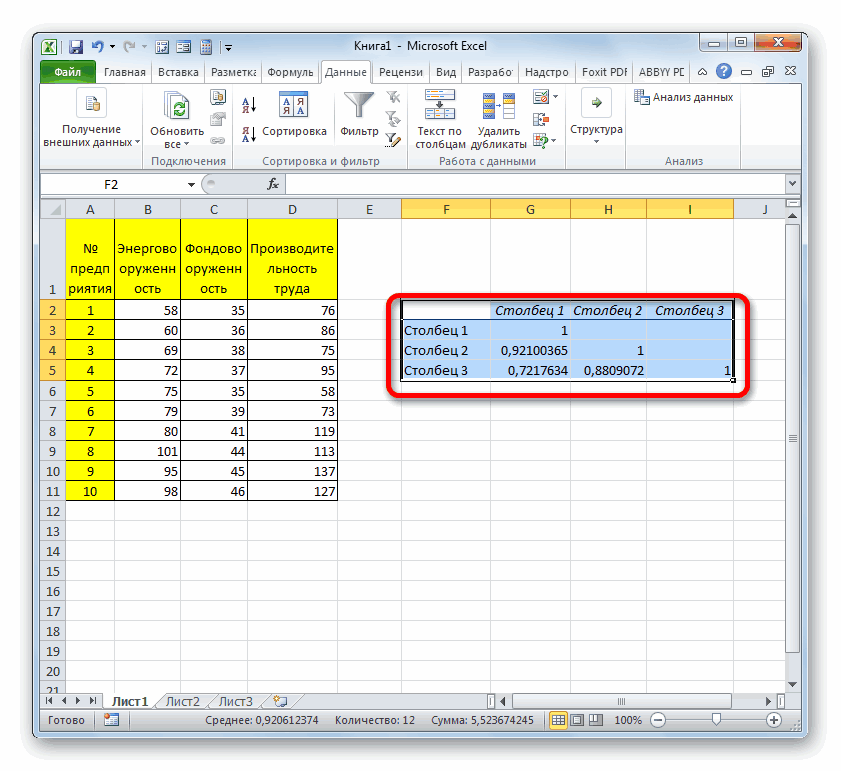
Коэффициент парной корреляции в Excel

Разберем, как правильно проводить коэффициент парной корреляции в табличном процессоре Excel.

Расчет коэффициента парной корреляции в Excel

К примеру, у вас есть значения величин х и у.

12

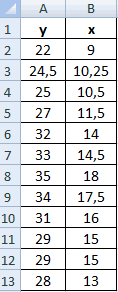
Х – это зависимая переменна, а у – независимая. Необходимо найти направление и силу связи между этими показателями. Пошаговая инструкция:

1. Выявим средние показатели величин при помощи функции СРЗНАЧ.

13

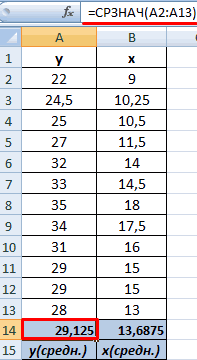
1. Произведем расчет каждого х и хсредн, у и усредн при помощи оператора «-».

14

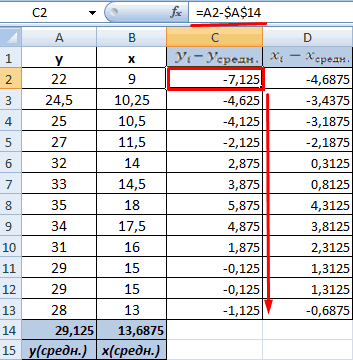
1. Производим перемножение вычисленных разностей.

15

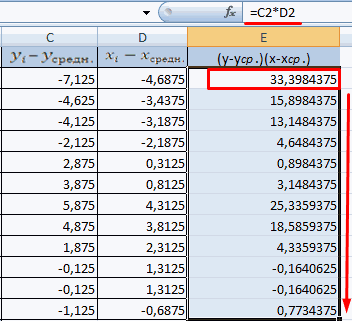
1. Вычисляем сумму показателей в этом столбце. Числитель – найденный результат.

16

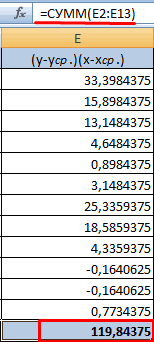
1. Посчитаем знаменатели разницы х и х-средн, у и у-средн. Для этого произведем возведение в квадрат.

17

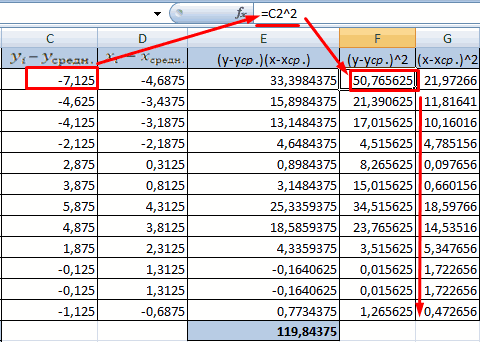
1. Используя функцию АВТОСУММА, найдем показатели в полученных столбиках. Производим перемножение. При помощи функции КОРЕНЬ возводим результат в квадрат.

18

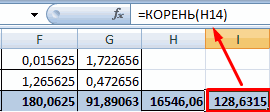
1. Производим подсчет частного, используя значения знаменателя и числителя.

19 20

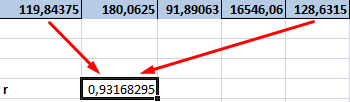
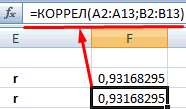
1. КОРРЕЛ – интегрированная функция, которая позволяет предотвратить проведение сложнейших расчетов. Заходим в «Мастер функций», выбираем КОРРЕЛ и указываем массивы показателей х и у. Строим график, отображающий полученные значения.

21

Матрица парных коэффициентов корреляции в Excel

Разберем, как проводить подсчет коэффициентов парных матриц. К примеру, есть матрица из четырех переменных.

22

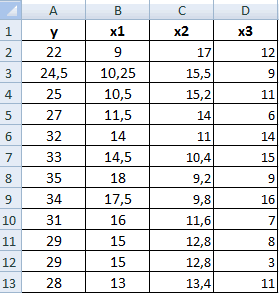
1. Заходим в «Анализ данных», находящийся в блоке «Анализ» вкладки «Данные». В отобразившемся списке выбираем «Корелляция».
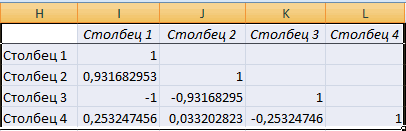
2. Выставляем все необходимые настройки. «Входной интервал» – интервал всех четырех колонок. «Выходной интервал» – место, в котором желаем отобразить итоги. Кликаем на кнопку «ОК».
3. В выбранном месте построилась матрица корреляции. Каждое пересечение строки и столбца – коэффициенты корреляции. Цифра 1 отображается при совпадающих координатах.

23

Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel

КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.

Примеры использования функции КОРРЕЛ в Excel

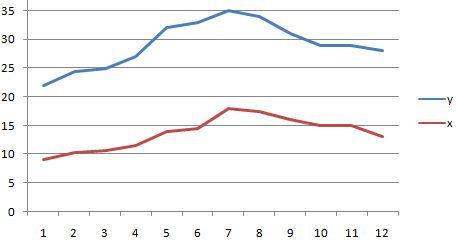
Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:

24

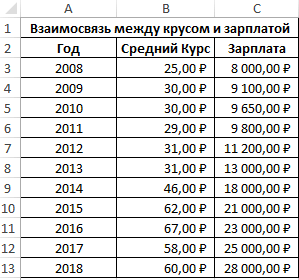
Алгоритм расчёта выглядит следующим образом:

25

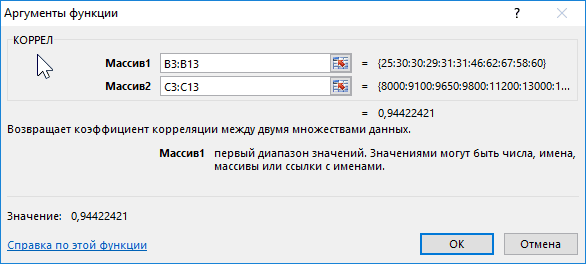
Отображенный показатель близок к 1. Результат:

26

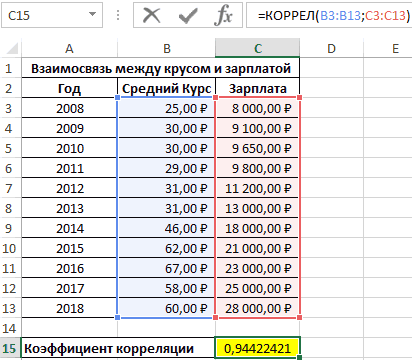
Определение коэффициента корреляции влияния действий на результат

Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.

27

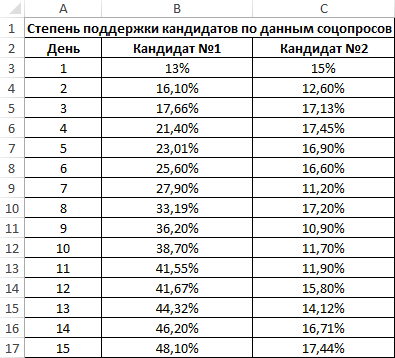
Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:

28

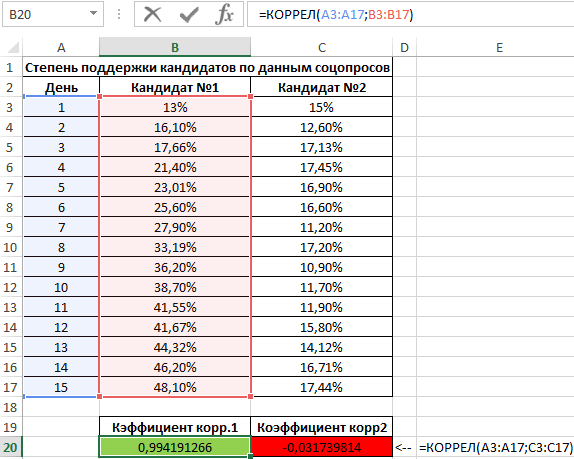
Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.

Анализ популярности контента по корреляции просмотров и репостов видео

Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:

29

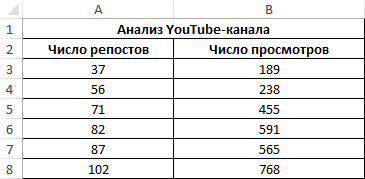
Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:

0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная прямая зависимость»;»Сильная обратная зависимость»);»Слабая зависимость или ее отсутствие»)’ >

Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:

30

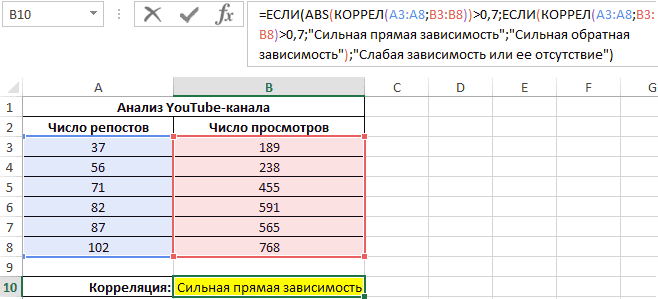
Теперь производим построение графика:

31

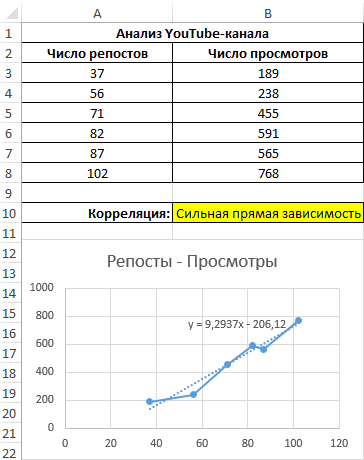
Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:

32

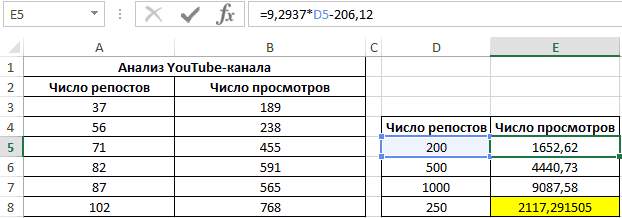
Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’ >. Получаем следующие результаты:

33

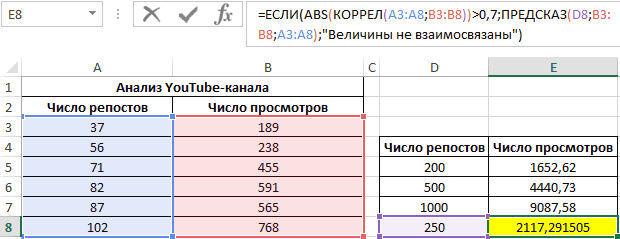
Особенности использования функции КОРРЕЛ в Excel

Данная функция имеет нижеприведенные особенности:

1. Не учитываются ячейки пустого типа.
2. Не учитываются ячейки, в которых находится информация типа Boolean и Text.
3. Двойное отрицание «—» применяется для учёта логических величин в виде чисел.
4. Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.

Оценка статистической значимости коэффициента корреляции

При проверке значимости корреляционного коэффициента нулевая гипотеза состоит в том, что показатель имеет значение 0, а альтернативная не имеет. Для проверки применяется нижеприведенная формула:

34

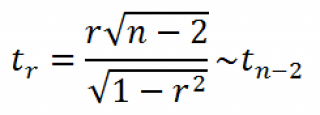
Заключение

Корреляционный анализ в табличном процессоре – это простой и автоматизированный процесс. Для его выполнения необходимо знать всего лишь, где находятся нужные инструменты и как их активировать через настройки программы.

Корреляции для начинающих

Апдейт для тех, кто сочтет статью полезной и занесет в избранное. Есть приличный шанс, что пост уйдет в минуса, и я буду вынужден унести его в черновики. Сохраняйте копию!

Краткий и несложный материал для неспециалистов, рассказывающий в наглядной форме о различных методах поиска регрессионных зависимостей. Это все и близко не академично, зато надеюсь что понятно. Прокатит как мини-методичка по обработке данных для студентов естественнонаучных специальностей, которые математику знают плохо, впрочем как и автор. Расчеты в Матлабе, подготовка данных в Экселе — так уж повелось в нашей местности

Введение

Зачем это вообще надо? В науке и около нее очень часто возникает задача предсказания какого-то неизвестного параметра объекта исходя из известных параметров этого объекта (предикторов) и большого набора похожих объектов, так называемой учебной выборки. Пример. Вот мы выбираем на базаре яблоко. Его можно описать такими предикторами: красность, вес, количество червяков. Но как потребителей нас интересует вкус, измеренный в попугаях по пятибалльной шкале. Из жизненного опыта нам известно, что вкус с приличной точностью равен 5*красность+2*вес-7*количество червяков. Вот про поиск такого рода зависимостей мы и побеседуем. Чтобы обучение пошло легче, попробуем предсказать вес девушки исходя из ее 90/60/90 и роста.

Исходные данные

В качестве объекта исследования возьму данные о параметрах фигуры девушек месяца Плейбоя. Источник — www.wired.com/special_multimedia/2009/st_infoporn_1702, слегка облагородил и перевел из дюймов в сантиметры. Вспоминается анекдот про то, что 34 дюйма — это как два семнадцатидюймовых монитора. Также отделил записи с неполной информацией. При работе с реальными объектами их можно использовать, но сейчас они нам только мешают. Зато их можно использовать для проверки адекватности полученных результатов. Все данные у нас непрерывные, то есть грубо говоря типа float. Они приведены к целым числам только чтобы не загромождать экран. Есть способы работы и с дискретными данными — в нашем примере это например может быть цвет кожи или национальность, которые принимают одно из фиксированного набора значений. Это больше имеет отношение к методам классификации и принятия решений, что тянет еще на один мануал. Data.xls В файле два листа. На первом собственно данные, на втором — отсеянные неполные данные и набор для проверки нашей модели.

Обозначения

W — вес реальный
W_p — вес, предсказанный нашей моделью
S — бюст
T — талия
B — бедра
L — рост
E — ошибка модели

Как оценить качество модели?

Задача нашего упражнения — получить некую модель, которая описывает какой-либо объект. Способ получения и принцип работы конкретной модели нас пока не волнует. Это просто функция f(S, T, B, L), которая выдает вес девушки. Как понять, какая функция хорошая и качественная, а какая не очень? Для этого используется так называемая fitness function. Самая классическая и часто используемая — это сумма квадратов разницы предсказанного и реального значения. В нашем случае это будет сумма (W_p — W)^2 для всех точек. Собственно, отсюда и пошло название «метод наименьших квадратов». Критерий не лучший и не единственный, но вполне приемлемый как метод по умолчанию. Его особенность в том, что он чувствителен по отношению к выбросам и тем самым, считает такие модели менее качественными. Есть еще всякие методы наименьших модулей итд, но сейчас нам это пока не надо.

Простая линейная регрессия

Самый простой случай. У нас одна переменная-предиктор и одна зависимая переменная. В нашем случае это может быть например рост и вес. Нам надо построить уравнение W_p = a*L+b, т.е. найти коэффициенты a и b. Если мы проведем этот расчет для каждого образца, то W_p будет максимально совпадать с W для того же образца. То есть у нас для каждой девушки будет такое уравнение:
W_p_i = a*L_i+b
E_i = (W_p-W)^2

Общая ошибка в таком случае составит sum(E_i). В результате, для оптимальных значений a и b sum(E_i) будет минимальным. Как же найти уравнение?

Матлаб

Для упрощения очень рекомендую поставить плагин для Excel под названием Exlink. Он в папке matlab/toolbox/exlink. Очень облегчает пересылку данных между программами. После установки плагина появляется еще одно меню с очевидным названием, и автоматически запускается Матлаб. Переброс информации из Экселя в Матлаб запускается командой «Send data to MATLAB», обратно, соответственно, — «Get data from MATLAB». Пересылаем в Матлаб числа из столбца L и отдельно из W, без заголовков. Переменные назовем так же. Функция расчета линейной регрессии — polyfit(x,y,1). Единица показывает степень аппроксимационного полинома. У нас он линейный, поэтому единица. Получаем наконец-то коэффициенты регрессии: regr=polyfit(L,W,1) . a мы можем получить как regr(1), b — как regr(2). То есть мы можем получить наши значения W_p: W_p=L*repr(1)+repr(2) . Вернем их назад в Эксель.

Графичек

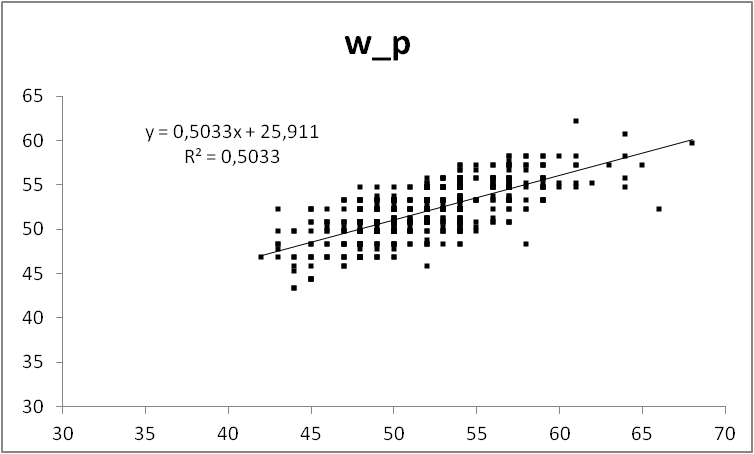
Мда, негусто. Это график W_p(W). Формула на графике показывает связь W_p и W. В идеале там будет W_p = W*1 + 0. Вылезла дискретизация исходных данных — облако точек клетчатое. Коэффициент корреляции ни в дугу — данные слабо коррелированы между собой, т.е. наша модель плохо описывает связь веса и роста. По графику это видно как точки, расположенные в форме слабо вытянутого вдоль прямой облака. Хорошая модель даст облако растянутое в узкую полосу, еще более плохая — просто хаотичный набор точек или круглое облако. Модель необходимо дополнить. Про коэффициент корреляции стоит рассказать отдельно, потому что его часто используют абсолютно неправильно.

Расчет в матричном виде

Можно и без всяких полифитов справиться с построением регрессии, если слегка дополнить столбец с величинами роста еще одним столбцом, заполненным единицами: L(:,2)=1 . Двойка показывает номер столбца, в который пишутся единицы. Тогда коэффициенты регрессии можно будет найти по такой формуле: repr=inv(L’*L)*L’*W . И обратно, найти W_p: W_p=L*repr . Когда осознаешь магию матриц, пользоваться функциями становится неприкольно. Единичный столбец нужен для расчета свободного члена регрессии, то есть просто слагаемого без умножения на параметр. Если его не добавлять, то в регрессии будет всего один член: W_p=a*L. Достаточно очевидно, что она будет хуже по качеству, чем регрессия с двумя слагаемыми. В целом, избавляться от свободного члена надо только в том случае, если он точно не нужен. По умолчанию он все-таки присутствует.

Мультилинейная регрессия

В русскоязычной литературе прошлых лет упоминается как ММНК — метод множественных наименьших квадратов. Это расширение метода наименьших квадратов для нескольких предикторов. То есть у нас в дело идет не только рост, но и все остальные, так сказать, горизонтальные размеры. Подготовка данных точно такая же: обе матрицы в матлаб, добавление столбца единиц, расчет по той же самой формуле. Для любителей функций есть b = regress(y,X) . Эта функция также требует добавления столбца единиц. Повторяем расчет по формуле из раздела про матрицы, пересылаем в Эксель, смотрим.

Попытка номер два

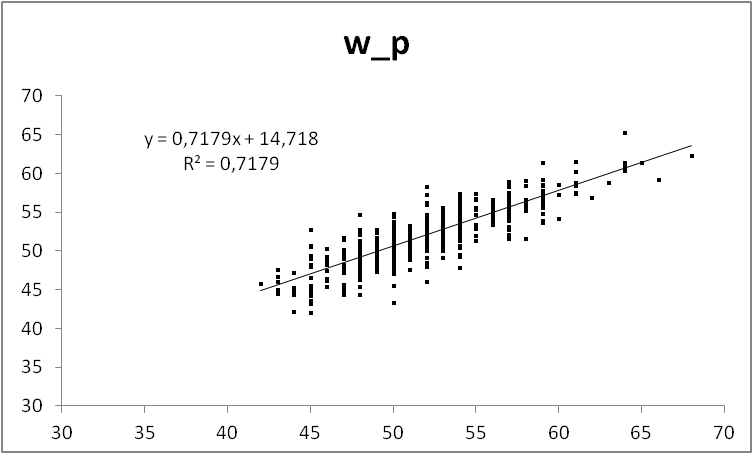
А так получше, но все равно не очень. Как видим, клетчатость осталась только по горизонтали. Никуда не денешься, исходные веса были целыми числами в фунтах. То есть после конверсии в килограммы они ложатся на сетку с шагом около 0.5. Итого финальный вид нашей модели:

W_p = 0.2271*S + 0.1851*T + 0.3125*B + 0.3949*L — 72.9132

Объемы в сантиметрах, вес в кг. Поскольку у нас все величины кроме роста в одних единицах измерения и примерно одного порядка по величине (кроме талии), то мы можем оценить их вклады в общий вес. Рассуждения примерно в таком духе: коэффициент при талии самый маленький, равно как и сами величины в сантиметрах. Значит, вклад этого параметра в вес минимален. У бюста и особенно у бедер он больше, т.е. сантиметр на талии дает меньшую прибавку к массе, чем на груди. А больше всего на вес влияет объем задницы. Впрочем, это знает любой интересующийся вопросом мужчина. То есть как минимум, наша модель реальной жизни не противоречит.

Валидация модели

Название громкое, но попробуем получить хотя бы ориентировочные веса тех девушек, для которых есть полный набор размеров, но нет веса. Их 7: с мая по июнь 1956 года, июль 1957, март 1987, август 1988. Находим предсказанные по модели веса: W_p=X*repr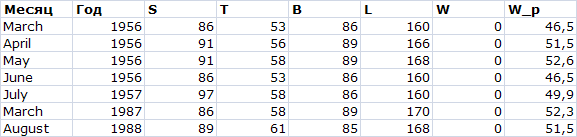

Что ж, по крайней мере в текстовом виде выглядит правдоподобно. А насколько это соответствует реальности — решать вам

Применимость

Если вкратце — полученная модель годится для объектов, подобных нашему набору данных. То есть по полученным корреляциям не стоит считать параметры фигур женщин с весом 80+, возрастом, сильно отличающимся от среднего по больнице итд. В реальных применениях можно считать, что модель пригодна, если параметры изучаемого объекта не слишком отличаются от средних значений этих же параметров для исходного набора данных. Могут возникнуть (и возникнут) проблемы, если у нас предикторы сильно коррелированы между собой. То есть, например это рост и длина ног. Тогда коэффициенты для соответствующих величин в уравнении регрессии будут определены с малой точностью. В таком случае надо выбросить один из параметров, или воспользоваться методом главных компонент для снижения количества предикторов. Если у нас малая выборка и/или много предикторов, то мы рискуем попасть в переопределенность модели. То есть если мы возьмем 604 параметра для нашей выборки (а в таблице всего 604 девушки), то сможем аналитически получить уравнение с 604+1 слагаемым, которое абсолютно точно опишет то, что мы в него забросили. Но предсказательная сила у него будет весьма невелика. Наконец, далеко не все объекты можно описать мультилинейной зависимостью. Бывают и логарифмические, и степенные, и всякие сложные. Их поиск — это уже совсем другой вопрос.

Содержание:

Корреляционный анализ:

Связи между различными явлениями в природе сложны и многообразны, однако их можно определённым образом классифицировать. В технике и естествознании часто речь идёт о функциональной зависимости между переменными x и у, когда каждому возможному значению х поставлено в однозначное соответствие определённое значение у. Это может быть, например, зависимость между давлением и объёмом газа (закон Бойля—Мариотта).

В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияния каждого из которых ничтожно, а число их велико. В этом случае связь теряет свою однозначность и изучаемая физическая система переходит не в определённое состояние, а в одно из возможных для неё состояний. Здесь речь может идти лишь о так называемой статистической связи. Статистическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения. Следовательно, для изучения статистической зависимости нужно знать аналитический вид двумерного распределения. Однако нахождение аналитического вида двумерного распределения по выборке ограниченного объёма, во-первых, громоздко, во-вторых, может привести к значительным ошибкам. Поэтому на практике при исследовании зависимостей между случайными переменными X и У обычно ограничиваются изучением зависимости между одной из них и условным математическим ожиданием другой, т.е.

Вопрос о том, что принять за зависимую переменную, а что — за независимую, следует решать применительно к каждому конкретному случаю.

Знание статистической зависимости между случайными переменными имеет большое практическое значение: с её помощью можно прогнозировать значение зависимой случайной переменной в предположении, что независимая переменная примет определенное значение. Однако, поскольку понятие статистической зависимости относится к осредненным условиям, прогнозы не могут быть безошибочными.    Применяя некоторые вероятностные методы, как будет показано далее, можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.

Введение в корреляционный анализ

Связь, которая существует между случайными величинами разной природы, например, между величиной X и величиной Y, не обязательно является следствием прямой зависимости одной величины от другой (так называемая функциональная связь).

В некоторых случаях обе величины зависят от целой совокупности разных факторов, общих для обеих величин, в результате чего и формируется связанные друг с другом закономерности. Когда связь между случайными величинами обнаружена с помощью статистики, мы не можем утверждать, что обнаружили причину происходящего изменения параметров, скорее мы лишь увидели два взаимосвязанных следствия.

Например, дети, которые чаще смотрят по телевизору американские боевики, меньше читают. Дети, которые больше читают, лучше учатся. Не так-то просто решить, где тут причины, а где следствия, но это и не является задачей статистики.

Статистика может лишь, выдвинув гипотезу о наличии связи, подкрепить ее цифрами. Если связь действительно имеется, говорят, что между двумя случайными величинами есть корреляция. Если увеличение одной случайной величины связано с увеличением второй случайной величины, корреляция называется прямой.

Например, количество прочитанных страниц за год и средний балл (успеваемость). Если, напротив рост одной величины связано с уменьшением другой, говорят об обратной корреляции. Например, количество боевиков и количество прочитанных страниц. Взаимная связь двух случайных величин называется корреляцией, корреляционный анализ позволяет определить наличие такой связи, оценить, насколько тесна и существенна эта связь. Все это выражается количественно.

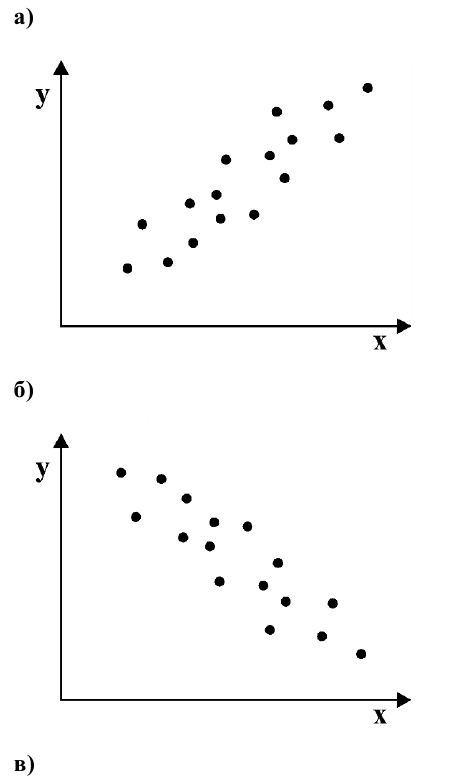
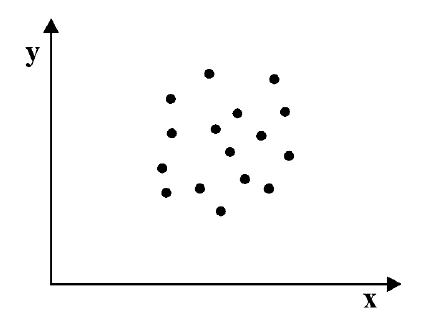
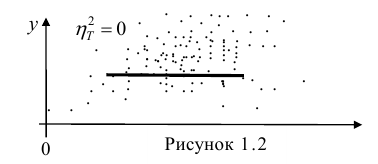
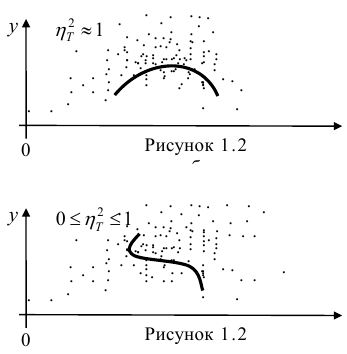
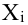
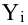
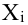
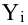
Как определить, есть ли корреляция между величинами? В большинстве случаев, это можно увидеть на обычном графике. Например, по каждому ребенку из нашей выборки можно определить величину (число страниц) и (средний балл годовой оценки), и записать эти данные в виде таблицы. Построить оси X и Y, а затем нанести на график весь ряд точек таким образом, чтобы каждая из них имела определенную пару координат (,) из нашей таблицы. Поскольку мы в данном случае затрудняемся определить, что можно считать причиной, а что следствием, не важно, какая ось будет вертикальной, а какая горизонтальной.

Если график имеет вид а), то это говорит о наличии прямой корреляции, в случае, если он имеет вид б) — корреляция обратная. Отсутствие корреляции тоже можно приблизительно определить по виду графика — это случай в).

С помощью коэффициента корреляции можно посчитать насколько тесная связь существует между величинами.

Пусть, существует корреляция между ценой и спросом на товар. Количество купленных единиц товара в зависимости от цены у разных продавцов показано в таблице: Видно, что мы имеем дело с обратной корреляцией. Для количественной оценки тесноты связи используют коэффициент корреляции:

Коэффициент r мы считаем в Excel, с помощью функции 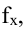далее статистические функции, функция KOPPEЛ. По подсказке программы вводим мышью в два соответствующих поля два разных массива (X и Y). В нашем случае коэффициент корреляции получился r = -0,988.

Надо отметить, что чем ближе к 0 коэффициент корреляции, тем слабее связь между величинами. Наиболее тесная связь при прямой корреляции соответствует коэффициенту r, близкому к +1. В нашем случае, корреляция обратная, но тоже очень тесная, и коэффициент близок к -1.

Что можно сказать о случайных величинах, у которых коэффициент имеет промежуточное значение? Например, если бы мы получили r = 0,65. В этом случае, статистика позволяет сказать, что две случайные величины частично связаны друг с другом. Скажем на 65% влияние на количество покупок оказывала цена, а на 35% — другие обстоятельства. И еще одно важное обстоятельство надо упомянуть.

Поскольку мы говорим о случайных величинах, всегда существует вероятность, что замеченная нами связь — случайное обстоятельство. Причем вероятность найти связь там, где ее нет, особенно велика тогда, когда точек в выборке мало, а при оценке Вы не построили график, а просто посчитали значение коэффициента корреляции на компьютере. Так, если мы оставим всего две разные точки в любой произвольной выборке, коэффициент корреляции будет равен или +1 или -1. Из школьного курса геометрии мы знаем, что через две точки можно всегда провести прямую линию. Для оценки статистической достоверности факта обнаруженной Вами связи полезно использовать так называемую корреляционную поправку:

Связь нельзя считать случайной, если:

В то время как задача корреляционного анализа — установить, являются ли данные случайные величины взаимосвязанными, цель регрессионного анализа — описать эту связь аналитической зависимостью, т.е. с помощью уравнения. Мы рассмотрим самый несложный случай, когда связь между точками на графике может быть представлена прямой линией. Уравнение этой прямой линии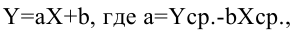

Зная уравнение прямой, мы можем находить значение функции по значению аргумента в тех точках, где значение X известно, a Y — нет. Эти оценки бывают очень нужны, но они должны использоваться осторожно, особенно, если связь между величинами не слишком тесная. Отметим также, что из сопоставления формул для b и r видно, что коэффициент не дает значение наклона прямой, а лишь показывает сам факт наличия связи.

Определение формы связи. Понятие регрессии

Определить форму связи — значит выявить механизм получения зависимой случайной переменной. При изучении статистических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т.д.).

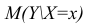
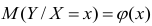
Условное математическое ожидание случайной переменной К, рассматриваемое как функция х, т.е. , называется

функцией регрессии случайной переменной Y относительно X (или функцией регрессии Y по X). Точно так же условное математическое ожидание

 случайной переменной X, т.е. называется функцией регрессии случайной переменной X относительно Y (или функцией регрессии X по Y).

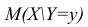
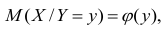
На примере, дискретного распределения найдём функцию регрессии.

Функция регрессии имеет важное значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной. Точность такого прогноза определяется дисперсией условного распределения.

Несмотря на важность понятия функции регрессии, возможности её практического применения весьма ограничены. Для оценки функции регрессии необходимо знать аналитический вид двумерного распределения (X, Y). Только в этом случае можно точно определить вид функции регрессии, а затем оценить параметры двумерного распределения. Однако для подобной оценки мы чаще всего располагаем лишь выборкой ограниченного объема, по которой нужно найти вид двумерного распределения (X, Y), а затем вид функции регрессии. Это может привести к значительным ошибкам, так как одну и ту же совокупность точек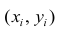на плоскости можно одинаково успешно описать с помощью различных функций. Именно поэтому возможности практического применения функции регрессии ограничены. Для характеристики формы связи при изучении зависимости используют понятие кривой регрессии.

Кривой регрессии Y по X (или Y на А) называют условное среднее значение случайной переменной У, рассматриваемое как функция определенного класса, параметры которой находят методом наименьших квадратов по наблюдённым значениям двумерной случайной величины (х, у), т.е.

Аналогично определяется кривая регрессии X по Y (X на Y):

Кривую регрессии называют также эмпирическим уравнением регрессии или просто уравнением регрессии. Уравнение регрессии является оценкой соответствующей функции регрессии.

Возникает вопрос:    почему для определения кривой регрессии

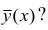
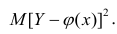
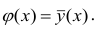
используют именно условное среднее Функция у(х) обладает одним замечательным свойством: она даёт наименьшую среднюю погрешность оценки прогноза. Предположим, что кривая регрессии — произвольная функция. Средняя погрешность прогноза по кривой регрессии определяется математическим ожиданием квадрата разности между измеренной величиной и вычисленной по формуле кривой регрессии, т.е. . Естественно потребовать вычисления такой кривой регрессии, средняя погрешность прогноза по которой была бы наименьшей. Таковой является Это следует из свойств минимальности рассеивания около центра распределения

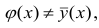
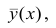
Если рассеивание вычисляется относительно то средний квадрат отклонения увеличивается. Поэтому можно сказать, что кривая регрессии, выражаемая как минимизирует среднеквадратическую погрешность прогноза величины Y по X.

Основные положения корреляционного анализа

Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. С помощью этих методов решают разные задачи; требования, предъявляемые к исследуемым переменным, в каждом методе различны.

Основная задача корреляционного анализа — выявление связи между случайными переменными путём точечной и интервальной оценки парных коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации, оценки частных коэффициентов корреляции. Корреляционный анализ позволяет также оценить функцию регрессии одной случайной переменной на другую.

Предпосылки корреляционного анализа следующие:  

•  1) переменные величины должны быть случайными;
• 2) случайные величины должны иметь совместное нормальное распределение.

Рассмотрим простейший случай корреляционного анализа — двумерную модель. Введём основные понятия и опишем принцип проведения корреляционного анализа. Пусть X и Y — случайные переменные, имеющие совместное нормальное распределение. В этом случае связь между X и Y можно описать коэффициентом корреляции p;. Этот коэффициент определяется как ковариация между X и Y, отнесённая к их среднеквадратическим отклонениям:
(1.1)

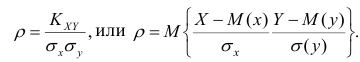
Оценкой коэффициента корреляции является выборочный коэффициент корреляции r. Для его нахождения необходимо знать оценки следующих параметров: 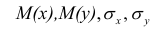  .    Наилучшей оценкой

математического ожидания является среднее арифметическое, т.е.

Оценкой дисперсии служит выборочная дисперсия, т.е.

Тогда выборочный коэффициент корреляции

Коэффициент р называют также парным коэффициентом корреляции, а r— выборочным парным коэффициентом корреляции.

При совместном нормальном законе распределения случайных величин X и Y, используя рассмотренные выше параметры распределения и коэффициент корреляции, можно получить выражение для условного математического ожидания, т. е, записать выражение для функции регрессии одной случайной величины на другую. Так, функция регрессии Y на X имеет вид:

функция регрессии X на Y — следующий вид:

Выражения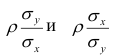 — называют коэффициентами регрессии.

Подставив в (1.3) соответствующие оценки параметров, получим уравнения регрессии, график которых — прямая линия, проходящая через точку 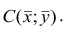Запишем уравнение регрессии у на х и х на у:

Таким образом, в корреляционном анализе на основе оценок параметров двумерной нормальной совокупности получаем оценки тесноты связи между случайными переменными и можем оценить регрессию одной переменной на другую. Особенностью корреляционного анализа является строго линейная зависимость между переменными. Это обусловливается исходными предпосылками. На практике корреляционный анализ можно применять для обработки наблюдений, сделанных на предприятиях при нормальных условиях работы, если случайные изменения свойства сырья или других факторов вызывают случайные изменения свойств продукции.

Свойства коэффициента корреляции

Коэффициент корреляции является одним из самых распространенных способов измерения связи между случайными переменными. Рассмотрим некоторые свойства этого коэффициента.

Теорема 1. Коэффициент корреляции принимает значения на интервале (-1, +1).

Доказательство. Докажем справедливость утверждения для случая дискретных переменных. Запишем явно неотрицательное выражение:

Возведём выражение под знаком суммы в квадрат:

Первое и третье из слагаемых равны единице, поскольку из определения дисперсии следует, что

Таким образом, окончательно получаем

Если коэффициент корреляции положителен, то связь между переменными также положительна и значения переменных увеличиваются или уменьшаются одновременно. Если коэффициент корреляции имеет отрицательное значение, то при увеличении одной переменной уменьшается другая.

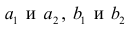
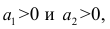
Приведём следующее важное свойство коэффициента корреляции: коэффициент корреляции не зависит от выбора начала отсчёта и единицы измерения, т. е. от любых постоянных таких, что т.е.

Таким образом, переменные X и У можно уменьшать или увеличивать в а раз, а также вычитать или прибавлять к значениям X и У одно и то же число b. В результате величина коэффициента корреляции не изменится.

Если коэффициент корреляции 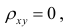то случайные переменные некоррелированы. Понятие некоррелированности не следует смешивать с понятием независимости, независимые величины всегда некоррелированы. Однако обратное утверждение невероятно: некоррелированные величины могут быть зависимы и даже функционально, однако эта связь не линейная.

Выборочный коэффициент корреляции вычисляют по формуле (1.2). Имеется несколько модификаций этой формулы, которые удобно использовать при той или иной форме представления исходной информации. Так, при малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по формуле

Если информация имеет вид корреляционной таблицы (см. п 1.5), то удобно пользоваться формулой

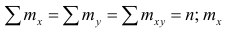
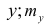
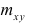
где — суммарная частота наблюдаемого значенияпризнака х при всех значениях — суммарная частота наблюдаемого значения признака упри всех значениях х; — частота появления пары признаков (x, у).

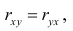
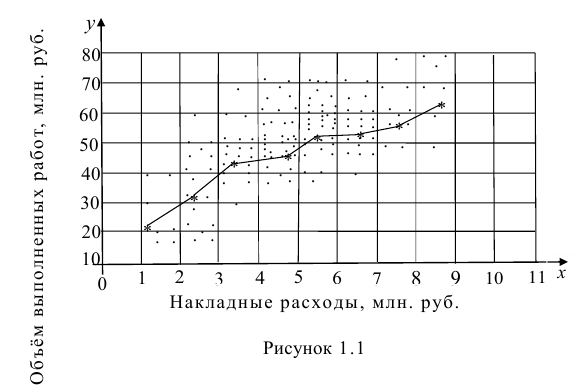
Из формулы (1.2) очевидно, что т.е. величина выборочного коэффициента корреляции не зависит от порядка следования переменных, поэтому обычно пишут просто r.

Поле корреляции. Вычисление оценок параметров двумерной модели

На практике для вычисления оценок параметров двумерной модели удобно использовать корреляционную таблицу и поле корреляции. Пусть, например, изучается зависимость между объёмом выполненных работ (у) и накладными расходами (x). Имеем выборку из генеральной совокупности, состоящую из 150 пар переменных 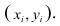   Считаем, что предпосылки корреляционного анализа выполнены.

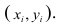
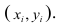
Пару случайных чисел    можно изобразить графически в виде точки с координатами. Аналогично можно изобразить весь набор пар случайных чисел (всю выборку). Однако при большом объёме выборки это затруднительно. Задача упрощается, если выборку упорядочить, т.е. переменные сгруппировать. Сгруппированные ряды могут быть как дискретными, так и интервальными.

По осям координат откладывают или дискретные значения переменных, или интервалы их изменения. Для интервального ряда наносят координатную сетку. Каждую пару переменных из данной выборки изображают в виде точки с соответствующими координатами для дискретного ряда или в виде точки в соответствующей клетке для интервального ряда. Такое изображение корреляционной зависимости называют полем корреляции. На рис. 1.1 изображено поле корреляции для выборки, состоящей из 150 пар переменных (ряд интервальный).
 

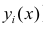
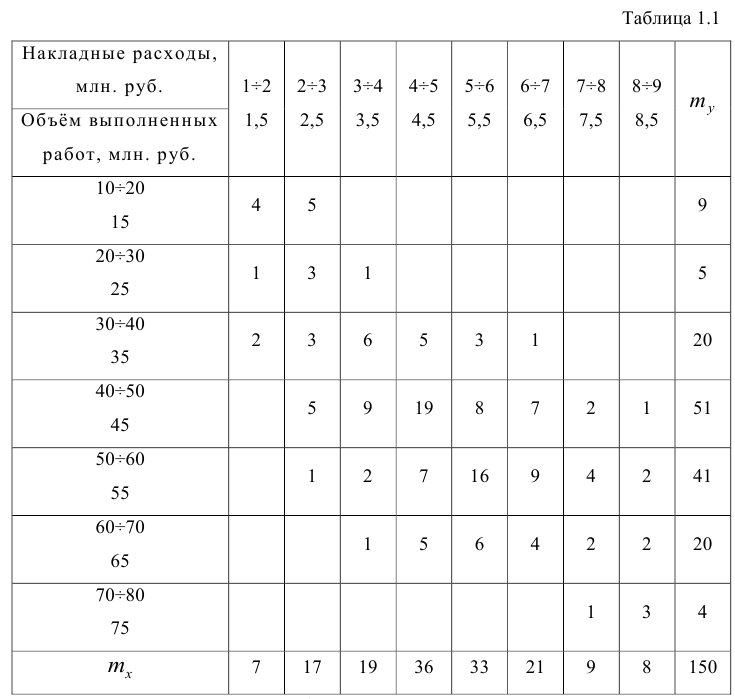
Если вычислить средние значения у в каждом интервале изменения х [обозначим их )], нанести эти точки на рис. 1.1 и соединить между собой, то получим ломаную линию, по виду которой можно судить, как в среднем меняются у в зависимости от изменения х. По виду этой линии можно также сделать предположение о форме связи между переменными. В данном случае ломаную линию можно аппроксимировать прямой линией, так как она достаточно хорошо приближается к ней. По выборочным данным можно построить также корреляционную табл. 1.1.

Корреляционную таблицу, как и поле корреляции, строят по
сгруппированному ряду (дискретному или интервальному). Табл. 1.1 построена на основе интервального ряда. В первой строке и первом столбце таблицы помещают интервалы изменения х и у и значения середин интервалов. Так, например, 1,5 — середина интервала изменения *=1-2,15— середина интервала изменения у= 10-20. В ячейки, образованные пересечением строк и столбцов, заносят частоты попадания пар значений (л у) в соответствующие интервалы по х и у. Например, частота 4 означает, что в интервал изменения у от 10 до 20 попало 4 пары наблюдавшихся значений. 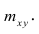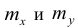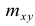Эти частоты обозначают В 9-й строке и 10-м столбце находятся значения — суммы по соответствующим столбцу и строке.

Как будет показано в дальнейшем, корреляционно таблицей удобно пользоваться при вычислении коэффициентов корреляций и параметров уравнений регрессии.

Корреляционная таблица построена на основе интервального ряда, поэтому для оценок параметров воспользуемся формулами гл. 1 для вычисления средней арифметической и дисперсии. Имеем:

(1.6)
 

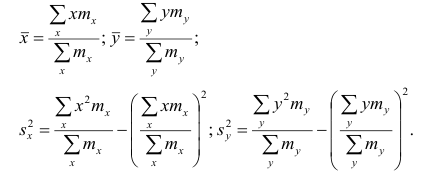
Проверка гипотезы о значимости коэффициента корреляции

На практике коэффициент корреляции р обычно неизвестен. По результатам выборки может быть найдена его точечная оценка — выборочный коэффициент корреляции r.

Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин X и Y. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции г, т.е. установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу 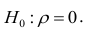. Предполагается наличие двумерного нормального распределения случайных переменных; объём выборки может быть любым. Вычисляют
которая имеет распределение Стьюдента с k=n-2
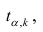
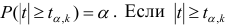
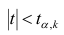
степенями свободы. Для проверки нулевой гипотезы по уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (t-распределение; см. табл. 1 приложения) критическое значение  удовлетворяющее условию, то нулевую гипотезу об отсутствии корреляционной связи между переменными X и Y следует отвергнуть. Переменные считают зависимыми. При нет оснований отвергать нулевую гипотезу.

В случае значимого выборочного коэффициента, корреляции есть смысл построить доверительный интервал для коэффициента корреляций р. Однако для этого нужно знать закон распределения выборочного коэффициента корреляции r.

Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся к хорошо изученным распределениям, например нормальному или Стьюдента. Чаще всего для подбора функции применяют преобразование Фишера. Вычисляют статистику:

где r=thz — гиперболический тангенс от z.

Распределение статистики z хорошо аппроксимируется нормальным распределением с параметрами

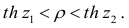
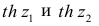
В этом, случае доверительный интервал для римеетвид Величины находят по таблицам по следующим значениям:

где 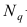— нормированная функция Лапласа для q % доверительного интервала (см. табл. 2 приложений значение функции

Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля, а интервальные оценки для них можно получить по следующим формулам:

где 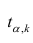имеет распределение Стьюдента с k=n—2 степенями свободы.
 

Корреляционное отношение

На практике часто предпосылки корреляционного анализа нарушаются: один из признаков оказывается величиной не случайной, или признаки не имеют совместного нормального распределения. Однако статистическая зависимость между ними существует. Для изучения связи между признаками в этом случае существует общий показатель зависимости признаков, основанный на показателе изменчивости — общей (или полной) дисперсии.

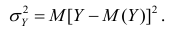
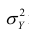
Полной называется дисперсия признака относительно его математического ожидания. Так, для признака Y это Дисперсию можно разложить на две составляющие, одна из которых характеризует влияние фактора X на Y, другая — влияние прочих факторов.

Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной. Представим 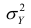в следующем виде:

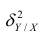
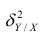
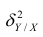
Первое слагаемое обозначимЭто дисперсия функции регрессии относительно математического ожидания признака (в данном случае признака У);.она измеряет влияние признака X на Y. Второе слагаемое обозначим. Это дисперсия признака Y относительно функции регрессии. Её называют также средней из условных дисперсий или остаточной дисперсией измеряет влияние на Y прочих факторов.

Покажем, что 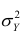действительно можно разложить на два таких слагаемых:

Для простоты полагаем распределение дискретным. Имеем

так как при любом х справедливо равенство

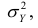
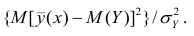
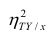
Третье слагаемое в равенстве (1.10) равно нулю, поэтому равенство (1.9) справедливо. Поскольку второе слагаемое в равенстве (1.9) оценивает влияние признака X на Y, то его можно использовать для оценки тесноты связи между X и Y. Тесноту связи удобно оценивать в единицах общей дисперсии т.е. рассматривать отношение. Эту величину обозначают и называют теоретическим корреляционным отношением. Таким образом,

Разделив обе части равенства (1.9) на 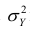получим

Из последней формулы имеем

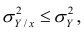
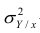
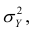
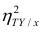
Поскольку так как — составная часть то из равенства (1.12) следует, что значение всегда заключено между нулем и единицей.

Все сделанные выводы справедливы и для 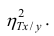   Из равенства (1.12)
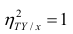
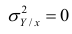
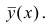
следует, что только тогда, когда , т.е. отсутствует влияние прочих факторов и всё распределение сконцентрировано на кривой регрессии . В этом случае между Y и X существует функциональная зависимость.

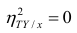
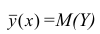
Далее, из равенства (1.12) следует, что тогда и только тогда, когда

= const, т.е. линия регрессии У по X — горизонтальная прямая, проходящая через центр распределения. В этом случае можно сказать, что переменная У не коррелирована с X (рис. 1.2,а, б, в).

Аналогичными свойствами обладает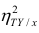— показатель тесноты связи между X и У.

Часто используют величину

Считают, что она не может быть отрицательной. Значения величины 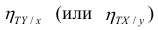также могут находиться лишь в пределах от нуля до единицы. Это очевидно из формулы (1.13).

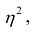
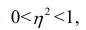
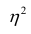
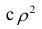
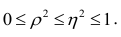
Значения лежащие в интервалеявляются показателями тесноты группировки точек около кривой регрессии независимо от её вида (формы связи). Корреляционное отношение связано следующим образом: В случае линейной зависимости между переменными

Разность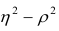 может быть использована как показатель нелинейности связи между переменными.

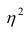
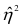
При вычислении по выборочным данным получаем выборочное корреляционное отношение. Обозначим его. Вместо дисперсий в этом случае используются их оценки. Тогда формула (1.12) принимает вид
 

Понятие о многомерном корреляционном анализе

Частный коэффициент корреляции. Основные понятия корреляционного анализа, введенные для двумерной модели, можно распространить на многомерный случай. Задачи и предпосылки корреляционного анализа были сформулированы в п. 1.3. Однако если при изучении взаимосвязи переменных по двумерной модели мы ограничивались рассмотрением парных коэффициентов корреляции, то для многомерной модели этого недостаточно. Многообразие связей между переменными находит отражение в частных и множественных коэффициентах корреляции.

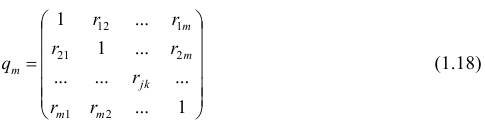
Пусть имеется многомерная нормальная совокупность с m признаками 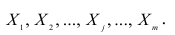В этом случае взаимозависимость между признаками

можно описать корреляционной матрицей. Под корреляционной матрицей будем понимать, матрицу, составленную из парных коэффициентов корреляции (вычисляются по формуле (1,1)):

где 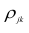— парные коэффициенты корреляции; m — порядок матрицы.

Оценкой парного коэффициента корреляции является выборочный парный коэффициент корреляции, определяемый по формуле (1.2), однако для m признаков формула (9.2) принимает вид

где 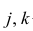— порядковые номера признаков.

Как и в двумерном случае, для оценки коэффициента корреляции необходимо оценить математические ожидания и дисперсии. В многомерном корреляционном анализе имеем т математических ожиданий и m дисперсий, а также m(m—1)/2 парных коэффициентов корреляции. Таким образом, нужно произвести оценку 2m+m(m—1)/2 параметров.

В случае многомерной корреляции зависимости между признаками более многообразны и сложны, чем в двумерном случае. Одной корреляционной матрицей нельзя полностью описать зависимости между признаками. Введём понятие частного коэффициента корреляции l-го порядка.

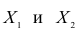
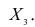
Пусть исходная совокупность состоит из т признаков. Можно изучать зависимости между двумя из них при фиксированном значении l признаков из m-2 оставшихся. Рассмотрим, например, систему из 5 признаков. Изучим зависимости между при фиксированном значении признака В этом случае имеем частный коэффициент корреляции первого порядка, так как фиксируем только один признак.

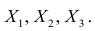
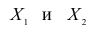
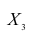
Рассмотрим более подробно структуру частных коэффициентов корреляции на примере системы из трёх признаков . Эта система позволяет изучить частные коэффициенты корреляции только первого порядка, так как нельзя фиксировать больше одного признака. Частный коэффициент корреляции первого порядка для признаков при фиксированном значении выражается через парные коэффициенты
корреляции и имеет вид

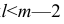
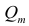
Частный коэффициент корреляции, так же как и парный коэффициент корреляции, изменяется от —1 до +1, В общем виде, когда система состоит из m признаков, частный коэффициент корреляции l-го порядка может быть найден из корреляционной матрицы. Если 1=m—2, то рассматривается матрица порядка m, при— подматрица порядкаl+2, составленная из элементов матрицы , которые отвечают индексам коэффициента частной
корреляции. Например, корреляционная матрица системы из пяти признаков имеет вид

Для определения частного коэффициента корреляции второго порядка, например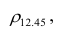 следует использовать подматрицу четвертого порядка,
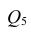
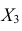
вычеркнув из исходной матрицы третью строку и третий столбец, так как признак не рассматривают.

В общем виде формулу частного коэффициента корреляции l-го порядка (1=m—2) можно записать в виде

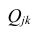
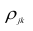
где — алгебраические дополнения к элементу корреляционной
матрицы — алгебраические дополнения к элементам и ркк корреляционной матрицы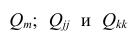

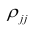
Очевидно, что выражение (1.16) является частым случаем выражения (1.17), в чём легко убедиться, рассмотрев корреляционную матрицу

Оценкой частного коэффициента корреляции l-го порядка является выборочный частный коэффициент корреляции l-го порядка. Он вычисляется на основе корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции:

Формула выборочного частного коэффициента корреляции имеет вид

где 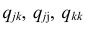— алгебраические дополнения к соответствующим элементам матрицы (1.18).

Частный коэффициент корреляции l-го порядка, вызволенный на основе п наблюдений над признаками, имеет такое же распределение, что и парный коэффициент корреляции, вычисленный 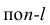наблюдениям. Поэтому значимость частных коэффициентов корреляции оценивают так же, как и в п. 1.6.

Множественный коэффициент корреляции

Часто представляет интерес оценить связь одного из признаков со всеми остальными. Это можно сделать с помощью множественного, или совокупного, коэффициента корреляции

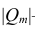
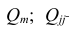
где —определитель корреляционной матрицы—алгебраическое
дополнение к элементу

Квадрат коэффициента множественной корреляции 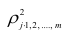называется

множественным коэффициентом детерминации. Коэффициенты множественной корреляции и детерминации — величины положительные, принимающие значения в интервале Оценками этих

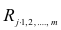
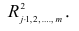
коэффициентов являются выборочные множественные коэффициенты корреляции и детерминации, которые обозначают соответственно и

Формула для вычисления выборочного множественного коэффициента корреляции имеет вид

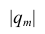
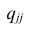
где —определитель корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции; алгебраическое дополнение к элементу

Многомерный корреляционный анализ позволяет получить оценку функции регрессии — уравнение регрессии. Коэффициенты в уравнении регрессии можно найти непосредственно через выборочные парные коэффициенты корреляции или воспользоваться методом многомерной регрессии, который мы рассмотрим в вопросе 2.7. В этом случае все предпосылки регрессионного анализа оказываются выполненными и, кроме того, связь между переменными строго линейна.

Ранговая корреляция

В некоторых случаях встречаются признаки, не поддающиеся количественной оценке (назовём такие признаки объектами). Попытаемся, например, оценить соотношение между математическими и музыкальными способностями группы учащихся. «Уровень способностей» является переменной величиной в том смысле; что он варьирует от одного индивидуума к другому. Его можно измерить, если выставлять каждому индивидууму отметки. Однако этот способ лишен объективности, так как разные экзаменаторы могут выставить одному и тому же учащемуся разные отметки. Элемент субъективизма можно исключить, если учащиеся будут ранжированы. Расположим учащихся по порядку, в соответствии со степенью способностей и присвоим каждому из них порядковый номер, который назовем рангом. Корреляция между рангами более точно отражает соотношение между способностями учащихся, чем корреляция между отметками.

Тесноту связи между рангами измеряют так же, как и между признаками. Рассмотрим уже известную формулу коэффициента корреляции

Пусть 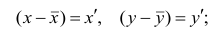     тогда,    учитывая,

что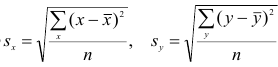,можно записать

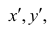
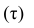
В зависимости от того, что принять за меру различия между величинами можно получить различные коэффициенты связи между рангами. Обычно используют коэффициент корреляции рангов Кэнделла и коэффициент корреляции рангов Спирмэна р.

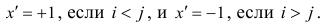
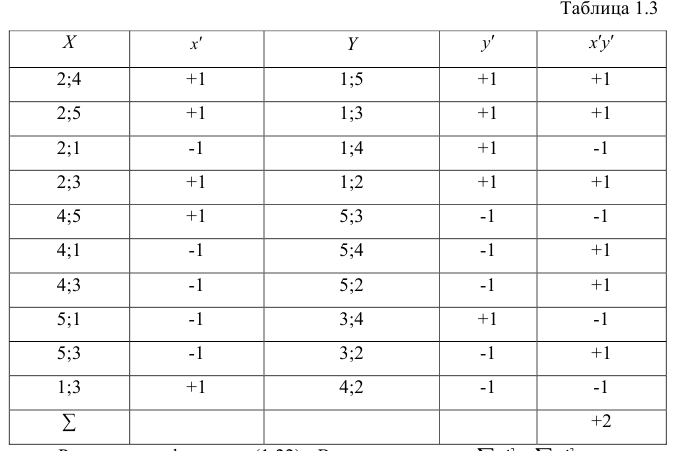
Введём следующую меру различия между объектами: будем считать Поясним сказанное на примере. Имеем две последовательности:

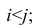
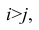
Рассмотрим отдельно каждую из них. В последовательности X первой паре элементов —2; 4 припишем значение +1, так как второй паре 2; 5 также припишем значение +1, третьей паре 2; 1 припишем значение —1, поскольку  и т.д. Последовательно перебираем все пары, причём каждая пара должна быть учтена один раз. Так, если учтена пара 2; 1, то не следует учитывать пару 1;    2. Аналогичные действия проделаем с последовательностью У, причём порядок перебора пар должен в точности повторять порядок перебора пар в последовательности X. Результаты этих действий представим в виде табл. 1.3.

Рассмотрим формулу (    1 .22). В нашем случае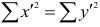 и равна

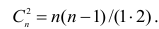
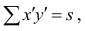
количеству пар, участвовавших в переборе. Каждая пара встречается только один раз, поэтому их общее количество равно числу сочетаний из n по 2, т.е. Обозначая получаем формулу коэффициента корреляции рангов Кэнделла:

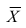
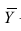
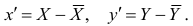
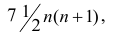
Теперь рассмотрим другую меру различия между объектами. Если обозначить через средний ранг последовательности X, через — средний ранг последовательности Т, тоПоскольку ранги последовательности X и Y есть числа натурального ряда, то их сумма равна     а    средний    ранг    
Тогда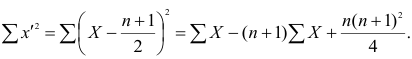 Сумма
чисел натурального ряда равна

Тогда 

Введём новую величину d, равную разности между рангами: d=X—Y, и определим через неё величину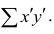. Имеем:

Коэффициент корреляции рангов Спирмэна

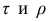
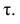
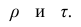
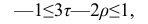
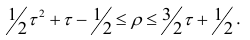
У коэффициентов разные масштабы, они отличаются шкалами измерений. Поэтому на практике нельзя ожидать, что они совпадут. Чаще всего, если значения обоих коэффициентов не слишком, близки к 1, p; по абсолютной величине примерно на 50% превышает Выведены неравенства, связывающие Например, при больших n можно пользоваться следующим приближённым соотношением:       или

Коэффициент p легче рассчитать, однако с теоретической точки зрения больший интерес представляет коэффициент

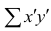
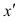
При вычислении коэффициента корреляций рангов Кэнделла для подсчёта s можно использовать следующий приём:    одну из последовательностей упорядочивают так, чтобы её элементы были числами натурального ряда; соответственно изменяют и другую последовательность. Тогда сумму можно подсчитывать лишь по последовательности К, так как все равны +1.

Если нельзя установить ранговое различие нескольких объектов, говорят, что такие объекты являются связанными. В этом случае объектам приписывается средний ранг. Например, если связанными являются объекты 4 и 5, то им приписывают ранг 4.5; если связанными являются объекты 1, 2, 3, 4 и 5, то их средний ранг (1+2+3+4+5)/5=3. Сумма рангов связанных объектов должна быть равна сумме рангов при ранжировании без связей. 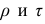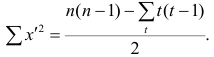Формулы коэффициентов корреляции для в этом случае также можно вывести из формулы обобщённого коэффициента корреляции, только знаменатель выражения (1.21) в этом случае не равен n(n—1)/2. Если / последовательных членов связаны, то все оценки, относящиеся к любой вобранной из них паре, равны нулю; число таких пар t(t—1), Следовательно,

Соответственно для другой последовательности

где t и u—число связанных пар в последовательностях.

Обозначая 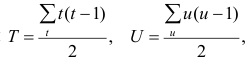получаем

Аналогично находим выражение для р. Только в этом случае

 , где е и г — число связанных пар в
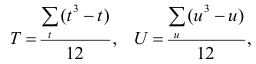
последовательностях, а

Если имеется несколько последовательностей, то возникает необходимость определить общую меру согласованности между ними. Такой мерой является коэффициент копкордации.

Пусть ь — число последовательностей, т — количество рангов в каждой последовательности. Тогда коэффициент конкордации

где d — фактически встречающееся отклонение от среднего значения суммы рангов одного объекта.

Коэффициент корреляции рангов может быть использован для быстрого оценивания взаимосвязи между признаками, не имеющими нормального распределения, и полезен в тех случаях, когда признаки поддаются ранжированию, но не могут быть точно измерены.

Пример:

Для данных табл. 13 найти выборочный коэффициент корреляции, проверить его значимость на уровне 

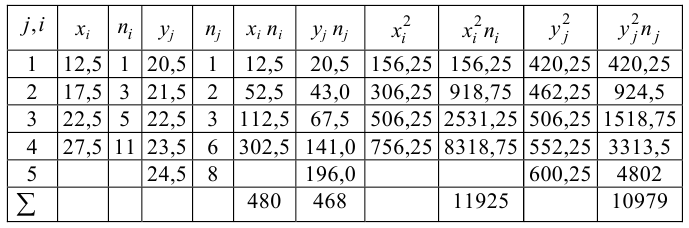
Решение. Для вычислений составим таблицу. Находим суммы

 и заносим их в таблицу. Вычислим

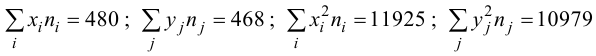
Подставляя полученные значения сумм в (8), найдем выборочный коэффициент корреляции

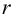
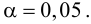
Проверим значимость  на уровне  Для этого вычислим статистику

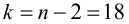
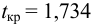
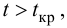
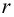
По таблице распределения П6 Стьюдента  находим критическое значение  Так как  то считаем  значимым.

Пример:

Для данных табл. 13 найти корреляционное отношение 

Для вычисления эмпирического корреляционного отношения найдем групповые средние 

Тогда

Вычисляем корреляционное отношение

После
установления характера и тесноты
корреляционной связи необходимо получить
математическую модель исследуемой
зависимости в виде уравнения связи.
Если связь нелинейная, то необходимо
подобрать функцию, график которой будет
максимально приближен ко всем исходным
точкам, а если линейная – то получить
конкретное уравнение прямой.

В
данной работе, независимо от того какой
характер связи получится фактически,
будем рассчитывать уравнение прямой,
условно принимая, что связь между
исследуемыми признаками линейная. Для
этого необходимо преобразовать исходное
уравнение прямой:

Подставив
в приведенное выше уравнение все
известные значения (M_y,
r,
σ_y,
σ_x,
M_x)
неизвестными останутся только х и у:

В
результате преобразований:
у=3,1+0,1112x–2,798

получим конкретное
уравнение прямой:

у_x
= 0,1112х + 0,3

Далее
заполняется таблица (табл. 3.7) для
построения графика. При этом значения
y_x
рассчитываются по найденному выше
конкретному уравнению прямой.

Таблица 3.7

На
графике изображаются исходные данные
(y_ср)
в виде отдельных точек и вероятные (y_x
– найденные по рассчитанному уравнению)
– в виде прямой (рис. 3.3).

Рис. 3.3 Графическое
изображение корреляционной связи.

4. Регрессионный анализ

4.1. Техника и способы регрессионного анализа

В
качестве примера для аналитического
выравнивания используются данные
взаимосвязи двух сопряженных признаков:
диаметров (Д), принимаемых за X, и высот
деревьев (H), принимаемых за Y.

Таблица
4.1

Взаимосвязь
диаметров и высот (невыравненные данные)

4.2 Выравнивание по уравнению прямой линии

Аналитическое
выравнивание имеет своей конечной целью
получение конкретного уравнения связи
между двумя сопряженными признаками.
В первую очередь исходные данные наносят
на систему координат и по характеру
расположения точек определяют функцию
для выравнивания. Её график должен
проходить максимально близко по отношению
ко всем исходным точкам. В данном примере
характер расположения точек линейный
следовательно выравнивание осуществляем
по уравнению прямой.

Как
известно, уравнение линейной зависимости
общего вида будет иметь вид: y
= а x+b.

Вычисление
конкретного уравнения сводится к
определению числовых значений
коэффициентов а, b,
для получения которых существует
несколько способов. Рассмотрим два,
наиболее широко применяемых способа,
характеризующихся различной точностью
и трудоемкостью:

а)
способ координат двух избранных точек,
обеспечивающий получение менее точных
результатов, но гораздо более простым
путем;

б)
способ наименьших квадратов, позволяющий
получить достаточно точные результаты
путем использования координат всех
выравниваемых точек (наблюдений).

Остановимся
на технике работ при вычислении
конкретного уравнения методом координат
избранных точек. В этом случае исходные
данные изображаются на графике, и
производится предварительное выравнивание.
Результирующая линия проводится между
точками с таким расчетом, чтобы разделить
их общее количество на две приблизительно
равные части. При этом необходимо
стремиться к такому положению, чтобы
расстояние между линией и исходными
точками было кратчайшим. Для облегчения
техники выравнивания и увеличения его
точности можно рекомендовать следующий
прием. Соединить все выравниваемые
точки и постараться провести плановую
выравнивающую линию по возможности
ближе к этим серединам. При этом желательно
провести прямую таким образом, чтобы
хотя бы две исходные точки попали на
неё. С полученной прямой линии снимаем
координаты двух любых точек исходных
данных (лежащих на проведенной прямой).
Если число наблюдений в классах известно,
то следует отдать предпочтение точкам,
обеспеченным наибольшим числом
наблюдений. В нашем примере в качестве
избранных использованы координаты
точек классов № 2 и № 6.

X₂=16; Y₂=18,00; X₆=32; Y₆=23,65.

Система двух
конкретных уравнений приобретет вид

После
подстановки координат избранных точек:

После
решения системы относительно а и b,
получим

а=0,35
b=12,4

Следовательно,
полученное конкретное уравнение связи
Y/Х
(Д/Н) будет иметь вид

у=0,35x+12,4

Для
краткости изложения в последующем
тексте полученным уравнениям присвоены
определенные номера: уравнение,
вычисленное методом координат точек,
получает номер I,
а уравнение, полученное методом наименьших
квадратов – номер II.

Пределы «работы»
полученного уравнения по диаметру от
10 см до 46 см.

Рассмотрим
технику вычислений при использовании
способа наименьших квадратов. Для
получения конкретного уравнения в этом
случае используются координаты всех
точек. Это учитывается при выведении
системы уравнений для этого метода.
Так, если записать уравнения прямой для
каждой точки, а потом просуммировать
левые и правые части всех уравнений, то
получим следующее:

y₁=
ax₁
+ b

y₂=
ax₂
+ b

y₃=
ax₃
+
b

……………

……………

∑y=a∑x+bn.

Так
как нам необходимо найти два неизвестных
значения (a
и b),
то в системе должно быть два уравнения.
Для получения второго уравнения системы
умножим обе части каждого уравнения на
соответствующий «х» и просуммируем
левые и правые части уравнений. Получим:

x₁y₁=
ax₁²
+ bх₁

x₂y₂=
ax₂²
+ bx₂

x₃y₃=
ax₃²
+
bx₃

….……………

….……………

∑хy=a∑x²+b∑х.

Таким
образом, мы вывели оба уравнения системы:

Для
удобства вычислений числовых значений
указанной системы составляется
вспомогательная таблица (табл.4.2).

Таблица 4.2

Вспомогательные
расчеты для вычисления конкретного
уравнения

прямой
линии

Подставим
итоговые данные в систему уравнений и
вычислим коэффициенты а, b,
имея в виду, что значение «n»
соответствует числу классов по X:

Следовательно,
конкретное уравнение будет иметь вид

Y=0,33Х+13,1

С
целью последующего анализа результатов
применения полученных уравнений
вычисляются вероятные (теоретические)
значения зависимого признака по первому
уравнению (y_в1)
и второму уравнению (y_в2).
Последние (y_в2)
сравниваются с исходными (опытными)
данными (у). Указанные сравнения (a
= y–y_в2)
производятся по всем классам X, а их
результат для
прямой линии показан
в табл.
4.3.

Таблица 4.3

Сравнение
исходных и вероятных высот деревьев,
полученных по уравнению прямой линии

Приведенные
данные позволяют, прежде всего, проверить
правильность вычислений, выполненных
при получении конкретных уравнений, на
предмет обнаружения грубых арифметических
ошибок.

Правильность
вычисления уравнений связи проверяется
путем сравнения исходных значений Y
с вероятными (у_в),
полученными по уравнению I
(у_в1)
и уравнению II
(у_в2)
Критерием правильности вычислений
уравнения I
будет совпадение вероятных значений
у_в1
с
исходными значениями Y
для тех классов, в которых использованы
координаты точек в качестве исходных
для получения конкретного уравнения
I.
В нашем примере для уравнения прямой
линии значение у_в1
равно
18,0, соответствует исходным данным Y
во втором классе, то есть также 18,0.
Аналогичное положение и в следующем,
шестом классе: у_в1
=23,6
практически не отличается от Y
=23,65. Совпадение Y
и

в остальных классах не обязательно и
может наступить только случайно.

Некоторый
контроль правильности уравнения II
можно получить
путем
сопоставления Y
и у_в2
– во
всех классах. В этом
случае
должно наблюдаться такое сочетание
знаков (плюс и минус), которое отражает
«срединное» положение выравнивающей
прямой между выравниваемыми исходными
значениями Y.

О
явной неправильности полученного
уравнения будет свидетельствовать
наличие во всех классах только +, равно
как и знаков -, а также, если в нескольких
начальных классах будут наблюдаться
отклонения с одним и тем же знаком ( +
или -), а во всех последующих классах с
противоположным, а именно:

+++++++

— — — — — — —

++++- — —

— — — -+++

Заметим,
что описанные критерии правильности и
вычислений I
и II
уравнений распространяются и на
выравнивание по всем другим линиям
связи.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Этот вид корреляционной зависимости весьма важен, так как очень многие корреляционные связи, характерные для количественных признаков наблюдаемых однородных фактов, близки к линейным. Данные наблюдения, представленные в виде корреляционной таблицы, и найденные из этой таблицы пары соответственных значений Х и или У и , используются для отыскания параметров уравнений прямых регрессии

и .

Эта операция, называемая Выравниванием, обычно выполняется по способу наименьших квадратов, сущность которого состоит в таком подборе параметров линии регресси, при котором достигается минимум .

Разберем применение данного способа в общем виде для каждого из записанных уравнений регрессии. При этом для иллюстрации используем данные корреляционной таблицы 1 распределения растений житняка по общему весу и по весу семян.

1. УравнеНИе прямой регрессии У по х. При отыскании по способу наименьших квадратов параметров линейной функции У=ах+B На основании данных наблюдения о парах значений Х и У, связанных однозначным соответствием, используется система нормальных уравнений

Здесь коэффициенты определяются простым суммированием слагаемых в соответствии с количеством пар значений Х и У.

Если же требуется с помощью способа наименьших квадратов определить параметры уравнения, связывающего значения Х с соответственными частными средними , по данным не простой, а корреляционной таблицы, то структура коэффициентов и свободных членов нормальных уравнений должна отразить все данные корреляционной таблицы.

А) Коэффициенты, соответствующие суммам и , должны включать в операцию суммирования все значения Х как повторяющиеся, так и неповторяющиеся. Количество значений определяется числом , поэтому сумма этих значений Х равна . Аналогично сумма значений равна и т. Д. Отсюда сумма всех значений Х выразится в виде

Суммирование квадратов переменной Х строится также и дает

Б) Свободный член, сооТВеТСтвуЮщИй сумме , должен представить сумму всех частных средних . При этом для каждого значения Х количество соответственных частных средних определяется количеством таких значений самого Х. Поэтому значению соответствует , частных средних , значенИЮ Соответствует частных средних и т. д. Сумма всех частных средних Имеет вид

.

В) Свободный член, соответствующий сумме , должен представить сумму всех воЗМожных произведений значений Х на соответствующие частные срЕДние . КоличестВО разных произведений здесь определяется количеством соответственных значений Х. Поэтому сумма всех произведений вида имеет вид

.

Удовлетворяющая указанным требованиям система нормальных уравнений для отыскания значений параметров уравнения прямой регрессии имеет следующий вид:

Определение корней этой системы предварительно требует некоторого преобразования коэффициентов и свободных членов.

Коэффициенты системы преобразуются так:

Развернутая запись свободного члена позволяет для каждого слагаемого воспользоваться переходом от частных средних к соответственным частным значениям У.

В самом деле, если , то

.

Поэтому

И аналогично

Почленное сложЕНие всех равеНСтв дает в СОответствии с ПРинятой структурой корреляционной таблицы 2

После приведения этого результата к выражению, Содержащему среднее значение У, получится

.

Преобразование свободного члена выполняется Аналогично. Здесь При слагаемое приводится к виду

Последующая запись всех остальных слагаемых такого же вИДа при , и суммирование соответствующих выражений дает реЗУльтаТ

Сохраняя эту запись для выполнения подсчетов, можно привести полученный результат к выражению со средним значением Ху.

Двойной знак суммирования позволяет выполнять суммирование в любом порядке: сНАчала по горизонтали (меняя нумерацию частных значений У), а ЗАтем по вертикали (меняя нумерацию частных значений Х), или, наоборот, сначала по вертикали, а затем по горизонтали.

По структуре корреляционной таблицы:

Или

Отсюда

Так как

В преобразованном виде система такова:

Или

Для определения параметра A достаточно после умножения членов второго уравнения на почленно вычесть это уравнение из первого: , или

Параметр B определяется непосредственно из второго уРАвНенИя:

.

Подставляя полученное выражение в уравнение прямой регрессии Y по Х, т. Е. , получим

,

Или .

КоэффИЦиент А в уравнении прямой регрессии называется КоЭФфициентом прямой регрессии у по х И обозначается символом .

Таким образом,

И окончательная запись уравнения прямой регрессии Y по X таково:

.

Составим такое уравнение с числовыми параметрами для распределения растений житняка по данным корреляционной таблицы 1 об общем весе (X) и весе семян (Y) растений. Вычисление необходимых параметров можно проводить по нижеследующей системе поДСчетов, соответствующей выполненному общему решению.

1) Составляем вспомогательную таблицу.

2) По данным табл. 4

Таблица 4

3) Определяем коэффициент регрессии У по Х:

4) Записываем уравнение прямой регрессии У по X:

,

Или окончательно

2. Уравнение прямой регрессии Х по У. Система нормальных уравнений для отыскания параметров С и D уравнения прямой регрессии Х по У, получаемая в результате применения способа наименьших квадратов, имеет вид

По аналогии с преобразованиями, проведенными для случая регрессии У по Х, можно записать, что

Нормальные уравнения можно переписать в упрощенном вИДе:

Или

Для определения параметра С из членов первого уравнЕнИя вЫЧитаются члены второго уравнения, умноженные на :

,

Или

Параметр D определяется непосредственно из второго уравнения:

.

Замена D этим выражением в уравнении прямой регрессии дает

Или .

Коэффициент С в этом уравнении называют Коэффициентом прямой Регрессии х по у И обозначают символом .

Таким образом,

И окончательная запись уравнения прямой регрессии Х по У такова:

.

Заметим, что обе прямые регрессии, как видно из их уравнений, проходят через точку .

На примере распределения растений житняка по данным корреляционной таблицы о весе семян (У) и общем весе (Х) растений составим уравнение прямой регрессии Х по У с числовыми параметрами. Все необходимые вычисления для подсчета параметров проводятся в таком же порядке, как это выполнено для уравнения прямой регрессии У по Х.

1) Составляем вспомогательную таблицу.

2) По данным табл. 5

3) Определяем коэффициент регрессии Х по У:

Таблица 5

4) Записываем уравнение прямой регрессии Х по Y:

,

Или окончательно

Ниже будет показано, что оба уравнения прямых регрессии могут быть получены одним расчетом с помощью коэффициента корреляции.