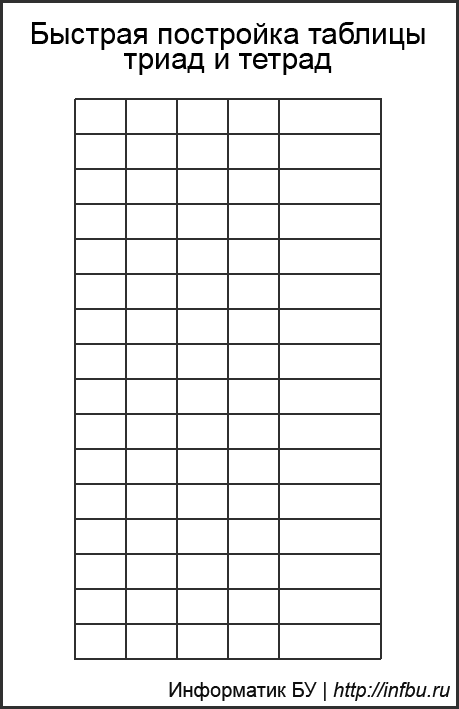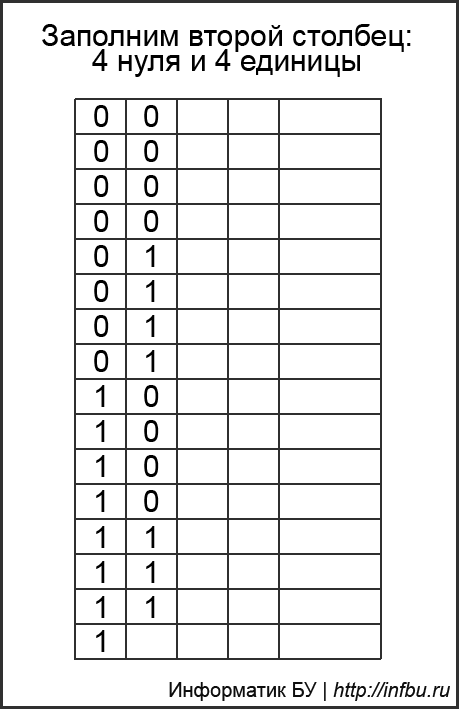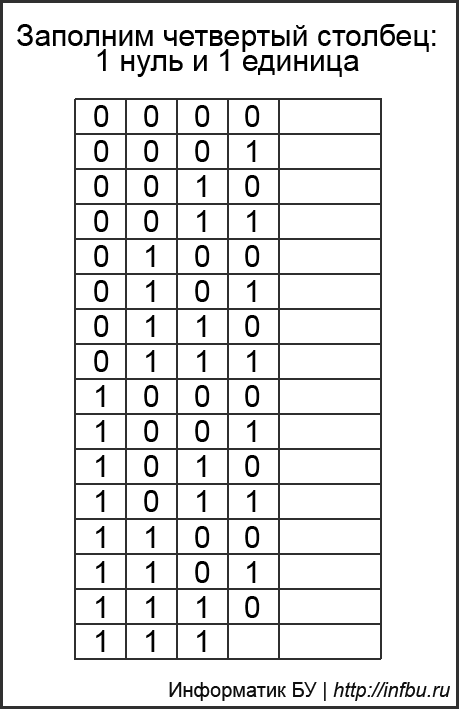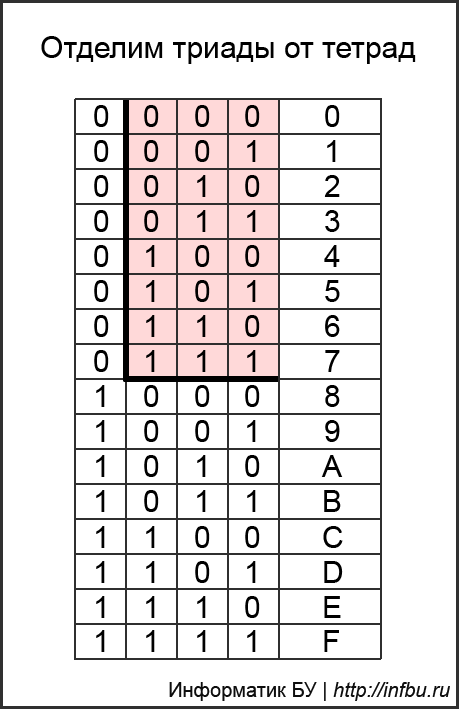
Таблица триад и тетрад, проще сгенерировать, чем запомнить.
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
1
1
0
1
0
1
0
1
2
0
1
0
0
1
1
3
1
1
0
1
0
4
1
0
5
1
0
1
0
1
0
0
6
1
7
1
1
0
1
1
1
8
0
9
1
0
1
1
0
1
1
0
10
1
A
1
11
1
1
12
B
0
1
C
13
14
D
E
15
F
Переводы в систему счисления с основанием, кратным двойке (2, 8, 16), наиболее эффективно выполнять при помощи триадно — тетрадного метода, суть которого заключается в независимом переводе триад (тетрад) в цифры требуемого 8-ричного (16-ричного) числа.
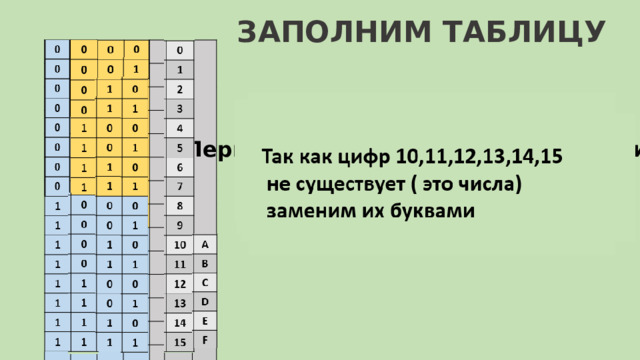
ЗАПОЛНИМ ТАБЛИЦУ
Первый столбик 8 ноликов и 8 единиц
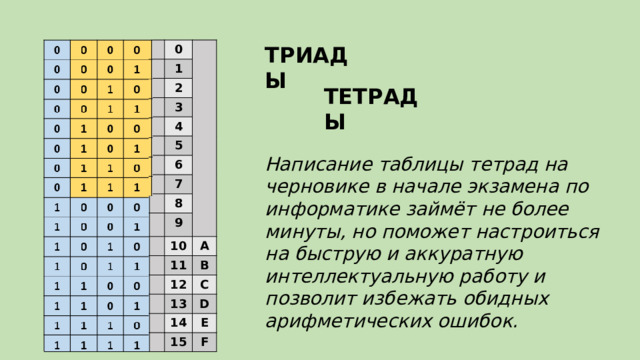
ТРИАДЫ
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
1
1
1
1
0
0
2
0
0
0
1
1
1
1
1
3
0
1
1
4
0
0
0
5
1
1
0
1
0
6
0
1
0
7
1
1
0
1
8
1
1
0
1
1
1
9
1
0
0
1
10
1
1
A
11
1
0
12
1
B
13
C
1
14
D
E
15
F
ТЕТРАДЫ
Написание таблицы тетрад на черновике в начале экзамена по информатике займёт не более минуты, но поможет настроиться на быструю и аккуратную интеллектуальную работу и позволит избежать обидных арифметических ошибок.
Описание презентации по отдельным слайдам:
-
1 слайд
Использование метода триад и тетрад в системах счисления
Преподаватель: Брык И.В.
Анапа
2023
ЧПОУ «Анапский индустриальный техникум -
2 слайд
Системы счисления
Система счисления – метод записи чисел, представление чисел с помощью письменных знаков.Системы счисления
Позиционные
Непозиционные -
3 слайд
Непозиционная и позиционная система счисления
В непозиционной системе счисления величина, которая обозначает цифру, не зависит от положения в числе. К таким системам счисления можно отнести египетскую и римскую системы счисления.
Например: число 67 в римской системе счисления можно записать, как LXVII.
Позиционная система счисления — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда) относительно десятичного разделителя. -
4 слайд
Порядок перевода из 2 в 10
Для того, чтобы перевести из двоичной системы счисления в десятеричную необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду
Пример: перевод в десятичную систему двоичное число 101110
1504131211002=1*25+1*23+1*22+1*21=32+8+4+2=4610 -
5 слайд
Порядок перевода из 10 в 2
Для того чтобы перевести из десятичной системы счисления в двоичную систему счисления необходимо целую часть числа разделить на основание 2 с выделением остатков, дробную умножить на 2. -
6 слайд
Как строится таблица триад и тетрад
Первый столбик — Выписывается 8 нулей, затем 8 единиц.
Второй столбик — уменьшается количество 0 и 1 в два раза, т.е. записывается 4 нуля и 4 единицы, повторяется это дважды.
Третий столбик — еще в два раза уменьшается нули и единицы. Чередуется 2 нуля и 2 единицы до конца столбика.
Четвертый столбик — чередуются нули и единицы. -
7 слайд
Пример разбора решения обычным способом
Имеется число СE516, которое нужно перевести в двоичную систему счисления
Переведем из 16 10
С2E150 = 12*162 +14*161 + 5*160 =3072+224+5=3301102) Затем из 10 2
-
8 слайд
Разбор с помощью таблицы тетрад
-
9 слайд
Рассмотрим пример когда у нас есть двоичное число и переведем его в восмеричную сс
Число 1101001011 в двоичной системе счисления, нужно перевести в восьмеричную систему счисления. Нужно разделить это число на триады, начиная справа.
Получается 1 101 001 011 и к единице добавляется два незначащих нуля. -
10 слайд
Заключение
С помощью метода диад, триад и тетрад можно намного проще и быстрее переводить числа из 4, 8, 16 системы счисления в двоичную и наоборот. Перевод можно осуществлять где угодно и когда угодно, при любых обстоятельствах. Для этого нужно лишь понять, как составить таблицу и правильно использовать её. -
Использование таблицы треад и тетрад
Таблицу триад и тетрад вы можете увидеть, щелкнув по кнопке в правом нижнем углу сайта. Она нужна для быстрого перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную и наоборот.
Многие зазубривают таблицу, но она строится очень просто без зубрёжки:
Перевод чисел из восьмеричной системы счисления в двоичную
Возьмем восьмеричное число 34568
Представим каждый разряд числа в виде триады:
3 – 011
4 – 100
5 – 101
6 – 110
Запишем последовательно:
011 100 101 110
Избавимся от первого незначащего нуля и получим результат:
111001011102 = 34568
Перевод чисел из двоичной системы счисления в восьмеричную
Возьмем число 111011012
Разделим его на триады, начиная с правого разряда:
11 101 101
Добавим один незначащий нуль:
011 101 101
Заменим триады значениями из таблицы:
3 5 5
Получается, что 3558 = 111011012
Перевод чисел из шестнадцатеричной системы счисления в двоичную
Возьмем число 15F16
Представим каждый разряд в виде тетрады:
1 – 0001
5 – 0101
F – 1111
Запишем последовательно:
0001 0101 1111
Избавимся от трех первых незначащих нулей и запишем результат:
101011111
Получается, что 1010111112 = 15F16
Перевод чисел из двоичной системы счисления в шестнадцатеричную
Возьмем число 100010110111012
Разделим его на тетрады, начиная с правого разряда:
0010 0010 1101 1101
Заменим тетрады значениями из таблицы:
2 2 D D
Получается, что 22DD16 = 100010110111012
Комментарии ()
|
# |
||
|
|
Наталья Пицык # 24 января 2018 в 22:10 0 |
||
|
По теме: методические разработки, презентации и конспекты
Таблица- справка. Итоги проверки тетрадей по русскому языку для контрольных и творческих работ.
Таблица- справка «Итоги проверки тетрадей по русскому языку для контрольных и творческих работ» экономит время завуча, руководителя методического объединения и т.д. при плановом ВШК….
Переводы из двоичной в восьмиричную и шестнадцатиричную системы счислений методом триад и тетрад
Подробное описание урока по изучению метода триад и тетрад…
Рабочая тетрадь «Таблицы и диаграммы» 7 класс
В рабочей тетради предложен ряд задач для формирования умение читать и интерпретировать количественную информацию, представленную в различной форме (таблиц, диаграмм, графиков реальных зависимостей) и…
Рабочая тетрадь «Технология создания и преобразования информационных объектов. Возможности электронных таблиц. Microsoft Excel»
Рабочая тетрадь «Технология создания и преобразования информационных объектов. Возможности электронных таблиц. Microsoft Excel» с практическими занятиями….
ЭЛЕКТРОННЫЕ ТАБЛИЦЫ EXCEL (рабочая тетрадь, методические материалы)
Электронные таблицы (табличные процессоры) – это прикладное программное обеспечение общего назначения, предназначенное для обработки различных данных, представимых в табличной форме.При пом…
Таблица триад и тетрад, проще сгенерировать, чем запомнить.
Презентация с анимацией как быстро составить таблицу триад и тетрад Написание таблицы тетрад на черновике в начале экзамена по информатике займёт не более минуты, поможет избежать обидных арифметическ…
Конспект урока «Перевод двоичных чисел в шестнадцатеричные и восьмеричные числа и наоборот «методом триад и тетрад»
Gознакомить с “методом триад и тетрад” для перевода двоичных, восьмеричных и шестнадцатеричных чисел из одной СС в другую….
Цели урока:
Образовательная — познакомить уч-ся с
“методом триад и тетрад” для перевода двоичных,
восьмеричных и шестнадцатеричных чисел из одной
СС в другую.
Развивающая – развивать познавательный
интерес учащихся, умения применять полученные
знания на практике.
Воспитательная – повысить уровень
информационной культуры учащихся.
I. Проверка домашнего задания
Вызывается ученик к доске для выполнения
домашнего упражнения
Уч-ся отвечают на вопросы:
- Как представить отрицательных десятичных
целых чисел в двоичном виде? - Что значит проинвертировать число?
- На что указывает при разрядной сетке в 8 бит
старший бит, равный 1?
II. Изучение нового материала
Так как основания 8-1 и 16-й СС являются степенями
двойки, то перевод чисел из этих СС в 2-ую и
наоборот прост и основан на методах триад и
тетрад. Число делится на триады (тетрады) вправо и
влево от десятичной точки. Если крайние триады
(тетрады) оказались неполными, они дополняются
нулями.
| Алфавит | Триады | Тетрады |
| 0 | 000 | 0000 |
| 1 | 001 | 0001 |
| 2 | 010 | 0010 |
| 3 | 011 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 0101 |
| 6 | 110 | 0110 |
| 7 | 111 | 0111 |
| 8 | 1000 | |
| 9 | 1001 | |
| А(10) | 1010 | |
| В(11) | 1011 | |
| С(12) | 1100 | |
| D(13) | 1101 | |
| E(14) | 1110 | |
| F(15) | 1111 |
[Приложение]
Примеры:
- 40118=100.000.001.0012 (точки отделяют триады)
- В7, А16=1011.0111,1012 (последняя тетрада
неполная) - 10110,12=010.110,1002=26,48
- 1110,12=0001.1110,10002=1Е,816
III. Закрепление
Упражнение: Выполнить перевод, используя
тетрады и триады:
101,012=?8; 1010001012=?16; 1110110,12=?8;
40118=?2; СВ7,916=?2
IV. Самостоятельная работа
Выполнить перевод, используя тетрады и триады:
В-1
1001,012=?8=?16;
СВ7, 916=?2=?8
В-2
1010001012=?8=?16;
40118=?2=?16;
В-3
1110110,12=?8=?16;
DE7, 816=?2=?8
Ответы для самопроверки:
В-1: 1001,012=11,28=9,416;
СВ7,916=110010110111,10012=6267,448
В-2: 1010001012=5058=14516;
40118=1000000010012=80916;
В-3: 1110110,12=166,48=76,816;
DE7, 816=110111100111,12=6747,48
V. Итог урока
- Как перевести с помощью триад из двоичной СС в
восьмеричную? - Как перевести с помощью триад из восьмеричной
СС в двоичную ? - Как перевести с помощью тетрад из двоичной СС в
шестнадцатеричную? - Как перевести с помощью тетрад из
шестнадцатеричной СС в двоичную?
VI. Домашнее задание
Выполнить перевод, используя тетрады и триады:
1101,12=?8=?16; 3 45,78=?2=?16;
ВС,516=?2=?8