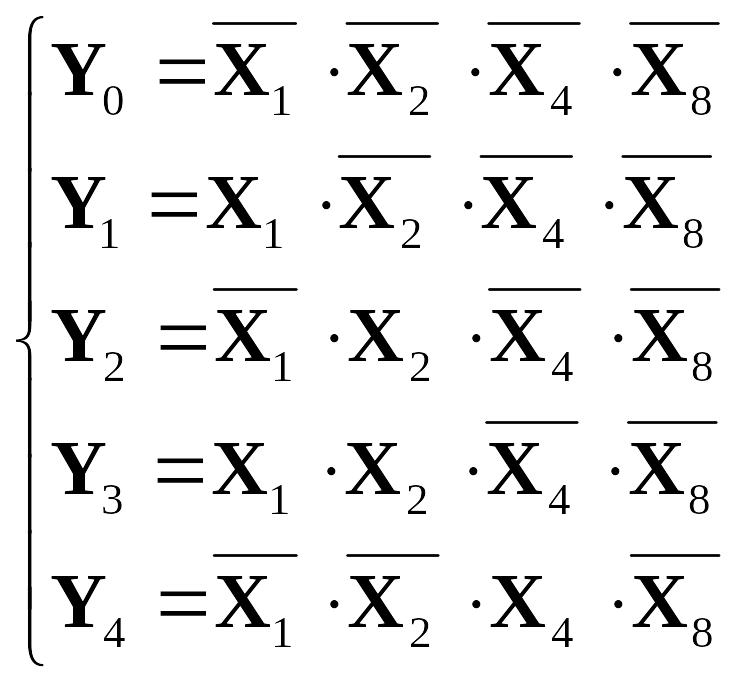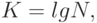Как составить схему дешифратора - Avtoru.top - решение различных проблем

Двоичные дешифраторы
относятся к преобразователям кода. На
вход дешифратора поступают коды символов,
которые преобразуются в значения
символов (двоичной код преобразуется
в код «один из N»).
Дешифратор, имеющий N
входов, не может иметь больше 2^N
выходов. В зависимости от входного
двоичного кода на выходе дешифратора
возбуждается один и только один выход.

В качестве примера рассмотрим построение
дешифратора двоичного кода (8421) цифр в
десятичные цифры, каждая из которых
имеет свой выход (задача, обратная
рассмотренной при изучении шифратора).

У дешифратора на входы
поступают коды символов, которые
преобразуются (декодируются) в символы,
вызывающие появление активного уровня
сигнала только на одном выходе. Его
работа описывается той же, что и работа
шифратора, таблицей 3.1, в которой
меняются местами входные и выходные
переменные: входными переменными будут
коды десятичных цифр — значения X1,
X2,
X4,
X8,
а выходными – выходы самих десятичных
цифр Y0
– Y9.

Построение дешифратора также начинается
с записи описывающих его работу логических
выражений. Так как на каждом выходе
активный уровень (единица по таблице
3.1) появляется только при строго
определенной комбинации входных
переменных, то следует взять конъюнкцию
входных переменных, а те из переменных,
которые в коде цифры принимают значение
нуля, проинвертировать, чтобы конъюнкция
оказалась равна единице:

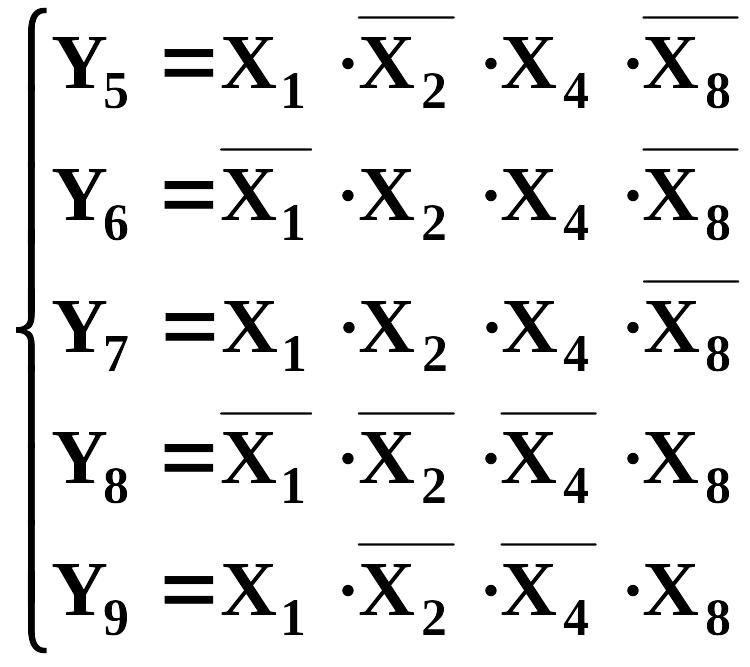
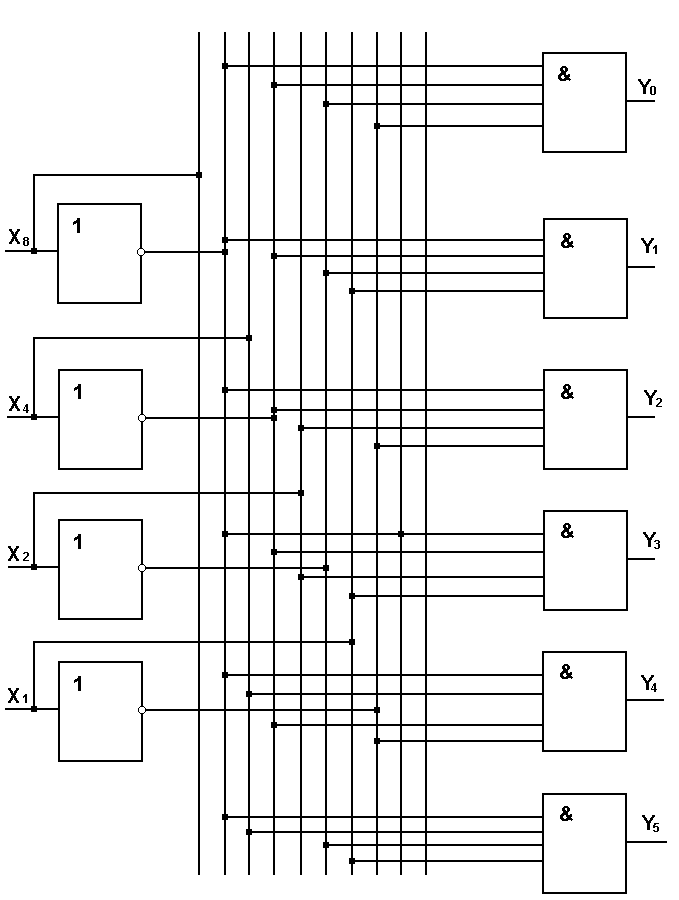
Для построения схемы рассматриваемого
дешифратора необходимо взять 10 элементов
И на 4 входа каждый и соединить их в
соответствии с выше приведенной системой
уравнений (рис. 3.4).

Рис 3.4. Схема дешифратора

Теперь, если подать на входы какой-либо
код в соответствии с таблицей 3.1, получим
уровень единицы только на одном выходе
(код символа которого задан входными
переменными), на остальных же выходах
будут уровни логического нуля.

Построение схем шифратора и дешифратора
состоит из одинаковых этапов (составление
таблицы работы, которая у них совпадает,
составление по таблице системы логических
выражений, в которой входные переменные
для шифратора являются выходными для
дешифратора и наоборот, приведение
системы логических выражений к требуемому
базису и построение схемы в соответствии
с полученной системой). Необходимо
обратить внимание на то, что при описании
работы шифратора используют логические
суммы (дизъюнкции) входных переменных,
тогда как у дешифратора – логические
произведения (конъюнкции).

Промышленностью выпускаются
микросхемы дешифраторов на ограниченное
число входов и выходов (обычно на четыре
входа). Обычно они имеют инвертированные
выходы (формируют инверсию выходных
сигналов) и один или несколько управляющих
входов. При запрещении работы микросхемы
на выходе обычно устанавливается высокий
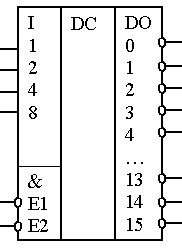
уровень. На рис. 3.5 в качестве примера
приведена ИМС дешифратора К155ИД3, работа
которого описывается таблицей 3.3. Входы
для подачи кодов сигналов обозначены
1, 2, 4, 8, соответствующие кодам выходы
обозначены числами 1-15. Входы Е₁и Е₂
служат для разрешения работы дешифратора.
Причем его работа разрешена только в
том случае, когда на оба разрешающих
входа поданы уровни логического нуля.

Работа дешифратора К155ИД3
Таблица 3.3

Входы	Выходы
Е1	Е2	1	2	4	8	0	1	2	3	4	…	15
1	*	*	*	*	*	1	1	1	1	1	…	1
*	1	*	*	*	*	1	1	1	1	1	…	1
0	0	0	0	0	0	0	1	1	1	1	…	1
0	0	1	0	0	0	1	0	1	1	1	…	1
0	0	0	1	0	0	1	1	0	1	1	…	1
0	0	1	1	0	0	1	1	1	0	1	…	1
.	.	.	.	.	.	.	.	.	.	.	…	.
0	0	1	1	1	1	1	1	1	1	1	…	0

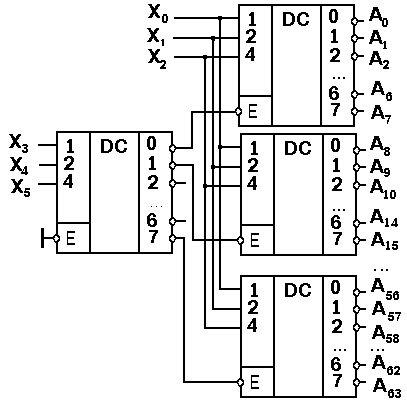
На базе выпускаемых микросхем
дешифраторов можно реализовать дешифратор
на любое число разрядов. Для расширения
числа входов и выходов дешифраторы
объединяют в несколько ступеней, причем
входы дешифраторов второй ступени
подключаются к выходам дешифраторов
первой ступени и так далее (рис. 3.6).
Дешифратор старших разрядов (входы
Х₃-Х₅)
определяет, какой из дешифраторов
младших разрядов (Х₀-Х₂)
входного кода будет работать. Младшие
разряды кодов поступают на все входы
младших дешифраторов параллельно.

Рис. 3.5 Дешифратор К155ИД3
Рис.3.6
Расширение входов

и выходов дешифраторов

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Аннотация: Рассматривается принцип действия дешифраторов на положительной и отрицательной логике.

Дешифратор является частным случаем преобразователей произвольных кодов, рассмотренных в
«Преобразователи произвольных кодов»
.

Дешифратор — это логическая схема, преобразующая двоичный код в унарный, когда только на одном из всех выходов появляется активный сигнал. Номер этого активного выхода в десятичном коде совпадает с двоичным кодом, подаваемым на входные линии дешифратора.

Принцип действия дешифратора лежит в основе работы всем известного устройства — домофона. Когда мы набираем номер на домофоне, звонок звенит только в одной квартире с указанным номером.

Рассмотрим схему дешифратора на три входа. Как при синтезе логической схемы по арифметическому выражению (
«Преобразователи произвольных кодов»
), составляем таблицу истинности. Поскольку в нашем примере у схемы должно быть три входа, количество комбинаций на этих входах будет равно 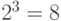$2^{3}=8$ , поэтому выходов у схемы будет также 8. Обозначим входные сигналы переменной с индексом, соответствующим весу двоичного разряда — 1, 2, 4 (табл. 4.1). Выходные сигналы обозначим как с индексом, соответствующим поданному на входы двоичному коду, при котором этот выход активен. Для синтезируемой схемы примем положительную логику, когда активным является уровень логической 1.

В соответствии с принципом синтеза логических схем по заданной формуле, после составления таблицы истинности нужно для каждого выхода написать логическое выражение. В данном случае задача упрощается, так как для каждого выхода логическая 1 имеет место быть только в одной строке таблицы. Поэтому в логическом выражении для каждого выхода будет только один минтерм:

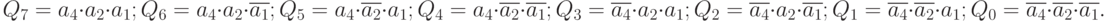$Q_{7}=a_{4}cdot a_{2}cdot a_{1}; \ Q_{6}= a_{4}cdot a_{2}cdot overline{a_{1}}; \ Q_{5}= a_{4}cdot overline{a_{2}}cdot a_{1}; \ Q_{4}= a_{4}cdot overline{a_{2}}cdot overline{a_{1}}; \ Q_{3}= overline{a_{4}}cdot a_{2}cdot a_{1};\ Q_{2}= overline{a_{4}}cdot a_{2}cdot overline{a_{1}}; \ Q_{1}= overline{a_{4}}cdot overline{a_{2}}cdot a_{1}; \ Q_{0}= overline{a_{4}}cdot overline{a_{2}}cdot overline{a_{1}}.$

(
4.1)

На рис. 4.1 показана функциональная схема данного дешифратора, соответствующая логическим выражениям (4.1).

В реальных дешифраторах обязательно присутствует входной управляющий сигнал, разрешающий работу данного дешифратора в соответствии со своей функцией. В простейшем случае разрешающий сигнал (от англ. enable — давать возможность) может подаваться на каждый из логических элементов И, осуществляющих вычисление по (4.1), так, как показано на рис. 4.2 красным цветом. Если Е=1 , то он не влияет на работу схемы (рис. 4.2). Дешифратор работает так, как описано выше. Если Е=0 , то на всех выходах дешифратора будут логические 0 независимо от состояния входных сигналов, т.е. все выходы дешифратора будут в пассивном (в рассматриваемом случае нулевом) состоянии.

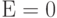
Все рассмотренные ранее логические элементы могут быть реализованы в виде отдельных интегральных микросхем (ИМС) малой степени интеграции. Так, сборка из четырёх 2-входовых элементов И-НЕ объединяется в одном корпусе ИС К155ЛА3 [4].

Интегральная микросхема (ИМС) — микроэлектронное изделие, выполняющее определенную функцию преобразования и обработки сигнала и имеющее высокую плотность упаковки электрически соединённых элементов, которое рассматривается как единое целое [4, с.9].

Степень интеграции ИМС — показатель степени сложности микросхемы, характеризующийся числом содержащихся в ней элементов и компонентов [4, с.10]:

K=lg N,

где — число входящих в ИМС элементов и компонентов.

Различают интегральные микросхемы малой ( МИС — малые интегральные схемы), средней ( СИС ), большой ( БИС ) и сверхбольшой ( СБИС ) степени интеграции.

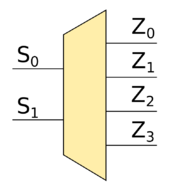
На рис. 4.3 показаны примеры условного графического обозначения (УГО) дешифраторов с активным единичным уровнем входных и выходных сигналов. Здесь и далее на УГО выделяется три поля. Центральное поле содержит обозначение функции, выполняемой ИМС. В данном случае это DC — от англ. D e c oder — дешифратор. Левое поле содержит обозначение входов ИМС, правое — обозначение выходов.

Рис.
4.3.
УГО дешифраторов с активными единичными входными и выходными сигналами: а — на один вход; б — на два входа; в — на три входа; г — на четыре входа.

При принятии отрицательной логики, когда активным уровнем всех сигналов является логический ноль, таблица истинности дешифратора на три входа (табл. 4.2) будет содержать в диагонали не единицы, а нули. При этом порядок следования комбинаций входных сигналов в данном случае удобно сделать обратным — в первой строке указать комбинацию 111 , далее 110 и т.д. до последней строки с комбинацией 000 .

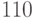
Активный нулевой уровень сигнала принято обозначать на УГО в виде инверсных входов и выходов так, как представлено на рис. 4.4. Поскольку в каждом столбце табл. 4.2 присутствует один ноль и семь единиц, логическое выражение удобнее представить в виде соответствующих макстермов:

$overline{Q_7} =a_4 + a_2 + a_1;\ overline{Q_6} =a_4 + a_2 + overline{a_1};\ overline{Q_5} =a_4 + overline{a_2} + a_1;\ overline{Q_4} =a_4 + overline{a_2} + overline{a_1};\ overline{Q_3} =overline{a_4} cdot a_2cdot a_1;\ overline{Q_2} =overline{a_4} cdot a_2cdot overline{a_1};\ overline{Q_1} =overline{a_4} + overline{a_2} + a_1;\ overline{Q_0} =overline{a_4} + overline{a_2} + overline{a_1}$

(
4.2)

Источник

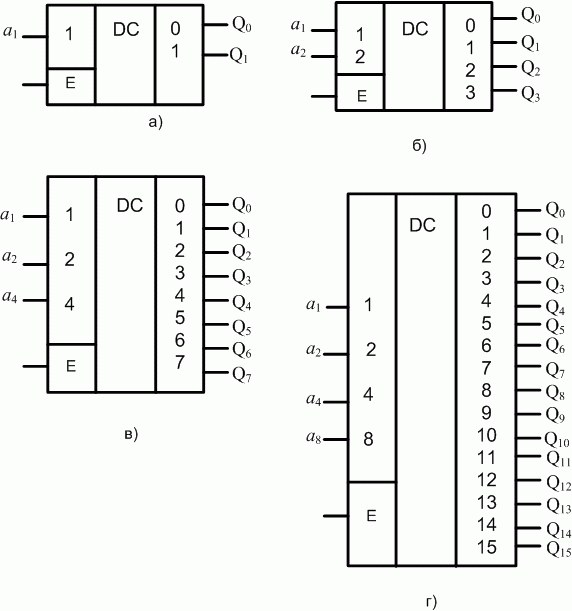
Синтез схем на дешифраторах

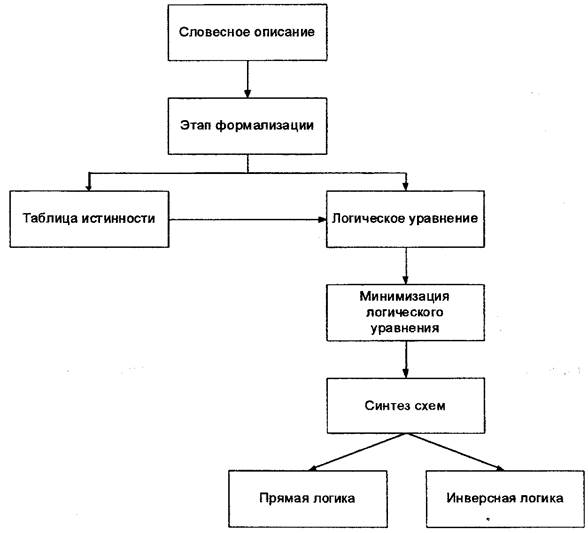
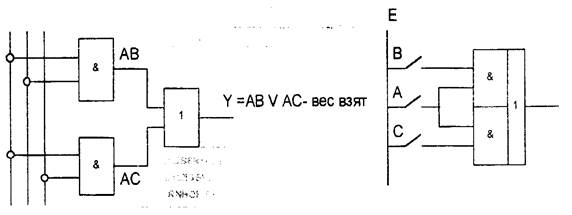
Нужно создать логическое автоматическое устройство для оповещения зрителей о результатах принятия решения судейской коллегии на соревнованиях по тяжелой атлетике. Судейская коллегия состоит из трех судей, один из которых старший -председатель. Если вес взят, то судья нажимает кнопку. Коллективное решение «вес взят» должно появляться при единогласном решении трех судей или двух из них при условии, что один — председатель.

Методологический прием формализации — метод «черного ящика».

Особенность синтеза логических схем с несколькими выходами

В некоторых случаях удается минимизировать логичеcкую схему за счет двоичных элементов, формирующих другие выходы.

у₁ = f(a,b) — функция, равная единице в случае, если а>b

у₂ = f(a,b) — функция, равная единице в случае, если а≥b

у_з = f(а, b) — функция, равная единице в случае, если а<b

Разложение Шеннона

Формула разложения Шеннона:

Последовательное разложение Шеннона:

Если применить метод разложения к нескольким функциям, то можно обнаружить одинаковые подфункции.

Имеем схему с двумя выходами:

В результате разложения Шеннона получили две одинаковые подфункции f₁₂ и f₂₁.

Анализ логических схем, построенных на микросхемах малой и средней степени интеграции

Известна логическая схема

Два метода анализа:

1) Построение таблицы истинности

2) Написание логического уравнения

По первому способу строим таблицу истинности, подавая на вход различные комбинации входных сигналов, последовательно определяя реакцию промежуточных логических элементов.

По второму способу вводим промежуточные переменные и пишем логические уравнения для каждого логического элемента.

у = х₁х₂х₃ — минимизированное логическое уравнение

Примечание: Часто при анализе схем встречается задача нахождения уравнений, когда неизвестно внутреннее содержание логической схемы, но известны последовательности входных и выходных сигналов

Задача идентификации решается с помощью методов тестирования. Один из таких методов — табличный метод.

Синтез схем на микросхемах средней степени интеграции

Дешифратор, шифратор, мультиплексор, демультиплексор — представители данного класса схем.

Синтез схем на дешифраторах

Дешифратор — логический многополюсник, который имеет n входов и 2 n выходов, причем при подаче на вход двоичной комбинации, возбуждается только один выход, который и указывает на наличие этой комбинации на выходе.

Дешифратор — это преобразователь двоичного кода в десятичный.

Как видно из уравнений выходов у_i каждый такой выход является функцией от всех входных сигналов. Это обстоятельство позволяет задавать с помощью дешифратора любую логическую функцию, которая представлена в СДНФ

Синтез комбинационной схемы на дешифраторе сводится к объединению соответствующих выходов дешифратора с помощью дизъюнктора.

1) не нужно минимизировать логическое уравнение

2) этап технологического проектирования значительно упрощается

1) ограниченное количество входов

2) логическая функция должна быть представлена в СДНФ

3) если функция представлена в ДНФ, то необходимо сначала найти ее СДНФ, что можно сделать двумя способами: либо с помощью таблицы истинности, либо через аналитические преобразования

Синтез дешифратора и шифратора

Дешифратором (декодером) называется устройство, распознающее различные кодовые комбинации. Сигналы четырехэлементной комбинации подаются на входы дешифратора. В зависимости от вида кодовой комбинации на входе сигнал логической единицы появится только на одном определённом выходе, а на всех других будет сигнал логического нуля. Таким образом, каждой кодовой комбинации на входе соответствует свой выход.[1, с.74]

Нам необходимо синтезировать декодер преобразующий двоичную комбинацию в соответствующее десятичное число. Для этого воспользуемся таблицей.

Таблица 1.3—таблица соответствия двоичных комбинаций десятичным числам

Теперь запишем логические выражения, определяющие значения выходных переменных:

Схема декодера приводится в приложении 1.3.1

Синтез шифратора

Шифратором (кодером) называется устройство, производящее преобразование сигнал логической единицы на одном из входов в соответствующую кодовую комбинацию на выходной шине. Шифраторы, например, используют в устройствах ввода информации в цифровые системы. В таких устройствах при нажатии выбранной клавиши подаётся сигнал на определённый вход шифратора и на его выходе возникает двоичное число, соответствующее данной клавише.

Нам необходимо построить шифратор для представления десятичного числа в двоичном коде «с избытком 3». Для этого воспользуемся выше приведенной таблицей 1.3, в которой приведено соответствие между значениями на входе и выходе и получим следующие логические выражения:

Схема шифратора приведена в приложении 1.3.2.

Синтез мультиплексора

В качестве преобразователя параллельной формы представления числа в последовательную будем использовать мультиплексор.

Мультиплексор является устройством, которое осуществляет выборку одного из нескольких входов и подключает его к своему выходу. Мультиплексор имеет несколько информационных входов (Dо,D1. ), адресные входы (A0, A1) и один выход Q. Каждому информационному входу присваивается номер, называемый адресом. Мультиплексор выбирает один из входов, адрес которого задается двоичным кодом на адресных входах, и подключает его к выходу.[1,c.78]

Таким образом, подавая на адресные входы адреса различных информационных входов, можно передавать цифровые сигналы с этих входов на выход Q. Число информационных входов N_инф и число адресных входов N_адр связаны соотношением N_инф?2 Nадр . В данном курсовом проекте мультиплексор имеет четыре информационных входа. Следовательно, число адресных входов равно двум.

Синтез дешифратора

Дешифратор — это устройство, предназначенное для обратного преобразования двоичного кода в единичный сигнал и выдачу его на одном определенном выходе, соответствующему двоичному коду, поступившему на вход.

Количество входов и выходов дешифратора определяется по формуле:

где у — число выходов; х — число входов.

В данном курсовом проекте х = 3, у = 8.

Слева показаны входы дешифратора. 1, 2, 4 обозначены весовые коэффициенты двоичных разрядов, соответствующие отдельным входам.

Источник

Определение:

Шифратор (англ. encoder) — логическая схема, имеющая входов , , , и выходов , , , . Если на -ый вход подать , а на остальные входы — , то выходы , , , будут кодировать число .

Определение:

Дешифратор (англ. decoder) — логическая схема, имеющая входов , , , и выходов , , , . На все выходы подаётся , кроме выхода , на который подаётся , где — число, которое закодировано входами , , ,

Содержание

1 Принцип работы шифратора
2 Логическая схема шифратора
3 Принцип работы дешифратора
4 Логическая схема дешифратора
5 Использование в реальной жизни
6 См. также
7 Источники информации

Принцип работы шифратора

Принцип работы шифратора заключается в том, что выходы , , , кодируют один из входов , , , в двоичной системе счисления. Очевидно, что если подать на несколько входов значение , то такая схема будет работать некорректно. В качестве примера рассмотрим шифратор -to-. Если , то , если же , то и . Остальные случаи разбираются аналогичным образом.

Логическая схема шифратора

Построить логическую схему шифратора можно следующим образом: давайте будем использовать гейт , который имеет входов (где — какое-то натуральное число), и на выходе возвращает , если на всех его входах будет подано , в противном случае этот гейт вернёт . Давайте рядом с каждым выходом поставим гейт , и будем, по необходимости, расширять этот гейт. Тогда для каждого входа рассмотрим двоичное представление номера этого входа, и если на -ом месте стоит , то соединим этот вход с гейтом , который соединён с выходом . Очевидно, если подать ровно на один вход , то выходы будут кодировать это число в двоичном представлении (если подать на вход , то на всех выходах будет , а сам вход не будет соединён ни с каким гейтом).

Логическая схема шифратора -to-

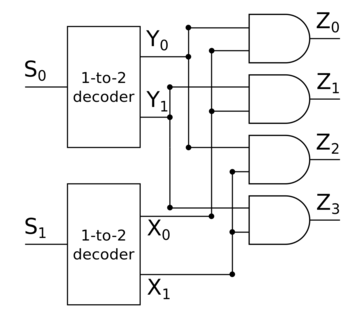
Принцип работы дешифратора

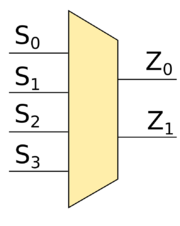
Суть дешифратора заключается в том, что с помощью входов , , , можно задавать выход, на который будет подаваться . Для того, чтобы лучше понять, как работает дешифратор, рассмотрим в качестве примера дешифратор -to- (это значит, что у этого дешифратора есть два входа и и четыре выхода , , и ). Если , то на выходе будет значение , на остальных выходах будет . Если же , , то на выходе будет , на остальных выходах будут . Если , , то на выходе будет , а на остальных входах будет . Если же , то на выходе будет , а на других — .

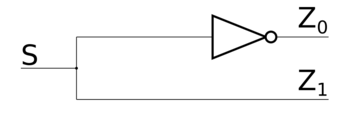
Логическая схема дешифратора

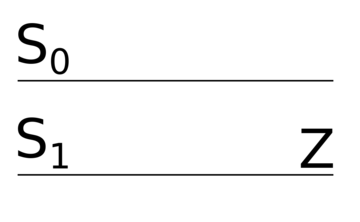
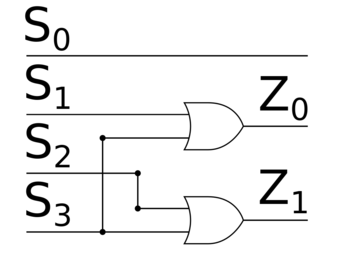
Давайте построим логическую схему дешифратора рекурсивным способом: допустим, что мы построили схему для входа, теперь попробуем слить -ый выход с предыдущими . Для схема выглядит тривиальным образом: от входа отходят два провода, один напрямую соединён с выходом , другой соединён с гейтом , а гейт соединён с выходом . Теперь допустим, что мы можем построить схему для входов. Тогда -ый вход соединим с дешифратором -to-, а первые входы соединим с дешифратором -to- и потом соединим каждый выход дешифратора -to- с каждым выходом дешифратора -to- с помощью гейтов , потом соединим соответствующие гейты с выходами таким образом, чтобы значение на входе было равно только в том случае, если число кодируется входами , , , . Очевидно, что мы таким образом перебрали всевозможные комбинации значений на входах , , , , поэтому наша схема будет работать верно.

Логическая схема дешифратора -to-

Использование в реальной жизни

Принцип работы дешифратора используется при построении мультиплексора и демультиплексора. Также шифраторы и дешифраторы используются в том случае, когда надо передавать большое количество данных, при этом использовать много проводов затруднительно (к примеру телеграф). В этом случае они позволяют использовать малое количество проводов, обеспечивая при этом наибольшее возможное количество состояний, которое может быть передано.

См. также

Реализация булевой функции схемой из функциональных элементов
Метод Лупанова синтеза схем
Мультиплексор и демультиплексор

Источники информации

Wikipedia — Priority encoder
Wikipedia — Binary decoder
Different Types of Encoder and Decoder and Its Uses

Источник

Синтез схем на дешифраторах

Синтез дешифратора и шифратора

Синтез шифратора

Синтез мультиплексора

Синтез дешифратора

Содержание

Принцип работы шифратора

Логическая схема шифратора

Принцип работы дешифратора

Логическая схема дешифратора

Использование в реальной жизни

См. также

Источники информации

Не пропустите также: