Сетевой график – это динамическая модель проекта, которая отражает последовательность и зависимость работ, необходимых для успешного завершения проекта. Сетевой график отражает сроки выполнения запланированных работ и ресурсы, необходимые для их выполнения, а также прямые финансовые затраты, возникающие при реализации этих работ.
В английском языке для определения сетевого графика используется термин Project Network — is a graph depicting the sequence in which a project’s terminal elements are to be completed by showing terminal elements and their dependencies.
Основной целью использования сетевого графика является эффективное планирование и управление работами и ресурсами проекта. При этом, под ресурсами в данном контексте понимается как оборудование, производственные мощности или денежные средства, так и трудовые ресурсы, внутренние или внешние для организации, выполняющей проект.
Наибольшая эффективность применения сетевого графика достигается при его использовании для планирования проектов или отдельных взаимосвязанных работ. Сетевой график позволяет довольно точно определить плановые сроки завершения проекта и выявить возможные варианты их сокращения. И, что более важно, сетевой график позволяет на ранней стадии планирования проекта выявить критический путь. Кроме этого сетевой график позволяет осуществлять базовый контроль над ходом работ проекта, их сроками и исполнением бюджета.
Виды сетевых графиков
Сетевой график — это граф, на котором события (состояния работ или объектов в определенный момент времени) представлены в виде вершин, а работы проекта представлены в виде дуг, соединяющих вершины графа. Сетевой график, представленный в таком виде, изначально является частью метода PERT (Program Evaluation and Review Technique).
На практике же чаще используется другой вариант сетевого графика, когда вершинами графа являются работы, а дуги обозначают взаимосвязь между ними. Такой вид сетевого графика является частью метода критического пути (англ., CPM — Critical Path Method).
Рассмотрим второй вариант графика и алгоритм его построения подробнее.
Алгоритм построения сетевого графика
Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.
Шаг 1. Определить основную цель проекта
Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.
Шаг 2. Выявить ограничения
Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.
Шаг 3. Определить состав работ
Определить состав работ, необходимых для достижения цели, поставленной на шаге 1.
Шаг 4. Оценить длительность работ
Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.
Шаг 5. Определить последовательность работ
Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.
Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.
Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.
Шаг 6. Указать связи между работами
Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.
Шаг 7. Определить раннее начало и раннее окончание
Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.
Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.
Шаг 8. Определить поздние начало и окончание
Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.
Шаг 9. Определить временной резерв
Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.
Шаг 10. Выявить критический путь
Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.
Пример построения сетевого графика
Несмотря на то, что описанный выше алгоритм может показаться сложным, на самом же деле построение сетевого графика задача несложная. Для того, чтобы убедиться в этом рассмотрим построение сетевого графика на простом примере ремонта детской комнаты.
Шаг 1. Определить основную цель проекта
Представьте, что сейчас лето, вашему сыну исполнилось 7 лет и в сентябре он идет в школу. Вы решил обновить его комнату к новому учебному году и сделать ее подходящей для школьника, т.е. должно появиться полноценной рабочее место, зонирование комнаты измениться, и т.д.
В этом случае целью нашего небольшого проекта будет — сделать комнату пригодной и приятной для проживания мальчика, который пойдет в начальную школу.
Шаг 2. Выявить ограничения
Бюджет не более 100,000 руб., ремонтные работы можно вести только в рабочие дни с 10:00 до 18:00 с обязательным перерывом с 12:00 до 14:00. Итого получается — 6 рабочих часов в день.
Шаг 3. Определить состав работ
Немного поразмыслив мы накидали основные работы, которые надо сделать, а именно:
- Нам нужен дизайн-проект новой комнаты;
- Нам надо закупить материалы для ремонта;
- Надо составить смету ремонта;
- Надо выполнить сам ремонт;
- И т.к. мы решили сделать небольшую перепланировку, то надо согласовать ее с ТСЖ.
Отобразим эти работы в виде блоков:
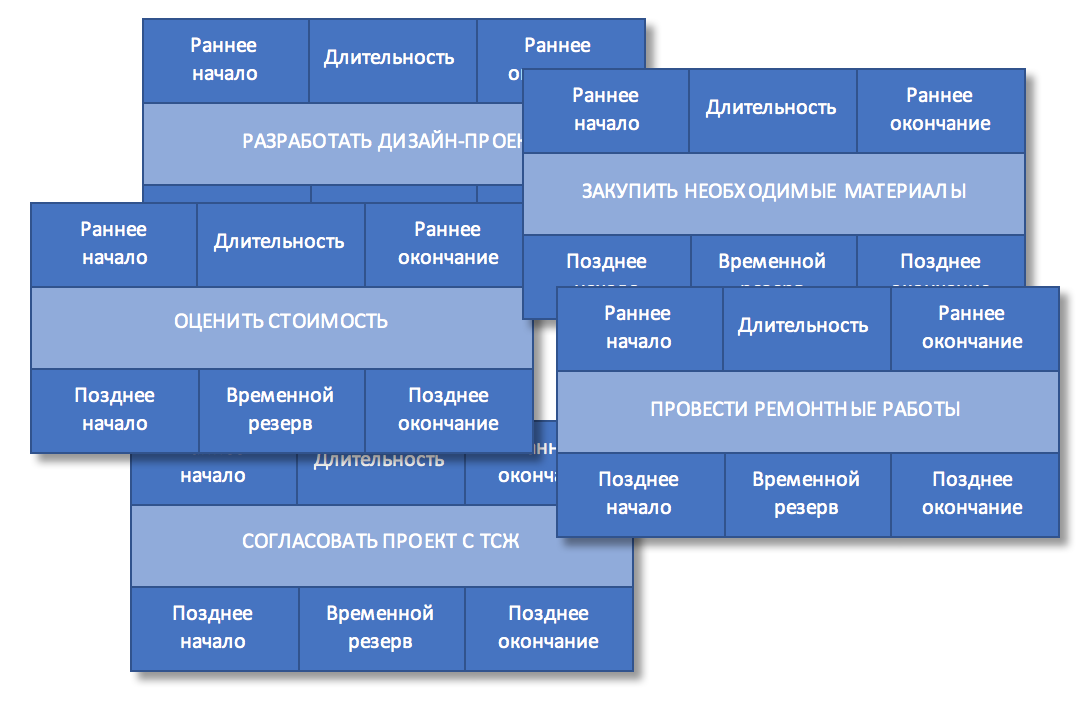
Рисунок 1. Состав работ
Шаг 4. Оценить длительность работ
Мы решили оценивать длительность работ в днях, т.к. до начала учебного года еще достаточно времени, то такая точность планирования нас вполне устраивает.

Рисунок 2. Длительность работ
Шаг 5. Определить последовательность работ
Теперь определим последовательность работ, мы будем использовать схему построения сетевого графика «сверху-вниз». Первая работа, которую необходимо выполнить — это работа «Разработать дизайн-проекта«. Затем мы оценим стоимость проекта, а параллельно начнем согласование с ТСЖ, т.к. эта задача занимает много времени. После того, как мы оценим проект и его согласуем, мы приступим к покупке всех необходимых материалов и уже затем начнем сам ремонт.

Рисунок 3. Последовательность работ
Шаг 6. Указать связи между работами
Укажем стрелками связи между работами.
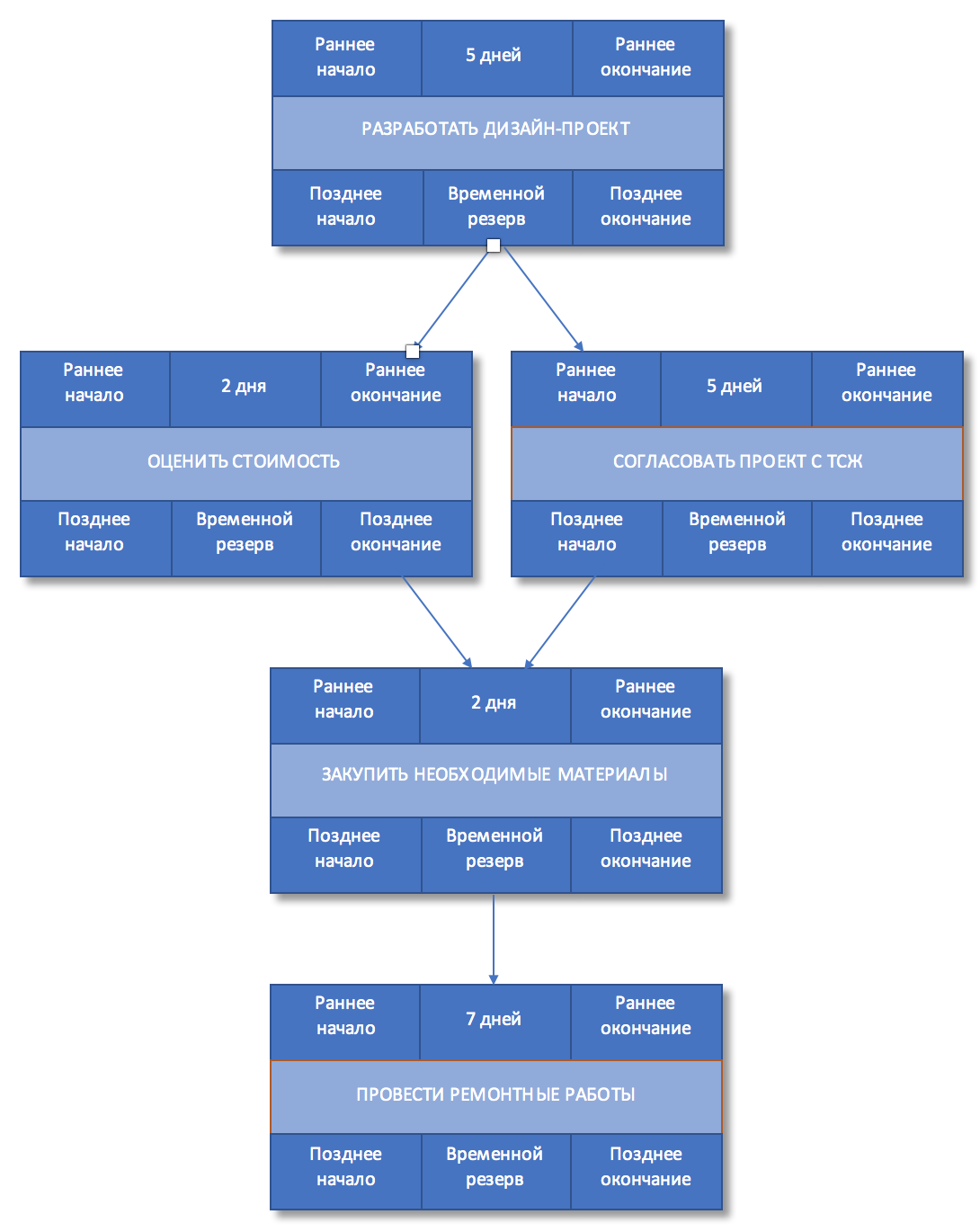
Рисунок 4. Связи между работами
Шаг 7. Определить раннее начало и раннее окончание
Т.к. мы выбрали модель сетевого график «сверху-вниз», то начинаем его и просматривать сверху вниз, начиная с самой верхней работы, и далее по очереди двигаемся к самой нижней работе.
Напомним, что раннее начало последующей работы будет совпадать с ранним завершением предшествующей, а раннее окончание каждой из работ определяется как раннее начало плюс длительность работ Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ.
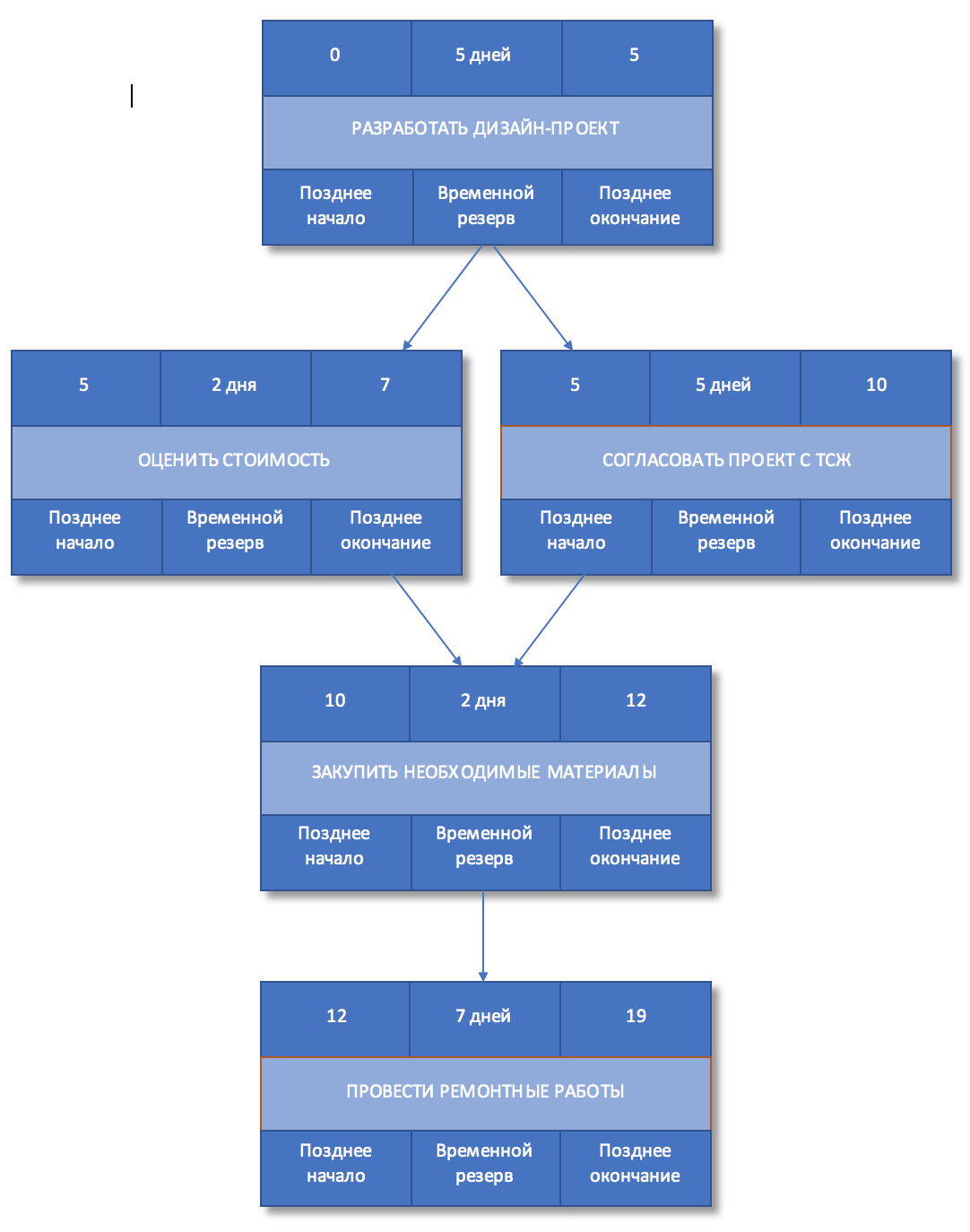
Рисунок 5. Раннее начало и окончание работ
Шаг 8. Определить поздние начало и окончание
Для того, чтобы определить поздние начало и окончание просмотрим сетевой график в обратном направлении — снизу вверх. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.
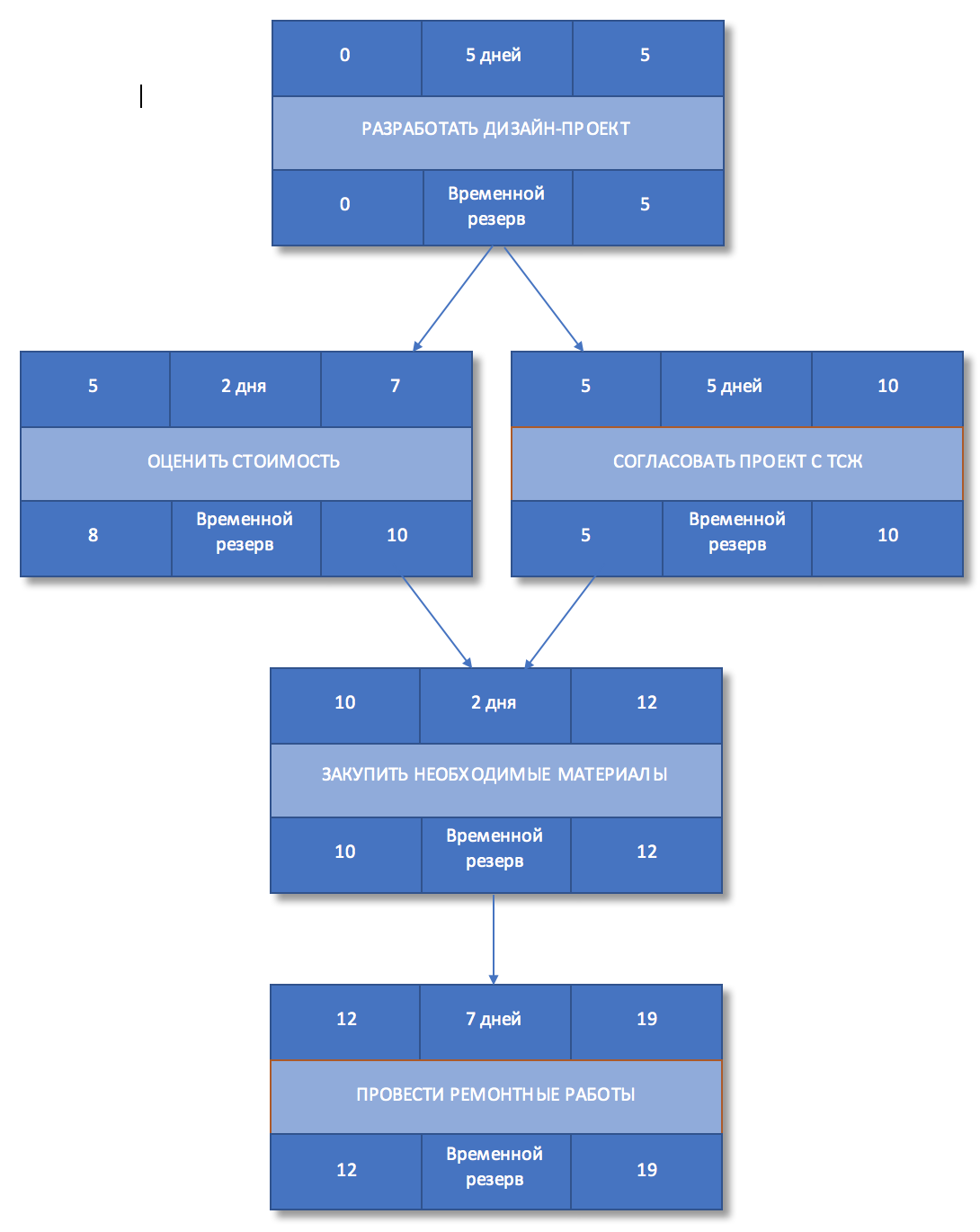
Рисунок 6. Позднее начало и окончание работ
Шаг 9. Определить временной резерв
Вычислим временной резерв для каждой из работ. Он вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.
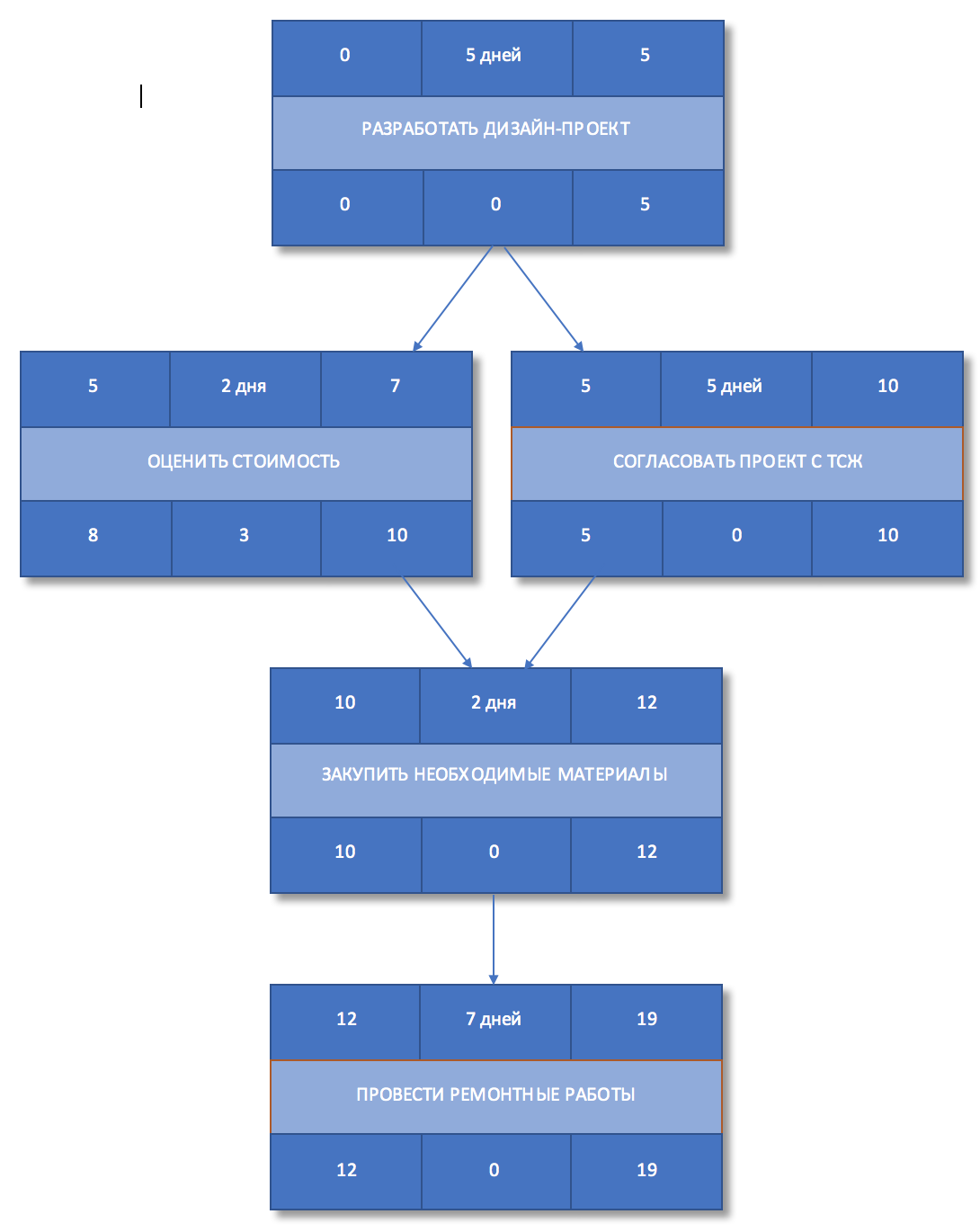
Рисунок 7. Временной резерв
Шаг 10. Выявить критический путь
Как мы уже знаем, критический путь — это цепочка работ, у которых резерв времени равен нулю. Выделим такие задачи на сетевом графике.
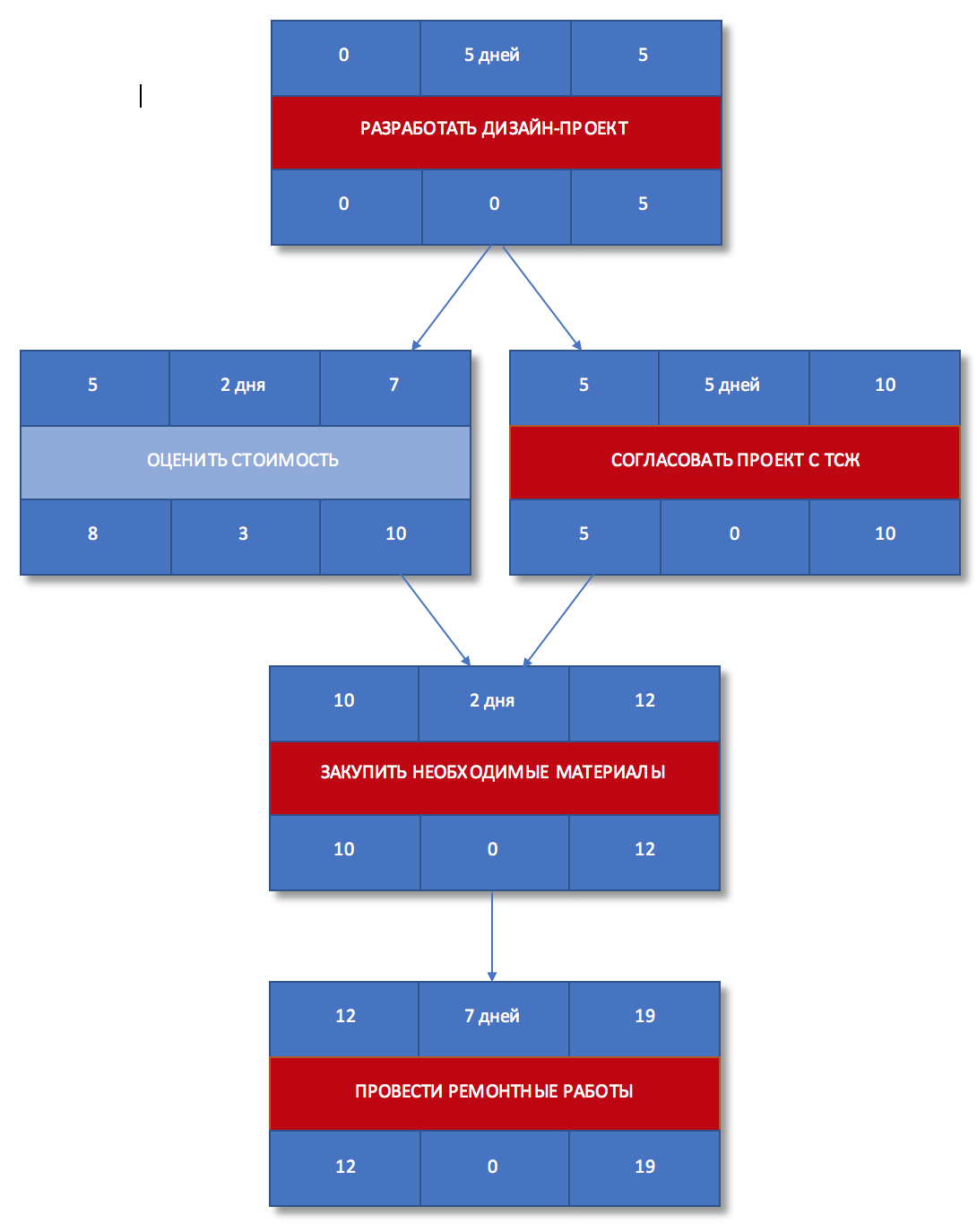
Рисунок 8. Критический путь
Задачи «Разработать дизайн-проект«, «Согласовать проект с ТСЖ» и «Закупить необходимые материалы«, «Провести ремонтные работы» составляю критический путь, а его длина составляет 19 дней. Это означает, что в текущем виде проект не может быть выполнен быстрее, чем за 19 дней. Если мы хотим сократить сроки проекта, то нам необходимо оптимизировать задачи, лежащие на критическом пути.
Например, мы можем начать ремонтные работы раньше получения согласования на перепланировку от ТСЖ, приняв на себя риски того, что согласование может быть не получено.
Просмотры: 138 115
Планирование работы всегда начинается с определения количества задач, ответственных за их исполнение лиц и времени, необходимого для полного завершения. При управлении проектами такие схемы просто необходимы. Во-первых, для того чтобы понимать, какое общее время будет затрачено, во-вторых, чтобы знать, как планировать ресурсы. Именно этим занимаются проектные менеджеры, они в первую очередь осуществляют построение сетевого графика. Пример возможной ситуации рассмотрим далее.
Исходные данные
Руководство рекламного агентства приняло решение о выходе в свет нового рекламного продукта для своих клиентов. Перед сотрудниками фирмы были поставлены такие задачи: рассмотреть идеи рекламных брошюр, привести аргументы в пользу того или иного варианта, создать макет, подготовить проект договора для клиентов и послать всю информацию руководству на рассмотрение. Для информирования клиентов необходимо провести рассылку, расклеить плакаты и обзвонить все фирмы, имеющиеся в базе данных.
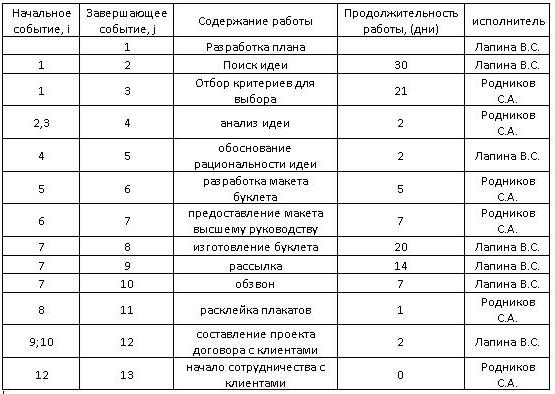
Кроме этого, главный руководитель составил детальный план всех необходимых действий, назначил ответственных сотрудников и определил время.
Начнем построение сетевого графика. Пример имеет данные, представленные на следующем рисунке:
Построение матрицы
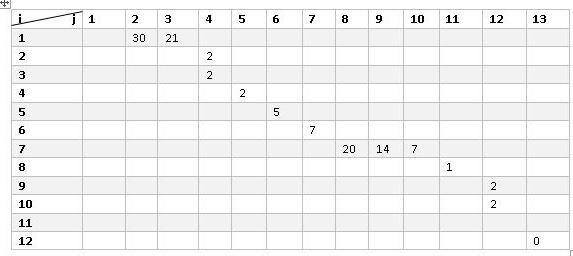
Перед тем как сформировать сетевой график, необходимо создать матрицу. Построение графиков начинается с этого этапа. Представим себе систему координат, в которой вертикальные значения соответствуют i (начальное событие), а горизонтальные строки – j (завершающее событие).
Начинаем заполнять матрицу, ориентируясь на данные рисунка 1. Первая работа не имеет времени, поэтому ею можно пренебречь. Рассмотрим детальнее вторую.
Начальное событие стартует с цифры 1 и заканчивается на втором событии. Продолжительность действия равняется 30 дням. Это число заносим в ячейку на пересечении 1 строки и 2 столбца. Аналогичным способом отображаем все данные, что представлено на рисунке ниже.
Основные элементы, используемые для сетевого графика
Построение графиков начинается с обозначения теоретических основ. Рассмотрим основные элементы, требующиеся для составления модели:
- Любое событие обозначается кружком, в середине которого находится цифра, соответствующая порядку действий.
- Сама работа – это стрелка, ведущая от одного события к другому. Над стрелкой пишут время, необходимое для ее совершения, а под стрелкой обозначают ответственное лицо.
Работа может выполниться в трех состояниях:
— Действующая – это обыкновенное действие, на совершение которого требуются затраты времени и ресурсов.
— Ожидание – процесс, во время которого ничего не происходит, но он требует затрат времени для перехода от одного события к другому.
— Фиктивная работа – это логическая связь между событиями. Она не требует ни времени, ни ресурсов, но чтобы не прервать сетевой график, ее обозначают пунктирной линией. Например, подготовка зерна и приготовление мешков для него — это два отдельных процесса, они не связаны последовательно, но их связь нужна для следующего события – фасовки. Поэтому выделяют еще один кружочек, который соединяют пунктиром.
Основные принципы построения
Правила построения сетевых графиков заключаются в следующем:
- Все события имеют начало и конец.
- Только к первому событию могут не идти стрелки, и только от последнего они не выходят.
- Все без исключения события должны быть связаны последовательными работами.
- График строится строго слева направо в последовательном порядке.
- Два события может соединять только одна работа. Нельзя ставить две стрелки; если нужно выполнить две работы, то вводят фиктивную с новым событием.
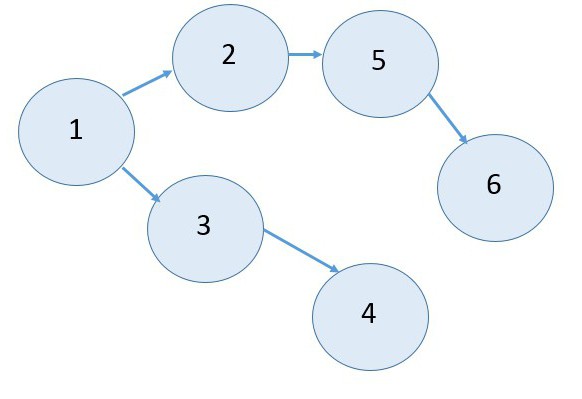
- В сети должны отсутствовать тупики. Нельзя допускать ситуации, указанной на рисунке 3.
- Нельзя допускать образования циклов и замкнутых контуров.
Построение сетевого графика. Пример
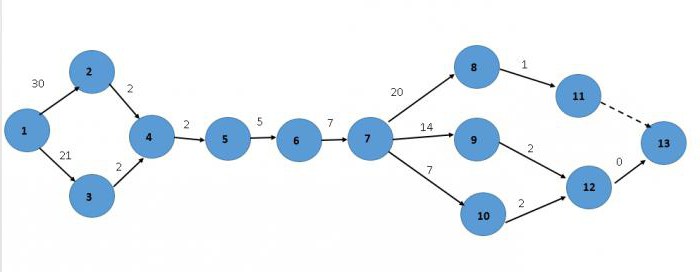
Вернемся к исходному примеру и попробуем начертить сетевой график, используя все данные, указанные ранее.
Начинаем с первого события. Из него выходят два – второе и третье, которые соединяются в четвертом. Далее все идет последовательно до седьмого события. Из него выходят три работы: восьмая, девятая и десятая. Постараемся все отобразить:
Критические значения
Это еще не все построение сетевого графика. Пример продолжается. Далее нужно рассчитать критические моменты.
Критический путь – это наибольшее время, затраченное на выполнение задания. Для того чтобы его рассчитать, нужно сложить все наибольшие значения последовательных действий. В нашем случае это работы 1-2, 2-4, 4-5, 5-6, 6-7, 7-8, 8-11. Суммируем:
30+2+2+5+7+20+1 = 67 дней
Таким образом, критический путь равен 67 дням.
Если такое время на проект не устраивает руководство, его нужно оптимизировать согласно требованиям.
Автоматизация процесса
На сегодняшний день мало кто из проектных менеджеров вручную рисует схемы. Программа для построения сетевых графиков – это простой и удобный способ быстро рассчитать затраты времени, определить порядок работ и назначить исполнителей.
Кратко рассмотрим самые распространенные программы:
- Microsoft Project 2002 – офисный продукт, в котором очень удобно рисовать схемы. Но проводить расчеты немного неудобно. Для того чтобы совершить даже самое простое действие, нужен немалый багаж знаний. Скачивая программу, позаботьтесь о приобретении инструкции по пользованию к ней.
- SPU v2.2. Очень распространенный бесплатный софт. Вернее, даже не программа, а файл в архиве, для использования которого не нужна установка. Изначально она была разработана для выпускной работы одного студента, но оказалась настолько полезной, что автор выложил ее в сеть.
- NetGraf – еще одна разработка отечественного специалиста из Краснодара. Очень легка, проста в использовании, не требует установки и огромного багажа знаний, как с ней управляться. Плюсом является то, что поддерживает импорт информации из других текстовых редакторов.
- Часто можно встретить вот такой экземпляр – Borghiz. О разработчике мало что известно, как и о том, как пользоваться программой. Но по примитивному методу «тыка» ее можно освоить. Главное, что она работает.
Практика построения сетевого графика

Свежие публикации автора:
Содержание
- 1 Перед стартом моделирования
- 2 Последовательность действий по моделированию
- 2.1 Шаг первый
- 2.2 Шаг второй
- 2.3 Шаг третий
- 2.4 Шаг четвертый
- 3 Дополнительные расчеты модели
- 4 Использование табличного метода
Представим себе ситуацию развития проекта капитального строительства на производственном предприятии. Проект успешно инициирован и полным ходом идут работы по его планированию. Сформирована и утверждена иерархическая структура работ, план по вехам принят. Разработан первичный вариант календарного плана. Поскольку задача оказалась достаточно масштабной, куратор принял решение о разработке еще и сетевой модели. Расчет сетевого графика в прикладном аспекте его исполнения является предметом настоящей статьи.
Перед стартом моделирования
Методологический базис сетевого проектного планирования представлен на нашем сайте несколькими статьями. Я лишь сошлюсь на две из них. Это материалы, посвященные этапу сетевого планирования проекта в целом и непосредственно моделированию сетевого графика проекта. Если в ходе повествования у вас будут возникать вопросы, просмотрите ранее представленные осмысления, основная суть методологии в них изложена. В настоящей статье мы рассмотрим небольшой пример локальной части комплекса строительно-монтажных работ в рамках значительной проектной реализации. Расчеты и моделирование будем выполнять методом «вершина-работа» и классическим табличным способом («вершина-событие») с применением МКР (метода критического пути).
Построение сетевого графика мы начнем на основе первой итерации календарного плана, выполненного в форме диаграммы Ганта. Для целей наглядности предлагаю не учитывать отношения предшествования и максимально упростить последовательность действий. Хотя на практике такое бывает редко, представим в нашем примере, что операции выстроены в последовательность вида «окончание-начало». Ниже вашему вниманию представляются две таблицы: выписка из списка работ проекта (фрагмент из 15-ти операций) и список параметров сетевой модели, необходимый для представления формул.
Пример фрагмента списка операций инвестиционного проекта
Список параметров сетевой модели, подлежащих расчету
Пусть вас не пугает обилие элементов. Построение сетевой модели и расчет параметров достаточно просто выполнить. Важно тщательно подготовиться, иметь под рукой иерархическую структуру работ, линейный график Ганта – в общем, все, что дает возможность определиться с последовательностью и взаимосвязями действий. Еще в первые разы выполнения графика я рекомендую иметь перед собой формулы расчета требуемых значений. Они представлены ниже.
Формулы расчета параметров сетевого графика
Что нам потребуется определить в ходе построения графика?
- Раннее начало текущей работы, в которую входят несколько связей от предыдущих операций. Выбираем максимальное значение из всех ранних окончаний предыдущих операций.
- Позднее окончание текущего действия, из которого выходят несколько связей. Выбираем минимальное значение из всех поздних начал последующих действий.
- Последовательность работ, формирующих критический путь. У этих действий раннее и позднее начала равны, как и раннее и позднее окончание соответственно. Резерв такой операции равен 0.
- Полные и частные резервы.
- Коэффициенты напряженности работ. Логику формул резервов и коэффициента напряженности работы мы рассмотрим в специальном разделе.
Последовательность действий по моделированию
Шаг первый
Построение сетевого графика начинаем путем размещения прямоугольников задач последовательно слева-направо, применяя правила, описанные в предыдущих статьях. При выполнении моделирования методом «вершина-работа» основным элементом диаграммы выступает семисегментный прямоугольник, в составе которого отражены параметры начала, окончания, длительности, резерва времени и наименования или номера операций. Схема представления ее параметров показана далее.
Схема изображения работы на сетевом графике
Результат первого этапа построения сетевого графика
В соответствии с логикой последовательности операций с помощью специализированной программы, MS Visio или любого редактора размещаем образы работ в заданном выше формате. В первую очередь заполняем наименования выполняемых действий, их номера и длительность. Рассчитываем раннее начало и раннее окончание с учетом формулы раннего начала текущего действия в условиях нескольких входящих связей. И так проходим до завершающей фрагмент операции. При этом, в нашем примере проекта тем же графиком Ганта не предусмотрены исходящие связи от операций 11, 12, 13 и 14. «Подвешивать» их на сетевой модели недопустимо, поэтому мы добавляем фиктивные связи к конечной работе фрагмента, выделенные на рисунке синим цветом.
Шаг второй
Находим критический путь. Как известно, это путь, имеющий самую большую продолжительность действий, которые в него входят. Просматривая модель, мы выбираем связи между работами, имеющими максимальные значения раннего окончания действий. Намеченный критический путь выделяем стрелочками красного цвета. Полученный результат представлен на промежуточной схеме далее.
Схема сетевого графика с выделенным критическим путем
Шаг третий
Заполняем значения позднего окончания, позднего начала и полного резерва работ. Для выполнения расчета переходим к конечной работе и берем ее за последнюю операцию критического пути. Это означает, что поздние значения окончания и начала идентичны ранним, и от последней операции фрагмента мы начинаем двигаться в обратную сторону, заполняя нижнюю строку схематического представления действия. Модель выполнения расчета показана ниже на схеме.
Схема расчета поздних начал и окончаний вне критического пути
Итоговый вид сетевого графика
Шаг четвертый
Четвертым шагом алгоритма сетевого моделирования и расчетов выполняется вычисление резервов и коэффициента напряженности. Первым делом имеет смысл обратить внимание на полные резервы путей некритических направлений (R). Они определяются путем вычитания из продолжительности критического пути временной длительности каждого из этих путей, пронумерованных на схеме итогового сетевого графика.
- R пути под номером 1 = 120 – 101 = 19;
- R пути под номером 2 = 120 – 84 = 36;
- R пути под номером 3 = 120 – 104 = 16;
- R пути под номером 4 = 120 – 115 = 5;
- R пути под номером 5 = 120 – 118 = 2;
- R пути под номером 6 = 120 – 115 = 5.
Дополнительные расчеты модели
Выполнение расчета общего резерва текущей операции производится путем вычитания из значения позднего начала раннего начала или из позднего окончания раннего окончания (см. схему расчета выше). Общий (полный) резерв показывает нам возможность начала текущей работы позже или увеличения продолжительности на длительность резерва. Но нужно понимать, что пользоваться полным резервом следует с большой осторожностью, потому что работы, стоящие от текущего события дальше остальных, могут оказаться без запаса времени.
Помимо полных резервов в сетевом моделировании оперируют также и частными или свободными резервами, которые представляют собой разницу между ранним началом последующей работы и ранним окончанием текущей. Частный резерв показывает, есть ли возможность сдвинуть ранее начало операции вперед без ущерба для начала следующей процедуры и всему графику в целом. Следует помнить, что сумма всех частных резервных значений тождественна полному значению резерва для рассматриваемого пути.
Главной задачей выполнения вычислений различных параметров является оптимизация сетевого графика и оценка вероятности выполнения проекта в срок. Одним из таких параметров является коэффициент напряженности, который показывает нам уровень сложности реализовать работу в намеченный срок. Формула коэффициента представлена выше в составе всех расчетных выражений, применяемых для анализа сетевого графика.
Коэффициент напряженности определяется как разница между единицей и частного от деления полного резерва времени работы на разницу длительности критического пути и особого расчетного значения. Это значение включает ряд отрезков критического пути, совпадающих с максимально возможным путем, к которому может быть отнесена текущая операция (i-j). Далее помещен расчет частных резервов и коэффициентов напряженности работ для нашего примера.
Таблица расчета частных резервов и коэффициента напряженности
Коэффициент напряженности варьируется от 0 до 1,0. Значение 1,0 устанавливается для работ, находящихся на критическом пути. Чем ближе значение некритической операции к 1,0, тем труднее удержаться в плановых сроках ее реализации. После того, как значения коэффициента по всем действиям графика посчитаны, операции, в зависимости от уровня этого параметра, могут быть отнесены к категории:
- критической зоны (Кн более 0,8);
- подкретической зоны (Кн более или равно 0,6, но менее или равно 0,8);
- резервной зоны (Кн менее 0,6).
Оптимизация сетевой модели, нацеленная на сокращение общей продолжительности проекта, как правило, обеспечивается следующими мероприятиями.
- Перераспределение ресурсов в пользу наиболее напряженных процедур.
- Снижение трудоемкости операций, расположенных на критическом пути.
- Распараллеливание работ критического пути.
- Переработка структуры сети и состава операций.
Использование табличного метода
Общепризнанные ПП календарного планирования (MS Project, Primavera Suretrack, OpenPlan и т.п.) способны вычислять ключевые параметры сетевой модели проекта. Мы же в настоящем разделе табличным методом выполним настройку подобного расчета обычными средствами MS Excel. Для этого возьмем наш пример фрагмента проектных операций проекта в области СМР. Расположим основные параметры сетевого графика в столбах электронной таблицы.
Модель расчета параметров сетевого графика табличным способом
Преимуществом выполнения расчетов табличным способом является возможность простой автоматизации вычислений и избежание массы ошибок, связанных с человеческим фактором. Красным цветом будем выделять номера операций, располагающихся на критическом пути, а синим цветом отметим расчетные позиции частных резервов, превышающих нулевое значение. Разберем пошагово расчет параметров сетевого графика по основным позициям.
- Ранние начала операций, следующих за текущей работой. Алгоритм расчета настраиваем на выбор максимального значения из раннего времени окончания нескольких альтернативных предыдущих действий. Взять, например, операцию под номером 13. Ей предшествуют работы 6, 7, 8. Из трех ранних окончаний (71, 76, 74 соответственно) нам нужно выбрать максимальное значение – 76 и проставить его в качестве раннего начала операции 13.
- Критический путь. Выполняя процедуру расчета по пункту 1 алгоритма, мы доходим до конца фрагмента, найдя значение продолжительности критического пути, которая в нашем примере составила 120 дней. Значения наибольших ранних окончаний среди альтернативных действий обозначают операции, лежащие на критическом пути. Отмечаем эти операции красным цветом.
- Поздние окончания операций, предшествующих текущей работе. Начиная с концевой работы начинаем движение в обратную сторону от действий с большими номерами к операциям с меньшими. При этом из нескольких альтернатив исходящих работ выбираем наименьшее знание позднего начала. Поздние начала вычисляем как разницу между выбранными значениями поздних окончаний и продолжительности операций.
- Резервы операций. Вычисляем полные (общие) резервы как разницу между поздними началами и ранними началами либо между поздними окончаниями и ранними окончаниями. Значения частных (свободных) резервов получаем в результате вычитания из числа раннего начала следующей операции раннего окончания текущей.
Мы рассмотрели практические механизмы составления сетевого графика и расчета основных параметров временной продолжительности проекта. Таким образом, вплотную приблизились к исследованию возможностей анализа, проводимого с целью оптимизации сетевой модели и формирования непосредственно плана действий по улучшению ее качества. Настоящая тема занимает немного места в комплексе знаний проект-менеджера и не так уж и сложна для восприятия. Во всяком случае, каждый РМ обязан уметь воспроизводить визуализацию графика и выполнять сопутствующие расчеты на хорошем профессиональном уровне.
Сетевые графики строительства отдельных объектов и комплексов.
Сетевой график
— это графическое изображение
технологической последовательности
выполнения работ на объекте или нескольких
объектах с указанием их продолжительности
и всех временных параметров, а также
общего срока строительства. В основе
управления строительством должна лежать
заранее разработанная модель процесса
производства СМР, начиная с подготовительных
работ и кончая вводом объекта в
эксплуатацию.
Отличительными
особенностями сетевого графика являются:
-
наличие
взаимосвязи между работами и
технологической последовательностью
их выполнения; -
возможность
выявления работ, от завершения которых
в первую очередь зависит продолжительность
строительства; -
возможность
выбора вариантов последовательности
и продолжительности работ с целью
улучшения сетевого графика; -
облегчение
осуществления контроля работ за ходом
строительства; -
возможность
использования ЭВМ для расчёта параметров
графика при планировании и управлении
строительством.
Элементов
сетевого
графика, приводим в таблице:
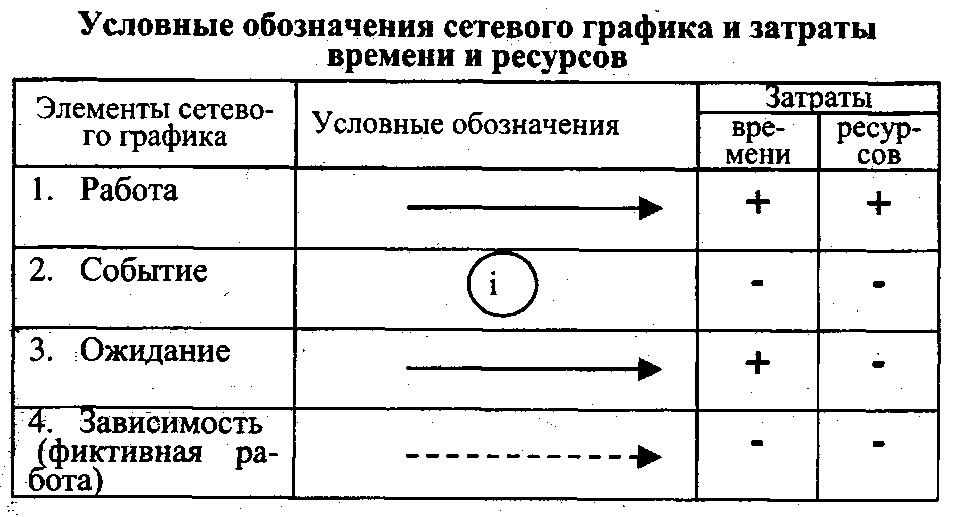
Работа
– это технологический процесс, требующий
затрат времени, трудовых и материальных
ресурсов, приводящий к достижению
определённого запланированного
результата. Работа на графике обозначается
сплошной стрелкой, длина которой может
быть не связана с продолжительностью
работ (если график выполнен не в масштабе
времени).
Событие
— это
факт
окончания одной или нескольких работ,
необходимых и достаточных для начала
последующих работ. Имеется в виду, что
событие свершается мгновенно, поэтому
оно не требует ни времени, ни материальных,
ни трудовых затрат. Событие изображается
в виде круга, внутри которого указывается
определённый номер – код события.
Виды
событий:
-
исходное
событие — начало строительства объекта,
не имеет предшествующих работ. Этим
событием начинается развитие сетевого
графика. -
завершающее
событие — не имеет последующих работ и
им заканчиваются работы в сетевом
графике.
События
ограничивают рассматриваемой работой
и по отношению к ней они могут быть
начальными и конечными:
-
начальное
событие — для рассматриваемой работы
определяет начало данной работы и
является конечным для предшествующих
работ. -
конечное
событие — определяет факт окончания
данной работы и является начальным для
последующих работ.

Ожидание
—
в
строительстве может возникать
необходимость в перерывах между
выполняемыми работами. Это процесс,
требующий времени и не потребляющий
материальных и трудовых ресурсов.
Ожидание изображается, как и работа,
сплошной стрелкой с указанием
продолжительности и наименованием
ожидания. Такие
перерывы могут быть:
-
технологические
перерывы могут быть связаны с
необходимостью набора прочности
бетоном, твердения стяжки под рулонную
кровлю, сушки штукатурки перед малярными
работами и т.п. -
организационные
перерывы могут возникать при занятости
бригад нужных профессий на другом
объекте, ожиданием тёплого времени
года для выполнения работ по благоустройству
и проч.
Зависимость
— между
отдельными видами СМР могут существовать
технологические зависимости (например,
нельзя вести отделочные работы, монтаж
технологического оборудования при
отсутствии кровли, работы по благоустройству
без прокладки подземных коммуникаций
и т.п.). Зависимость (иногда её ещё называют
фиктивной работой) отражает технологическую
или организационную взаимосвязь работ,
она не требует ни времени, ни ресурсов,
определяет технологическую
последовательность событий, изображается
на сетевом графике пунктирной стрелкой.
Зависимость
может быть:
-
технологической
(показывает необходимую последовательность
выполнения работ); -
ресурсной
или организационной, связанной с
переходом бригад или перегоном
строительных машин с объекта на объект.
Путь
—
это
непрерывная последовательность работ
в сетевом графике (т.к. каждая работа в
графике имеет свою продолжительность,
рассчитанную на основе подлежащих к
выполнению объёмов работ, то пройдя от
исходного события к завершающему, по
цепочке работ и зависимостей, можно
подсчитать общую продолжительность
работ в каждой цепочке). В сетевом графике
между исходным и завершающим событием
может быть несколько путей, различных
по продолжительности.
Полный
путь
– это путь от исходного до завершающего
события сетевого графика. Участок пути
от исходного события до данного события
называют предшествующим, а путь от
данного события до любого последующего
называют последующим путём.
Критический
путь
сетевого графика – это полный путь от
исходного до завершающего события,
имеющий наибольшую длину (продолжительность)
из всех полных путей. Его временная
длина определяет срок выполнения всех
работ в сетевом графике. В сетевом
графике может быть несколько критических
путей. Увеличение продолжительности
работ, лежащих на критическом пути,
увеличивает общую продолжительность
работ; соответственно сокращение этих
работ приводит к общему сокращению
срока строительства объекта. Критический
путь на сетевом графике выделяется
утолщённой линией или каким-либо другим
способом.
Подкритический
путь –
это путь,
длина которого несколько меньше
критического пути, но при сокращении
продолжительности работ на критическом
пути подкритический путь может стать
критическим.
Критическая
зона
— совокупность критических и подкритических
путей на сетевом графике. Выявление в
сетевом графике критической зоны
позволяет выявить работы, на которые
нужно обращать внимание при необходимости
сокращения сроков строительства, либо
при проектировании сетевого графика,
либо при контроле за ходом строительства.
Код
работы –
т.к. в
сетевом графике каждая работа находится
между двумя событиями (начальным, из
которого она выходит, и конечным, в
которое она входит), то каждое событие
имеет свой номер, поэтому каждая работа
приобретает свой код, состоящий из
номеров её начального и конечного
события.
Основные
правила построения сетевого графика:
-
для
удобства построения сетевого графика
направление стрелок следует принимать
слева направо, избегая по возможности
пересечения линий; -
каждая
работа должна иметь свой код. В случае
выполнения параллельных работ, имеющих
единое начало и окончание, необходимо
вводить дополнительные события, иначе
разные работы получат единое наименование.

-
в
сетевом графике не должно быть «тупиков»
(событий, из которых не выходит ни одной
работы) и «хвостов» (событий, в которые
не входит ни одна работа);
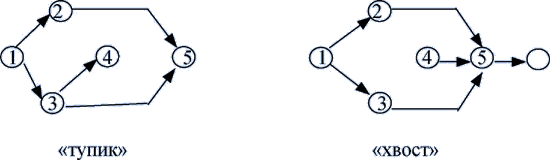
-
нумерация
(кодирование) событий должна соответствовать
последовательности работ во времени,
т.е. предшествующим событиям присваиваются
меньшие номера; -
нумерацию
событий нужно производить только после
полного построения сети и убеждённости,
что технологически сеть построена
правильно; -
первоначальный
вариант сетевого графика строится без
учёта продолжительности составляющих
его работ, обеспечивая только
технологическую последовательность
(в этом случае длина стрелок значения
не имеет).
Резерв
времени
– определяется при сравнении
длины критического пути с длиной любого
некритического пути, устанавливая при
этом возможность на определённое
количество времени увеличить длину
некритических работ без увеличения
общего срока строительства объекта.
Эти дни и составляют резерв времени,
который
может быть:
-
частным
— количество рабочего времени, на которое
может быть увеличена продолжительность
этой работы или перенесено её начало
так, чтобы при этом не изменилось раннее
начало последующих работ. -
общим
— количество рабочего времени, на которое
может быть увеличена продолжительность
данной работы при условии, что
продолжительность самого наибольшего
из путей, проходящих через эту работу,
не превышает длины критического пути.
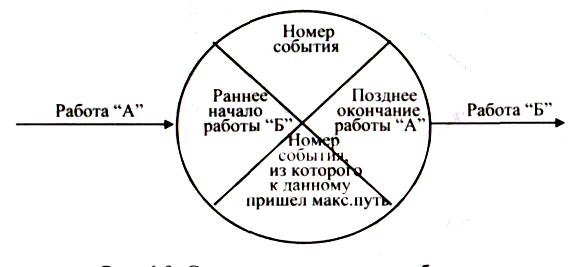
Для расчета
непосредственно на сетевом графике
каждое событие делится на 4 сектора:
При
разработке сетевой график представляет
собой немасштабную модель, но возникает
необходимость представить его в привычной
форме в масштабе времени, доступной для
использования на любом уровне управления.
Для привязки графика к календарному
времени используется календарная
линейка. При привязке событий сетевого
графика к календарю наглядно видно,
когда какая работа выполняется и когда
она должна быть закончена. Масштабный
график, как правило, строят по ранним
срокам событий.
Раннее
начало работы
— срок, раньше которого нельзя начать
данную работу, не нарушив принятой
технологической последовательности.
Он определяется наиболее долгим путем
от исходного события до начала данной
работы
Позднее
окончание работы
— самый поздний срок окончания работы,
при котором не увеличивается общая
продолжительность работ. Он определяется
самым коротким путем от данного события
до завершения всех работ.
Карточка-определитель
сетевого графика
является исходным документом для расчёта
сетевого графика.
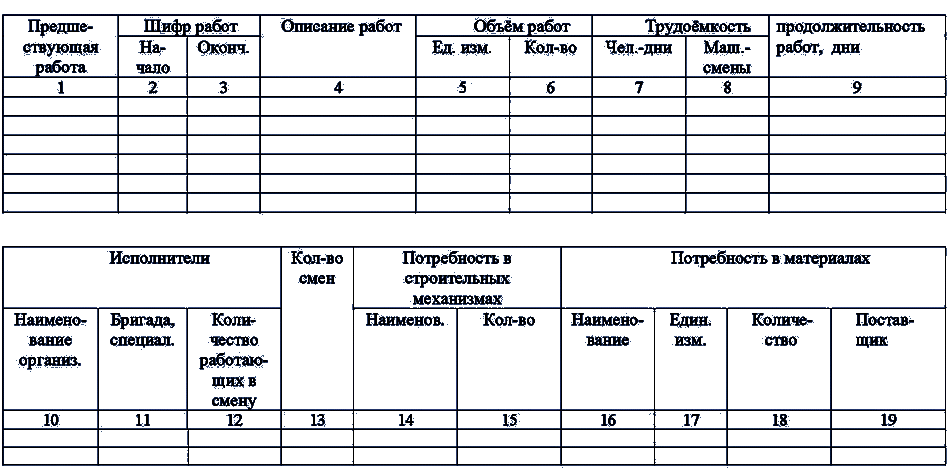
С
помощью карточки-определителя назначается
продолжительность выполнения каждой
работы на основе принятых методов
производства работ, назначается состав
бригады и сменность. Исходными
данными для разработки карточки-определителя
сетевого графика являются:
-
точное
наименование и состав каждой работы; -
данные
об имеющихся в строительной организации
бригадах и их составах; -
информация
о достигнутой этими бригадами
производительности труда; -
данные
о поставках строительных материалов
и конструкций, оборудования; -
сведения
о действующих нормативных документах
(СНиП, ЕНиР, инструкции и указания по
производству работ); -
данные
о механизмах, которыми располагают
строительные и монтажные организации.
Определение
продолжительности работ осуществляется
после определения
трудоёмкости работы двумя
способами:
-
назначив
численный состав бригады, разделить
трудоёмкость работ на число рабочих
бригады; -
назначив
продолжительность работ в днях, разделить
трудоёмкость работ на её продолжительность;
в этом случае мы узнаем необходимый
численный состав бригады.
Но
эти положения не распространяются на
выполнение механизированных работ. В
этом случае надо определить требуемое
количество машино-смен работы и, разделив
на количество механизмов и их сменность,
получить продолжительность работы в
днях; в соответствии с ЕНиР назначается
состав монтажной бригады.
В
результате расчёта параметров сети и
возможности её привязки к календарю
можно выявить потребность
в трудовых и материальных ресурсах в
каждый момент строительства объекта.
Для этого строится эпюра потребности
ресурсов, горизонтальный вектор которой
привязан к календарю, а вертикальный
вектор указывает на количество
потребляемых ресурсов. В основу построения
эпюры закладывается постоянство
расходования ресурсов при выполнении
каждой работы. Сложение потребностей
работ по вертикали в определённый
календарный срок даёт необходимую
информацию.
Чтобы
правильно привязать сеть к календарю,
даты начала той или иной работы должны
соответствовать ранним началам работ,
расположенные в левом секторе событий.
Работы,
имеющие резерв времени, должны быть на
сетевом графике выделены (могут иметь
прерывистую линию в той части работы,
где есть частный резерв времени), и на
эпюру проецируется только та часть
работы, где есть ресурсы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Анализ сетевого графика
С помощью данной программы можно онлайн определить параметры сетевого графика (рассчитать сроки свершения событий, резервы времени и критический путь), найти коэффициенты напряженности. Оптимизация сетевого графика проводится по следующим критериям: число исполнителей, резервы-затраты, сокращение сроков (см. вкладку Параметры сетевого графика).
Сетевой график можно нарисовать, а также задать в виде матрицы или таблицы (меню Действия).
- Ввод данных
- Параметры сетевого графика
- Решение
- Видеоинструкция
- Оформление Word
Нумерация вершин с №1
Выберите нужный тип вершины и нажмите левой кнопкой мыши на графическом полотне
Размеры графического полотна
Ширина
Высота
Созданный сетевой график можно сохранить в форматах docx и png (меню Действия).
Далее можно найти параметры сетевой модели (критический путь, резервы времени, построить диаграмму Ганта и многое другое).
Для сформированного графа можно выполнить следующие действия:
Здесь будет показано решение
Инструкция к сервису
Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить. Новый объект также можно вставить, предварительно выделив его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле. Нумерация вершин может начинаться с 0, для этого нужно снять отметку с пункта Нумерация вершин с №1.
1234
1103015
Нумерация вершин с 0
0123
1103015
Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить.
Сетевая модель может быть представлена в табличной форме и в виде матрицы весов (матрицы расстояний). Чтобы использовать данные представления, выберите меню Операции.
Построенный граф можно сохранить в формате docx или png.
Если в качестве формы вершин используется прямоугольник, то при построении секторальной диаграммы применяется методология Microsoft Visio с отображением параметров duration, ES, EF, LS, LF, and slack.
Основные определения
Ориентированный граф, в котором существует лишь одна вершина, не имеющая входящих дуг, и лишь одна вершина, не имеющая выходящих дуг, называется сетью. Сеть, моделирующая комплекс работ, называется его сетевой моделью или сетевым графиком. Дуги, соединяющие вершины графа, ориентированы в направлении достижения результата при осуществлении комплекса работ.
Наиболее распространен способ представления моделируемого комплекса работ в понятиях работ и событий.
Понятие «работа» имеет следующие значения:
- «действительная работа» – процесс, требующий затрат времени и ресурсов;
- «фиктивная работа» – логическая связь между двумя или несколькими работами, указывающая на то, что начало одной работы зависит от результатов другой. Фиктивная работа не требует затрат времени и ресурсов, продолжительность ее равна нулю.
Работа на графике изображается стрелкой, над которой указывается затрачиваемое на нее время. Длина стрелки и ее ориентация на графике не имеют значения. Желательно только выдерживать направление стрелок так, чтобы начальное событие для работы (обозначается i) располагалось слева в сетевом графике, а конечное (обозначается j) — справа. Для отображения фиктивных работ используют пунктирные стрелки, над которыми время не указывается или проставляется ноль.
На сетевой модели событиям соответствуют вершины графа.
Правила построения сетевой модели
Правило 1. Каждая операция в сети представляется одной и только одной дугой (стрелкой). Ни одна из операций не должна появляться в модели дважды. При этом следует различать случай, когда какая-либо операция разбивается на части; тогда каждая часть изображается отдельной дугой.
Правило 2. Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно.
Правило 3. При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы:
а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?
б) Какие операции должны непосредственно следовать после завершения данной операции?
в) Какие операции могут выполняться одновременно с рассматриваемой?
При построении сетевого графика следует соблюдать следующие правила:
- в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
- В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
- в сети не должно быть замкнутых контуров (рис.1);
- Любые два события должны быть непосредственно связаны не более чем одной работой.
- В сети рекомендуется иметь одно исходное и одно завершающее событие.
- Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.
Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1 и обводится кружком. Из начального события выпускают стрелки, соответствующие работам, которым не предшествуют какие-либо другие работы. По определению, момент завершения работы является событием. Поэтому каждая стрелка
завершается кружком – событием, в котором проставляется номер этого события. Нумерация событий произвольная. На следующем этапе построения изображаем работы, которым предшествуют уже нарисованные работы (то есть которые опираются на уже построенные работы) и т. д. На следующем этапе отражаем логические взаимосвязи между работами и определяем конечное событие сетевого графика, на которое не опираются никакие работы. Построение закончено, далее необходимо провести упорядочение сетевого графика.
Методы оптимизации сетевого графика
Логико-математическое описание, формирование планов и управляющих воздействий осуществляется на базе использования особого класса моделей, называемых сетевыми моделями.
После построения и расчета сетевого графика (определения его параметров), выполнения анализа графика, заключающегося в оценке его целесообразности и структуры, оценке загрузки исполнителей, оценке вероятности наступления завершающего события в заданный срок, следует приступать к оптимизации сетевого графика. Процедура оптимизации заключается в приведение графика в соответствие с заданными сроками выполнения работ, возможностями подрядных организаций и т.д. В общем случае под оптимизацией следует понимать процесс улучшения организации выполнения работ.
Для возможности оптимизации сетевой модели, все исходные данные вводятся в виде таблицы (Операции/Добавить в виде таблицы).
- Оптимизация сетевой модели по критерию «число исполнителей». Заполняется столбец Количество исполнителей Ч
- Оптимизация сетевой модели по критерию «время – стоимость» (
время — затраты
). В случае известных коэффициентов затрат на ускорение работ заполняется только этот столбец h(i,j). Иначе, заполняются столбцы tопт (Нормальный режим), Минимальное время работ, tmin (Ускоренный режим), Нормальная стоимость, Cн и Срочная стоимость, Cc.
Графики привязки (а) и загрузки (b) до оптимизации
1,261,311,452,532,613,684,644,725,866,817,83 1122 3194175 6 7 8189 10 11 12 13 141315 16 17 181019 20 21 22423 24 25 26127
Графики привязки (а) и загрузки (b) после оптимизации
1,261,311,452,532,613,684,644,725,866,817,83 1122 3114145 6 7158 9 10 111812 13 14 151016 17 18419 20 21 221023 24 25 26727
Диаграмма Ганта
1,241,331,452,5112,6143,64,6174,75,8196,8277,825
Чтобы построить диаграмму Ганта по графику работ, необходимо выделить пункт Строить диаграмму Ганта
. Также можно создать график на основе введенных данных. Для этого следует указать количество работ (мероприятий) и даты их проведения.
Количество работ
Примеры сетевых моделей
Рассмотрим варианты сетевых графиков из кулинарной области на примере варки борща из курицы.
а) Варка в обычной посуде
12345
11030157
Работы:
1,2: чистка овощей (капуста, морковь, картофель, свекла, лук), 10 мин.
1,3: варить курицу, 30 мин.
2,3: положить капусту и варить 10 мин.
3,4: положить 1/2 свеклы, морковь и картофель. Варить 15 мин.
4,5: доложить остатки свеклы, лук, зелень. Варить 7 мин.
б) Варка в посуде с эффектом русской печи
(трехслойное дно, крышка без отверстий)
12345
1010203060
Работы:
1,2: чистка овощей (капуста, морковь, картофель, свекла, лук), 10 мин.
1,4: варить курицу в обычной посуде, 30 мин.
2,3: положить овощи в спецпосуду, добавить 3 ложки воды, нагреть до T=70 C и выключить, 10 мин.
3,4: приготовление овощей в собственном соку, 20 мин.
4,5: добавить к курице приготовленные овощи. Настаивается 60 мин.
Список литературы
- Мушик Э., Мюллер П. Методы принятия технических решений. Пер. с нем. –М.: Мир, 1990.
- Таха Х. Введение в исследование операций. В 2-х книгах. Кн. 2. Пер. с англ. –М.: мир, 1985.
- Управление в системах РАВ: Учебник. –Л.: Воениздат, 1980.
Текст
РазмерЦвет
Линия
ТолщинаЦвет
пунктирная — — — —
Размеры в px и фон
wh
Текст (вес)
РазмерЦвет
Линия
ТолщинаЦвет
пунктирная — — —
концевой маркер →
Тип
Число строк
Минимальное время работ, tmin
Максимальное время работ, tmax
Количество исполнителей, чел., Ч
Коэффициент затрат на ускорение работ, руб./сут., h(i,j)
Нормальная стоимость, Cн
Срочная стоимость, Cc
По умолчанию минимальное количество заполняемых столбцов равно трем: i, j, tопт. Чтобы иметь возможность ввести и другие данные, выделите соответствующий пункт.
В каждой строке укажите вершины в формате:v1-v2:n, например1-2:4
1-3:8
2-4:12
4-1:6
Выберите номер критического пути.