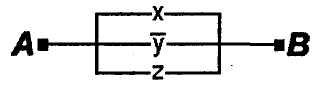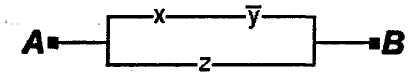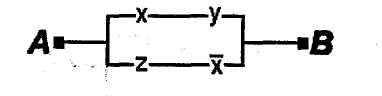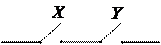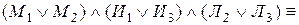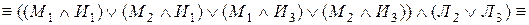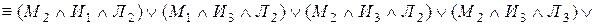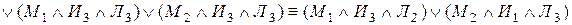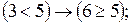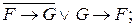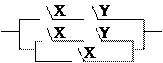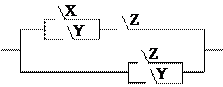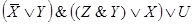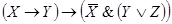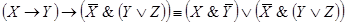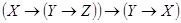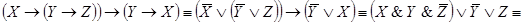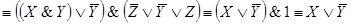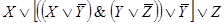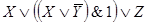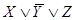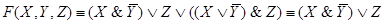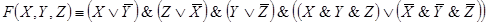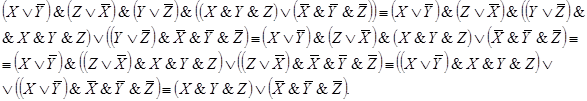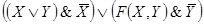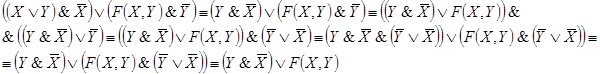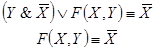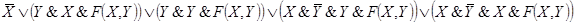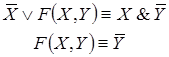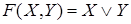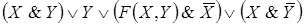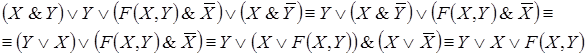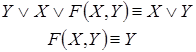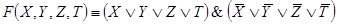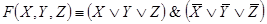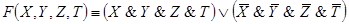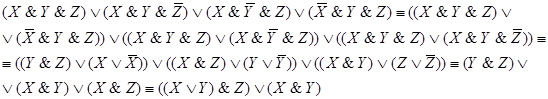I. Приложение алгебры высказываний к релейно-контактным схемам (ркс).
Релейно-контактные схемы (их часто
называют переключательными схемами)
широко используются в технике
автоматического управления.
Под переключательной схемой понимают
схематическое изображение некоторого
устройства, состоящее из следующих
элементов:
1) переключателей, которыми могут
быть механические устройства,
электромагнитные реле, полупровод-вики
и т.д.;
2) соединяющие их проводники;
3) входыв схему ивыходыиз нее
(клеммы, на которые подается
электрическое напряжение). Они называются
полюсами.
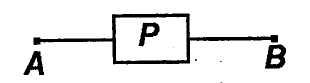
Простейшая схема содержит один
переключатель Ри имеет один входАи один выходВ. ПереключателюР поставим в соответствие высказываниер, гласящее: «ПереключательРзамкнут». Если р истинно, то импульс,
поступающий на полюсА, может быть
снят на полюсеВ без потери напряжения,
т.е. схема пропускает ток. Еслирложно, то переключатель разомкнут, и
схема тока не проводит. Таким образом,
если принять во внимание не смысл
высказывания, а только его значение, то
можно считать, что любому высказыванию
может быть поставлена в соответствие
переключательная схема с двумя полюсами
(двухполюсная схема).
Формулам, включающим основные логические
операции, также могут быть поставлены
в соответствие переключательные
схемы.
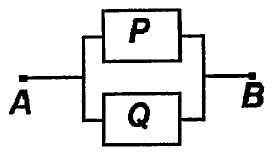
Так, конъюнкции двух высказываний p&qставится в соответствие схема:
а дизъюнкции схема:
Т.к. любая формула алгебры логики может
быть записана в ДНФ или КНФ, то ясно,
что каждой формуле алгебры логики
можно поставить в соответствие некоторую
РКС, а каждой РКС можно поставить в
соответствие некоторую формулу алгебры
логики. Поэтому возможности схемы можно
выявить, изучая соответствующую ей
формулу, а . упрощение схемы можно свести
к упрощению формулы.
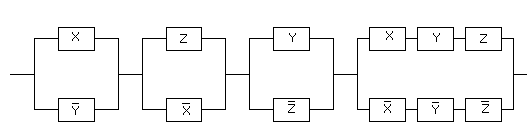
Пример 1. Составить РКС для формулы
Решение. Упростим данную формулу с
помощью равносильных преобразований:
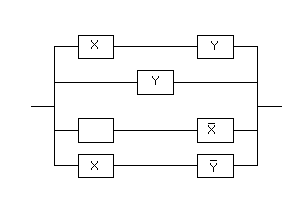
Тогда РКС для данной формулы имеет вид*:
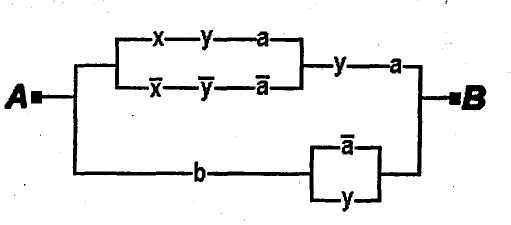
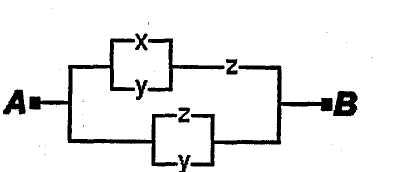
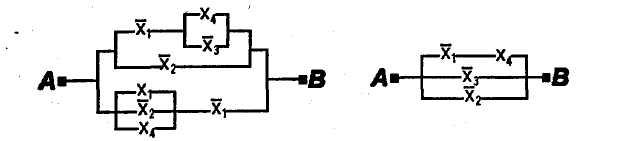
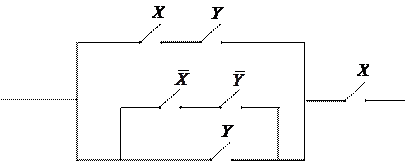
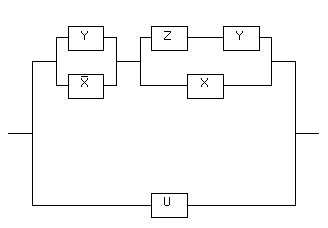
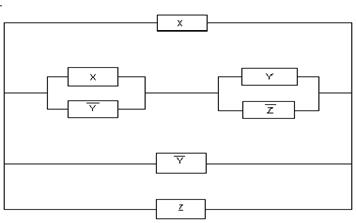
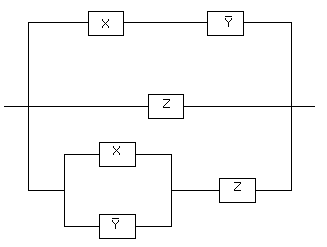
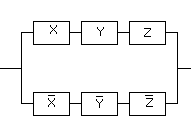
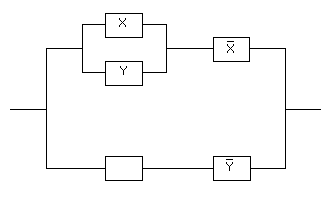
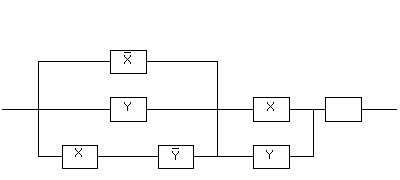
Пример 2. Упростить РКС:
Решение.Составим по данной РКС
формулу (функцию проводимости) и
упростим ее:
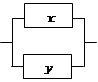
(к последним двум слагаемым применили
закон поглощения).
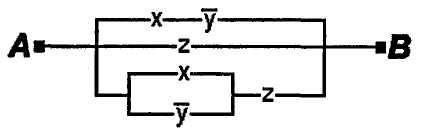
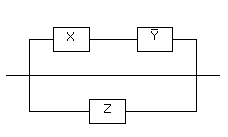
Тогда упрощенная схема выглядит так:
II. Решение логических задач с помощью алгебры логики.
Условие логической задачи с помощью
соответствующих обозначений записывают
в виде формулы алгебры логики. После
равносильных преобразований формулы
получают ответ на все вопросы задачи.
Пример 3.После обсуждения состава
участников предполагаемой экспедиции
было решено, что должны выполняться два
условия:
а) если поедет Арбузов, то должны поехать
еще Брюквин или Вишневский;
б) если поедут Арбузов и Вишневский, то
поедет и Брюквин.
Требуется:
1) ввести краткие обозначения для
сформулированных условий и составить
логическую формулу, выражающую
принятое решение в символической форме;
2) для полученной формулы найти возможно
более простую равносильную формулу;
3) пользуясь найденной более простой
формулой, дать новую и более простую
словесную формулировку принятого
решения о составе участников экспедиции.
Решение.Назначение в экспедицию
Арбузова, Брюквина и Вишневского
обозначим буквамиА, Б,Всоответственно. Тогда условие а)
можно записать в виде,
а условие б) в виде,.
Так как оба условия должны выполняться
одновременно, то они должны быть
соединены логической связкой «и».
Поэтому принятое решение можно записать
в виде следующей символической формулы:
(
)&(
).
2. ()&(
)=
3. Символическую формулу читаем так:
«Если поедет Арбузов, то поедет и
Брюквин». Это и есть наиболее простая
словесная формулировка принятого
решения о составе экспедиции.
1.45. Составить РКС для формулы:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;

;
1.46. Построить схемы, реализующие
следующие булевы операции:
1) импликацию;
2) эквивалентность;
3) альтернативу (см. задачу 1.28);
4) штрих Шеффера (см. задачу 1.29);
5) штрих Лукасевича (см. задачу 1.30).
1.47. Построить РКС дляF{x,y,z),
если известно, что:
1) F(0,l,0) = F(l,0,l) = F(l,l,l) = 1;
2) F(l,0,l) = F(l,l,0) = l;
3) F(0,0,1) = F(0,l,l) =F(1,0,1) = F(l,l,l) = 1;
4) F(1,1,0) = .F(1,1,1) = 1;
5) F(0,0,l) = F{l,0,l) = F(l,0,0) = 1;
6) F(0,0,1) = F(0,l,0) = F(0,l,l) = F(l,0,l) = 1,
а остальные значения функции Fравны нулю.
1.48. Упростить РКС:
1
2)
3)
4)
5)
6)
7)

1.49. По данной схеме найти функцию
проводимости и условия работы:
1)
2)
3)
4)
5)
6)
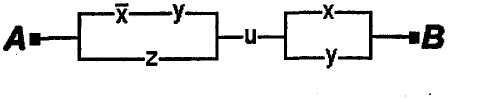
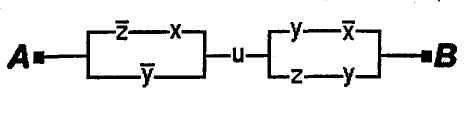
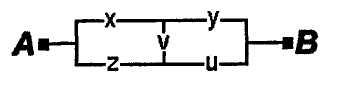
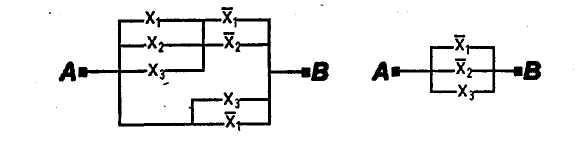
1.50.Проверить равносильность схем:
1)
2)
3)
4)
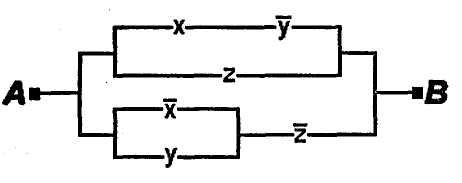
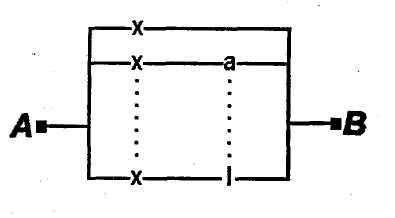
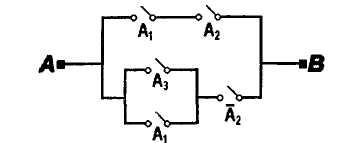
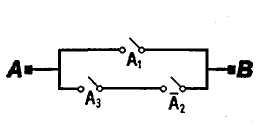
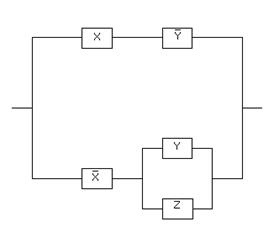
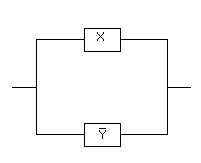
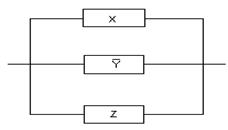
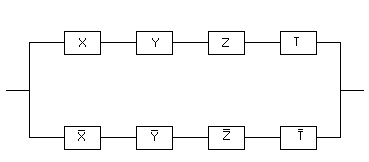
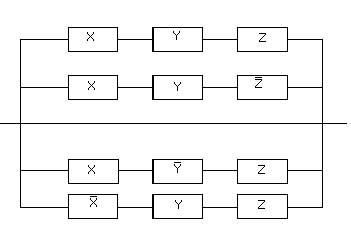
1.51.Электрическая цепь, изображенная
на рис. 1, содержит только двухпозиционные
выключатели (при одном состоянии
переключателя ток через него проходит,
при другом не проходит). Можно ли эту
цепь заменить более простой цепью,
изображенной на рис. 2?
рис.1 рис.2
1.52.В школе, перешедшей на
самообслуживание, четырем
старшеклассникам: Андрееву, Костину,
Савельеву и Давыдову поручили убрать
7-ой, 8-ой, 9-ый и 10-ый классы. При проверке
оказалось, что 10-ый класс убран плохо.
Не ушедшие домой ученики сообщили о
следующем:
1. Андреев: «Я убирал 9-ый класс, а Савельев
— 7-ой».
2. Костин: «Я убирал 9-ый класс, а Андреев
— 8-ой».
3. Савельев: «Я убирал 8-ой класс, а Костин
— 10-ый».
Давыдов уже ушел домой. В дальнейшем
выяснилось, что каждый ученик в одном
из двух высказываний говорил правду, а
во втором ложь. Какой класс убирал каждый
ученик?
1.53.Пять школьников из пяти различных
городов Брянской области прибыли для
участия в областной олимпиаде по
математике. На вопрос: «Откуда Вы?»
каждый дал ответ:
Иванов: «Я приехал из Клинцов, а Дмитриев
— из Новозыбкова».
Сидоров: «Я приехал из Клинцов, а Петров
— из Труб-чевска».
Петров: «Я приехал из Клинцов, а Дмитриев
— из Дятькова».
Дмитриев: «Я приехал из Новозыбкова, а
Ефимов -из Жуковки».
Ефимов: «Я приехал из Жуковки, а Иванов
живет в Дятькове».
Откуда приехал каждый из школьников,
если одно
егс^ухверждение верно, а другое ложно?
1.54. Семья, состоящая из отца А, матери
В и трех дочерей С,D, Е
купила телевизор. Условились, что в
первый вечер будут смотреть передачи
в таком порядке:
1. Когда отец А смотрит передачу, то мать
В делает то же.
2. Дочери Dи Е, обе или одна
из них, смотрят передачу.
3. Из двух членов семьи — мать В и дочь С
— смотрят передачу одна и только одна.
4. Дочери С и Dили обе
смотрят, или обе не смотрят.
5. Если дочь Е смотрит передачу, то отец
А и дочь Dделают то же.
Кто из членов семьи в этот вечер смотрит
передачу?
1.55.На вопрос: «Кто из трех студентов
изучал математическую логику?»
получен верный ответ — «Если изучал
первый, то изучал и третий, но неверно,
что если изучал второй, то изучал и
третий.». Кто изучал математическую
логику?
1.56. Определите, кто из четырех
студентов сдал экзамен, если известно:
1. Если первый сдал, то и второй сдал.
2. Если второй сдал, то третий сдал или
первый не сдал.
3. Если четвертый не сдал, то первый сдал,
а третий не сдал.
4. Если четвертый сдал, то и первый сдал.
1.57. Известно следующее: если Петя
не видел Колю на улице, то либо Коля
ходил в кино, либо Петя сказал правду;
если Коля не ходил в кино, то Петя не
видел Колю на улице, и Коля сказал правду;
если Коля сказал правду, то либо он ходил
в кино, либо Петя солгал. Выясните, ходил
ли Коля в кино.
1.58.Чтыре студентки, имена которых
начинаются буквами А, Е, С, Р посещают
институт по очереди и ведут общий
конспект лекций. Необходимо составить
график посещения на ближайшую неделю,
учитывая, что:
1. Понедельник — день самостоятельной
работы на курсе, и в институт не ходит
никто, а в субботу необходимо быть
всем.
2. С и Р не смогут пойти на занятия во
вторник в связи с большой загруженностью
в понедельник.
3. Если С выйдет в среду или Р — в четверг,
то Е согласится побывать на занятиях в
пятницу.
4. Если А не пойдет в ВУЗ в четверг, то Е
позволит себе сходить туда в среду.
5. Если А или Р будут в институте в среду,
то С сможет пойти в пятницу.
6. Если Р в пятницу вместо института
пойдет на свадьбу подруги, то А придется
сходить в институт во вторник, а С — в
четверг.
1.59.Четыре друга — Антонов (А), Вехов
(В), Сомов (С), Деев (Д) решили провести
каникулы в четырех различных городах
— Москве, Одессе, Киеве и Ташкенте.
Определите, в какой город должен поехать
каждый из них, если имеются следующие
ограничения:
1. Если А не едет в Москву, то С не едет
в Одессу.
2. Если В не едет ни в Москву, ни в Ташкент,
то А едет в Москву.
3. Если С не едет в Ташкент, то В едет в
Киев.
4. Если Д не едет в Москву, то В не едет
в Москву.
5. Если Д не едет в Одессу, то В не едет в
Москву.
1.60.Однажды следователю пришлось
одновременно
допрашивать трех свидетелей: Клода,
Жака и Дика. Их показания противоречили
друг другу, и каждый из них обвинял
кого-нибудь во лжи.
1. Клод утверждал, что Жак лжет.
2. Жак обвинял во лжи Дика.
3. Дик уговаривал следователя не верить
ни Клоду, ни Жаку.
Но следователь быстро вывел их на чистую
воду, не задав им ни одного вопроса. Кто
из свидетелей говорил правду?
.
РКС для формулы в дискретной математике: как справиться с задачей
РКС (расстановка кванторов по Сколему) – это метод, который позволяет привести формулу с кванторами к эквивалентной формуле без кванторов. РКС широко применяется в дискретной математике, особенно в теории автоматов, формальных языках, а также в теории графов и комбинаторике.
Пример использования РКС
Предположим, нам нужно привести следующую формулу к эквивалентной формуле без кванторов:
$$ forall x exists y (x + y = 0) $$
Сначала нам нужно найти все свободные переменные в формуле – это переменные, которые не связаны кванторами. В данном случае свободной переменной является переменная $x$.
Затем мы вводим новые функциональные символы и выражаемсвязанные переменные через них. В нашем случае мы можем использовать функциональный символ $f$ для выражения переменной $y$:
$$ forall x exists f (x + f(x) = 0) $$
Теперь мы можем применить к формуле РКС. Для этого мы последовательно выражаем каждую связанную переменную через новый функциональный символ:
$$ forall x (x + f(x) = 0) $$
Таким образом, исходная формула была преобразована к эквивалентной формуле без кванторов.
Заключение
РКС – это важный метод в дискретной математике, позволяющий упростить вычисления с формулами, содержащими кванторы. Несмотря на некоторые технические сложности, РКС может применяться для широкого круга задач, от теории автоматов до комбинаторики.
Релейно-контактные схемы
Укажем на применение алгебры логики к анализу и синтезу релейно-контактных схем. Среди технических средств автоматизации значительное место занимают устройства релейно-контактного действия. Они находят широкое применение в телефонии, телеуправлении, автоматике и телемеханике, на железнодорожном транспорте, в вычислительной технике. Сейчас при конструировании таких устройств все больше и больше используется алгебра логики. Впервые идея использования алгебры логики для построения автоматических устройств была выдвинута в 1910 году известным физиком П.Эренфестом. Но только в 30-х годах эта идея нашла свое воплощение в работах советского физика В.И. Шестакова, американского математика К.Шеннона и японского инженера А.Накосима.
Контактная схема представляет собой устройство из проводников и контактов, связывающих полюса источника тока. Контакт бывает в двух состояниях:
а) контакт разомкнут и тогда ему приписывают 0;

Контакт «не 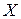
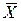
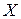
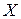
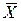
Дизъюнкции 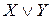
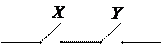
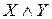
Каждый контакт подключен к некоторому реле. В схеме одинаковыми буквами обозначаются контакты, подключенные к одному и тому же реле. Всей схеме ставится в соответствие булева функция F, которая равна 1, если схема проводит ток, и 0 в противном случае. Эта функция называется функцией проводимости схемы, а ее таблица – условиями работы схемы. Две схемы с одинаковыми функциями проводимости называются равносильными. Средства алгебры высказываний позволяют упрощать схемы, используя отношение равносильности формул алгебры высказываний.
□ По данной схеме запишем формулу, определяющую функцию проводимости, и упростим ее:
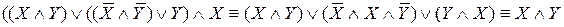
Таким образом, 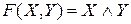
§5. Решение логических задач методами алгебры логики.
Под логической задачей будем понимать задачу, где основным видом деятельности является выявление отношений между объектами задачи, а не нахождение количественных характеристик объектов. Суть применения алгебры логики к решению логических задач состоит в том, что, имея конкретные условия логической задачи, стараются записать их в виде формулы алгебры логики. В дальнейшем путем равносильных преобразований упрощают полученную формулу. Простейший вид формулы, как правило, приводит к ответу на все вопросы задачи.
Покажем на ряде конкретных примеров, как использовать возможности алгебры логики для решения элементарных логических задач.
Пример 1. При составлении расписания уроков на некоторый день учителя просили, чтобы их уроки были:
1. математик – первым или вторым;
2. историк – первым или третьим;
3. литератор – вторым или третьим.
Можно ли удовлетворить просьбы всех учителей?
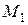
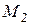
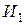
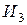
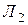
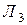
Тогда на языке алгебры эту задачу можно записать в виде формулы , после равносильных преобразований которой можно будет дать ответ на вопрос задачи:
Выяснили, что имеется две возможности:
1. 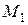
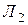
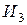
2. 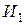
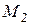
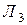
Вопросы для самоконтроля по теме «Логика высказываний»
1. Что понимается под высказыванием? Привести примеры.
2. Являются ли высказываниями следующие предложения:
а) два плюс два равно пяти;
б) функция 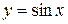
в) существует рациональное число такое, что х > 7.
3. Определить операции отрицания, дизъюнкции, конъюнкции, импликации, эквиваленции и задать их с помощью таблиц истинности.
4. Найти истинностные значения следующих высказываний:
а)
б) 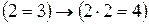
в) 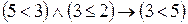
5. Что понимается под формулой алгебры высказываний?
6. Найти значения формул при заданных значениях высказывательных переменных:
а) 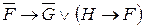
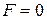
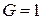
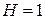
б) 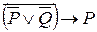
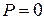
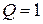
7. Построить таблицу истинности формулы 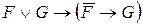
8. Что называется тождественно истинной (ложной) формулой? Проверить, является ли каждая из формул тождественно истинной:
а)
б) 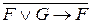
9. Какие формулы называются равносильными? Как доказать равносильность формул? Проверить равносильность
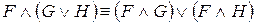
10. Записать первые десять основных равносильностей алгебры высказываний. Доказать законы поглощения и законы де Моргана.
11. Записать законы двойного отрицания; исключения импликации; введения дизъюнкции; введения конъюнкции; замены эквиваленции; контрапозиции; противоположностей; доказательства от противного; транзитивности импликации; транзитивности эквиваленции. Обосновать законы доказательства от противного и закон контрапозиции.
12. Упростить формулу 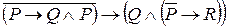
13. Преобразовать формулу 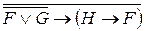
14. Перевести предложение на логический язык и построить его отрицание: «Если вечером я буду не занята, то пойду в кино или на дискотеку».
15. Упростить релейно-контактную схему:
16. Ввести понятие функции проводимости для релейно-контактной схемы. Найти функцию проводимости и условия работы для схемы:
17. Один из братьев Витя, Толя, Коля разбил окно. В разговоре участвуют еще двое братьев – Андрей и Дима.
– Это мог сделать только Витя или Толя – сказал Андрей.
– Я окно не разбивал, – возразил Витя, – Коля тоже.
– Вы оба говорите неправду, – заявил Толя.
– Нет, Толя, один из них сказал правду, а другой неправду, – возразил Дима.
–Ты, Дима, неправ, – вмешался Коля.
Их отец, которому, конечно, можно доверять, уверен, что трое братьев сказали правду. Кто разбил окно?
Источник
Анализ и синтез релейно-контактных схем
Одно из применений алгебры высказываний – анализ и синтез релейно-контактных схем.
Еще в 1910 году физик П.С. Эренфест указал на возможность применения аппарата алгебры логики при исследовании релейно-контактных схем. Каждой схеме можно поставить в соответствие некоторую формулу алгебры высказываний, и каждая формула алгебры высказываний реализуется с помощью некоторой схемы.
Рассмотрим 2-х-полюсные переключатели, т.е. такие, которые имеют два состояния: «замкнуто» — 1, «разомкнуто» — 0. На схеме будем изображать:
Определение 7. Переключатель, который сблокирован с X так, что он замкнут, если X разомкнут, и разомкнут, если X замкнут, называется инверсным и обозначается 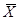
Конъюнкция двух высказываний X и Y будет представлена двухполюсной схемой с последовательным соединением двух переключателей X и Y.
Эта схема пропускает ток тогда и только тогда, когда истины и X, и Y одновременно, то есть истина конъюнкция X&Y.
Дизъюнкция двух высказываний X и Y изобразится двухполюсной схемой с параллельным соединением двух переключателей X и Y.
X 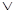
Эта схема пропускает ток в случае, если истинно высказывание X или истинно высказывание Y, то есть истина дизъюнкция X 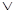
Таким образом, всякую булеву формулу можно трактовать как некоторую последовательно-параллельную схему от 2-х-полюсных переключателей. Все свойства булевых операций переносятся на соответствующие операции над переключателями. Формула, которую можно составить для каждой схемы называется функцией проводимости схемы, а таблица значений – условиями работы схемы.
Определение 8. Две схемы называются равносильными, если имеют одинаковые функции проводимости.
Анализ схемы заключается в следующем: для данной схемы составляется функция проводимости, которая на основании законов булевых функций упрощается и для нее строится новая, более простая схема, которая обладает теми же электрическими свойствами.
Синтез схем заключается в построении схем с заданными электрическими свойствами. На основании заданных электрических свойств строится таблица условий работы схемы и затем функция проводимости, представляющая собой СДНФ, а по ней строится схема.
Задача 1.Составить РКС, обладающая следующей функцией проводимости:
Задача 2.Составить РКС обладающая следующей функцией проводимости:
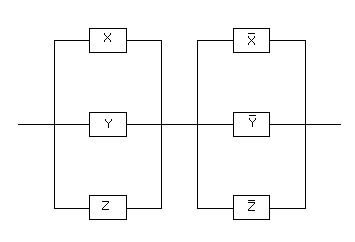
Задача 3.Составить РКС обладающая следующей функцией проводимости:
Ей соответствует функция проводимости:
F(X,Y,Z)
F(X,Y,Z) 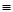
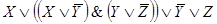
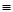
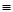
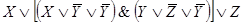
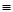
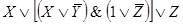
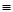
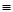
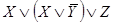
Этой же функции проводимости соответствует более простая схема.
Ей соответствует функция проводимости:
Этой же функции проводимости соответствует более простая схема.
Ей соответствует функция проводимости:
Задача 7.Какой контакт необходимо вставить в вакантное место, чтобы функция проводимости полученной схемы стала бы равна данной булевой функции:
Данной схеме соответствует функция проводимости:
Задача 8.Какой контакт необходимо вставить в вакантное место, чтобы функция проводимости полученной схемы стала бы равна данной булевой функции:
Данной схеме соответствует функция проводимости:
Задача 9.Какой контакт необходимо вставить в вакантное место, чтобы функция проводимости полученной схемы стала бы равна данной булевой функции:
Данной схеме соответствует функция проводимости:
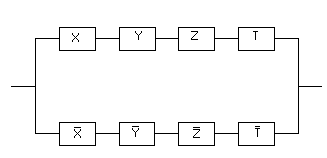
Задача 10.Построить РКС с четырьмя переключателями, которая проводит ток тогда и только тогда, когда замыкаются не все переключатели, а только некоторые из них.
Составим таблицу значений функции проводимости F (X, Y, Z, T) этой схемы:
В правом столбце звездочками отметим те строки, на которых функция F (X, Y, Z, T) обращается в 0, запишем для неё выражение, используя СКНФ, потому что наборов значений аргументов, на которых функция обращается в 0, значительно меньше, чем наборов значений аргументов, на которых функция обращается в 1, и значит, СКНФ будет более простой, чем СДНФ:
Задача 11. Построить схему с тремя переключателями, которая замыкается тогда и только тогда, когда замкнут либо один, либо два переключателя. При построении использовать не более шести контактов.
Составим таблицу значений функции проводимости F (X, Y, Z) этой схемы:
В правом столбце звездочками отметим те строки, на которых функция
F (X, Y, Z, T) обращается в 1, запишем для неё выражение, используя СКНФ, потому что наборов значений аргументов, на которых функция обращается в 0, значительно меньше, чем наборов значений аргументов, на которых функция обращается в 1, и значит, СКНФ будет более простой, чем СДНФ:
Задача 12.Требуется составить схему с четырьмя переключателями X, Y, Z, T. Схема должна проводить ток тогда и только тогда, когда будут замкнуты переключатели X и Y или Z и T.
Составим таблицу значений функции проводимости F (X, Y, Z, T) этой схемы:
В правом столбце звездочками отметим те строки, на которых функция
F (X, Y, Z, T) обращается в 1, запишем для неё выражение, используя СДНФ:
Задача 13.Построить контактную схему для оценки результатов некоторого спортивного соревнования тремя судьями при следующих условиях: судья, засчитывающий результат, нажимает имеющуюся в его распоряжении кнопку, а судья, не засчитывающий результат, кнопки не нажимает. В случае, если кнопки нажали не менее двух судей должна загореться лампочка (положительное решение судей принято простым большинством голосов).
Работа РКС описывается функцией Буля трех переменных F (X, Y, Z), где переменные высказывания X, Y, Z означают:
Таблица истинности функции F (X, Y, Z) имеет вид:
| X Y Z | F(X, Y, Z) |
| 1 1 1 | |
| 1 1 0 | |
| 1 0 1 | |
| 0 1 1 | |
| 1 0 0 | |
| 0 1 0 | |
| 0 0 1 | |
| 0 0 0 |
Этой же функции проводимости соответствует более простая схема.
Источник