Содержание
- Процедура прогнозирования
- Способ 1: линия тренда
- Способ 2: оператор ПРЕДСКАЗ
- Способ 3: оператор ТЕНДЕНЦИЯ
- Способ 4: оператор РОСТ
- Способ 5: оператор ЛИНЕЙН
- Способ 6: оператор ЛГРФПРИБЛ
- Вопросы и ответы
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
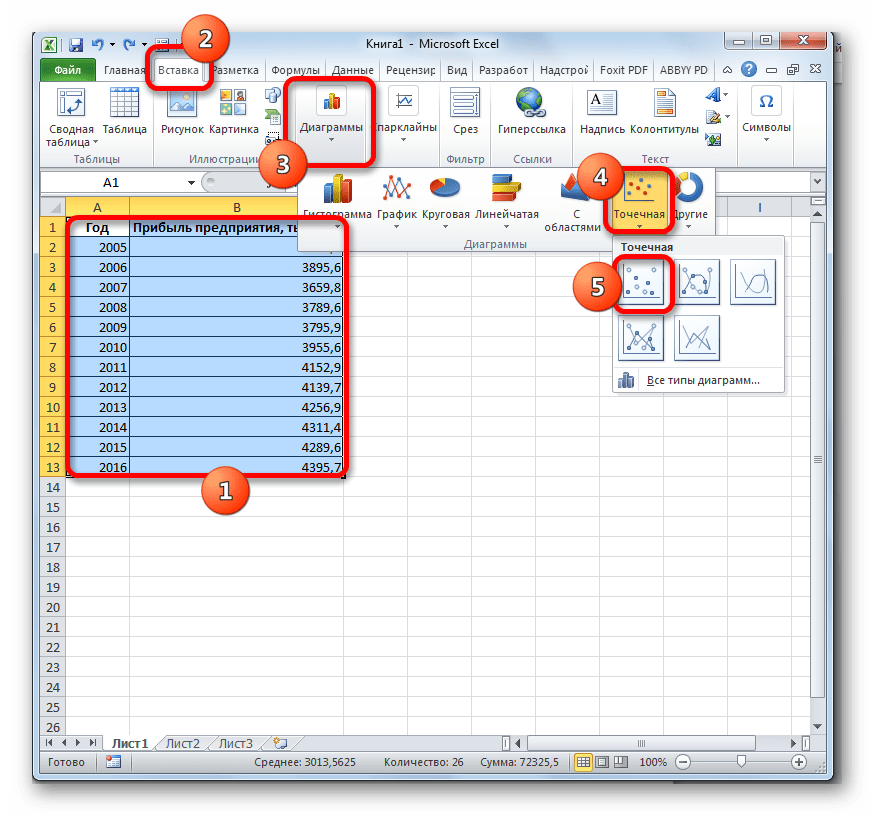
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
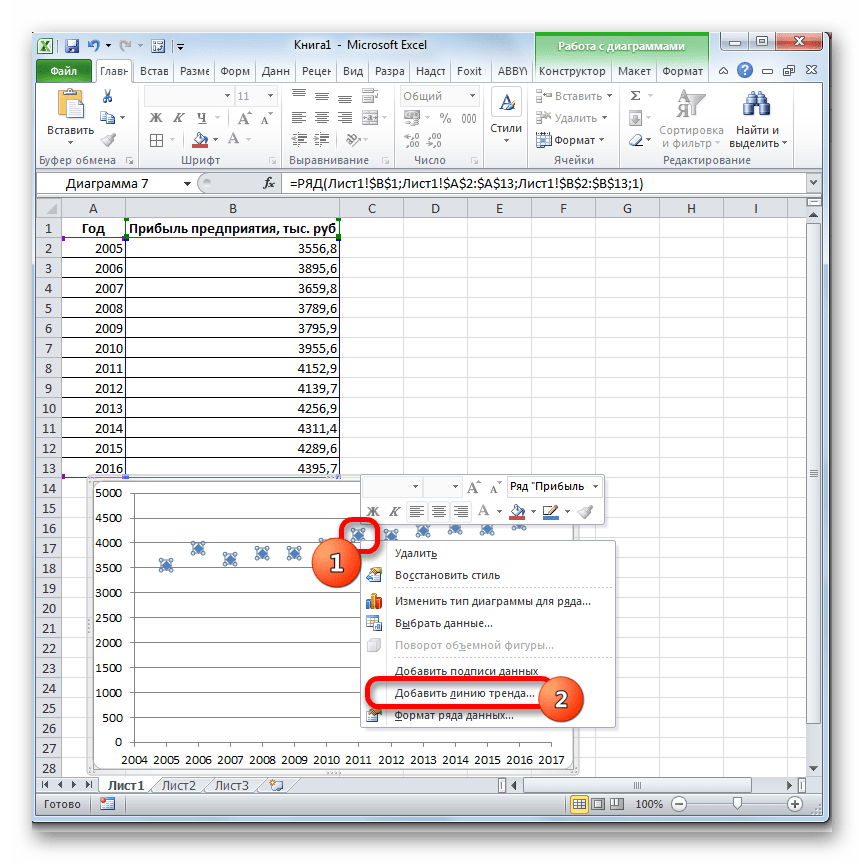
- Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».
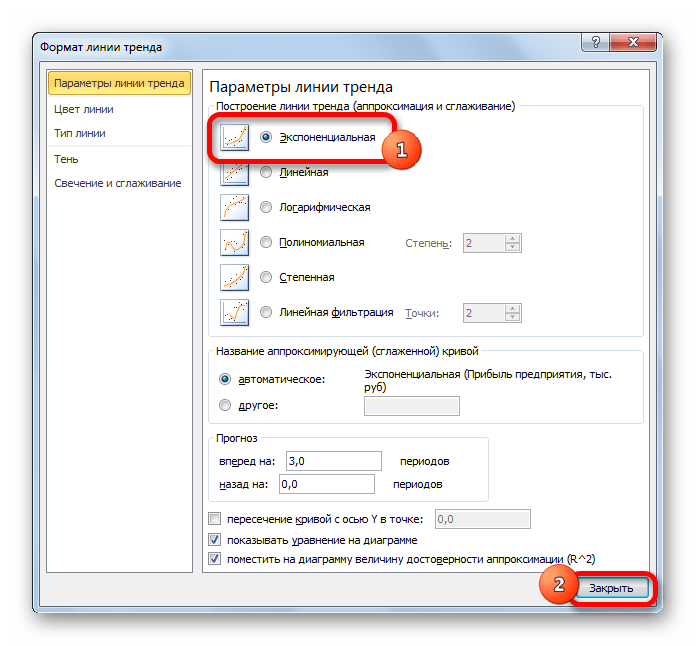
- Открывается окно форматирования линии тренда. В нем можно выбрать один из шести видов аппроксимации:
- Линейная;
- Логарифмическая;
- Экспоненциальная;
- Степенная;
- Полиномиальная;
- Линейная фильтрация.
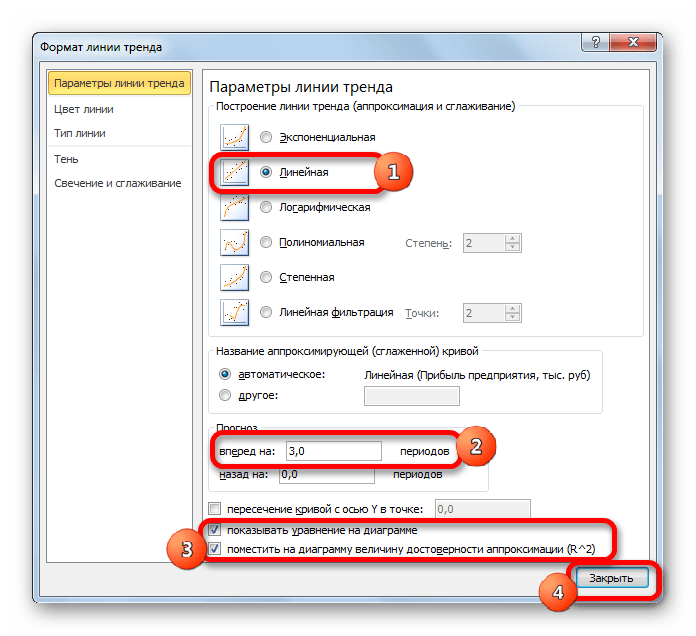
Давайте для начала выберем линейную аппроксимацию.
В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».
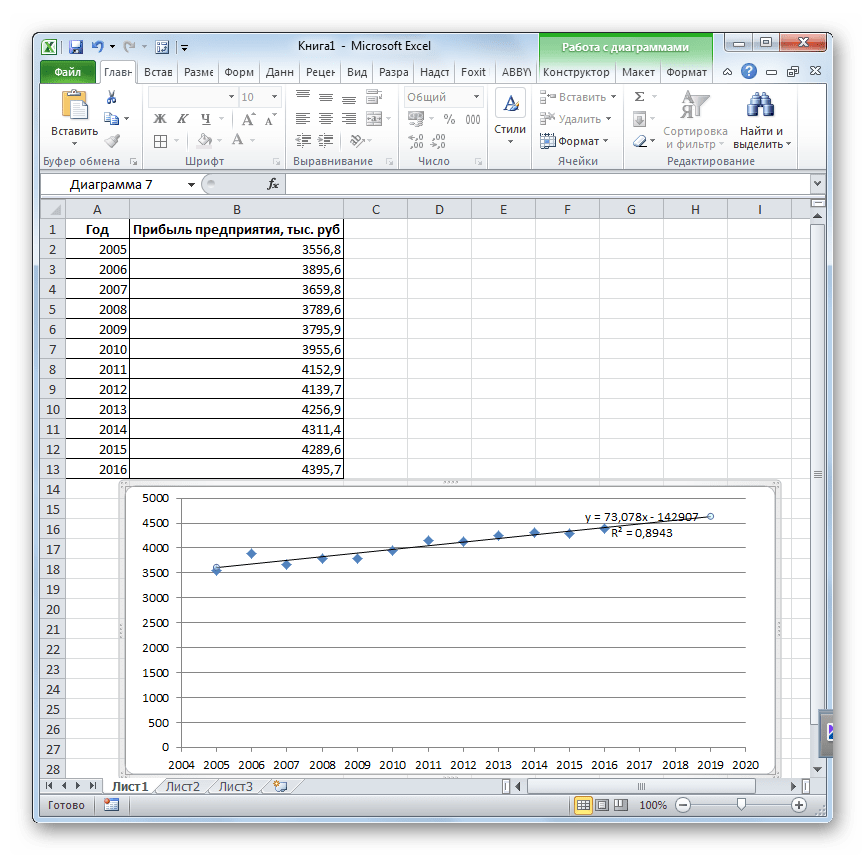
- Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.
- Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.
Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.
Урок: Как построить линию тренда в Excel
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
=ПРЕДСКАЗ(X;известные_значения_y;известные значения_x)
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
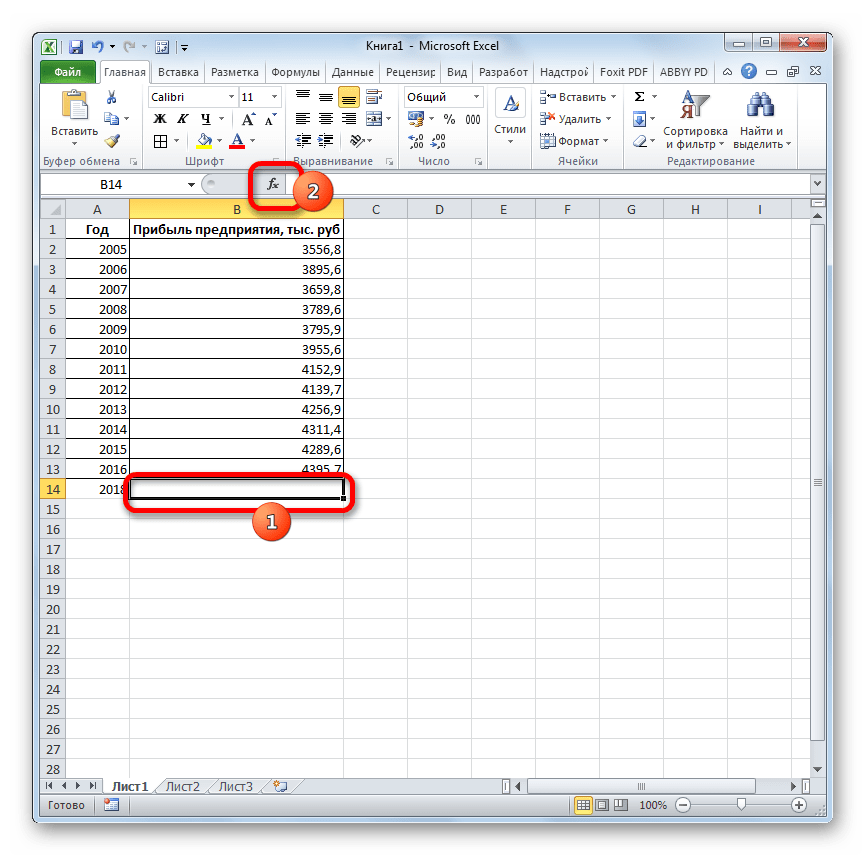
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
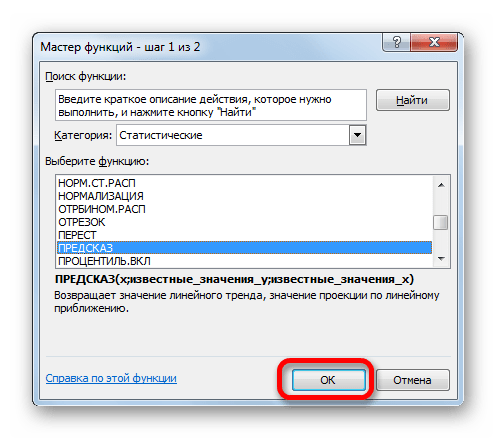
- Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».
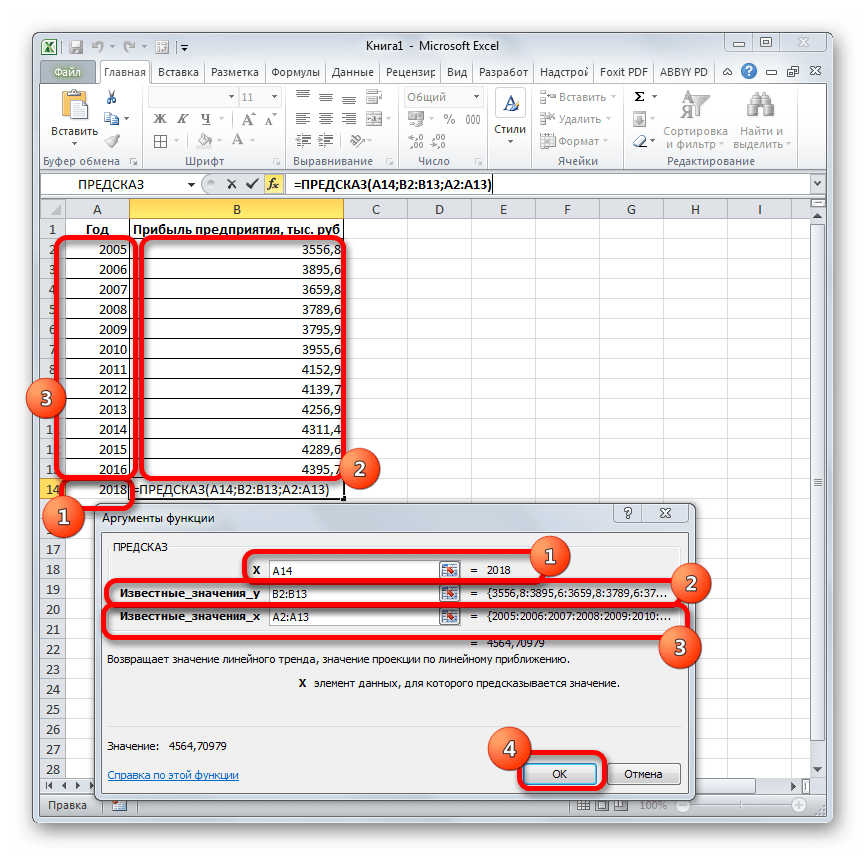
- Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
После того, как вся информация внесена, жмем на кнопку «OK».
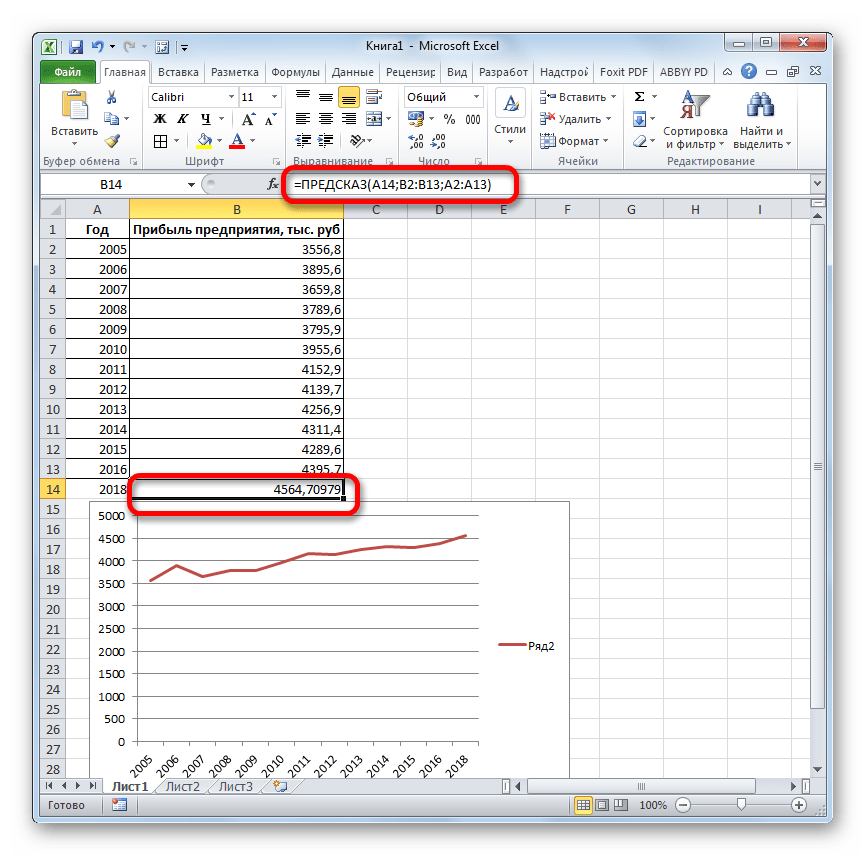
- Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.
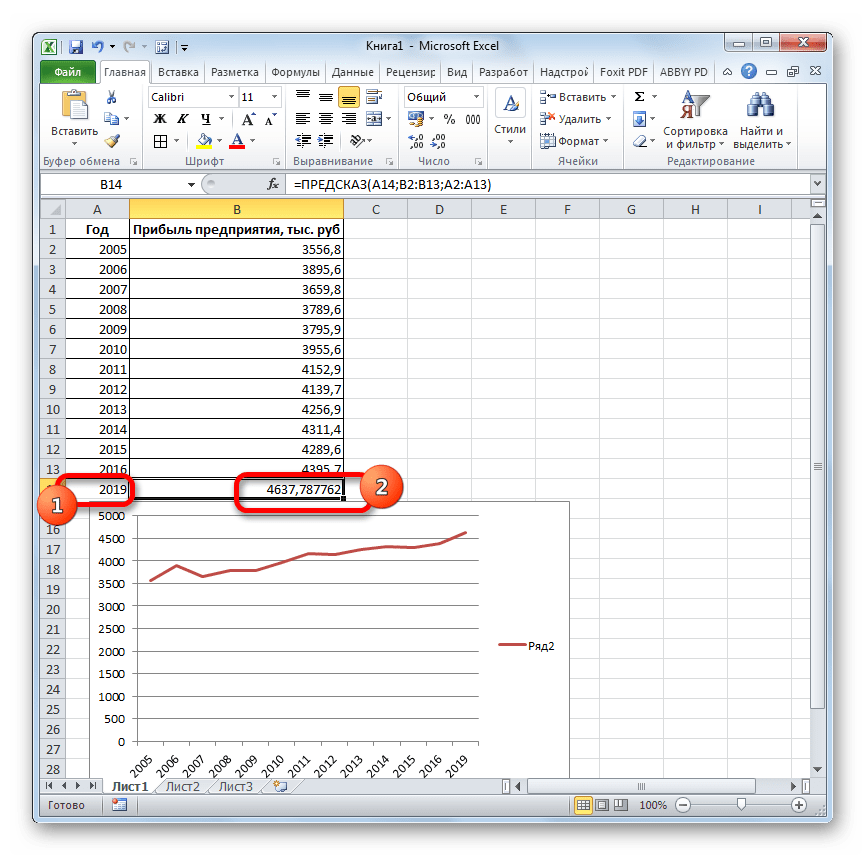
- Если поменять год в ячейке, которая использовалась для ввода аргумента, то соответственно изменится результат, а также автоматически обновится график. Например, по прогнозам в 2019 году сумма прибыли составит 4637,8 тыс. рублей.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Урок: Экстраполяция в Excel
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
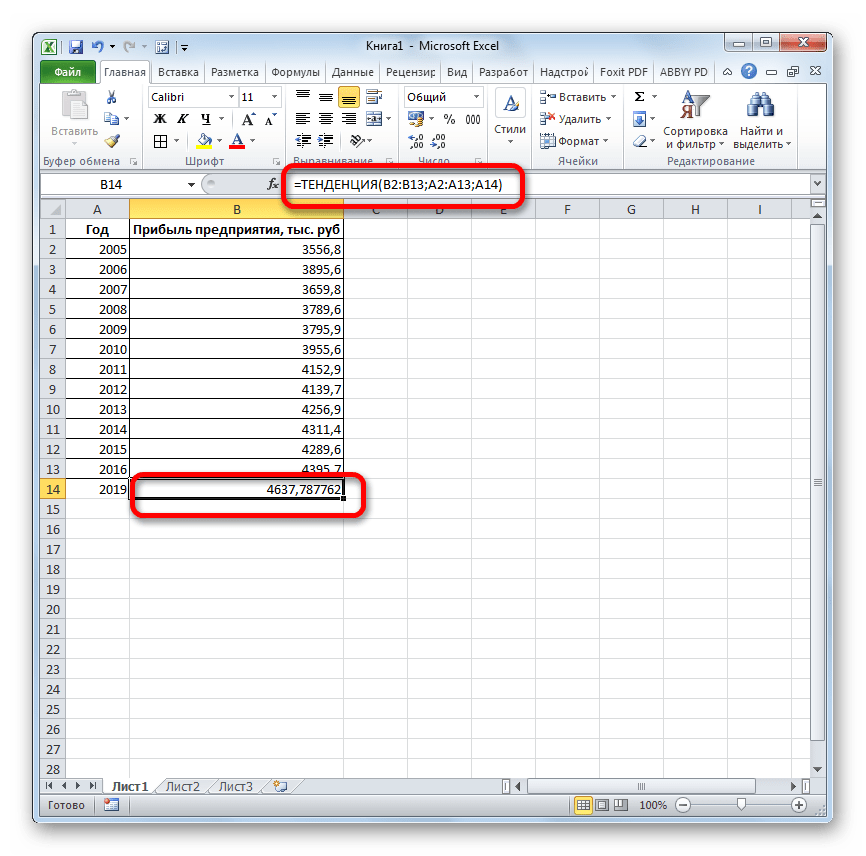
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
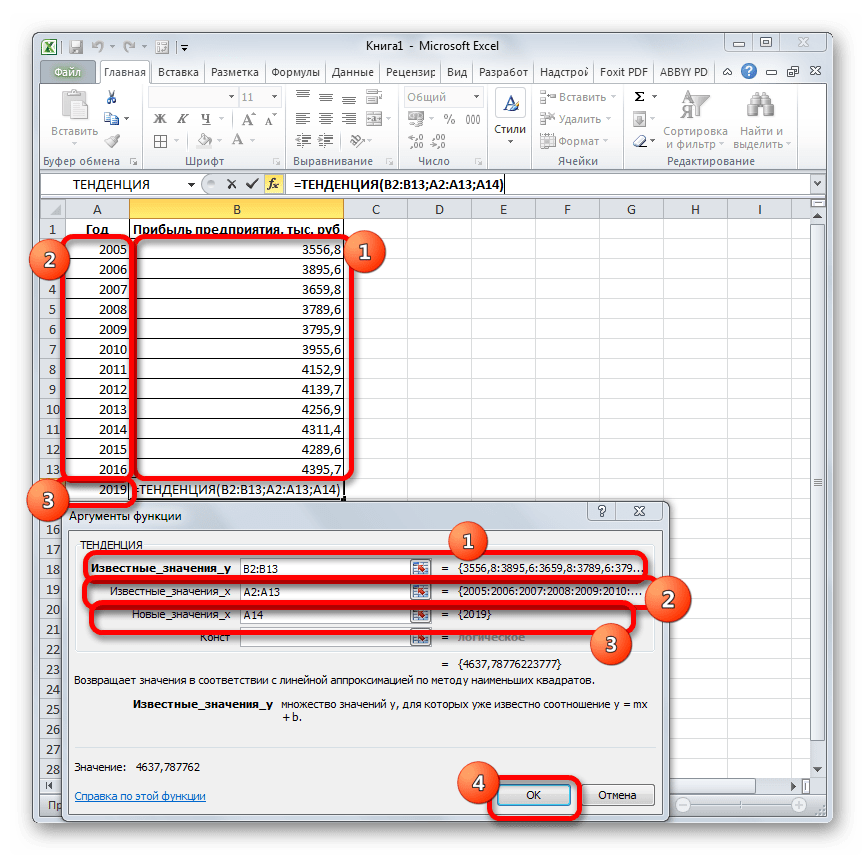
- Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».
- Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
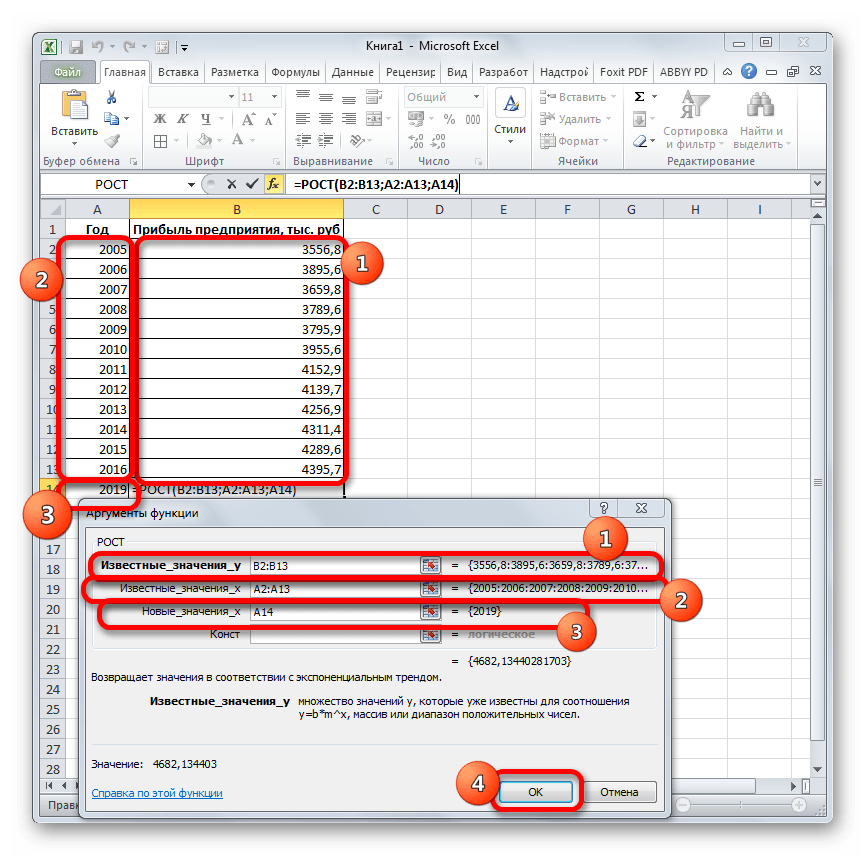
- Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».
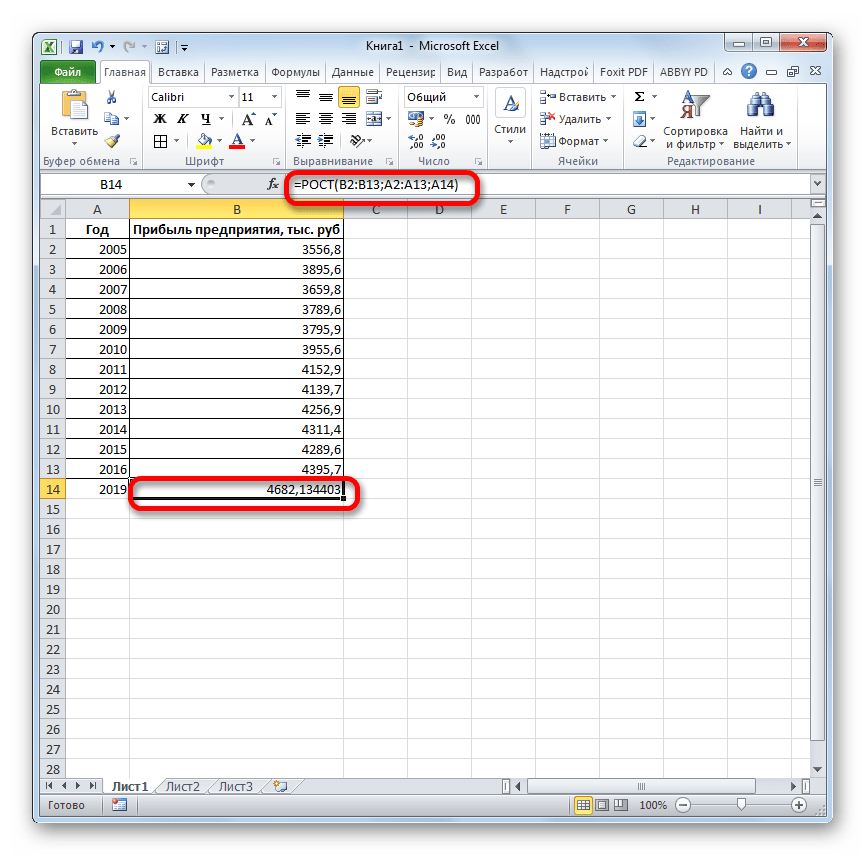
- Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
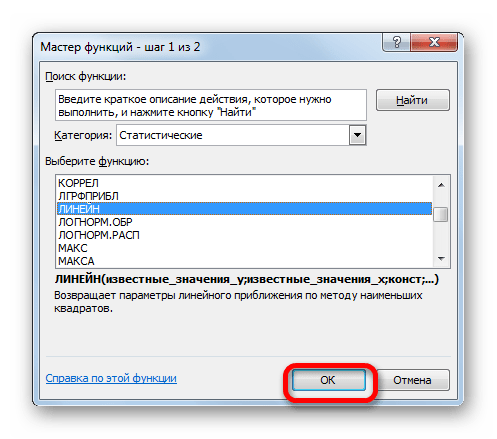
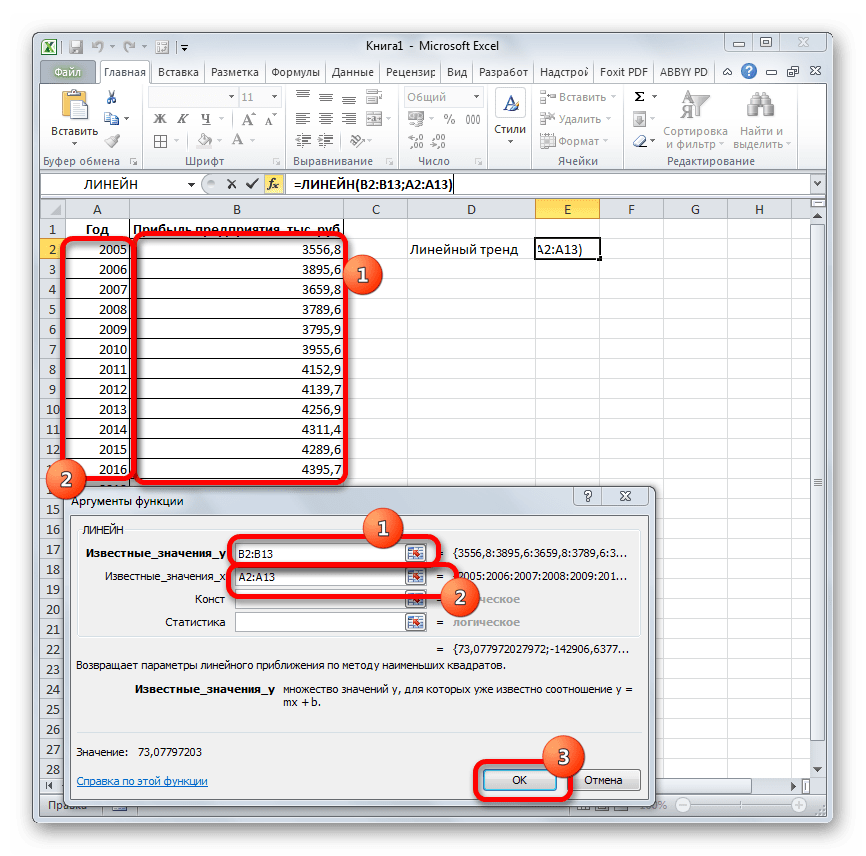
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
- В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».
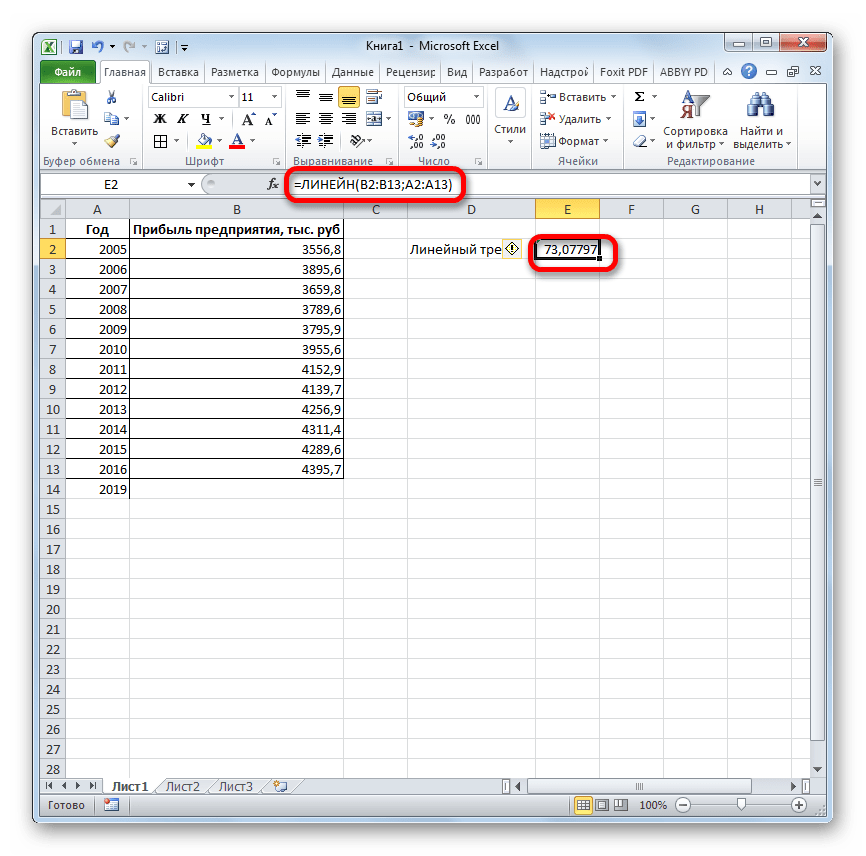
- Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.
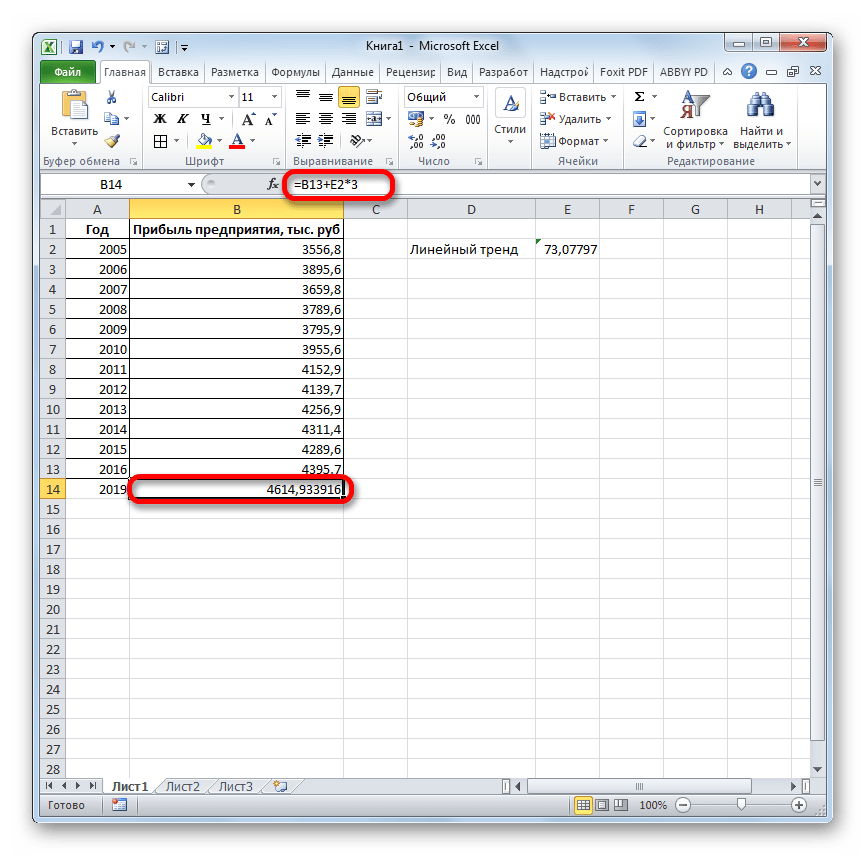
- Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
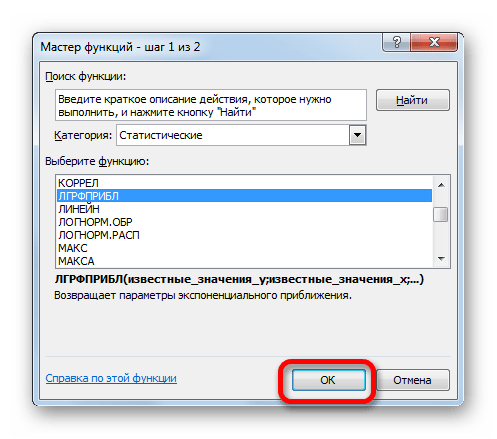
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
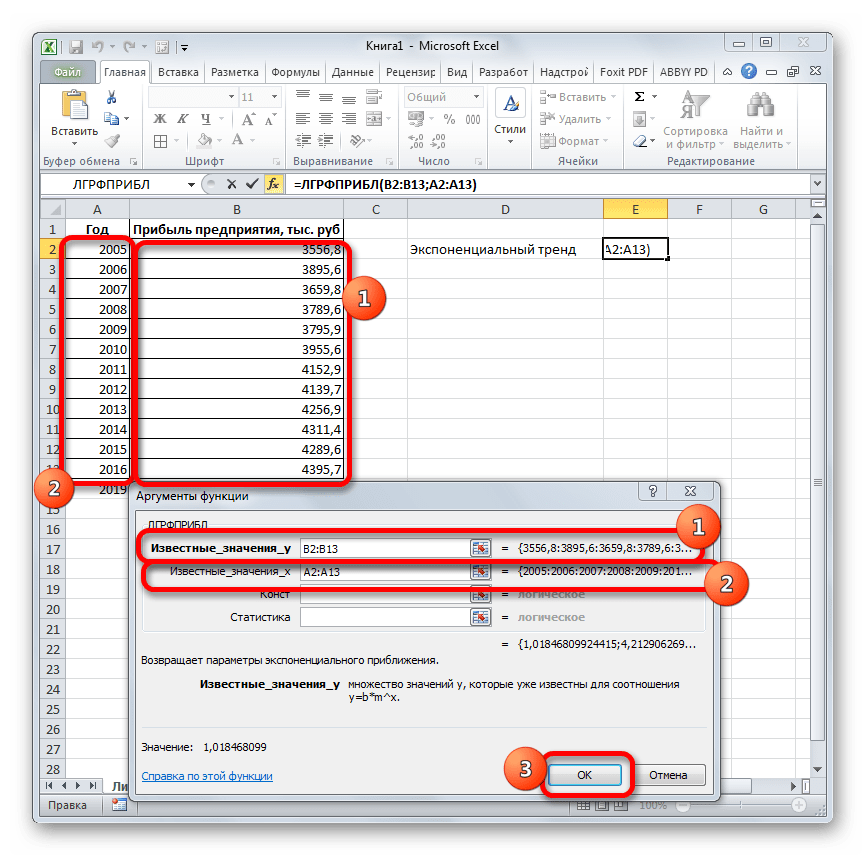
- Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».
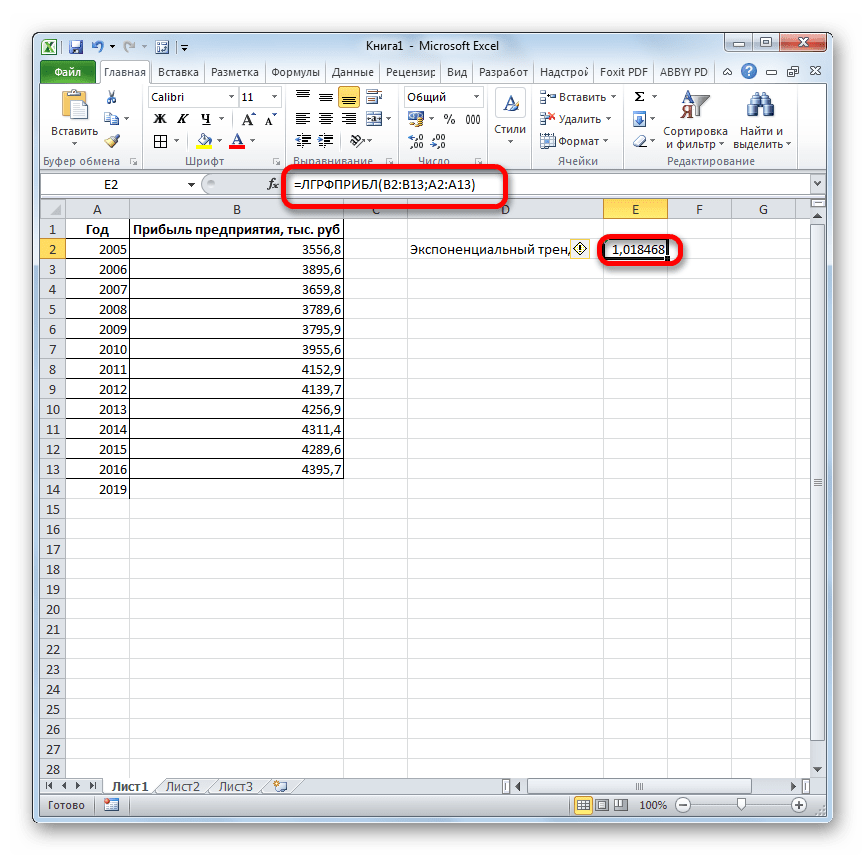
- Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.
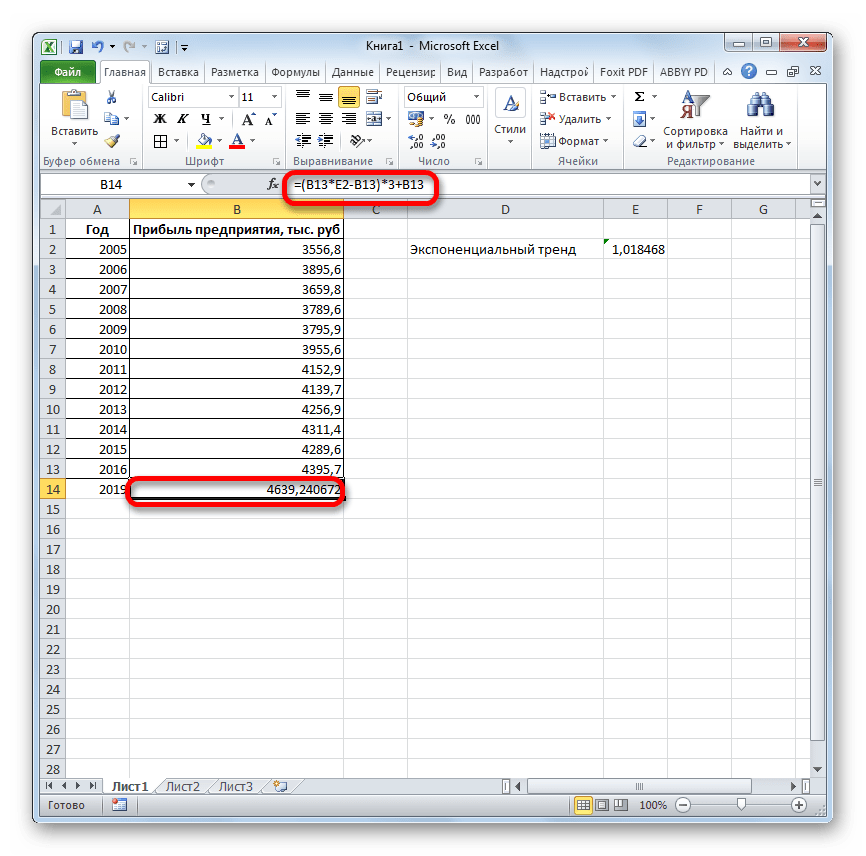
- Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Урок: Другие статистические функции в Excel
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.
Можно выделить
два метода разработки прогнозов,
основанных на методах математической
статистики: экстраполяцию и моделирование.
В первом случае в
качестве базы прогнозирования используется
прошлый опыт, который пролонгируется
на будущее. Делается предположение,
что система развивается эволюционно в
достаточно стабильных условиях. Чем
крупнее система, тем более вероятно
сохранение ее параметров без изменения
— конечно, на срок, не слишком большой.
Обычно рекомендуется, чтобы срок
прогноза не превышал одной трети
длительности расчетной временной
базы.
Во втором случае
строится прогнозная модель, характеризующая
зависимость изучаемого параметра от
ряда факторов, на него влияющих. Она
связывает условия, которые, как ожидается,
будут иметь место, и характер их влияния
на изучаемый параметр.
Данные модели не
используют функциональные зависимости;
они основаны только на статистических
взаимосвязях.
Здесь опять же
возникает вопрос: как еще до наступления
будущего оценить точность прогнозных
оценок? Для этого обычно расчеты по
выбранной прогнозной модели сравнивают
с данными, полученными в прошлом, и для
каждого момента времени определяют
различие оценок. Затем определяется
средняя разность оценок, скажем, среднее
квадратическое отклонение. По его
величине определяется прогнозная
точность модели.
При построении
прогнозных моделей чаще всего используется
парный и множественный регрессионный
анализ
Парный регрессионный
анализ
основан на использовании уравнения
прямой линии. При использовании уравнения
регрессии в целях прогнозирования надо
иметь в виду, что перенос закономерности
связи на динамику не является, строго
говоря, корректным и требует проверки
условий допустимости такого переноса
(экстраполяции), что выходит за рамки
статистики и может быть сделано только
специалистом, хорошо знающим объект
исследования и возможности его
развития в будущем.
Ограничением
прогнозирования на основе регрессионного
уравнения, тем более парного, служит
условие стабильности или, по крайней
мере, малой изменчивости других факторов
и условий изучаемого процесса, не
связанных с ними. Если резко изменится
«внешняя среда» протекающего процесса,
прежнее уравнение потеряет свое значение.
Следует соблюдать
еще одно ограничение: нельзя подставлять
значения факторного признака,
существенно отличающиеся от входящих
в базисную информацию, по которой
вычислено уравнение регрессии. При
качественно иных уровнях фактора, если
они даже возможны в принципе, были
бы иными параметры уравнения. Можно
рекомендовать при определении значений
факторов не выходить за пределы трети
размаха вариации как за минимальное,
так и за максимальное значения
признака-фактора, имеющиеся в исходной
информации.
Анализ на основе
множественной регрессии
основан на использовании более чем
одной независимой переменной в уравнении
регрессии. Это усложняет анализ, делая
его многомерным. Однако регрессионная
модель более полно отражает действительность,
так как в реальности исследуемый
параметр, как правило, зависит от
множества факторов.
Так, например, при
прогнозировании спроса идентифицируются
факторы, определяющие спрос, определяются
взаимосвязи, существующие между
ними, и прогнозируются их вероятные
будущие значения; из них при условии
реализации условий, для которых уравнение
множественной регрессии остается
справедливым, выводится прогнозное
значение спроса.
Многофакторное
уравнение множественной регрессии
имеет следующий вид:
Термин «коэффициент
условно-чистой регрессии» означает,
что каждая из величин b
измеряет среднее по совокупности
отклонение зависимой переменной
(результативного признака) от ее средней
величины при отклонении зависимой
переменной (фактора) х от своей средней
величины на единицу ее измерения. При
этом все прочие факторы, входящие в
уравнение регрессии, закреплены на
средних значениях и не изменяются.
Помимо целей
прогнозирования множественная регрессия
может использоваться для отбора
статистически значимых независимых
факторов, которые следует использовать
при исследовании результативного
признака. В частности, при поиске
критериев сегментации исследователь
может использовать регрессионный анализ
для выделения демографических
факторов, которые оказывают наиболее
сильное влияние на какой-то результирующий
показатель, характеризующий поведение
покупателей, например выбор товара
определенной марки.
Кроме того,
множественная регрессия может
использоваться для определения
относительной важности независимых
переменных.
Поскольку независимые
переменные имеют различные размерности,
проводить их сравнение прямым образом
нельзя. Например, нельзя прямым образом
сравнивать коэффициенты b
для размера семьи и величины среднего
для семьи дохода.
Обычно в данном
случае поступают следующим образом.
Делят каждую разницу между независимой
переменной и ее средней на среднее
квадратическое отклонение для этой
независимой переменной. Далее возможно
прямое сравнение полученных величин
(коэффициентов).
Многие данные
маркетинговых исследований представляются
для различных интервалов времени,
например на ежегодной, ежемесячной и
другой основе. Такие данные называются
временными
рядами.
Анализ временных рядов направлен на
выявление трех видов закономерностей
изменения данных: трендов, цикличности
и сезонности.
Тренд
характеризует общую тенденцию в
изменениях показателей ряда.
В таблице 5
приводятся данные объема продаж коньков
определенной компании за 15 лет.
Таблица
5 — Объем продаж коньков
|
Год |
Годовой |
|
1 |
1300 |
|
2 |
1250 |
|
3 |
1005 |
|
4 |
1437 |
|
5 |
908 |
|
6 |
1170 |
|
7 |
1380 |
|
8 |
1245 |
|
9 |
1111 |
|
10 |
1508 |
|
11 |
1970 |
|
12 |
2115 |
|
13 |
2460 |
|
14 |
3040 |
|
15 |
3520 |
|
16 |
???? |
Необходимо
определить прогнозную оценку объема
продаж на шестнадцатый год. Представив
в графическом виде данные табл. 2, можно
с помощью метода наименьших квадратов
подобрать прямую линию, в наибольшей
степени соответствующую полученным
данным (рис. 1), и определить прогнозную
величину объема продаж.
Сущность метода
наименьших квадратов состоит в отыскании
параметров модели тренда, минимизирующих
ее отклонение от точек исходного
временного ряда, т. е.

где

уi
– фактические значения исходного ряда;
n – число наблюдений. Если модель тренда
представить в виде
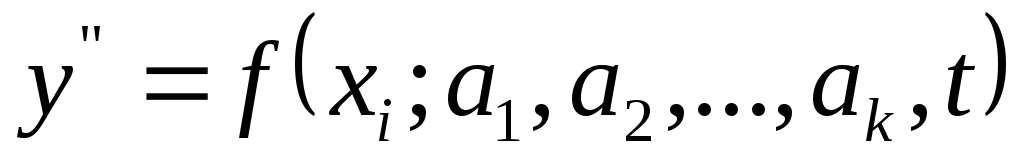
где a1
,a2
,…, ak
– параметры модели;
t – время;
xi
— независимые переменные, то для того,
чтобы найти параметры модели,
удовлетворяющие условию (1), необходимо
приравнять нулю первые производные
величины S по каждому из коэффициентов
a . Решая полученную систему уравнений
с k неизвестными, находим значения
коэффициентов a .
В то же время более
внимательное рассмотрение рис. 1 позволяет
сделать вывод о том, что не все точки
близко расположены к прямой. Особенно
эти расхождения велики для последних
лет, а верить последним данным, видимо,
следует с достаточным основанием.
В данном случае
можно применить метод экспоненциального
сглаживания, назначая разные весовые
коэффициенты (большие для последних
лет) данным для разных лет. В последнем
случае прогнозная оценка в большей
степени соответствует тенденциям
последних лет.
Алгоритм расчета
экспоненциально сглаженных значений
в любой точке ряда i основан на трех
величинах:
— фактическое
значение Ai в данной точке ряда i;
— прогноз в точке
ряда Fi;
— некоторый заранее
заданный коэффициент сглаживания W,
постоянный по всему ряду.
Новый прогноз
можно записать формулой:
(3)
Коэффициент
сглаживания W может принимать любые
значения из диапазона 0 < W < 1.Однако,
аналитики большинства фирм при обработке
рядов используют свои традиционные
значения W. Так, по опубликованным данным
в аналитическом отделе Kodak, традиционно
используют значение 0,38, а на фирме Ford
Motors – 0,28 или 0,3.
Рисунок 3 —
Прогнозирование объема продаж коньков
Циклический
характер колебаний статистических
показателей характеризуется длительным
периодом (солнечная активность,
урожайность отдельных культур,
экономическая активность). Такие явления,
как правило, не являются предметом
исследования маркетологов, которых
обычно интересует динамика проблемы
на относительно коротком интервале
времени.
Сезонные колебания
показателей имеют регулярный характер
и наблюдаются в течение каждого года.
Они и являются предметом изучения
маркетологов (спрос на газонокосилки,
на отдых в курортных местах в течение
года, на телефонные услуги в течение
суток и т.д.). Поскольку выявленные
закономерности носят регулярный
характер, то их вполне обоснованно можно
использовать в прогнозных целях.
Как и любые прогнозы,
оценки, полученные при помощи статистических
методов нужно уметь правильно использовать.
Предположим, что была получена прогнозная
оценка величины спроса на какой-то
товар. Она говорит о том, что при тех
же условиях внешней среды, структуре
и силе действия исходных факторов
величина спроса к определенному
моменту времени достигнет такой-то
величины. Менеджерам, которые
используют результаты данного прогноза,
следует ответить на вопрос: «А
устраивает ли нас данная величина
спроса?» Если «да», то надо приложить
максимум усилий, чтобы все сохранить
без изменения. Если «нет», то необходимо
использовать внутренние возможности
(например, провести дополнительную
рекламную компанию) и постараться
повлиять на определенные факторы внешней
среды, поддающиеся косвенному воздействию
(например, повлиять на деятельность
посредников, пролоббироавть изменение
определенных тарифов, импортных пошлин).
Вся эта деятельность направлена на
обеспечение получения желаемой величины
спроса.
-
.
Внутренний анализ и анализ конкуренции
Для полноты
информации проводиться исследования
не только потребителей, но внутренний
анализ и анализ конкуренции.
Внутренняя среда
организации –
та часть общей среды, которая находится
в ее пределах. Она оказывает постоянное
и самое непосредственное воздействие
на функционирование организации.
Внутренняя среда имеет несколько срезов,
состояние которых в совокупности
определяет тот потенциал и те возможности,
которыми располагает организация.
Изучение внутренней среды направлено
на уяснение того, какими сильными и
слабыми сторонами обладает организация.
Сильные стороны служат базой, на которую
организация опирается в конкурентной
борьбе и которую она должна стремиться
расширять и укреплять. Слабые стороны
— это предмет пристального внимания
со стороны руководства, которое должно
делать все возможное, чтобы избавиться
от них.
Анализ внутренней
среды организации обычно
проводится для сравнения положения
компании с положением ближайших
конкурентов (для оценки конкурентной
стратегической позиции организации).
Внутренний анализ
— это большое количество взаимосвязанных
переменных, которые могут быть объединены
в несколько групп, где важнейшими будут:
ресурсы и организация корпорации; рынки
и сбыт; финансирование; производство,
операции и технические аспекты; персонал.
Рассмотрим
последовательно компоненты каждой
группы.
·
Образ
и престиж корпорации.
• Размеры корпорации.
• Гибкие и
подстраивающиеся структуры.
• Эффективные
исследования и разработки.
• Эффективные
системы управленческойинформации;
• Уровень подготовки
высшего руководства.
• Стандартные
процедуры деятельности.
• Система контроля
и планирования
Целью внутреннего
анализа является устранение разногласий
между системными и стратегическими
задачами организации
Обратимся к анализу
конкуренции. Конкуренция —
это, как известно, механизм формирования
новых рыночных ниш и наиболее
эффективное использование существующих.
Поэтому освоение таких ниш компанией
должно сопровождаться изучением
конкурентных механизмов на данном
рынке. Причем такой анализ должен
предшествовать работе маркетологов
и разработчиков продуктов.
Первоочередность
анализа конкуренции гарантирует от
возможных просчетов в будущем,
поскольку определяет реалистичную
модель поведения на рынке.
Анализ проводиться
по следующим направлениям:
-
Определение
конкурентов; -
Сбор
сведений о конкуренте; -
Анализ
конкурентов; -
Анализ
конкурентоспособности предприятия.
На основе
маркетинговых исследований делаются
прогнозные оценки маркетинговой
информации.
Прогнозная
информация есть результат ряда основных
этапов поиска: предпрогнозная
ситуация
(проблемы, цели, рабочие гипотезы и др.),
прогнозный
фон (сбор и
анализ данных, влияющих на производство
продукта, товара и т.д.), исходная
модель
(совокупность признаков, показателей,
отражающих содержание объекта); поисковый
прогноз
(выявление текущего развития предполагаемой
модели); нормативный
прогноз
(ожидаемое будущего состояния с заданными
нормами и целями); оценка
степени точности
прогнозов (например с помощью экспертов);
Прогноз должен
учитывать следующие потребности:
1)
психологические,
2) этнокультурные,
3) социальные,
4)
трудовые,
5)
экономические
Однако
прогнозная информация может оказаться
недостаточной (ущербной), если не
учитывать интересы потребителей при
личных встречах. Данное партнерство
позволяет фирме оценить продукт в
реальных условиях, а покупатель получает
изделие с учетом его требований. Без
учета мнения покупателей можно
«промахнуться», имея в виду тот
факт, когда изделие не найдет своего
потребителя. Выявление мнения покупателя —
один из важных источников получения
прогнозной информации в маркетинге.
линия тренда
Одним
из самых популярных видов графического прогнозирования в Экселе является
экстраполяция выполненная построением линии тренда.
Попробуем
предсказать сумму прибыли предприятия через 3 года на основе данных по этому
показателю за предыдущие 12 лет.
1.
Строим график зависимости на основе табличных данных, состоящих из
аргументов и значений функции. Для этого выделяем табличную область, а затем,
находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы,
который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной
ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой
вид, но тогда, чтобы данные отображались корректно, придется выполнить
редактирование, в частности убрать линию аргумента и выбрать другую шкалу
горизонтальной оси.
2.
Теперь нам нужно построить линию тренда. Делаем щелчок правой
кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню
останавливаем выбор на пункте «Добавить линию тренда».
3.
Открывается окно форматирования линии тренда. В нем можно выбрать
один из шести видов аппроксимации:
o
Линейная;
o
Логарифмическая;
o
Экспоненциальная;
o
Степенная;
o
Полиномиальная;
o
Линейная фильтрация.
Давайте для начала выберем линейную аппроксимацию.
В
блоке настроек «Прогноз» в
поле «Вперед на» устанавливаем
число «3,0»,
так как нам нужно составить прогноз на три года вперед. Кроме того, можно
установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме
величину достоверности аппроксимации (R^2)». Последний показатель
отображает качество линии тренда. После того, как настройки произведены, жмем
на кнопку «Закрыть».
4.
Линия тренда построена и по ней мы можем определить примерную
величину прибыли через три года. Как видим, к тому времени она должна
перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество
линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность
линии. Максимальная величина его может быть равной 1. Принято считать,
что при коэффициенте свыше 0,85 линия тренда является достоверной.
5.
Если же вас не устраивает уровень достоверности, то можно
вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации.
Можно перепробовать все доступные варианты, чтобы найти наиболее точный.
Нужно заметить, что эффективным прогноз с помощью экстраполяции
через линию тренда может быть, если период прогнозирования не превышает 30% от
анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем
составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он
будет относительно достоверным, если за это время не будет никаких форс-мажоров
или наоборот чрезвычайно благоприятных обстоятельств, которых не было в
предыдущих периодах.
2.оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну
функцию – ТЕНДЕНЦИЯ.
Она также относится к категории статистических операторов. Её синтаксис во
многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные
значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью
соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего
инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он
не является обязательным и используется только при наличии постоянных факторов.
Данный
оператор наиболее эффективно используется при наличии линейной зависимости
функции.
Посмотрим,
как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить
полученные результаты, точкой прогнозирования определим 2019 год.
1.
Производим обозначение ячейки для вывода результата и
запускаем Мастер
функций обычным способом. В категории «Статистические» находим
и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
2.
Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В
поле «Известные
значения y» уже описанным выше способом заносим координаты
колонки «Прибыль
предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим
ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В
нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по
кнопке «OK».
3.
Оператор обрабатывает данные и выводит результат на экран. Как
видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной
зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.
оператор РОСТ
Ещё
одной функцией, с помощью которой можно производить прогнозирование в Экселе,
является оператор РОСТ. Он тоже относится к статистической группе инструментов,
но, в отличие от предыдущих, при расчете применяет не метод линейной
зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким
образом:
=РОСТ(Известные
значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в
точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании
останавливаться не будем, а сразу перейдем к применению этого инструмента на
практике.
1.
Выделяем ячейку вывода результата и уже привычным путем
вызываем Мастер
функций. В списке статистических операторов ищем пункт «РОСТ», выделяем
его и щелкаем по кнопке «OK».
2.
Происходит активация окна аргументов указанной выше функции.
Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в
окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на
кнопку «OK».
3.
Результат обработки данных выводится на монитор в указанной ранее
ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия
от результатов обработки данных оператором ТЕНДЕНЦИЯнезначительны, но они имеются. Это связано с
тем, что данные инструменты применяют разные методы расчета: метод линейной
зависимости и метод экспоненциальной зависимости.
оператор
ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного
приближения. Его не стоит путать с методом линейной зависимости, используемым
инструментом ТЕНДЕНЦИЯ.
Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные
значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются
необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы,
наверное, заметили, что в этой функции отсутствует аргумент, указывающий на
новые значения. Дело в том, что данный инструмент определяет только изменение
величины выручки за единицу периода, который в нашем случае равен одному году,
а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему
фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный
на количество лет.
1.
Производим выделение ячейки, в которой будет производиться
вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в
категории «Статистические» и
жмем на кнопку «OK».
2.
В поле «Известные значения y», открывшегося окна аргументов,
вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим
адрес колонки «Год».
Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».
3.
Программа рассчитывает и выводит в выбранную ячейку значение
линейного тренда.
4.
Теперь нам предстоит выяснить величину прогнозируемой прибыли на
2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по
ячейке, в которой содержится фактическая величина прибыли за последний
изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится
рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним
годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз
(2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы
произвести расчет кликаем по кнопке Enter.
Как
видим, прогнозируемая величина прибыли, рассчитанная методом линейного
приближения, в 2019 году составит 4614,9 тыс. рублей
оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим,
будет ЛГРФПРИБЛ.
Этот оператор производит расчеты на основе метода экспоненциального
приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ
(Известные значения_y;известные значения_x;
новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют
соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного
изменится. Функция рассчитает экспоненциальный тренд, который покажет, во
сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно
будет найти разницу в прибыли между последним фактическим периодом и первым
плановым, умножить её на число плановых периодов (3) и
прибавить к результату сумму последнего фактического периода.
1.
В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем
щелчок по кнопке «OK».
2.
Запускается окно аргументов. В нем вносим данные точно так, как
это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».
3.
Результат экспоненциального тренда подсчитан и выведен в обозначенную
ячейку.
4.
Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем
ячейку, которая содержит значение выручки за последний фактический период.
Ставим знак «*» и
выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем
по элементу, в котором находится величина выручки за последний период.
Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке,
которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.
Прогнозируемая
сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального
приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от
результатов, полученных при вычислении предыдущими способами.
Урок: Другие статистические функции в Excel
Мы
выяснили, какими способами можно произвести прогнозирование в программе Эксель.
Графическим путем это можно сделать через применение линии тренда, а
аналитическим – используя целый ряд встроенных статистических функций. В
результате обработки идентичных данных этими операторами может получиться
разный итог. Но это не удивительно, так как все они используют разные методы
расчета. Если колебание небольшое, то все эти варианты, применимые к
конкретному случаю, можно считать относительно достоверными.
|
Можно считать, что прогнозирование является чуть ли не основной целью и задачей большого числа специалистов, занимающихся анализом данных. Современные методы статистического прогнозирования позволяют с высокой точностью прогнозировать практически все возможные показатели. |
Автоматизируйте решение задачи прогнозирования с помощью системы Sales-Forecast. Смотреть видео |
При анализе временных рядов можно выделить две основные цели:
-
определение природы временного ряда
-
прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям)
Однако надо помнить, что не существует универсальных методов прогнозирования на все случаи жизни. Выбор метода прогнозирования и его эффективность зависят от многих условий, и в частности от требуемой длины или времени прогнозирования.
По времени прогнозирования различают краткосрочный, среднесрочный и долгосрочный прогноз.
Краткосрочный прогноз характеризует собой прогноз «на завтра», то есть прогноз на несколько шагов вперед. Для него применяют практически все известные методы: экспоненциальное сглаживание, АРПСС (ARIMA) и нейронные сети.
Среднесрочный прогноз – это обычно прогноз на один или на половину сезонного цикла. Для него используют АРПСС и экспоненциальное сглаживание, которые позволяют отслеживать качество прогноза в зависимости от срока прогноза.
А при построении долгосрочного прогноза стандартные статистические методы прогнозирования практически не используют, и требуется использование комплексных подходов. Например, использование нейронных сетей или регрессионных моделей.
Для построения прогноза, важно правильно понимать термины, используемые при построении моделей и хорошо ими оперировать. Это и выделение тренда, циклической составляющей ряда, трендциклической, сезонной составляющей и шумовой компоненты; и исследование автокорреляционной и частной автокорреляционной функции для нахождения сезонности; и построение периодограммы, и вычисление сезонного лага (например, при помощи спектрального анализа Фурье).
После построения любой модели важно проверять, насколько адекватно она построена. Для этого можно, во-первых, провести визуальный анализ со сдвигом прогноза на несколько шагов назад. А во-вторых, воспользоваться анализом остатков – стандартным методом проверки адекватности любой построенной статистической модели.
Для наглядного представления применимости моделей в зависимости от интересующей длительности прогноза удобно пользоваться следующей таблицей:
Программа STATISTICA является комплексным аналитическим инструментом, предназначенным для построения точных прогнозов в любых областях, используя различные методы прогнозирования, а справка системы своевременно напомнит необходимую терминологию.
STATISTICA — полностью на русском языке!
При решении задач прогнозирования могут применяться процедуры и модули следующих продуктов STATISTICA:
STATISTICA Base
Продукт необходим для расчета описательных статистик, построения графиков, сравнения нескольких групп (например, рядов продаж за несколько лет) и оценки правомерности использования «старых» данных при построении прогнозов, оценки изменчивости ряда, «чистки данных» (нахождения и обработки выбросов), расчета корреляций, выявления зависимостей между временными рядами и т.д.
В этом блоке реализован один из наиболее часто используемых методов прогнозирования — построение классической линейной модели многомерной регрессии, описывающей зависимость между переменной, которую необходимо прогнозировать, и влияющими на нее факторами.
Например, может быть смоделирована зависимость объемов продаж от таких факторов как цены на продукцию, расходы на проведение рекламных и маркетинговых акций, сезонность в распределении продаж, цены конкурентов и др. При известных значениях факторов на основе объясняющей модели легко могут быть спрогнозированы объемы продаж.
Таким образом, анализ зависимостей между переменными не ограничивается проведением корреляционного анализа, а включает также построение на основе исходных данных численной зависимости, которая может быть использована для прогнозирования значений независимых переменных при известных значениях факторов. Кроме этого проводится оценка статистической значимости как самой модели, так и предикторов, входящих в ее состав.
Например, зная запланированные на следующий месяц объемы скидок, уровни цен, затраты на проведение рекламных акций и т.д., можно получить предполагаемый уровень продаж и его доверительный интервал, подставив соответствующие значения в уравнение зависимости.
STATISTICA Advanced
Продукт содержит все возможности STATISTICA Base и расширяет их углубленными методами анализа.
Модуль STATISTICA Advanced Linear/Non-Linear Models (Линейные и Нелинейные Модели)
Позволяет перейти от построения простейших линейных регрессионных моделей к более общим и сложным нелинейным моделям, которые обеспечивают более точное моделирование рынка. Например, в модель могут входить не только сами факторы, но и их различные функциональные преобразования. Для построения подобных моделей доступны модули Общие линейные и нелинейные модели, Общие регрессионные модели, Нелинейное оценивание и др.
Кроме этого, при построении нелинейных моделей появляется возможность нахождения оптимальных значений факторов, при которых будут достигаться наиболее желательные значения зависимой переменной (например, максимальные объемы продаж). Для этого используются специальные оптимизационные алгоритмы и графические методы, например, инструмент Профили желательности.
Модуль Временные ряды и прогнозирование, также входящий в блок Линейные и Нелинейные Модели STATISTICA, широко используется для построения прогнозов временных рядов без привлечения сопутствующих факторов, т.е. для прогнозирования поведения ряда на основе его собственной истории. Модуль включает наиболее эффективные и популярные методы и анализа временных рядов, такие как экспоненциальное сглаживание, модель авторегрессии и скользящего среднего, сезонная декомпозиция, спектральный анализ Фурье и другие. Для каждого из методов имеется большое число настроек, что позволяет наилучшим образом адаптировать его под исследуемый временной ряд.
При исследовании временных рядов часто очень эффективными оказываются графические и описательные методы и анализа, большинство из которых для удобства интегрированы в модуль Временные ряды и прогнозирование. Модуль также содержит полный набор средств для проведения всевозможных преобразований временных рядов, таких как взятие разности различных порядков (исследование изменчивости ряда), сглаживание ряда (обнаружение тенденций в поведении ряда), выделение тренда (выделение детерминированной систематической составляющей ряда), вычисление автокорреляционных и кросскорреляционных функций, а также построение их графиков (коррелограмм).
Процедура Анализ распределенных лагов, представленная в модуле, позволяет исследовать запаздывающие влияния сопутствующих факторов на изучаемый временной ряд. Например, при анализе зависимости между фактором рекламных акций и объемом продаж логично предположить, что реклама может подействовать не моментально, а через некоторое время. Как раз при решении подобных задач может быть применена эта процедура, она позволит выявить наличие зависимости и определить, через какое время следует ожидать «отдачи» от рекламы.
Модуль STATISTICA Multivariate Exploratory Techniques (Многомерные разведочные технологии анализа)
Предоставляет широкий выбор разведочных технологий анализа различных типов данных в сочетании с богатыми интерактивными средствами визуализации.
Модули этого блока могут быть использованы при решении задач, связанных с сегментацией исходных объектов в данных, снижением размерности данных, задач классификации и др. Применение многомерных статистических методов анализа позволяет снизить трудоемкость решения задачи прогнозирования.
Модуль Кластерный анализ позволяет разбить исходную, вообще говоря, неоднородную совокупность объектов на максимально однородные группы, или кластеры. Например, в крупных торговых сетях ассортимент продаваемых товаров насчитывает тысячи единиц. Анализ и прогнозирование каждого временного ряда по отдельности не представляются возможными в связи с высокой трудоемкостью такого подхода. Мы можем разбить все множество временных рядов на однородные кластеры, которые будут содержать ряды, обладающие сходной динамикой, после чего анализировать уже не отдельные ряды, а целые кластеры. Таким образом, значительно (иногда в десятки раз) снижается размерность задачи, а следовательно и трудоемкость прогнозирования продаж.
Кроме этого, можно кластеризовать временные ряды исходя из абсолютных значений оборота по каждому из товаров, и выделить товары, продажи которых приносят наибольшую прибыль. Как показывает опыт, часто около 20% ассортимента обеспечивают 80% оборота (так называемый принцип Парето).
STATISTICA Automated Neural Networks
Единственный в мире программный продукт для нейросетевых исследований, полностью переведенный на русский язык. Поддержка различных типов анализов: регрессия, классификация, временные ряды (прогнозирование), временные ряды (классификация), кластерный анализ, визуализация данных.
Продукт содержит мощное собрание встроенных интеллектуальных возможностей, которые позволяют решить реальные задачи, не имея практически никакого опыта работы с нейронными сетями. В то же время, опытный пользователь нейронных сетей может полностью управлять почти всеми аспектами нейросетевой структуры и обучения.
STATISTICA Data Miner
Продукт содержит наиболее полный набор методов Data Mining на рынке программного обеспечения, в удобном пользовательском интерфейсе позволяет исследовать большие массивы информации и выявлять в них скрытые правила и закономерности (продукт также содержит все возможности STATISTICA Advanced, STATISTICA Automated Neural Networks).
Кроме того, StatSoft Russia ведет разработку готовых отраслевых решений, позволяющих автоматизировать процесс построения прогнозов (в том числе для сотен рядов), а также учесть всю специфику задач Заказчика.
Ниже представлены некоторые примеры применения системы STATISTICA для решения задач прогнозирования в различных областях:
Видео на канале StatSoft TV по прогнозированию:
Узнать о применении STATISTICA для решения Ваших задач Вы можете, заказав бесплатную выездную презентацию или online семинар StatSoft.
Академия Анализа Данных предлагает всеохватывающий набор курсов по современным технологиям анализа данных и прогнозирования:
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Еще…Меньше
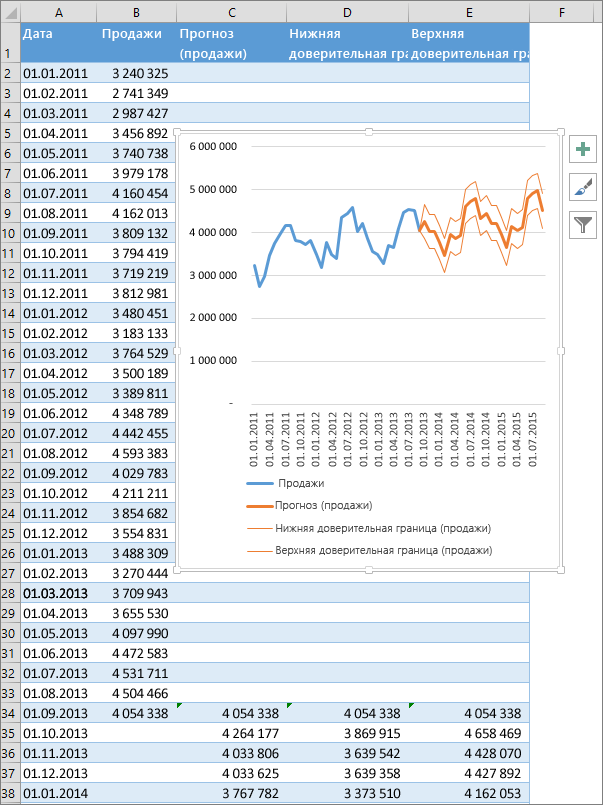
Если у вас есть статистические данные с зависимостью от времени, вы можете создать прогноз на их основе. При этом в Excel создается новый лист с таблицей, содержащей статистические и предсказанные значения, и диаграммой, на которой они отражены. С помощью прогноза вы можете предсказывать такие показатели, как будущий объем продаж, потребность в складских запасах или потребительские тенденции.
Сведения о том, как вычисляется прогноз и какие параметры можно изменить, приведены ниже в этой статье.
Создание прогноза
-
На листе введите два ряда данных, которые соответствуют друг другу:
-
ряд значений даты или времени для временной шкалы;
-
ряд соответствующих значений показателя.
Эти значения будут предсказаны для дат в будущем.
Примечание: Для временной шкалы требуются одинаковые интервалы между точками данных. Например, это могут быть месячные интервалы со значениями на первое число каждого месяца, годичные или числовые интервалы. Если на временной шкале не хватает до 30 % точек данных или есть несколько чисел с одной и той же меткой времени, это нормально. Прогноз все равно будет точным. Но для повышения точности прогноза желательно перед его созданием обобщить данные.
-
-
Выделите оба ряда данных.
Совет: Если выделить ячейку в одном из рядов, Excel автоматически выделит остальные данные.
-
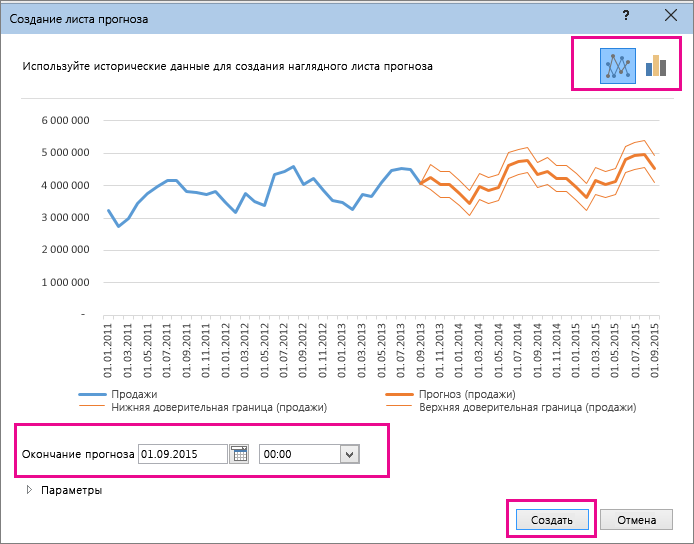
На вкладке Данные в группе Прогноз нажмите кнопку Лист прогноза.
-
В окне Создание прогноза выберите график или гограмму для визуального представления прогноза.
-
В поле Завершение прогноза выберите дату окончания, а затем нажмите кнопку Создать.
В Excel будет создан новый лист с таблицей, содержащей статистические и предсказанные значения, и диаграммой, на которой они отражены.
Этот лист будет находиться слева от листа, на котором вы ввели ряды данных (то есть перед ним).
Настройка прогноза
Если вы хотите изменить дополнительные параметры прогноза, нажмите кнопку Параметры.
Сведения о каждом из вариантов можно найти в таблице ниже.
|
Параметры прогноза |
Описание |
|
Начало прогноза |
Выберите дату, с которой должен начинаться прогноз. При выборе даты начала, которая наступает раньше, чем заканчиваются статистические данные, для построения прогноза используются только данные, предшествующие ей (это называется «ретроспективным прогнозированием»). Советы:
|
|
Доверительный интервал |
Установите или снимите флажок Доверительный интервал, чтобы показать или скрыть его. Доверительный интервал — это диапазон вокруг каждого предсказанного значения, в который в соответствии с прогнозом (при нормальном распределении) предположительно должны попасть 95 % точек, относящихся к будущему. Доверительный интервал помогает определить точность прогноза. Чем он меньше, тем выше достоверность прогноза для данной точки. Доверительный интервал по умолчанию определяется для 95 % точек, но это значение можно изменить с помощью стрелок вверх или вниз. |
|
Сезонность |
Сезонность — это число для длины (количества точек) сезонного шаблона и автоматически обнаруживается. Например, в ежегодном цикле продаж, каждый из которых представляет месяц, сезонность составляет 12. Автоматическое обнаружение можно переопрепредидить, выбрав установить вручную и выбрав число. Примечание: Если вы хотите задать сезонность вручную, не используйте значения, которые меньше двух циклов статистических данных. При таких значениях этого параметра приложению Excel не удастся определить сезонные компоненты. Если же сезонные колебания недостаточно велики и алгоритму не удается их выявить, прогноз примет вид линейного тренда. |
|
Диапазон временной шкалы |
Здесь можно изменить диапазон, используемый для временной шкалы. Этот диапазон должен соответствовать параметру Диапазон значений. |
|
Диапазон значений |
Здесь можно изменить диапазон, используемый для рядов значений. Этот диапазон должен совпадать со значением параметра Диапазон временной шкалы. |
|
Заполнить отсутствующие точки с помощью |
Для обработки отсутствующих точек в Excel используется интерполяция, то есть отсутствующие точки будут заполнены в качестве взвешенного среднего значения соседних точек, если отсутствует менее 30 % точек. Чтобы нули в списке не были пропущены, выберите в списке пункт Нули. |
|
Использование агрегатных дубликатов |
Если данные содержат несколько значений с одной меткой времени, Excel находит их среднее. Чтобы использовать другой метод вычисления, например Медиана илиКоличество,выберите нужный способ вычисления из списка. |
|
Включить статистические данные прогноза |
Установите этот флажок, если хотите поместить на новом листе дополнительную статистическую информацию о прогнозе. При этом добавляется таблица статистики, созданная с помощью прогноза. Ets. Функция СТАТ и показатели, такие как коэффициенты сглаживания («Альфа», «Бета», «Гамма») и метрики ошибок (MASE, SMAPE, MAE, RMSE). |
Формулы, используемые при прогнозировании
При использовании формулы для создания прогноза возвращаются таблица со статистическими и предсказанными данными и диаграмма. Прогноз предсказывает будущие значения на основе имеющихся данных, зависящих от времени, и алгоритма экспоненциального сглаживания (ETS) версии AAA.
Таблицы могут содержать следующие столбцы, три из которых являются вычисляемыми:
-
столбец статистических значений времени (ваш ряд данных, содержащий значения времени);
-
столбец статистических значений (ряд данных, содержащий соответствующие значения);
-
столбец прогнозируемых значений (вычисленных с помощью функции ПРЕДСКАЗ.ЕTS);
-
два столбца, представляющие доверительный интервал (вычисленные с помощью функции ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ). Эти столбцы отображаются только при проверке доверительный интервал в разделе Параметры.
Скачивание образца книги
Щелкните эту ссылку, чтобы скачать книгу с Excel FORECAST. Примеры функции ETS
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Статьи по теме
Функции прогнозирования
Нужна дополнительная помощь?
Нужны дополнительные параметры?
Изучите преимущества подписки, просмотрите учебные курсы, узнайте, как защитить свое устройство и т. д.
В сообществах можно задавать вопросы и отвечать на них, отправлять отзывы и консультироваться с экспертами разных профилей.