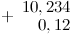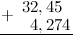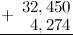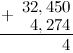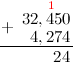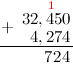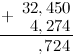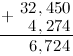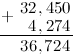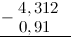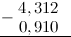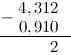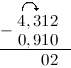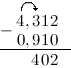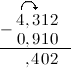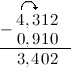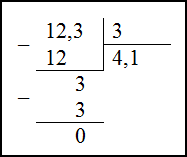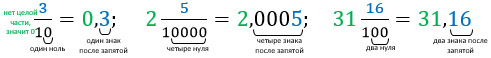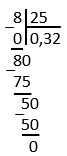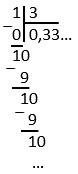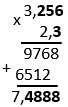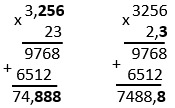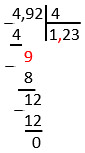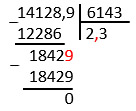Десятичные дроби — для чайников
Действия с десятичными дробями – деление умножение, сложение, вычитание, сравнение. Разбор примеров.
Все это здесь.
Между прочим, большинство ошибок на экзаменах происходят как раз из-за незнания простейших действий вроде этих.
Так что читай эту статью и отрабатывай скиллы.
Десятичные дроби — коротко о главном
1. Определение
Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени.
2. Конечная и бесконечная десятичная дробь
Десятичная дробь может быть:
- конечной, если она содержит конечное число цифр после запятой (( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}));
- бесконечной, в том числе периодичной, если конечное число цифр определить не определено (( 0,05882352941…));
- периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right)))
3. Свойства десятичных дробей
- Десятичная дробь не меняется, если справа добавить нули ( displaystyle frac{3}{100}=0,03=0,030=0,030000)и т.д.;
- Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: ( 0,014330000=0,01433);
- Десятичная дробь возрастает в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо: ( 0,0125cdot 100=1,25) (перенесли запятую на ( 2) знака вправо – умножили на ( 100) и дробь возросла в ( 100) раз);
- Десятичная дробь уменьшается в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево: ( 124,56:100=1,2456) (перенесли запятую на ( 2) знака влево – разделили на ( 100) и дробь уменьшилась в ( 100) раз).
4. Сложение десятичных дробей
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.
5. Вычитание десятичных дробей
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:
6. Умножение десятичных дробей
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
7. Деление десятичных дробей
Деление десятичной дроби на натуральное число
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Деление десятичных дробей друг на друга
- Считаем количество знаков справа от запятой в десятичной дроби.
- Умножаем и делимое, и делитель на 10, 100 или 1000 и т.д., в зависимости от того, сколько мы насчитали знаков в первом пункте. Умножать необходимо, чтобы превратить десятичную дробь в целое число.
Десятичные дроби — подробнее
Конечно, ты знаешь, что такое обыкновенная дробь. Например, ( displaystyle frac{1}{3}, frac{1}{4},frac{5}{112}).
Наравне с приведенными выше дробями существуют дроби ( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}) и т.д.
Такие дроби можно записать намного удобнее и более кратко, то есть:
( displaystyle frac{8}{10}=0,8)
( displaystyle frac{13}{100}=0,13)
( displaystyle frac{49}{1000}=0,049)
Данного вида дроби называются десятичными. Иными словами:
Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени (первый пример – ( 10) в первой степени, второй – ( 10) во второй степени и т.д.).
Ты наверняка знаешь, что каждая цифра после запятой имеет свое название. На всякий случай напомню тебе про них, чтобы в дальнейшем мы говорили на одном языке:
Это огромное число читается по следующему алгоритму:
- Сначала читается число, стоящее до запятой и добавляется слово «целых»: ««( 46) целых»;
- Затем читается как обыкновенное число слева после запятой и добавляется слово, обозначающее название самой последней цифры. В нашем случае – «одна тысяча двести тридцать четыре десятитысячные».
А теперь прочитаем все вместе – «( 46) целых одна тысяча двести тридцать четыре десятитысячные». Разобрался? Переходим к визуализации полученных знаний!
Итак, небольшая тренировка на понимание, что такое эта десятичная дробь! Нарисуй квадрат ( 10) на ( 10) и закрась какую-нибудь его часть равную:
- ( 0,05;)
- ( 0,4;)
- ( 0,27;)
- ( 0,245)
Справился? Проверяем, что у тебя получилось.
Во-первых, квадрат ( 10) на ( 10) состоит из ( 100) клеточек. Соответственно, ( 0.05) – ( 5) клеточек из ( 100); ( 0,4) – ( 40) клеточек из ( 100) и так далее.
Наверняка, наибольшее затруднение составило последнее число – ( -0,245). На картинке это необходимо отразить как 24,5 клетки.
В общем, смотри:
С понятиями разобрались, теперь научимся переводить из десятичной дроби в обыкновенную и обратно.
Перевод из десятичной дроби в обыкновенную и обратно
Попробуй перевести:
- ( 0,136)
- ( 0,2436)
- ( 0,0456)
- ( 0,21)
Сравним ответы:
- ( displaystyle 0,136=frac{136}{1000})
- ( displaystyle 0,2436=frac{2436}{10000})
- ( displaystyle 0,0456=frac{456}{10000})
- ( displaystyle 0,21=frac{21}{100})
Уверена, что ты с легкостью справился! А как насчет обратного перевода? Из обыкновенных в десятичные?
Попробуй свои силы на вот этих дробях:
- ( displaystyle frac{2}{10})
- ( displaystyle frac{3}{100})
- ( displaystyle frac{4}{1000})
- ( displaystyle frac{4562}{100})
А вот и ответы:
- ( displaystyle frac{2}{10}=0,2)
- ( displaystyle frac{3}{100}=0,03)
- ( displaystyle frac{4}{1000}=0,004)
- ( displaystyle frac{4562}{100}=45frac{62}{100}=45,62)
Если ты со всем справился, можешь пропускать следующий абзац, а если где-то допустил ошибку, внимательно прочти о том, как легко и 100% правильно переводить дроби из обыкновенных в десятичные.
- Смотрим на дробь и определяем, есть ли у нее целая часть? Если есть, выделяем целую часть, записываем ее, и ставим запятую.
- После запятой должно быть столько знаков, сколько нулей стоит в знаменателе. Например, дробь ( displaystyle frac{4}{1000}) — ( 3) нуля в знаменателе, соответственно, мы как бы мысленно выделяем ( 3) ячейки.
- Затем записываем числитель – ( 4), но выравниваем его по правому краю, а в пустые ячейки вставляем нули.
Разобрался? Посмотри еще раз эту маленькую «инструкцию»:
Я думаю, ты во всем-всем разобрался! Потренируемся? Попробуй поработать еще с вот этими дробями:
- ( displaystyle frac{26}{10})
- ( displaystyle frac{43}{100})
- ( displaystyle frac{99}{1000})
- ( displaystyle frac{3562}{100})
А теперь ответы:
- ( displaystyle frac{26}{10}=2,6)
- ( displaystyle frac{43}{100}=0,43)
- ( displaystyle frac{99}{1000}=0,099)
- ( displaystyle frac{3562}{100}=35,62)
Виды десятичных дробей
Десятичная дробь может быть:
- конечной, если она содержит конечное число цифр после запятой (( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}));
- бесконечной, в том числе периодичной, если конечное число цифр определить не определено (( 0,05882352941…));
- периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right))).
Поговорим сначала о конечных дробях.
Конечная десятичная дробь
Само собой понятно, что дроби ( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}) являются конечными, ведь знаменатель дроби уже представлен как единица с последующими нулями, и поэтому мы сразу можем сказать, что данную обыкновенную дробь можно перевести в конечную десятичную. А что ты скажешь насчет этой дроби: ( displaystyle frac{1}{4})? Ее знаменатель далеко не единица с последующими нулями, но ты четко знаешь, что у нее есть десятичный «аналог»:
( displaystyle frac{1}{4}=frac{1cdot 25}{4cdot 25}=frac{25}{100}=0,25)
То есть, чтобы определить, можно ли перевести дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число, такое, чтобы знаменатель стал равен ( 10), ( 100), ( 1000) и так далее.
Усвоил? Постарайся представить в виде конечной десятичной дроби следующие обыкновенные дроби:
- ( displaystyle frac{1}{5})
- ( displaystyle frac{1}{8})
- ( displaystyle frac{3}{5})
- ( displaystyle frac{1}{16})
Сравним наши ответы:
- ( displaystyle frac{1cdot 2}{5cdot 2}=frac{2}{10}=0,2)
- ( displaystyle frac{125}{1000}=0,125)
- ( displaystyle frac{3}{5}=frac{6}{10}=0,6)
- ( displaystyle frac{1}{16}=frac{625}{10000}=0,0625)
Справился? Молодец. Выходим на новый уровень и переходим к бесконечным десятичным дробям.
Бесконечная десятичная дробь
Итак, бери калькулятор и дели ( 1) на ( 17). Поделил? Ты получил ( 0,05882352941) и дальше окошко калькулятора не показывает… Это тоже является десятичной дробью, только данная десятичная дробь является бесконечной. Ты сейчас скажешь, а как же наше определение?
Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени (первый пример – ( 10) в первой степени, второй – ( 10) во второй степени и т.д.).
Все очень просто и никаких противоречий с определением нет. В данном случае нам необходимо привести наш знаменатель к ( {{10}^{n}}), с учетом, что ( n) это какое-либо бесконечное число, которое мы не можем «обозреть» взглядом», или иными словами – ( nto +infty )
Таким образом:
Бесконечной десятичной дробью называется обыкновенная дробь, в записи которой после запятой содержится бесконечное количество цифр.
Как правило, в задачах, где встречаются бесконечные десятичные дроби, просят указать ответ либо с округлением (например, до десятых, или до сотых), либо записать в виде обыкновенной дроби, то есть как ( displaystyle frac{1}{17}).
Подумай, какой самый популярный пример можно привести на тему «бесконечная десятичная дробь»? Правильно! Число ( pi ) является бесконечной десятичной дробью. Во всем мире люди договорились, что для решения математических задач принято, что ( pi =3,14), но это далеко не так. Число ( pi ) не имеет определенного завершения. Оно настолько бесконечно, что ежегодно в мире проводятся соревнования по запоминанию числа ( pi ). Мировой рекорд по запоминанию знаков числа ( pi ) после запятой принадлежит китайцу Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки! Все 67 890 знаков после запятой мы приводить не будем, а приведем несколько сокращенную запись:
( pi =3,1415926535text{ }8979323846text{ }2643383279text{ }5028841971)
Думаю, этого хватит, чтобы оценить «масштабы» данного числа.
Наравне с бесконечными десятичными дробями существуют периодические десятичные дроби. Они так же не имеют конца, но последующие числа в них повторяются, например, попробуй перевести в десятичную дробь ( displaystyle frac{1}{3}). Что у тебя получилось?
( displaystyle frac{1}{3}=0,333333333….)
Чтобы не повторять число ( 3) много много раз, решили говорить «ноль целых и три в периоде», так как тройка будет повторяться после запятой бесконечное число раз. Из этого умозаключения следует определение:
Дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр.
Чтобы кратко записать такую дробь, период (повторяющиеся цифры после запятой) пишут в скобках:
( displaystyle frac{1}{3}=0,underbrace{3}_{период}33333333….=0,left( 3 right))
( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right))
Важно, что период не может начинаться слева от запятой:
( displaystyle frac{100}{7}=underbrace{14,2857}_{не период}1428571428571…=14,left( 285714 right)).
Свойства десятичных дробей
Существует четыре свойства десятичных дробей. Они очень простые, и ты 100% знаешь о всех них, но давай их перечислим и вспомним:
1. Десятичная дробь не меняется, если справа добавить нули
( displaystyle frac{3}{100}=0,03=0,030=0,030000)и т.д.
2. Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби:
( 0,014330000=0,01433)
ВНИМАНИЕ!!! Нельзя удалять нули, расположенные не в конце десятичной дроби!!!!
( 0,014330000ne 0,1433)
3. Десятичная дробь возрастает в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо:
( 0,0125cdot 100=1,25) (перенесли запятую на ( 2) знака вправо – умножили на ( 100) и дробь возросла в ( 100) раз)
4. Десятичная дробь уменьшается в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево:
( 124,56:100=1,2456) (перенесли запятую на ( 2) знака влево – разделили на ( 100) и дробь уменьшилась в ( 100) раз)
Последние два свойства позволяют быстро умножать и делить десятичные дроби на ( 10), ( 100), ( 1000) и т.д. о чем подробнее мы поговорим чуть ниже.
Действия с десятичными дробями
Десятичные дроби – это обычные числа. Мы можем складывать их, вычитать из одной другую, умножать и делить.
Очень важно уметь правильно производить с ними математические действия, так как зачастую именно от арифметических ошибок зависит твоя оценка на экзамене.
Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению.
Как складывать десятичные дроби
При сложении десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. Соответственно, запятые стоят четко друг под другом.
Разберемся на примере:
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставится четко на том же месте, как и в складываемых числах.
Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.
Если при сложении в сумме мы получаем больше ( 10), то одна единица прибавляется к сумме при сложении цифр следующего разряда.
Решим наш пример, учтя все правила:
Разобрался? Посчитай в столбик самостоятельно:
- ( 0,0125+0,141)
- ( 2,4225+0,34)
- ( 122,4355+1,34)
- ( 2,435+12,3)
Сравним ответы:
- ( 0,0125+0,141=0,1535)
- ( 2,4225+0,34=2,7625)
- ( 122,4355+1,34=123,7755)
- ( 2,435+12,3=14,735)
Как вычитать десятичные дроби
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения.
Соответственно, запятые стоят четко друг под другом.
Вычитание происходит, как и вычитание натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в числах, с которыми мы работаем.
Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.
Если при вычитании получается, что мы из меньшего числа вычитаем большее, то мы как бы занимаем десяток у более высокого разряда (при вычитании сотых частей, берем десяток у десятых, при вычитании десятых – у единиц и так далее), не забывая уменьшить вычитаемое число у заимствованного разряда.
Посмотрим подробно на примере:
Думаю, с рисунком тебе стало все понятно. Попробуй посчитать в столбик следующие выражения:
- ( 0,0125-0,141)
- ( 2,4225-0,34)
- ( 122,4355-1,34)
- ( 12,435-12,3)
Сравним полученные ответы:
- ( 0,0125-0,141=-0,1285)
- ( 2,4225-0,34=2,0825)
- ( 122,4355-1,34=121,0955)
- ( 12,435-12,3=0,135)
Как умножать десятичные дроби
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
Мы начинаем запись числа, получающего при перемножении, под тем разрядом второго числа, на который умножаем. Далее мы суммируем полученные числа и только затем ставим запятую.
Чтобы определить, между какими числами должна стоять запятая, мы должны посмотреть, сколько чисел стоит после знака запятой у первого множителя, сколько у второго, сложить их и отсчитать справа данное количество чисел.
Непонятно? Смотри:
Как ты видишь, при перемножении мы будем складывать столько слагаемых, сколько разрядов содержится во втором множителе, поэтому удобней записывать числа так, чтобы первый множитель был по количеству чисел больше, чем второй.
Таким способом мы значительно снизим вероятность ошибок.
Не веришь? Смотри:
Если при умножении мы получаем число, которое больше ( 9), например ( 12), то единицу мы прибавляем к значению, полученному при умножении последующих чисел следующего десятка.
Соответственно, если получаем, например, ( 24), то прибавляем ( 2).
Проиллюстрируем данное правило:
Разобрался? Дорешай данный пример самостоятельно.
Сколько у тебя получилось? У меня ( 10,33911).
А теперь пора приступить к некоторым очень важным моментам, которые помогут сохранить время на экзамене.
Как делить десятичные дроби
Теперь ты знаешь о десятичных дробях почти все. Осталось только разобраться с тем, как их делить друг на друга.
Если ты отлично это представляешь, смело пропускай данный подраздел. Если нет – смотри инструкцию к применению.
Итак. Мы рассмотрим два вида деления:
- деление десятичной дроби на натуральное число;
- деление десятичной дроби на десятичную дробь.
Начнем с деления десятичной дроби на натуральное число.
Чтобы делить десятичную дробь на натуральное число, необходимо пользоваться следующими правилами:
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Важно!!!
Если целая часть делимого меньше делителя, то в частном ставим ( 0) целых. Логично, правда?
Рассмотрим на конкретном примере:
Усвоил? Раздели столбиком следующие числа:
- ( 135,2:5)
- ( 16,4:2)
- ( 158,14:4)
- ( 2,456:2)
- ( 0,626:2)
Сравним наши ответы:
- ( 135,2:5=27,04)
- ( 16,4:2=8,2)
- ( 158,14:4=39,535)
- ( 2,456:2=1,228)
- ( 0,626:2=0,313)
Вспомни теперь свойства десятичных дробей, описанные ранее: если нам необходимо разделить дробь на ( 10), ( 100), ( 1000) и так далее, нет необходимости делать это в столбик – мы можем просто перенести запятую на столько цифр влево, сколько нулей у нас в делителе.
Например: ( 135,2:10=13,52).
А теперь попробуй самостоятельно:
- ( 135,2:100)
- ( 16,4:10)
- ( 158,14:1000)
- ( 2,456:10)
Перенес? Смотри, что у меня получилось:
- ( 135,2:100=1,352)
- ( 16,4:10=1,64)
- ( 158,14:1000=0,15814)
- ( 2,456:10=0,2456)
Молодец! Переходим к делению десятичных дробей друг на друга.
Деление десятичных дробей друг на друга
Итак, для того чтобы это делать существует три правила:
- Считаем количество знаков справа от запятой в десятичной дроби.
- Умножаем и делимое, и делитель на ( 10), ( 100) или ( 1000) и т.д., в зависимости от того, сколько мы насчитали знаков в первом пункте. Умножать необходимо, чтобы превратить десятичную дробь в целое число.
- Делим числа как натуральные.
ВАЖНО!!! При умножении мы смотрим, в каком из чисел, участвующих в делении, присутствует наибольшее количество знаков после запятой? Ориентируясь именно на это число мы умножаем на ( 10), ( 100), ( 1000) и так далее.
Рассмотрим на примере ( 16,4:0,02)
В каком числе у нас стоит наибольшее количество знаков после запятой? Правильно, во втором, то есть в делителе: после нуля стоит два знака. Что из этого следует? Что мы умножаем и делимое и делитель на ( 100)!
Что дальше? Мы получаем следующий пример: ( 1640:2) Посчитай, сколько это будет самостоятельно. У меня получилось ( 820).
Рассмотрим примерчик посложнее: ( 5,31:0,3)
Самое большое количество знаков после запятой содержится в первом числе – их два, соответственно, умножаем оба числа, участвующего в делении на ( 100). Получаем: ( 531:30).
А теперь делим в столбик:
Ты видишь, что нацело разделить не получилось, мы «снесли» еще один ноль, и только тогда пришли к ответу, поэтому сразу после окончания деления нашего делимого, мы ставим запятую.
Теперь ты полностью готов совершать любые действия с десятичными дробями. Молодец! Рассмотрим только, как их сравнивать, хотя я думаю, ты уже и сам с этим справишься!
Как сравнивать десятичные дроби
Мы можем сравнивать десятичные дроби двумя способами.
Способ первый – поразрядно.
Допустим, нам необходимо сравнить ( 5,365 V 5,36)
1. Смотрим, одинаковое ли количество знаков после запятой стоит у каждой дроби? Нет? Значит дописываем справа необходимое количество нулей (ты же помнишь, что от дописывания нулей дробь неизменна, правда?)
Что у нас получилось? Верно: ( 5,365 V 5,360)
2. Начинаем сравнивать слева направо: целую часть с целой, десятые части с десятыми и так далее. Когда одна из частей дроби оказывается больше аналогичной части другой, эта дробь и больше.
Перейдем к нашему примеру: целые части у нас одинаковы – их значение ( 5). Десятые тоже – ( 3). Сотые – ( 6), а вот тысячные у первой дроби ( 5), а у второй ( 0). Что больше: ( 5) или ( 0)? Верно, ( 5), соответственно:
( 5,365 > 5,360)
Способ второй – с помощью умножения.
Внимательно смотрим на дроби. На сколько нам нужно умножить два числа, чтобы сравнивать целые числа? Смотрим на ту дробь, у которой знаков после запятой больше, то есть на первую. У нее после запятой ( 3) знака, соответственно, чтобы сделать из нее целое число, необходимо умножить на ( 1000) Умножаем обе дроби на это значение:
( 5,365cdot 1000 V 5,36cdot 1000)
( 5365 V 5360)
Эти числа ты сравнишь без проблем:
( 5365 > 5360)
Заметь, результат получился одинаковый. Теперь попробуй сравнить дроби самостоятельно любым наиболее удобным для тебя способом:
- ( 21,34 V 20,34)
- ( 0,34 V 0,341)
- ( 120,15 V 1210,16)
- ( 10,565 V 10,465)
Справился? Смотри что вышло:
- ( 21,34 > 20,34)
- ( 0,34 < 0,341)
- ( 120,15 < 1210,16)
- ( 10,565 > 10,465)
Вот теперь ты усвоил дроби полностью!
Подготовка к ЕГЭ на 90+ в мини-группах
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).
Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:
4,56 – четыре целых пятьдесят шесть сотых
18,234 – восемнадцать целых двести тридцать четыре тысячных
78,6 – семьдесят восемь целых шесть десятых
Чтение десятичных дробей
Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять – один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:
- Записать их друг под другом так, чтобы при записи запятая оказалась под запятой и соответствующий разряд под соответствующим.
- Уравнять количество знаков после запятой, добавляя недостающие нулями.
- Выполнить сложение (вычитание) в столбик, не обращая внимания на запятую.
- Поставить запятую под запятыми.
Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.
Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.
34,145 + 5,678 = 39,823
34,145
5,678
39,823
Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.
9,235 – 2,34 = 6,895
9,235
2,340
6,895
Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.
56 + 12,74 = 68,74
56,00
12,74
68,74
Умножение десятичных дробей
При умножении двух десятичных дробей в столбик необходимо:
- Написать числа одно под другим, не обращая внимания на запятую
- Выполнить умножение в столбик
- В ответе отделить столько цифр справа запятой, сколько их в обоих множителях вместе. Если в одном из чисел нет запятой, то считать цифры только в одном числе.
Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.
0,125 × 2,3
0,125
× 2,3
00375
0250
0,2875
Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.
34,2 × 8
34,3
× 8
274,4
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.
Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.
Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.
Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.
Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.
Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.
Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.
Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.
Деление десятичных дробей
- При делении десятичной дроби на целое число выполняют сначала деление целой части, а затем десятичной.
- При делении десятичной дроби на другую десятичную дробь необходимо в делителе убрать запятую, а в делимом передвинуть ее вправо на столько цифр, сколько их в делителе после запятой. Затем выполнить деление на целое число.
- Есть случаи, когда цифр после запятой при переносе запятой у дроби не хватает. Тогда необходимо дополнить число нулями.
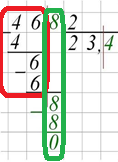
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4
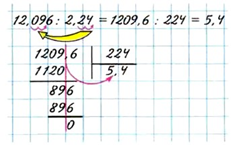
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.
Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.
Деление десятичной дроби на 10, 100, 1000…
При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.
Пример №15. 45,982 : 10 = 4,5982 Перенесли запятую влево на 1 цифру, так как у 10 один нуль.
Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.
Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.
Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.
Пример №18. 6,5746 : 0,1 = 65,746 Перенос запятой на 1 цифру вправо, так как в числе 0,1 одна цифра после запятой.
Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.
Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.
Задание OM0706o
На координатной прямой точки А, В, С и D соответствуют числам -0,201; -0,012; -0,304; 0,021.
Какой точке соответствует число -0,304?
1) А
2) В
3) С
4) D
Сформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.
Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304<–0,201<–0,012.
В итоге имеем возрастающий ряд: –0,304; –0,201; –0,012; 0,021.
Поскольку стрелка положительного направления на координатной прямой направлена вправо, то А<B<C<D. Следовательно, А=–0,304; В=–0,201; С=–0,012; D=0,021. Значит, числу –0,304 соответствует точка А.
Ответ: A
pазбирался: Даниил Романович | обсудить разбор
Задание OM0606o
Найдите значение выражения:
–0,3·(–10)4+4·(–10)2–59
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
–0,3·(–10)4+4·(–10)2–59 =
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
= –0,3·10000+4·100–59 =
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
= –3000+400–59 =
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
= –2600–59 =
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
= –(2600+59) = –2659
Ответ: -2659
pазбирался: Даниил Романович | обсудить разбор
Задание OM0605o
Найдите значение выражения:
–13•(–9,3)–7,8
Это задание требует простого умения выполнять арифметические действия с десятичными дробями.
–13·(–9,3)–7,8 =
Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:
= 120,9–7,8 =
Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:
= 113,1
Ответ: 113,1
pазбирался: Даниил Романович | обсудить разбор
Задание OM0601o
Найдите значение выражения:
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
4,5 • 2,5
Можно произвести вычисления в столбик, тогда получим:
4,5 • 2,5 = 11,25
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции – деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
Ответ: 0,8
pазбирался: Даниил Романович | обсудить разбор
Алла Василевская | Просмотров: 10.2k
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Действия над десятичными дробями
Содержание:
- Умножение и деление десятичной дроби на 10, 100, 1000 и т.д.
- Сложение и вычитание десятичных дробей
- Умножение десятичных дробей
- Деление десятичных дробей
Умножение и деление десятичной дроби на 10, 100, 1000 и т.д.
Чтобы умножить десятичную дробь на 10, 10, 1000 и т.д. надо
перенести десятичную запятую на столько знаков вправо, сколько нулей содержит число 10, 100, 1000 и т.д.
Замечание
Если десятичных знаков дроби меньше, чем количество нулей у единицы, то на пустые места записывают нули.
Пример
Задание. Выполнить умножение: 1)
$2,34 cdot 10$ ; 2)
$2,34 cdot 100$ ; 3)
$2,34 cdot 1000$
Решение. 1) Так заданная дробь умножается на 10 (один нуль), то
десятичную запятую переносим на один знак вправо:
$$2,34 cdot 10=23,4$$
2) Число умножается на 100, поэтому десятичную запятую переносим на
два знака вправо:
$$2,34 cdot 100=234$$
3) В данном случае запятую у десятичной дроби надо перенести на три знака вправо, и так как
дробь содержит только два десятичных знака, то справа дописываем один нуль:
$$2,34 cdot 1000=2340$$
Чтобы поделить десятичную дробь на 10, 100, 1000 и т.д., надо перенести десятичную запятую на один, два,
три и т.д. знака влево соответственно.
Замечание
Если для перенесения запятой в дроби не хватает знаков, их число дополняют соответствующим количеством нулей слева.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Выполнить действия: 1)
$23,4 : 10$ ; 2)
$23,4 : 100$ ; 3)
$23,4 : 1000$
Решение. 1) Переносим запятую на один знак влево, так как делим на 10 и это
число содержит один нуль. Будем иметь:
$$23,4 : 10=2,34$$
2) В этом случае при делении на 100 переносим запятую на
два знака влево:
$$23,4 : 100=0,234$$
3) Запятая переносится на три знака влево, недостающий один знаки дополняем одним нулем. Получаем:
$$23,4 : 1000=0,0234$$
Сложение и вычитание десятичных дробей
При сложении (вычитании) десятичных дробей поступают следующим образом:
-
При необходимости уравнивают количество знаков после запятой, добавляя справа нули к соответствующей дроби,
что, согласно основному свойству десятичных дробей, не влияет на величину дроби.Например. Если надо, например, сложить дроби $0,123$ и
$4,56$ , то справа ко второй дроби надо дописать
один нуль, чтобы десятичных знаков стало три: $4,560$ -
Записывают дроби так, чтобы их запятые находились друг под другом (или, что то же самое, разряд под разрядом).
Например. Правильная запись:
Неправильная запись:
или
- Сложить/вычесть, не обращая внимания на запятую, как целые числа. Складываем по
одной цифре, начиная с самого крайнего правого разряда и двигаясь влево к следующему - Поставить запятую в сумме/разности под запятыми, складываемых/вычитаемых дробей.
Пример
Задание. Найти сумму дробей
$32,45$ и $4,274$
Решение. Распишем решение пошагово. Итак, нам надо найти сумму
$$32,45+4,274$$
Действия будем производить в столбик, то есть запишем сумму следующим образом (помним,
что для десятичных дробей при выполнении сложения/вычитания десятичные запятые дробей должны находиться на одной вертикальной линии):
Вначале к первой дроби справа дописываем нуль, чтобы уравнять количество десятичных знаков:
Складываем по одной цифре (знаку, разряду) справа налево. Результат сложения записываем под соответствующими
слагаемыми под чертой. На первом этапе складываем 0 и 4: 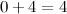
Теперь складываем 5 и 7: 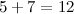
число большее 10, а поэтому под чертой записываем только последнюю цифру полученного числа, то есть 2, а над соседним левым
разрядом — 4 — ставим оставшиеся цифры, то есть 1. (Обычно при решении говорят так: «два пишем, один в уме»):
Единица над 4 означает, что после того как будет выполнено сложение следующего разряда:
которую мы «держим в уме».
Итак, складываем далее, к 4 прибавляем 2: 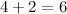
прибавляем «красную» единицу: 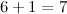
Под десятичными запятыми слагаемых, ставим запятую суммы:
И продолжаем сложение далее по выше описанному алгоритму: 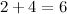
И, снеся 3 (под ней во втором слагаемом нет соответствующей цифры), окончательно будем иметь:
Таким образом, $32,45+4,274=36,724$
Ответ. $32,45+4,274=36,724$
Пример
Задание. Вычислить $4,312-0,91$
Решение. Выполним вычитание в столбик, для этого запишем заданные десятичные дроби одна
под другой так, чтобы их десятичные запятые находились на одной вертикали:
Для того, чтобы десятичных знаков было равное число, допишем ко второй дроби справа нуль:
Вычитание столбиком начинаем с самой правой цифры: 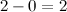
Далее от 1 отнимаем 1:
Теперь нам нужно вычесть из тройки девять. Это сделать нельзя, так как #3 < 9# . Поэтому «займем десяток» в соседнем слева от 3 разряде — у 4. Это действие отметим стрелкой сверху. Занятый десяток прибавим к 3: $3+10=13$ . Соответственно 4 уменьшилась на 1:
$4-1=3$ . Итак, далее из 13 вычтем 9: $3-9=4$ :
Далее ставим запятую:
Далее от 3 (то, что осталось от 4, после того, как мы забрали нее одну единицу) отнимем 0:
Итак, в итоге получаем, что $4,312-0,91=3,402$
Ответ. $4,312-0,91=3,402$
Умножение десятичных дробей
Чтобы умножить одно десятичное число на другое, необходимо перемножить их как
целые числа, не обращая внимания на
запятые, а затем в полученном произведении отделить справа столько десятичных знаков, сколько их было вместе в обоих сомножителях.
Пример
Задание. Вычислить $2,34 cdot 4,12$
Решение. Умножаем заданные числа, не обращая внимания на запятые:
$234 cdot 412 = 96408$
Так как первый множитель содержит два десятичных знака и второй также, то у результата отделяем $2+2=4$ знака справа:
$2,34 cdot 4,12 = 9,6408$
Ответ. $2,34 cdot 4,12 = 9,6408$
Деление десятичных дробей
Для деления десятичной дроби на натуральное число придерживаются следующего алгоритма:
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую.
- Ставим в полученном частном запятую, когда заканчивается деление целой части делимого. Если целая часть
делимого меньше делителя, то в частном ставим 0 целых.
Пример
Задание. Выполнить деление $1,176:21$
Решение. Так как целая часть десятичной дроби, которая равна 1, меньше, чем делитель, который равен 21,
то в частном в целой части ставим 0. Далее делим как целые числа:
Таким образом, $1,176:21 = 0,056$
Ответ. $1,176:21 = 0,056$
Для того, чтобы поделить число на десятичную дробь, необходимо делитель превратить в целое число, умножив его на
10, 100, 1000 и т.д. раз соответственно. Чтобы величина дроби не изменилась, на это же число (10, 100, 1000 и т.д.)
надо умножить и делимое, после чего деление сведется к делению на целое число, алгоритм которого описан выше.
Пример
Задание. Поделить дробь $1,23$ на дробь $0,3$
Решение. Так как делитель $0,3$ не является целым числом, то его надо таковым сделать. Так как у данного числа один знак после запятой, тогда для перемещения
десятичной запятой вправо на один знак его (число) надо умножить на 10:
$0,3 cdot 10=3$ . Чтобы результат не изменился, надо и делимое
$0,3$ умножить на 10: $1,23 cdot 10=12,3$
Таким образом, пришли к равносильному делению $12,3:3$ . Деление произведем в столбик:
Ответ. $1,23:0,3 = 4,1$
Читать следующую тему: периодические десятичные дроби.
Не получается написать работу самому?
Доверь это кандидату наук!
Действия с десятичными дробями
Изначально существовали только обыкновенные дроби, но со временем появилась более удобная запись дробей со знаменателями 10, 100, 1000 и т.д.
Такая запись состояла из целой части и числителя, разделенные между собой запятой; при этом количество знаков после нее должно было быть равно количеству нулей в знаменателе.
Но любую другую дробь тоже можно перевести в десятичную. Для этого надо в столбик разделить числитель на знаменатель. Тут возможны два варианта развития событий: дробь может быть конечной или бесконечной.
Чтобы смешанное число перевести в десятичную дробь не надо переводить его в неправильную. Достаточно лишь разделить числитель на знаменатель, т.к. целая часть остается без изменений.
Бесконечная десятичная дробь бывает периодической и непериодической.
Обыкновенную дробь можно представить только в бесконечной периодической, если она не конечная, конечно же)
Период у дроби необязательно начинается сразу после запятой.
Может быть и такое: 2,721541541541… = 2,72(154).
Сложение и вычитание десятичных дробей.
Чтобы в столбик сложить/вычесть десятичные дроби надо записать их так, чтобы запятая была под запятой, уровнять количество знаков после запятых, сложить/вычесть их, не обращая внимания на запятую, а затем поставить запятую под запятыми (вот это я лихо написала!).
На примерах будет совсем всё понятно)
1) Сложим сначала целое число с десятичной дробью. Целое число тоже представимо в виде десятичной дроби — достаточно поставить после него запятую и дописать столько нулей, сколько необходимо для сложения и вычитания.
4 + 3,25 = ?
А теперь тот же пример, только с минусом:
2) Сложим/вычтем две десятичные, у которых количество знаков после запятой одинаковое.
3) А теперь примеры с разным количеством знаков после запятой в дробях. Возьмем дроби 6,2 и 3,064.
Умножение десятичных дробей.
Чтобы в столбик умножить десятичные дроби надо записать их как при умножении натуральных чисел, не обращая внимания на запятые; умножить; в ответе с конца отсчитать столько знаков после запятой, сколько их стоит после запятой в обеих дробях.
При умножении десятичной дроби на число действует это же правило.
Чтобы каждый раз не умножать десятичную дробь на 10, 100, 1000 и т.д. достаточно запомнить, что при умножении на эти числа запятая у дроби перемещается вправо на столько знаков, сколько нулей стоит в числе.
Деление десятичных дробей.
Сначала разберем деление десятичной дроби на натуральное число. Деление в столбик происходит как обычно: делим не обращая внимания на запятую, НО, как только мы снесли вниз первую цифру из дробной части, надо в частное поставить запятую.
Например, при делении 4,92 на 4 запятая ставится в частное при снесении цифры 9. Другими словами, как только мы заканчиваем делить целую часть, сразу ставим запятую.
Теперь рассмотрим деление на десятичную дробь.
На десятичную дробь делить просто так нельзя — нужно сначала перенести запятые в обоих числах на столько цифр, сколько их после запятой в делителе. Делитель — это второе число)
Вообще, этот перенос запятых осуществляется умножением обоих чисел на 10, 100, 1000 и т.д.
Попробуем разделить две дроби на примере: 14,1289 : 6,143.
В делителе три знака после запятой. Значит, оба числа надо умножить на 1000 или просто перенести запятые на три знака вправо.
14,1289 : 6,143 = 14128,9 : 6143 = …
При делении опять, как только снесли первую цифру из дробной части, сразу поставили запятую в частное.
14,1289 : 6,143 = 2,3.
Чтобы каждый раз не делить десятичную дробь на числа 10, 100, 1000 и т.д. достаточно запомнить, что при делении на эти числа запятая у дроби перемещается влево на столько знаков, сколько нулей стоит в числе.
Округление.
Очень часто в экзаменационных задачах мы видим «округлите до десятых» или «округлите до целого»… Что это вообще значит?
Округление — это замена какого-то числа ближайшим к нему числом, причем, если число округляют до какого-нибудь разряда, то все следующие за ним цифры до запятой становятся нулями, а цифры после запятой отбрасываются.
Если первая замененная нулем или отброшенная цифра была равна 0, 1, 2, 3 или 4, то стоящую перед ней цифру оставляют без изменений. В остальных случаях (5, 6, 7, 8, 9) ее увеличивают на 1.
Возьмем число 9814,3516 и округли его до тысячных, сотых, десятых, единиц, десятков, сотен, единиц тысяч (разряд округления буду подчеркивать).
1) До тысячных: 9814,3516 ≈ 9814,352 (после единицы стоит цифра 6, значит надо прибавить единицу к разряду тысячных, а шестерка обращается в 0 и отбрасывается).
2) До сотых: 9814,3516 ≈ 9814,35 (после пятерки стоит 1, значит разряд сотых остается без изменений; все остальное отбрасыватся).
3) До десятых: 9814,3516 ≈ 9814,4 (после тройки стоит 5, значит к разряду десятых прибавляем 1; остальное отбрасываем).
4) До единиц: 9814,3516 ≈ 9814 (после четверки стоит 3; разряд не меняем, остальное отбрасываем).
5) До десятков: 9814,3516 ≈ 9810 (после единицы стоит 4 — разряд не меняется; после разряда десятков цифры до запятой обращаются в нули (в данном случае это только одна цифра), после запятой — отбрасываются).
6) До сотен: 9814,3516 ≈ 9814,352 (после 8 стоит 1, разряд не меняется, цифры до запятой обращаются в нули, после запятой — отбрасываются).
7) До единиц тысяч: 9814,3516 ≈ 10000 (после девятки стоит 8, значит к разряду единиц тысяч прибавляется 1, цифры до запятой обращаются в 0, после запятой — отбрасываеются).
Ну что, скил прокачан? Если да, то супер)
Успехов в учебе!
Десятичная дробь – это форма записи обыкновенной дроби, у которой знаменатель равен (10), (100), (1000) и т.д.
Пример:



Запятая в десятичной дроби отделяет:
1) целую часть от дробной;
2) столько знаков, сколько нулей в знаменателе обыкновенной дроби.

Как перевести десятичную дробь в обыкновенную?
Десятичную дробь можно представить как обыкновенную: для этого «прочитайте» десятичную дробь и запишите прочитанное в виде смешанной дроби.
Например, (0,35) читается как «ноль целых, тридцать пять сотых». Так и пишем: (0 frac{35}{100}). Целая часть равна нулю, то есть ее можно просто не писать, а дробную часть – сократить на (5).
Получим: (0,35=0frac{35}{100}=frac{35}{100}=frac{7}{20}).
Еще примеры: (2,14=2frac{14}{100}=frac{214}{100}=frac{107}{50});
(7,026=7frac{26}{1000}=frac{7026}{1000}).
Этот переход можно делать и быстрее:
Запишите в числитель все число без запятой, а в знаменатель – единицу и столько нулей, столько цифр было отделено запятой.
Звучит сложно, поэтому смотрите картинку:

Как обыкновенную дробь перевести в десятичную?
Для этого надо домножить числитель и знаменатель дроби на такое число, чтобы в знаменателе получилось (10), (100), (1000) и т.д., а потом записать результат в десятичном виде.
Примеры: (frac{3}{5})(=)(frac{3cdot 2}{5cdot 2})(=)(frac{6}{10})(=0,6); (frac{63}{25})(=frac{63 cdot 4}{25cdot 4})(=)(frac{252}{100})(=2,52); (frac{7}{200})(=)(frac{7 cdot 5}{200cdot 5})(=)(frac{35}{1000})(=0,035).
Этот способ хорошо работает, когда в знаменателе дроби: (2), (5), (20), (25)… и т.д., то есть когда сразу понятно, на что надо домножать. Однако в остальных случаях:
Для превращения обыкновенной дроби в десятичную нужно поделить числитель дроби на ее знаменатель.
Например, дробь (frac{7}{8}) проще преобразовать делением (7) на (8), чем догадываться, что (8) можно домножить на (125) и получить (1000).
Далеко не все обыкновенные дроби без проблем превращаются в десятичные. Точнее, превращаются-то все, но вот записать результат такого превращения бывает весьма трудно. Например, дробь (frac{9}{17}) в десятичном виде будет выглядеть как (0,52941…) — и так далее, бесконечный ряд неповторяющихся цифр. Такие дроби обычно оставляют в виде обыкновенных.
Однако некоторые дроби, дающие бесконечный ряд цифр в десятичном виде записаны быть могут. Так происходит в случае, если цифры в этом ряду повторяются. Например, дробь (frac{2}{3}) в десятичном виде выглядит так (0,66666…) — бесконечный ряд шестерок. Ее записывают вот так: (0,(6)). Содержимое скобки – это как раз и есть бесконечно повторяющаяся часть (так называемый период дроби).
Еще примеры: (frac{100}{27})(=)(3,7037037037…=3,(703)).
(frac{579}{110})(=5,2636363636…=5,2(63)).
Виды десятичных дробей:

Сложение и вычитание десятичных дробей
Сложение (вычитание) десятичных дробей выполняется так же, как сложение (вычитание) натуральных чисел: главное, чтобы запятая во втором числе стояла под запятой в первом.



Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые. Потом сложить количество знаков после запятой в первом числе и во втором, а затем отделить полученное количество знаков в итоговом числе, считая справа налево.
Лучше (1) раз посмотреть на картинку, чем (10) раз прочитать, поэтому наслаждайтесь:

Деление десятичных дробей
Чтобы разделить десятичную дробь на десятичную дробь, надо перенести запятую во втором числе (делителе) до тех пор, пока оно не станет целым. Потом на столько же перенести запятую в первом числе (делимом). Затем нужно разделить получившиеся числа как обычно. При этом в ответе нужно будет не забыть поставить запятую сразу же, как мы «перейдем за запятую» в делимом.
Снова картинка объяснит принцип лучше любого текста.
На практике бывает легче представлять деление как обыкновенную дробь, потом домножением числителя и знаменателя убирать запятые (или просто сразу передвигать запятые, как делали выше), а затем сокращать получившиеся числа.
(13,12:1,6=)(frac{13,12}{1,6})(=)(frac{13,12·100}{1,6·100})(=)(frac{1312}{160})(=)(frac{328}{40})(=)(frac{82}{10})(=8,2).
Пример. Вычислите (0,0625:()(frac{1}{8})(+)(frac{5}{16})()cdot 2,8).
Решение:
|
(0,0625:()(frac{1}{8})(+)(frac{5}{16})()cdot 2,8=) |
Приведем дроби в скобке к общему знаменателю и сложим: (frac{1}{8})(+)(frac{5}{16})(=)(frac{2}{16})(+)(frac{5}{16})(=)(frac{7}{16}). |
|
|
(=0,0625:()(frac{7}{16})()cdot 2,8=) |
Поделим (7) на (16), то есть запишем полученную дробь в десятичном виде. |
|
|
(=0,0625:0,4375cdot 2,8=) |
Представим знак деления как дробную черту и перенесем запятые на (4) знака вправо. |
|
|
(=)(frac{625}{4375})(cdot 2,8=) |
Сократим дробь на (625). |
|
|
(=)(frac{1}{7})(cdot 2,8=) |
Представим десятичную дробь (2,8) как обыкновенную и перемножим две дроби. |
|
|
(=)(frac{1}{7})(cdot)(frac{28}{10})(=)(frac{28}{70})(=)(frac{4}{10})(=0,4). |
Ответ: (0,4).
Пример.Вычислите (frac{0,4 — 0,9}{0,5 + frac{1}{3}}).
Решение:
|
(frac{0,4 — 0,9}{0,5 + frac{1}{3}})(=) |
В числителе сделаем вычитание. В знаменателе переведем (0,5) в обыкновенную дробь. |
|
|
(=) (frac{- 0,5}{frac{1}{2} + frac{1}{3}})(=) |
С трехэтажными дробями работать неудобно, поэтому большую дробную черту представим как деление. |
|
|
(=)(- 0,5:)(({frac{1}{2} + frac{1}{3})})(=) |
Приведем дроби в скобке к общему знаменателю… |
|
|
(=) (- 0,5:)(({frac{3}{6} + frac{2}{6})})(=) |
…и сложим их. |
|
|
(=)(- 0,5:)(frac{5}{6})(=) |
Представим десятичную дробь в обыкновенном виде и заменим знак деления умножением, перевернув вторую дробь. |
|
|
(=-)(frac{1}{2})∙(frac{6}{5})(=-)(frac{6}{10})(=) |
Получим ответ, переведя дробь в десятичную. |
|
|
(=-0,6). |
Ответ: (-0,6).

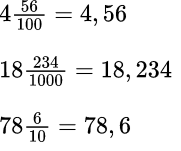
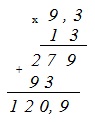
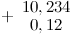
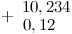 или
или