Полином Жегалкина (англ. Zhegalkin polynomial) — полином с коэффициентами вида и , где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или. Полином был предложен в 1927 году И. И. Жегалкиным в качестве средства для представления функций булевой логики. Полином Жегалкина имеет следующий вид:
Содержание
- 1 Полнота
- 2 Существование и единственность представления (теорема Жегалкина)
- 3 Построение полинома Жегалкина
- 3.1 По таблице истинности
- 3.2 Преобразование дизъюнктивной нормальной формы
- 3.3 Метод треугольника
- 3.4 Преобразование Мёбиуса
- 4 См. также
- 5 Источники информации
Полнота
По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали
- Хотя бы одна функция, не сохраняющая ;
- Хотя бы одна функция, не сохраняющая ;
- Хотя бы одна нелинейная функция;
- Хотя бы одна немонотонная функция;
- Хотя бы одна несамодвойственная функция.
Исходя из этого, система функций является полной:
| Сохраняет 0 | ||||||
|---|---|---|---|---|---|---|
| Сохраняет 1 | ||||||
| Самодвойственная | ||||||
| Монотонная | ||||||
| Линейная |
На основе этой системы и строятся полиномы Жегалкина.
Существование и единственность представления (теорема Жегалкина)
| Теорема (Жегалкина): |
|
Каждая булева функция единственным образом представляется в виде полинома Жегалкина. |
| Доказательство: |
|
Заметим, что различных булевых функций от переменных штук. При этом конъюнкций вида существует ровно , так как из возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит или , то есть существует различных полиномов Жегалкина от переменных. Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него (любой один, если таких несколько). Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом. |
Построение полинома Жегалкина
Существует несколько способов построения полинома Жегалкина.
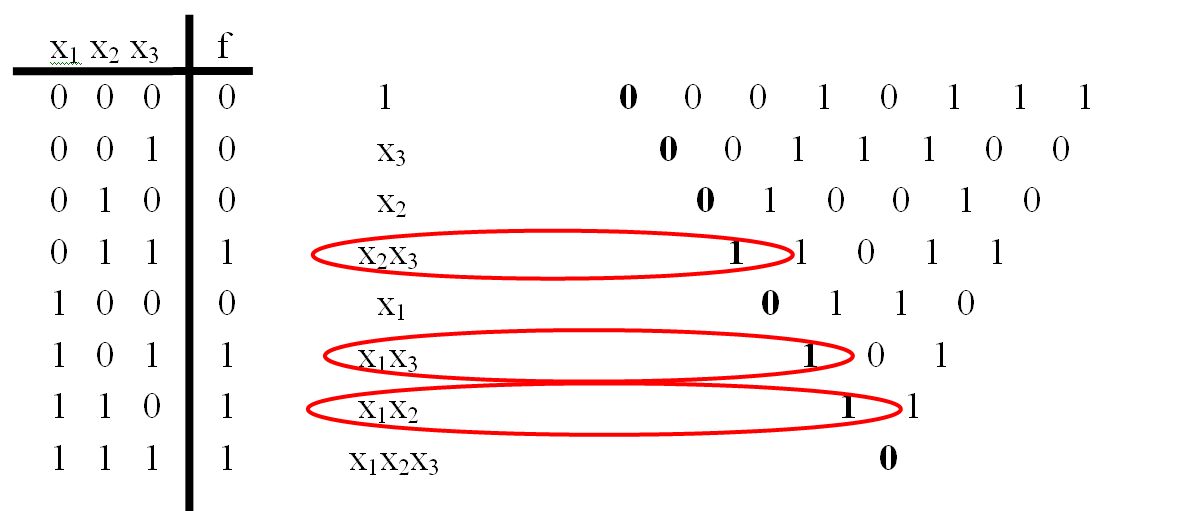
По таблице истинности
Пусть для функции задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что , а . За каждую подстановку находим только один коэффициент.
Пример:
Дана функция и её таблица истинности:
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Построим для неё полином Жегалкина:
Так как , то .
Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы:
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
Таким образом, полином Жегалкина выглядит так:
Преобразование дизъюнктивной нормальной формы
Этот способ основан на том, что . Если функция задана в виде ДНФ, то можно сначала убрать дизъюнкцию, используя правило де Моргана, а все отрицания заменить прибавлением единицы по модулю два, после чего раскрыть скобки по обычным правилам, при этом учитывая, что четное число одинаковых слагаемых равно нулю (так как ), а нечетное число одинаковых слагаемых равно одному такому слагаемому. Либо же можно заменить дизъюнкцию по следующему правилу:
.
Если функция задана в СДНФ, то так как при любых значениях входных переменных в единицу обращается не более одного члена выражения, то достаточно просто заменить все дизъюнкции исключающим ИЛИ.
Пример:
Дана функция в ДНФ , построим полином Жегалкина.
Запишем функцию так:
;
Сгруппируем слагаемые и воспользуемся преобразованием (1):
Воспользуемся свойствами конъюнкции и , а также тем, что , и упростим выражение:
Ещё раз воспользуемся преобразованием (1):
Раскроем скобку по алгебраическим правилам:
Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ:
Заменим отрицание на прибавление :
Раскроем скобки:
Выкинем парные слагаемые и получим окончательную формулу:
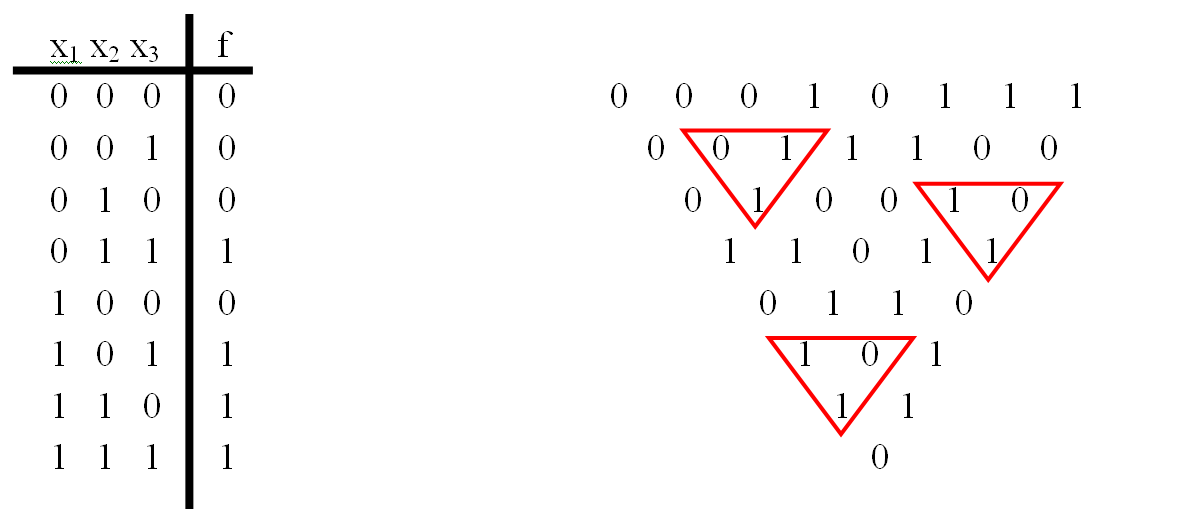
Метод треугольника
Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами:
- Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от до .
- Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности.
- Ячейка в каждом последующем столбце получается путём сложения по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже.
- Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности.
- Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке соответствует член , ячейке — член , ячейке — член , ячейке — член и т.д.
- Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина.
Фактически, этот метод является модификацией метода построения по таблице истинности, описанного выше. По сравнению с ним он удобнее тем, что расчёты занимают мало места и в них сложнее ошибиться, но метод треугольника требует бо́льшего количества операций.
Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных показан на рисунке.
Чтобы получить формулу, по которой рассчитывается какой-либо коэффициент, нужно из клетки, в которой он записан, пройтись всеми возможными путями влево, до столбца таблицы истинности, делая ходы влево и влево-вниз, записать значения в конечных ячейках и сложить их все между собой по модулю 2.
Таким образом, в первом столбце сверху записан коэффициент ,
во втором — ,
в третьем — ,
в четвёртом —
и так далее, то есть при построении вспомогательной таблицы коэффициенты полинома просчитываются автоматически.
Преобразование Мёбиуса
Пусть задана булева функция .
Любая булева функция представима в виде полинома Жегалкина, притом единственным образом.
Пусть , и введем обозначение
Тогда полином Жегалкина можно записать как:
, где .
Множество коэффициентов можно рассматривать как функцию , заданной на множестве индексов , то есть .
Очевидно, функцию можно записать и следующим образом: если если если .
Тут запись если означает, что элелемент присутствует в соответствующем члене полинома только если .
Тогда если для какого-то , ,то в слагаемом будет существовать хотя бы один множитель, равный нулю, и такое слагаемое на сумму не повлияет.
Отсюда ясно, что
Найдем отображение (То есть такое, которое по заданной функции вычисляет значения всех коэффициентов).
обозначает, что «меньше» как последовательность бит
| Теорема: |
|
Пусть задана функция . Тогда функцию можно найти по формуле: . |
| Доказательство: |
|
Докажем при помощи индукции по количеству единиц в векторе ( иначе говоря, по сумме ) и для удобства обозначим это количество единиц(сумму) . 1) База: если , то, очевидно 2) Пускай теорема справедлива для всех сумм . Покажем, что в таком случае она верна и для . По , а далее по предположению индукции видим: . Рассмотрим сумму . Каждый элемент содержится в ней, только если , и для фиксированных и элемент встречается ровно столько раз, сколько существует , таких, что . Несложно увидеть, что таких существует ровно , то есть нечетное количество раз. Тогда . То есть при формула также выполняется, значит при любых выполняется . |
Отображение также называется преобразованием Мёбиуса.
Видно, что и — это одно и тоже преобразование. Значит, если применить преобразование Мёбиуса к функции, а затем вновь применить то же преобразование к получившейся функции, тогда вновь получим исходную функцию . То есть преобразование Мёбиуса обратно самому себе, иными словами, является инволюцией.
См. также
- Булевы функции
- Полные системы функций, теорема Поста
- ДНФ
- КНФ
Источники информации
- Cтатистика | Математика НГУ
- Википедия — Полином Жегалкина
- Е.Л Рабкин, Ю.Б. Фарфоровская, дискретная математика
- Логачёв О.А, Сальников А.А., Ященко В.В. Булевы фунции в теории кодирования и криптологии — МЦНМО, 2004. — 470с. — ISBN 5-94057-117-4.
поэтому ее сокращенная ДНФ содержит всего 2 простые конъюнкции,
а она имеет вид f = x1 x3 x 2.
Следующий пример показывает использование карт Карно при п = 4:
|
x3, x4 /x1, x2 |
0 0 |
0 1 |
1 1 |
1 0 |
|
0 0 |
1 |
0 |
1 |
1 |
|
0 1 |
0 |
0 |
0 |
0 |
|
1 1 |
0 |
0 |
0 |
1 |
|
1 0 |
1 |
1 |
1 |
1 |
|
Здесь сокращенная ДНФ содержит 4 слагаемых (СДНФ содержит |
||||
|
имеет вид f = x2 x4 x3 x4 |
x1 x4 x1 x2 x3 . |
При п = 5 использование карт Карно является несколько более сложным и здесь не приводится.
Обоснование приведенного алгоритма сокращения. Пусть для опреде-
ленности в карте Карно стоят рядом 2 единицы в первой строке и в первом и во втором столбцах. По алгоритму записи ДНФ функции по ее таблице истинности этим единицам в ДНФ соответствуют 2 дизъюнктных слагае-
мых: x1t1 x2t2 x3t3 x4t4 x1t1 x2t2 x3s3 x4s4 . По определению карты Карно (1-е условие)
впарах (t3, t4) и (s3, s4) либо t3 = t4, либо s3 = s4; для определенности, пусть
впервой паре – равенство, а во второй – неравенство. Тогда, вынося общие множители за скобки, получим:
x1t1 x2t2 x3t3 x4t4 x1t1 x2t2 x3s3 x4s4 x1t1 x2t2 x3t3 x4t4 x4s4 x1t1 x2t2 x3t3 1 0 x1t1 x2t2 x3t3 .
Такие же рассуждения применимы и к любому другому прямоугольнику из единиц в карте Карно.
Полиномом (многочленом) Жегалкина от п переменных называется функция, в которой для получения ее значений (из набора значений аргументов) используется фиксированная цепочка операций 3 видов: конъюнкций, сложений по модулю 2 и констант (т. е. нулей и единиц).
Ясно, что любой полином Жегалкина можно (после преобразований) записать в виде
|
P 0 1x1 2 x2 |
n xn n 1x1x2 |
n C2 xn 1xn |
2n 1x1x2 xn. (2.6) |
|
n |
Всего здесь 2п слагаемых. Напомним, что + сейчас означает сложение по модулю 2, коэффициенты 0 , 1, , 2n 1 являются константами (рав-
ными нулю или единице).
35

Например, полином Жегалкина от 3 переменных всегда можно привести к виду
P(x, y, z) 0 1x 2 y 3z 4xy 5xz 6 yz 7 xyz. (2.7)
Замечание. При помощи сложения по модулю 2 легко записать отрицание любой логической функции: K K 1 , в частности, х + 1 = x
Теорема. Любая логическая функция может быть представлена полиномом Жегалкина.
Доказательство. Любую функцию можно записать в виде ДНФ. Запишем двойное отрицание этой ДНФ (что не меняет функции). При помощи нижнего отрицания и правила Де Моргана избавимся от дизъюнкций. В оставшейся записи данной функции будут присутствовать только конъюнкции и отрицания. Каждое отрицание заменим на прибавление единицы. В получившейся записи функции на переменные будут действовать только конъюнкции, сложения по модулю 2 и присутствовать константы. Это и значит, что функция записана в виде полинома Жегалкина, и теорема доказана.
Замечания: 1) в доказательстве приведен алгоритм перехода от записи функции в виде ДНФ к ее записи в виде полинома Жегалкина.
Пример:
f(x, y, z) = xy x y y z xy x y y z = (xy + 1)((x + 1)(y + 1) + 1)((y + 1) z + 1) + 1 =
=(xy + 1)(xy + x+ y)(yz + z + 1) + 1 = (x+ y)(yz + z + 1) + 1 =
=xyz + yz + xz + yz + x + y + 1 = xyz + xz + x + y + 1;
2)напоминаем, что при сложении (по модулю 2) 1 + 1 = 0. Поэтому сумма четного числа одинаковых слагаемых всегда равна 0. Например, xyz + xyz + xyz = xyz;
3)надо уметь переходить к полиному Жегалкина не только от ДНФ (по алгоритму, приведенному в доказательстве теоремы), но и от таблицы истинности данной функции. Для такого перехода надо знать 2 алгоритма: метод неопределенных коэффициентов и «метод бабочки».
Метод неопределенных коэффициентов. Запишем сначала нашу функ-
цию в виде полинома Жегалкина с неопределенными коэффициентами, т. е. перепишем формулу (2.6), в частности, для функции 3 переменных – формулу (2.7). Затем в написанную формулу по очереди подставляем всевозможные наборы значений переменных и приравниваем полученные выражения соответствующим значениям функции из ее таблицы истинности.
Из полученных равенств, в которых неизвестными являются коэффициенты полинома Жегалкина, находим эти коэффициенты. Легко видеть, что за каждую подстановку мы находим ровно один коэффициент. Так как
число наборов равно числу коэффициентов (и равно 2п), то мы сможем найти все коэффициенты и, подставляя их в исходную формулу (2.6) (в частности, в формулу (2.7)), получим полином Жегалкина данной функции.
36
Метод бабочки. Пусть дана функция z = f (x1, x2,…, xп) от п переменных. В ее таблице истинности записаны 2п ее значений. Алгоритм метода бабочки заключается в последовательном проведении п операций, обычно называемых итерациями. 1-я итерация: рядом со столбцом значений данной функции записывается новый столбец; в верхнюю его половину (т. е. от 1-й строчки до строчки с номером 2п–1) переписываются числа из столбца значений функции, т. е числа f (0, x2,…, xп), а в нижнюю его половину (т. е. в строчках с номерами от 2п–1 + 1 до 2п) записываются суммы по модулю 2 соответствующих значений данной функции из верхней и нижней
половины таблицы, т. е. числа f (0, x2,…, xп) + f (1, x2,…, xп). Во 2-й итерации ту же процедуру проделывают отдельно с верхней и отдельно с ниж-
ней частью столбца, полученного в результате проведения 1-й итерации. В результате проведения второй итерации появляется новый столбец, у которого в верхней четверти записаны числа f (0, 0, x3,…, xп), во второй четверти – числа f (0, 0, x3,…, xп) + f (0, 1, x3,…, xп), в третьей четверти – числа f(0, 0, x3,…, xп) + f (1, 0, x3,…, xп), а в нижней четверти – числа
f(0, 0, x3,…, xп) + f (1, 0, x3,…, xп) + f (0, 1, x3,…, xп) + f (1, 1, x,…, xп).
Эта процедура повторяется п раз. При проведении последней, п-й, итерации в последнем, п-м, столбце в строках с номерами 1, 3, 5, …, 2п – 1 переписываются значения из предыдущего, п – 1—го столбца, а в строках с номерами 2, 4, 6,…, 2п записывается сумма (по модулю 2) того, что было записано в этой строке в п – 1—м столбце со значением, записанном в этом же п – 1—м столбце в предыдущей строке. По полученному п-му столбцу составляется полином Жегалкина данной функции: каждой единице этого столбца сопоставляется конъюнкция тех переменных, значения которых в строке с рассматриваемой единицей тоже равны единице, а затем эти конъюнкции переменных складываются по модулю 2. Последнее выражение и есть полином Жегалкина данной функции.
Например, f(x)= {01101001}.
|
x y z |
f(x, y, z) |
i1 |
i2 |
i3 |
|
0 0 0 |
0 |
0 |
0 |
0 |
|
0 0 1 |
1 |
1 |
1 |
1 |
|
0 1 0 |
1 |
1 |
1 |
1 |
|
0 1 1 |
0 |
0 |
1 |
0 |
|
1 0 0 |
1 |
1 |
1 |
1 |
|
1 0 1 |
0 |
1 |
1 |
0 |
|
1 1 0 |
0 |
1 |
0 |
0 |
|
1 1 1 |
1 |
1 |
0 |
0 |
37
В последнем столбце – 3 единицы, которым соответствуют наборы значений аргументов (0, 0, 1), (0, 1, 0) и (1, 0, 1) соответственно. Значит, в полиноме Жегалкина этой функции складываются три простых конъюнкции, каждая из которых содержит всего по одной переменной – x, y и z соответственно, и поэтому искомый полином имеет вид: f(x, y, z) = x+ y+ z.
Обоснование метода бабочки. Докажем по индукции, что указанный метод действительно приводит к полиному Жегалкина.
База индукции. Для всех 4 функций одной переменной (т. е. для 0, 1, х, x ) это утверждение проверяется непосредственно при помощи одной итерации над их таблицами истинности. Индукционный переход. Пусть это утверждение уже доказано для всех логических функций от п переменных (х1, х2, …, хп). Докажем, что тогда оно верно и для функции f от п+1 переменной, т. е. для z = f(х1, х2, …, хп, хп +1). Считаем, что таблица истинности этой функции записана стандартным образом, т. е. по возрастанию двоичных чисел, соответствующих наборам значений аргументов. Тогда в п-м столбце, полученном в результате п-й итерации, в строках с номерами 1, 3, 5, …, 2п –1 стоят числа, соответствующие значению 0 последнего аргумента: хп+1 = 0. Иными словами, в них стоят значения, соответствующие z = f(х1, х2, …, хп, 0), т. е. функции от п переменных. По индукционному предположению, по их значениям можно записать полином Жегалкина для этой функции, поэтому мы записываем этот полином (у которого простые конъюнкции не содержат переменной хп+1), а значения из этих строк переписываем без изменений в последний, (п + 1)-й столбец (т. е. для (п + 1)-й итерации). В том же п-м столбце в строках с номерами 2, 4, 6, …, 2п стоят числа, соответствующие тем же наборам значений аргументов, что и
встроках с номерами 1, 3, 5, …, 2п–1 (так как наборы значений аргументов
встроках с номерами 2k–1 и 2k отличаются только значениями последнего
аргумента: хп+1 = 0 и хп+1 = 1 соответственно). Поэтому, если мы уже получили для полинома Жегалкина простую конъюнкцию xk1 xk2 …xkm (km < n + 1),
рассматривая строку с нечетным номером для f(х1, х2, …, хп, 0) = 1, то в строке со следующим номером в последнем, (п + 1)-м, столбце должен стоять 0, так как иначе в полиноме Жегалкина нужно будет записать сумму (по модулю 2) 2 простых конъюнкций xk1 xk2 …xkm + xk1 xk2 …xkm xn 1, которая
при хп+1 = 1 и при любом наборе значений остальных переменных равна 0 (даже для тех наборов значений переменных, у которых соответствующая простая конъюнкция входит в полином Жегалкина с коэффициентом 1). Иными словами, если в столбце, соответствующем предпоследней итерации, стоят подряд две единицы, то в столбце последней итерации должны стоять 1 и 0. Это достигается сложением двух единиц предпоследнего столбца, что и требуется для доказательства индукционного перехода (так как 1 + 0 = 0 + 1 = 1, а 0 + 0 = 0, то рассуждения в остальных вариантах расположения значений в предпоследнем столбце очевидны).
38
Что нам стоит полином Жегалкина построить…
Время на прочтение
2 мин
Количество просмотров 130K
Думаю, каждый, кто изучал или изучает в университете дискретную математику, знаком с понятием многочлена Жегалкина.
Главная особенность этих многочленов состоит в том, что любую булеву функцию можно представить полиномом Жегалкина, причем единственным образом.
Чаще всего для построения полиномов Жегалкина студентам предлагаются два метода построения таких полиномов: метод неопределенных коэффициентов и метод эквивалентных преобразований.
Расчеты с использованием данных методов часто оказываются громоздкими. По невнимательности допустить ошибку не составляет труда.
Под катом приведен один удобный алгоритм, для построения полиномов Жегалкина, который студенты воспринимают «на ура», т.к. требует только выполнение «механических действий» без применения каких-либо умственных усилий. Краткое описание метода можно найти в Википедии, но на мой взгляд по нему не совсем понятно, как быстро проводить вычисления. Мне метод известен под названием «метод треугольника Паскаля».
Порядок проведения вычислений проще показать на примере. Далее я буду по шагам показывать, как должен выглядеть расчет на бумаге (или как его удобно проводить).
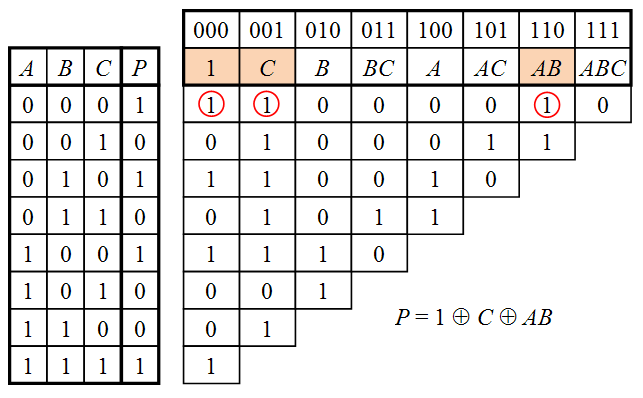
Метод треугольника Паскаля
Требуется построить полином Жегалкина для функции f. Для примера, в качестве функции f возьмем функцию голосования .
Шаг 1. Строим таблицу значений функции (строки в таблице идут в порядке возрастания двоичных кодов). Таблицу лучше разместить в левой части листа.
Шаг 2. Построение треугольника.
Для этого берем вектор значения функции и выписываем его напротив первой строки таблицы:
Далее заполняем треугольник, складывая попарно соседние значения по модулю 2, результат сложения выписываем ниже.
Продолжаем вычисления, пока в строке не останется лишь одна цифра.
Шаг 3. Построение полинома Жегалкина.
Нас интересует левая сторона треугольника (значения выделены жирным):
Числа на левой стороне (выделены жирным шрифтом) треугольника есть коэффициенты полинома при монотонных конъюнкциях, соответствующих наборам значений переменных.
Теперь выпишем для наглядности эти конъюнкции. Конъюнкции выписываем по двоичным наборам в левой части таблицы по следующему принципу: если напротив переменной xi стоит 1, то переменная входит в конъюнкцию; в противном случае переменная отсутствует в конъюнкции. Набору (0,0,0) соответствует константа 1.
Если принцип получения конъюнкций понятен, то столбец с ними можно (даже лучше) не выписывать, а сразу переходить к построению полинома.
Для построения полинома нужны только конъюнкции из строк с единицами на левой стороне треугольника.
Это и есть конъюнкции, входящие в состав полинома Жегалкина. Осталось лишь выписать сам полином:
Если переменных в функции не 3, а 4 или больше, то метод работает без изменений, только увеличатся размеры таблиц. Тем не менее, в отличие от метода неопределенных коэффициентов, расчеты можно без особых усилий выполнить на листе бумаги.
Литература
К сожалению, мне не удалось найти и посмотреть источник, указанный в Википедии:
В.П. Супрун Табличный метод полиномиального разложения булевых функций // Кибернетика. — 1987. — № 1. — С. 116-117.
ДНФ, КНФ, СДНФ, СКНФ, полином Жегалкина
На этой странице вы найдете готовые примеры задач, связанных с упрощением и преобразованием булевых функций к нормальным формам (ДНФ, КНФ), совершенным нормальным формам (СДНФ, СКНФ) и к каноническому многочлену Жегалкина.
Самый простой метод построения совершенной дизъюнктивной и конъюнктивной нормальных форм — с помощью таблиц истинности. Для перехода к ДНФ и КНФ используют методы эквивалентных преобразований, правила де Моргана, свойства поглощения, правило Блейка и т.п.
Полином Жегалкина может быть построен как с помощью последовательных преобразований, так и по таблице истинности (метод неопределенных коэффициентов).
Все эти примеры разобраны ниже. Типовые задачи снабжены подробным решением, формулами, пояснениями. Используйте их, чтобы научиться решать подобные задачи или закажите решение своей работы нам.
Другие примеры решений о булевых функциях:
- Булевы формулы
- Таблицы истинности
- Минимизация ДНФ булевых функций
- Полнота системы функций
Задачи и решения о представлении булевых функций
Нормальные формы (КНФ, СКНФ, ДНФ и СДНФ): примеры решений
Задача 1. Привести к КНФ и СКНФ.
$$((((Ato B)to bar A) to bar B) to bar C).$$
Задача 2. С помощью эквивалентных преобразований построить д.н.ф. функции:
$$f(x)=(overlinex_2 oplus x_3) cdot (x_1 x_3 to x_2) $$
Задача 3. Используя СКНФ, найдите наиболее простую формулу алгебры высказываний от четырех переменных, принимающую значение 0 на следующих наборах значений переменных, и только на них:
Задача 4. Привести данные выражения к ДНФ, пользуясь правилами де Моргана. Если возможно, сократить ДНФ, используя свойство поглощения и правило Блейка.
Многочлен Жегалкина: примеры решений
Задача 5. Представив функцию формулой над множеством связок $$, преобразовать затем полученную формулу в полином Жегалкина функции $f(x)$ (используя эквивалентности):
$$f(x) = (x_1 vee x_2) cdot (x_2 | x_3)$$
Задача 6. Задана булева функция: $$ f(x_1, x_2, x_3) = overline vee ((x_1 wedge overline ) | overline)>$$ А) Построить таблицу истинности, найти двоичную форму булевой функции и привести ее к СДНФ и СКНФ.
Б) Найти многочлен Жегалкина.
Задача 7. Для заданной логической функции перейти к полиному Жегалкина.
Решение задач на заказ
Выполняем для студентов очников и заочников решение заданий, контрольных и практических работ по любым разделам булевой алгебры, в том числе задачи по построению СДНФ, СКНФ, полинома Жегалкина на заказ. Также оказываем помощь в сдаче тестов. Подробное оформление, таблицы, графики, пояснение, использование специальных программ при необходимости. Стоимость примера от 100 рублей , оформление производится в Word, срок от 2 дней.
Как построить полином жегалкина по таблице истинности
Полином Жегалкина — полином с коэффициентами вида 0 и 1, в котором конъюнкция используется как произведение, сумма по модулю 2 используется как сложение. Полином был предложен в 1927 году Иваном Жегалкиным в качестве удобного средства для представления функций булевой логики. В зарубежной литературе представление в виде полинома Жегалкина обычно называется алгебраической нормальной формой (АНФ).
Полином Жегалкина имеет вид:
где C0, C1, …, C1…n – коэффициенты при переменных 1, x1, x2,…xn, x1x2,…, x1…xn соответственно.
Теорема. Любая функция п переменных может быть представлена полиномом Жегалкина и это представление единственно.
Доказательство. Любая функция f(x1, x2, …, xn) имеет свою таблицу истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределенными коэффициентами. Затем по очереди подставляем всевозможные наборы переменных и находим коэффициенты. Легко видеть, что за каждую подстановку находим только один коэффициент. Так как число наборов равно числу коэффициентов (и равно 2п), отсюда следует утверждение теоремы.
Доказательство этой теоремы показывает, как по таблице истинности построить полином Жегалкина.
Для булевых функций двух переменных полином Жегалкина имеет вид:
Определим булевы функции двух переменных через операции алгебры Жегалкина (т. е. через конъюнкцию и сумму по модулю 2).
Предварительно дадим решение простейших уравнений, вытекающих из определения суммы по модулю 2:
Если a ⊕ 1 = 1, то a = 0
Если a ⊕ 0 = 1, то a = 1
Если a ⊕ 1 = 0, то a = 1
Если a ⊕ 0 = 0, то a = 0.
Функция f0(x1,x2)= есть тождественный ноль.
Функция f1(x1,x2)= есть конъюнкция.
Для функции f2(x1,x2)= определим значения коэффициентов полинома Жегалкина:
f2(0,0) = C0=0
f2(0,1) = C0⊕ C2=0
f2(1,0) = C0⊕ C1=1
f2(1,1) = C0⊕ C1⊕ C2⊕ C12=0
Метод треугольника
Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами:
- Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от 000. 00 до 111. 11.
- Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности.
- Ячейка в каждом последующем столбце получается путём сложения по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже.
- Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности.
- Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке 111 соответствует член ABC, ячейке 101 — член AC, ячейке 010 — член B, ячейке 000 — член 1 и т.д.
- Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина.
Фактически, этот метод является модификацией метода построения по таблице истинности, описанного выше. По сравнению с ним он удобнее тем, что расчёты занимают мало места и в них сложнее ошибиться, но метод треугольника требует бо́льшего количества операций. Достоинством метода является то, что при построении вспомогательной таблицы коэффициенты полинома просчитываются автоматически.
Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных P(A,B,C) показан на рисунке.
ЛЕКЦИЯ 9
Пополним список уже известных логических операций, а именно, познакомимся со штрихом Шеффера, стрелкой Пирса и операцией двоичного сложения. На последней остановимся более подробно.
Штрих Шеффера – это новое высказывание , обозначаемое х|y, ложное тогда и только тогда, когда оба высказывания х и у истинны. Приведем таблицу истинности:
Легко заметить, что штрих Шеффера – это отрицание конъюнкции или дизъюнкция отрицаний х и у: Следовательно, штрих Шеффера можно прочесть следующим образом: не х или не у.
Используя основные равносильности, можно эту операцию выразить и через другие, например:
Отрицание высказывания можно представить в виде :
Стрелка Пирса – это новое высказывание, обозначаемое х¯ у, истинное тогда и только тогда, когда оба высказывания ложны. Приведем таблицу истинности:
Стрелка Пирса – это отрицание дизъюнкции или конъюнкция отрицаний х и у:
Стрелку Пирса можно прочесть так: не х и не у.
Отрицание высказывания выражается через стрелку Пирса:
Пример: составить КНФ и ДНФ для формулы
Используя новые равносильности и основные равносильности , преобразуем формулу:
Полученная формула является одновременно ДНФ и КНФ.
Двоичное сложение – это новое высказывание, обозначаемое х+у, ложное тогда и только тогда. Когда оба высказывания имеют одинаковые логические значения. Приведем таблицу истинности:
Двоичное сложение – это отрицание эквиваленции:
Познакомимся с законами для двоичного сложения:
1. коммутативность: х+у º у+х;
2. ассоциативность: х+у+z º x+(y+z);
3. дистрибутивность: x(y+z) º xy +xz;
Рассмотрим использование данной операции в вопросе представления булевой функции единственным образом, наряду с совершенными формулами.
2. Полином Жегалкина.
Познакомимся с определением полинома:
Любую булеву функцию можно представить в виде двоичной суммы различных одночленов (конъюнкций), в которые все переменные входят не выше, чем в первой степени и константы 1 или 0, т.е. булева функция представима в виде:
Причем, такое представление единственное.
Эта сумма называется многочленом Жегалкина.
Существует два способа представления булевой функции в виде полинома: метод неопределенных коэффициентов и метод построения полином по формуле. Опишем каждый метод подробно.
Метод неопределенных коэффициентов.
Перепишем полином в виде :
где Ki – конъюнкции, число которых равно 2 n – 1, — вектор коэффициентов, где bI Î.
Коэффициент bI указывает на присутствие или отсутствие соответствующей конъюнкции в полиноме.
Алгоритм поиска вектора коэффициентов и составления полинома.
1. по таблице истинности составить систему уравнений ,где (a1 , a2 , …, an) — все наборы значений переменных таблицы истинности для данной булевой функции (вместо переменных в полином подставить их соответствующие значения, в левой части уравнения – соответствующее этому набору значение функции).
3. пользуясь таблицей истинности для двоичного сложения и конъюнкции, вычислить коэффициенты bI ;
4. подставить в полином значения коэффициентов и составить полином.
Представление булевой функции в виде полинома называется разложением функции в многочлен или в полином.
Разложить функцию f(x, y, z) = (01101000).
Cоставляя уравнения, нулевые конъюнкции будем исключать:
Решая систему , получим вектор коэффициентов: (0,0,1,0,1,1,0,1), тогда функция раскладывается в полином:
P(x,y,z) = 0 + y +xy + xz +xyz.
Проверку можно выполнить, составив таблицу истинности для полинома.
Построение полинома по формуле.
Данный метод основан на применении равносильных преобразований данной булевой функции, представленной в виде формулы, к виду полинома.
Алгоритм построения полинома по формул:
1. заменить формулу равносильной, содержащей только операции конъюнкцию и отрицание;
2. снять отрицания, пользуясь равносильностью:
3. раскрыть скобки:
4. упростить, используя идемпотентность : х+х =0, равносильность х+0=х.
Задачи для самостоятельного решения.
1. Построить таблицу истинности для формулы Составить для данной формулы КНФ и ДНФ.
2. Методом неопределенных коэффициентов разложить функции в полиномы: а) f(x,y,z)= (01001110); б) f(x,y,z) = (11000101); в) f(x,y)= (0101); г) f(x,y)=(1011)
3. Методом неопределенных коэффициентов и путем равносильных преобразований построить полиномы для формул: а) х®у; б) (х|y)¯z; в) (x®y)(y¯z); г) ((x®y)v)|x.
1. Привести таблицу истинности для штриха Шеффера. Выразить штрих Шеффера через отрицание и конъюнкцию. Выразить отрицание через штрих Шеффера.
2. Привести таблицу истинности для стрелки Пирса. Выразить стрелку Пирс через отрицание и дизъюнкцию. Выразить отрицание через стрелку Пирса.
3. Привести таблицу истинности для двоичного сложения. Выразить двоичное сложение через отрицание и эквиваленцию.

 и
и