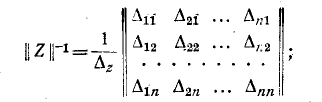
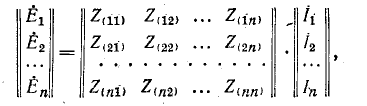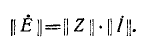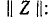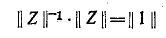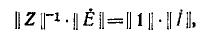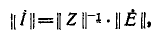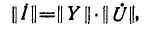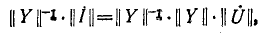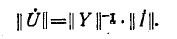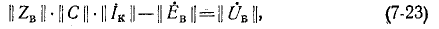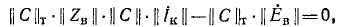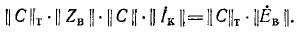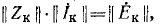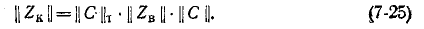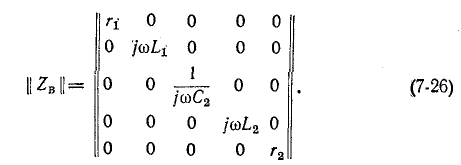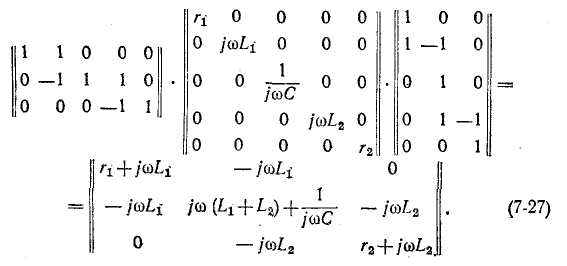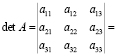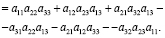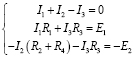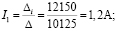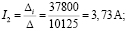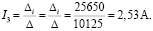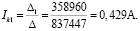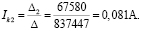Рассмотренные методы расчета электрических цепей – непосредственно по законам
Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально
рассчитать любую схему. Однако их применение без использования введенных ранее
топологических матриц рационально для относительно простых схем. Использование
матричных методов расчета позволяет формализовать процесс составления уравнений
электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно
существенно при расчете сложных разветвленных схем.
Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.
Пусть имеем схему по рис. 1, где — источник тока. В соответствии
с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы
можно записать:
| (1) |
Однако, для дальнейших выкладок будет удобнее представить ток
как сумму токов k-й
ветви и источника тока, т.е.:
| (2) |
Подставив (2) в (1), получим:
| (3) |
Формула (3) представляет собой аналитическое выражение закона Ома для участка
цепи с источниками ЭДС и тока (обобщенной ветви).
Соотношение (3) запишем для всех n ветвей схемы
в виде матричного равенства

или
| (4) |
где Z
– диагональная квадратная (размерностью n x n)
матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не
учитываем), за исключением элементов главной диагонали, равны нулю.
Соотношение (4) представляет собой матричную запись закона Ома.
Если обе части равенства (4) умножить слева на контурную матрицу В
и учесть второй закон Кирхгофа, согласно которому
| (5) |
то
| (6) |
то есть получили новую запись в матричной форме второго закона Кирхгофа.
Метод контурных токов в матричной форме
В соответствии с введенным ранее понятием матрицы главных контуров
В, записываемой для
главных контуров, в качестве независимых переменных примем токи ветвей связи,
которые и будут равны искомым контурным токам.
Уравнения с контурными токами получаются на основании второго закона Кирхгофа;
их число равно числу независимых уравнений, составляемых для контуров, т.е.
числу ветвей связи c=n—m+1.
Выражение (6) запишем следующим образом:
| (7) |
В соответствии с методов контурных токов токи всех ветвей могут быть выражены
как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей
связи. Если элементы j–го столбца матрицы В
умножить соответствующим образом на контурные токи, то сумма таких произведений
и будет выражением тока j–й
ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано
в виде матричного соотношения
| (8) |
где — столбцовая матрица контурных
токов; — транспонированная контурная
матрица.
С учетом (8) соотношение (7) можно записать, как:
| (9) |
Полученное уравнение представляет собой контурные уравнения в матричной форме. Если обозначить
| (10) |
| (11) |
то получим матричную форму записи уравнений, составленных по методу контурных
токов:
| (12) |
где — матрица контурных сопротивлений;
— матрица контурных ЭДС.
В развернутой форме (12) можно записать, как:
 , , |
(13) |
то есть получили известный из
метода контурных токов результат.
Рассмотрим пример составления контурных уравнений.
Пусть имеем схему по рис. 2. Данная схема имеет четыре узла (m=4)
и шесть обобщенных ветвей (n=6). Число независимых контуров, равное числу ветвей связи,
c=n-m+1=6-4+1=3.
Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.
Запишем матрицу контуров, которая
будет являться матрицей главных контуров, поскольку каждая ветвь связи входит
только в один контур. Принимая за направление обхода контуров направления ветвей
связи, получим:
B
Диагональная матрица сопротивлений ветвей
Z
Матрица контурных сопротивлений
Zk=BZBT


Матрицы ЭДС и токов источников
Тогда матрица контурных ЭДС

Матрица контурных токов
Таким образом, окончательно получаем:

где ;
;
;
;
;
;
;
;
.
Анализ результатов показывает, что полученные три уравнения идентичны тем,
которые можно записать непосредственно из рассмотрения схемы по известным правилам
составления уравнений по методу контурных токов.
Метод узловых потенциалов в матричной форме
На основании полученного выше соотношения (4), представляющего собой, как было
указано, матричную запись закона Ома, запишем матричное выражение:
| (14) |
где

ветвей, все члены которой, за исключением элементов главной диагонали, равны
нулю.
Матрицы Z
и Y взаимно обратны.
Умножив обе части равенства (14) на узловую матрицу А и учитывая первый закон Кирхгофа,
согласно которому
| (15) |
получим:
| (16) |
Выражение (16) перепишем, как:
| (17) |
Принимая потенциал узла, для которого отсутствует строка в матрице А, равным нулю, определим напряжения
на зажимах ветвей:
| (18) |
Тогда получаем матричное уравнение вида:
| (19) |
Данное уравнение представляет собой узловые уравнения в матричной форме. Если
обозначить
| (20) |
| (21) |
то получим матричную форму записи уравнений, составленных по методу узловых
потенциалов:
| (22) |
где — матрица узловых проводимостей;
— матрица узловых токов.
В развернутом виде соотношение (22) можно записать, как:
 |
(23) |
то есть получили известный из метода узловых потенциалов результат.
Рассмотрим составление узловых уравнений на примере схемы по рис. 4.
Данная схема имеет 3 узла (m=3)
и 5 ветвей (n=5). Граф схемы с выбранной ориентацией ветвей представлен
на рис. 5.
Узловая матрица (примем )
А
Диагональная матрица проводимостей ветвей:
Y
где .
Матрица узловых проводимостей

Матрицы токов и ЭДС источников
Следовательно, матрица узловых токов будет иметь вид:
Таким образом, окончательно получаем:

где ;
;
;
;
.
Анализ результатов показывает, что полученные уравнения идентичны тем, которые
можно записать непосредственно из рассмотрения схемы по известным правилам составления
уравнений по методу узловых потенциалов.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В чем заключаются преимущества использования матричных методов
расчета цепей? - Запишите выражения матрицы контурных сопротивлений и матрицы контурных ЭДС.
- Запишите выражения матрицы узловых проводимостей и матрицы узловых токов.
- Составить узловые уравнения для цепи на рис. 2.
- Составить контурные уравнения для цепи рис. 4, приняв, что дерево образовано
ветвями 3 и 4 (см. рис. 5).
Ответ:

Ответ:

В
соответствии с введенным ранее понятием
матрицы главных
контуров
В,
записываемой для
главных контуров, в качестве независимых
переменных примем токи ветвей связи,
которые и будут равны искомым контурным
токам.
Уравнения
с контурными токами получаются на
основании второго закона Кирхгофа; их
число равно числу независимых уравнений,
составляемых для контуров, т.е. числу
ветвей связи c=n—m+1.
Выражение (6) запишем следующим образом:
|
|
(7) |
В
соответствии с методов контурных токов
токи всех ветвей могут быть выражены
как линейные комбинации контурных токов
или в рассматриваемом случае токов
ветвей связи. Если элементы j–го
столбца матрицы В
умножить соответствующим образом на
контурные токи, то сумма таких произведений
и будет выражением тока j–й
ветви через контурные токи (через токи
ветвей связи). Сказанное может быть
записано в виде матричного соотношения
|
|
(8) |
где
—
столбцовая матрица контурных токов;
—
транспонированная контурная матрица.
С
учетом (8) соотношение (7) можно записать,
как:
|
|
(9) |
Полученное
уравнение представляет собой
контурные уравнения
в матричной
форме. Если обозначить
|
|
(10) |
|
|
(11) |
то
получим матричную форму записи уравнений,
составленных по методу контурных токов:
|
|
(12) |
где
—
матрица контурных сопротивлений;
—
матрица контурных ЭДС.
В
развернутой форме (12) можно записать,
как:
|
|
(13) |
то
есть получили известный из метода
контурных токов результат.
Р
пример составления контурных уравнений.
Пусть
имеем схему по рис. 2. Данная схема имеет
четыре узла (m=4)
и шесть обобщенных
ветвей (n=6).
Число независимых
контуров, равное числу ветвей связи,
c=n—m+1=6-4+1=3.
Граф
схемы с выбранным деревом (ветви 1, 2, 3)
имеет вид по рис. 3.

матрицу контуров, которая будет являться
матрицей главных контуров, поскольку
каждая ветвь связи входит только в один
контур. Принимая за направление обхода
контуров направления ветвей связи,
получим:
|
В |
|
.Диагональная
матрица сопротивлений ветвей
|
Z |
|
Матрица
контурных сопротивлений
|
Zk=BZBT |
|

Матрицы
ЭДС и токов источников
|
|
|
|
|
|
Тогда
матрица контурных ЭДС
|
|
|

Матрица
контурных токов
|
|
|
Таким
образом, окончательно получаем:

где
;
;
;
;
;
;
;
;
.
Анализ
результатов показывает, что полученные
три уравнения идентичны тем, которые
можно записать непосредственно из
рассмотрения схемы по известным правилам
составления уравнений по методу контурных
токов.
15) Матричная запись метода узловых напряжений
На
основании полученного выше соотношения
(4), представляющего собой, как было
указано, матричную запись закона Ома,
запишем матричное выражение:
|
|
(14) |
где

диагональная матрица проводимостей
ветвей, все члены которой, за исключением
элементов главной диагонали, равны
нулю.
Матрицы
Z
и Y
взаимно обратны.
Умножив
обе части равенства (14) на узловую матрицу
А
и учитывая первый
закон Кирхгофа, согласно которому
|
|
(15) |
получим:
|
|
(16) |
Выражение
(16) перепишем, как:
|
|
(17) |
Принимая
потенциал узла, для которого отсутствует
строка в матрице А,
равным нулю, определим
напряжения на зажимах ветвей:
|
|
(18) |
Тогда
получаем матричное уравнение вида:
|
|
(19) |
Данное
уравнение представляет собой узловые
уравнения в матричной форме. Если
обозначить
|
|
(20) |
|
|
(21) |
то
получим матричную форму записи уравнений,
составленных по методу узловых
потенциалов:
|
|
(22) |
где
—
матрица узловых проводимостей;
—
матрица узловых токов.
В
развернутом виде соотношение (22) можно
записать, как:
|
|
(23) |
то
есть получили известный из метода
узловых потенциалов результат.
Рассмотрим
составление узловых уравнений на примере
схемы по рис. 4.
|
|
|
Данная
схема имеет 3 узла (m=3)
и 5 ветвей (n=5).
Граф схемы с выбранной ориентацией
ветвей представлен на рис. 5.
Узловая
матрица (примем
)
|
А |
|
Диагональная
матрица проводимостей ветвей:
|
Y |
|
где
.
Матрица
узловых проводимостей
|
|
|

Матрицы
токов и ЭДС источников
|
|
|
|
|
|
.
.Следовательно,
матрица узловых токов будет иметь вид:
|
|
|
.Таким
образом, окончательно получаем:

где
;
;
;
;
.
Анализ
результатов показывает, что полученные
уравнения идентичны тем, которые можно
записать непосредственно из рассмотрения
схемы по известным правилам составления
уравнений по методу узловых потенциалов.
Соседние файлы в папке Экзамен
- #
- #
- #
- #
- #
13.06.2014246 б220Шпора по электронике
Применение матриц к расчету электрических цепей:
Математическая символика и правила матричной алгебры позволяют упростить запись систем уравнений, получающихся при расчете сложных электрических цепей. В этом отношении матричную алгебру можно сравнить со стенографией, которая облегчает и ускоряет запись.
Напомним, что матрица представляет собой совокупность величин, называемых ее элементами и расположенных в виде прямоугольной таблицы 1. Если число строк равно числу столбцов, то матрица называется квадратной. Матрица, содержащая один столбец, называется столбцовой или матрицей-столбцом.
Приведенная система уравнений, записанных по второму закону Кирхгофа для контурных э. д. с. и контурных токов, может быть представлена в виде произведений квадратной матрицы собственных и общих сопротивлений контуров на столбцовую матрицу контурных токов.
При этом следует помнить, что произведением двух матриц называется матрица, элементы которой равны сумме произведений всех элементов соответствующей строки первой матрицы на соответствующие элементы столбца второй матрицы. Итак, уравнения (7-2) в матричной форме имеют вид:
или сокращенно
Данное матричное уравнение может быть решено относительно матрицы 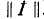
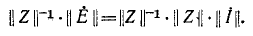
Как известно, для получения обратной матрицы необходимо заменить в исходной матрице-каждый элемент его алгебраическим дополнением, затем заменить строки соответствующими столбцами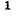
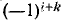
здесь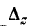
Произведение обратной матрицы на исходную матрицу равно единичной матрице, т. е. квадратной матрице, у которой все элементы главной диагонали (идущей от левого верхнего угла к правому нижнему) равны единице, а остальные элементы равны нулю.
Следовательно,
и
где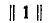
Произведение единичной матрицы на матрицу 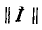
или в развернутой форме
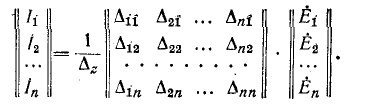
В результате умножения матриц получаются выражения для контурных токов вида (7-4).
Аналогично решается матричное уравнение для узловых напряжений
где
откуда
В результате умножения матрицы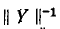
Матричная алгебра широко применяется для расчета сложных четырехполюсников.
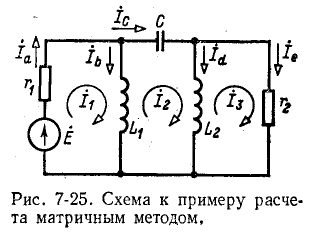
В случае относительно простой электрической схемы без взаимной индукции матрица контурных сопротивлений легко записывается непосредственно по заданной схеме. В более сложных случаях матрица контурных сопротивлений может быть получена с помощью матрицы сопротивлений ветвей. Ниже показана связь, существующая между матрицами контурных сопротивлений и сопротивлений ветвей 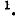
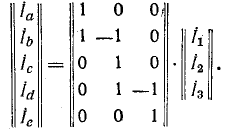
•Обозначим токи, напряжения, э. д. с. и сопротивления ветвей индексом «в», а соответствующие контурные величины — индексом «к». Связь между токами в ветвях и контурными токами выражается зависимостью
Здесь 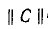
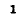
Например, для схемы рис. 7-25 имеем:
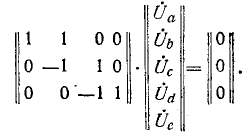
Уравнения вида (М2) по второму закону Кирхгофа в матричной форме записываются так:
где 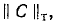
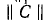
Строка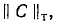
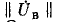
любом контуре равна нулю, т. е. «произведение» любой строки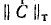
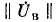
Например, для схемы рис, 7-25 имеем:
Считая, что направления э. д. с. и токов в ветвях совпадают, получаем матрицу напряжений на ветвях в виде
Подстановка (7-20) и (7-22) дает:
а подстановкой (7-23) в (7-21) получаем:
откуда
Сопоставив это уравнение с уравнением для контурных токов
приходим к выводу, что э. д. с. в ветвях и контурные э. д. с. связаны матричным уравнением
а матрица контурных сопротивлений получается по формуле
Для схемы рис. 7-25 матрица сопротивлений ветвей записывается в виде
Матрица контурных сопротивлений согласно (7-25) равна:
- Дуальные цепи
- Электромеханические аналогии
- Индуктивно связанные электрические цепи
- Фильтры и топологические методы анализа линейных электрических цепей
- Теорема обратимости (или взаимности)
- Теорема компенсации
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
- Теорема об эквивалентном источнике
2.5 Метод узловых потенциалов
За неизвестные аргументы принимаются потенциалы узлов NУП = n − 1, т.к.
потенциал одного из узлов определён (его условно заземляют) и равен
нулю.
Исходным для обоснования метода является закон Ома.
С другой стороны, U(В) = ATφ.
После обозначения Y(У) = AY(В)AT, J(У) = AJ(В) − AY(В)E(В), получим
узловые уравнения:
где
Y(У) – квадратная матрица узловых проводимостей размера (n − 1) � (n − 1);
J(У) – столбцовая матрица узловых токов.
Пример.
n = 4
m = 6
Граф схемы
Принимаем, что φ4 = 0.
Узловая матрица:
Матрица проводимостей ветвей:
где
gk = 1∕Rk, k = 1,…, 6.
Матрица узловых проводимостей:
При умножении матрицы размера k � l на матрицу размером l � r
получается матрица размером k � r.
Матрица токов источников тока ветвей:
Матрица ЭДС источников ЭДС ветвей:
Матрица узловых токов:
Таким образом, узловые уравнения принимают вид:
Порядок составления матриц
- Столбцовая матрица φ – матрица неизвестных потенциалов.
- Матрица узловых
проводимостей Y(У) – квадратная. На главной диагонали записываются
суммы проводимостей ветвей, присоединённых к соответствующему
узлу – собственные узловые проводимости, Y pp > 0.Остальные элементы матрицы Y ij – общие узловые проводимости,
которые равны сумме проводимостей ветвей, присоединённых между
узлами i и j, Y ij < 0.Матрица Y(У) симметрична, т.е Y ij = Y ji и Y(У) =
T.
- Столбцовая матрица узловых токов J(У) состоит из элементов Jp(У),
равных сумме токов источников тока, присоединённых к p-му узлу,
включая и токи источников тока, эквивалентных источникам ЭДС.Jp(У) > 0, если ток направлен к узлу, в противном случае Jp(У) < 0.
После нахождения неизвестных потенциалов по закону Ома определяются токи
ветвей
(знак «+» у слагаемых числителя используется в том случае, если направление
тока İi совпадает с направлением i или Ėk).
Частным случаем метода узловых потенциалов является метод двух узлов
для схем, имеющих лишь два узла. После заземления одного из узлов
определяется узловое напряжение:
Слагаемые Ekgk и Jk суммируются с положительным знаком, если они
направлены к узлу 1.
С учётом данного метода можно привести следующие преобразования
схем.
1. Рассмотрим фрагмент схемы, состоящей из m параллельных ветвей.
Заземлим 2-ой узел. U = φ1 − φ2 = φ1.
Уравнение по методу узловых потенциалов представляется в виде:
Вводя обозначения
получим U = E − RI.
Данному уравнению соответствует следующая схема:
Таким образом, ряд параллельных ветвей можно заменить эквивалентной
ветвью. При определении эквивалентной ЭДС, слагаемые Ekgk и Jk суммируются
с положительным знаком, если они направлены к узлу 1.
2. Аналогичное преобразование можно осуществить для источников
тока.
⇒
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Искандарова К.Р.
1
Чубанов А.А.
1
1 ФГБОУ ВО «Ставропольский государственный аграрный университет»
Статья посвящена матричному методу расчета электрических цепей. В ней рассмотрены основные теоретические понятия. На примере показана практичность и рациональность матричного метода в электротехнической инженерной практике. Использование матричных методов расчета позволяет оформить процесс составления уравнений электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно существенно при расчете сложных разветвленных схем. Также поднимаются вопросы взаимодействия математики и техники в целом. В этой статье мы разберем расчет электрических цепей с использованием матрицы и ее детерминанта, который применяется на практике. Для этого необходимо вспомнить, что такое матрица и ее детерминанты. Рассмотрим, с какой целью в электротехнике применяют матричные методы расчёта сложных электрических цепей.
матричный метод
электрическая цепь
матрица и ее детерминант
1. Бондаренко В.А., Цыплакова О.Н. Задачи с экономическим содержанием на занятиях по дифференциальному исчислению // Актуальные вопросы теории и практики бухгалтерского учета, анализа и аудита: ежегодная 75-я научно-практическая конференция. – 2011. – С. 124–127.
2. Гулай Т.А., Гатауллина К.Р., Фурсов Д.И., Применение классического метода при математическом расчете переходных процессов // Международный студенческий научный вестник. – 2017. – № 4–4. – С. 511–513.
3. Гулай Т.А., Желтяков В.И., Применение систем линейных алгебраических уравнений при расчете электрических цепей // Международный студенческий научный вестник. – 2017. – № 4–4. – С. 522–524.
4. Гулай Т.А., Жукова В.А., Мелешко С.В., Невидомская И.А., Математика: рабочая тетрадь. – Ставрополь, 2015.
5. Гулай Т.А., Мелешко С.В., Невидомская И.А., Применение технических средств обучения в процессе математической подготовки студентов инженерных направлений // Вестник АПК Ставрополья. – 2014. – № 1 (13). – С. 10–13.
6. Долгополова А.Ф., Колодяжная Т.А. Руководство к решению задач по математическому анализу. Часть 1 // Международный журнал экспериментального образования. – 2011. – № 12. – С. 62–63.
7. Долгополова А.Ф., Гулай Т.А., Литвин Д.Б. Руководство к решению задач по математическому анализу. Часть 2 // Международный журнал экспериментального образования. – 2012. – №2. – С. 81–82.
8. Мелешко С.В., Зорина Е.Б., Попова С.В., Гулай Т.А., Самостоятельная работа как важнейшее средство повышения профессионально-познавательной и творческой активности будущих специалистов // Theoretical & Applied Science. – 2016. – № 11 (43). – С. 135–138.
В настоящее время трудно переоценить значение инженерной практики в современном мире науки и техники. Инженеры пользуются огромными познаниями в математике, стимулируют научно-технический прогресс, результаты которого определяют поступательное развитие общества. Однако стоит отметить, что данное развитие имеет место, только при тесном взаимодействии математики и технической практики. Инженерное дело, как область интеллектуальной деятельности человека, не может быть реализовано без математического аппарата, на основе которого решаются основные научно-технические задачи. Соответственно и математика не имела бы возможности интенсивного развития, если бы не являлась основным инструментом в научно-технической деятельности. Это значит, что математика и инженерное дело взаимно дополняют друг друга. Таким образом, мы приходим к выводу, что современный инженер, воплощающий инновационные идеи, не может обойтись без уверенных знаний математики [3, 8].
Например, инженер-электротехник для решения основных задач в своей области, в частности расчет параметров электрических цепей, использует уравнения Кирхгофа в матричной форме. В данном случае мы наблюдаем, как благодаря линейной алгебре и ее методам, значительно упрощается процесс длительных расчетов, а значит, увеличивается эффективность инженерной деятельности.
Рассмотрим базовую теорию. Матрица – это прямоугольная таблица чисел, в которой содержатся m строк (или n столбцов) идентичной длины [7].
сокращенно можно записать, где 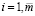
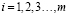
Матрицу размером 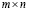
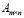
Квадратной матрице A n-го порядка можно сопоставить число 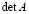
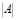
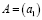
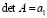
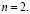
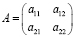
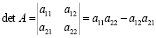
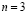
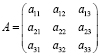
Минором некоторого элемента 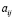
Алгебраическим дополнением элемента aij, детерминанта называется минор, взятый со знаком «+», если сумма i+j – четное число, и со знаком «-», если сумма нечетная. Обозначается как Aij: 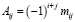
Метод Крамера – это способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с нулевым главным детерминантом матрицы коэффициентов системы [5].
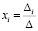
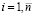
На примере продемонстрируем расчет электрической цепи с помощью данной теории.
Пример 1.
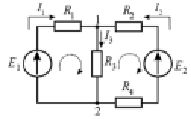
Дана электрическая цепь (рисунок). Надо определить токи в ветвях, с помощью законов Кирхгофа. Параметры элементов электрической цепи следующие: R1=45 Ом, R2=15 Ом, R3=45 Ом, R1=75 Ом, E1=60 В, E2=450 В.
Схема электрической цепи
Решение. Необходимо выбрать положительные направления искомых токов ветвей и обозначить их на схеме.
Составим уравнение, используя первый закон Кирхгофа для узла 1. Выбрав направления обходов контуров, можно записать уравнение по второму закону Кирхгофа. В итоге можно получить систему из трех уравнений:
Решаем полученную систему по методу Крамера с помощью детерминантов:
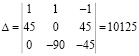
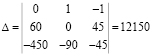
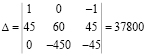
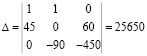
Находим значения токов по формуле Крамера
Пример 2.
Второй закон Кирхгофа используется для метода контурных токов. С помощью этого метода можно уменьшить число уравнений в системе на n–1. Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока – контурного тока, являющегося расчетной величиной. В заданной системе рассмотрим три контура-ячейки и введем для них контурные токи Ik1, Ik2, Ik3. Смежными ветвями называются ветви, принадлежащие двум смежным контурам. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления. При составлении этих уравнений по второму закону Кирхгофа алгебраически суммируются ЭДС источников в левой части равенства, входящих в контур-ячейку. В правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура. На основании ранее приведенного материала контурные токи рассчитываются следующим образом:
E1=Ik1(r01+R1+R3+R4)+Ik2R3–Ik3R4;
E2=Ik1R3+Ik2(r02+R2+R3+R5)+Ik3R5;
0= –Ik1R4+Ik2R5+Ik3(R4+R5+R6).
Подставляем в уравнение численные значения ЭДС и сопротивлений:
40=102Ik1+24Ik2–41Ik3;
20=24Ik1+93Ik2+16Ik3;
0=–41Ik1+16Ik2+118Ik3.
Решим систему с помощью определителей. Вычислим определитель системы Δ и частные определители Δ1, Δ2, Δ3:
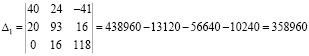
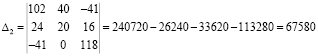
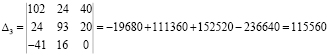
Вычисляем контурные токи:
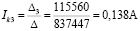
Действительные токи ветвей:
I1=Ik1=0,429 А;
I6=Ik3=0,138 А;
I1=Ik1=0,081 А;
I3=Ik1+Ik2=0,429+0,081=0,510 А;
I4=Ik1–Ik3=0,429–0,138=0,291 А;
I5=Ik2+Ik3=0,081+0,138=0,219 А.
Библиографическая ссылка
Искандарова К.Р., Чубанов А.А. РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ С ИСПОЛЬЗОВАНИЕМ МАТРИЦЫ И ЕЕ ДЕТЕРМИНАНТА // Международный студенческий научный вестник. – 2018. – № 3-1.
;
URL: https://eduherald.ru/ru/article/view?id=18211 (дата обращения: 29.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)














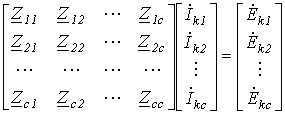 ,
,








 ,
,