Факультативное занятие по математике «Магический треугольник»
Цели:
- Познакомить с понятием «магический треугольник», сформировать умение решать магический треугольник.
- Развитие зрительной памяти на цифровом материале, концентрации и объёма внимания, мышления, речи.
- Повторить сложения и вычитания в пределах 100.
Ход занятия
I. Разминка.
Ответьте на вопросы
- Титул самого «правдивого» человека на свете. (Барон Мюнхаузен)
- Ребёнок лошади. (Жеребёнок)
- Страна, где жил великий сказочник Андерсен. (Дания)
- Северная ездовая охотничья собака. (Лайка)
- Полосатая африканская лошадь. (Зебра)
- Часть одежды, куда кладут деньги. (Карман)
- Дедов сын. (Отец)
- Метательное оружие, возвращающееся к охотнику. (Бумеранг)
II. а) Упражнения на развитие зрительной памяти на цифровом материале.
Посмотрите внимательно (20 сек. ) на предлагаемые вашему вниманию ряды чисел.
Постарайтесь запомнить их взаимное расположение, порядок следования.
- Каких чисел в ряду больше – однозначных или двузначных?
- Каким по счёту стоит наименьшее двузначное число?
- Чему равна сумма третьего и последнего чисел?
- Каким по счёту идёт число, в котором меньше букв?
- Какое число по счёту соответствует количеству гласных букв в русском алфавите?
- Правда ли , что разность между вторым и последним числами является 3?
- Сколько раз в ряду повторяется цифра 2?
- Правда ли, что сумма первого и третьего чисел равна круглому числу?
- В каких сказках встречается второе число ряда?
б)Упражнения на развитие зрительной памяти.
Внимательно прочитайте три раза слова, попытайтесь их запомнить, а затем напишите
| ключ | арбуз | ведро | дерево |
| груша | книга | птица | чашка |
в) Упражнения на развитие концентрации и объёма внимания.
Назовите в обратном порядке.
4 – 23
6 – 1 – 15
61 – 7 – 43 – 8
97 – 4 – 6 – 9 – 31
6 – 1 – 6 – 93 – 4 – 23
III. Магический треугольник.
Магический треугольник составлен из девяти маленьких треугольников, в которые вписали числа. В каждом магическом треугольнике можно найти 3 треугольника, которые составлены из четырёх маленьких треугольников.
– Найдите суммы в этих треугольниках.
7 + 1 + 6 + 3 = 17
2 + 1 + 5 + 9 = 17
3 + 2 + 4 + 8 = 17
– Суммы одинаковы, значит треугольник магический
Посчитайте ещё один треугольник.
6 + 12 + 13 + 7 = 38
12 + 15 + 9 + 2 = 38
13 + 9 + 10 + 6 = 38
Суммы одинаковы, значит треугольник магический
11 + 5 + 4 + 10 = 30
5 + 2 + 7 + 16 = 30
4 + 7 + 6 + 13 = 30
Суммы одинаковы, значит треугольник магический
Суммы одинаковы, значит треугольник магический
7 + 8 + 9 + 5 = 29
2 + 8 + 6 + 1 = 17
3 + 1 + 4 + 9 = 17
Суммы не одинаковы, значит треугольник не магический
5 + 2+1 + 16 = 24
2 + 13 + 6 + 3 = 24
3 + 1 + 6 + 14 =24
Головоломка Волшебный треугольник
Головоломка «Волшебный треугольник» будет интересна и доступна для решения детям школьного возраста.
Есть несколько разных видов волшебных треугольников, и я поделюсь с вами двумя из них. Самое замечательное то, что у каждой головоломки есть несколько решений.
Решение волшебных треугольников развивает у детей базовые навыки сложения, а также критическое и логическое мышление.
Вам понадобится
- Ребенок! (подойдет один или несколько).
- Распечатанный шаблон.
Или свой собственный карандашом и бумагой.
Можно решить волшебный треугольник, написав цифры внутри кругов. Но проще исправлять ошибки, имея возможность перемещать круги вдоль периметра треугольника.
Цель игры
Расположите числа для каждого треугольника (1-6 для треугольника 3x3x3; 1-9 для треугольника 4x4x4) так, чтобы сумма чисел на каждой стороне была равна сумме чисел на каждой другой стороне.
Для маленького треугольника расположите числа так, чтобы сумма каждой стороны равнялась 9. Есть также решения для 10, 11 и 12.
Для большого треугольника расположите числа так, чтобы сумма каждой стороны равнялась 17. Вы также можете найти решения для чисел 19, 20, 21 и 23.
Если ребенок силен в математике, не говорите ему, какой будет сумма для каждой стороны волшебного треугольника. Просто дайте указание расположить числа так, чтобы сумма на каждой стороне была равна остальным. Пусть он попробует вычислить, например, что каждая сторона должна давать в сумме 9.
Эту загадку можно собрать с треугольниками еще большего размера — по 5 или 6 цифр на каждой стороне. Однако вам придется сделать свою собственную игровую доску!
Треугольник Паскаля — формула, свойства и применение
Основная формула
Строки треугольника обычно нумеруются, начиная со строки n = 0 в верхней части. Записи в каждой строке целочисленные и нумеруются слева, начиная с k = 0, обычно располагаются в шахматном порядке относительно чисел в соседних строчках. Построить фигуру можно следующим образом:
- В центре верхней части листа ставится цифра «1».
- В следующем ряду — две единицы слева и справа от центра (получается треугольная форма).
- В каждой последующей строке ряд будет начинаться и заканчиваться числом «1». Внутренние члены вычисляются путём суммирования двух цифр над ним.
Запись в n строке и k столбце паскалевской фигуры обозначается (n k). Например, уникальная ненулевая запись в самой верхней строке (0 0) = 1. С помощью этого конструкция предыдущего абзаца может быть записана следующим образом, образуя формулу треугольника Паскаля (n k) = (n — 1 k-1) + (n — 1 k), для любого неотрицательного целого числа n и любого целого числа k от 0 до n включительно. Трёхмерная версия называется пирамидой или тетраэдром, а общие — симплексами.
История открытия
Паскаль ввёл в действие многие ранее недостаточно проверенные способы использования чисел треугольника, и он подробно описал их в, пожалуй, самом раннем из известных математических трактатов, специально посвящённых этому вопросу, в труде об арифметике Traité du triangle (1665). За столетия до того обсуждение чисел возникло в контексте индийских исследований комбинаторики и биномиальных чисел, а у греков были работы по «фигурным числам».
Из более поздних источников видно, что биномиальные коэффициенты и аддитивная формула для их генерации были известны ещё до II века до нашей эры по работам Пингала. К сожалению, бо́льшая часть трудов была утеряна. Варахамихира около 505 года дал чёткое описание аддитивной формулы, а более подробное объяснение того же правила было дано Халаюдхой (около 975 года). Он также объяснил неясные ссылки на Меру-прастаара, лестницы у горы Меру, дав первое сохранившееся определение расположению этих чисел, представленных в виде треугольника.
Примерно в 850 году джайнский математик Махавира вывел другую формулу для биномиальных коэффициентов, используя умножение, эквивалентное современной формуле. В 1068 году Бхаттотпала во время своей исследовательской деятельности вычислил четыре столбца первых шестнадцати строк. Он был первым признанным математиком, который уравнял аддитивные и мультипликативные формулы для этих чисел.
Примерно в то же время персидский учёный Аль-Караджи (953–1029) написал книгу (на данный момент утраченную), в которой содержалось первое описание треугольника Паскаля. Позднее работа была переписана персидским поэтом, астрономом и математиком Омаром Хайямом (1048–1131). Таким образом, в Иране фигура упоминается как треугольник Хайяма.
Известно несколько теорем, связанных с этой темой, включая биномы. Хайям использовал метод нахождения n-x корней, основанный на биномиальном разложении и, следовательно, на одноимённых коэффициентах. Треугольник был известен в Китае в начале XI века благодаря работе китайского математика Цзя Сианя (1010–1070). В XIII веке Ян Хуэй (1238–1298) представил этот способ, и поэтому в Китае он до сих пор называется треугольником Ян Хуэя.
На западе биномиальные коэффициенты были рассчитаны Жерсонидом в начале XIV века, он использовал мультипликативную формулу. Петрус Апиан (1495–1552) опубликовал полный треугольник на обложке своей книги примерно в 1527 году. Это была первая печатная версия фигуры в Европе. Майкл Стифель представил эту тему как таблицу фигурных тел в 1544 году.
В Италии паскалевский треугольник зовут другим именем, в честь итальянского алгебраиста Никколо Фонтана Тарталья (1500–1577). Вообще, современное имя фигура приобрела благодаря Пьеру Раймонду до Монтрмору (1708), который назвал треугольник «Таблица Паскаля для сочетаний» (дословно: Таблица мистера Паскаля для комбинаций) и Абрахамом Муавром (1730).
Отличительные черты
Треугольник Паскаля и его свойства — тема довольно обширная. Главное, в нём содержится множество моделей чисел. Обзор следует начать с простого — ряды:
- Сумма элементов одной строки в два раза больше суммы строки, предшествующей ей. Например, строка 0 (самая верхняя) имеет значение 1, строчка 1–2, а 2 имеет значение 4 и т. д. Это потому что каждый элемент в строке производит два элемента в следующем ряду: один слева и один справа. Сумма элементов строки n равна 2 n .
- Принимая произведение элементов в каждой строке, последовательность продуктов можно связать с основанием натурального логарифма.
- В треугольнике Паскаля через бесконечный ряд Нилаканты можно найти число Пи.
- Значение строки, если каждая запись считается десятичным знаком (имеется в виду, что числа больше 9 переносятся соответственно), является степенью 11 (11 n для строки n). Таким образом, в строке 2 ⟨1, 2, 1⟩ становится 11 2 , равно как ⟨1, 5, 10, 10, 5, 1⟩ в строке пять становится (после переноса) 161, 051, что составляет 11 5 . Это свойство объясняется установкой x = 10 в биномиальном разложении (x + 1) n и корректировкой значений в десятичной системе.
- Некоторые числа в треугольнике Паскаля соотносятся с числами в треугольнике Лозанича.
- Сумма квадратов элементов строки n равна среднему элементу строки 2 n. Например, 1 2 + 4 2 + 6 2 + 4 2 + 1 2 = 70.
- В любой строчке n, где n является чётным, средний член за вычетом члена в двух точках слева равен каталонскому числу (n / 2 + 1).
- В строчке р, где р представляет собой простое число, все члены в этой строке, за исключением 1s, являются кратными р.
- Чётность. Для измерения нечётных терминов в строке n необходимо преобразовать n в двоичную форму. Пусть x будет числом 1s в двоичном представлении. Тогда количество нечётных членов будет 2 х . Эти числа являются значениями в последовательности Гулда.
- Каждая запись в строке 2 n -1, n ≥ 0, является нечётной.
- Полярность. Когда элементы строки треугольника Паскаля складываются и вычитаются вместе последовательно, каждая строка со средним числом, означающим строки с нечётным числом целых чисел, даёт 0 в качестве результата.
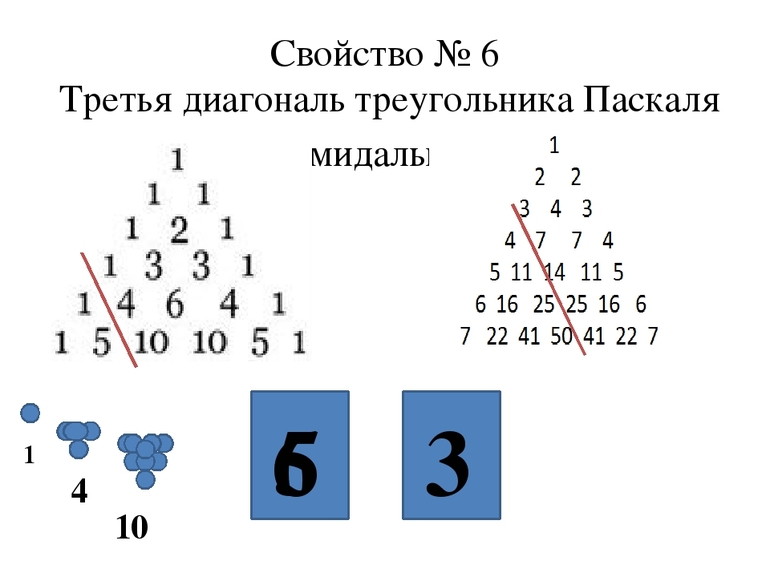
Диагонали треугольника содержат фигурные числа симплексов. Например:
- Идущие вдоль левого и правого краёв диагонали содержат только 1.
- Рядом с рёбрами диагонали содержат натуральные числа по порядку.
- Двигаясь внутрь, следующая пара содержит треугольные числа по порядку.
- Следующая пара — тетраэдрические, а следующая пара — числа пятиугольника.
Существуют простые алгоритмы для вычисления всех элементов в строке или диагонали без вычисления других элементов или факториалов.
Общие свойства
Образец, полученный путём раскраски только нечётных чисел, очень похож на фрактал, называемый треугольником Серпинского. Это сходство становится всё более точным, так как рассматривается больше строк в пределе, когда число рядов приближается к бесконечности, получающийся в результате шаблон представляет собой фигуру, предполагающую фиксированный периметр. В целом числа могут быть окрашены по-разному в зависимости от того, являются ли они кратными 3, 4 и т. д.
В треугольной части сетки количество кратчайших путей от заданного до верхнего угла треугольника является соответствующей записью в паскалевском треугольнике. На треугольной игровой доске Плинко это распределение должно давать вероятности выигрыша различных призов. Если строки треугольника выровнены по левому краю, диагональные полосы суммируются с числами Фибоначчи.
Благодаря простому построению факториалами можно дать очень простое представление фигуры Паскаля в терминах экспоненциальной матрицы: треугольник — это экспонента матрицы, которая имеет последовательность 1, 2, 3, 4… на её субдиагонали, а все другие точки — 0.
Количество элементов симплексов фигуры можно использовать в качестве справочной таблицы для количества элементов (рёбра и углы) в многогранниках (треугольник, тетраэдр, квадрат и куб).
Шаблон, созданный элементарным клеточным автоматом с использованием правила 60, является в точности паскалевским треугольником с биномиальными коэффициентами, приведёнными по модулю 2. Правило 102 также создаёт этот шаблон, когда завершающие нули опущены. Правило 90 создаёт тот же шаблон, но с пустой ячейкой, разделяющей каждую запись в строках. Фигура может быть расширена до отрицательных номеров строк.
Секреты треугольника
Конечно, сейчас большинство расчётов для решения задач не в классе можно сделать с помощью онлайн-калькулятора. Как пользоваться треугольником Паскаля и для чего он нужен, обычно рассказывают в школьном курсе математики. Однако его применение может быть гораздо шире, чем принято думать.
Начать следует со скрытых последовательностей. Первые два столбца фигуры не слишком интересны — это только цифры и натуральные числа. Следующий столбец — треугольные числа. Можно думать о них, как о серии точек, необходимых для создания групп треугольников разных размеров.
Точно так же четвёртый столбец — это тетраэдрические числа или треугольные пирамидальные. Как следует из их названия, они представляют собой раскладку точек, необходимых для создания пирамид с треугольными основаниями.
Столбцы строят таким образом, чтобы описывать «симплексы», которые являются просто экстраполяциями идеи тетраэдра в произвольные измерения. Следующий столбец — это 5-симплексные числа, затем 6-симплексные числа и так далее.
Полномочия двойки
Если суммировать каждую строку, получатся степени основания 2 начиная с 2⁰ = 1. Если изобразить это в таблице, то получится следующее:
| 1 | ||||||||||||||
| 1 | + | 1 | = | 2 | ||||||||||
| 1 | + | 2 | + | 1 | = | 4 | ||||||||
| 1 | + | 3 | + | 3 | + | 1 | = | 8 | ||||||
| 1 | + | 4 | + | 6 | + | 4 | + | 1 | = | 16 | ||||
| 1 | + | 5 | + | 10 | + | 10 | + | 5 | + | 1 | = | 32 | ||
| 1 | + | 6 | + | 15 | + | 20 | + | 15 | + | 6 | + | 1 | = | 64 |
Суммирование строк показывает силы базы 2.
Силы одиннадцати
Треугольник также показывает силы основания 11. Всё, что нужно сделать, это сложить числа в каждом ряду вместе. Как показывает исследовательский опыт, этого достаточно только для первых пяти строк. Сложности начинаются, когда записи состоят из двузначных чисел. Например:
| 1 | = | 11° |
| 11 | = | 11¹ |
| 121 | = | 11² |
| 1331 | = | 11³ |
Оказывается, всё, что нужно сделать — перенести десятки на одно число слева.
Совершенные квадраты
Если утверждать, что 4² — это 6 + 10 = 16, то можно найти идеальные квадраты натуральных чисел в столбце 2, суммируя число справа с числом ниже. Например:
- 2² → 1 + 3 = 4
- 3² → 3 + 6
- 4² → 6 + 10 = 16 и так далее.
Комбинаторные варианты
Чтобы раскрыть скрытую последовательность Фибоначчи, которая на первый взгляд может отсутствовать, нужно суммировать диагонали лево-выровненного паскалевского треугольника. Первые 7 чисел в последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, 13… найдены. Используя исходную ориентацию, следует заштриховать все нечётные числа, и получится изображение, похожее на знаменитый фрактальный треугольник Серпинского.
Возможно, самое интересное соотношение, найденное в треугольнике — это то, как можно использовать его для поиска комбинаторных чисел, поскольку его первые шесть строк написаны с помощью комбинаторной записи. Поэтому, если нужно рассчитать 4, стоит выбрать 2, затем максимально внимательно посмотреть на пятую строку, третью запись (поскольку счёт с нуля), и будет найден ответ.
Действия с биномами
Например, есть бином (x + y), и стоит задача повысить его до степени, такой как 2 или 3. Обычно нужно пройти долгий процесс умножения (x + y)² = (x + y)(x + y) и т. д. Если воспользоваться треугольником, решение будет найдено гораздо быстрее. К примеру, нужно расширить (x + y)³. Поскольку следует повышать (x + y) до третьей степени, то необходимо использовать значения в четвёртом ряду фигуры Паскаля (в качестве коэффициентов расширения). Затем заполнить значения x и y. Получится следующее: 1 x³ + 3 x²y + 3 xy² + 1 y³. Степень каждого члена соответствует степени, до которой возводится (x + y).
В виде более удобной формулы этот процесс представлен в теореме бинома. Как известно, всё лучше разбирать на примерах. Итак — (2x – 3)³. Пусть x будет первым слагаемым, а y — вторым. Тогда x = 2x, y = –3, n = 3 и k — целые числа от 0 до n = 3, в этом случае k = <0, 1, 2, 3>. Следует внести эти значения в формулу. Затем заполнить значения для k, которое имеет 4 разные версии, их нужно сложить вместе. Лучше упростить условия с показателями от нуля до единицы.
Как известно, комбинаторные числа взяты из треугольника, поэтому можно просто найти четвёртую строку и подставить в значения 1, 3, 3, 1 соответственно, используя соответствующие цифры Паскаля 1, 3, 3, 1. Последнее — необходимо завершить умножение и упрощение, в итоге должно получиться: 8 x³ — 36 x² + 54x — 27. С помощью этой теоремы можно расширить любой бином до любой степени, не тратя время на умножение.
Биномиальное распределение описывает распределение вероятностей на основе экспериментов, которые можно разделить на группы с двумя возможными исходами. Самый классический пример этого — бросание монеты. Например, есть задача выбросить «решку» — успех с вероятностью p. Тогда выпадение «орла» является случаем «неудачи» и имеет вероятность дополнения 1 – p.
Если спроектировать этот эксперимент с тремя испытаниями, с условием, что нужно узнать вероятность выпадения «решки», можно использовать функцию вероятности массы (pmf) для биномиального распределения, где n — это количество испытаний, а k — это число успехов. Предполагаемая вероятность удачи — 0,5 (р = 0,5). Самое время обратиться к треугольнику, используя комбинаторные числа: 1, 3, 3, 1. Вероятность получить ноль или три «решки» составляет 12,5%, в то время как переворот монеты один или два раза на сторону «орла» — 37,5%. Вот так математика может применяться в жизни.
http://www.analogi.net/razvivashki/golovolomka-volshebnyy-treugolnik
http://nauka.club/matematika/treugolnik-paskalya.html
From Wikipedia, the free encyclopedia
A magic triangle is a magic arrangement of the integers from 1 to n to triangular figure.
Perimeter magic triangle[edit]
A magic triangle or perimeter magic triangle[1] is an arrangement of the integers from 1 to n on the sides of a triangle with the same number of integers on each side, called the order of the triangle, so that the sum of integers on each side is a constant, the magic sum of the triangle.[1][2][3][4] Unlike magic squares, there are different magic sums for magic triangles of the same order.[1] Any magic triangle has a complementary triangle obtained by replacing each integer x in the triangle with 1 + n − x.[1]
Examples[edit]
Order-3 magic triangles are the simplest (except for trivial magic triangles of order 1).[1]
Other magic triangles[edit]
Other magic triangles use Triangular number or square number of vertices to form magic figure. Matthew Wright and his students in St. Olaf College developed magic triangles with square numbers. In their magic triangles, the sum of the k-th row and the (n-k+1)-th row is same for all k.[5] Its one modification uses triangular numbers instead of square nubers. (sequence A355119 in the OEIS) Another magic tringle form is magic triangles with triangluar numbers with different summation. In this magic triangles, the sum of the k-th row and the (n-k)-th row is same for all k. (sequence A356643 in the OEIS)
See also[edit]
- Magic hexagon
- Antimagic square
- Magic polygon
References[edit]
- ^ a b c d e «Perimeter Magic Triangles». www.magic-squares.net. Retrieved 2016-12-27.
- ^ «Perimeter Maghic Polygons». www.trottermath.net. Retrieved 2016-12-27.
- ^ «Magic Triangle : nrich.maths.org». nrich.maths.org. Retrieved 2016-12-27.
- ^ «P4W8: Magic Triangles and Other Figures» (PDF). Retrieved December 27, 2016.
- ^ Magic Triangles
Для быстрого запоминания формул и верного их применения тожемного различных способов. Какой из них использовать – дело вкуса.Нам на уроках математики на помощь приходит «волшебный»треугольник . Почему «волшебный»?
Этот треугольник помогает быстро составить формулу зависимостиодной переменной от двух других.
Чтобы не заучивать правил нахождения арифметическихдействий, научимся рисовать «волшебный» треугольник. На «верхний этаж» «селим» самое большое число — СУММУ. А внизу будут жить «малыши» — слагаемые. Между слагаемыми,естественно, живёт «+». А «гордая» СУММА отгородилась ото всех» стеной» — минусами.
Что нам говорит правило?
Чтобы найти неизвестное слагаемое, нужно из суммывычесть известное слагаемое.
На «верхний этаж» «селим» самое большое число -УМЕНЬШАЕМОЕ. А внизу будут жить «малыши» — вычитаемое и разность. Между жителями нижнего этажа живёт «+».
А «гордое» УМЕНЬШАЕМОЕ отгородилась ото всех » стеной» — минусами.
Что нам говорит правило?
Чтобы найти неизвестное уменьшаемое,
нужно к вычитаемому прибавить разность.
Чтобы найти неизвестное вычитаемое,
нужно из уменьшаемого вычесть разность
Нарисуем сразу же «волшебный» треугольник и будем использоватьего при решении всех задач на цену, количество, стоимость.
Чтобы найти стоимость, нужно цену умножить на количество. Ст = Ц х К
Чтобы найти цену, нужно стоимость разделить на количество. Ц= Ст : К
Чтобы найти количество, нужно стоимость разделить на цену. К= Ст : Ц
Нарисуем сразу же «волшебный» треугольник и будем использовать его при решении всех задач на движение.
Чтобы найти расстояние,нужно скорость умножить на время. S = V х t
Чтобы найти скорость, нужно расстояние разделить на время. V = S : t
Чтобы найти время, нужно расстояние разделить на скорость. t = S : V
Прием «волшебный» треугольник» очень прост вприменении. Нет необходимости тратить много времени иматериала на его изображение. Даже схематическая записьпоможет восстановить нужную зависимость величин. В тоже время этот треугольник помогает снять неуверенностьслабого ученика при решении задач на движение, нанахождение площади многоугольника, что особенно важно при подготовке к всероссийскимпроверочным работам уже с 4 класса.
Данный прием не является инновационным. Занимаясь вопросами изучения работы левого и правогополушарий, я пришла к выводу, что любой изучаемыйматериал должен быть хорошо структурирован и повозможности зарисован в виде схемы или опорногоконспекта. Тогда ребятам легче воспроизводить теорию наследующем уроке, а так же материал лучше запоминаетсяи легче используется в дальнейшем обучении.
Использование таких приемов повышаетуверенность обучающихся в своих силах, дает имвозможность верно выполнить задание и получитьположительную отметку на уроке, а так жесправиться с домашней работой без помощивзрослых.
А для сильных обучающихся эта подсказкапомогает быстро выучить новую формулу иструктурировать изучаемый материал, чтоположительно сказывается на мотивацииизучения предмета.
Сначала проссумируем все числа от 1 до 9. Получим 1 + 2 + и так далее = 45
Но сумма каждой стороны = 20, тогда сумма всех сторон равна 60
Но при этом каждая вершина будет участвовать в суммировании по 2 раза.
Таким образом получаем сумма трех вершин (трех чисел) = 60-45 = 15
Возможны варианты троек в вершинах
( Далее расписывал сколько всего способов и как всё это получается. Но кому всё это нужно. Система, ответы с математическими выкладками считает не уникальными, потому как там много цифр и символов. Поэтому сухой ответ без разбора)
Итого 4 варианта. Но каждую тройку вершин можно переставить 6 способами
Получается 6•4 = 24 способов расставить номера по вершинам
Для двух способов (1; 5; 9) и (3; 5; 7) однозначно определяется пара чисел на стороне.
Для двух других способов (2; 5; 
Но каждую пару можно поменять внутри стороны местами получится 8 различных перестановок. Получаем (24+12)•8 = 288 вариантов расположения шаров удовлетворяющих условию.
Какой именно был вариант угадать не предоставляется возможным. Но можно выбрать любой
Давайте возьмем для примера расстановку 1; 5; 9 в вершинах.
Максимальная сторона 5 + 9 = 14. Добавить 6 = 2 + 4
Минимальная сторона 1 + 5 = 6. Добавить 14 = 6 + 8
Остается 3-я сторона 1 + 9 = 10. Добавить 10 = 3 + 7
Нарисуем для каждого из 4 вариантов 6 различных комбинаций. Остальные комбинации будут получаться перестановкой вершин или перестановками внутри стороны.