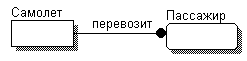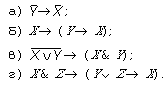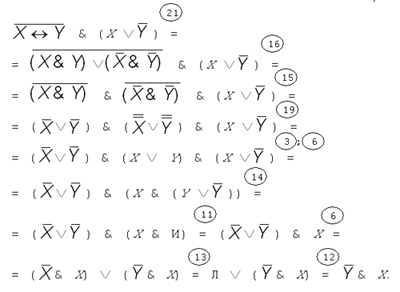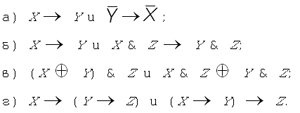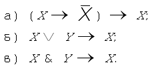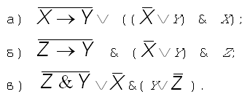Логическими
уровень – это абстрактный взгляд на
данные, на нем данные представляются
так, как выглядят в реальном мире, и
могут называться так, как они называются
в реальном мире.
Объекты
модели, представляемые на логическом
уровне, называются сущностями
и атрибутами.
Логическая модель данных может быть
построена на основе другой логической
модели, например на основе модели
процессов. Логическая модель данных
является универсальной и никак не
связана с конкретной реализацией СУБД.
Различают
три уровня логической модели, отличающихся
по глубине представления информации о
данных:
-
диаграмм
сущность-связь
(Entity Relationship Diagram, ERD); -
модель
данных, основанная на ключах (Key Based
model, KB); -
полная
атрибутная
модель
(Fully Attributed model, FA).
Диаграмма сущность-связьпредставляет
собой модель данных верхнего уровня.
Она включает сущности и взаимосвязи,
отражающие основные бизнес-правила
предметной области. Такая диаграмма не
слишком детализирована, в нее включаются
основные сущности и связи между ними,
которые удовлетворяют основным
требованиям, предъявляемым к ИС.
Диаграмма сущность-связь может включать
связи многие-ко-многим и не включать
описание ключей. Как правило, ERD
используется для презентаций и обсуждения
структуры данных с экспертами предметной
области.
Модель данных, основанная на ключах,
— более подробное представление данных.
Она включает описание всех сущностей
и первичных ключей и предназначена для
представления структуры данных и ключей,
которые соответствуют предметной
области.
Полная атрибутивнаямодель –
наиболее детальное представление
структуры данных: представляет данные
в третьей нормальной форме ивключает
все сущности, атрибуты и связи.
В данных методических указаниях будет
рассмотрена модель данных, основанная
на ключах.
Основные компоненты диаграммы ERwin –
это сущности, атрибуты и связи.
Каждая сущностьявляется множеством
подобных индивидуальных объектов,
называемых экземплярами. Каждый экземпляр
индивидуален и должен отличаться от
всех остальных экземпляров. Построение
модели данных предполагает определение
сущностей и атрибутов, т.е. необходимо
определить, какая информация будет
храниться в конкретной сущности или
атрибуте.Сущностьможно определить
как объект, событие или концепцию,
информация о которой должна сохраняться.
Сущности должны иметь наименование с
четким смысловым значением, именоваться
существительным в единственном числе,
не носить «технических» наименований
и быть достаточно значимыми для того,
чтобы их моделировать. Именование
сущности в единственном числе облегчает
в дальнейшем чтение модели. Фактически
имя сущности дается по имени ее экземпляра.
Сущность на диаграмме изображается
прямоугольником. В зависимости от режима
представления диаграммы прямоугольник
может содержать имя сущности, ее описание,
список ее атрибутов и другие сведения
(см. рис. 34).
Рис.
34.
Сущность с заполненными атрибутами.
Экземпляры независимойсущности
могут быть уникально идентифицированы
без определения ее связей с другими
сущностями;зависимаясущность,
наоборот, не может быть уникально
идентифицирована без определения ее
связей с другими сущностями. Зависимая
сущность отображается в ERwin прямоугольником
с закругленными углами (см. рис. 35).
Рис.
35.
Зависимая сущность с заполненными
атрибутами.
Зависимая сущность может наследовать
один и тот же внешний ключ от более чем
одной родительской сущности, или от
одной и той же родительской сущности
через использование несколько связей.
Если не введены различные роли для
такого множественного наследования,
ERwin считает, что в зависимой сущности
атрибуты внешнего ключа появляются
только один раз.
В зависимости от того, все ли возможные
сущности-подтипы включены в модель,
категорийная связь является полной или
неполной. Например, если супертип может
содержать данные об уволенных сотрудниках,
то эта связь — неполной категоризации,
так как для него не существует записи
в сущностях — подтипах. В ERwin полная
категория изображается окружностью с
двумя подчеркиваниями, а неполная —
окружностью с одним подчеркиванием.
Унификация— это объединение двух
или более групп атрибутов внешних ключей
в один внешний ключ (группу атрибутов),
в предположении, что значения одноименных
атрибутов в дочерней сущности всегда
одинаковы. Рассмотрим пример: сущность
«сотрудник» имеет первичный ключ
«код сотрудника» и связан
идентифицирующей связью с сущностями
«супруга» и «дети». При этом
происходит миграция первичного ключа
в зависимые сущности. В свою очередь,
сущность «супруга» связана не
идентифицирующей связью с сущностью
«дети». Имеются два пути миграции
ключа, однако в сущности «дети»
атрибут «код сотрудника» появляется
один раз в качестве элемента первичного
ключа. Существуют случаи, когда унификация
атрибутов дает неверный с точки зрения
предметной области результат. Для отмены
унификации для атрибутов вводятся имена
ролей.
Атрибутвыражает свойство объекта,
характеризующее его экземпляр
(определенное свойство объекта. С точки
зрения БД (физическая модель) сущности
соответствует таблица, экземпляру
сущности – строка в таблице, а атрибуту
– колонка таблицы. Горизонтальная линия
прямоугольника разделяет атрибуты
сущности на два набора: атрибуты,
составляющие первичный ключ (в верхней
части) и прочие, не входящие в первичный
ключ (в нижней части).
Первичный ключ— это атрибут или
набор атрибутов, уникально идентифицирующий
экземпляр сущности. Если несколько
наборов атрибутов могут уникально
идентифицировать сущность, то выбор
одного из них осуществляется разработчиком
на основании анализа предметной области.
Для каждого первичного ключа ERwin создает
при генерации структуры БД уникальный
индекс.
Если между некоторыми сущностями
существует связь, то факты из одной
сущности ссылаются или некоторым образом
связаны с фактами из другой сущности.
Связь– это функциональная зависимость
между сущностями. Поддержание
непротиворечивости функциональных
зависимостей между сущностями называется
ссылочной целостностью. Поскольку связи
содержатся «внутри» реляционной
модели, реализация ссылочной целостности
может выполняться как приложением, так
и самой СУБД (с помощью механизмов
декларативной ссылочной целостности,
триггеров). Связь это понятие логического
уровня, которому соответствует внешний
ключ на физическом уровне. Связь
называетсяидентифицирующей, если
экземпляр дочерней сущности идентифицируется
через ее связь с родительской сущностью.
Атрибуты, составляющие первичный ключ
родительской сущности, при этом входят
в первичный ключ дочерней сущности.
Дочерняя сущность при идентифицирующей
связи всегда является зависимой. Связь
называетсяне идентифицирующей,
если экземпляр дочерней сущности
идентифицируется иначе, чем через связь
с родительской сущностью. Атрибуты,
составляющие первичный ключ родительской
сущности, при этом входят в состав не
ключевых атрибутов дочерней сущности.
Для добавления сущности следует нажать
кнопку
,
а затем – щелкнуть «мышью» по свободному
месту диаграммы. После этого по созданному
элементу
следует щелкнуть два раза левой кнопкой
«мыши». В открывшемся диалоговом окне
Attributes(см. рис. 36) следует:
-
при
нажатии кнопки
ввести название сущности;
-
при
нажатии кнопки Newввести название и тип добавляемого
атрибута (список форматов возможных
типов представлен в табл. 5), а при
необходимости установить ему ключевой
признак вводом флажкаPrimary Key.
Рис.
36.
Окно для заполнения атрибутов сущности.
Таблица 5.
Расшифровка назначения типов атрибутов
-
Тип
Формат
Unknown
Не определен
Blob
Счетчик
Datetime
Дата или время
Number
Числовой
String
Текстовый
Для каждого атрибута имеется возможность
ввода дополнительных характеристик,
расположенных на вкладках окна Attributes:
-
General(основные характеристики атрибута);
-
Datatype(выбранный формат атрибута);
-
Definition(пояснения);
-
Note(комментарий для данного атрибута);
-
UDP(свойства атрибутов сущности, добавляемых
пользователем); -
Key
Group(отношение выбранного атрибута
к ключевым признакам); -
History(история возникновения атрибута).
Для связывания таблиц следует, нажав
кнопку
или
(идентифицирующая связь) или
(не идентифицирующая связь), щелкнуть
левой кнопкой «мыши» на одной таблице,
а затем щелкнуть «мышью» на другой
таблице, с которой требуется выполнить
связь.
Пример логической модели данных
представлен на рис. 37.
Для компактного расположения модели
на листе бумаги при печати следует
вызвать в меню FileрежимPrint, а в
открывшемся окнеPrint(см. рис.
38) нажать кнопкуFit
model.
Рис.
37.
Пример логической модели данных
Рис.
38.
Окно для настройки параметров печати.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- ознакомиться с технологией построения логической модели в ERWin,
- изучить методы определения ключевых атрибутов сущностей,
- освоить метод проверки адекватности логической модели,
- изучить типы связей между сущностями.
Первым шагом при создании логической модели БД является построение диаграммы ERD (Entity Relationship Diagram). ERD-диаграммы состоят из трех частей: сущностей, атрибутов и взаимосвязей. Сущностями являются существительные, атрибуты — прилагательными или модификаторами, взаимосвязи — глаголами.
ERD-диаграмма позволяет рассмотреть систему целиком и выяснить требования, необходимые для ее разработки, касающиеся хранения информации.
ERD-диаграммы можно подразделить на отдельные куски, соответствующие отдельным задачам, решаемым проектируемой системой. Это позволяет рассматривать систему с точки зрения функциональных возможностей, делая процесс проектирования управляемым.
ERD-диаграммы
Как известно основным компонентом реляционных БД является таблица. Таблица используется для структуризации и хранения информации. В реляционных БД каждая ячейка таблицы содержит одно значение. Кроме того, внутри одной БД существуют взаимосвязи между таблицами, каждая из которых задает совместное пользование данными таблицы.
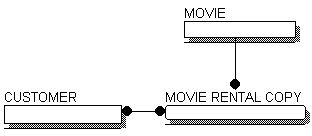
ERD-диаграмма графически представляет структуру данных проектируемой информационной системы. Сущности отображаются при помощи прямоугольников, содержащих имя. Имена принято выражать существительными в единственном числе, взаимосвязи — при помощи линий, соединяющих отдельные сущности. Взаимосвязь показывает, что данные одной сущности ссылаются или связаны с данными другой.
Рис. 6.1. Пример ERD-диаграммы,
Определение сущностей и атрибутов
Сущность — это субъект, место, вещь, событие или понятие, содержащие информацию. Точнее, сущность — это набор (объединение) объектов, называемых экземплярами. В приведенном на рис. 6.1 примере сущность CUSTOMER (клиент) представляет всех возможных клиентов. Каждый экземпляр сущности обладает набором характеристик. Так, каждый клиент может иметь имя, адрес, телефон и т. д. В логической модели все эти характеристики называются атрибутами сущности.
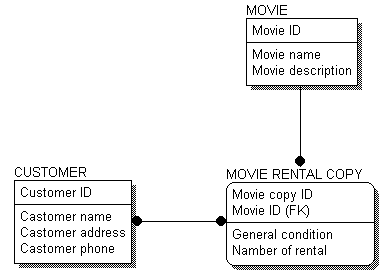
На рис. 6.2 показана ERD-диаграмма, включающая в себя атрибуты сущностей.
Рис. 6.2. ERD-диаграмма с атрибутами
Логические взаимосвязи
Логические взаимосвязи представляют собой связи между сущностями. Они определяются глаголами, показывающими, как одна сущность относится к другой.
Некоторые примеры взаимосвязей:
- команда включает много игроков,
- самолет перевозит много пассажиров,
- продавец продает много продуктов.
Во всех этих случаях взаимосвязи отражают взаимодействие между двумя сущностями, называемое «один-ко-многим». Это означает, что один экземпляр первой сущности взаимодействует с несколькими экземплярами другой сущности. Взаимосвязи отображаются линиями, соединяющими две сущности с точкой на одном конце и глаголом, располагаемым над линией.
Кроме взаимосвязи «один-ко-многим» существует еще один тип — это «многие-ко-многим». Этот тип связи описывает ситуацию, при которой экземпляры сущностей могут взаимодействовать с несколькими экземплярами других сущностей. Связь «многие-ко-многим» используют на первоначальных стадиях проектирования. Этот тип взаимосвязи отображается сплошной линией с точками на обоих концах.
Связь «многие-ко-многим» может не учитывать определенные ограничения системы, поэтому может быть заменена на «один-ко-многим» при последующем пересмотре проекта.
Проверка адекватности логической модели
Если взаимосвязи между сущностями были правильно установлены, то можно составить предложения, их описывающие. Например, по модели, показанной на рис. 6.3, можно составить следующие предложения:
Самолет перевозит пассажиров. Много пассажиров перевозятся одним самолетом.
Составление таких предложений позволяет проверить соответствие полученной модели требованиям и ограничениям создаваемой системы.
Рис. 6.3. Пример логической модели со взаимосвязью
Модель данных, основанная на ключах
Каждая сущность содержит горизонтальную линию, разделяющую атрибуты на две группы. Атрибуты, расположенные над линией, называются первичным ключом. Первичный ключ предназначен для уникальной идентификации экземпляра сущности.
Выбор первичного ключа
При создании сущности необходимо выделить группу атрибутов, которые потенциально могут стать первичным ключом (потенциальные ключи), затем произвести отбор атрибутов для включения в состав первичного ключа, следуя следующим рекомендациям:
Первичный ключ должен быть подобран таким образом, чтобы по значениям атрибутов, в него включенных, можно было точно идентифицировать экземпляр сущности. Никакой из атрибутов первичного ключа не должен иметь нулевое значение. Значения атрибутов первичного ключа не должны меняться. Если значение изменилось, значит, это уже другой экземпляр сущности.
При выборе первичного ключа можно внести в сущность дополнительный атрибут и сделать его ключом. Так, для определения первичного ключа часто используют уникальные номера, которые могут автоматически генерироваться системой при добавлении экземпляра сущности в БД. Применение уникальных номеров облегчает процесс индексации и поиска в БД.
Первичный ключ, выбранный при создании логической модели, может быть неудачным для осуществления эффективного доступа к БД и должен быть изменен при проектировании физической модели.
Потенциальный ключ, не ставший первичным, называется альтернативным ключом (Alternate Key). ERWin позволяет выделить атрибуты альтернативных ключей, и по умолчанию в дальнейшем при генерации схемы БД по этим атрибутам будет генерироваться уникальный индекс. При создании альтернативного ключа на диаграмме рядом с атрибутом появляются символы (АК).
Атрибуты, участвующие в неуникальных индексах, называются инверсионными входами (Inversion Entries). Инверсионные входы — это атрибут или группа атрибутов, которые не определяют экземпляр уникальным образом, но часто используются для обращения к экземплярам сущности. ERWin генерирует неуникальный индекс для каждого инверсионного входа.
При проведении связи между двумя сущностями в дочерней сущности автоматически образуются внешние ключи (foreign key). Связь образует ссылку на атрибуты первичного ключа в дочерней сущности, и эти атрибуты образуют внешний ключ в дочерней сущности. Атрибуты внешнего ключа обозначаются символами (FK) после своего имени.
Пример
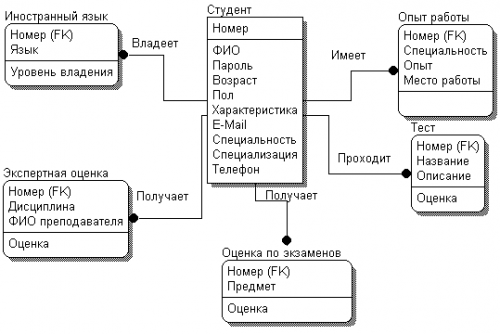
Рассмотрим процесс построения логической модели на примере БД студентов системы «Служба занятости в рамках вуза». Первым этапом является определение сущностей и атрибутов. В БД будут храниться записи о студентах, следовательно, сущностью будет студент.
Таблица 6.1. Атрибуты сущности «Студент»
| Атрибут | Описание |
| Номер | Уникальный номер для идентификации пользователя |
| Ф.И.О. | Фамилия, имя и отчество пользователя |
| Пароль | Пароль для доступа в систему |
| Возраст | Возраст студента |
| Пол | Пол студента |
| Характеристика | Memo-поле с общей характеристикой пользователя |
| Адреса электронной почты | |
| Телефон | Номера телефонов студента (домашний, рабочий) |
| Опыт работы | Специальности и опыт работы студента по каждой из них |
| Специальность | Специальность, получаемая студентом при окончании учебного заведения |
| Специализация | Направление специальности, по которому обучается студент |
| Иностранный язык | Список иностранных языков и уровень владения ими |
| Тестирование | Список тестов и отметки о их прохождении |
| Экспертная оценка | Список предметов с экспертными оценками по каждому из них |
| Оценки по экзаменам | Список сданных предметов с оценками |
В полученном списке существуют атрибуты, которые нельзя определить в виде одного поля БД. Такие атрибуты требуют дополнительных определений и должны рассматриваться как сущности, состоящие, в свою очередь, из атрибутов. К таковым относятся: опыт работы, иностранный язык, тестирование, экспертная оценка, оценки по экзаменам. Определим их атрибуты.
Таблица 6.2. Атрибуты сущности «Опыт работы»
|
Атрибут |
Описание |
| Специальность | Название специальности, по которой у студента есть опыт работы |
| Опыт | Опыт работы по данной специальности в годах |
| Место работы | Наименование предприятия, где приобретался опыт |
Таблица 6.3. Атрибуты сущности «Иностранный язык»
| Атрибут | Описание |
| Язык | Название иностранного языка, которым владеет студент |
| Уровень владения | Численная оценка уровня владения иностранным языком |
Таблица 6.4. Атрибуты сущности «Тестирование»
| Атрибут | Описание |
| Название | Название теста, который прошел студент |
| Описание | Содержит краткое описание теста |
| Оценка | Оценка, которую получил студент в результате прохождения теста |
Таблица 6.5. Атрибуты сущности «Экспертная оценка»
| Атрибут | Описание |
| Дисциплина | Наименование дисциплины, по которой оценивался студент |
| Ф.И.О. преподавателя | Ф.И.О. преподавателя, который оценивал студента |
| Оценка | Экспертная оценку преподавателя |
| Атрибут | Описание |
| Предмет | Название предмета, экзамен по которому сдавался |
| Оценка | Полученная оценка |
Составим ERD-диаграмму, определяя типы атрибутов и проставляя связи между сущностями (рис. 6.4). Все сущности будут зависимыми от сущности «Студент». Связи будут типа «один-ко-многим».
Рис. 6.4. ERD-диаграмма БД студентов
На полученной диаграмме рядом со связью отражается ее имя, показывающее соотношение между сущностями. При проведении связи между сущностями первичный ключ мигрирует в дочернюю сущность.
Следующим этапом при построении логической модели является определение ключевых атрибутов и типов атрибутов.
Таблица 6.7. Типы атрибутов
| Атрибут | Тип |
|
Номер |
Number |
|
Ф.И.О. |
String |
|
Пароль |
String |
|
Возраст |
Number |
|
Атрибут |
Тип |
|
Пол |
String |
|
Характеристика |
String |
|
|
String |
|
Специальность |
String |
|
Специализация |
String |
|
Опыт |
Number |
|
Место работы |
String |
|
Язык |
String |
|
Уровень владения |
Number |
|
Название |
String |
|
Описание |
String |
|
Оценка |
Number |
|
Дисциплина |
String |
|
Ф.И.О. преподавателя |
String |
|
Предмет |
String |
Выберем для каждой сущности ключевые атрибуты, однозначно определяющие сущность. Для сущности «Студент» это будет уникальный номер, для сущности «Опыт работы» все поля являются ключевыми, так как по разным специальностям студент может иметь разный опыт работы в разных фирмах. Сущность «Тест» определяется названием, так как студент по одному тесту может иметь только одну оценку. Оценка по экзамену определяется только названием предмета, экспертная оценка зависит от преподавателя, который ее составил, поэтому в качестве ключевых атрибутов выберем «Дисциплину» и «Ф.И.О. преподавателя». У сущности «Иностранный язык» уровень владения зависит только от наименования языка, следовательно, это и будет являться ключевым атрибутом.
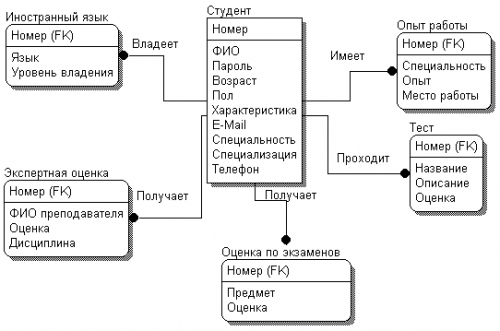
Получим новую диаграмму, изображенную на рис. 6.5, где все ключевые атрибуты будут находиться над горизонтальной чертой внутри рамки, изображающей сущность.
Рис. 6.5. ERD-диаграмма БД студентов с ключевыми атрибутами
Контрольные вопросы
- Назовите основные части ERD-диаграммы.
- Цель ERD-диаграммы.
- Что является основным компонентом реляционных БД?
- Что называется сущностью?
- Сформулируйте принцип именования сущностей.
- Что показывает взаимосвязь между сущностями?
- Назовите типы логических взаимосвязей.
- Каким образом отображаются логические взаимосвязи?
- Опишите механизм проверки адекватности логической модели.
- Что называется первичным ключом?
- Назовите принципы, согласно которым формируется первичный ключ.
- Что называется альтернативным ключом?
- Что называется инверсионным входом?
- В каком случае образуются внешние ключи?
Содержание отчета
- Тема, цель работы.
- ERD-диаграмма БД Служба занятости с атрибутами и ключами.
- Выводы по работе
Курсы повышения квалификации
Математические основы информатики
А.Г. Гейн
Учебный план
| №_ГАЗЕТЫ |
Лекция |
|
17/2007 |
Лекция 1. Что Информация и ее кодирование. |
|
18/2007 |
Лекция 2. Математические модели формальных исполнителей. Что такое формальная обработка информации? Конеч- ные автоматы. Что первично: язык или исполнитель? Грамматика языка. Распознаваемые языки. Универсальные исполни- тели (машина Тьюринга, машина Поста). |
|
19/2007 |
Лекция 3. Алгоритм и его свойства. Алгоритмическая неразрешимость. Вычислимость. Сложность. |
| Контрольная работа № 1. | |
|
20/2007 |
Лекция 4. Графы. Графы и орграфы. В каких задачах они возникают? Различные свойства графов (эйлеровость, гамильто- новость, планарность, двудольность). Сети. Потоки в сетях. Представление графов. Основные алгоритмы на графах. |
|
21/2007 |
Лекция 5. Логические модели в информатике. Алгебра высказываний. Булевы функции. Нормальные формы. Полные классы булевых функций. Релейно-контактные схемы. Вентили. Математические модели процессора и памяти компьютера. Предикаты и отношения. Реляционная алгебра. Теоретические основы реляционных СУБД. Языки логического программирования и их математическое основание. |
| Контрольная работа № 2. | |
|
22/2007 |
Лекция 6. Компьютерная теория чисел и вычислительная геометрия. Зачем нужна теория чисел в компьютерных науках? Гонка за простыми числами. Как разложить число на множители? Чем отличается теоретическая геометрия от вычислительной? Почему гладко на бумаге, но коряво на компьютере? Основные правила и алгоритмы вычислительной геометрии. |
| 23/2007 | Лекция 7. Защита информации. Защита символьной информации. Что нужно защищать? Электронная подпись. Системы верификации. Криптосистемы с открытым ключом. Защита графической информации. Математика электронных водяных знаков. |
| 24/2007 | Лекция 8. Основы методики преподавания математических основ информатики. |
| Итоговая работа |
Лекция 5. Логические модели в
информатике
Уже много сказано о возможностях
компьютеров и применяемых информационных
технологий, чтобы каждый понял, какую неоценимую
помощь может оказывать компьютер в
предоставлении и обработке информации. Однако за
человеком остается право (и обязанность) делать
выводы на основе предоставляемой информации и
принимать соответствующие решения. Конечно,
иногда мы говорим, что решение принимает
компьютер. Например, если компьютер, управляя
каким-либо автоматом, получает от датчиков этого
автомата информацию об опасности его разрушения
в тех условиях, в которых он оказался, то
компьютер может “принять решение” об эвакуации
автомата из этой обстановки. Но каждому ясно, что
на самом деле это решение было заранее
запрограммировано человеком и компьютер, как
обычно, безоговорочно следует инструкции.
Принятие решения — это в конечном
счете всегда прерогатива человека. Во-первых,
потому что любая информация в компьютере лишь
модельно отражает реальную действительность, и,
следовательно, принимаемое компьютером решение
может оказаться неадекватным сложившейся
ситуации.
В вышеприведенном примере вполне вероятна
ситуация, что автомат должен погибнуть, чтобы
предотвратить большее несчастье. Во-вторых,
передать компьютеру право принимать решения —
значит вверить судьбу человечества электронике.
И хотя сегодня бунт роботов — это все еще удел
фантастических произведений, в их основе лежит
именно предположение о предоставлении
компьютеру права принимать решения наравне с
человеком.
Тем не менее помощь компьютера в
решении человеком информационных задач намного
бы выросла, если бы компьютер “научился”
предлагать человеку на выбор обоснованные
варианты возможных решений. Но для этого надо
научить компьютер делать выводы из имеющейся
информации. Иными словами, надо в компьютере
смоделировать процесс рассуждений, которые
проводит человек.
О тех подходах к решению данной проблемы, которые
сегодня разрабатываются в информатике, и пойдет
речь в этой лекции.
Первым, кто предпринял удачную попытку
построить модель человеческих рассуждений, был,
по мнению историков науки, древнегреческий
ученый Аристотель. Именно он сформулировал
первые законы рассуждений, заложив основы новой
науки, названной им логикой. В дальнейшем
вклад в эту науку вносили психологи и философы,
лингвисты и математики. У этой науки появились
разные направления исследований, она
разделилась на ряд областей, одна из которых
называется формальной, или математической,
логикой. Более того, происходила не только
специализация исследований внутри логики, но и
расширение сферы исследований на всю
интеллектуальную деятельность человека. Как
человек распознает предметы и явления, как
происходит обучение и самообучение, как
вырабатываются стратегии в реальной жизни или
играх, каковы механизмы стихосложения и
сочинения музыки — все это стало предметом
исследований ученых. А модели, создаваемые в
результате таких исследований, стали называть
моделями искусственного интеллекта.
§ 16. Элементы логики высказываний
Психологи давно установили, что
мыслительная деятельность человека всегда
осуществляется посредством какого-либо языка.
Использование языка придает мыслительной
деятельности форму рассуждений. Что такое
рассуждение? Ответить можно так: это
последовательность вопросов, задаваемых самому
себе или собеседнику, и ответов на них.
Вопросы могут быть разного типа. Можно
спросить: “Сколько существует простых чисел?”
Ответом служит утверждение: “Простых чисел
бесконечно много”. Можно спросить: “Как найти
тысячное простое число?” Ответом будет алгоритм,
позволяющий вычислить требуемое простое число.
Информацию, содержащуюся в ответе на первый
вопрос, обычно относят к декларативному типу,
а информацию, содержащуюся в ответе на второй
вопрос, — к процедурному.
Напомним, что среди свойств
алгоритмов, обсуждавшихся нами в лекции 3, есть,
например, результативность и правильность. А вот
информацию, представленную декларативно, можно,
пожалуй, оценить только с одной позиции —
истинна она или ложна.
Повествовательное предложение, в
отношении которого имеет смысл говорить о его
истинности или ложности, называется высказыванием.
Такое определение высказыванию дал Аристотель,
который, как было сказано выше, считается
основоположником логики как науки.
Рассмотрим следующие предложения.
1. Число иррационально.
2. Число рационально.
3. Любое натуральное число х
рационально.
4. Любое число х рационально.
5. Существует число х, которое
иррационально.
6. Число х рационально.
7. Если число х иррационально, то
число х + 1 тоже иррационально.
8. Число называется рациональным, если
оно равно отношению целого числа к натуральному.
9. Верно ли, что число иррационально?
10. Докажите, что число иррационально.
Первые пять предложений, очевидно,
являются высказываниями, причем первое, третье и
пятое истинны, а второе и четвертое ложны. Два
последних предложения не являются
высказываниями, поскольку они вовсе не
повествовательные: одно из них вопросительное, а
другое — побудительное. Предложение 8 не
является высказыванием, поскольку об его
истинности говорить бессмысленно — оно лишь
определяет новое понятие через ранее введенные.
В повествовательном предложении 6
истинность заключенной в нем информации зависит
от значения переменной х: при одних ее
значениях утверждение окажется истинным, при
других — ложным. Так что это предложение нельзя
отнести к высказываниям (мы рассмотрим подобные
утверждения несколько позже). Точно так же
переменную х содержит предложение 7, поэтому
и его не следует относить к высказываниям. Но
если задуматься о смысле этого предложения, то
станет ясно, что оно истинно при любом значении
переменной х.
Пример предложения 7 показывает, что
данное Аристотелем объяснение, что такое
высказывание, не является, строго говоря,
определением. Более того, оно фактически
перекладывает на плечи других научных дисциплин
— математики, физики, химии, биологии, истории
(список вы легко продолжите сами) — саму проблему
получения ответа на вопрос, будет ли истинным то
или иное утверждение. И вот если ответ на такой
вопрос будет получен, то это утверждение получит
право называться высказыванием.
Впрочем, для некоторых утверждений
ответ об их истинности или ложности нельзя
получить никакими средствами. Вот одно из таких
утверждений: “Это предложение ложно”. Если
предположить, что само это утверждение истинно,
то оно обязано быть ложным. Если же считать, что
утверждение ложно, то оно обязано быть истинным.
Выявление и недопущение в рассуждениях подобных
внутренне противоречивых утверждений — тоже
одна из задач логики.
Оставляя другим наукам отвечать на
вопрос об истинности конкретного утверждения,
логика интересуется, как из набора истинных
утверждений можно получать новые истинные
утверждения. Это означает, что логика изучает
такие операции над высказываниями, в результате
применения которых снова получается
высказывание. При этом вовсе не требуется
вникать в смысл высказываний, над которыми
производятся операции. Математическая логика
предлагает формализованный язык для описания
этих операций, что позволяет построить
формальную модель человеческих рассуждений.
С некоторыми логическими операциями
вы наверняка знакомы еще по базовому курсу
информатики. Это прежде всего операция
конъюнкции (по-другому, операция и),
дизъюнкции (по-другому, операция или) и
операция отрицания (по-другому, операция не).
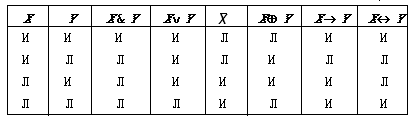
Но есть и другие операции, они перечислены в табл.
5.1.
Таблица 5.1
В названиях и обозначениях логических
операций, приведенных в табл. 5.1, на первом месте
указаны те, которые будут использоваться нами. В
другой литературе по математической логике
употребляются и другие из указанных названий и
обозначений.
Во всех логических операциях, кроме
операции отрицания, участвуют два аргумента.
Поэтому применение, например, конъюнкции к
высказываниям X и Y обычно записывают как X
& Y, а применение импликации к тем же
высказываниям как X Y. Отрицание высказывания X
записывают в виде .
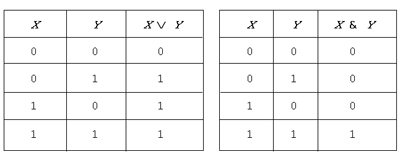
Значения логических операций задаются
с помощью так называемых таблиц истинности. В
них для всевозможных комбинаций значений
аргументов записывается результат применения
операции. Для всех операций одновременно эти
таблицы собраны в табл. 5.2; в ней значения
аргументов и результат применения операции
обозначены буквами И (истина) и Л (ложь).
Таблица 5.2
Как видно из таблицы, истинность
высказывания, полученного применением
дизъюнкции, имеет место, когда истинно либо одно
высказывание, либо другое, либо оба одновременно.
К примеру, истинность высказывания “Идет дождь или
дует ветер” означает, что на улице имеет место
одна из трех ситуаций: идет дождь и нет ветра; нет
дождя, но дует ветер; одновременно идет дождь и
дует ветер. Поэтому, записывая данную фразу
средствами математической логики, естественно
представить ее в виде X
Y, где X — это высказывание “Идет дождь”,
а Y — высказывание “Дует ветер”.
А вот высказывание “Петя сидит на
уроке физики или Петя сидит на уроке
истории”, когда оба высказывания, из которых оно
составлено, истинны, следует признать ложным —
не может Петя одновременно быть и на уроке
физики, и на уроке истории. Здесь по смыслу
применена операция исключающего ИЛИ. Поэтому,
переводя эту фразу на язык математической
логики, естественно воспользоваться операцией “” и, соответственно,
записать X Y,
где X — это высказывание “Петя сидит на уроке
физики”, а Y — высказывание “Петя сидит на
уроке истории”.
Возможно, вас удивила таблица
истинности для операции следования. Многим
кажется, что утверждение “Если X, то Y”
истинно в том и только том случае, когда X и Y
одновременно истинны, т.е. совпадает с
конъюнкцией этих высказываний. Но давайте
подумаем, когда ложно каждое из высказываний X
& Y и X ® Y. Легко понять, что
конъюнкция X и Y ложна тогда и только
тогда, когда ложно хотя бы одно из высказываний X
или Y. А ложность высказывания “Если X, то Y”
означает, что хотя высказывание Х истинно,
высказывание Y ложно. Отсюда и вытекает то
формальное определение импликации, которое
приведено в табл. 5.2. В частности, высказывание
“Если 2 х 2 = 5, то 2 х 2 = 4” истинно. Как, впрочем,
истинно и высказывание “Если
2 х 2 = 5, то 2 х 2 = 3”. Нередко отмеченное свойство
импликации формулируют так: из истины следует
истина, а из лжи — что угодно.
Обычно с помощью логических операций
стараются свести любое высказывание к таким
высказываниям, в которых уже нельзя выделить
другие высказывания. Такие высказывания, никакая
часть которых высказыванием не является,
называются простыми.
Вопросы и задания
1. Из приведенных ниже предложений
выберите высказывания и обоснуйте свой выбор.
а) Выхожу один я на дорогу.
б) Я спросил у ясеня: “Где моя
любимая?”
в) Зачем вы, девушки, красивых любите?
г) Если у вас нет собаки, ее не отравит
сосед.
д) Давайте восклицать, друг другом
восхищаться.
е) Не пой, красавица, при мне ты песен
Грузии печальной.
ж) Вот кто-то с горочки спустился.
з) Ничего на свете лучше нету, чем
бродить друзьям по белу свету.
и) Умом Россию не понять.
к) Но кто-то камень положил ему в
протянутую руку.
2. Для приведенных ниже высказываний
укажите, какие из них истинны и какие ложны.
а) Число 3 является делителем любого
числа, у которого сумма цифр равна 6.
б) Некоторые млекопитающие не живут на
суше.
в) Никто не может объять необъятное.
г) Демосфен утверждал: “В одну реку
нельзя войти дважды”.
д) Каждый год есть месяц, в котором 13-е
число приходится на пятницу.
3. Для приведенных ниже высказываний
попытайтесь указать, какие из них истинны и какие
ложны.
а) Натуральных чисел бесконечно много.
б) Если диагональ выпуклого
четырехугольника разбивает его на два равных
треугольника, то этот четырехугольник
параллелограмм.
в) Серединный перпендикуляр к отрезку
— это множество точек, равноудаленных от концов
данного отрезка.
г) В десятичной записи числа p
встречается 100 раз подряд цифра 9.
д) В записи числа 1/7 в виде бесконечной
десятичной дроби не встречается цифра 9.
е) Каждое натуральное число либо
простое, либо произведение простых чисел.
ж) Для всех действительных значений х
выполнено неравенство .
з) Для всех действительных значений х
выполнено неравенство .
и) Любое натуральное число, у которого
сумма цифр равна 2, не делится на 7.
Для всех ли высказываний вам удалось
выполнить задание? Почему тем не менее можно
утверждать, что все приведенные в пунктах а) — и)
предложения являются высказываниями?
4. В приведенных ниже высказываниях
выделите два простых, обозначьте их буквами и
запишите все высказывания с помощью этих
обозначений и логических операций.
а) Петя и Коля идут гулять.
б) Петя идет гулять, а Коля гулять не
идет.
в) Если Коля идет гулять, то Петя гулять
не идет.
5. Укажите, какую, на ваш взгляд,
дизъюнкцию — обычную или разделительную — надо
употребить при записи следующих высказываний на
языке математической логики.
а) На деревьях распустились листья или
раскрылись бутоны.
б) На улице замерз ртутный градусник
или от жары пересохла речка.
в) На небе светит Солнце или видна Луна.
6. Определите, какие из приведенных
ниже импликаций истинны.
а) Если число 1357 нечетно, то оно делится
на 3.
б) Если число 1357 четно, то оно делится
на 3.
в) Если число 1357 нечетно, то оно не
делится на 3.
г) Если число 1357 делится на 3, то оно
нечетно.
д) Если число 1357 не делится на 3, то оно
нечетно.
е) Если число 1357 не делится на 3, то оно
четно.
7. Составьте таблицы истинности для
высказываний
§ 17. Законы алгебры высказываний
В математике алгеброй называется
дисциплина, изучающая свойства операций на
множествах. Школьная алгебра изучает множество
действительных чисел и операции сложения,
умножения, вычитания, деления, возведения в
степень, которые над этими числами можно
выполнять. Некоторые свойства операций известны
всем еще по начальной школе, например,
переместительный закон сложения: от перемены
мест слагаемых сумма не меняется. Справедлив
аналогичный закон и для умножения чисел.
Одно из важных изобретений человека,
которое легло в основу алгебры, — это введение
буквенной символики для записи свойств операций.
К примеру, тот же переместительный закон
сложения записывается с помощью букв совсем
просто: a + b = b + a. Такие равенства,
которые верны при любых значениях букв,
называются тождествами. По мере изучения
алгебры тождеств появлялось все больше и больше,
скажем,
(a + b)2 = a2 + 2ab + b2,
(ab)n = anbn и т.д.
Прелесть тождеств состоит в том, что, подставляя
одни тождества в другие, можно получать новые
тождества. Такую процедуру называют тождественными
преобразованиями.
Математическая логика, а точнее, тот
раздел, о котором мы сейчас рассказываем, имеет
дело с множеством высказываний. В предыдущем
параграфе мы ввели несколько операций над
высказываниями. Следовательно, существует
алгебра высказываний — раздел математической
логики, изучающий свойства операций над
высказываниями. Нас прежде всего будут
интересовать те свойства, которые записываются
как тождества. Только в нашем случае буквы будут
обозначать произвольные высказывания, а знак
равенства будет по-прежнему выражать тот факт,
что значение левой части равенства совпадает со
значением правой части равенства, какие бы
высказывания мы в них не подставляли (разумеется,
вместо одинаковых букв мы должны подставлять
одно и то же высказывание, хотя вовсе не
обязательно, чтобы разные буквы заменялись
разными высказываниями). В математической логике
такие тождественно равные высказывания принято
называть равносильными. Сами высказывания, в
которых фигурируют буквы, обозначающие
произвольные высказывания и соединенные знаками
логических операций, называются формулами.
Буквы, входящие в такие формулы, называют логическими
переменными. Формулы называются тождественно
равными или равносильными, если
равносильны представленные ими высказывания.
В алгебре действительных чисел
доказательство тождеств подчас является
довольно трудным делом, требующим определенной
изобретательности. В алгебре высказываний
доказательство тождества — процесс несложный,
хотя и может оказаться весьма трудоемким.
Причина здесь в том, что действительных чисел
бесконечно много и все не перепробуешь,
подставляя их вместо переменных. Что касается
алгебры высказываний, то, как вы знаете, значение
выражения, составленного с помощью логических
операций из других высказываний, зависит только
от истинности и ложности входящих в его состав
высказываний. Поэтому, составив таблицы
истинности для двух таких высказываний, мы можем
легко убедиться, равносильны они или нет.
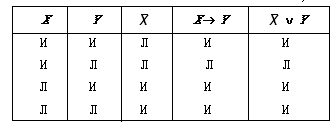
Убедимся, к примеру, в равносильности
высказываний X Y
и XY.
Таблица 5.3
Всем видно, что столбцы для X Y и X
Y совпали. Значит, можно записать X
Y = X
Y.
Приведем список основных тождеств
алгебры высказываний.
Мы выше проверили равенство под
номером 20. Остальные равенства можно проверить
тем же способом — составить таблицы истинности.
Мы оставляем это читателю.
Приведенные выше законы алгебры
логики обычно используют для преобразования
одних формул в другие, им равносильные. Вот
пример (в кружочках над равенствами указаны
применяемые законы):
Приведенные 22 тождества вовсе не
являются независимыми друг от друга — можно одни
из них получать, используя другие тождества того
же списка. Вот как, например, выводится закон
поглощения (тождество 17) из тождеств 11, 1, 6 и 10:
Закон ассоциативности для операции
конъюнкции позволяет не писать скобки, если эта
операция применяется подряд к нескольким
переменным. Например, вместо можно писать просто X & Y
& Z & U & V. Именно так мы и будем
делать. Аналогично будем записывать выражения с
операцией “”. Если же в
записи высказывания встречаются разные операции
— отрицание, конъюнкция, дизъюнкция, импликация,
— то договоримся, что приоритет их выполнения
отдается в указанном порядке: сначала
выполняется отрицание, затем конъюнкция, а уже
затем дизъюнкция. Если же порядок выполнения
операций надо изменить, то применяют скобки.
Поэтому выражения (X & Y) (Z & U) и X & Y
Z & U совпадают, но
отличаются от X & (Y Z) & U. Операции “
” и “
”
имеют самый низкий приоритет.
Формула называется тождественно
истинной, или тавтологией, если она
принимает значение истина при любых значениях
входящих в нее переменных. Примером простейшей
тавтологии является формула X X.
Из определения операции “” следует, что формулы F1 и F2
равносильны тогда и только тогда, когда формула F1
F2 является
тавтологией.
Подчеркнем еще раз, что математическая
логика лишь моделирует логику человеческого
рассуждения. К примеру, высказывания X & Y
и Y & X математическая логика признает
равносильными. И действительно, высказывания
“идет дождь и дует ветер” и “дует ветер и идет
дождь” в смысловом содержании идентичны друг
другу. Но сравните высказывания: “Она вошла в
зал, и заиграла музыка”, и “Заиграла музыка, и
она вошла в зал”, — и вы почувствуете тонкую, но
вполне уловимую разницу, идущую от человеческого
восприятия союза “и” как некой упорядоченности
событий по времени. Впрочем, в некоторых
трансляторах с языков программирования операции
дизъюнкции и конъюнкции также не коммутативны
(например, в некоторых версиях языка Пролог).
Каким бы ни было сложное высказывание,
для него всегда можно составить таблицу
истинности. А если дана некоторая таблица
истинности, то всегда ли можно записать сложное
высказывание, у которого была бы именно такая
таблица истинности? Ответ на этот вопрос
положителен. Мы покажем на примере, как строить
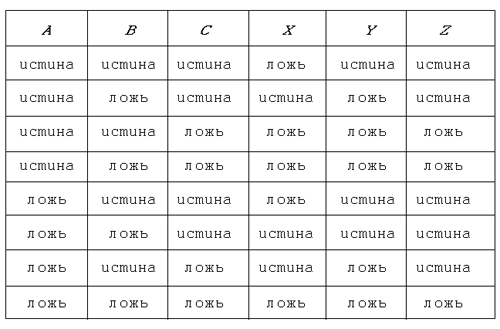
сложное высказывание по таблице истинности, а
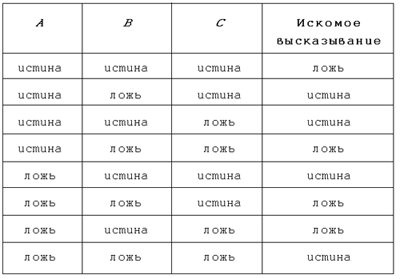
потом сформулируем общее правило. Пусть, к
примеру, таблица истинности выглядит так:
Таблица 5.4
Выберем строки, в которых для
искомого высказывания стоит значение истина.
Для каждой такой строки вместо значения истина
в столбце простого высказывания напишем само
высказывание, а вместо значения ложь напишем
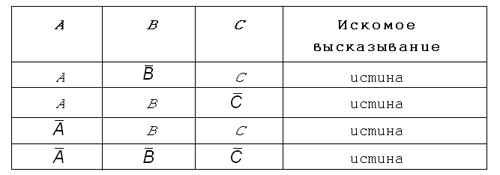
его отрицание. Получится так:
Таблица 5.5
Теперь в каждой строке соединим
получившиеся высказывания конъюнкцией, а
полученные таким способом сложные высказывания
— дизъюнкцией. У нас получится следующее
высказывание:
Конечно, это высказывание можно
теперь преобразовывать по указанным ранее
законам.
В общем случае надо поступать точно
так же:
— оставить в таблице те строки, в
которых значение искомого выражения — истина;
— в каждой клетке этих строк записать
вместо слова истина само высказывание из
заголовка столбца, а вместо слова ложь
записать его отрицание;
— соединить конъюнкцией высказывания,
стоящие в одной строке, а затем соединить
дизъюнкцией получившиеся высказывания для всех
отобранных строк.
Обратите внимание, что по этому
алгоритму всегда получается формула, в которой
используются только операции отрицания,
конъюнкции и дизъюнкции, причем так, что
отрицание применяется только к переменным,
конъюнкцией соединены переменные или их
отрицания, причем каждая переменная в таком
конъюнктивном выражении фигурирует ровно один
раз, и, наконец, дизъюнкции соединяют
получившиеся конъюнктивные выражения.
Выражение, записанное в таком виде, называется совершенной
дизъюнктивной нормальной формой (сокращенно
СДНФ). В силу договоренностей о порядке
выполнения операций в СДНФ скобки не требуются.
Вопросы и задания
1. Какие высказывания, содержащие
переменные, обозначающие высказывания,
называются равносильными?
2. Составьте таблицы истинности и
выясните, равносильны ли следующие высказывания.
3. а) Составив таблицы истинности,
проверьте равенства 1) — 6), приведенные в
объяснительном тексте параграфа.
б) Проверьте законы де Моргана,
составив соответствующие таблицы истинности.
4. а) Выведите тождество 18 из тождеств с
меньшими номерами.
б) Покажите, что законы де Моргана
выводятся друг из друга с помощью закона
двойного отрицания.
5. Проверьте, что следующие формулы
являются тавтологиями.
а) X X;
б) X (Y
X).
6. Выясните, какие из следующих формул
являются тавтологиями.
7. Выразите высказывание X через
высказывания А и В, если имеет место
равенство .
8. Выясните, существует ли такая
формула F, при подстановке которой в
следующую формулу эта формула становится
тавтологией.
9. а) Запишите через А, В и С
высказывания Х, Y и Z, заданные
следующей таблицей истинности.
Таблица 5.6
б) Запишите выражения , и преобразуйте их в
равносильные выражения, не содержащие скобок.
10. а) Известно, что высказывание F,
зависящее от трех высказываний А, В и С,
принимает то значение для каждого данного набора
значений А, В
и С, которое принимает большинство из этих
трех высказываний. Функцию F поэтому называют
функцией голосования. Составьте для F
логическую формулу.
б) Составьте логическую формулу для
функции голосования от четырех переменных.
§ 18. Контактные схемы
Контактом (или переключателем)
называется устройство, которое в процессе работы
может находиться в одном из двух состояний:
замкнутом или разомкнутом.
Контакт Х на чертеже будем
изображать следующим образом:
Рис. 1. Изображение контакта
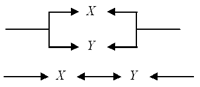
Два контакта X и Y можно
соединить между собой различными способами. Вот
два из них:
Рис. 2. Параллельное и
последовательное соединения контактов
Первое соединение называется
параллельным, второе — последовательным.
Контакты, соединенные между собой, называют контактной
схемой. Будем предполагать наличие у схемы
двух выделенных точек — входа и выхода. Схему
назовем замкнутой, если существует
последовательность замкнутых контактов Х1,
Х2, …, Хn такая, что Xi
соединен с Хi+1, X1 соединен с
входом, Хn — с выходом. Схему, не
являющуюся замкнутой, назовем разомкнутой.
Каждому контакту поставим в соответствие
высказывание, которое истинно тогда и только
тогда, когда контакт замкнут. Высказывание и
контакт будем обозначать одной буквой.
Пусть схема S построена из
контактов Х1, Х2, …, Хn
с помощью параллельного и последовательного
соединений. Тогда по схеме S можно построить
формулу логики высказываний FS так, что
параллельному соединению соответствует
дизъюнкция, последовательному — конъюнкция.
Кроме того, действия некоторых контактов могут
быть согласованными между собой. Если, к примеру,
контакт Y замкнут тогда и только тогда, когда
замкнут контакт X, то естественно такие
контакты обозначить одной и той же буквой,
скажем, X. Если же, наоборот, контакт Y
замкнут тогда и только тогда, когда контакт X
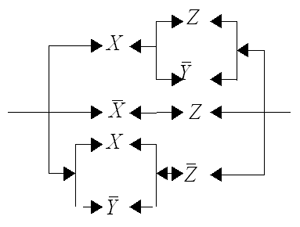
разомкнут, то контакт Y будем обозначать . На рис. 3
представлена некоторая схема S0, для
которой соответствующая формула выглядит так:
Рис. 3. Контактная схема
Формула FS “представляет”
схему S в следующем смысле: схема S
замкнута в том и только в том случае, если Fs
принимает значение истина. Нетрудно понять,
что по всякой такой формуле F можно
восстановить схему, которую формула F
представляет.
Пусть схемам S и T соответствуют
формулы FS и FT в описанном выше
смысле. Тогда если схемы S и T эквивалентны
(т.е. замкнуты и разомкнуты одновременно), то FS
и FT равносильны, и обратно. Этот факт
используется для решения задачи минимизации
контактных схем, которая состоит в том, чтобы по
данной схеме S найти схему Т,
эквивалентную S и содержащую меньше
контактов. Один из путей решения этой задачи
состоит в переходе к формуле FS и в
отыскании формулы G, равносильной FS
и содержащей меньше вхождений атомарных формул
(разумеется, G построена только с помощью
“&”, “” и “_”,
причем отрицание применяется лишь к переменным).
Так, например, формула FS0
равносильна формуле . Следовательно, схема, приведенная на рис.
3, эквивалентна следующей схеме (см. рис. 4), в
которой на три контакта меньше.
Рис. 4
Скажем откровенно: сегодня еще не
придуман алгоритм, позволяющий гарантированно
строить схему с минимальным количеством
контактов, хотя есть некоторые методы,
позволяющие оптимизировать некоторые схемы.
Большой вклад в создание таких методов внесли
российские ученые Ю.И. Журавлев, С.В. Яблонский и
др.
Впрочем, отсутствие такого алгоритма
частично объясняется тем, что существуют
контактные схемы, в которых параллельные и
последовательные соединения осуществляются не
столь прямолинейно. Рассмотрим, для примера,
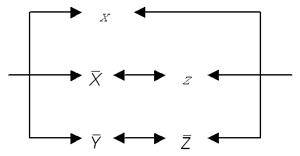
такую схему (рис. 5):
Рис. 5. Мостовая схема
Как в этой схеме контакт Z соединен
с контактом X? Последовательно или
параллельно? Однозначного ответа тут не дать.
Между двумя параллельными ветками переброшен
мостик. Поэтому и схему такую называют мостовой.
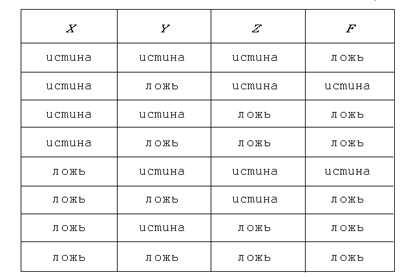
Тем не менее для нее нетрудно составить таблицу
“истинности”.
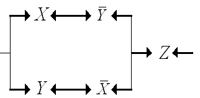
По этой таблице уже нетрудно записать
формулу для F, а затем построить реализующую
ее последовательно-параллельную схему:
Здесь уже потребуется 6 контактов.
Впрочем, воспользовавшись дистрибутивным
законом, формулу F можно привести к более
экономному виду:
Таблица 5.7
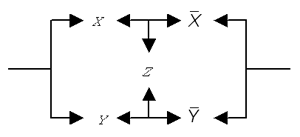
А схема для нее выглядит так:
Рис. 6. Последовательно-параллельная
схема, эквивалентная мостовой
В данном случае обе схемы получились
содержащими один и тот же набор контактов. Но
мостовые схемы, как правило, оказываются
экономнее последовательно-параллельных.
Вопросы и задания
1. Для следующих цепей построить
эквивалентные им более простые цепи:
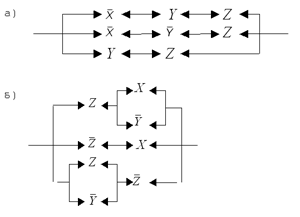
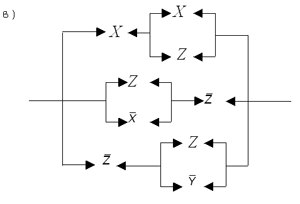
2. Для каждой мостовой схемы,
изображенной на рис. 8, построить
эквивалентную ей последовательно-параллельную
схему.
Рис. 8
3. Требуется, чтобы включение света в
комнате осуществлялось с помощью трех различных
переключателей таким образом, чтобы нажатие на
любой из них приводило к включению света, если
света не было, и выключению света, если тот горел.
Построить по возможности наиболее простую
переключательную схему, удовлетворяющую этому
требованию.
§ 19. Сумматор
В предыдущем параграфе мы
отождествили каждый контакт с некоторой
переменной. Пусть X и Y — два контакта, или,
по-другому, две переменные, каждая из которых
способна принимать ровно два значения: 1 или 0.
Тогда их параллельное соединение соответствует
дизъюнкции этих переменных (по-другому, операции
ИЛИ), а последовательное соединение — их
конъюнкции (операции И). В табл. 5.8 мы уже в
символах 1 и 0 (а не истины и лжи) еще раз
описали эти операции.
Таблица 5.8
Можно считать, что у нас имеются
два устройства, которые выполняют указанные
операции. Кроме того, естественно считать, что у
нас есть еще операция инверсии — логическое
отрицание. Для этих операций имеются даже
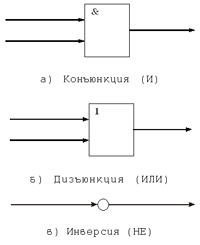
специальные обозначения (ГОСТ 2.745.91):
Рис. 9
Принято указанные операции называть вентилями:
вентиль И, вентиль ИЛИ, вентиль НЕ.
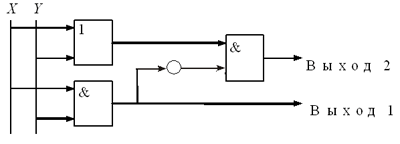
А теперь из вентилей соберем схему,
указанную на рис. 10.
Рис. 10
Чтобы понять, как преобразует входные
сигналы X и Y предложенная схема, составим
таблицу результатов (см. табл. 5.9).
Таблица 5.9
Сравнивая получившуюся таблицу с
таблицей сложения однозначных чисел в двоичной
системе счисления, приходим к выводу, что наше
устройство на выходах дает два сигнала, которые
поразрядно кодируют сумму двух однозначных
чисел в двоичной системе счисления. А поскольку
действия над числами, записанными в позиционной
системе, выполняются поразрядно, то ясно, что
аналогичным образом можно построить электронные
схемы для сложения многозначных чисел,
представленных в двоичной системе счисления.
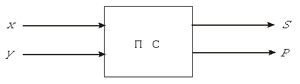
Электронную схему, изображенную на рис. 10,
называют полусумматором. В дальнейшем для
краткости полусумматор будем изображать одним
блоком (см. рис. 11).
В нем буквой S обозначен младший разряд суммы,
а буквой Р — старший разряд или, по-другому,
перенос единицы в следующий разряд суммы.
Рис. 11. Полусумматор
При сложении многозначных чисел в
старших разрядах приходится учитывать появление
так называемой “единицы переноса”. Это
означает, что в этих разрядах складываются не два
однозначных числа, а три. Используя полусумматор
как самостоятельный блок, схему сумматора
для сложения чисел в двоичной системе счисления
можно изобразить так, как показано на рис. 12.
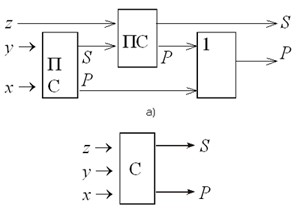
Здесь x и y — единицы разрядов слагаемых, а
z — перенос из суммы предыдущих разрядов;
выходы S и Р имеют тот же смысл, что и для
полусумматора.
Рис. 12. Схема сумматора (а) и его
обозначение
в виде блока (б)
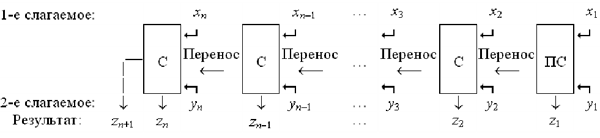
Чтобы сложить два многозначных числа,
нужно выстроить батарею сумматоров так, как
показано на рис. 13.
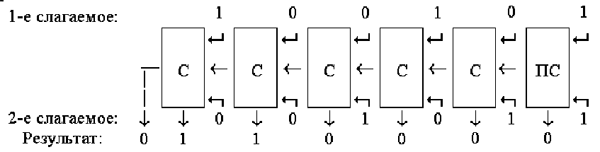
А на рис. 14 показана работа такой
батареи для чисел 100101 и 1011.
В современном компьютере никто,
конечно, не выстраивает подобных батарей. Они
входят составной частью в ту или иную микросхему,
которая обеспечивает выполнение не только
операции сложения, но и целого комплекса
операций по обработке двоично закодированной
информации.
Вопросы и задания
1. Из вентилей И, ИЛИ, НЕ постройте схему
по заданному логическому выражению.
Рис. 13. Батарея сумматоров для сложения
двух n-разрядных чисел xnxn-1x3x2x1
и ynyn-1y3y2y1
Рис. 14. Сложение чисел 100101 и 1011
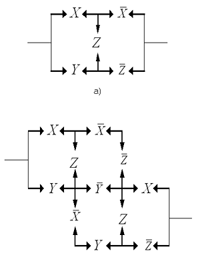
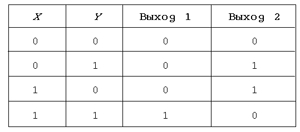
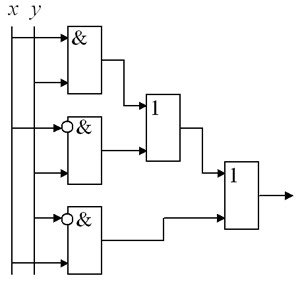
2. а) Составьте таблицу значений
булевой функции, реализованной схемой,
изображенной на рис. 15.
б) Составьте формулу, описывающую
схему, изображенную на рис. 15, и попытайтесь
ее упростить.
Рис. 15
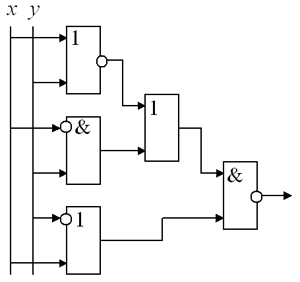
3. а) Составьте таблицу значений
булевой функции, реализованной схемой,
изображенной на рис. 16.
б) Составьте формулу, описывающую
схему, изображенную на рис. 16, и попытайтесь
ее упростить.
Рис. 16
Оксана Богуцкая
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Место логической модели в процессе проектирования
При проектировании программного обеспечения или других инженерных систем выделяют три уровня моделей:
- концептуальные: отображают предметную область в форме взаимосвязанных объектов без указаний способов их физического хранения; на этом этапе важно выявить номенклатуру участвующих в интересующем разработчиков процессе объектов, процессов и связей; примером такой модели могут служить диаграммы Use Case семейства UML;
- логические: строятся на основе концептуальной и сосредотачивается на детальном описании объектов, их атрибутов и взаимосвязей; пример — диаграммы классов UML;
- наконец, физические модели являются материальными воплощениями логических: компьютерными программами, механическими устройствами, экономическими структурами и т.п.
Таким образом, логическая модель является непосредственной основой для реализации физической. На основе логических моделей можно проектировать базы данных, компьютерные приложения и т.п.
Рисунок 1. Пример логической модели. Автор24 — интернет-биржа студенческих работ
Элементы логической модели
Обычно логическая модель графически выражается с помощью диаграмм, состоящих из следующих элементов:
- сущности: описывают объекты предметной области, и субъекты, воздействующие на нее;
- атрибуты: свойства объектов и субъектов;
- связи: взаимоотношения между сущностями;
- свойства связей: правила и ограничения этих взаимоотношений.
Сущности на диаграммах отображаются в виде прямоугольников, разбитых на горизонтальные фрагменты. В самом верхнем из них указывается наименование сущности (субъекта, объекта). Затем перечисляются атрибуты.
Наиболее ценными элементами графически выраженных логических моделей являются отношения (связи) между сущностями. Это не просто линии, а нотации, оформляемые по определенным правилам. Одиночная линия на конце линии означает «один», ветвление — «многие». Таким образом можно изобразить отношения «один к одному», «один ко многим», «многие к многим».
«Логическая информационная модель» 👇
Рисунок 2. Элементы линии для обозначения связей на диаграмме. Автор24 — интернет-биржа студенческих работ
Замечание 1
Кроме того, вертикальная черта у конца линии означает «обязательно», кружок — «не обязательно». Связи всегда надписываются для того, чтобы было понятно их функциональное назначение.
Набор взаимоисключающих отношений между сущностями обозначается с помощью дуги.
Рисунок 3. Обозначение взаимоисключающих связей. Автор24 — интернет-биржа студенческих работ
В примере о заказе пиццы можно предусмотреть сущность «Позиция заказа» с атрибутом «Количество» и соотнести ее с сущностями «Клиент» и «Сорт пиццы». Клиент может заказать разные сорта пиццы, при этом может отличаться и количество заказанных единиц. Заказ оформляется как таблица, где каждая строка («Позиция заказа») указывает приобретаемые клиентом в рамках заказа сорт пиццы и количество изделий данного сорта.
Основные требования к логической модели
Существуют критерии, в соответствии с которыми можно оценить полноценность логической модели:
- она должна содержать все значимые сущности и связи;
- все они должны быть поименованы в терминах предметной области;
- связи должны быть отмечены кратностью (например, один — многие);
- для каждой связи следует указать направление чтения;
- для каждой сущностей должны быть перечислены основные атрибуты.
Модель должна читаться следующим образом:
[Сущность 1] — [Связь] — [Сущность 2]
Возвращаясь к рассмотренному примеру, можно сказать, что сущность «Клиент» связана с сущностью «Заказ» отношением «может оформлять». При этом «Заказ» состоит из «Позиций», обладающих атрибутами «Сорт» и «Количество», при этом «Сорт» выделен в отдельную сущность с атрибутом «Название». Клиент может сделать любое количество заказов (в том числе нулевое), но заказ невозможен без указания клиента. В заказе может быть любое количество позиций (следует уточнить максимальное и минимальное значения и допустимость нулевых значений).
Существует ряд дополнительных требований к оформлению логической модели:
- сущности следует группировать по смыслу;
- следует избегать пересечения связей;
- расположение объектов на диаграмме должно способствовать удобству ее восприятия.
При создании логических моделей рекомендуется руководствоваться следующими правилами:
- необходимо определить границы моделирования, ответив на вопрос: какую часть исследуемой предметной области модель должна охватить? границы моделирования определяются исследуемыми процессами (например, продажа пиццы), либо фрагментом информационного пространства, соответствующим решаемой задаче (например, обработка электронной почты);
- разработка логической модели начинается с начала исследования предметной области и ведется на протяжении всего процесса проектирования; это итеративный, многоступенчатый процесс, в ходе которого последовательно уточняются и детализируются представления о предметной области;
- при разработке логических моделей следует сущности называть именами существительными, связи — глаголами, чтобы чтение диаграммы хотя бы приближенно соответствовало конструкциям обычного человеческого языка.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
§ 1.2. Знаковые модели
Информатика. 9 класса. Босова Л.Л. Оглавление
Ключевые слова:
- словесные модели
- математические модели
- компьютерные модели
Словесные модели
Словесные модели — это описания предметов, явлений, событий, процессов на естественных языках.
Например, гелиоцентрическая модель мира, которую предложил Коперник, словесно описывалась следующим образом:
- Земля вращается вокруг своей оси и вокруг Солнца;
- все планеты движутся по орбитам, центром которых является Солнце.
Множество словесных моделей содержится в ваших школьных учебниках: в учебнике истории представлены модели исторических событий, в учебнике географии — модели географических объектов и природных процессов, в учебнике биологии — модели объектов животного и растительного мира.
Произведения художественной литературы — это тоже модели, так как они фиксируют внимание читателя на определённых сторонах человеческой жизни. Анализируя литературное произведение, вы выделяете в нём объекты и их свойства, отношения между героями, связи между событиями, проводите параллели с другими произведениями и т. п. Самое непосредственное отношение к понятию модели имеет такой литературный жанр, как басня. Смысл этого жанра состоит в переносе отношений между людьми на отношения между вымышленными персонажами, например животными.
Такие особенности естественного языка, как многозначность, использование слов в прямом и переносном значении, синонимия, омонимия и т. п., придают человеческому общению выразительность, эмоциональность, красочность. Вместе с тем наличие этих особенностей делает естественный язык непригодным для создания информационных моделей во многих сферах профессиональной деятельности (например, в системах «человек — компьютер»).
Математические модели
Основным языком информационного моделирования в науке является язык математики.
Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями.
Язык математики представляет собой совокупность множества формальных языков; с некоторыми из них (алгебраическим, геометрическим) вы познакомились в школе, другие сможете узнать при дальнейшем обучении.
Язык алгебры позволяет формализовать функциональные зависимости между величинами, записав соотношения между количественными характеристиками объекта моделирования. В школьном курсе физики рассматривается много функциональных зависимостей, которые представляют собой математические модели изучаемых явлений или процессов.
Пример 1. Зависимость координаты тела от времени при прямолинейном равномерном движении имеет вид:
- х = х0 + ?xt.
Изменение координаты тела х при прямолинейном равноускоренном движении в любой момент времени t выражается формулой:

С помощью языка алгебры логики строятся логические модели — формализуются (записываются в виде логических выражений) простые и сложные высказывания, выраженные на естественном языке. Путём построения логических моделей удаётся решать логические задачи, создавать логические модели устройств и т. д.
Пример 2. Рассмотрите электрические схемы (рис. 1.3).

На них изображены известные вам из курса физики последовательное и параллельное соединения переключателе З. В первом случае, чтобы лампочка загорелась, должны быть включены оба переключателя. Во втором случае достаточно, чтобы был включён один из переключателе З. Можно провести аналогию между элементами электрических схем и объектами и операциями алгебры логики:

Спроектируем электрическую цепь, показывающую итог таЗного голосования комиссии в составе председателя и двух рядовых членов. При голосовании «за» каждыЗ член комиссии нажимает кнопку. Предложение считается принятым, если члены комиссии проголосуют за него единогласно либо если свои голоса «за» отдадут председатель и один из рядовых членов комиссии. В этих случаях загорается лампочка.
Решение. Пусть голосу председателя соответствует переключатель А, голосам рядовых членов — переключатели В и С. Тогда F(A, B,C) = A & B & C ? A & B ? A & C.
Упростим полученное логическое выражение:
- F(A, В, С) = А & В & (С ? 1) ? A & C = A & B & 1 ? A & C = A & B ? A & C = A & (B ? С).
Мы получили логическую модель, позволяющую построить схему проектируемой электрической цепи, изображённую на рис. 1.4.

Компьютерные математические модели
Многие процессы, происходящие в окружающем нас мире, описываются очень сложными математическими соотношениями (уравнениями, неравенствами, системами уравнений и неравенств). До появления компьютеров, обладающих высокой скоростью вычислений, у человека не было возможности проводить соответствующие вычисления, на счёт «вручную» уходило очень много времени.
В настоящее время многие сложные математические модели могут быть реализованы на компьютере. При этом используются такие средства, как:
- системы программирования;
- электронные таблицы;
- специализированные математические пакеты- и программные средства для моделирования.
Математические модели, реализованные с помощью систем программирования, электронных таблиц, специализированных математических пакетов и программных средств для моделирования, называются компьютерными математическими моделями.
Средства компьютерной графики позволяют визуализировать результаты расчётов, получаемых в процессе работы с компьютерными моделями.
С помощью ресурса «Демонстрационная математическая модель» (119324) вы сможете смоделировать полёт снаряда, выпущенного из пушки при различных исходных данных (http://sc.edu.ru/).
Особый интерес для компьютерного математического моделирования представляют сложные системы, элементы которых могут вести себя случайным образом. Примерами таких систем являются многочисленные системы массового обслуживания: билетные кассы, торговые предприятия, ремонтные мастерские, служба «Скорой помощи», транспортные потоки на городских дорогах и многие другие модели. Многим знакома ситуация, когда, придя в кассу, магазин, парикмахерскую, мы застаём там очередь. Приходится либо вставать в очередь и какое-то время ждать, либо уходить, т. е. покидать систему необслу- женным. Возможны случаи, когда заявок на обслуживание в системе мало или совсем нет; в этом случае она работает с недогрузкой или простаивает. В системах массового обслуживания количество заявок на обслуживание, время ожидания и точное время выполнения заявки заранее предсказать нельзя — это случайные величины.
Имитационные модели воспроизводят поведение сложных систем, элементы которых могут вести себя случайным образом.
Имитационное моделирование — это искусственный эксперимент, при котором вместо проведения натурных испытаний с реальным оборудованием проводят опыты с помощью компьютерных моделей. Для получения необходимой информации осуществляется многократный «прогон» моделей со случайными исходными данными, генерируемыми компьютером. В результате образуется такой же набор данных, который можно было бы получить при проведении опытов на реальном оборудовании или в реальной системе. Однако имитационное моделирование на компьютере осуществляется гораздо быстрее и обходится значительно дешевле, чем натурные эксперименты.
С помощью ресурса «Демонстрационная имитационная модель» (119425) вы сможете смоделировать ситуацию в системе массового обслуживания — магазине (http://sc.edu.ru/).
САМОЕ ГЛАВНОЕ
Словесные модели — это описания предметов, явлений, событий, процессов на естественных языках.
Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями.
Математические модели, реализованные с помощью систем программирования, электронных таблиц, специализированных математических пакетов и программных средств для моделирования, называются компьютерными математическими моделями.
Имитационные модели воспроизводят поведение сложных систем, элементы которых могут вести себя случайным образом.
Знаковые модели: Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
2. Приведите 2-3 собственных примера словесных моделей, рассматриваемых на уроках истории, географии, биологии.
3. Вспомните басни И. А. Крылова: «Волк и ягнёнок», «Ворона и лисица», «Демьянова уха», «Квартет», «Лебедь, Щука и Рак», «Лисица и виноград», «Слон и Моська», «Стрекоза и Муравей», «Тришкин кафтан» и др. Какие черты характера людей и отношения между людьми смоделировал в них автор?
4. Решите, составив математическую модель, следующую задачу. Теплоход прошёл 4 км против течения реки, а затем прошёл ещё 33 км по течению, затратив на весь путь один час. Найдите собственную скорость теплохода, если скорость течения реки равна 6,5 км/ч.
5. Требуется спроектировать электрическую цепь, показывающую итог тайного голосования комиссии в составе трёх членов. При голосовании «за» член комиссии нажимает кнопку. Предложение считается принятым, если оно собирает большинство голосов. В этом случае загорается лампочка.
6. Решите, составив логическую модель, следующую задачу. На международных соревнованиях по прыжкам в воду первые пять мест заняли спортсмены из Германии, Италии, Китая, России и Украины. Ещё до начала соревнований эксперты высказали свои предположения об их итогах: 1) Первое место займёт спортсмен из Китая, а спортсмен из Украины будет третьим. 2) Украина будет на последнем месте, а Германия — на предпоследнем. 3) Германия точно будет четвёртой, а первое место займёт Китай. 4) Россия будет первой, а Италия — на втором месте. 5) Италия будет пятой, а победит Германия.
По окончании соревнований выяснилось, что каждый эксперт был прав только в одном утверждении. Какие места в соревновании заняли участники?
7. В середине прошлого века экономисты оценили ежегодный объём вычислений, необходимых для эффективного управления народным хозяйством страны. Он составил 1017 операций. Можно ли справиться с таким объёмом вычислений за год, если привлечь к работе миллион вычислителей, каждый из которых способен выполнять одну операцию в секунду?
8. Приведите примеры использования компьютерных моделей. Найдите соответствующую информацию в сети Интернет.
9. В Единой коллекции цифровых образовательных ресурсов найдите лабораторную работу «Изучение закона сохранения импульса». В её основу положена математическая модель, описывающая движение тела, брошенного под углом к горизонту, с последующим делением тела на два осколка. Экспериментально проверьте закон сохранения импульса, выполнив работу согласно имеющемуся в ней описанию.
10. В Единой коллекции цифровых образовательных ресурсов найдите игру «Равноплечий рычаг». Изучите правила игры. Вспомните физическую закономерность, положенную в её основу. Попытайтесь «победить» компьютер и сформулировать выигрышную стратегию.
§ 1.1. Моделирование как метод познания
§ 1.2. Знаковые модели
§ 1.3. Графические информационные модели