|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Выбираем строки, где
и
выписываем конъюнкции всех переменных,
при чем, если переменная в этом наборе
равна 1, то записываем ее саму, а если
переменная = 0, то ее отрицание.
Для данного примера
коньюнкция этих дизъюнкций и будет
искомой формулой:
Определение:Конъюнкция
называетсяэлементарной, если
все переменные, входящие в нее, различны.
Количество букв, входящих в элементарную
конъюнкцию или элементарную дизъюнкцию,
называетсярангом.
Число 1 считается элементарной конъюнкцией
ранга 0. Переменная считается элементарной
конъюнкцией или элементарной дизъюнкцией
ранга 1. Число 0 считается элементарной
дизъюнкцией ранга 0. Любую конъюнкцию
переменных, не являющуюся тождественно
ложной, можно привести к виду элементарной,
а любую дизъюнкцию букв, не являющуюся
тождественно истинной, также можно
привести к виду элементарной. Для этого
надо применить свойства коммутативности,
идемпотентности и ассоциативности
конъюнкции и дизъюнкции.
Строго доказано, что любую формулу
булевой алгебры можно выразить с помощью
операций , &,.
Интуитивно этот факт очевиден, вспомним
алгоритм составления формулы по таблице
истинности. При этом мы используем
только эти операции. Такая форма записи
называетсядизъюнктивной нормальной
формой(ДНФ). Это своеобразный механизм
нормализации формул алгебры логики.
Определение:ДНФ– это
дизъюнкция различных элементарных
конъюнкций (т.е. каждая конъюнкция
состоит из элементарных высказываний
или их отрицаний).
Аналогично определяется КНФ – коньюктивная
нормальная форма.
Определение:Если в ДНФ все
элементарные конъюнкции имеют один и
тот же ранг, равный числу переменных,
от которых зависит ДНФ, то она называетсясовершенной (СДНФ).
Теорема. Для любой функции, не
являющейся тождественно ложной,
существует и притом единственная СДНФ.
Следствие. Любую булеву функцию,
не являющуюся тождественно ложной можно
представить в виде суперпозиции&,,,
причем отрицание относится только к
переменным.
Определение:Система логических
операций называется функционально
полной, если с помощью этих операций и
констант этой системы можно представить
любую функцию булевой алгебры.
Системы {&,,};
{,};
{&,},{/}
– являются функционально полными
{&,}
– функционально неполная.
Мы примем эти факты без доказательства,
и решая задачи, будем стараться любую
формулу представить с помощью {&,,}.
Позже мы более подробно обсудим вопрос
функциональной полноты и неполноты
системы операций.
Тема 1.7. Методы упрощения логических выражений. Методы решения логических задач.
Рассмотрим пример решения логической
задачи.
Пример:
После обсуждения состава участников
экспедиции решено, что должны выполняться
два условия.
-
Если поедет Арбузов, то должны ехать
Брюквин или Вишневский -
Если поедут Арбузов и Вишневский то
поедет Брюквин
Составить логическую формулу принятия
решения в символической форме, упростить
полученную формулу и сформулировать
по ней новое условие формирования
экспедиции.
Введём переменные и соответствующие
им элементарные высказывания.
— поедет Арбузов
— поедет Брюквин
— поедет Вишневский
Тогда выработанные условия формирования
экспедиции будут выглядеть следующим
образом:
Составим общую формулу и упростим
выражение
т.е. если поедет Арбузов, то поедет
Брюквин.
Пример:
Если завтра будет хорошая погода, то мы
пойдем на пляж или поедем в лес. Составим
формулу нашего поведения на завтра.
–
хорошая погода
– мы пойдем на пляж
– мы поедем в лес
Теперь построим отрицание этой фразы
т.о. получим высказывание «Завтра
будет хорошая погода, и мы не пойдем в
лес и на пляж.
Желающие могут построить таблицу
истинности и проверить это утверждение.
Пример:
По подозрению в совершенном преступлении,
задержаны Браун, Джон и Смит. Один из
них уважаемый в городе старик, второй
чиновник, а третий известный мошенник.
В ходе следствия старик говорил правду,
мошенник лгал, а третий задержанный в
одном случае говорил правду, а в другом
лгал.
Вот что они говорили:
Браун: Я совершил это. Джон не виноват.
(Б&Д)
Джон: Браун не виноват. Преступник Смит.
(Б&С)
Смит: Я не виноват. Виноват Браун (С&Б)
Опишем эти высказывания формально:
— преступление совершил Браун
— преступление совершил Джон
— преступление совершил Смит
Тогда их слова описываются следующими
выражениями:
Браун:
Джон:
Смит:
Т.к. по условиям задачи две из этих &ложны и одна истинна, то
Составим таблицу истинности
|
NN |
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
3 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|
5 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
6 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
7 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
8 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
-
Исключим из рассмотрения те наборы, на
которых
(по условию задачи одна из&- истинна, следовательно,
)
1, 3, 8 -
Исключим случай 5, т.к. в нем две &истинны, что противоречит условию
задачи. -
В случаях 4, 6, 7 у нас в начальном наборе
две 1 , т.е. 2 преступника, а по условию
задачи он один.
Остается только случай 2 , т.е. преступник
Смит, и оба его высказывания ложны.
следовательно
–
ложно и—
истинно
=
1 – Джон уважаемый старик
Остается, что Браун чиновник, и поскольку
– ложно , то
– истинно.
Пользуясь законами и тождествами булевой
алгебры можно упрощать логические
выражения.
Пример:
Упражнение:
(X&Y&Z)(X&Y&Z)X&Y
Соседние файлы в папке Коспект лекций
- #
16.03.2016266 б10desktop.ini
- #
16.03.201611.67 Кб10Folder.htt
- #
- #
- #
- #
- #
- #
Диана Загировна Филиппенкова
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Решение логических задач с помощью алгебры логики является мощным средством.
Алгоритм решения логических задач с помощью алгебры логики
-
изучение условия;
-
выделение простых высказываний, которым даются имена;
-
запись условия задачи языком алгебры логики;
-
составление конечной формулы, для чего объединяются формулы каждого утверждения с помощью логического умножения и приравнивается полученная формула единице;
-
упрощение формулы, анализ полученного результата или составление таблицы истинности, нахождение по таблице значения переменных, для которых $F=1$, анализ результатов.
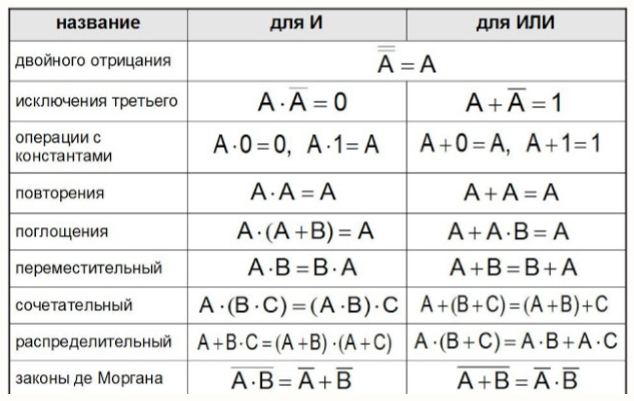
Законы алгебры логики
Рисунок 1.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Примеры решения логических задач с помощью алгебры логики
Пример 1
Задача «Кто преступник»
Определить участника преступления, зная, что:
-
«Если Иван не участвовал или Петр участвовал, то Семен участвовал»;
-
«Если Иван не участвовал, то Семен не участвовал».
Решим задачу с помощью таблиц истинности и с помощью алгебры логики.
Решение:
Решение с помощью таблицы истинности
Пусть:
$I$ — «Иван участвовал в преступлении»;
$P$ — «Петр участвовал в преступлении»;
$S$ — «Семен участвовал в преступлении».
Запишем условия задачи в виде формул:
$overline{I}vee Pto S$ и $overline{I}vee Pto overline{S}$
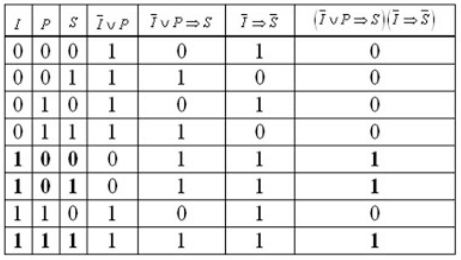
Построим таблицу истинности для всех возможных наборов:
Рисунок 2.
Из таблицы видно, что преступление совершил Иван.
Решение с помощью алгебры логики
[Fleft(I,P,Sright)=left(overline{I}vee Pto Sright)wedge left(overline{I}to overline{S}right)=left(left(overline{overline{I}vee P}right)vee Sright)wedge left(Ivee overline{S}right)=] [=left(Iwedge overline{P}vee Sright)wedge left(Ivee overline{S}right)=Iwedge overline{P}vee Iwedge Svee Iwedge overline{P}wedge overline{S}vee 0=Iwedge overline{P}vee Iwedge S=] [=Iwedge left(overline{P}vee Sright)]
Из получившегося выражения получаем, что выражение верно, когда $I=1$. Таким образом, преступник — Иван.
«Применение инструмента алгебры логики при решении логических задач» 👇
Пример 2
Задача о погоде
Определить погоду на завтра, если синоптик сказал, что:
-
Если не будет ветра, то будет пасмурная погода и не будет дождя.
-
Если будет дождь, то будет пасмурно и не будет ветра.
-
Если будет пасмурная погода, то будет дождь и не будет ветра.
Решим эту задачу средствами алгебры логики.
Решение:
-
Пусть:
$A$ — «Не будет ветра»;
$B$ — «Пасмурно»;
$C$ — «Дождь».
-
Запишем с помощью переменных $A$, $B$, $C$ высказывания синоптика:
Если не будет ветра, то будет пасмурная погода и не будет дождя:
[Ato Bwedge overline{C}]
Если будет дождь, то будет пасмурно и не будет ветра:
[Cto Bwedge A]
Если будет пасмурная погода, то будет дождь и не будет ветра
[Bto Cwedge A]
Составим конъюнкцию указанных функций:
[F=left(Ato Bwedge overline{C}right)wedge left(Cto Bwedge Aright)wedge left(Bto Cwedge Aright)]
Используя законы алгебры логики(закон де Моргана, переместительный закон, закон противоречия), упростим формулу:
[F=left(Ato Bwedge overline{C}right)wedge left(Cto Bwedge Aright)wedge left(Bto Cwedge Aright)=] [=left(overline{A}vee Bwedge overline{C}right)wedge left(overline{C}vee Bwedge Aright)wedge left(overline{B}vee Cwedge Aright)=] [=left(overline{A}vee Bwedge overline{C}right)wedge left(overline{B}vee Cwedge Aright)wedge left(overline{C}vee Bwedge Aright)=] [=left(overline{A}wedge overline{B}vee Bwedge overline{C}wedge overline{B}vee overline{A}wedge Cwedge Avee Bwedge overline{C}wedge Cwedge Aright)wedge left(overline{C}vee Bwedge Aright)=] [=overline{A}wedge overline{B}wedge left(Cvee Bwedge overline{A}right)=overline{A}wedge overline{B}wedge Cvee overline{A}wedge overline{B}wedge Bwedge overline{A}=overline{A}wedge overline{B}wedge overline{C}]
-
Приравниваем результат к единице, т.е. проверяем, при каких условиях выражение будет истинным:
[F=overline{A}wedge overline{B}wedge overline{C}=1.]
Проанализируем полученный результат:
Функция будет истинной, если каждый множитель будет истинным, т.е. $overline{A}=1$, $overline{B}=1$, $overline{C}=1$. Отсюда следует, что $A=0$, $B=0$, $C=0$.
Ответ: погода будет без ветра, ясная и без дождя.
Пример 3
История с амфорой
Антон, Борис и Григорий нашли в земле сосуд, о котором каждый высказал по два предположения:
-
Антон: «Сосуд греческий и изготовлен в V столетии»;
-
Борис: «Сосуд финикийский и изготовлен в III столетии»;
-
Григорий: «Сосуд не греческий и изготовлен в IV столетии».
Специалист сказал ученикам, что каждый из них не ошибся только в одном из двух предположений. Определить место и столетие изготовления сосуда.
Решение:
Введем следующие обозначения:
$G$ — «Сосуд греческий»;
$F$ — «Сосуд финикийский»;
$S_3$ — «Сосуд изготовлен в $III$ столетии»;
$S_4$ — «Сосуд изготовлен в $IV$ столетии»;
$S_5$ — «Сосуд изготовлен в $V$ столетии».
Запишем условие задачи с помощью обозначений:
Антон прав только в одном предположении: $G = 1$ или $S_5 = 1$. Тогда $Goverline{S_5}vee overline{G}S_5=1$.
Аналогично для слов Бориса: $Foverline{S_3}vee overline{F}S_3=1$.
Для слов Григория: $overline{G}overline{S_4}vee GS_4=1$.
Т.к. сосуд может быть изготовлен только в одном из столетий и только в одной из стран, запишем условия:
[S_3overline{S_4}overline{S_5}vee overline{S_3}S_4overline{S_5}vee overline{S_3}overline{S_4}S_5=1,] [Foverline{G}vee overline{F}G=1.]
Применим операцию логического умножения к полученным тождественно истинным высказываниям, результат которого также должен быть тождественно истинным:
[left(Goverline{S_5}vee overline{G}S_5right)wedge left(Foverline{S_3}vee overline{F}S_3right)wedge left(overline{G}overline{S_4}vee GS_4right)wedge left(Foverline{G}vee overline{F}Gright)wedge ] [wedge left(S_3overline{S_4}overline{S_5}vee overline{S_3}S_4overline{S_5}vee overline{S_3}overline{S_4}S_5right)=]
Перемножим первую на третью скобку и вторую на четвертую:
[=left(Goverline{S_5}overline{G}overline{S_4}vee overline{G}S_5overline{G}overline{S_4}vee Goverline{S_5}GS_4vee overline{G}S_5GS_4right)wedge ] [wedge left(Foverline{S_3}Foverline{G}vee overline{F}S_3Foverline{G}vee Foverline{S_3}overline{F}Gvee overline{F}S_3overline{F}Gright)wedge left(S_3overline{S_4}overline{S_5}vee overline{S_3}S_4overline{S_5}vee overline{S_3}overline{S_4}S_5right)=]
Т.к. $Goverline{G}=0$, $GG=G$, $overline{G}overline{G}=overline{G}$, упростим выражения:
[=left(overline{G}S_5overline{S_4}vee Goverline{S_5}S_4right)wedge left(Foverline{S_3}overline{G}vee overline{F}S_3Gright)wedge left(S_3overline{S_4}overline{S_5}vee overline{S_3}S_4overline{S_5}vee overline{S_3}overline{S_4}S_5right)=]
Перемножим первые две скобки и упростим выражение:
[=left(overline{G}S_5overline{S_4}overline{F}S_3Gvee Goverline{S_5}S_4overline{F}S_3Gvee overline{G}S_5overline{S_4}Foverline{S_3}overline{G}vee Goverline{S_5}S_4Foverline{S_3}overline{G}right)wedge ] [wedge left(S_3overline{S_4}overline{S_5}vee overline{S_3}S_4overline{S_5}vee overline{S_3}overline{S_4}S_5right)=] [=left(Goverline{S_5}S_4overline{F}S_3vee overline{G}S_5overline{S_4}Foverline{S_3}right)wedge left(S_3overline{S_4}overline{S_5}vee overline{S_3}S_4overline{S_5}vee overline{S_3}overline{S_4}S_5right)=] [=left(Goverline{S_5}S_4overline{F}S_3vee overline{G}S_5overline{S_4}Foverline{S_3}right)wedge left(S_3overline{S_4}overline{S_5}vee overline{S_3}S_4overline{S_5}vee overline{S_3}overline{S_4}S_5right)=overline{G}S_5overline{S_4}Foverline{S_3};]
$overline{G}S_5overline{S_4}Foverline{S_3}=1$, что возможно только в случае:
[overline{G}=1, S_5=1, overline{S_4}=1, F=1, overline{S_3}=1.]
Ответ: сосуд финикийский и изготовлен в $V$ столетии.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Информатика, 10 класс. Урок № 12.
Тема — Преобразование логических выражений
Перечень вопросов, рассматриваемых в теме: основные законы алгебры логики, преобразование логических выражений, логические функции, построение логического выражения с данной таблицей истинности и его упрощение, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ).
Глоссарий по теме: основные законы алгебры логики, логические функции, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ)
Основная литература по теме урока:
Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса
— М.: БИНОМ. Лаборатория знаний, 2017 (с.197—209)
Открытые электронные ресурсы по теме:
http://lbz.ru/metodist/authors/informatika/3/eor10.php
http://kpolyakov.spb.ru/school/ege.htm
Теоретический материал для самостоятельного изучения.
Способ определения истинности логического выражения путем построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т.к. за счет существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики.
Основные законы алгебры логики
Справедливость законов можно доказать построением таблиц истинности.
Пример 1. Упростим логическое выражение
Последовательно применим дистрибутивный закон и закон исключенного третьего:
В общем случае можно предложить следующую последовательность действий:
- Заменить операции строгая дизъюнкция, импликация, эквиваленция на их выражения через операции конъюнкция, дизъюнкция, инверсия;
- Раскрыть отрицания сложных выражений по законам де Моргана.
- Используя законы алгебры логики, упростить выражение.
Пример 2. Упростим логическое выражение 
Здесь последовательно использованы замена операции импликация, закон де Моргана, распределительный закон, закон противоречия и операция с константой, закон идемпотентности и поглощения.
Аналогичные законы выполняются для операции объединения, пересечения и дополнения множеств. Например:
Пример 3. На числовой прямой даны отрезки B = [2;12] и C = [7;18]. Каким должен быть отрезок A, чтобы предикат 
Преобразуем исходное выражение, избавившись от импликации:
A, B, C — множества. Для них можно записать 
Будем считать, что
Тогда 
Так как множество B — это отрезок [2;12], а множество 



Пример 4. Для какого наименьшего неотрицательного целого десятичного числа а выражение

Введем обозначения:
Перепишем исходное выражение в наших обозначениях и преобразуем его:

Рассмотрим предикат 

Рассмотрим предикат 

Рассмотрим предикат 
По условию задачи надо, чтобы 
Запишем это выражение для рассмотренных множеств истинности:
Так как 

Объединением множеств M и N являются все двоичные числа, у которых хотя бы один из битов с номерами 5, 4, 3, 2, 0 содержит единицу. Пересечением этого множества с множеством K будут все двоичные числа, у которых биты с номерами 4 и 0 будут заняты нулями, т.е. такие двоичные числа, у которых хотя бы один из битов с номерами 5, 3, 2 содержит 1. Все эти числа образуют множество А.
Искомое число a должно быть таким, чтобы при любом неотрицательном целом значении переменной х: 
Значение любого логического выражения определяется значениями входящих в него логических переменных. Тем самым логическое выражение может рассматриваться как способ задания логической функции.
Совокупность значений n аргументов удобно интерпретировать как строку нулей и единиц длины n. Существует ровно различных двоичных строк длины n. Так как на каждой такой строке некая функция может принимать значение 0 или 1, общее количество различных булевых функций от n аргументов равно
.
Для n=2 существует 16 различных логических функций. Рассмотрим их подробнее.
|
A |
B |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
F12 |
F13 |
F14 |
F15 |
F16 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
F1(A,B) = 0 — константа «ложь»;
F2(A,B) = A&B — конъюнкция;
F3(A,B) = 
F4(A,B) = A — функция, равная первому аргументу;
F5(A,B) = 
F6(A,B) = B — функция, равная второму аргументу;
F7(A,B) = 
F8(A,B) = A˅B — дизъюнкция;
F9(A,B) = 
F10(A,B) = 
F11(A,B) = 
F12(A,B) = 
F13(A,B) = 
F14(A,B) = 
F15(A,B) = 
F16(A,B) = 1 — константа «истина».
С увеличением числа аргументов количество логических функций резко возрастает. Отметим, что путем преобразований функция любого количества переменных может быть выражена через функции только двух переменных. Более того, можно использовать не все, а лишь некоторые логические функции двух переменных. Например:
- F2 и F11 (конъюнкция и отрицание второго аргумента);
- F8 и F13 (дизъюнкция и отрицание первого аргумента);
- F9 (стрелка Пирса, отрицание дизъюнкции);
- F15 (штрих Шеффера, отрицание конъюнкции).
Последние два примера говорят о том, что при желании всю алгебру логики можно свести к одной функции.
Любую логическую формулу путем тождественных преобразований можно привести к формуле, содержащей только операции отрицания, конъюнкции и дизъюнкции:
Такой способ представления логической формулы называется нормальной формой.
При решении задач часто требуется по таблице истинности логической формулы записать ее аналитическое выражение. Для этого используются понятия совершенной дизъюнктивной нормальной формы (СДНФ) и совершенной конъюнктивной нормальной формы (СКНФ).
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, в которой каждая переменная встречается не более одного раза (либо сама, либо ее отрицание). Например, запись 
Аналогично, выражение 
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций. Например, выражение 
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций. Например, выражение 
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные (либо сами, либо их отрицания). Например, выражение 

Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные (либо сами, либо их отрицания). Например, выражение 
Для всякой таблицы истинности можно составить соответствующее ей логическое выражение. Для этого необходимо:
- Отметить в таблице истинности наборы переменных, при которых значение логического выражения равно единице;
- Для каждого отмеченного набора записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — её отрицание;
- Все полученные конъюнкции связать операциями дизъюнкции.
Пример 5. Имеется следующая таблица истинности:
После выполнения первых двух шагов алгоритма получим:
После выполнения третьего шага получаем логическое выражение:
Попробуем упростить полученное выражение. Прежде всего, вынесем за скобки 
Решение логических задач
Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распространение получили следующие три способа решения логических задач:
- средствами алгебры логики;
- табличный;
- с помощью рассуждений.
Познакомимся с ними поочередно.
Решение логических задач средствами алгебры логики
Обычно используется следующая схема решения:
1. изучается условие задачи;
2. вводится система обозначений для логических высказываний;
3. конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
4. определяются значения истинности этой логической формулы;
5. из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.
Пример 1. Трое друзей, болельщиков автогонок «Формула-1», спорили о результатах предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Решение. Введем обозначения для логических высказываний:
Ш — победит Шумахер; Х — победит Хилл; А — победит Алези.
Реплика Ника «Алези пилотирует самую мощную машину» не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
Джон: ¬Ш/Х
Ник: Ш/¬А
Питер: ¬Х
Высказывание Ш / ¬ А/ ¬Х истинно только при Ш=1, А=0, Х=0.
Ответ. Победителем этапа гонок стал Шумахер.
Решение логических задач табличным способом
При использовании этого способа условия, которые содержит задача, и результаты рассуждений фиксируются с помощью специально составленных таблиц.
Пример 2. В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что:
- Смит самый высокий;
- играющий на скрипке меньше ростом играющего на флейте;
- играющие на скрипке и флейте и Браун любят пиццу;
- когда между альтистом и трубачом возникает ссора, Смит мирит их;
- Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как музыкантов трoе, инструментов шесть и каждый владеет только двумя инструментами, получается, что каждый музыкант играет на инструментах, которыми остальные не владеют.
Из условия 4 следует, что Смит не играет ни на альте, ни на трубе, а из условий 3 и 5, что Браун не умеет играть на скрипке, флейте, трубе и гобое. Следовательно, инструменты Брауна — альт и кларнет. Занесем это в таблицу, а оставшиеся клетки столбцов «альт» и «кларнет» заполним нулями:
Из таблицы видно, что на трубе может играть только Вессон.
Из условий 1 и 2 следует, что Смит не скрипач. Так как на скрипке не играет ни Браун, ни Смит, то скрипачом является Вессон. Оба инструмента, на которых играет Вессон, теперь определены, поэтому остальные клетки строки «Вессон» можно заполнить нулями:
Из таблицы видно, что играть на флейте и на гобое может только Смит.
Ответ: Браун играет на альте и кларнете, Смит — на флейте и гобое, Вессон — на скрипке и трубе.
Решение логических задач с помощью рассуждений
Этим способом обычно решают несложные логические задачи.
Пример 3. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Решение. Имеется три утверждения:
- Вадим изучает китайский;
- Сергей не изучает китайский;
- Михаил не изучает арабский.
Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно.
Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно.
Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.
Пример 4. Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты соглашения о полном разоружении, представленные каждой из стран. Отвечая затем на вопрос журналистов: «Чей именно проект был принят?», министры дали такие ответы:
Россия — «Проект не наш, проект не США»;
США — «Проект не России, проект Китая»;
Китай — «Проект не наш, проект России».
Один из них (самый откровенный) оба раза говорил правду; второй (самый скрытный) оба раза говорил неправду, третий (осторожный) один раз сказал правду, а другой раз — неправду.
Определите, представителями каких стран являются откровенный, скрытный и осторожный министры.
Решение. Для удобства записи пронумеруем высказывания дипломатов:
Россия — «Проект не наш» (1), «Проект не США» (2);
США — «Проект не России» (3), «Проект Китая» (4);
Китай — «Проект не наш» (5), «Проект России» (6).
Узнаем, кто из министров самый откровенный.
Если это российский министр, то из справедливости (1) и (2) следует, что победил китайский проект. Но тогда оба утверждения министра США тоже справедливы, чего не может быть по условию.
Если самый откровенный — министр США, то тогда вновь получаем, что победил китайский проект, значит оба утверждения российского министра тоже верны, чего не может быть по условию.
Получается, что наиболее откровенным был китайский министр. Действительно, из того, что (5) и (6) справедливы, cледует, что победил российский проект. А тогда получается, что из двух утверждений российского министра первое ложно, а второе верно. Оба же утверждения министра США неверны.
Ответ: Откровеннее был китайский министр, осторожнее — российский, скрытнее — министр США.