Как составить интерполяцию - Avtoru.top - решение различных проблем

Загрузить PDF

Линейная интерполяция (или просто интерполяция)^[1]
— процесс нахождения промежуточных значений величины по ее известным значениям. Многие люди могут провести интерполяцию, полагаясь исключительно на интуицию, но в этой статье описан формализованный математический подход к проведению интерполяции.

Шаги

1
Определите величину, для которой вы хотите найти соответствующее значение. Интерполяция может быть проведена для вычисления логарифмов или тригонометрических функций или для вычисления соответствующего объема или давления газа при данной температуре.^[2] Научные калькуляторы в значительной степени заменили логарифмические и тригонометрические таблицы; поэтому в качестве примера проведения интерполяции мы вычислим давление газа при температуре, значение которой не указано в справочных таблицах (или на графиках).
- В уравнении, которое мы выведем, «x» будет обозначать известную величину, а «у» — неизвестную величину (интерполированное значение). При построении графика эти значения откладываются соответственно их обозначениям — величина «x» — по оси X, величина «у» — по оси Y.
- В нашем примере под «x» будет подразумеваться температура газа, равная 37 °С.
2
В таблице или на графике найдите ближайшие значения, расположенные ниже и выше значения «x». В нашей справочной таблице не приведено давление газа при 37 °С, но приведены значения давления при 30 °С и при 40 °С. Давление газа при температуре 30 °С = 3 кПа, а давление газа при 40 °С = 5 кПа.
- Так как мы обозначили температуру в 37 °С как «x», то теперь обозначим температуру в 30 °С как x₁, а температуру в 40 °С как x₂.
- Так как мы обозначили неизвестное (интерполированное) давление газа как «у», то теперь обозначим давление в 3 кПа (при 30 °С) как у₁, а давление в 5 кПа (при 40 °С) как у₂.
3
Найдем интерполированное значение. Уравнение для нахождения интерполированного значения можно записать в виде y = y₁ + ((x — x₁)/(x₂ — x₁) * (y₂ — y₁))^[3]
- Подставим значения x, x₁, x₂ и получим: (37 — 30)/(40 — 30) = 7/10 = 0,7.
- Подставим значения у₁, у₂ и получим: (5 — 3) = 2.
- Умножив 0,7 на 2, получим 1,4. Сложим 1,4 и у₁: 1,4 + 3 = 4,4 кПа. Проверим ответ: найденное значение 4,4 кПа лежит между 3 кПа (при 30 °С) и 5 кПа (при 40 °С), а так как 37 °С ближе к 40 °С, чем к 30 °С, то и окончательный результат (4,4 кПа) должен быть ближе к 5 кПа, чем к 3 кПа.
Реклама

Советы

Если вы умеете работать с графиками, вы можете сделать грубую интерполяцию, отложив известное значение по оси X и найдя соответствующее значение на оси Y.^[4] В приведенном выше примере можно построить график, на котором по оси X откладывается температура (в десятках градусов), а по оси Y — давление (в единицах кПа). На этом графике вы можете нанести точку 37 градусов, а затем найти точку на оси Y, соответствующую этой точке (она будет лежать между точками 4 и 5 кПа). Приведенное выше уравнение просто формализует процесс мышления и обеспечивает получение точного значения.
В отличие от интерполяции, экстраполяция позволяет вычислить приблизительные значения величины вне диапазона значений, приведенных в таблицах или отображенных на графиках.^[5]

Об этой статье

Эту страницу просматривали 98 219 раз.

Была ли эта статья полезной?

Источник

Интерполяция данных: соединяем точки так, чтобы было красиво

Время на прочтение
7 мин

Количество просмотров 150K

Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:

Немного матчасти

Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек P₁ … P_n, называется интерполяцией. Есть множество способов интерполяции, но все они могут быть сведены к тому, что надо найти n – 1 функцию для расчёта промежуточных точек на соответствующих сегментах. При этом заданные точки обязательно должны быть вычислимы через соответствующие функции. На основе этого и может быть построен график:

Функции f_i могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками P_i) называется сплайном.

В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.

Ставим опыты

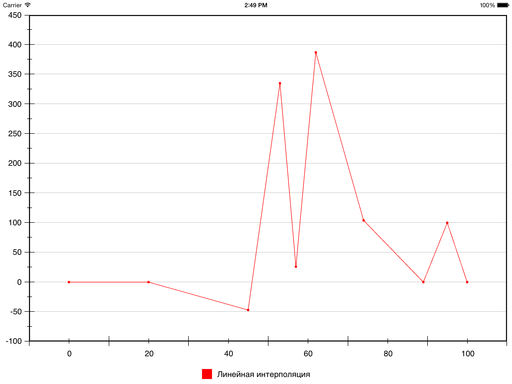
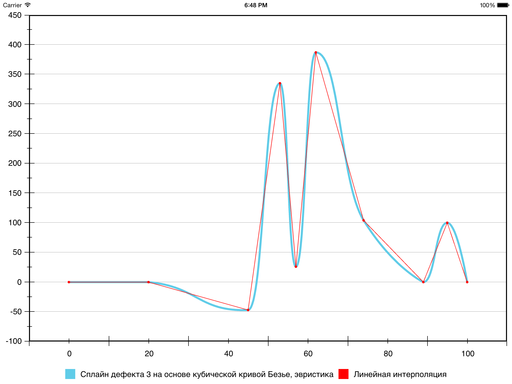
Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
Давайте добавим немного конкретики. Вот набор точек (взяты почти с потолка):

Результат линейной интерполяции этих точек выглядит так:

Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.

Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a; b], это означает, что на [a; b] она имеет непрерывную первую производную, а вот вторая производная уже терпит разрыв в каких-то точках.
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.
Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз P_i, то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.

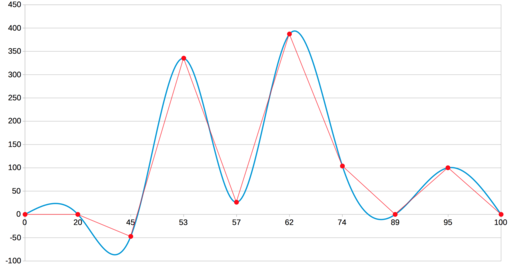
Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1. Вот как он выглядит для наших данных:

Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.

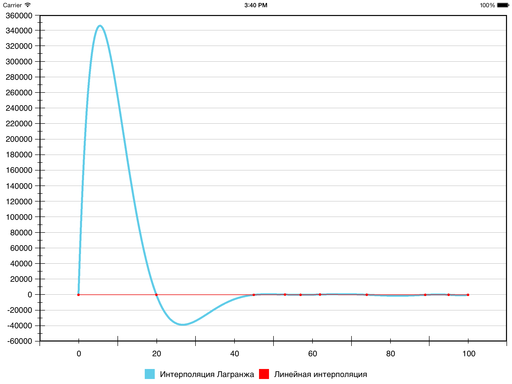
Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа. Это полиномы степени n – 1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
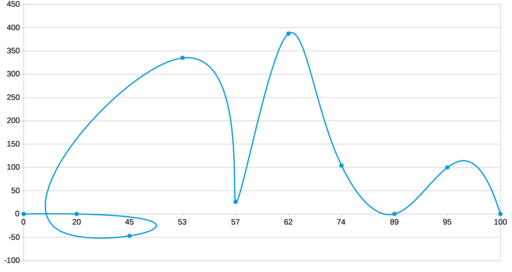
Но вот что получается:

Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.

В компьютерной графике очень широко применяются кривые Безье, представленные полиномами k-й степени.
Они не являются интерполирующими, так как из k + 1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные k – 1 точек играют роль своего рода «гравитационных центров», притягивающих к себе кривую.
Вот пример кубической кривой Безье:

Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k-й степени (кстати, k = 1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k – 1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k = 3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (P_i), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено здесь.
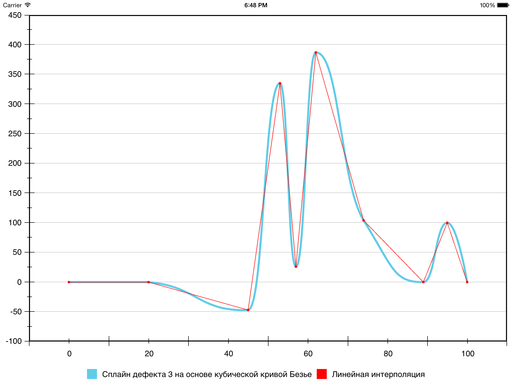
Вот что получится на нашем тестовом наборе:

Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.

Думаем и экспериментируем

Можно попробовать ослабить условие гладкости: потребовать дефект 2, а не 1, то есть сохранить непрерывность одной только первой производной.
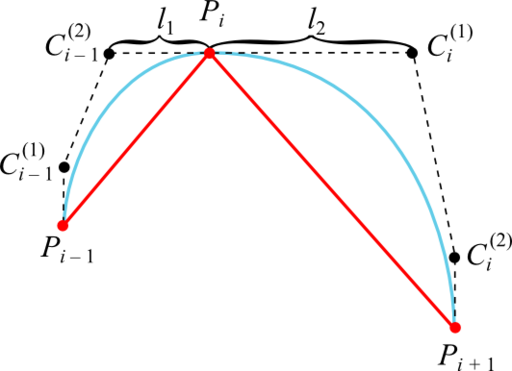
Достаточное условие достижения дефекта 2 в том, что промежуточные контрольные точки кубической кривой Безье, смежные с заданной точкой интерполируемой последовательности, лежат с этой точкой на одной прямой и на одинаковом расстоянии:

В качестве прямых, на которых лежат точки C_i – 1⁽²⁾, P_i и C_i⁽¹⁾, целесообразно взять касательные к графику интерполируемой функции в точках P_i. Это гарантирует отсутствие ложных экстремумов, так как кривая Безье оказывается ограниченной ломаной, построенной на её контрольных точках (если эта ломаная не имеет самопересечений).

Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:

Эвристика 1

Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки C₁⁽¹⁾ и C_n – 1⁽²⁾ совпадают с точками P₁ и P_n соответственно).
В этом случае получается вот такая кривая:

Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.

К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно сделать это ещё раз: пусть сплайн будет иметь дефект 3. По факту, тем самым формально функция не будет гладкой вообще: даже первая производная может терпеть разрывы. Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Отказываемся от требования равенства расстояний от точки P_i до точек C_i – 1⁽²⁾ и C_i⁽¹⁾, но при этом сохраняем их все лежащими на одной прямой:

Эвристика для вычисления расстояний будет такой:

Эвристика 2

Расчёт l₁ и l₂ такой же, как в «эвристике 1».
При этом, однако, стоит ещё проверять, не совпали ли точки P_i и P_i + 1 по ординате, и, если совпали, полагать l₁ = l₂ = 0. Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).

Результат получается такой:

В результате на шестом сегменте ошибка уменьшилась, а на седьмом — увеличилась: кривизна у Безье на нём оказалась больше, чем хотелось бы. Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:

Эвристика 3

Если абсцисса точки пересечения касательных в точках P_i(x_i, y_i) и P_i + 1(x_i + 1, y_i + 1) лежит в отрезке [x_i; x_i + 1], то l₁ либо l₂ полагаем равным нулю. В том случае, если касательная в точке P_i направлена вверх, нулю полагаем максимальное из l₁ и l₂, если вниз — минимальное.

Результат следующий:

На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код.

А как люди-то делают?

Обещанный обзор. Конечно, перед решением задачи мы посмотрели, кто чем может похвастаться, а уже потом начали разбираться, как сделать самим и по возможности лучше. Но вот как только сделали, не без удовольствия ещё раз прошлись по доступным инструментам и сравнили их результаты с плодами наших экспериментов. Итак, поехали.

MS Excel

Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.

LibreOffice Calc

В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.

Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат

Highcharts, одна из самых популярных JS-библиотек для построения диаграмм

Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).

amCharts, ещё одна популярная JS-библиотека

Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.

Coreplot, самая популярная библиотека построения графиков для iOS и OS X

Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.

aChartEngine, вроде как самая популярная библиотека построения графиков для Android

Больше всего похоже на кривую Безье степени n – 1, хотя в самой библиотеке график называется «cubic line». Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.

Вместо заключения

В конечном счёте получается, что из «больших ребят» лучше всех проблему решили Highcharts. Но метод, описанный в этой статье, обеспечивает ещё меньшую ошибку относительно линейной интерполяции.
Вообще, заняться этим пришлось по просьбе покупателей, которые зарепортили нам «острые углы» в качестве бага в нашем движке диаграмм. Будем рады, если описанный опыт кому-то пригодится.

Источник

Наиболее часто для определения функции φ(Х) используется постановка, называемая постановкой задачи интерполяции.

В этой классической постановке задачи интерполяции требуется определить приближенную аналитическую функцию φ(Х), значения которой в узловых точках Хi совпадают со значениями Y(Хi) исходной таблицы, т.е. условий

ϕ( X i ) =Yi (i = 0,1,2,…, n)

(2)

Построенная таким образом аппроксимирующая функция φ(Х) позволяет получить достаточно близкое приближение к интерполируемой функции Y(X) в пределах интервала значений аргумента [Х0; Хn], определяемого таблицей. При задании значений аргумента Х, не принадлежащих этому интервалу, задача интерполяции преобразуется в задачу экстраполяции. В этих случаях точность значений, получаемых при вычислении значений функции φ(Х), зависит от расстояния значения аргумента Х от Х0 , если Х < Х0 ,

или от Хn , если Х > Хn .

При математическом моделировании интерполирующая функция может быть использована для вычисления приближенных значений исследуемой функции в промежуточных точках подынтервалов [Хi; Хi+1]. Такая процедура называется уплотнением таблицы.

Алгоритм интерполяции определяется способом вычисления значений функции φ(Х). Наиболее простым и очевидным вариантом реализации интерполирующей функции является замена исследуемой функции Y(Х) на интервале [Хi; Хi+1] отрезком прямой, соединяющим точки Yi , Yi+1. Этот метод называется методом линейной интерполяции.

2.2 Линейная интерполяция

При линейной интерполяции значение функции в точке Х, находящейся между узлами Хi и Хi+1, определяется по формуле прямой, соединяющей две соседние точки таблицы

Y( X ) =Y( Xi )+	Y( Xi+1 ) −Y( Xi )	( X −Xi ) (i =0,1,2, …,n),	(3)

	Xi+1 −Xi

На рис. 1 приведен пример таблицы, полученной в результате измерений некоторой величины Y(X). Строки, исходной таблицы

выделены заливкой. Справа от таблицы построена точечная диаграмма, соответствующая этой таблице. Уплотнение таблицы выполнено благодаря вычислению по формуле (3) значений аппроксимируемой функции в точках Х, соответствующих серединам подынтервалов [Xi; Xi+1] (i=0, 1, 2, … , n).

Рис.1. Уплотненная таблица функции Y(X) и соответствующая ей диаграмма

При рассмотрении графика на рис. 1 видно, что точки, полученные в результате уплотнения таблицы по методу линейной интерполяции, лежат на отрезках прямых, соединяющих точки исходной таблицы. Точность линейной интерполяции, существенно зависит от характера интерполируемой функции и от расстояния между узлами таблицы Xi,, Xi+1.

Очевидно, что если функция плавная, то, даже при сравнительно большом расстоянии между узлами, график, построенный путем соединения точек отрезками прямых, позволяет достаточно точно оценить характер функции Y(Х). Если же функция изменяется достаточно быстро, а расстояния между узлами большие, то линейная интерполирующая функция не позволяет получить достаточно точное приближение к реальной функции.

Линейная интерполирующая функция может быть использована для общего предварительного анализа и оценки корректности результатов интерполяции, получаемых затем другими более точными методами. Особенно актуальной такая оценка становится в тех случаях, когда вычисления выполняются вручную.

2.3 Интерполяция каноническим полиномом

Метод интерполяции функции каноническим полиномом основывается на построении интерполирующей функции как полинома в виде [ 1 ]

ϕ( x) = Pn ( x) = c0 + c1 x + c2 x 2 + … + cn x n

( 4 )

Коэффициенты сi полинома (4) являются свободными параметрами интерполяции, которые определяются из условий

Лагранжа:					( 5 )
Pn ( xi ) = Yi ,	( i = 0 , 1 , … , n )
Используя (4) и (5) запишем систему уравнений
c +c x +c x 2	+…+c x n =Y
0	1 0	2 0	n 0	0
c +c x +c x 2	+…+c x n	=Y	( 6 )
0	1 1	2 1	n 1	1
. . . . . .
c +c x +c x 2	+…+c x n =Y
0	1 n	2 n	n n	n

Вектор решения сi ( i = 0, 1, 2, …, n) системы линейных алгебраических уравнений (6) существует и может быть найден, если среди узлов хi нет совпадающих. Определитель системы (6) называется определителем Вандермонда1 и имеет аналитическое выражение [ 2 ].

Для определения значений коэффициентов сi (i = 0, 1, 2, … , n)

систему уравнений (5) можно записать__ в векторно-матричной форме
A* C =Y ,	( 7 )

где А, матрица коэффициентов, определяемых таблицей степеней вектора аргументов X= (xi0, xi, xi2, … , xin)T (i = 0, 1, 2, … , n)

	1	x	x2	…	xn
		0	0		0
А=	1	x1	x12	…	x1n	( 8 )
. .	.	.	.	,
	1	x	x2	…	xn
		n	n		n

Определителем Вандермонда называется определитель

Он равен нулю тогда и только тогда, когда xi = xj для некоторых . (Материал из Википедии — свободной энциклопедии)

С — вектор-столбец коэффициентов сi	(i = 0, 1, 2, … , n), а Y	— вектор-
	__

столбец значений Yi (i = 0, 1, 2, … , n) интерполируемой функции в узлах интерполяции.

Решение этой системы линейных алгебраических уравнений может быть получено одним из методов, описанных в [ 3 ]. Например,

по формуле	__	( 9 )
	С = A−1 Y ,

где А-1 — матрица обратная матрице А. Для получения обратной матрицы А-1 можно воспользоваться функцией МОБР(), входящей в набор стандартных функций программы Microsoft Excel.

После того, как будут определены значения коэффициентов сi, используя функцию (4), могут быть вычислены значения интерполируемой функции для любого значения аргумента х.

Запишем матрицу А для таблицы, приведенной на рис.1, без учёта строк уплотняющих таблицу.

Рис.2 Матрица системы уравнений для вычисления коэффициентов канонического полинома

Используя функцию МОБР(), получим матрицу А-1 обратную матрице А (рис. 3). После чего, по формуле (9) получим вектор коэффициентов С={c0, c1, c2, …, cn }T, приведенный на рис. 4.

Для вычисления значений канонического полинома в ячейку

столбца Yканонич, соответствующую значению х0, введем преобразованную к следующему виду формулу, соответствующую

нулевой строке системы (6)

=(((( c5 * х0+ c4)* х0+ c3)* х0+ c2)* х0+ c1)* х0+ c0

(10)

Вместо записи «ci» в формуле, вводимой в ячейку таблицы Excel, должна стоять абсолютная ссылка на ячейку, содержащую этот коэффициент (см. рис. 4). Вместо «х0» — относительная ссылка на ячейку столбца Х (см. рис. 5).

Соседние файлы в папке PDF_ЛЕКЦИИ_2-й_семестр

Источник

Общие сведения о интерполяции

26.05.2023
Просмотров: 30374
Печатать

По учебе в университете и по работе, выполняя различные расчеты, крайне часто приходится делать интерполяцию. В этой статье на примере таблицы 72 СНиП II-23-81* мы поймем что это такое и овладеем принципом расчета. В конце статьи приведена онлайн интерполяция этой таблицы, чтобы каждый смог проверить правильность своих расчетов.

Итак, например, нам нужно найти коэффициент продольного изгиба центрально-сжатых элементов (табл. 72 СНиП II-23-81*), зная его гибкость, равную 137 и расчетное сопротивление 240 МПа.

Таблица 72 (СНиП II-23-81*) — Коэффициентыпродольного изгиба центрально-сжатых элементов

Примечание. Значение коэффициентов фи в таблице увеличены в 1000 раз.

Мы видим, что 137 находится между 130 и 140, которым соответствуют свои значения 0,364 и 0,315 соответственно.

Запишем систему уравнений (1)

140 0,315
130 0,364

Разница значений получается следующей:

10 -0,049 (2)

Запишем систему уравнений (3)

137 х
130 0,364

Разница значений получается следующей:

7 х— 0,364 (4)

Запишем уравнения (2) и (4) в виде пропорции:

10 -0,049
7 х— 0,364

Решаем пропорцию и получаем:

-0,0343 = х— 0,364
х = 0,364 — 0,0343 = 0,329

Таким образом, для гибкости равной 137 коэффициент продольного изгиба равен 0,329

В качестве онлайн примера ниже приведена таблица 72 из СНиП II-23-81*. Введите в синие ячейки полученные Вами числа и через 2 секунды в красной ячейке получите искомое значение.

Источник

Интерполяция и аппроксимация#

from matplotlib import pyplot as plt


def configure_matplotlib():
    plt.rc('text', usetex=True)
    plt.rcParams["axes.titlesize"] = 28
    plt.rcParams["axes.labelsize"] = 24
    plt.rcParams["legend.fontsize"] = 24
    plt.rcParams["xtick.labelsize"] = plt.rcParams["ytick.labelsize"] = 18
    plt.rcParams["text.latex.preamble"] = r"""
    usepackage[utf8]{inputenc}
    usepackage[english,russian]{babel}
    usepackage{amsmath}
    """

configure_matplotlib()

Интерполяция#

Подмодуль scipy.interpolate содержит в себе методы для интерполяции.

Коротко про интерполяцию можно почитать в википедии. Более подробное изложение можно найти в [2].

Задача интерполирования состоит в том, чтобы по значениям функции (f(x)) в нескольких точках отрезка восстановить ее значения в остальных точках этого отрезка. Разумеется, такая задача допускает сколь угодно много решений. Задача интерполирования возникает, например, в том случае, когда известны результаты измерения (y_h= f(x, k)) некоторой физической величины (f(x)) в точках (x_k, k = 0, 1, …, n), и требуется определить ее значения в других точках. Интерполирование используется также при сгущении таблиц, когда вычисление значений (f(x)) трудоемко. Иногда возникает необходимость приближенной замены или аппроксимации данной функции другими функциями, которые легче вычислить. В частности, рассматривается задача о наилучшем приближении в нормированном пространстве (H), когда заданную функцию (fin H) требуется заменить линейной комбинацией (varphi) заданных элементов из (H) так, чтобы отклонение (||f—varphi||) было минимальным. Результаты и методы теории интерполирования и приближения функций нашли широкое применение в численном анализе, например при выводе формул численного дифференцирования и интегрирования, при построении сеточных аналогов задач математической физики [2].

Для того чтобы рассмотреть интерполяцию, сгенерируем данные. Т.е. сгенерируем массив узлов интерполяционной сетки x_data и значений y_data некоторой функции (f) в узлах этой сетки при разном количестве известных точек.

import numpy as np

L = 0
R = np.pi
n_points = (4, 10, 64, 65)
f = np.sin

xh = np.linspace(L, R, 100) 
yh = f(xh)
    

def generate_data(f, L, R, n):
    x_data = np.linspace(L, R, n-1)
    y_data = f(x_data)
    return x_data, y_data    


def plot_problem(ax, x_data, y_data):
    ax.plot(xh, yh, linewidth=0.5, label="Исходная зависимость")
    ax.scatter(x_data, y_data, marker="x", color="red", label="Известные данные")
    ax.set_xlabel("$x$")
    ax.set_ylabel("$y$")
    

fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(16, 16), layout="tight")
for ax, N in zip(axs.flatten(), n_points):
    x_data, y_data = generate_data(f, L, R, N)
    plot_problem(ax, x_data, y_data)
    ax.set_title(f"Исходные данные ${N=}$")
    ax.legend()

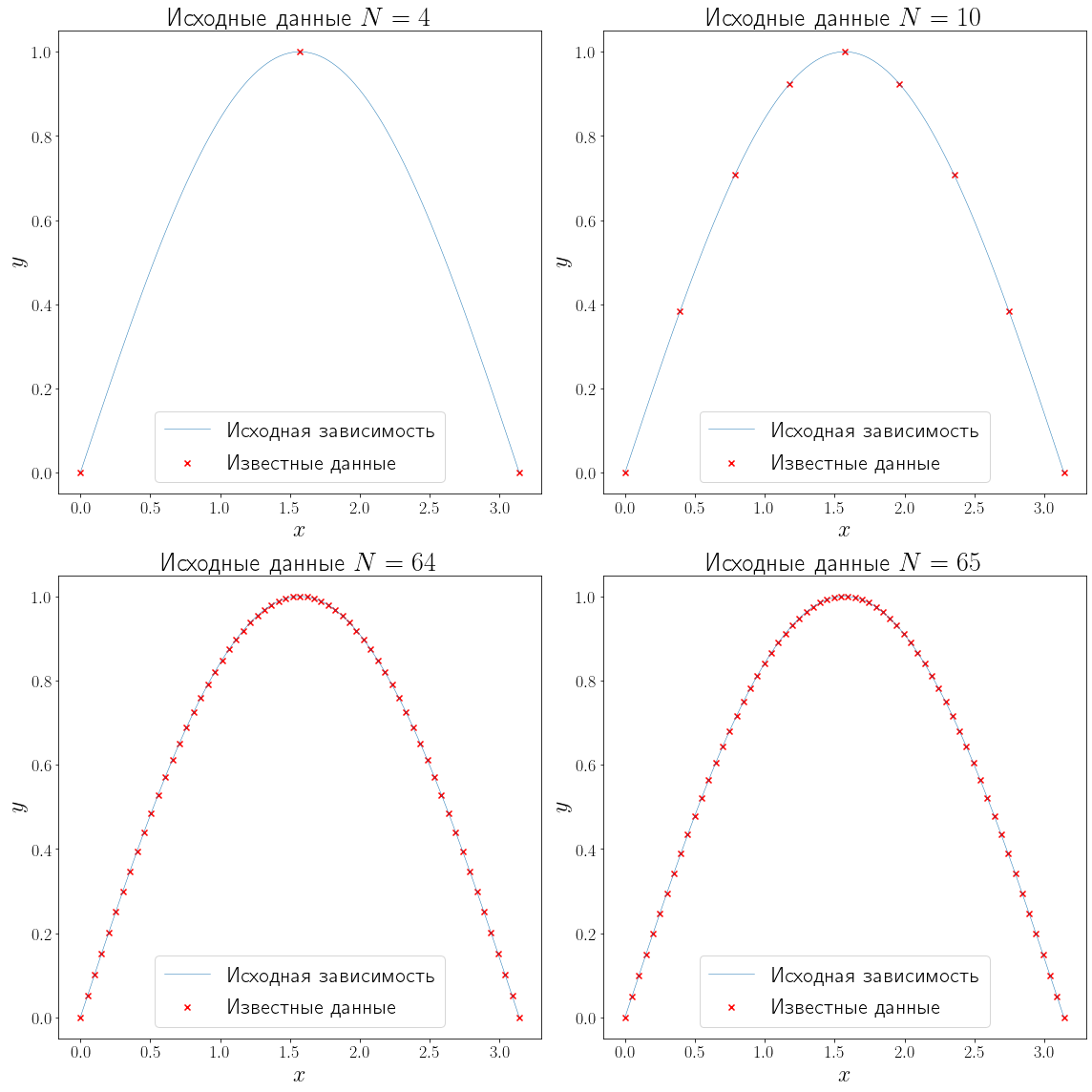
Теперь когда данные готовы, осталось произвести интерполяцию. Методов интерполяции существует очень много. Рассмотрим полиномиальную интерполяцию и сплайн интерполяцию.

Полиномиальная интерполяция#

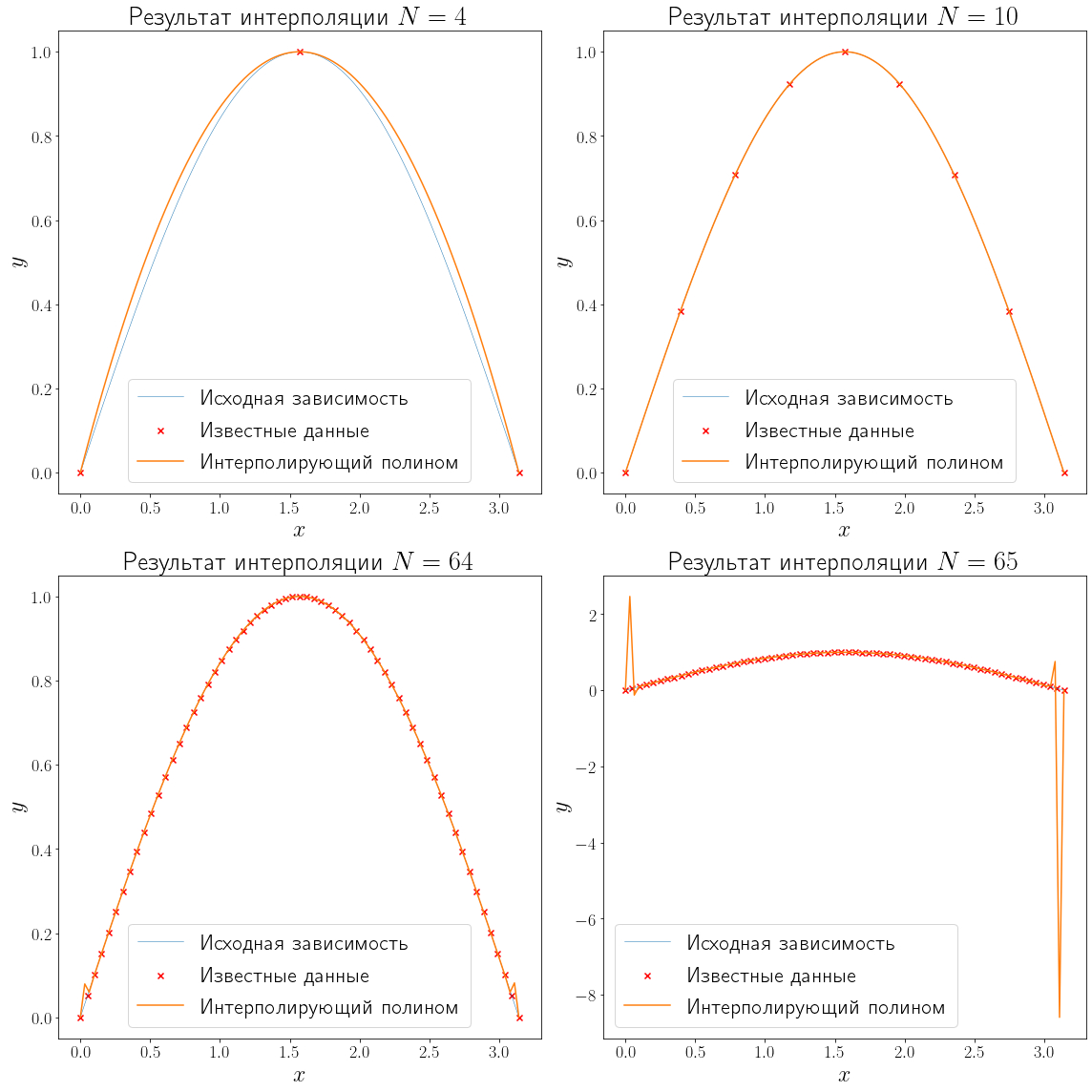
Полиномиальная интерполяция основывается на том факте, что существует единственный полином (P_{N}(x) = a_0 + a_1 x + cdots + a_{N} x ^ N ) степени (N), проходящий через точки ({(x_1, y_1), …, (x_{N + 1}, y_{N + 1})}), если (x_i neq x_j quad forall i, j = 1, cdots, N + 1, quad i neq j).

Недостатком полиномиальной интерполяции является её нестабильность. Полиномиальная интерполяция проявляет себя очень плохо при больших (N).

from scipy import interpolate

fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(16, 16), layout="tight")
for ax, N in zip(axs.flatten(), n_points):
    x_data, y_data = generate_data(f, L, R, N)
    plot_problem(ax, x_data, y_data)

    poly = interpolate.KroghInterpolator(x_data, y_data)
    y_poly = poly(xh)
    ax.plot(xh, y_poly, label="Интерполирующий полином")
    
    ax.set_title(f"Результат интерполяции ${N=}$")
    ax.legend()

Сплайн интерполяция#

Интерполирование многочленом … на всем отрезке ([a, b]) с использованием большого числа узлов интерполяции часто приводит к плохому приближению, что объясняется сильным накоплением погрешностей в процессе вычислений. Кроме того, из-за расходимости процесса интерполяции увеличение числа узлов не обязано приводить к повышению точности. Для того чтобы избежать больших погрешностей, весь отрезок ([a, b]) разбивают на частичные отрезки и на каждом из частичных отрезков приближенно заменяют функцию (f(х)) многочленом невысокой степени (так называемая кусочно-полиномиальная интерполяция). Одним из способов интерполирования на всем отрезке является интерполирование с помощью сплайн-функций. Сплайн-функцией или сплайном называют кусочно-полиномиальную функцию, определенную на отрезке ([a, b]) и имеющую на этом отрезке некоторое число непрерывных производных [2].

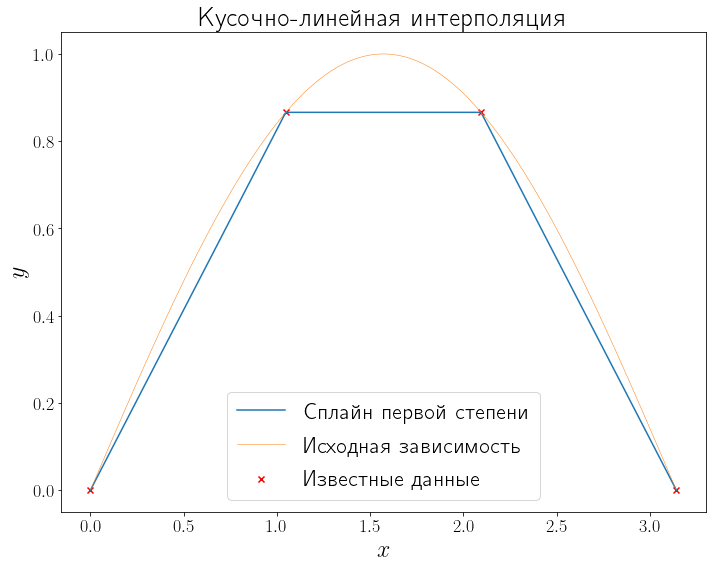
Например, если взять в качестве сплайн-функции полином первой степени, то на выходе получится кусочно-линейная интерполяция.

x_data, y_data = generate_data(f, L, R, 5)
linear = interpolate.interp1d(x_data, y_data, kind="linear")
y_linear = linear(xh)

fig, ax = plt.subplots(figsize=(10, 8), layout="tight")
ax.plot(xh, y_linear, label="Сплайн первой степени")
plot_problem(ax, x_data, y_data)
ax.legend()
ax.set_title("Кусочно-линейная интерполяция")

Text(0.5, 1.0, 'Кусочно-линейная интерполяция')

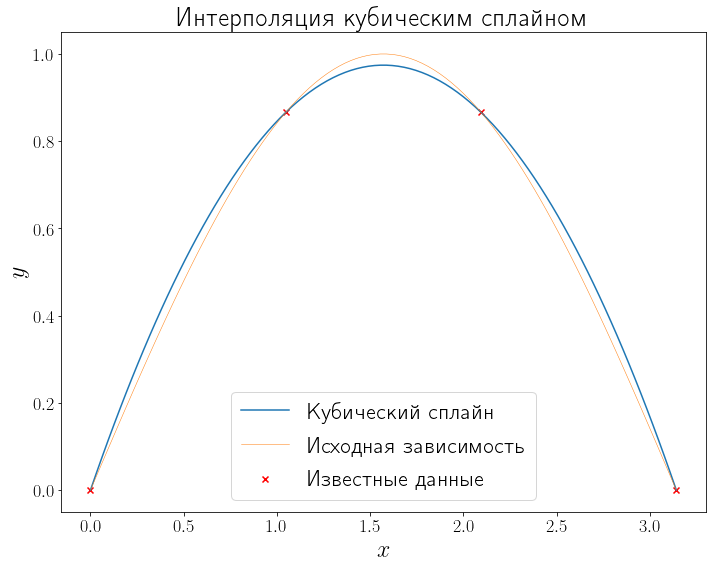
Очень часто выбирают полином третьей степени, которые позволяют строить гладкие интерполирующие полиному и разумно ведут себя между точками во многих случаях.

cubic = interpolate.interp1d(x_data, y_data, kind="cubic")
y_cubic = cubic(xh)

fig, ax = plt.subplots(figsize=(10, 8), layout="tight")
ax.plot(xh, y_cubic, label="Кубический сплайн")
plot_problem(ax, x_data, y_data)
ax.legend()
ax.set_title("Интерполяция кубическим сплайном")

Text(0.5, 1.0, 'Интерполяция кубическим сплайном')

Аппроксимация функций#

При интерполировании ставится цель восстановить исходную зависимость (y = f(x)) таким образом по набору точек, через которые функция (f) проходит в точности. Но что если значение исходной функции (f) в точках (x_i, , i=0,ldots,N) известно не точно, а в пределах какой-то погрешности или с точностью до какой-то случайной величины, т.е., например, (y_i = f(x_i) + varepsilon_i, , i = 0, ldots, N). В таком случае такое строгое требование на то, чтобы решение (varphi(x)) в точности проходило через все точки ((x_i, y_i), , i=0, …, N) не имеет большого смысла и может быть ослаблено, например, до поиска такой функции (varphi) из определенного класса функций, которая меньше всего отклоняется от значений ((x_i, y_i),, i=0,…, n).

Очень распространенным подходом в таком случае является метод наименьших квадратов, при котором отклонение формализуется в виде суммы квадратов отклонений аппроксимирующей функции (varphi) в точках (x_i, , i=0,ldots,N) от измерений (y_i, , i=0,ldots,N). Пусть решение ищется в классе функций ({varphi_pcolon mathbb{R}tomathbb{R}mid pin P}), тогда задача аппроксимации сводится к задаче минимизации

[
sum_{i=0}^{N}||varphi_p(x_i) — y_i||^2 sim min_{pin P}.
]

Note

Многие методы аппроксимации легко обобщаются на многомерные случаи.

При такой постановке часто выделяют линейную и нелинейную аппроксимации. Аппроксимация является линейной, если (varphi_p(x)) линейно зависит от параметров (p).

Note

Аппроксимация функций реализована во множестве других библиотек, таких как statsmodels, scikit-learn и некоторых других.

Линейная аппроксимация#

Очень распространенным случаем линейной аппроксимации является полиномиальная аппроксимация, при которой решение ищется в виде полинома (P_{N}(x) = a_0 + a_1 x + cdots + a_{n} x^n), т.е. решается задача

[
sum_{i=0}^{N}||a_0 + a_1 x_i + cdots + a_{n} x_i^n — y_i||^2 sim min_{a_0, a_1, ldots, a_n in mathbb{R}^{n+1}}.
]

Если все (x_i, , i=1,ldots,N) все различны, то при (n=N) существует глобальный минимум, который соответствует проходящему через все точки интерполирующему полиному, поэтому обычно решение ищется при (n<N).

Сгенерируем данные для тестирования полиномиальной интерполяции при различных (n). В качестве исходной зависимости выберем функцию

[
f(x)=2e^{-3x} + 4,
]

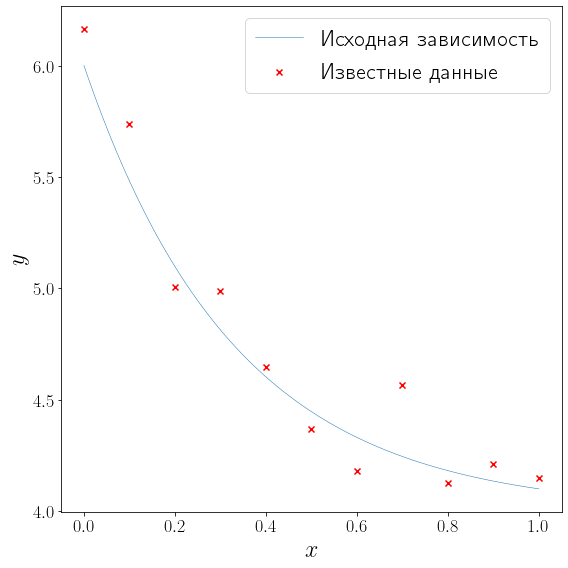
сгенерируем (N = 11) точек (x_i, , i=0, ldots, 10) равномерно распределенных на отрезке ([0, 1]) и искусственно добавим распределенный по Гауссу шум к значениям функции (f) в этих точках: ({y_i=f(x_i) + varepsilon_i, , varepsilon_i sim mathcal{N}(0, sigma^2), , i=0, ldots, 10}).

L = 0
R = 1

def f(x):
    return 2*np.exp(-3*x) + 4


N = 11
sigma = 0.2
x_data = np.linspace(L, R, N)
y_data = f(x_data) + np.random.normal(loc=0, scale=sigma, size=N)

xh = np.linspace(0, 1, 100) 
yh = f(xh)                   


fig, ax = plt.subplots(figsize=(8, 8), layout="tight")
plot_problem(ax, x_data, y_data)
ax.legend()

<matplotlib.legend.Legend at 0x1c71e0beb50>

Решить задачу полиномиальной аппроксимации можно средствами модуля numpy.polynomial. В частности подогнать полином заданной степени методом наименьших квадратов можно с помощью метода numpy.polynomial.Polynomial.fit.

from numpy.polynomial import Polynomial

degrees = (1, 2, 3, 4, 5, 10)


fig, axs = plt.subplots(figsize=(16, 24), nrows=3, ncols=2, layout="tight")
for ax, degree in zip(axs.flatten(), degrees):
    approximation = Polynomial.fit(x_data, y_data, degree)
    plot_problem(ax, x_data, y_data)
    ax.plot(xh, approximation(xh), color="green", label="Аппроксимация")
    ax.set_title(f"$n = {degree}$")
    ax.legend()

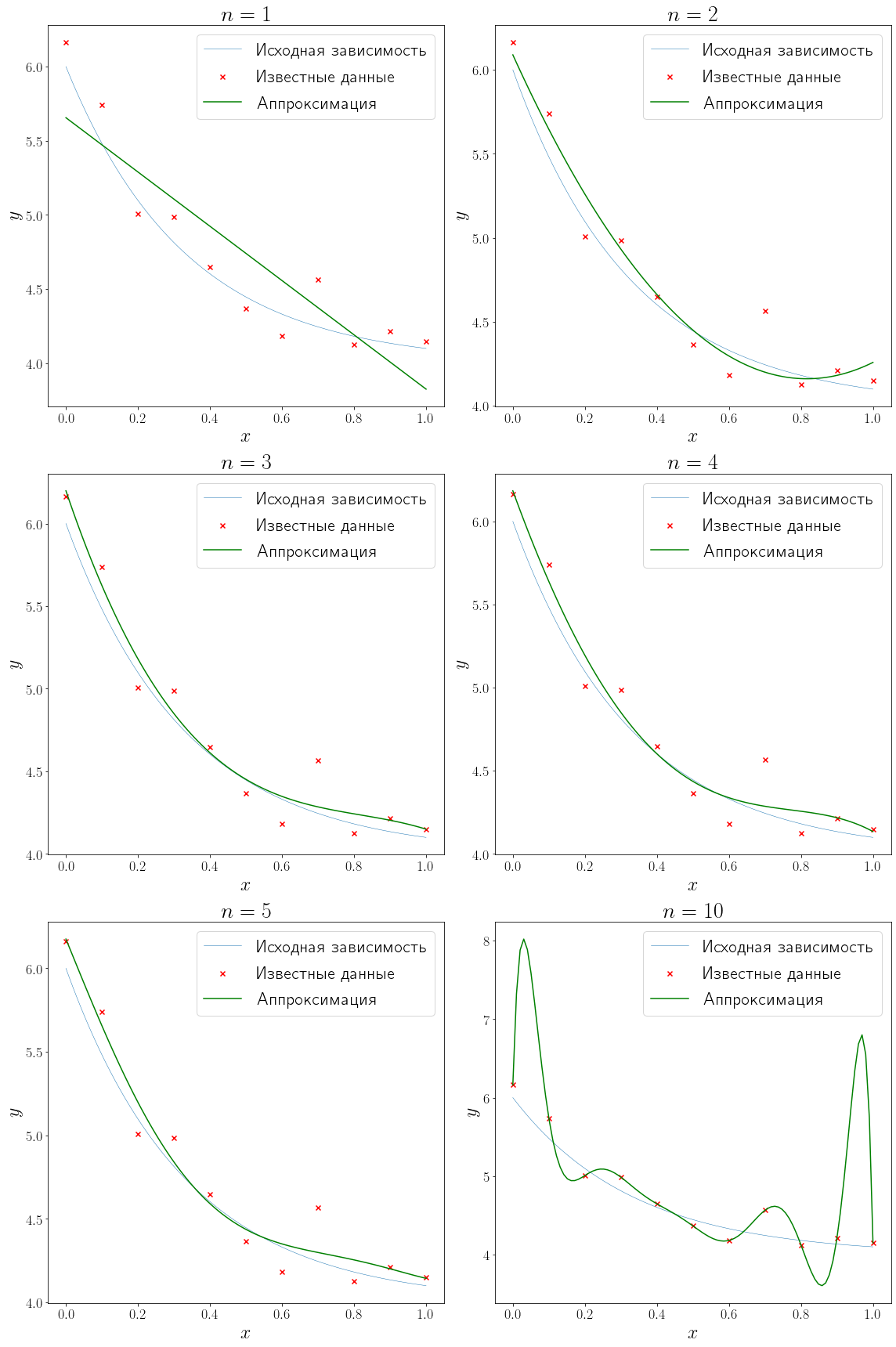
В более общем случае при линейной аппроксимации решение ищется в виде линейной комбинации любых функций (varphi(x) = c_1varphi_1(x) + cdots + c_nvarphi_n(x)) и задача аппроксимации сводится к подбору коэффициентов (c_i, , i=1,ldots,n) посредством минимизации

[
sum_{i=0}^{N}||c_1 varphi_1(x_1) + cdots + c_n varphi_n(x_i) — y_i||^2 sim min_{c_1, ldots, c_n in mathbb{R}^n}.
]

Полиномиальная интерполяция получается при (varphi_i(x) = x^i). Можно показать, что решение оптимизационной задачи выше эквивалентно минимизации невязки системы линейных алгебраических уравнений

[begin{split}
begin{pmatrix}
varphi_1(x_0) &cdots & varphi_k(n_0) \
vdots & ddots & vdots \
varphi_1(x_N) &cdots & varphi_k(n_N)
end{pmatrix}
begin{pmatrix}
c_1 \ vdots \ c_n
end{pmatrix}=
begin{pmatrix}
y_0 \ vdots \ y_N
end{pmatrix}.
end{split}]

За решение таких задач отвечает метод linalg.lstsq. В качестве примера аппроксимируем тот же набор точек, но решение будем искать в виде

[
varphi_{alpha, beta, gamma}(x) = alpha + beta e^{-x} + gamma x^2.
]

from scipy import linalg

def approximation(x, alpha, beta, gamma):
    return alpha + beta*np.exp(-x) + gamma*np.square(x)


A = np.vstack([
    np.ones_like(x_data), np.exp(-x_data), np.square(x_data)
]).T

b = y_data

(alpha, beta, gamma), *_ = linalg.lstsq(A, b)

fig, ax = plt.subplots(figsize=(8, 8), layout="tight")
plot_problem(ax, x_data, y_data)
ax.plot(xh, approximation(xh, alpha, beta, gamma), color="green", label="Аппроксимация")
ax.legend()

<matplotlib.legend.Legend at 0x1c71e1393d0>

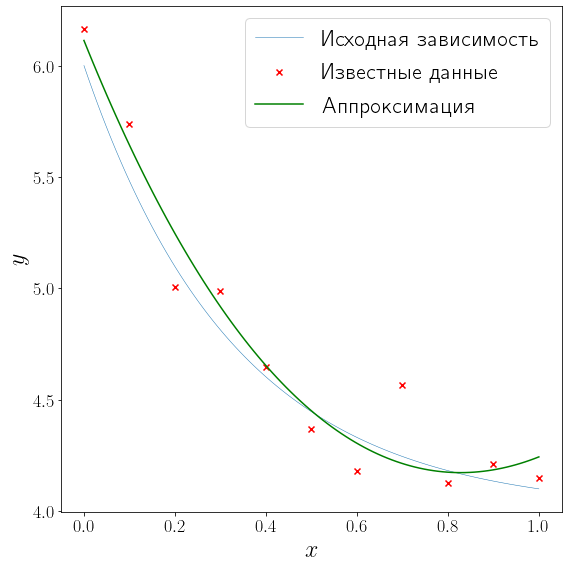
Нелинейная аппроксимация#

Будем аппроксимировать данные функцией вида

[
varphi_{alpha, beta, gamma}(x) = alpha e^{beta x} + gamma.
]

Исходная функция (f(x)=2e^{-3x} + 4) совпадает с (varphi_{alpha, beta, gamma}(x)) при (alpha=2), (beta=-3) и (gamma=4), т.е. теоретически можно восстановить точное решение.
Аппроксимация не является линейной, т.к. (varphi_{alpha, beta, gamma}) зависит от параметра (beta) экспоненциально. Метод optimize.curve_fit позволяет искать приближенное решение задачи нелинейной аппроксимации.

Чтобы воспользоваться методом optimize.curve_fit, необходимо определить функцию, которая первым своим аргументом принимает (x) (может быть скаляром, а может быть и вектором), а остальными аргументами принимает параметры (p). В примере ниже это функция approximation.

Далее этому методу optimize.curve_fit передаётся эта самая функция, данные, под которые эту функцию необходимо подогнать, и начальное приближение (p_0) используемое в качестве стартовой точки для подбора параметров, при которых достигается минимальное среднее квадратичное отклонение (varvarphi_p) от заданного набора точек.

from scipy import optimize

def approximation(x, alpha, beta, gamma):
    return alpha * np.exp(beta * x) + gamma

(alpha, beta, gamma), _ = optimize.curve_fit(approximation, x_data, y_data, p0=[3, -6, 10])


fig, ax = plt.subplots(figsize=(8, 8), layout="tight")
plot_problem(ax, x_data, y_data)
ax.plot(xh, approximation(xh, alpha, beta, gamma), color="green", label="Аппроксимация")
ax.legend()

print(f"""
Найденные параметры: 
{alpha = :.3f},
{beta = :.3f},
{gamma = :.3f},
""")

Найденные параметры: 
alpha = 2.130,
beta = -3.378,
gamma = 4.081,

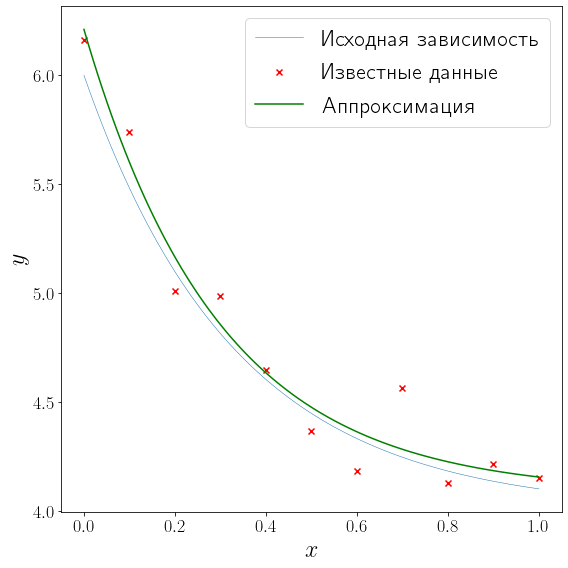
Видим, что найденные значения коэффициентов (alpha, beta) и (gamma) с неплохой точностью совпали с истинными и аппроксимирующая кривая довольно близко проходит к исходной (f(x)).

Note

В случае нелинейной аппроксимации следует проявлять особую осторожность, т.к. функционал среднеквадратичного отклонения минимизируется численными методами и начальное приближение (p_0) играет большую роль: при не удачном (p_0) алгоритм может сойтись не туда или не сойтись вообще.

Список литературы#

1: Брайан К. Джонс Дэвид Бизли. Python. Книга рецептов. М. ДМК Пресс, 2019. ISBN 978-5-97060-751-0.
2(1,2,3): Гулин А.В. Самарский А.А. Численные методы. М. Наука, 1989. ISBN 5-02-013996-3.

Источник

Шаги

Советы

Об этой статье

Была ли эта статья полезной?

Интерполяция данных: соединяем точки так, чтобы было красиво

Немного матчасти

Ставим опыты

Думаем и экспериментируем

А как люди-то делают?

MS Excel

LibreOffice Calc

Highcharts, одна из самых популярных JS-библиотек для построения диаграмм

amCharts, ещё одна популярная JS-библиотека

Coreplot, самая популярная библиотека построения графиков для iOS и OS X

aChartEngine, вроде как самая популярная библиотека построения графиков для Android

Вместо заключения

2.2 Линейная интерполяция

2.3 Интерполяция каноническим полиномом

Общие сведения о интерполяции

Интерполяция и аппроксимация#

Интерполяция#

Полиномиальная интерполяция#

Сплайн интерполяция#

Аппроксимация функций#

Линейная аппроксимация#

Нелинейная аппроксимация#

Список литературы#

Не пропустите также: