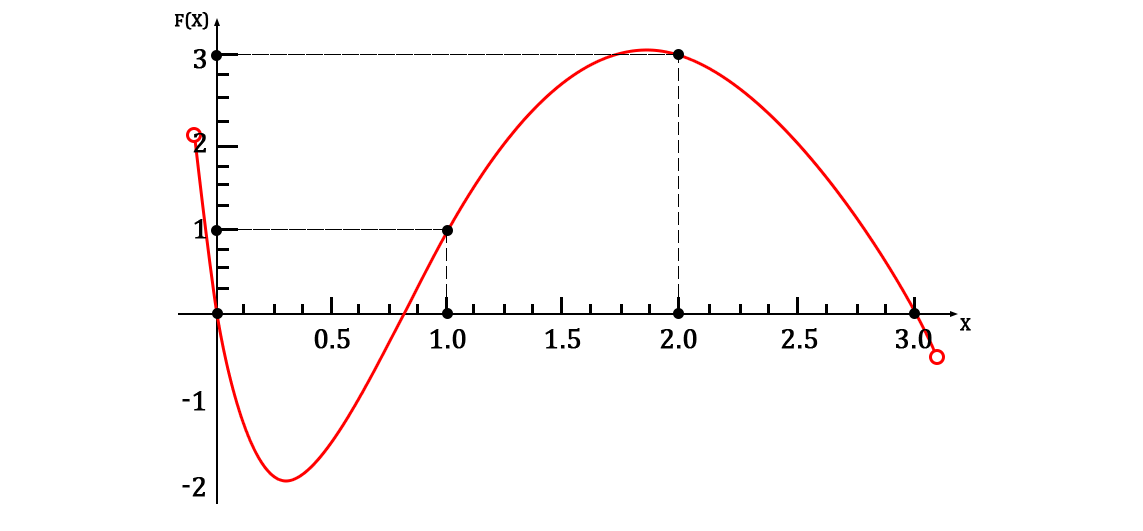
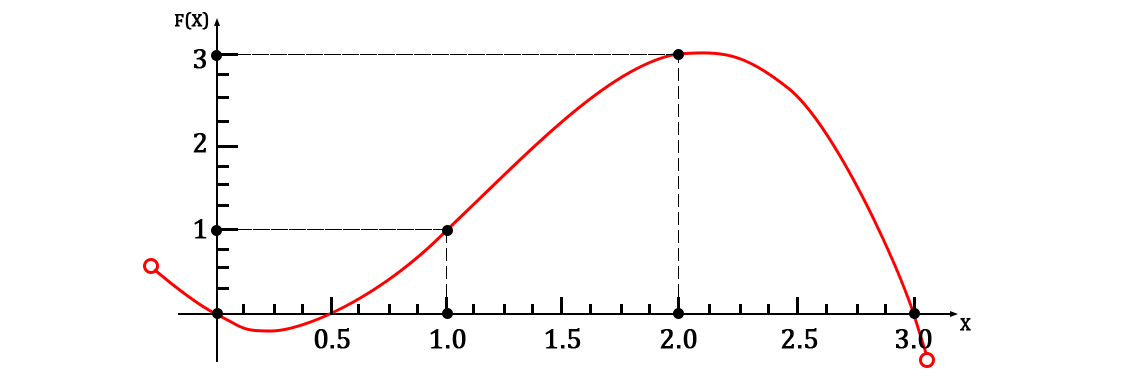
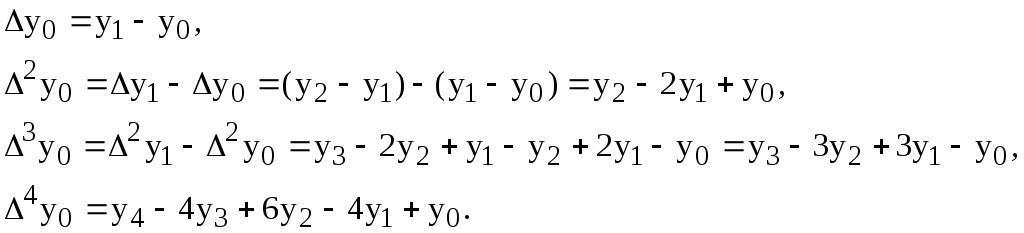Пусть
на отрезке
в некоторой последовательности
узлов
задана функция
своими значениями
,
где.
Задача алгебраического интерполирования
состоит в построении многочленастепени
,
удовлетворяющего условию интерполирования:.
Известно,
что существует единственный полином
степени не выше
,
принимающий в исходных точках заданные
значения. Коэффициентыполинома
можно определить из системы уравнений:
Определитель
этой системы есть определитель
Вандермонда, и, следовательно, система
имеет единственное решение.
Пример.
Построить интерполяционный многочлен
,
совпадающий с функциейв точках
.
Решение.
Пусть
,
поэтому имеем

Отсюда
.
Поэтому
при
.
Многочлен Лагранжа
Будем
искать многочлен в виде линейной
комбинации множеств степени
:
.
При
этом потребуем, чтобы каждый многочлен
во всех узлах интерполяции, за исключением
одного,
где он равен 1. Легко проверить, что этим
условиям отвечает многочлен вида
.
Действительно,
.
Причислитель выражения равен 0. По аналогии
получим:
,
.
Подставив эти
формулы в исходный многочлен, получим:
.
Эта формула
называется интерполяционным многочленом
Лагранжа.
Пример.
Построить интерполяционный многочлен
Лагранжа
,
совпадающий с функциейв точках
.
Решение.
Составим таблицу
-
х
-2
-4/3
0
4/3
2
у
0
1
2
1
0
Подставляя эти
значения в формулу Лагранжа, получим:
Если
функция
непрерывно дифференцируема до
-го
порядка включительно, то остаточный
член интерполяционного многочлена в
форме Лагранжа имеет вид
,
где
– внутренняя точка минимального отрезка,
содержащего узлы интерполированияи точку
.
Многочлен Ньютона с конечными разностями
Рассмотрим
случай равноотстоящих узлов интерполяции,
т. е.
– называется шагом.
Введем
понятие конечных разностей. Пусть
известны значения функции в узлах
.
Составим разности значений функции:
Эти разности
называются разностями первого порядка.
Можно составить
разности второго порядка:
.
Аналогично
составляются разности k-го
порядка:
.
Выразим
конечные разности непосредственно
через значение функции:
Таким
образом, для любого k
можно записать:
Запишем
эту формулу для значений разности в
узле
:
.
Используя конечные
разности, можно определить
.
Перейдем к построению
интерполяционного многочлена Ньютона.
Этот многочлен будем искать в виде
.
График
многочлена должен проходить через
заданные узлы, то есть
.
Используем эти условия для нахождения
коэффициентов многочлена:
Найдем
отсюда коэффициенты
:
Таким
образом, для любого
-го
коэффициента формула примет вид
.
Подставляя
эти формулы в выражение многочлена
Ньютона, получим его следующий вид:
Полученную
формулу можно записать в другом виде.
Для этого введем переменную
.
В этом
случае
С
учетом этих соотношений формулу
многочлена Ньютона можно записать в
виде
.
Полученное
выражение может аппроксимировать данную
функцию
на всем отрезке изменения аргумента
.
Однако более целесообразно (с точки
зрения повышения точности расчетов и
уменьшения числа слагаемых в полученой
формуле) ограничиться случаем,
то есть использовать эту формулу для
всех.
Для других случаев вместопринять
,
еслипри
.
В этом случае интерполяционный многочлен
можно записать в виде
Полученная
формула называется первым интерполяционным
многочленом Ньютона для интерполяции
вперед. Эту интерполяционную формулу
обычно используют для вычисления
значений функции в точках левой половины
рассматриваемого отрезка. Это объясняется
следующим: разности
вычисляются через значения функции
,
причем.
Из-за этого при больших значенияхмы не можем вычислить высших порядков
.
Для
правой половины рассматриваемого
отрезка разности лучше вычислять справа
налево. В этом случае
,
то есть,
и интерполяционный многочлен Ньютона
можно получить в виде:
.
Полученная
формула называется вторым интерполяционным
многочленом назад.
Пример.
Используя интерполяционный полином
Ньютона, вычислить
,
где функциязадана таблицей
|
х |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
у |
0 |
0,1002 |
0,2013 |
0,8045 |
0,4108 |
0,5211 |
Решение.
Составляем
таблицу конечных разностей.
|
х |
у |
|
|
|
|
|
|
0 |
0 |
|||||
|
0,1002 |
||||||
|
0,1 |
0,1002 |
0,0009 |
||||
|
0,1011 |
0,0012 |
|||||
|
0,2 |
0,2013 |
0,0021 |
-0,0002 |
|||
|
0,1032 |
0,0010 |
0,0001 |
||||
|
0,3 |
0,3045 |
0,0031 |
-0,0001 |
|||
|
0,1063 |
0,0009 |
|||||
|
0,4 |
0,4108 |
0,0040 |
||||
|
0,1103 |
||||||
|
0,5 |
0,5211 |
Для
вычисления
положим в интерполяционном многочлене
Ньютона впередтогда
и
Пример.
Задана таблица. Найти
.
|
х |
|
|
|
|
|
|
0,2588 |
|||
|
0,0832 |
||||
|
|
0,3420 |
-0,026 |
||
|
0,0806 |
0,0006 |
|||
|
|
0,4226 |
-0,032 |
||
|
0,0774 |
0,0006 |
|||
|
|
0,5 |
0,038 |
||
|
0,0736 |
||||
|
|
0,5736 |
При
вычислении
положим
.
При
вычислении
положим
.
Оценим погрешности
формул Ньютона вперед и назад:
где
и
где
.
Формулы
приближенного дифференцирования
основаны на первой интерполяционной
формуле Ньютона. Интерполяционный
многочлен Ньютона имеет вид
,
где
Производя
перемножение биномов, получим
так
как
,
то
.
Аналогично
можно вычислять производные функции
любого порядка.
В
некоторых случаях требуется находить
производные функций
в основных табличных точках
.
Так как табличное значение можно считать
за начальное, то положив,
имеем
,
Для
производной многочлена Ньютона первого
порядка погрешность может быть вычислена
по формуле
,
где
– число конечных разностей в многочлене
Ньютона.
Пример.
Найти
функции
,
заданной таблично.
Решение.
|
х |
у |
|
|
|
|
50 |
1,6990 |
|||
|
0,0414 |
||||
|
55 |
1,7404 |
-0,0036 |
||
|
0,0378 |
0,0005 |
|||
|
60 |
1,7782 |
-0,0031 |
||
|
0,0347 |
||||
|
65 |
1,8129 |
Здесь
;

Вычисляя погрешность,
получим:

Действительно,

Таким образом,
результаты совпадают до четвертого
знака.
Соседние файлы в папке ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интерполяционный многочлен на произвольных функциях
Время на прочтение
3 мин
Количество просмотров 18K
Введение
Приветствую, уважаемые читатели! Сегодня предлагаю поразмышлять о следующей задачке:
Дано
пар точек на плоскости
. Все
различны. Необходимо найти многочлен
такой, что
, где
Переводя на русский язык имеем: Иван загадал
точек на плоскости, а Мария, имея эту информацию, должна придумать функцию, которая (по меньшей мере) будет проходить через все эти точки. В рамках текущей статьи наша задача сводится к помощи Марии окольными путями.
«Почему окольными путями?» — спросите вы. Ответ традиционный: это статья является продолжением серии статей дилетантского характера про математику, целью которых является популяризация математического мира.
Процесс
Для начала стоит отметить, что некоторое кол-во интерполяционных многочленов уже, разумеется, существует. Оные полиномы как раз предназначены для решения искомой задачи. Среди них особенно известны такие как полином Лагранжа и Ньютона.
А также необходимо внести ясность, что такое «произвольные функции» (термин приходит из названия текущей статьи). Под ними понимается любая унарная функция, результат которой есть биективное отображение аргумента.
В рамках статьи предлагаю за такую функцию взять десятичный логарифм
и следующие точки:
Представляя их на плоскости, должно получится нечто следующее:
Нетрудно заметить, что сейчас кол-во пар точек равно
.
При решении данной задачи приходит на ум некая системы уравнений, где кол-во линейно-независимых строк равно
. Что же это за система уравнений такая?
Давайте попробуем функцию записать в виде суммы десятичных логарифмов с коэффициентами про оных (да так, чтобы кол-во коэффициентов было равно
):
Аргументы при
различные чтобы
избежать линейной зависимости
строк в будущем (можно придумать другие). А также, учитывая, что область определения функции как минимум
(на основе заданных условием точек), мы таким образом обеспечиваем существование области значений для функции
в этой области определения.
Так как нам известны
пар точек, то обратимся к ним для того, чтобы построить следующую тривиальную систему:
Тривиальность системы заключается в том, что мы просто найдем такие
, которые будет удовлетворять всему набору условия.
Собственно решая данную систему относительно
получим следующее решение:
На этом задача естественным образом подходит к концу, остается только записать это в единую функцию:
Она, разумеется, будет проходить через заданный набор точек. А график функции будет выглядеть следующим образом:
Также, ради наглядности, можно привести аппроксимированную систему решений:
Тогда аппроксимированный вид функции будет следующий:
Разумеется, никто не говорит о том, что полученная функция будет минимальной (тот же полином Лагранжа даст более короткую форму). Однако, данный метод позволяет выразить функцию через набор произвольных функций (правда, имея в виду ограничения, заданные выше по статье).
Различные примеры
На десерт аналогично построим функцию в радикалах:
Составим систему уравнения для нахождения коэффициентов:
Её решение единственно и выглядит следующим образом:
Тогда готовая функция выглядит следующим образом:
Что по совместительтву является полином Лагранжа для данного набора точек (т.к. оный в неявном виде реализует радикальную форму алгоритма из статьи). График на области заданных точек выглядит так:
Самым интересным в данной истории является то, что произвольные функции для построения конечной функции можно
и нужно
комбинировать. Иными словами, функция может быть построена сразу на радикалах и логарифмах, а может и на чем-то другом (показательные функции, факториалы, и т.п. ). Лишь бы полученный набор функций обеспечивал линейную независимость строк при подборе коэффициентов. В общем виде для заданных
пар точек это выглядит так:
Где
— коэффициенты которые предстоит найти через систему уравнений (СЛАУ), а
— некоторые функции, которые обеспечат линейную независимость при нахождении коэффициентов.
А дальше — по алгоритму выше, всё совершенно аналогично. Не забывая о том, что
должны быть определены на заданных условием точках.
К примеру можно показать функцию, состоящую из полностью различных базовых функций:
Дабы удовлетворить заданному набору точек, коэффициенты будут в таком случае следующие (найдены строго по алгоритму из статьи):
А сама функция будет такой:
График же будет выглядит практически также как предыдущий (на области заданных точек).
Если хочется более «гладкий» график, то можно посмотреть в сторону факториальной формы, например такой:
Найдем коэффициенты:
Подставим оные в готовую функцию:
А также полюбуемся очень хорошим графиком:
Зачем это нужно?
Да хотя бы для того, чтобы представить себе пучок веревок, стянутых пластиковыми хомутами 
(* Тут мы просто наложили все графики друг на друга)
На этом в рамках текущей статьи все, рекомендую поиграться самостоятельно.
Всего наилучшего,
с вами был Петр.
Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для 





В простейшем случае 
Определение
Файл:Lagrangepolys.png Этот пример показывает интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и (7,9), а также полиномы yj lj(x), каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных xi
Лагранж предложил способ вычисления таких многочленов:
где базисные полиномы определяются по формуле:
Легко видеть что 
Отсюда следует, что 



Применения
Полиномы Лагранжа используются для интерполяции, а также для
численного интегрирования.
Пусть для функции 

В частности,
Значения интегралов от 


Для случая равномерного распределения по отрезку узлов интерполяции
В указанном случае можно выразить 

,
и, следовательно,
.
Подставив эти выражения в формулу полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим
Теперь можно ввести замену переменной
и получить полином от XY, который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования алгоритмов с многобайтным представлением чисел.
cs:Lagrangeova interpolace
nl:Lagrange-polynoom
sr:Лагранжов полином
uk:Многочлен Лагранжа
Содержание
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом ПОЛИНОМ ОДНОЙ ПЕРЕМЕННОЙ.
Интерполяция
Интерполяция или интерполирование — приближенное
или точное нахождение какой-либо величины по известным отдельным значениям
этой же величины, или других величин, с ней связанных.
Различают интерполяцию и экстраполяцию: образно говоря, интерполяция занимается восстановлением неизвестной функции в промежутках между точками, где известны ее значения (например, при известных значениях $ f(1) $ и $ f(2) $ требуется оценить $ f(1.5) $), в то время как
экстраполяция предполагает, что мы пытаемся «растянуть» множество задания функции (например, при
известных $ f(1) $ и $ f(2) $ оцениваем $ f(2.5) $ или $ f(0.5) $).
П
Пример. Вставить пропущенные буквы:
ИНТ…РПО…ЯЦИЯ
;
…КСТРАПОЛЯЦ…
.
И
Происхождение слова «интерполяция»
☞
ЗДЕСЬ.
Задача интерполяции решается в разных классах функций — полиномов алгебраических или тригонометрических, комбинаций экспонент; в классе рациональных функций. Начинаем изложение материала с самого простого случая —
Полиномиальная интерполяция
Задача. Построить полином $ y_{}=f(x) $, принимающий значения
согласно следующей таблице:
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & y_1 & y_2 &dots & y_n
end{array}
$$
Здесь числа $ { x_{j}, y_{j} }_{j=1}^n $ — рациональные (т.е. из $ mathbb Q_{} $), вещественные (из $ mathbb R_{} $) или комплексные (из $ mathbb C_{} $); числа $ { x_{j} }_{j=1}^n $ называются узлами интерполяции; искомый полином называется интерполяционным. Для однообразия любое из упомянутых множеств будем обозначать через $ mathbb A_{} $.


Геометрическая интерпретация для случая $ mathbb A_{} = mathbb R_{} $: построить алгебраическую кривую $ y_{} = f(x) $, проходящую через заданные точки $ (x_{j},y_{j}) $ плоскости $ (x_{},y_{}) $.
Т
Теорема. При $ x_{1},dots,x_{n} $ различных существует единственный полином $ f(x) in mathbb A_{}[x] $ степени $ le n_{}-1 $ такой, что
$$ f(x_{1})=y_{1},dots,f(x_{n})=y_{n} . $$
Доказательство. Коэффициенты полинома $ f(x)=A_{0}+A_1x+dots+A_{n-1}x^{n-1} $ можно определить из системы уравнений
$$
left{begin{array}{ccl}
A_0+A_1x_1+dots+A_{n-1}x_1^{n-1}&=&y_1 \
A_0+A_1x_2+dots+A_{n-1}x_2^{n-1}&=&y_2 \
dots & & dots \
A_0+A_1x_n+dots+A_{n-1}x_n^{n-1}&=&y_n,
end{array}
right.
$$
которая имеет единственное решение поскольку определитель системы (см.
☞
определитель Вандермонда, формулы Крамера ) отличен от нуля.
♦
Иногда интерполяционным полиномом называют полином из теоремы — т.е. полином минимально возможной степени. Но я в дальнейшем не ставлю такого ограничения.
=>
Все множество интерполяционных полиномов, принимающих значения по таблице, можно представить в виде
$$
f(x)+(x-x_1)times dots times(x-x_n)q(x) ,
$$
где $ f_{}(x) $ – полином из предыдущей теоремы, а $ q_{}(x) in mathbb A[x] $ – произвольный полином.
?
Придумать упрощение схемы вычисления интерполяционного полинома для таблицы
с набором узлов симметричным относительно $ 0_{} $:
$$
begin{array}{c|cccccccc}
x & -x_n & -x_{n-1} & dots & -x_1 & x_1 & dots & x_{n-1} & x_n \
hline
y & y_{-n} & y_{-(n-1)} &dots & y_{-1} & y_1 & dots & y_{n-1} & y_n
end{array}
$$
Решение
☞
ЗДЕСЬ.
?
Пусть имеется интерполяционная таблица
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & F(x_1) & F(x_2) &dots & F(x_n)
end{array}
$$
построенная для полинома $ F_{}(x) $ степени $ ge n $. Какое отношение имеет интерполяционный полином, построенный по этой таблице, к полиному $ F_{}(x) $?
Вычисление интерполяционного полинома посредством решения системы линейных уравнений из теоремы в общем случае затрудняется тем обстоятельством, что матрица Вандермонда является плохо обусловленной, т.е. небольшая погрешность в представлении ее элементов или значений $ y_1,dots,y_n $ может приводить к существенному изменению решений системы уравнений.
П
Пример. Интерполяционный полином для таблицы
$$
begin{array}{c|ccccc}
x & 1 & 2 & 3 & 4 & 5 \ hline
y & 1 & -2 & 33 & 166 & 481
end{array}
$$
имеет вид
$$ x^4-6,x^2 + 6 .$$
Если немного изменить значения $ y $:
$$
begin{array}{c|ccccc}
x & 1 & 2 & 3 & 4 & 5 \ hline
y & 1.05 & -2.05 & 32.95 & 166.05 & 480.95
end{array}
$$
то полином изменится не очень существенно:
$$
0.9875x^4+0.125x^3-6.3875x^2+0.375x+5.95 , .
$$
Но вот если осуществить следующие изменения того же порядка малости
$$
begin{array}{c|ccccc}
x & 1 & 2 & 3 & 4 & 5 \ hline
y & 1.02 & -2.05 & 33.05 & 165.95 & 481
end{array}
$$
то полином меняется гораздо существенней:
$$ 1.03x^4-0.361(6)x^3-4.495x^2-2.50(3)x+7.35 , . $$
Следовательно, применение вычислительных методов решения систем линейных уравнений — типа метода Гаусса — к системе с матрицей Вандермонда столкнется с необходимостью строгого контроля округлений.
♦
Практическое построение интерполяционного полинома производится альтернативными алгоритмами — посредством вспомогательных промежуточных представлений полинома в специальных, сравнительно просто вычисляемых, видах. Самыми распространенными являются формы Лагранжа и Ньютона.
Интерполяционый полином в форме Лагранжа
Уравнение для определения интерполяционного полинома можно записать в детерминантной форме:
$$
0equiv
left|
begin{array}{llrrrl}
1 & x_1 & x_1^2 & dots & x_1^{n-1} & -y_1 \
1 & x_2 & x_2^2 & dots & x_2^{n-1} & -y_2 \
vdots & & & & & vdots \
1 & x_n & x_n^2 & dots & x_n^{n-1} & -y_n \
1 & x & x^2 & dots & x^{n-1} & — f(x)
end{array}
right|_{(n+1)times (n+1)} .
$$
Представив последний столбец в виде суммы, получим отсюда:
$$
f(x) equiv
left|
begin{array}{llrrrr}
1 & x_1 & x_1^2 & dots & x_1^{n-1} & -y_1 \
1 & x_2 & x_2^2 & dots & x_2^{n-1} & -y_2 \
dots & & & & & dots \
1 & x_n & x_n^2 & dots & x_n^{n-1} & -y_n \
1 & x & x^2 & dots & x^{n-1} & 0
end{array}
right|
Big/
left|
begin{array}{lrrrr}
1 & x_1 & x_1^2 & dots & x_1^{n-1} \
1 & x_2 & x_2^2 & dots & x_2^{n-1} \
dots & & & & dots \
1 & x_n & x_n^2 & dots & x_n^{n-1}
end{array}
right| .
$$
Теперь разложим определитель из числителя по последнему столбцу и вспомним выражение определителя Вандермонда. Обозначим
$$
W(x) = (x-x_1)times dots times (x-x_n) ,
$$
$$
W_j(x) = frac{W(x)}{x-x_j} =(x-x_1)times dots times (x-x_{j-1})
(x-x_{j+1})times dots times (x-x_n) .
$$
Тогда интерполяционный полином в форме Лагранжа записывается в виде:
$$
f(x) equiv sum_{j=1}^n frac{y_jW_j(x)}{W_j(x_j)}=
$$
$$
=
y_1frac{(x-x_2)times dots times (x-x_n)}{(x_1-x_2)times dots times (x_1-x_n)}+
$$
$$
+y_2frac{(x-x_1)(x-x_3)times dots times (x-x_n)}{(x_2-x_1)(x_2-x_3)times dots times (x_2-x_n)}+
dots+
$$
$$
+y_nfrac{(x-x_1)times dots times (x-x_{n-1})}{(x_n-x_1)times dots times (x_n-x_{n-1})} .
$$
Образно говоря, каждое слагаемое в форме Лагранжа «отвечает» исключительно только за свой узел интерполяции (т.е. обеспечивает в нем нужное значение полинома) — и при этом «не портит» остальные узлы (обращается в них в нуль). Полиномы
$$ {{widetilde W}_j(x):= W_j(x)/W_j(x_j) }_{j=1}^n $$
называются базисными интерполяционными полиномами. Эта система полиномов действительно образует базис линейного пространства полиномов степеней, не превосходящих $ n-1 $.
?
Доказать, что
а) $ W_j(x_j)=W^{prime}(x_j) $;
б) $ displaystyle sum_{j=1}^n {widetilde W}_j(x) equiv 1 $ .
П
Пример. Построить интерполяционный полином по таблице
$$
begin{array}{c|ccccc}
x & -2 & -1 & 1 & 2 \ hline
y & -29 & -8 & -2 & 7
end{array}
$$
и с его помощью интерполировать значение неизвестной функции при $ x_{}=0 $.
Решение. Имеем: $ W_{}(x)=(x+2)(x+1)(x-1)(x-2) $, и полином в форме Лагранжа:
$$
f(x)=frac{-29}{-12}(x+1)(x-1)(x-2)+ frac{-8}{6}(x+2)(x-1)(x-2)+
frac{-2}{-6}(x+2)(x+1)(x-2) +
$$
$$
+ frac{7}{12} (x+2)(x+1)(x-1) .
$$
Подставляем сюда $ x_{}=0 $:
Ответ. $ f_{}(0)=-3 $.
Рекурсивное вычисление коэффициентов
Заметим, что представление интерполяционного полинома в форме Лагранжа еще не дает его канонической формы, т.е. явного выражения для коэффициентов $ A_0,A_1,dots, A_{n-1} $. Для получения последних требуется разложить по степеням переменной базисные интерполяционные полиномы.
$$
{widetilde W}_j(x)equiv w_{j0}+w_{j1}x+dots+ w_{j,n-1}x^{n-1} , .
$$
Кстати, осуществив такие разложения, мы получим и возможность обращения матрицы Вандермонда:
$$ left(
begin{array}{lllll}
1& x_1 &x_1^2 & ldots& x_1^{n-1}\
1& x_2& x_2^2 & ldots& x_2^{n-1}\
vdots& vdots & vdots & & vdots \
1 & x_{n}& x_{n}^2& ldots& x_n^{n-1}
end{array}
right)^{-1}=
left(
begin{array}{llll}
w_{10}& w_{11}& ldots& w_{1,n-1}\
w_{20}& w_{21}& ldots& w_{2,n-1}\
dots & dots & & dots \
w_{n0}& w_{n1}& ldots& w_{n,n-1}\
end{array}
right)^{top} , .
$$
Подробности
☞
ЗДЕСЬ; решение этой задачи востребовано не только для целей интерполяции.
В настоящем пункте мы произведем «доводку» метода Лагранжа до коэффициентов интерполяционного полинома
Т
Теорема. Пусть числа $ x_{1},dots,x_n $ все различны. Для полинома
$$ W(x)=(x-x_{1})times dots times (x-x_n) $$
справедливы следующие равенства Эйлера-Лагранжа :
$$
sum_{j=1}^n frac{x_j^k}{W'(x_j)}=left{
begin{array}{cc}
0 & npu k< n-1; \
1 & npu k= n-1.
end{array}
right.
$$
Доказательство. Построим интерполяционный полином по следующей таблице:
$$
begin{array}{c|ccc}
x & x_1 & dots & x_n \ hline
y & x_1^k & dots & x_n^k
end{array}
$$
С одной стороны, ответ известен заранее: $ f(x)equiv x^k $. С другой стороны,
формула Лагранжа дает его же в виде суммы:
$$
x^k equiv sum_{j=1}^n x_j^k frac{W_j(x)}{W_j(x_j)}
equiv
x^{n-1}sum_{j=1}^n frac{x_j^k}{W'(x_j)}+ dots ,
$$
где в правой части стоит разложение по убывающим степеням $ x_{} $.
В этом тождестве степени полиномов слева и справа должны быть одинаковыми.
Если $ k< n-1 $, то старший коэффициент правого полинома должен обратиться в
нуль. Если же $ k= n-1 $, то должны совпасть старшие коэффициенты обоих полиномов.
♦
=>
Для любого полинома $ g(x)in mathbb C[x], deg g < n-1 $ выполняется равенство
$$
sum_{j=1}^n frac{g(x_j)}{W'(x_j)}=0 , .
$$
В следующем результате изменен порядок нумерации коэффициентов интерполяционного полинома!
Т
Теорема. Обозначим
$$
sigma_k = sum_{j=1}^{n} frac{x_j^{n+k-1}}{W^{prime}(x_j)} ,
tau_k = sum_{j=1}^{n} y_j frac{x_j^{k}}{W^{prime}(x_j)} .
$$
Имеют место равенства, связывающие коэффициенты интерполяционного
полинома
$$ f(x)=A_{0}x^{n-1}+dots+A_{n-1} $$
с величинами $ sigma_{} $ и $ tau_{} $:
$$
tau_0=A_0,
tau_k=A_0sigma_k+A_1sigma_{k-1}+dots+A_{k-1}sigma_1 + A_k npu
kin {1,dots,n-1 } .
$$
Формулы позволяют рекурсивно, начиная со старшего, вычислить
коэффициенты интерполяционного полинома по величинам $ sigma_{} $ и $ tau_{} $.
П
Пример. Найти корни интерполяционного полинома, заданного таблицей
$$
begin{array}{c|ccccc}
x & 1 & 2 & 3 & 4 & 5 \ hline
y & 1 & -2 & 33 & 166 & 481
end{array}
$$
Решение. Здесь $ W(x)=(x-1)(x-2)(x-3)(x-4)(x-5)_{} $,
$$ W^{prime}(1)=24, W^{prime}(2)=-6, W^{prime}(3)=4, W^{prime}(4)=-6,
W^{prime}(5)=24 . $$
$$ sigma_1=frac{1^5}{W^{prime}(1)}+frac{2^5}{W^{prime}(2)}+
frac{3^5}{W^{prime}(3)}+frac{4^5}{W^{prime}(4)}+frac{5^5}{W^{prime}(5)}=15 ,
$$
$$
sigma_2=frac{1^6}{W^{prime}(1)}+frac{2^6}{W^{prime}(2)}+
frac{3^6}{W^{prime}(3)}+frac{4^6}{W^{prime}(4)}+frac{5^6}{W^{prime}(5)}=140,
$$
$$sigma_3=1050, sigma_4=6951 . $$
$$
tau_0=frac{1^0 cdot 1}{W^{prime}(1)}+frac{2^0cdot (-2)}{W^{prime}(2)}+
frac{3^0 cdot 33}{W^{prime}(3)}+frac{4^0 cdot 166}{W^{prime}(4)}
+frac{5^0 cdot 481}{W^{prime}(5)}=1,
$$
$$
tau_1=frac{1^1 cdot 1}{W^{prime}(1)}+frac{2^1cdot (-2)}{W^{prime}(2)}+
frac{3^1 cdot 33}{W^{prime}(3)}+frac{4^1 cdot 166}{W^{prime}(4)}
+frac{5^1 cdot 481}{W^{prime}(5)}=15,
$$
$$ tau_2=134, tau_3= 960, tau_4=6117 . $$
Формулы:
$$
begin{array}{lcll}
1 &=&A_0 & Rightarrow A_0=1 , \
15&=&15, A_0 +A_1 & Rightarrow A_1=0 , \
134&=&140, A_0+ 15, A_1 +A_2 & Rightarrow A_2=-6 , \
960&=&1050, A_0+ 140, A_1+ 15, A_2 +A_3 & Rightarrow A_3=0 , \
6117&=&6951, A_0+ 1050, A_1+ 140, A_2+ 15, A_3 +A_4 & Rightarrow A_4=6 .
end{array}
$$
Уравнение $ x^{4}-6, x^2 +6=0 $ легко решается подстановкой $ X = x^{2} $.
Ответ. $ sqrt{3 pm sqrt{3}},, — sqrt{3_{} pm sqrt{3}} $.
Величины $ sigma_k $,рассматриваемые как функции $ x_1,dots,x_n $, известны в классической алгебре XIX века под названием
алеффункции. Несмотря на их рациональный вид, они являются полиномами (симметрическими) по $ x_1,dots,x_n $. Подробности
☞
ЗДЕСЬ.
Можно организовать и альтернативную схему вычисления коэффициентов интерполяционного полинома, начав с его свободного члена.
Так, при условии $ {x_j ne 0 }_{j=1}^n $, имеем:
$$
A_{n-1}=(-1)^{n-1} tau_{-1} prod_{j=1}^n x_{j} quad npu quad tau_{-1}= sum_{j=1}^{n} y_j frac{1}{x_jW^{prime}(x_j)} , .
$$
Интерполяционный полином в форме Ньютона
Основной недостаток построения интерполяционного полинома по методу (в форме) Лагранжа
заключается в том, что при добавлении в таблицу нового узла (новых результатов измерений), в формуле приходится пересчитывать все слагаемые. От этого недостатка свободен метод Ньютона, в котором добавление нового узла ведет к добавлению лишь одного слагаемого к построенному ранее полиному.
Вывод представления этого полинома с помощью аппарата определителей
☞
ЗДЕСЬ. А само представление имеет вид
$$
f(x)=B_1+(x-x_1)B_2+(x-x_1)(x-x_2)B_3 + dots + (x-x_1)times dots times (x-x_{n-1})B_n
;
$$
он и называется интерполяционным полиномом в форме Ньютона.
Коэффициенты $ B_{1},B_2,dots,B_n $ в этой форме определяются с помощью интерполяционной таблицы:
$$
begin{array}{rcl}
y_1 & = & B_1, \
y_2 & = & B_1 +(x_2-x_1)B_2, \
y_3 & = & B_1 +(x_3-x_1)B_2+ (x_3-x_1)(x_3-x_2)B_3, \
dots & & dots \
y_n&= & B_1+(x_n-x_1)B_2+(x_n-x_1)(x_n-x_2)B_3 + dots + (x_n-x_1)times dots times (x_n-x_{n-1})B_n
end{array}
$$
Получаем последовательно:
$$
B_1 = y_1, B_2= frac{y_2-y_1}{x_2-x_1}, B_3=frac{displaystyle frac{y_3-y_1}{x_3-x_1}-frac{y_2-y_1}{x_2-x_1}}{x_3-x_1},dots
$$
Схему вычисления коэффициентов можно оформить в виде таблицы, если ввести следующее обозначение. Выражение
$$ [x_j,x_k]=frac{y_j-y_k}{x_j-x_k} quad npu quad j,k in {1,dots,n }, jne k $$
называется разделенной разностью первого порядка. Выражение
$$[x_{j+p},x_{j+p-1},dots,x_{j+1},x_j]=frac{[x_{j+p},x_{j+p-1},dots,x_{j+1}]-[x_{j+p-1},dots,x_{j+1},x_j]}{x_{j+p}-x_j}
$$
называется разделенной разностью порядка $ mathbf p $.
Т
Теорема. Интерполяционный полином в форме Ньютона записывается в виде:
$$
f(x)=y_1+[x_2,x_1](x-x_1)+[x_3,x_2,x_1](x-x_1)(x-x_2)+dots+
$$
$$
+[x_n,x_{n-1},dots,x_1] (x-x_1)times dots times (x-x_{n-1})
$$
Поясним схему вычисления разделенных разностей для случая $ n_{}=5 $. В первых двух столбцах стоят данные интерполяционной таблицы (со вставленными пустыми строками между соседними):
$$
begin{array}{r|ccccc}
x & y & \ hline
x_1 & y_1 & \
& & [x_2,x_1] \
x_2 & y_2 & & [x_3,x_2,x_1] & \
& & [x_3,x_2] & & [x_4,x_3,x_2,x_1] \
x_3 & y_3 & & [x_4,x_3,x_2] & & [x_5,x_4,x_3,x_2,x_1] \
& & [x_4,x_3] & & [x_5,x_4,x_3,x_2] \
x_4 & y_4 & & [x_5,x_4,x_3] \
& & [x_5,x_4] \
x_5 & y_5
end{array}
$$
Для вычисления третьего столбца мы вычитаем соседние значения $ y_{} $ и делим на соответствующую разность $ x_{} $:
$$
[x_2,x_1] = frac{y_2-y_1}{x_2-x_1}, [x_3,x_2]= frac{y_3-y_2}{x_3-x_2},dots
$$
и ставим получившиеся числа между соответствующими значениями $ x_{} $. Четвертый столбец заполняется аналогично: вычитаются соседние числа третьего столбца и делятся на разность крайних задействованных значений $ x_{} $:
$$
[x_3,x_2,x_1] = frac{[x_3,x_2]-[x_2,x_1]}{x_3-x_1}, [x_4,x_3,x_2] = frac{[x_4,x_3]-[x_3,x_2]}{x_4-x_2}, dots
$$
И так далее. После получения треугольной таблицы выбираются числа из верхней стороны треугольника: именно они и являются искомыми коэффициентами интерполяционного полинома в форме Ньютона.
П
Пример. Построить интерполяционный полином по таблице
$$
begin{array}{c|ccccr}
x & 1 & -2 & 3 & 0 & -1 \ hline
y & 2 & 17 & 82 & 1 & 2
end{array}
$$
Решение.
$$
begin{array}{r|ccccc}
x & y & \ hline
1 & underline{2} & \
& & underline{-5} \
-2 & 17 & & underline{9} & \
& & 13 & & underline{2} \
3 & 82 & & 7 & & underline{1} \
& & 27 & & 0 \
0 & 1 & & 7 \
& & -1 \
-1 & 2
end{array}
$$
Ответ.
$$ f(x)=2 -5(x-1)+9(x-1)(x+2)+2(x-1)(x+2)(x-3)+(x-1)(x+2)(x-3)x equiv x^4+1 . $$
Вычисления особенно упрощаются в случае равноотстоящих узлов интерполяции. Если
$$
x_2-x_1=x_3-x_2=dots=x_n-x_{n-1}=h ,
$$
то
$$
f(x)=y_1+Delta y_1 frac{x-x_1}{h}+Delta^2 y_1 frac{(x-x_1)(x-x_2)}{2!h^2}+dots+
Delta^{n-1} y_1 frac{(x-x_1)(x-x_2)times dots times (x-x_{n-1})}{(n-1)!h^{n-1}}
$$
где
$$
Delta^k y_1=y_{k+1}-C_{k}^1y_{k}+ C_{k}^2y_{k-1}+dots+(-1)^{k}y_1 ,
$$
и $ C_{k}^j $ означает биномиальный коэффициент.
Предельным переходом при $ h_{} to 0 $ из этой формулы может быть получена формула Тейлора.
Возвращаясь к соображениям, высказанным в начале пункта: можно ли считать, что метод Ньютона всегда выгоднее метода Лагранжа? — Ответ оказался положительным в случае увеличения количества узлов интерполяции при сохранении интерполяционных значений в изначальной таблице:
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & y_1 & y_2 &dots & y_n
end{array}
quad longrightarrow
begin{array}{c|cccccc}
x & x_1 & x_2 & dots & x_n & x_{n+1} \ hline
y & y_1 & y_2 &dots & y_n & y_{n+1}
end{array}
$$
Но вот в случае перехода
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & y_1 & y_2 &dots & y_n
end{array}
quad longrightarrow
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & tilde y_1 & tilde y_2 &dots & tilde y_n
end{array}
$$
т.е. в случае изменения хотя бы одного значения $ y_j $ в исходной таблице1) метод Ньютона теряет свое преимущество — приходится пересчитывать всю схему; в то время как в форме Лагранжа достаточно поменять значения числовых сомножителей базисных полиномов $ {W_j(x)/W_j(x_j)} $.
Применение полиномиальной интерполяции в задаче о разделении секрета
Обратная интерполяция
В одном из предшествующих
☝
пунктов решалcя следующий
П
Пример. Найти корни интерполяционного полинома, заданного таблицей
$$
begin{array}{c|ccccc}
x & 1 & 2 & 3 & 4 & 5 \ hline
y & 1 & -2 & 33 & 166 & 481
end{array}
$$
Способ решения этой задачи предлагался стандартный: сначала строился интерполяционный полином $ f_{}(x) $,
потом искались его корни. Можно, однако, попробовать идти следующим обходным путем. Именно, исходя из заданной таблицы попытаться восстановить обратную функцию для неизвестной, т.е. функцию $ g_{}(y) $ такую, что $ g(f(x)) equiv x $ или же, эквивалентно, $ f(g(y)) equiv y $. Разумеется, точно эту функцию — для полинома $ f_{}(x) $ — построить крайне сложно2), но ведь и сам интерполяционный полином является лишь некоторым приближением реальности! Имеет смысл решить поставленную задачу непосредственным использованием результатов таблицы, которая задает соответствие $ xleftrightarrow y_{} $ для некоторых пар значений; это соответствие можно использовать не только в направлении $ xrightarrow y_{} $, но и в направлении $ x leftarrow y_{} $, т.е. строить интерполяционный полином для $ x_{} $ как функции от $ y_{} $ (фактически, «перевернуть» интерполяционную таблицу).
Для рассматриваемого примера форма Лагранжа дает представление полинома в виде:
$$ g(y) =1 times frac{(y+2)(y-33)(y-166)(y-481)}{(1+2)(1-33)(1-166)(1-481)}+
2times frac{(y-1)(y-33)(y-166)(y-481)}{(-2-1)(-2-33)(-2-166)(-2-481)}+
$$
$$
+3times frac{(y-1)(y+2)(y-166)(y-481)}{(33-1)(33+2)(33-166)(33-481)}+4times
frac{(y-1)(y+2)(y-33)(y-481)}{(166-1)(166+2)(166-33)(166-481)}+
$$
$$
+5times frac{(y-1)(y+2)(y-33)(y-166)}{(481-1)(481+2)(481-33)(481-166)} .
$$
Чтобы найти какому значению $ x_{} $ соответствует значение $ y_{}=0 $ мы просто подставляем это последнее в формулу и получаем
$$
g(0) =frac{33789444007}{25901164800} approx 1.304553 .
$$
Сравнивая этот ответ с полученным
☝
ВЫШЕ, мы видим некоторое соответствие с корнем $ sqrt{3-sqrt{3}} approx 1.126032 $.
♦
Понятно, что исключительным случаем для обратной интерполяции будет случай «коллизии»3): двум разным узлам интерполяции соответствует одно и то же значение $ y_{} $.
Ряд проведенных численных экспериментов показал, что бывают очень сильные расхождения в результатах «прямого» и обратного интерполирования — например, при сравнении корней $ f(x)=c $ со значением $ g(c_{}) $. Кажется, что результаты более адекватны реальности если величины аргументов и значений интерполируемой функции не слишком различаются по величине (хотя это еще надо проверять). Еще один пример см. в пункте
Замена переменных и обратное отображение.
Интерполяционный полином Эрмита
Задача [Эрмит]. Построить полином $ y_{}=f(x) $, имеющий заданные значения своих производных в
узлах интерполяции $ {x_j}_{j=1}^s $:
$$
begin{array}{ccc}
P(x_1), & dots &, P^{(m_1-1)}(x_1), \
P(x_2), & dots &, P^{(m_2-1)}(x_2), \
dots ,& & dots, \
P(x_s), & dots & , P^{(m_s-1)}(x_s) . \
end{array}
$$
При $ m_j=1 $ узел $ x_{j} $ называется простым узлом интерполяции, при $ m_j>1 $ узел $ x_{j} $ называется кратным узлом.
Для случая вещественной интерполяционной таблицы ( $ mathbb A = mathbb R_{} $ ) задаче можно придать следующую геометрическую интерпретацию: требуется провести алгебраическую кривую $ y_{}=f_{}(x) $ через заданные точки $ (x_{j}, y_j) $ так, чтобы в каждой точке обеспечить заданные наклоны касательных (а также, возможно, кривизны и т.п.).


Интерполяционная таблица дает $ m_{1}+dots + m_{s} $ условий на коэффициенты неизвестного полинома. По аналогии со стандартной задачей полиномиальной интерполяции, можно ожидать, что искомый полином будет существовать среди полиномов степени $ le m_{1}+dots + m_s -1 $. Будем искать этот полином методом неопределенных коэффициентов. Обозначим
$$
widehat{W}(x) = (x-x_1)^{m_1}times dots times (x-x_s)^{m_s} ,
$$
$$
widehat{W_j}(x) = frac{widehat{W}(x)}{(x-x_j)^{m_j}} =(x-x_1)^{m_1}times dots times (x-x_{j-1})^{m_{j-1}}
(x-x_{j+1})^{m_{j+1}}
times dots times (x-x_s)^{m_s} .
$$
Пусть $ f_{}(x) $ — произвольный полином степени $ le m_1+dots + m_{s} -1 $. Разложим дробь
$ f_{}(x)big/widehat{W}(x) $ на сумму простейших над множеством $ mathbb A_{} $:
$$
begin{array}{lcll}
displaystyle
frac{f(x)}{widehat{W}(x)} &equiv &
displaystyle frac{A_{1,1}}{(x-x_1)}+frac{A_{1,2}}{(x-x_1)^2}+
dots+ frac{A_{1,m_1}}{(x-x_1)^{m_1}}+ & \
\
&+& displaystyle frac{A_{2,1}}{(x-x_2)}+frac{A_{2,2}}{(x-x_2)^2}+
dots+ frac{A_{2,m_2}}{(x-x_2)^{m_2}}+ & \
\
&+&dots + & \
\
&+& displaystyle frac{A_{s,1}}{(x-x_s)}+frac{A_{s,2}}{(x-x_s)^2}+
dots+ frac{A_{s,m_s}}{(x-x_s)^{m_s}} & \
&& & displaystyle = sum_{j=1}^{s} sum_{ell=1}^{{mathfrak m}_j}frac{A_{j,ell}}{(x-lambda_j)^{ell}}
end{array}
$$
Определим числители дробей $ A_{jk}^{} $ с помощью интерполяционных данных. Домножим обе части тождества на $ (x-x_{1})^{m_1} $, получим:
$$
frac{f(x)}{widehat{W_1}(x)} equiv A_{1,1}(x-x_1)^{m_1-1}+A_{1,2}(x-x_1)^{m_1-2}+
dots+ A_{1,m_1} + (x-x_1)^{m_1} G(x) ; $$
здесь через $ G_{}(x) $ обозначена дробно-рациональная функция по $ x_{} $, знаменатель которой не обращается в нуль при $ x=x_{1} $. Подставим это значение $ x_{} $ в обе части последнего равенства:
$$ A_{1,m_1} = frac{P(x_1)}{widehat{W_1}(x_1)} . $$
Теперь продифференцируем последнее тождество по $ x_{} $, подставим $ x=x_{1} $ и воспользуемся данными интерполяционной таблицы:
$$ A_{1,m_1-1} = frac{d}{d, x} left[ frac{f(x)}{widehat{W_1}(x)} right] Bigg|_{_{x=x_1}} = frac{P^{prime}(x_1)widehat{W_1}(x_1)-P(x_1)widehat{W_1}^{prime}(x_1)}{left[widehat{W_1}(x_1)right]^2} . $$
Снова продифференцируем по $ x_{} $ и т.д. В результате получаем:
$$
A_{1,m_1-k}=frac{1}{k!}frac{d^k}{d, x^k} left[ frac{f(x)}{widehat{W_1}(x)} right] Bigg|_{_{x=x_1}} . $$
Аналогично поступаем и с другими узлами интерполяции. В результате, получаем решение задачи в виде интерполяционного полинома Эрмита:
$$
f(x)=sum_{j=1}^s left[ A_{j,1}(x-x_j)^{m_j-1}+A_{j,2}(x-x_j)^{m_j-2}+
dots+ A_{j,m_j} right] widehat{W_j}(x) .
$$
В литературе имеется неоднозначность терминологии — этот же полином называется и интерполяционным полиномом Лагранжа-Сильвестра, и интерполяционным полиномом Серре.
Т
Теорема. Подмножество всевозможных полиномов из $ mathbb A[x] $, принимающих значения по таблице, можно представить в виде
$$
{ f(x)+widehat{W}(x)q(x) big| q_{}(x) in mathbb A[x] } ;
$$
здесь $ f_{}(x) $ — интерполяционный полином Эрмита.
Интерполяционный полином Эрмита является естественным обобщением обычного интерполяционного полинома в форме Лагранжа ( $ s=n, m_{1}=1,dots,m_s=1 $) и формулы Тейлора
( $ s=1, m_{1}=n $).
Можно указать и явное представление для этого полинома — с использованием формализма определителей. На основании правила дифференцирования дробно-рациональной функции, получаем:
$$
f(x) =
$$
$$
=- sum_{j=1}^s frac{widehat{W_j}(x)}{left[ widehat{W_j} (x_j)right]^{mathfrak m_j}}
left|begin{array}{cccccc}
widehat{W_j} (x_j) & 0 & 0 & dots & 0 & P(x_j) \
widehat{W_j}^{prime} (x_j) & widehat{W_j} (x_j) & 0 & dots & 0 & P^{prime}(x_j) \
widehat{W_j}^{prime prime}(x_j) & 2 widehat{W_j}^{prime}(x_j) & widehat{W_j}(x_j) & dots & 0 & P^{prime prime}(x_j) \
vdots & vdots & vdots & ddots & vdots & vdots \
widehat{W_j}^{[mathfrak m_j-1]}(x_j) & C_{mathfrak m_j-1}^1 widehat{W_j}^{[mathfrak m_j-2]}(x_j) & C_{mathfrak m_j-1}^2 widehat{W_j}^{[mathfrak m_j-3]}(x_j) & dots & widehat{W_j} (x_j) & f^{[mathfrak m_j-1]}(x_j) \
1 & displaystyle{frac{x-x_j}{1!}} & displaystyle{frac{(x-x_j)^2}{2!}} & dots & displaystyle{frac{(x-x_j)^{mathfrak m_j — 1} }{(mathfrak m_j-1)!}}& 0
end{array}
right|_{(mathfrak m_j+1)times (mathfrak m_j+1)} .
$$
Здесь $ C_N^M $ — биномиальный коэффициент. Еще один подход к построению полинома см.
☞
[8].
П
Пример. Построить интерполяционный полином по таблице
$$
begin{array}{c|crrr}
x & -1 & 0 & 1 & 2 \ hline
f(x) & 16 & 7 & 8 & 217 \ hline
f^{prime}(x) & & -1 & -4 & 1375 \ hline
f^{prime prime}(x) & & 6 & -44 & \ hline
f^{prime prime prime}(x) & & & -126 &
end{array}
$$
Решение. Здесь
$$ widehat{W}(x) = (x+1)x^3(x-1)^4(x-2)^2 . $$
Для $ x_{}=-1 $ имеем $ m_{1}=1 $ и в формуле Эрмита этому узлу соответствует одно слагаемое:
$$
16 frac{x^3(x-1)^4(x-2)^2}{(-1)^3(-1-1)^4(-1-2)^2} .
$$
Для $ x_{}=0 $ имеем $ m_{2}=3 $ и этому узлу соответствует полином
$$
left[ A_{2,1}x^{2}+A_{2,2}x+ A_{2,3} right] (x+1)(x-1)^4(x-2)^2 ,
$$
значения которого — вместе с первой и второй производной — в точке $ x_{}=0 $ должны совпадать с табличными:
$$
A_{2,3} = frac{7}{1cdot(-1)^4 cdot (-2)^2}=frac{7}{4} ;
$$
$$
4,A_{2,2}-16 A_{2,3} = -1 quad Rightarrow quad A_{2,2}= 27/4 ;
$$
$$
8,A_{2,1}-32,A_{2,2}+42,A_{2,3}= 6 quad Rightarrow quad A_{2,1} = 297/16 .
$$
Для $ x_{}=1 $ имеем $ m_{3}=4 $:
$$
left[ A_{3,1}(x-1)^{3}+A_{3,2}(x-1)^2+ A_{3,3}(x-1) +A_{3,4} right] underbrace{(x+1)x^3(x-2)^2}_{=widehat{W_3}(x)} ,
$$
и для определения четырех коэффициентов этого полинома мы имеем четыре условия из таблицы:
$$
2, A_{3,4}=8 quad Rightarrow quad A_{3,4}=4 ,
$$
$$
2, A_{3,3}+3, A_{3,4}=-4 quad Rightarrow quad A_{3,3}=-8 ,
$$
$$
4,A_{3,2}+6,A_{3,3}-6,A_{3,4}= -44 quad Rightarrow quad A_{3,2}=7 ,
$$
$$
12,A_{3,1}+18,A_{3,2}-18,A_{3,3}-36,A_{3,4} =-126 quad Rightarrow quad A_{3,1}=-21 .
$$
Этот же результат можно получить и в виде альтернативного — детерминантного — представления:
$$
widehat{W_3}(1)=2, widehat{W_3}^{prime}(1)=3, widehat{W_3}^{prime prime}(1)=-6, widehat{W_3}^{prime prime prime}(1)=-36,
$$
и
$$
-frac{widehat{W_3}(x)}{[widehat{W_3}(1)]^4}
left|
begin{array}{ccccc}
widehat{W_3}(1) & 0 & 0 & 0 & f(1) \
widehat{W_3}^{prime}(1) & widehat{W_3}(1) & 0 & 0 & f^{prime}(1) \
widehat{W_3}^{prime prime}(1) & 2 , widehat{W_3}^{prime}(1) & widehat{W_3}(1) & 0 & f^{prime prime}(1) \
widehat{W_3}^{prime prime prime}(1) & 3, widehat{W_3}^{prime prime}(1) & 3, widehat{W_3}^{prime}(1) & widehat{W_3}(1) &
f^{prime prime prime}(1) \
1 & x-1 & frac{1}{2}(x-1)^2 & frac{1}{6}(x-1)^3 & 0
end{array}
right|=
$$
$$
=-
frac{widehat{W_3}(x)}{16}
left|
begin{array}{ccccc}
2 & 0 & 0 & 0 & 8 \
3 & 2 & 0 & 0 & -4 \
-6 & 6 & 2 & 0 & -44 \
-36 & -18 & 9 & 2 & -126 \
1 & x-1 & frac{1}{2}(x-1)^2 & frac{1}{6}(x-1)^3 & 0
end{array}
right| .
$$
Наконец, для $ x_{}=2 $ имеем $ m_{4}=2 $:
$$
left[frac{655}{144}(x-2)+ frac{217}{24} right](x+1)x^3(x-1)^4 .
$$
Ответ. $ 2,x^{9}-3,x^8-4,x^5+5,x^4-x^3+3,x^2-x+7 $.
?
Построить уравнение «горки»: найти полином из условий
$$ f_{}(1)=f'(1)=0,f(2)=1,f'(2)=0 , . $$

Следующий результат не очень связан с содержанием настоящего пункта, но надо было куда-то поместить.
Т
Теорема [1]. При заданных $ {y_1,dots,y_n } subset mathbb C_{} $ существуют
а) полином
$$ f(x)=x^{n+1}+a_1x^n+dots+a_{n}x $$
(т.е. $ f(0)=0 $) и
б) числа $ {x_{1},dots,x_n } subset mathbb C $ такие, что
$$ f(x_j) = y_j, f^{prime}(x_j)=0 quad npu quad j in {1,dots, n } . $$
Зачем этот результат (формулировка — J.W.Andrushkiw, доказательство — R.Thom)
нужен — не разобрался.
Рациональная интерполяция
Задача. Для таблицы значений
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_N \ hline
y & y_1 & y_2 &dots & y_N
end{array}
$$
построить рациональную функцию в виде $ f(x)=p(x)/q(x) $ при $ p_{}(x) $ — полиноме степени $ le n $, $ q_{}(x) $ — полиноме степени $ le m $,
так, чтобы $ { f(x_j)=y_j }_{j=1}^N $. При этом $ N,n,m $ связаны соотношением:
$$ N=m+n+1 , . $$
Общее число неопределенных коэффициентов полиномов $ p_{} $ и $ q_{} $ равно $ n+m+2 $; но мы не будем различать решения задачи отличающиеся на общий числовой множитель числителя и знаменателя.
Первое решение задачи было предложено Коши в 1821 г. [9].
Т
Теорема [Коши]. Обозначим:
$$ W(x) = prod_{j=1}^N (x-x_j) , $$
$$ W_{overline{j_1j_2dots j_{ell}}} (x)=prod_{s=1}^{ell} (x-x_{j_s}) quad u quad W_{j_1j_2dots j_{ell}} (x)= frac{W(x)}{W_{overline{j_1j_2dots j_{ell}}}(x)}=
prod_{jin{1,dots,N}setminus {j_1,dots,j_{ell}}} (x-x_j), .
$$
Решение задачи рациональной интерполяции задается формулами:
$$
p(x)=sum_{(j_1,j_2,dots,j_{m+1})} frac{displaystyle prod_{s=1}^{m+1} y_{j_s}}{displaystyle prod_{s=1}^{m+1} W_{j_1j_2dots j_{m+1}} (x_{j_s}) } W_{j_1j_2dots j_{m+1}} (x)
$$
и
$$
q(x)=(-1)^{mn}sum_{(j_1,j_2,dots,j_{m})} frac{displaystyle prod_{ell=1}^{m} y_{j_{ell}}}{displaystyle prod_{jin{1,dots,N}setminus {j_1,dots,j_m}} W_{overline{j_1j_2dots j_{m}}} (x_{j}) } W_{overline{j_1j_2dots j_{m}}} (x) , .
$$
Первая сумма берется по всем возможным сочетаниям из $ {1,dots, N} $ по $ m+1 $ чисел, а вторая — по $ m_{} $ чисел.
=>
При $ m=0 $ получаем представление интерполяционного полинома в форме Лагранжа.
П
Пример. $ n =1, m=2, N=4 $
$$
p(x)=frac{y_1y_2y_3(x-x_4)}{(x_1-x_4)(x_2-x_4)(x_3-x_4)}+frac{y_1y_2y_4(x-x_3)}{(x_1-x_3)(x_2-x_3)(x_4-x_3)} +
$$
$$
+frac{y_1y_3y_4(x-x_2)}{(x_1-x_2)(x_3-x_2)(x_4-x_2)}+frac{y_2y_3y_4(x-x_1)}{(x_2-x_1)(x_3-x_1)(x_4-x_1)} ,
$$
$$
q(x)=frac{y_1y_2(x_1-x)(x_2-x)}{(x_1-x_3)(x_1-x_4)(x_2-x_3)(x_2-x_4)}+frac{y_1y_3(x_1-x)(x_3-x)}{(x_1-x_2)(x_1-x_4)(x_3-x_2)(x_3-x_4)}+
$$
$$
+frac{y_1y_4(x_1-x)(x_4-x)}{(x_1-x_3)(x_1-x_2)(x_4-x_3)(x_4-x_2)}+frac{y_2y_3(x_2-x)(x_3-x)}{(x_2-x_1)(x_2-x_4)(x_3-x_1)(x_3-x_4)}+
$$
$$
+frac{y_2y_4(x_2-x)(x_4-x)}{(x_2-x_1)(x_2-x_3)(x_4-x_1)(x_4-x_3)}+frac{y_3y_4(x_3-x)(x_4-x)}{(x_3-x_1)(x_3-x_2)(x_4-x_1)(x_4-x_2)} .
$$
♦
И
Биографические заметки о Коши
☞
ЗДЕСЬ.
§
Другие примеры на применение теоремы Коши
☞
ЗДЕСЬ
Теорема Коши дает решение задачи в смысле «как правило». Дело в том, что задача рациональной интерполяции (в указанной постановке) не всегда разрешима.
П
Пример. Для таблицы
$$
begin{array}{c|c|c|c|c|c}
x & -1 & 0 & 1 & 2 & 3 \
hline
y & 1 & 1 & 1/3 & 3 & 1/13
end{array}
$$
построить удовлетворяющую ей рациональную функцию $ f(x)=p(x)/q(x) $ при $ deg p(x)=1,deg q(x) =3 $.
Решение. Теорема Коши дает решение в виде
$$ p(x)equiv x-2, quad q(x)equiv x^3-x^2-x-2 , . $$
Однако $ p(2)=0 $ и $ q(2)=0 $, и условие $ f(2)=3 $ не выполняется. Оно не выполнится даже если мы разделим полученные полиномы на общий линейный делитель.
Вместе с тем, той же таблице удовлетворяют (безо всяких проблем) рациональные дроби
$$
frac{-860,x^2+3573,x-2932}{133,x^3-1079,x^2+3221,x-2932} , quad frac{-1587,x+3948}{860,x^4-4167,x^3+1501,x^2+4941,x+3948}, dots
$$
для которых нарушено поставленное ограничение $ N=m+n+1 $, связывающее степени числителя и знаменателя с количеством узлов интерполяции.
♦
Альтернативный подход к решению задачи основывается на следующей теореме, развивающей результат К.Якоби [10,11];
он основан на идее из пункта
☝
о рекурсивном вычислении коэффициентов интерполяционного полинома.
Предварим теоремы двумя определениями. Для произвольной числовой последовательности
$$ { mathbf c }= c_0,c_1,dots, c_{2k-2}, dots $$
определитель
$$
H_{k}({c})=
left|begin{array}{llllll}
color{Brown}c_0 & color{Blue}c_1 & color{Green}c_2 & color{Violet}c_3 & dots & c_{k-1} \
color{Blue}c_1 & color{Green}c_2 & color{Violet}c_3 & c_4 & dots & c_k \
color{Green}c_2 & color{Violet}c_3 & c_4 & &dots & c_{k+1} \
color{Violet}c_3 & c_4 & & & & \
vdots & & & ddots & vdots \
c_{k-1} & c_{k} & c_{k+1} & &dots & c_{2k-2}
end{array}
right|= det
left[ c_{j+k}right]_{j,k=0}^{k-1}
$$
называется ганкелевым определителем порядка $ k_{} $, порожденным этой последовательностью.
Определитель, зависящий от переменной $ x_{} $,
$$
mathcal H_k(x; {c}) =
left|
begin{array}{lllll}
c_0 & c_1 & c_2 & ldots & c_{k} \
c_1 & c_2 & c_3 &ldots & c_{k+1} \
vdots & & & ddots& vdots \
c_{k-1} & c_{k} & c_{k+1} & ldots & c_{2k-1} \
1 & x & x^2 & ldots & x^{k}
end{array} right|_{(k+1) times (k+1)}
$$
будет полиномом по $ x_{} $; он называется ганкелевым полиномом k-го порядка (порожденным последовательностью $ {c} $).
Т
Теорема. Пусть $ left{ y_j ne 0 right}_{j=1}^N $. Вычислим последовательности
$$
left{
tau_k=sum_{j=1}^N y_j frac{x_j^k}{W^{prime}(x_j)}
right}_{k=0}^{2m} quad mbox{ и } quad
left{ widetilde tau_k=sum_{j=1}^N frac{1}{y_j} frac{x_j^k}{W^{prime}(x_j)} right}_{k=0}^{2n-2} , ,
$$
и вычислим порожденные ими ганкелевы полиномы $ mathcal H_m (x;{tau}) $ и $ mathcal H_n (x;{widetilde tau}) $.
Если
$$
H_{n}({widetilde tau}) ne 0
$$
и
$$
left{ mathcal H_m (x_j;{tau})ne 0 right}_{j=1}^{N} ,
$$
то существует единственное решение задачи рациональной интерполяции при $ deg p(x)=n, deg q(x) le m=N-n-1 $.
Это решение можно представить в виде
$$
p(x) = H_{m+1}({tau}) mathcal H_n (x;{widetilde tau}) =
$$
$$
=left|
begin{array}{llll}
tau_0 & tau_1 & dots & tau_m \
tau_1 & tau_2 & dots & tau_{m+1} \
vdots & vdots & & vdots \
tau_{m-1} & tau_{m} & dots & tau_{2m-1} \
tau_{m} & tau_{m+1} & dots & tau_{2m}
end{array}
right| cdot
left|
begin{array}{llll}
widetilde tau_0 & widetilde tau_1 & dots & widetilde tau_n \
widetilde tau_1 & widetilde tau_2 & dots & widetilde tau_{n+1} \
vdots & vdots & & vdots \
widetilde tau_{n-1} & widetilde tau_n & dots & widetilde tau_{2n-1} \
1 & x & dots & x^n
end{array}
right| , ,
$$
$$
q(x) = H_{n}({widetilde tau}) mathcal H_m (x;{tau}) =
$$
$$
=left|
begin{array}{llll}
widetilde tau_0 & widetilde tau_1 & dots & widetilde tau_{n-1} \
widetilde tau_1 & widetilde tau_2 & dots & widetilde tau_{n} \
vdots & vdots & & vdots \
widetilde tau_{n-1} & widetilde tau_n & dots & widetilde tau_{2n-2}
end{array}
right| cdot
left|
begin{array}{llll}
tau_0 & tau_1 & dots & tau_m \
tau_1 & tau_2 & dots & tau_{m+1} \
vdots & vdots & & vdots \
tau_{m-1} & tau_{m} & dots & tau_{2m-1} \
1 & x & dots & x^m
end{array}
right|
, .
$$
§
Подробнее о методе Якоби (в том числе и об эффективном способе вычисления ганкелевых полиномов)
☞
ЗДЕСЬ.
.
Тригонометрическая интерполяция
Потребность в подобной интерполяции возникает в случае, когда приближаемая функция по своей природе предполагается периодической с известным периодом, например $ 2 pi_{} $.
Задача. Построить периодическую функцию периода $ 2 pi_{} $, принимающую значения
согласно следующей таблице:
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_n \ hline
y & y_1 & y_2 &dots & y_n
end{array}
$$
Здесь узлы интерполяции предполагаются различными вещественными $ {x_{1},dots,x_n} subset [0,2 pi] $ (хотя
все приведенные в этом пункте результаты будут справедливы и для комплексных узлов при
различных $ { mathfrak{Re} (x_k)}_{k=1}^{n}
subset [0,2pi[ $).
Т
Теорема [Эрмит ?]. Функция
$$
F(x)=y_1frac{sin(x-x_2)timesdots timessin (x-x_n)}{sin(x_1-x_2)times dots times sin (x_1-x_n)} +
$$
$$
+y_2frac{sin(x-x_1)sin(x-x_3)times dots times sin (x-x_n)}{sin(x_2-x_1)sin(x_2-x_3)times dots times sin (x_2-x_n)} + dots +
$$
$$
+y_nfrac{sin(x-x_1) times dots times sin (x-x_{n-1})}{sin(x_n-x_1)times dots times sin (x_n-x_{n-1})}
$$
решает поставленную задачу.
Доказательство тривиально, если обратить внимание на аналогию с интерполяционным полиномом в форме Лагранжа.
♦
Проанализируем полученный ответ, сначала преобразовав его. Каждое произведение в числителе можно представить в виде комбинации синусов и косинусов от аргументов кратных $ x_{} $. Так, например,
$$ sin(x-x_1) sin (x-x_2) equiv frac{1}{2} left( cos (x_2-x_1) — cos(2,x-x_1-x_2) right)equiv
$$
$$
equiv frac{1}{2} cos (x_2-x_1) — frac{1}{2} cos(x_1+x_2) cos, 2,x — frac{1}{2} sin(x_1+x_2) sin ,2,x ;
$$
$$
sin(x-x_1) sin (x-x_2) sin (x-x_3) equiv frac{1}{2} left( cos (x_2-x_1) sin (x-x_3) — cos(2,x-x_1-x_2) sin (x-x_3) right) equiv
$$
$$
equiv
frac{1}{4}left[cos(x_1-x_2)cos(x_3)+cos(x_1-x_3)cos , x_2+cos(x_2-x_3)cos(x_1)right]sin,x-
$$
$$
— frac{1}{4}left[cos(x_1-x_2)sin, x_3+cos(x_1-x_3)sin, x_2+cos(x_2-x_3)sin,x_1right]cos,x
—
$$
$$
-frac{1}{4}cos (x_1+x_2+x_3) sin 3,x +frac{1}{4} sin(x_1+x_2+x_3)cos, 3, x ,
$$
и т.д. Таким образом, функцию $ F_{}(x) $ можно представить в виде линейной комбинации тригонометрических функций $ sin ,x, cos , x $, $ sin 2,x, cos 2,x , dots, sin , (n-1) x, cos , (n-1) x $.
Функция от $ x_{} $ вида
$$
begin{matrix}
f_n(x)=a_0 & + & a_1 cos x + a_2 cos 2x+dots + a_n cos nx + \
&+&b_1 sin x + b_2 sin 2x+dots + b_n sin nx .
end{matrix}
$$
при постоянных $ {a_0,a_1,b_1,a_2,b_2,dots,a_n,b_n} $ называется тригонометрическим полиномом по переменной $ x_{} $. Если хотя бы одно из чисел $ a_{n} $ или $ b_{n} $ отлично от нуля, то говорят, что тригонометрический полином имеет порядок $ mathbf n $.
Тригонометрический полином порядка $ n_{} $ определяется заданием $ (2, n+1) $-го своего коэффициента
$ {a_0,a_1,b_1,a_2,b_2,dots,a_n,b_n} $. Возникает гипотеза, что, по аналогии со случаем полиномиальной интерполяции, задание $ (2,n+1) $-го значения интерполяционной таблицы определит такой полином однозначно. Полином, построенный по теореме Эрмита, не удовлетворяет этому условию: указанные выше преобразования, проведенные для случая $ (2, n+1) $-го узла интерполяции приведут к тригонометрическому полиному порядка $ 2, n $. Тем не менее, идея, лежащая в основе той теоремы, допускает естественное обобщение.
Т
Теорема. Функция
$$
begin{matrix}
F(x)&=&y_1frac{displaystyle sinfrac{x-x_2}{2}timesdots timessin frac{x-x_{2n+1}}{2}}{displaystyle sin frac{x_1-x_2}{2}times dots times sin frac{x_1-x_{2n+1}}{2}} + \
&+&y_2frac{displaystyle sinfrac{x-x_1}{2}sinfrac{x-x_3}{2}times dots times sinfrac{x-x_{2n+1}}{2}}{displaystyle sinfrac{x_2-x_1}{2}sinfrac{x_2-x_3}{2}times dots times sinfrac{x_2-x_{2n+1}}{2}} + \
& + & dots + \
&+& y_{2n+1}frac{displaystyle sin frac{x-x_1}{2} times dots times sin frac{x-x_{2n}}{2}}{ displaystyle sin frac{x_{2n+1}-x_1}{2} times dots times sin frac{x_{2n+1}-x_{2n}}{2}}
end{matrix}
$$
удовлетворяет условиям $ { F(x_j)=y_j }_{j=1}^{2n+1} $. Эта функция является тригонометрическим полиномом порядка не выше $ n_{} $. При таком ограничении на порядок полином, удовлетворяющий заданным интерполяционным условиям, определяется единственным образом.
Задача. Найти явные выражения для коэффициентов тригонометрического полинома из последней теоремы.
«Лобовое» решение аналогично решению задачи полиномиальной интерполяции — сведением ее к подходящей системе линейных уравнений.
П
Пример. Построить интерполяционный полином второго порядка по следующей таблице
$$
begin{array}{c|cccccc}
x & 0 & 2pi/5 & 4pi/5 & 6pi/5 & 8pi/5 \ hline
y & 1 & -1 & 3 & -2 & 2
end{array}
$$
Решение. Будем искать коэффициенты полинома традиционным методом неопределенных коэффициентов: полином
$$ a_0 + a_1 cos x + b_1 sin x + a_2 cos 2, x + b_2 sin 2, x $$
должен удовлетворять таблице. Получаем систему линейных уравнений, которую перепишем в матричном виде:
$$
left(
begin{array}{ccccc}
1 & 1 & 0 & 1 & 0 \
1 & cos 2pi/5 & sin 2pi/5 & cos 4pi/5 & sin 4pi/5 \
1 & cos 4pi/5 & sin 4pi/5 & cos 8pi/5 & sin 8pi/5 \
1 & cos 6pi/5 & sin 6pi/5 & cos 12pi/5 & sin 12pi/5 \
1 & cos 8pi/5 & sin 8pi/5 & cos 16pi/5 & sin 16pi/5
end{array}
right)
left(
begin{array}{c}
a_0 \ a_1 \ b_1 \ a_2 \ b_2
end{array}
right)
=
left(
begin{array}{r}
1 \ -1 \ 3 \ -2 \ 2
end{array}
right) .
$$
Согласно теореме эта система должна иметь решение относительно $ a_0,a_1,b_1,a_2,b_2 $, причем единственное. Так оно и оказывается: на акцентируя внимания на методе решения этой системы (см.
☞
ЗДЕСЬ ) , а также на том, как можно выразить в виде квадратичных иррациональностей косинусы и синусы углов кратных $ pi/5 $ (см.
☞
ЗДЕСЬ ), приведу лишь конечный результат —
$$ a_0 =3/5, a_1 =1/5, a_2 =1/5, $$
$$ b_1=-frac{1}{20}sqrt{2(5+sqrt{5})}(11-5sqrt{5})approx
0.034302, b_2=
-frac{1}{20}sqrt{2(5+sqrt{5})}(7+3sqrt{5})approx -2.607455 . $$
♦
?
По таблице
$$
begin{array}{c|ccccccccccccccccccccc}
x =frac{2}{21}pi times & scriptstyle 1 & scriptstyle 2 & scriptstyle 3 & scriptstyle 4 & scriptstyle 5 & scriptstyle 6 & scriptstyle 7 & scriptstyle 8 & scriptstyle 9 & scriptstyle 10 & scriptstyle 11 & scriptstyle 12 & scriptstyle 13 & scriptstyle 14 & scriptstyle 15 & scriptstyle 16 & scriptstyle 17 & scriptstyle 18 & scriptstyle 19 & scriptstyle 20 & scriptstyle 21 \ hline
y & scriptstyle 175 & scriptstyle 196& scriptstyle 230& scriptstyle 253& scriptstyle 245& scriptstyle 205& scriptstyle 135& scriptstyle 100& scriptstyle 82& scriptstyle 85& scriptstyle 82& scriptstyle 64& scriptstyle 29& scriptstyle 10& scriptstyle 15& scriptstyle 50& scriptstyle 110& scriptstyle 158& scriptstyle 174& scriptstyle 173& scriptstyle 175
end{array}
$$
построить (алгебраический) полином $ 20 $-й степени и тригонометрический полином $ 10_{} $-го порядка и сравнить их значения при $ x=pi/7 $ и $ x=pi/5 $.
Решение
☞
ЗДЕСЬ.
Для случая системы равноотстоящих узлов решение задачи значительно упрощается.
Задача. Построить полином $ f_{n} (x) $ такой, что
$$ f_nleft( frac{2pi j}{2n+1} right) = y_j quad npu quad j in{-n,-n+1,dots,-1,0,1,dots n } . $$
Т
Теорема. Коэффициенты полинома $ f_{n} (x) $ определяются формулами
$$
a_0= frac{1}{2n+1} sum_{j=-n}^n y_j,
$$
$$
a_m= frac{2}{2n+1} sum_{j=-n}^n y_j cos left( frac{2pi jm}{2n+1} right),quad
b_m= frac{2}{2n+1} sum_{j=-n}^n y_j sin left(frac{2pi jm}{2n+1} right)
$$
при $ min {1,dots,n } $.
При бесконечном увеличении числа узлов интерполяции $ n_{} $ в пределе получаем коэффициенты ряда Фурье для функции $ y_{}=f(x) $:
$$
a_0= frac{2}{pi} int_{-pi}^{pi} f(x) d, x ,
$$
$$
a_m = frac{1}{pi} int_{-pi}^{pi} f(x) cos mx d, x ,
b_m = frac{1}{pi} int_{-pi}^{pi} f(x) sin mx d, x mbox{ при } min mathbb N .
$$
§
Подробное изложение теории тригонометрической интерполяции (и дискретного преобразования Фурье)
☞
ЗДЕСЬ
Интерполяция суммами экспонент
§
Материал настоящего пункта — сильная «выжимка» из [2]. Числовой пример — мой.
Если Вы решили упражнение из предыдущего пункта, то могли обнаружить что интерполяционный алгебраический полином $ A_0+A_1x+A_2x^2+dots $ не всегда является подходящим средством приближения неизвестной функции, особенно если та, по своей «скрытой природе», принципиально неполиномиальна. В последней фразе слово «приближение» пока не формализовано — оно связано с понятием
аппроксимации, которое дается
☟
НИЖЕ. Забегая вперед, заметим, что алгебраический полином, построенный в задаче интерполяции, подходит не для всех задач,связанных с приближением неизвестной функции. Так, интуитивно понятно, почему для приближения периодической функции в предыдущем пункте использовались периодические функции с соизмеримыми периодами.
Другой класс таких «специфических» функций составляют функции, имеющие определенную асимптотику при неограниченном возрастании их аргументов (по абсолютной величине или в определенном направлении). В этом случае ставят задачу приближения функции $ F_{}(x) $ суммой экспонент:
$$ f(x) = c_1e^{m_1x}+c_2e^{m_2x}+dots+c_ne^{m_nx} ; $$
как видим, эта функция задается $ 2,n $ параметрами — коэффициентами $ {c_{k}}_{k=1}^n $ и показателями $ {m_k}_{k=1}^n $.
П
Пример. Пусть имеется вещество, представляющее из себя смесь двух радиоактивных материалов с различными периодами полураспада. По закону радиоактивного распада изменение количества $ N(t) $ радиоактивного материала (измеряемого в граммах или в количестве атомов) во времени вычисляется по формуле
$$ N(t)=N(0) e^{-lambda t} , $$
где $ N(0) $ — исходное количество материала, а $ lambda_{} > 0 $ — постоянная распада, различная для различных материалов. Тогда для смеси двух материалов получаем зависимость
$$
N_{1,2}(t)=N_1(0) e^{-lambda_1 t}+ N_2(0) e^{- lambda_2 t} .
$$
Требуется определить параметры процесса $ N_1(0), N_2(0), lambda_1, lambda_2 $ по показаниям счетчика Гейгера в различные моменты времени.
♦
Задача. Построить функцию $ displaystyle f(x) = sum_{k=1}^n m_k e^{m_kx} $, удовлетворяющую условиям интерполяции:
$$ {f(x_j)=y_j}_{j=0}^{2n-1} ; $$
узлы интерполяции $ {x_j}_{j=0}^{2n-1} $ предполагаются различными.
В отличие от рассмотренных выше задач алгебраической или тригонометрической интерполяции, поставленная задача является, во-первых, принципиально нелинейной относительно параметров, и, во-вторых, не всегда разрешимой.
П
Пример. $ f(x_0)=0, f(x_1)=1 $.
♦
Ограничимся случаем вещественных равноотстоящих узлов:
$$ x_j= j h quad npu quad h>0, jin{0,dots,2,n-1} . $$
Обозначим
$$ u_1=e^{m_1h},dots, u_n=e^{m_nh} ; $$
в этих обозначениях условия интерполяции можно переписать в виде:
$${c_1u_1^{j}+c_2u_2^{j}+dots+ c_nu_n^{j}=y_j }_{j=0}^{2n-1} . $$
Получилась система из $ 2, n $ уравнений относительно $ 2, n $ неопределенных параметров $ {c_{k}}_{k=1}^n $ и $ {u_k}_{k=1}^n $. Вхождение первых — хорошее, поскольку линейное. Со вторыми приходится обращаться с помощью «обходного манёвра», который я пока изложу в виде формального алгоритма4).
1.
Составляется система линейных уравнений, ее матричный вид:
$$
left(begin{array}{lllll}
y_0 & y_1 & y_2 & dots & y_{n-1} \
y_1 & y_2 & y_3 & dots & y_n \
y_2 & y_3 & y_4 & dots & y_{n+1} \
vdots & & & & vdots \
y_{n-1} & y_n & y_{n+1} & dots & y_{2n-2}
end{array}right)
left(
begin{array}{l}
a_n \ a_{n-1} \ a_{n-2} \ vdots \ a_1
end{array}
right)=
left(
begin{array}{l}
y_n \ y_{n+1} \ y_{n+2} \ vdots \ y_{2n-1}
end{array}
right)
$$
здесь неизвестными являются5) $ a_1,a_2,dots,a_{n} $. На числа $ {y_j}_{j=0}^{2n-1} $ накладываются два ограничения:
$$
left|begin{array}{lllll}
y_0 & y_1 & y_2 & dots & y_{n-1} \
y_1 & y_2 & y_3 & dots & y_n \
y_2 & y_3 & y_4 & dots & y_{n+1} \
vdots & & & & vdots \
y_{n-1} & y_n & y_{n+1} & dots & y_{2n-2}
end{array}right| ne 0,
left|begin{array}{lllll}
y_1 & y_2 & y_3 & dots & y_{n} \
y_2 & y_3 & y_4 &dots & y_{n+1} \
y_3 & y_4 & y_5 &dots & y_{n+2} \
vdots & & & & vdots \
y_n & y_{n+1} & y_{n+2} & dots & y_{2n-1}
end{array}right| ne 0 ;
$$
эти два определителя относятся к типу ганкелевых6).
2.
При выполнении этих ограничений система линейных уравнений имеет единственное решение
$$ a_{n},a_{n-1},dots,a_1 , $$
у которого $ a_{n} ne 0 $ (см.
☞
Формулы Крамера ). Находим это решение.
3.
Составляем алгебраическое уравнение относительно новой переменной $ lambda $:
$$ g(lambda)= lambda^n — a_1 lambda^{n-1}-a_2 lambda^{n-2}-dots-a_n = 0 , $$
коэффициенты которого найдены в предыдущем пункте. Проверяем это уравнение на отсутствие кратных корней
(см. методы
☞
ЗДЕСЬ или
☞
ЗДЕСЬ ). Находим все корни (в общем случае, они — комплексные и, как правило, могут быть найдены разве лишь приближенно). Эти корни и будут искомыми числами $ u_1,u_2,dots,u_n $.
4.
Оставшиеся параметры $ c_1,c_2,dots,c_n $ определяем из системы линейных уравнений
$$
left(begin{array}{llll}
1 & 1 & dots & 1 \
u_1 & u_2 & dots & u_n \
u_1^2 & u_2^2 & dots & u_n^2 \
vdots & & & vdots \
u_{1}^{n-1} & u_{2}^{n-1} & dots & u_{n}^{n-1}
end{array}right)
left(
begin{array}{l}
c_1 \ c_2 \ c_3 \ vdots \ c_n
end{array}
right)=
left(
begin{array}{l}
y_0 \ y_{1} \ y_{2} \ vdots \ y_{n-1}
end{array}
right) ,
$$
в которую подставлены величины $ u_1,u_2,dots,u_n $, найденные в предыдущем пункте.
Ее определитель — определитель Вандермонда, который, по предположению пункта
3
, отличен от нуля. Следовательно система имеет единственное решение.
П
Пример. Построить экспоненциальную функцию вида
$$ f(x)=c_1e^{m_1x}+c_2e^{m_2x}+c_3e^{m_3x}+c_4e^{m_4x} , , $$
принимающую значения согласно следующей таблице:
$$
begin{array}{c|cccccccc}
x & 0 & 0.1 & 0.2 & 0.3 & 0.4 & 0.5 & 0.6 & 0.7 \ hline
y & 0.5 & 0.378907 & 0.232694 & 0.088027 & -0.016793 & -0.028242 & 0.127344 & 0.550507
end{array}
$$
Решение. Для данного примера $ h=0.1, n=4 $. Система из пункта
1
приведенного алгоритма имеет решение
$$ a_1 approx 4.462091, a_2 approx — 7.447287, a_3approx 5.521117, a_4 approx -1.537257 . $$
Полином
$$ g(lambda)=lambda^4-4.462091, lambda^3+7.447287, lambda^2-5.521117, lambda+1.537257 $$
из пункта
3
алгоритма имеет корни
$$ u_1 approx 1.127497, u_2 approx 1.363425, u_{3,4} approx 0.985585pm 0.169182, mathbf i . $$
Составляем на основании этих значений систему линейных уравнений из пункта
4
алгоритма и решаем ее:
$$ c_1 approx -2.399999, c_2 approx 0.600001, c_{3,4} approx 1.149999mp 0.0000004 mathbf i . $$
Теперь осталось только перевести найденные величины $ {u_j}_{j=1}^4 $ в искомые показатели $ {m_j}_{j=1}^4 $ по формулам $ m_j=(operatorname{ln} u_j)/h $:
$$ m_1 approx 1.200001, m_2 approx 3.0999996, m_{3,4} approx -0.0000003pm 1.700000 mathbf i . $$
Я не объясняю как вычисляется натуральный логарифм мнимого числа, но вот правило
вычисления $ e^{a+mathbf i b} $ можно обнаружить
☞
ЗДЕСЬ.
Окончательно:
$$ f(x)approx -2.399999, e^{1.200001,x}+0.600001, e^{3.0999996,x}+ 2.299999, cos 1.700000 +
0.0000008, mathbf i , sin 1.700000 , $$
при истинном ответе:
$$ f(x) = -2.4e^{1.2,x}+0.6e^{3.1,x}+2.3cos , 1.7x . $$
♦
Последний пример дает интересный «поворот мысли». Представленный алгоритм отработал правильно и обнаружил периодическую функцию, наличие которой в гипотезе постановки задачи изначально не предполагалось! Алгоритм оказался «умнее» постановщика задачи… Этот эффект является проявлением замечательного свойства функций комплексного аргумента: в терминах комплексных чисел свойства функций $ e^{z} $ практически совпадают со свойствами $ cos z $ и $ sin z $, поскольку две последние линейно выражаются через первую:
$$ cos z= frac{1}{2}e^{mathbf i z} + frac{1}{2} e^{-mathbf i z}, sin z = — frac{mathbf i}{2}e^{mathbf i z} + frac{mathbf i}{2}e^{-mathbf i z} .$$
Возникает ужасное подозрение, что весь материал пункта о тригонометрической интерполяции может быть получен
средствами настоящего пункта . — Так оно и есть. Однако универсальный подход оказывается более громоздким, и в частном случае когда приближаемая функция предполагается периодической он менее эффективен, чем частный алгоритм построения тригонометрического полинома. Другое дело, если интерполируемая функция имеет вид:
$$ sin x + 3 cos sqrt{2} x $$
— т.е. представляет комбинацию двух периодических функции, но с несоизмеримыми периодами! В этом случае для ее идентификации придется применять «тяжелую артиллерию» в виде комбинации экспонент…
Аппроксимация
Задача интерполяции является частным случаем более общей задачи аппроксимации функций, т.е. замены одной неизвестной или сложной для вычисления функции другой, более простой. Здесь существенно понятие «близости» функций, которое может быть различным в конкретных задачах.
Можно определить «расстояние» между функциями $ f_{}(x) $ и $ g_{}(x) $, заданными на отрезке $ [a_{},b] $, как
$$ max_{xin [a,b]} |f(x) -g(x)| , $$
т.е. как величину максимального «разноса» ординат графиков этих функций. С точки зрения этого определения, интерполяционный полином не всегда дает подходящий способ аппроксимации. Это показывает
и упражненение из пункта о тригонометрической интерполяции и следующий пример.
П
Пример [Рунге]. Пусть на интервале $ [-1,1] $ задана функция
$$F(x)=frac{1}{26,x^2+1} . $$
Построим для нее интерполяционный полином $ f_{n}(x) $ степени $ n_{} $ по равноотстоящим узлам
$$ x_{k+1}=-1+frac{2k}{n} npu k in {0,dots,n } , $$
и будем оценивать
$$ max_{xin [-1,1]} |f_n(x) -F(x)| . $$
Имеем
$$
begin{array}{lcl}
f_3(x)&=&-frac{26}{105},x^2+frac{269}{945}, \
& & \
f_6(x)&=&-frac{52728}{3955},x^6+frac{252148}{11865},x^4-frac{948506}{106785},x^2+1, \
& & \
f_{10}(x)&=& -frac{4641162500000}{20289063627},x^{10}+frac{3463021250000}{6763021209},x^8- \
&-&frac{22398415000}{56832111},x^6+frac{2578375455500}{20289063627},x^4-frac{38842240814}{2254340403},x^2+1, \
& & \
f_{14}(x)&=& -frac{111170591389930357376}{28071734843750625},x^{14}+frac{610827425219397568}{53267049039375},x^{12} + dots + 1, \
& & \
f_{20}(x)&=& frac{137858491849000000000000000}{485257804458375856761}x^{20}-frac{178685814435050000000000000}{161752601486125285587},x^{18}+dots + 1
end{array}
$$
$$
begin{array}{c|cccccc}
n & 3 & 6 & 10 & 14 & 20 \ hline
max |f_n(x) -F(x)| & 0.678306 & 0.627383 & 1.98668 & 7.620721 & 65.42256
end{array}
$$
Вывод: точность приближения функции $ F_{}(x) $ полиномом $ f_{n}(x_{}) $ падает с увеличением его степени хотя — во все более частых узлах интерполяции — значения этих функций совпадают!
♦
Почему это происходит? Вопрос оказывается связанным со сходимостью ряда. Интерполяционный ряд
$$ f_1+(f_2-f_1)+(f_3-f_2) + dots $$
будет сходиться в некоторой окрестности нуля и расходиться при значениях $ x_{} $ близких к краю рассмотренного интервала. Для приведенного примера я, правда, оценок не нашел, но вот для другого примера Рунге
$$
F(x)=frac{1}{(1+x)^2}
$$
в [3] указывается7), что интерполяционный ряд построенный для равноотстоящих на интервале $ [-5,5_{}] $ узлов сходится при $ x_{} in ] -3.63, 3.63 [ $ и расходится вне этого интервала.
♦
§
Еще одна иллюстрация проблемы — аппроксимация ступенчатой функции
$$
F(x)=left{ begin{array}{cc} -1 & mbox{при} x<0 \
+1 & mbox{при} x>0
end{array} right.
$$
на отрезке $ [-1,1] $ — обсуждается
☞
ЗДЕСЬ.
Можно определить «расстояние» между функциями $ f_{}(x) $ и $ g(x_{}) $, непрерывными на отрезке $ [a_{},b] $, как
$$ int_a^b |f(x) -g(x)| d,x , $$
или же
$$ int_a^b [f(x) -g(x)]^2 d,x . $$
Для выяснения геометрического смысла этих определений, вспомним, что
геометрический смысл
интеграла $ int_a^{b} f(x) d, x $ от неотрицательной на $ [a_{},b] $ функции $ f_{}(x) $ — площадь криволинейной трапеции на плоскости
$ (x_{},y) $, ограниченной прямыми $ x=a_{},,x=b,,y=0 $ и графиком $ y=f(x_{}) $.
Следовательно, интеграл
$$
int_a^b left| f(x) -g(x) right| d, x
$$
определяет площадь фигуры, ограниченной прямыми $ x=a_{},,x=b $ и графиками $ y=f(x_{}), y=g(x) $ (закрашена голубым на рисунке). Чем меньше эта площадь, тем «теснее» друг к другу расположены графики $ y=f_{}(x) $ и $ y=g_{}(x) $ на отрезке $ [a_{},b] $. Величина
$$
int_a^b [f(x) -g(x)]^2 d,x ,
$$
вообще говоря, не совпадает с предыдущей, но смысл ее тот же:
она позволяет оценивать близость графиков на всем отрезке $ [a_{},b] $. С вычислительной точки зрения, проще вычислять интеграл от квадрата функции, чем от ее модуля.
Задача. Для функции $ f(x_{}) $, непрерывной на $ [0_{},1] $, построить полином $ f_{n-1}(x_{})=a_0+a_1x+dots+a_{n-1}x^{n-1} $ такой, чтобы величина
$$ int_0^1 left[f(x)-f_{n-1}(x) right]^2 d, x $$
была наименьшей.
Т
Теорема. Коэффициенты полинома $ f_{n-1}(x_{}) $ находятся из системы уравнений
$$
left(
begin{array}{lllll}
1 & frac{1}{2} & frac{1}{3} & dots & frac{1}{n} \
&&&& \
frac{1}{2} & frac{1}{3} & frac{1}{4} & dots & frac{1}{n+1} \
&&&& \
frac{1}{3} & frac{1}{4} & frac{1}{5} & dots & frac{1}{n+2} \
&&&& \
dots & & & & dots \
&&&& \
frac{1}{n} & frac{1}{n+1} & frac{1}{n+2} & dots & frac{1}{2n-1}
end{array}
right)
left(
begin{array}{l}
a_0 \
a_1 \
a_2 \
vdots \
a_{n-1}
end{array}
right)=
left(
begin{array}{l}
b_0 \
b_1 \
b_2 \
vdots \
b_{n-1}
end{array}
right) .
$$
Здесь
$$
b_{j}=int_0^1 f(x) x^{j} d, x quad npu quad jin {0,dots,n-1 } .
$$
Матрица $ {mathfrak H}_{n} $ системы называется матрицей Гильберта. Ее определитель равен
$$
frac{[1!,2!, 3! dots (n-1)!]^3}
{n!, (n+1)!, (n+2)!, dots (2n-1)!} ,
$$
т.е. отличен от нуля, и, следовательно, система имеет единственное решение.
Хотя определитель Гильберта и отличен от нуля, но очень близок к нему:
$$
det {mathfrak H}_3=frac{1}{2160}, det {mathfrak H}_4=frac{1}{6,048,000},
det {mathfrak H}_6=frac{1}{186313420339200000}
$$
поэтому при решении линейной системы надо внимательно следить за ошибками округлений [4],[5].
Задача. Для функции $ f_{}(x) $, непрерывной на $ [-pi,pi_{}] $, построить тригонометрический полином
$$
begin{matrix}
f_n(x)=a_0 & + & a_1 cos x + a_2 cos 2x+dots + a_n cos nx + \
&+&b_1 sin x + b_2 sin 2x+dots + b_n sin nx .
end{matrix}
$$
такой, чтобы величина
$$ int_{-pi}^{pi} left[f(x)-f_{n}(x) right]^2 d, x $$
была наименьшей.
Т
Теорема. Коэффициенты тригонометрического полинома $ f_{n}(x_{}) $ являются коэффициентами Фурье функции $ f(x_{}) $:
$$ a_0=frac{1}{2pi} int_{-pi}^{pi} f(x) d, x , $$
$$
a_m = frac{1}{pi} int_{-pi}^{pi} f(x) cos mx d, x ,quad
b_m = frac{1}{pi} int_{-pi}^{pi} f(x) sin mx d, x quad
$$
при $ min {1,dots n} $ .
Аппроксимация в случае недостоверности данных
Предположим теперь, что данные исходной таблицы не являются достоверными: значения обеих переменных подвержены воздействию случайных погрешностей одинакового порядка. Как воспользоваться этими данными для задачи аппроксимации? Мы рассмотрим здесь только две подобные задачи.
Все числа в настоящем и следующем пунктах предполагаются вещественными.
Задача. Найти координаты точки $ (x, y) $, сумма квадратов расстояний до которой от точек $ P_1=(x_{1},y_1),dots, P_n=(x_n,y_n) $ будет минимальной.
Можно дать этой задаче следующее наглядное толкование: предположим, что на лист бумаги прикрепляется точечная мишень, в которую стрелок стреляет из пистолета. После стрельбы лист бумаги с пулевыми отверстиями, но со снятой мишенью, передается эксперту с требованием установить вероятное положение мишени. Предположения, в которых эта задача решается, стандартные: пистолет пристрелян и не дает сносов, а сам стрелок не страдает косоглазием.
Т
Теорема 1. Координаты искомой точки определяются средними значениями координат точек $ { P_j}_{j=1}^n $:
$$
overline{x}=frac{x_1+x_2+ dots+x_n}{n},quad
overline{y}=frac{y_1+y_2+ dots+y_n}{n} .
$$
Обозначение среднего значения числовой последовательности через $ overline{color{White}{x}} $ является традиционным; не следует его путать с комплексным сопряжением. Точку $ (overline{x},overline{y}) $ иногда называют центроидом для системы точек $ { P_j}_{j=1}^n $.
=>
Координаты точки, для которой величина
$$
sum_{j=1}^n m_j left[(x-x_j)^2+(y-y_j)^2 right] ,
$$
($ m_{1},dots,m_n $ — положительные константы) будет минимальной:
$$
hat x=frac{m_1x_1+m_2x_2+ dots+m_nx_n}{m_1+m_2+ dots+m_n},quad
hat y=frac{m_1y_1+m_2y_2+ dots+m_ny_n}{m_1+m_2+ dots+m_n} .
$$
Иными словами: искомая точка совпадает с центром масс (барицентром) системы масс $ {m_j}_{j=1}^n $,
расположенных в точках $ {P_j}_{j=1}^n $.
Задача. Найти уравнение прямой в виде
$$ ax+by+1 =0 , $$
сумма квадратов расстояний до которой от точек $ {P_j}_{j=1}^n $ будет минимальной.
Если обозначить $ delta_j $ расстояние от $ P_j $ до некоторой прямой, то речь идет о поиске такой прямой, которая бы обеспечивала
$$ min (delta_1^2+delta_2^2+dots + delta_n^2) , . $$

Т
Теорема 2 [3],[4]. Обозначим
$$
u=frac{a}{b},
X=left( begin{array}{cc}
1 & x_1 \
1 & x_2 \
vdots & vdots \
1 & x_n
end{array}
right)_{ntimes 2},
Y=left( begin{array}{cc}
1 & y_1 \
1 & y_2 \
vdots & vdots \
1 & y_n
end{array}
right)_{ntimes 2} ,
$$
а $ overline{x} $ и $ overline{y} $ — те же, что и в теореме $ 1 $.
Тогда коэффициенты $ a_{} $ и $ b_{} $ искомой прямой, как правило, определяются из системы уравнений
$$
u^2+K,u-1 =0, a overline{x} + b overline{y} +1 =0 ;
$$
здесь
$$
K=frac{det(X^{top}X)-det(Y^{top}Y)}{det(X^{top}Y)} .
$$
В исключительном случае возможно решение
$$ b=0, x= overline{x} mbox{ или } a=0, y= overline{y} . $$
Геометрическая интерпретация. Линейное уравнение из теоремы означает, что искомая прямая обязательно проходит через центр тяжести системы точек. Уравнение для определение тангенса угла наклона этой прямой к оси $ Ox_{} $ — квадратное, оно имеет два корня $ mu_{1}, mu_2 $, т.е. имеется два кандидата на решение задачи. По формулам Виета $ mu_{2}=-1/mu_1 $,
что означает: две прямые взаимно перпендикулярны. На рисунке
эти прямые показаны для случая
$$
begin{array}{c|cccccc}
x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \ hline
y & 0.35 & 0.80 & 1.70 & 1.85 & 3.51 & 1.02
end{array}
$$
Их уравнения:
$$-1.59, x +1.16, y +1=0, -0.26, x — 0.35, y +1 =0 ; $$
они пересекаются в центроиде системы точек $ {(x_j,y_j)} $:
$$ overline{x} =1.75, overline{y} approx 1.54 . $$
Сумма квадратов расстояний от данных точек до этих прямых:
$$ 2.25 mbox{ и } 8.36 $$
соответственно. Следовательно, решением задачи является первая прямая (зеленая).
♦
Т
Теорема 3 [Пирсон]. Пусть матрицы $ X $ и $ Y $ определены как в теореме $ 2 $. Тогда минимум суммы квадратов расстояний точек $ {(x_{j},y_j)}_{j=1}^n $ до прямой
$$ ax+by+c=0 $$
равен минимальному положительному корню $ lambda_{min} $ уранения
$$
left| begin{array}{ccc}
sum_{j=1}^n x_j^2 — lambda & sum_{j=1}^n x_jy_j & sum_{j=1}^n x_j \
sum_{j=1}^n x_jy_j & sum_{j=1}^n y_j^2 — lambda & sum_{j=1}^n y_j \
sum_{j=1}^n x_j & sum_{j=1}^n y_j & n
end{array}
right|=0 , .
$$
Коэффициенты $ a, b $ и $ c $ уравнения искомой прямой определяются из системы уравнений
$$
left( begin{array}{ccc}
sum_{j=1}^n x_j^2 — lambda_{min} & sum_{j=1}^n x_jy_j & sum_{j=1}^n x_j \
sum_{j=1}^n x_jy_j & sum_{j=1}^n y_j^2 — lambda_{min} & sum_{j=1}^n y_j
end{array}
right)
left( begin{array}{c}
a \ b \ c
end{array}
right)=
left( begin{array}{c}
0 \ 0 \ 0
end{array}
right) , .
$$
П
Пример [Пирсон]. Построить прямую из теоремы $ 3 $ для точек
$$
begin{array}{c|cccccccccc}
x & 0.0 & 0.9 & 1.8 & 2.6 & 3.3 & 4.4 & 5.2 & 6.1 & 6.5 & 7.4 \ hline
y & 5.9 & 5.4 & 4.4 & 4.6 & 3.5 & 3.7 & 2.8 & 2.8 & 2.4 & 1.5
end{array}
$$
Решение. Здесь $ n=10 $ и
$$
sum_{j=1}^{10} x_j= 38.2, sum_{j=1}^{10} y_j= 37.0 quad Rightarrow quad overline x =3.82, overline y = 3.70 , .
$$
Далее,
$$
sum_{j=1}^{10} x_j^2= 202.32, sum_{j=1}^{10} y_j^2= 154.12, sum_{j=1}^{10} x_jy_j =110.91 , .
$$
Вычисляем определитель
$$
left|
begin{array}{ccc}
202.32 -lambda & 110.91 & 202.32 \
110.91 & 154.12 — lambda & 37.0 \
202.32 & 37.0 & 10
end{array}
right|equiv 10lambda^2-736.16lambda+451.5422 , .
$$
Корни полинома:
$$ lambda_1 approx 0.618573, lambda_2 approx 72.997427 , . $$
Следовательно, минимальное значение суммы квадратов расстояний от заданных точек до наилучшей прямой равна $ lambda_1 $
Подставляем это значение в систему линейных уравнений относительно $ a, b, c $. Она имеет бесконечное множество решений, из которого мы выберем, например,
$$ aapprox -0.094322, b approx -0.172889, c=1 , . $$
Уравнение прямой совпадает с решением Пирсона, но вот значение для минимума у него приведено другое: $ 0.2484 $. Прямая проверка подтверждает значение $ lambda_1 $.
♦
П
Пример [Гальтон]. В каждой семье, имеющей взрослых детей, замерим рост родителей и рост взрослых детей. Именно это проделал Ф.Гальтон в последней четверти XIX века. Результаты его измерений по $ 205 $ семьям и $ n= 898 $ детям можно найти
☞
ЗДЕСЬ. Целью исследования было установление зависимости между усредненным ростом обоих родителей и ростом их детей. Если изобразить полученные данные в виде точек $ {(x_j,y_j)}_{j=1}^n $ плоскости, то получим следующую картину:

Здесь размеры указаны в дюймах ($ 1 $ дюйм $ approx 2.54 $ см), а усредненный рост родителей вычисляется по формуле
$$
frac{1}{2}(mbox{рост отца} + 1.08 times mbox{рост матери}) , .
$$
Координаты центроида: $ overline{x}approx 69.22, overline{y}approx 66.76 $. Уравнение
$$
898lambda^2-13002110lambda+27405100000=0
$$
имеет два положительных корня
$$
lambda_{min}approx 2560.575, quad lambda_{max}approx 11918.389 , .
$$
Уравнение прямой, обеспечивающей минимум сумме квадратов расстояний от экспериментальных точек:
$$ y approx 4.71, x-259.40 , , $$

=>
В случае, когда координаты точек $ {(x_{j},y_j)}_{j=1}^n $ центрированы к началу координат, т.е.
$$ sum_{j=1}^n x_j = sum_{j=1}^n y_j =0 , ,$$
то обе прямые из теоремы $ 3 $ проходят через начало координат ($ c=0 $), числа $ lambda_{min} $ и $ lambda_{max} $ являются собственными числами (т.е. корнями характеристического полинома) матрицы
$$
G=left( begin{array}{cc}
X^{top} X & X^{top} Y \
X^{top} Y & Y^{top} Y
end{array}
right) quad npu quad X^{top}=[x_1,x_2,dots,x_n], Y^{top}=[y_1,y_2,dots,y_n] , .
$$
Собственный вектор этой матрицы, соответствующий числу $ lambda_{max} $ будет направляющим вектором прямой, обеспечивающей минимум сумме квадратов.
По аналогии хочется утверждать, что собственный вектор, соответствующий числу
$ lambda_{min} $ будет направляющим вектором прямой, обеспечивающей максимум сумме квадратов. Однако, это утверждение неверно. Оно будет верно, если мы добавим условие «…среди всех прямых, проходящих через начало координат».
Матрица $ G $, составленная для произвольных векторов $ {X,Y} subset mathbb R^n $, известна как матрица Грама этих векторов. Но более интересна другая ее интерпретация — статистическая. Матрица
$$
frac{1}{n} left( begin{array}{cc}
X^{top} X & X^{top} Y \
X^{top} Y & Y^{top} Y
end{array}
right) , ,
$$
составленная для векторов $ {X,Y} subset mathbb R^n $, каждый из которых имеет нулевое среднее значение, называется ковариационной матрицей этих векторов.
Метод наименьших квадратов
Предположим снова, что данные исходной таблицы не являются достоверными: значения обеих переменных подвержены воздействию случайных погрешностей, но — в отличие от предыдущего пункта — эти погрешности имеют разные порядки. Например, будем считать, что в заданной
таблице значений
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_m \ hline
y & y_1 & y_2 &dots & y_m
end{array}
$$
величины $ x_{} $ нам известны практически без искажений (т.е. на входе процесса мы имеем абсолютно достоверные данные), а вот измерения величины $ y_{} $ подвержены случайным погрешностям.
Задача. Построить полином $ f_{}(x) $ такой, чтобы величина
$$
sum_{j=1}^m (f(x_j)-y_j)^2
$$
стала минимальной.
В случае $ deg f_{} =m-1 $ мы возвращаемся к задаче интерполяции в ее классической постановке. Практический интерес, однако, представляет случай $ deg f_{} < m-1 $: экспериментальных данных больше (обычно — много больше) чем значений параметров (коэффициентов полинома $ f_{} $), которые требуется определить.
Так, в случае $ deg f_{}=1 $ речь идет о построении прямой $ y=ax+b $ на плоскости $ (x,y) $, обеспечивающей
$$ min (varepsilon_1^2+varepsilon_2^2+dots + varepsilon_m^2) , . $$
Здесь $ varepsilon_j = |a,x_j+b-y_j| $.

Обратите внимание на отличие этого рисунка от его аналога из предыдущего ПУНКТА.
Т
Теорема. Если $ mge n_{} $ и $ x_{1},dots,x_m $ все различны, то
существует единственный набор коэффициентов $ a_{0},dots,a_{n-1} $, обеспечивающий
минимальное значение для
$$
sum_{j=1}^m (a_0+a_1x_j+dots+a_{n-1}x_j^{n-1} -y_j)^2 .
$$
Этот набор определяется как решение системы нормальных уравнений
$$
underbrace{
left(begin{array}{llllll}
s_0 &s_1&s_2&ldots&s_{n-2}& s_{n-1}\
s_1 &s_2&s_3&ldots&s_{n-1}& s_{n}\
s_2 &s_3&s_4&ldots&s_{n}& s_{n+1}\
vdots& & & && vdots\
s_{n-1} &s_n&s_{n+1}&ldots &s_{2n-3}&s_{2n-2}
end{array}right)}_{displaystyle S_{ntimes n}}
left(begin{array}{l}
a_0 \ a_1 \ a_2 \ vdots \ a_{n-1} end{array} right)=
left(begin{array}{l}
t_0 \ t_1 \ t_2 \ vdots \ t_{n-1} end{array} right)
$$
при $ s_{k} = x_1^k+dots+x_m^k, t_{k} = x_1^ky_1+dots+x_m^k y_m $.
Если одно из значений $ x_{j} $ равно $ 0_{} $ , то полагаем $ 0^{0} = 1 $, так что $ s_{0}=m $
при любых $ {x_{1},dots, x_m} subset mathbb R $.
Доказательство
☞
ЗДЕСЬ.
?
Показать, что линейный полином $ y=a_{0}+a_1x $, построенный по методу наименьших квадратов, определяет на плоскости $ (x_{},y) $ прямую, проходящую через центроид
$$
overline{x}=frac{x_1+x_2+ dots+x_m}{m},quad
overline{y}=frac{y_1+y_2+ dots+y_m}{m} .
$$
системы точек $ (x_{1},y_1),dots,(x_m,y_m) $.
П
Пример. По методу наименьших квадратов построить уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы
$$
begin{array}{c|cccccc}
x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \ hline
y & 0.35 & 0.80 & 1.70 & 1.85 & 3.51 & 1.02
end{array}
$$
Решение. Имеем
$$
s_0=6, s_1=0.5 + 1 + 1.5 + 2 + 2.5 + 3=10.5, $$
$$ s_2=0.5^2 + 1^2 + 1.5^2 + 2^2 + 2.5^2 + 3^2=22.75,
$$
$$t_0=0.35 + 0.80 + 1.70 + 1.85 + 3.51 + 1.02=9.23,
$$
$$
t_1
=0.5cdot 0.35 + 1 cdot 0.80 + 1.5 cdot 1.70 + 2 cdot 1.85 +
$$
$$
+2.5 cdot 3.51 + 3 cdot 1.02=19.06 .
$$
Решаем систему нормальных уравнений
$$
left(
begin{array}{cc}
6 & 10.5 \
10.5 & 22.75
end{array}
right)
left(
begin{array}{c}
a_0 \ a_1
end{array}
right)=
left(
begin{array}{c}
9.23 \ 19.06
end{array}
right),
$$
получаем уравнение прямой в виде
$$ y= 0.375 + 0.664, x .$$
На рисунке
она изображена в цвете охры (для сравнения оставлена также зеленая прямая, полученная по методу предыдущего пункта).
♦
§
Дальнейшее развитие идеологии МНК
☞
ЗДЕСЬ.
Многомерная интерполяция
По аналогии с одномерным случаем можно поставить задачу интерполяции в многомерном пространстве. Пусть заданы точки (узлы интерполяции)
$$ (x_{j1},dots,x_{jell}) in mathbb C^{ell} npu jin {1,dots, N } $$
и заданы значения $ {z_j}_{j=1}^N $ функции в этих точках. Требуется построить полином от $ ell $ переменных, принимающий заданные значения в узлах интерполяции.
Сложности: парадокс Крамера
Задача. Построить полином $ f_{}(x,y) $ с комплексными коэффициентами по его значениям на конечном наборе точек:
$$ f(x_1,y_1)=z_1,dots, f(x_N,y_N)=z_N .$$
Задача аналогична одномерной, однако ее решение в двумерном случае имеет одну особенность. Коэффициенты полинома $ f_{}(x) in mathbb C[x] $ степени не выше, чем $ n_{}-1 $, однозначно восстанавливаются по значениям этого полинома в произвольном наборе из $ n_{} $ различных точек $ x_{1},dots,x_{n} $. Полином $ f_{}(x,y) in mathbb C[x,y] $ третьей степени определяется своими 10-ю коэффициентами:
$$
f(x,y)equiv a_{30}x^3+a_{21}x^2y+a_{12}xy^2+a_{03}y^3+a_{20}x^2+a_{11}xy+a_{02}y^2+a_{10}x+a_{01}y+a_{00} .
$$
По аналогии с одномерным случаем, можно было бы ожидать, что задание этого полинома его значениями в 9-ти произвольных узлах всегда позволит установить его коэффициенты, причем бесконечным числом способов. Эти ожидания, однако, опровергаются примером.
П
Пример [7]. Построить полином $ f_{}(x,y) $ третьей степени такой, что
$$ f(0,0)=0,f(1,1){=}z_{2},f(-2,1){=}z_{3},f(3,2)=z_{4},
f(6,5)=z_{5},f(-3,-7)=z_{6} ,$$
$$ f(2,-4)=z_{7},fleft(-2,-frac{scriptstyle 1}{scriptstyle 2}right)=z_{8},fleft({{scriptstyle
82110385798} over {scriptstyle 32539385899}}{,}{{scriptstyle 36830918404}
over {scriptstyle 32539385899}} right)=z_{9} . $$
Решение. В каноническом представлении полинома $ f_{}(x,y) $ имеется 10
коэффициентов, которые мы считаем неопределенными и ищем из заданных условий. Разрешая получающуюся систему из 9-ти линейных уравнений
относительно этих коэффициентов, мы приходим к ответу: матрица системы имеет ранг 7, т.е., согласно теореме Кронекера-Капелли, сама система будет совместной только при дополнительном условии «связи» величин $ z_{2},dots,z_9 $. Именно, последние должны удовлетворять определенному линейному соотношению
$$ p_2z_2+dots+p_9z_9=0 $$
при целых $ p_{2},dots,p_9 $ (мы не указываем эти числа ввиду их громоздкости). Таким образом, в общем случае поставленная
задача неразрешима (например, она не имеет решения при $ z_{2}=dots=z_9=1 $).
При $ z_{2},dots,z_9 $, удовлетворяющих упомянутому уравнению «связи»,
поставленная задача имеет решение. Однако, оно неединственно в силу
все той же теоремы Кронекера-Капелли, поскольку число совместных линейных уравнений меньше числа определяемых ими коэффициентов.
Как удалось подобрать узлы настолько «неудачные» для задачи интерполяции? Крамер предложил выбирать узлы как точки пересечения двух кривых третьего порядка (кубик). Согласно теореме Безу, две такие кривые пересекаются как раз в 9 точках. Например, если взять
$$
{scriptstyle 241},x^{3}
{-}{scriptstyle 1659},x^{2}y{-}
{scriptstyle 6043},xy^{2}{+}{scriptstyle 6300},y^{3}+
{scriptstyle 1633} ,x^{2}{-}
{scriptstyle 6592},xy{+}
{scriptstyle 23100},y^{2}{+}
{scriptstyle 11886},x{-}
{scriptstyle 28866},y=0
$$
и
$$
{scriptstyle 3814},x^{3}
{-}
{scriptstyle 3814},x^{2}y+
{scriptstyle 4493},xy^{2}{-}{scriptstyle 4112},y^{3}
{-}{scriptstyle 2040},x^{2}{+}{scriptstyle 4195},xy{-}
{scriptstyle 15550},y^{2}{-}{scriptstyle 25984},x{+}
{scriptstyle 38998},y=0 .
$$
то все точки пересечения этих кривых будут иметь рациональные координаты — как раз те, что приведены выше. Система из 9-ти линейных уравнений для определения 10-ти коэффициентов
интерполяционного полинома при $ z_{2}=dots=z_9=0 $ становится однородной. Поскольку она имеет 2 линейно независимых набора решений (соответствующие коэффициентам двух рассмотренных кубик), то ранг ее матрицы должен быть не выше 8. Если мы «сдвинем» хоть одно из значений $ z_{j} $ из нуля, то почти наверняка соответствующая неоднородная система станет несовместной, а задача интерполяции — неразрешимой среди полиномов третьей степени.
♦
Прямоугольная сетка
В достаточно важном — с практической точки зрения — частном случае задачу интерполяции можно решить.
Пусть узлы интерполяции расположены в точках
$$
(x_j,y_k) npu j in {1,dots,n}, kin {1,dots,m} ,
$$
и в них известны значения функции $ z_{jk} $. Требуется построить полином $ f_{}(x,y) $ по этим значениям. Такая задача возникает, например, при восстановлении рельефа морского дна с помощью промеров глубин эхолотом.

Т
Теорема. Если все числа $ { x_{j} }_{j=1}^n $ различны и все числа $ {y_{k}}_{k=1}^m $ различны, то существует единственный полином $ f_{}(x,y) $, степень
которого по переменной $ x_{} $ не превосходит $ n_{}-1 $, а по переменной $ y_{} $ — не превосходит $ m_{}-1 $, принимающий значения по заданной таблице.
Доказательство. Построить выражение для полинома можно обобщением формы Лагранжа. Обозначим
$$
W(x) = (x-x_1)times dots times (x-x_n) ,quad mathfrak W(y) = (y-y_1)times dots times (y-y_m)
$$
и
$$
W_j(x) = frac{W(x)}{x-x_j} =(x-x_1)times dots times (x-x_{j-1})
(x-x_{j+1})times dots times (x-x_n) quad npu quad j in {1,dots,n},
$$
и
$$
mathfrak W_k(y) = frac{mathfrak W(y)}{y-y_k} =(y-y_1)times dots times (y-y_{k-1})
(y-y_{k+1})times dots times (y-y_m) quad npu quad k in {1,dots,m} , .
$$
Тогда
$$
f(x,y)=sum_{j=1}^n sum_{k=1}^m z_{jk} frac{W_j(x)}{W_j(x_j)} frac{mathfrak W_k(y)}{mathfrak W_k(y_k)} , .
$$
Легко проверить, что этот полином удовлетворяет условиям теоремы:
$$ f(x_j,y_k)=z_{jk}, deg f_x le n-1, deg f_y le m-1 . $$
Осталось показать его единственность при этих условиях. Распишем этот полином по степеням $ x_{} $ и $ y_{} $:
$$
begin{array}{lllll}
a_{00} &+ a_{10}x &+a_{20}x^2 &+dots &+ a_{n-1,0}x^{n-1} + \
+a_{01}y &+ a_{11}xy &+a_{21}x^2y &+dots &+ a_{n-1,1}x^{n-1}y +\
+dots &&&& + \
+a_{0,m-1}y &+ a_{1,m-1}xy &+a_{2,m-2}x^2y &+dots &+ a_{n-1,m-1}x^{n-1}y^{m-1}
end{array}
$$
(лексикографическое упорядочение $ x succ y $ с возрастанием полной степени: см.
☞
ЗДЕСЬ ). Представим его в матричном виде, используя операцию умножения матриц:
$$
(1,y,y^2,dots,y^{m-1})
left(begin{array}{lllll}
a_{00} & a_{10} & a_{20} & dots & a_{n-1,0} \
a_{01} & a_{11} & a_{21} & dots & a_{n-1,1} \
dots & & & & dots \
a_{0,m-1} & a_{1,m-1} & a_{2,m-1} & dots & a_{n-1,m-1} \
end{array}
right) left( begin{array}{l} 1\ x \ x^2 \ vdots \ x^{n-1} end{array} right) .
$$
Условия
$$
f(x_j,y_k)=z_{jk} npu j in {1,dots,n}, kin {1,dots,m}
$$
можно также объединить в матричном представлении:
$$
left( begin{array}{llll}
1 & y_1 & dots & y_{1}^{m-1} \
1 & y_2 & dots & y_{2}^{m-1} \
vdots & & & vdots \
1 & y_m & dots & y_{m}^{m-1}
end{array} right)
underbrace{left(begin{array}{lllll}
a_{00} & a_{10} & a_{20} & dots & a_{n-1,0} \
a_{01} & a_{11} & a_{21} & dots & a_{n-1,1} \
dots & & & & dots \
a_{0,m-1} & a_{1,m-1} & a_{2,m-1} & dots & a_{n-1,m-1}
end{array}
right)}_{A}
left( begin{array}{llll} 1 & 1 & dots & 1 \
x_1 & x_2 & dots & x_{n} \
x_1^2 & x_2^2 & dots & x_{n}^2 \
vdots & & & vdots \
x_1^{n-1} & x_2^{n-1} & dots & x_{n}^{n-1}
end{array} right)=
$$
$$
=
underbrace{left( begin{array}{llll} z_{11} & z_{21} & dots & z_{n1} \
z_{12} & z_{22} & dots & z_{n2} \
z_{13} & z_{23} & dots & z_{n3} \
vdots & & & vdots \
z_{1m} & z_{2m} & dots & z_{nm}
end{array} right)}_{Z} .
$$
Матричное равенство имеет вид
$$
tilde V_{mtimes m}cdot A_{mtimes n} V_{ntimes n}^{top}= Z_{mtimes n} .
$$
Здесь матрицы $ V_{} $ и $ tilde V $ — матрицы Вандермонда. Их определители отличны от нуля, поскольку все $ {x_{j}}_{j=1}^n $ различны и все $ {y_{k}}_{k=1}^m $ различны. Следовательно, существуют обратные к этим матрицам и для матрицы $ A_{} $ коэффициентов полинома $ f_{} $ мы получаем однозначное представление:
$$
A=tilde V^{-1} Z left( V^{-1}right)^{top} .
$$
♦
Задачи
Источники
[1]. Mycielski J. Polynomials with Preassigned Values at their Branching Points. The American Mathematical Monthly, 77 (8).1970, pp. 853-855
[2]. Henrici P. Applied and Computational Complex Analysis. V. 1. 1974. NY. Wiley
[3]. Скарборо Дж. Численные методы математического анализа. М.-Л.ГТТИ. 1934, с.93
[4]. Hilbert D. Ein Beitrag zur Theorie des Legendreschen Polynoms. Acta Math. Bd.18, 1894, S.155-160
[5]. Форсайт Дж., Молер К. Численное решение систем линейных алгебраических уравнений. М. Мир. 1969
[6]. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. М.ГИФМЛ. 1958
[7]. Калинина Е.А., Утешев А.Ю. Теория исключения. Учеб. пособие. СПб.: НИИ Химии СПбГУ, 2002. 72 с.
[8]. Утешев А.Ю., Тамасян Г.Ш. К задаче полиномиального интерполирования с кратными узлами. Вестник СПбГУ. Серия 10. 2010. Вып. 3, С. 76-85. Текст (pdf)
☞
ЗДЕСЬ
[9]. Cauchy A.-L. Cours d’Analyse de l’École Royale Polytechnique: Part I: Analyse Algébrique. Paris, France: L’Imprimerie Royale, 1821, pt. 1.
[10]. Jacobi C.G.J. Űber die Darstellung einer Reihe gegebner Werthe durch eine gebrochne rationale Function. J.reine angew. Math. 1846. Bd. 30, S. 127-156
[11]. Утешев А.Ю., Боровой И.И. Решение задачи рациональной интерполяции с использованием ганкелевых полиномов. Вестник СПбГУ. Серия 10. 2016. Вып. 4, С. 31-43.
Текст
☞
ЗДЕСЬ (pdf).
[12]. Pearson K. On lines and planes of closest fit to systems of points in space. Phil. Mag. 1901. V.2, pp. 559-572