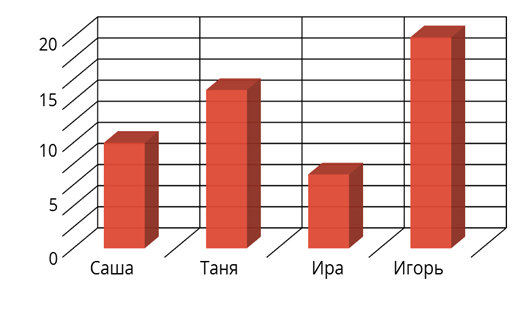Как составить графическую модель чисел

КСП

 Предмет математика.

Ход
урока

На этой странице сайта вы найдете ответы на вопрос Нарисуй графические модели чисел 30, 50, 51, 15, 38, 83?,
относящийся к категории Математика. Сложность вопроса соответствует базовым
знаниям учеников 1 — 4 классов. Для получения дополнительной информации
найдите другие вопросы, относящимися к данной тематике, с помощью поисковой
системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и
задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям.
Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы
помогут найти нужную информацию.

Графические информационные модели. Многообразие графических информационных моделей

Урок 5. Информатика 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Графические информационные модели. Многообразие графических информационных моделей»

Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений. Графические информационные модели являются простейшим видом моделей. С их помощью передаются внешние признаки объекта – размер, форма, цвет. Графические модели несут в себе больше информации, чем словесные.

Для более наглядного и понятного представления информации в графических информационных моделях используются графические изображения (образные элементы), которые могут быть дополнены текстами, числами и символами. Примерами графических информационных моделей являются схемы, карты, чертежи, графики, диаграммы и много другое.

Разберёмся более подробно с каждой из них.

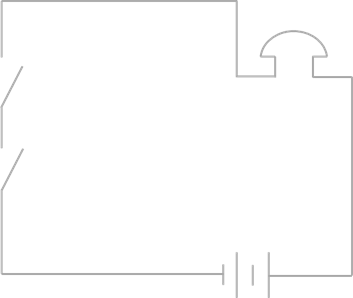
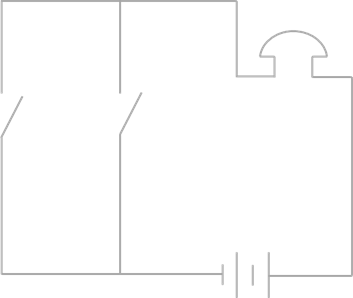
Cхема – это графическое отображение состава и структуры сложной системы. Можно обратиться к ранее рассматриваемому примеру: две электрические схемы соединения переключателей.

Схема последовательного соединения переключателей

Схема параллельного соединения переключателей

На первой представлено последовательное соединение, а на второй – параллельное. Можно заметить, что с помощью схемы легче разбираться с такими задачами, нежели использовать словесное описание. Схемы используются на уроках биологии, истории и так далее.

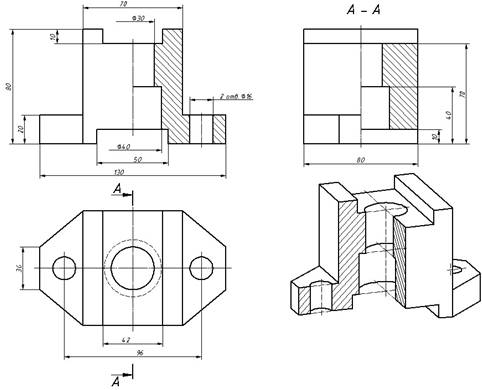
Следующая графическая информационная модель – чертеж. Чертеж – это условное графическое изображение предмета с точным соотношением его размеров, получаемое методом моделирования. При построении чертежа используются изображения, числа, текст. С помощью изображений мы получаем представление о форме объекта, с помощью чисел – о размере, с помощью текста – о названии объектов, размерах, в которых выполнены изображения. Примером чертежа является изображение детали перед её изготовлением.

На чертеже изображена деталь в разрезе, чтобы лучше было видно все части, составляющие нашу деталь, присутствуют размеры (числа).

Рассмотрим такую графическую информационную модель как карта. Карта используется для отображения местности в уменьшенном масштабе, которая является для нее объектом моделирования. Например, с помощью карты мы можем узнать сколько километров от Москвы до Санкт-Петербурга, как добраться на метро или автобусе с одного остановочного пункта до другого, где находится Будапешт и много другое. Для различных целей используются разнообразные карты: политическая, географическая, тематическая и другие.

Перейдем к графикам. График – это графическое изображение, которое отображает зависимость одной величины от другой, динамику какого-либо процесса в течение какого-либо периода и много другое.

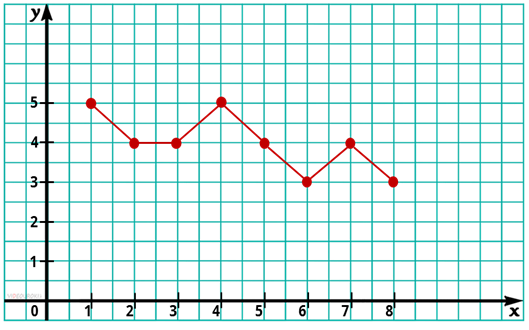
Например, Максим учится в девятом классе. В течение 8 лет учёбы в школе он получал следующие годовые оценки по математике: первый класс – 5, второй класс – 4, третий класс – 4, четвёртый – 5, пятый – 4, шестой – 3, седьмой – 4, восьмой — 3. Посмотрим, как это можно отобразить на графике. Ось X будет отображать классы с 1 по 8. Ось Y оценки с 1 до 5. Обратите внимание, что в данном графике за единицу будем брать две клеточки.

Расставим точки в соответствии с данными на координатной плоскости и соединим их линиями.

Мы получили необходимый график, с помощью которого можно сделать вывод, что знания Максима по математике ухудшились. Ещё одним примером графика является кардиограмма сердца. Кардиограмма точно определяет в каком ритме бьётся сердце.

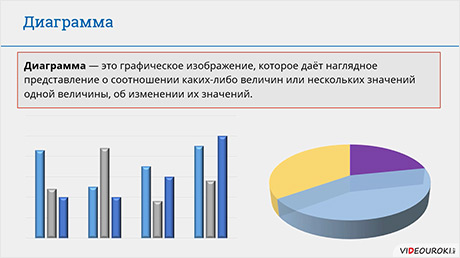
Перейдём к диаграммам. Диаграмма – это графическое изображение, которое даёт наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Диаграммы бывают нескольких видов, но более подробно мы с ними познакомимся при изучении электронных таблиц.

А сейчас рассмотрим несколько примеров.

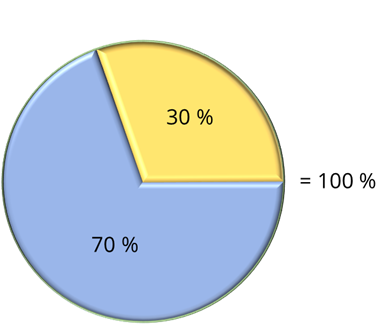
Первый: Наша планета состоит из воды и суши. Вода составляет семьдесят процентов от планеты, а суша – тридцать. Изобразим всё это с помощью круговой диаграммы. Нарисуем круг. Он будет изображать планету и соответственно будет равен ста процентам. Затем изобразим семьдесят процентов суши и тридцать процентов воды.

На данной диаграмме мы можем увидеть соотношение воды и суши.

Теперь рассмотрим ещё один пример. Саша тратит на дорогу от дома до школы 10 минут, Таня – 15 минут, Ира – 7 минут и Игорь – 20 минут. Давайте все это изобразим с помощью диаграммы. На оси X напишем имена учащихся, а на оси Y – время, затраченное на дорогу. Затем каждому учащемуся нарисуем столбик по высоте соответствующий времени его пути.

Таким образом мы получили столбчатую диаграмму.

· Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений.

· Схема – это графическое отображение состава и структуры сложной системы.

· Чертёж – это условное графическое изображение предмета с точным соотношением его размеров, получаемое методом моделирования.

· График – это графическое изображение, которое отображает зависимость одной величины от другой, динамику какого-либо процесса в течение какого-либо периода и много другое.

· Диаграмма – это графическое изображение, которое дает наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений.

Источник

Урок математики «Графическая модель трёхзначного числа».(3 класс) обновлёнка

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Раздел долгосрочного планирования:

1А Числа в пределах 1000. Сложение и вычитание/ «Живая и неживая природа», «Что такое хорошо и что такое плохо».

Школа: КГУ «СОШ№ 58»

ФИО учителя: Лисицына Светлана Михайловна

Графическая модель трёхзначного числа .

Цели обучения, достигаемые на этом уроке

3.5.2.1 строить графические модели многозначных чисел, использовать таблицу разрядов и классов 3.1.1.2 читать, записывать и сравнивать трехзначные числа

Все смогут строить графические модели многозначных чисел, используя таблицу разрядов и классов читать, записывать и сравнивать трехзначные числа.

Большинство смогут находить ошибки в графических моделях многозначных чисел.

Некоторые смогут придумать и записать трёхзначные числа , используя числа Древнего Египта.

строит графические модели многозначных чисел (оценивание через формативное задание)

читает, записывает и сравнивает трехзначные числа.(оценивание через наблюдение за парами, группами)

С отрудничество, социальная ответствпенност, творчество, бережное отношение к природе

Учащиеся знают разрядный состав и графические модели двузначных чисел и числа 100 из программы 2 класса.

Карточки с цифрами от 0 до10, модели двузначных чисел, модели трёхзначных чисел для каждого, постеры для групп, маркеры, карточки желтого, красного, зеленого цвета для каждого на рефлексию «Светофор», фишки, компьютер.

Каким образом я достигну целей обучения?

(метод/ прием/ техника/ стратегия)

-Кто готов к уроку- хлопните в ладоши.

-У кого хорошее настроение –топните ногами.

-Кто готов добиваться цели- погладьте себя по голове.

-Вижу, что все готовы добиваться цели, садитесь.

2. Стартер: подготовить к выходу на тему и цель урока.

Что вы знаете о трёхзначных числах?

-Что такое разряд?

-Из каких разрядов состоят трёхзначные числа?

-Каким образом отсчитываются разряды?

3 . Угадать число и показать ответ в виде графической модели, которую они составят из кубиков или конструктора «Лего» или клеточек из тетради: вспомнить, как строить графические модели двузначных чисел.

1. В первом разряде этого числа столько единиц, сколько колес у легковой машины.

Во втором разряде этого числа единиц столько, сколько ног у муравья.

2.Это число равно сумме чисел17 и 35 .

3.Это число является произведением 5и 6.

4.Это число является результатьм деления32 и 8

-Сделайте вывод, как составлять графическую модель двузначного числа?

— Как построить модель трёхзначного числа?

— Значит какая тема урока ?

— Подумайте в паре.

— Сформулируйте цель урока.

— Проговорите хором цель урока.

(Ф)-Это место цифры в записи числа: единицы, десятки, сотни.

-Трёхзначные числа состоят из трёх разрядов.

-Разряды отсчитываются с конца числа, с разряда единиц.

(Г) Приклеивают на постер№1

Строят модель числа 46.

Строят модель числа 52.

Строят модель числа 30

Строят модель числа 4

-Для единиц берем отдельные клеточки, для десятков столбики из 10 клеточек.

— Она строится так же, как и двузначного числа, но нужно добавить единицы разряда сотен, пластину из 100 кубиков. Это 10 столбиков, скрепленных между собой, показывающих десятки.

— Узнаем , как образуются трёхзначные числа.

Научимся читать и записывать трёхзначные числа по её графической модели, строить графические модели трёхзначных чисел.

спикеры выходят к доске, вывешивают постеры групп , сверяют, доказывают по очереди почему они так составили схемы.

Остальные учащиеся оценивают и подают сигнал с помощью «хлопка» в случае согласия с выступающим.

Способ поддержки групп с помощью диалога учителя и обучающихся для постановки цели урока.

— Сколько в числе 46 дес. и единиц?

1. Соберите модель трёхзначного числа 1 группа-548, 2 группа — 627, 3 группа — 329, 4 группа — 860, 5 группа – 307.

— Какое из этих чисел самое большое?

— Какое самое маленькое? Почему?

— С какого разряда нужно начинать сравнивать числа?

— Какова цель урока?

-Достигли ее? (не полностью)

— Рассмотрите задание №1 учебника стр.8

2.Определи числа по их модели , запиши их в тетрадь. Разложи на сумму разрядных слагаемых :выяснить, понимание разряда трёхзначных чисел.

-Какая цель урока?

-Достигли мы цели урока?

-Мы должны научиться строить модель трёхзначного числа. Но возникнет затруднение построение моделей сотен, так как рисование 100 кубиков или клеток является трудоемким процессом и занимает много места в тетрадях.

-Рассмотрите задание 2 (А) учебника стр. 9.Что вы заметили?

3. Пронаблюдайте за изменением модели числа:

наблюдать за изменением модели числа.

4. № 2 (Б) учебника. Нарисуй модели чисел в тетради 305,600,990,1000. По графической модели числа определи, сколько в нём сотен, десятков и единиц: тренироваться в составлении моделей .

5. Игра «Найди верную модель »

Задание 3 Один ребенок уходит в коридор, три других составляют модели (одна правильная): выбрать правильную модель числа.

— Прочитайте следующее задание .

— Кто из детей правильно составил графическую модель числа 543. Почему?

— Вернёмся к цели урока. Для чего мы выполняли это задание.

4. Составьте числа и используя знаки чисел: закрепление навыков записи чисел по их графической модели.

Числа Древнего Египта.

Древние египтяне сотню обозначали знаком- ₪,

Десяток – знаком ∩, единицу – знаком I.

5.Придумай и запиши числа древнеегипетскими знаками.

6.***Игра «Покажи число»(резервное задание) : закрепление темы.

1.Первый игрок выходит к доске, показывает модель заданного числа

2.Остальные игроки используя карточки с цифрами составляют увиденное число и показывают его.

3. За правильный ответ игрок получает фишку.

4. Игра повторяется 3 раза.

Игроки меняются ролями.

5. Выигрывает тот, кто набрал больше фишек.

— Какая была тема урока?

— Какую цель ставили?

— Достигли ли мы цели, выполняя это задание.

-Тогда давайте проверим.

(Г) Составляют и приклеивают на постер №2 графические модели чисел.

Выходят к доске спикеры и рассказывают о разрядах этого числа.

Составляли модели чисел, читали и сравнивали их.

(И) Рассматривают и

Определяют числа по модели

(Ф) — Научиться читать и записывать трёхзначные числа по её графической модели, строить графические модели трёхзначных чисел.

(Ф) — Заменили квадратик на красный кружок-это единицы.

Заменили 10 квадратиков на один красный треугольник-это 1 десяток.

Заменили сто квадратиков на 1большой квадрат.

(И)- Рисуют модели чисел.

(Г) Выбирают правильную модель, объясняют почему.

-Чтобы не путать разряды числа, учились выбирать правильную модель.

(П) Составляют и записывают числа.

-Придумывают и записывают числа.

Играют в игру. Собирают фишки.

Передают постеры по часовой стрелке, отмечают «звёздочкой» правильные модели.

— графическая модель сотен соответствует количеству сотен в числе;

— графическая модель десятков соответствует количеству десятков в числе;

— графическая модель единиц соответствует количеству единиц в числе.

Осознают свои ошибки.

Метод взаимооценки в парах по эталону на экране.

Осознают что получилось, что не получилось.

Метод взаимооценки в парах :

меняются тетрадями, исправляют ошибки и ставят «+» за правильную модель по эталону на экране.

Взаимооценка по эталону на экране .

Самооценка по эталону на экране.

Способ поддержки групп с помощью диалога учителя и обучающихся для достижения цели задания.

Способ по темпу .

Кто быстрее справился с заданием, помогает тем, кто затрудняется составить схему .

Способ поддержки с помощью вопросов .

-Как обозначаются сотни, дес., ед.?

Способ поддержки через диалог учителя с помощью вопросов.

-Как обозначены сотни?

-Сколько таких значков?

-Какой цифрой обозначим?

1. Итог урока: подвести итоги учебной деятельности на уроке.

-Какая была тема урока?

-Какие цели ставили?

-Кто достиг цели урока, поднимите руку.

2. Задание для формативного оценивания: определить уровень достижения урока.

1. Составить графическую модель чисел.Заполни таблицу.

2. Составь два верных неравенства, используя числа в таблице.

строит графические модели многозначных чисел, читает, записывает и сравнивает трехзначные числа

3. Обсуждение домашнего задания: закрепить тему самостоятельно.

Составить 3 модели трёхзначного числа.

Раб. тет. стр. 5-6 По графической модели числа определить, сколько в нем сотен, десятков и единиц.

Рефлексия учащихся: выяснить, что получилось, что необходимо улучшить в своём обучении.

Красная карточка – вам было всё понятно, вы помогали друзьям.

Жёлтая карточка : «Урок для вас был интересным, вы отвечали на вопросы учителя, урок был в полезен для вас, все задания выполнили.

Зелёная карточка : у вас остались вопросы, было не всё понятно.

(И) Показывают карточку.

Задание для оценивания.

1.-строит модель первого числа и записывает его ;-2б.

— строит модель второго числа и записывает его;2

— строит модель 3 числа и записывает его;-2 б.

-строит модель 4 числа и записывает его-2 б.

2. Составляет первое неравенство-1б.

Составляет второе неравенство -1б.

Рефлексия учителя по проведенному уроку

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 935 человек из 81 региона

Курс повышения квалификации

Скоростное чтение

• Сейчас обучается 879 человек из 79 регионов

Курс повышения квалификации

Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО

• Курс добавлен 23.09.2021
• Сейчас обучается 287 человек из 63 регионов

Ищем педагогов в команду «Инфоурок»

Урок по обновлённому содержанию образования, защищён на курсах ПК

Все смогут строить графические модели многозначных чисел, используя таблицу разрядов и классов читать, записывать и сравнивать трехзначные числа.

Большинство смогут находить ошибки в графических моделях многозначных чисел.

Некоторые смогут придумать и записать трёхзначные числа , используя числа Древнего Египта.

Номер материала: ДБ-422006

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Россияне чаще американцев читают детям страшные и печальные книжки

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Онлайн-конференция о профориентации и перспективах рынка труда

Время чтения: 3 минуты

Школьник из Челябинской области стал победителем конкурса «Ученик года — 2021»

Время чтения: 2 минуты

Минпросвещения намерено расширить программу ускоренного обучения рабочим профессиям

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Модели натурального ряда чисел и его элементов: Геометрическая (плоскостная) модель натурального ряда

Задача криптографического анализа шифра (атака на шифр) предполагает построение и исследование модели криптографической системы (алгоритма шифра и его элементов), а также ситуации, в рамках которой осуществляется криптоанализ. Для шифра RSA такой моделью его элемента должны быть модели нечетного числа, которые криптоаналитик стремится факторизовать.

Эта статья является первой из цикла, в котором будут показаны различные модели натурального ряда чисел (НРЧ), отдельного числа и некоторые другие, а также подходы для решения задачи факторизации, основанные на этих моделях.

Введение

Хорошо ли мы знакомы с натуральным рядом чисел? Много ли знаем о нём? Да, это целые положительные числа, которые следуют одно за другим, начинаясь единицей (1) и увеличиваясь на 1 в каждом очередном числе, и так до бесконечности (∞).

Ещё все числа НРЧ делятся на два класса по делимости на 2: четные и нечетные. Единица — нечетное число (нуль не включается в НРЧ), двойка (1 + 1 = 2) — четное, за двойкой — тройка (2 + 1 = 3) — снова нечетное, а за ней следует четная четверка (3 + 1 = 4). Так в НРЧ нечетные и четные числа чередуются.

Числа умноженные на себя — это квадраты в НРЧ. Они занимают свои определенные места в НРЧ, так, что образуют такую же чередующуюся по четности последовательность — нечетный — четный квадрат. Между квадратами соседних чисел разность всегда нечетное число позиций, занимаемых не квадратами. Из этого следует, что сумма 1 + 3 + …+ 2k — 1 = k², где k число нечетных, подряд следующих чисел, равна квадрату числа слагаемых. Это неформальное рассмотрение НРЧ.

А как в теории определяется НРЧ? Натуральным рядом чисел называют непустое множество N = {1, 2, 3,…} с унарной операцией S, здесь через S обозначено отображение N в N, удовлетворяющее условиям или следующим аксиомам Пеано:

1. для любого а ∊ N, 1 ≠ S_а;
2. для любых а, b ∊ N, если S_а = S_b, то а = b;
3. любое подмножество N, c 1 ∊ N, которое содержит вместе с каждым элементом а элемент S_а, совпадает с N. Элемент S_а множества N обычно называют элементом, непосредственно следующим за а.

Натуральный ряд чисел представляет собой вполне упорядоченное множество. В теории чисел доказывается, что следующие условия:

1. а + 1 = S_а, а + S_b = S(а + b);
2. а · 1 = а, а · S_b = а · b + а,

где а и b — любые элементы из N, определяют во множестве N, бинарные операции (+) и (·).

Система <N, +, ·, 1> является системой натуральных чисел.
Натуральное число — одно из основных понятий математики натуральных чисел и может быть истолковано как кардинальное число непустого конечного множества. Множество N = {1, 2,…} всех натуральных чисел и операции над ними: сложение (+) и умножение (·) образуют систему натуральных чисел <N, +, ·, 1>. В этой системе обе бинарные операции ассоциативны, коммутативны и связаны законом дистрибутивности; 1 — нейтральный элемент умножения, т.е. а · 1 = 1· а = а для любого натурального числа а; сложение не имеет нейтральных элементов и, более того, (а + b) ≠ а для любых натуральных чисел а и b. При этом выполняется аксиома индукции: любое подмножество множества N, содержащее 1 и вместе с каждым элементом а сумму а + 1, совпадает с N.

В дедуктивных научных теориях аксиомами называют основные исходные положения, т.е. аксиомы — это основные положения, самоочевидные принципы. Из аксиом в рамках таких теорий путем дедукции извлекается все их содержание.

На самом деле чисто формальный подход хотя и обеспечивает определенную строгость и доказательность результатов весьма ограничен и мало что дает практике. Проявление ограниченности мы можем видеть в отсутствии решений актуальных задач современной математики: установление простоты числа, нахождение дискретного логарифма, делителей большого натурального числа и др. Надо заметить при этом, что время и усилия, затраченные на поиск ответов специалистами весьма значительные.

Одним из разделов аддитивной теории чисел является исследование суммирования последовательностей. Важной является ситуация, когда в результате суммирования ограниченного числа последовательностей, получаются все достаточно большие числа или другой вариант — все натуральные числа, что в сущности эквивалентно моделированию НРЧ.
В теории вводится понятие базиса k-го порядка, под которым понимают многократную (k-кратную) сумму последовательности П с собой k раз и при этом формируются все натуральные числа. Дальнейшее суммирование последовательности П к предыдущему результату k = k + 1-й раз не меняет полученный базис.

Так, например, известна теорема Лагранжа о том, что любое натуральное число есть сумма четырех квадратов. Таким образом, последовательность квадратов Q есть базис 4-го порядка [1]. Известно [2, 3], что последовательность кубов образует базис 9-го порядка. Последний результат доказывается более сложным путем.

Усеченные модели НРЧ (не все натуральные числа присутствуют в модели), в которых обязательно присутствие лишь достаточно больших чисел, получаются при меньшем числе слагаемых последовательностей. Так из теоремы И.М. Виноградова [1] следует, что достаточно трижды просуммировать последовательность Р + Р + Р, где Р — последовательность простых чисел и эта сумма будет содержать все достаточно большие нечетные числа. Таким образом, последовательность Р образует базис 4-го порядка для достаточно больших чисел. Последовательность кубов в этой ситуации образует базис базис 7-го порядка для достаточно больших чисел. Таковы в общем результаты строгой теории чисел.

Мы при изложении материала не будем прибегать к строгим доказательствам, в части положений они пока отсутствуют, а где имеются занимают много места

Как было упомянуто выше, предлагается дополнить модель нечётного числа плоскостной моделью натурального ряда чисел. Данная модель удобна тем, что содержит все нечетные числа, а потенциальное знание их позиции (координат клетки с числом) приводит практически к мгновенной факторизации. Остается найти способ локализации заданного числа (указания на его клетку). Числовые примеры приведённые ниже по тексту иллюстрируют возможности предлагаемой модели и я надеюсь, простимулируют читателя к поиску решения названной задачи.

Ранее было показано, что использование геометрической (плоскостной) модели натурального ряда чисел в форме–плоскости позволяет формулировать задачу факторизации больших чисел (ЗФБЧ) в терминах и понятиях этой модели и сводить ее по существу к определению координат целой точки гиперболы, характеризуемой модулем сравнения N шифра RSA, который доступен всем абонентам сети. Использование другого доступного ключевого параметра (показателя шифрующей экспоненты е), найденных факторов и модуля обеспечивает простое вычисление закрытого ключа шифра d и доступ к исходному виду сообщения.

Наиболее сложной частью проведения криптоаналитической атаки представляется поиск целой точки гиперболы при известном модуле N. При огромной разрядности RSA-чисел отрезок ветви гиперболы, лежащей в выделенной области ненадежных ключевых параметров (НКП) содержит единственную целую точку среди бесконечного множества других точек. Поиск такой точки переборными алгоритмами – длительный и трудоемкий процесс, сводящийся к проверке принадлежности вычисляемой точки множеству натуральных чисел. Процедура в сущности проста: задается натуральное значение одной координаты клетки и определяется целочисленность второй координаты, либо задается и вычисляется.

Среди множества возможных моделей НРЧ весьма эффективной представляется следующая, обозначенная как Г^s∓. Модель удовлетворяет практически всем требованиям, обычно предъявляемым к ним.

Сформулируем ряд положений для обоснования выбора рассматриваемой модели:

1. Г^s∓ — модель содержит все нечетные числа НРЧ, а факторизовать всегда требуется нечетное число, так как четные легко делятся на степени двойки.
2. Соотношения, реализующие разложение числа на множители – это формулы сокращенных вычислений, суммы и разности одинаковых степеней переменных, среди которых наиболее предпочтительное соотношение: x₁² — x₀² = (x₁ + x₀)(x₁ — x₀)
3. Все нечетные числа в НРЧ лежат между квадратами чисел разной четности.
4. Любое составное нечетное натуральное число представимо суммой нечетного числа слагаемых — нечетных последовательных чисел и, возможно, не единственным образом.
5. Сумма из пункта 4 легко преобразуется в произведение среднего слагаемого (больший dб делитель N) на число слагаемых (меньший dм делитель N).
6. Значение в каждой клетке на пересечении горизонтали и вертикали подмодели Г^2- с одной стороны, равно разности квадратов номеров этих линий, а с другой – равно произведению номеров короткой и длинной диагоналей, встречающихся в этой клетке.
7. Значения чисел в клетках диагоналей кратны номеру диагонали, в которой они лежат.

Конструктивное описание Г ^2∓ модели

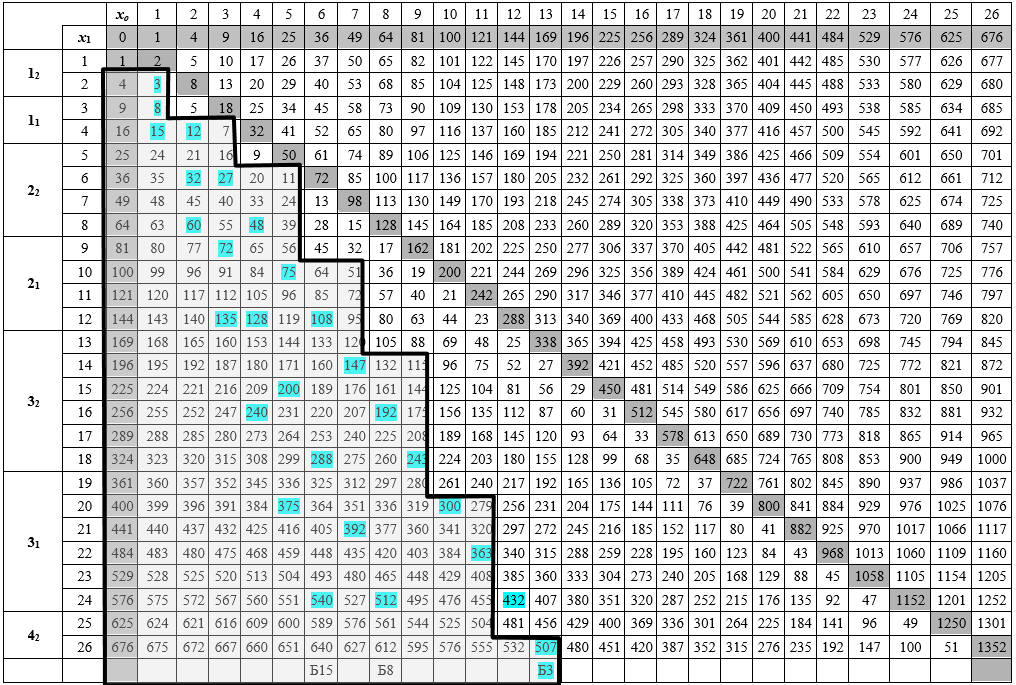
Для построения модели на плоскости задаются две пересекающихся ортогональных координатных числовых оси, направленных х₁ — вертикально вниз и х₀ — горизонтально вправо. Точки осей, равноотстоящие одна от другой, размечаются числами натурального ряда. Пересечение осей помечается нулем. Через размеченные точки проводятся линии, образующие границы полос перпендикулярных направлений. На плоскости возникает рисунок решетки, подобие паркета из клеток размером 1х1. В работе фрагмент плоскости ограничим возможностями рисуночного представления и в нем выделим главную диагональ, подобно главной диагонали числовой матрицы. С каждой клеткой под главной диагональю свяжем значение N(x₁, x₀) = x₁² — x₀², а над главной диагональю и на диагонали клеткам припишем значения N(x₁, x₀) = x₁² + x₀², где х₁ и х₀ — координаты клетки (x₁, x₀).

_{Визуальное представление модели}

Отметим, что клетки такой дискретной плоскости уникальны, а значения в них могут повторяться. При таком определении четность значений в клетках соответствует чередующемуся порядку, как цвет клеток на шахматной доске. Клетки при этом будем называть соответственно четными или нечетными. Клетки, размещаемые под главной диагональю образуют полуплоскость, которую будем называть Г^2- (Г от слова гипербола), а над главной диагональю — К = Г²⁺ (К от слова круг). Обобщенную модель обозначим Г^s∓, где s — может принимать значения 2, 3,… и др.

Элементами модели являются клетки (аналог точки плоскости), прямые линии (совокупности клеток-точек, примыкающих одной из сторон или вершиной, одна к другой) горизонтальные (Н_i), вертикальные (V_i), наклонные (совокупности примыкающих вершинами клеток-точек или клетками без контакта, формирующих направление линий с разрывами — лучей): длинные (Д_i) и короткие (К_i) диагонали, которые содержат либо только четные значения и при этом называются четными, либо нечетными диагоналями, образованными нечетными клетками. Короткие диагонали заканчиваются и начинаются в точках координатных осей с совпадающими координатами (номерами диагоналей). Длинные диагонали (Д_i) проходят параллельно главной (с номером (Д₀)) имеют только начальные точки на координатных осях и продолжаются вниз до ∞. Их положение выше и ниже (Д₀) характеризуется совпадающими номерами и для их различения диагонали верхней полуплоскости снабжаются дополнительным (+) значком (Д_i⁺). Нечетная диагональ (Д₁⁺) начинается на оси х₀ клеткой с 1 и содержит в своих клетках нечетные числа. Нечетная диагональ Д₁ начинается на оси х₁ клеткой с N=1 и содержит все без исключения нечетные числа, упорядоченные по возрастанию. Тем самым обеспечивается требование к модели НРЧ содержать все нечетные числа.

В рамках такой модели появляется удобная возможность исследовать гипотетические числовые закономерности и решать, например, задачи определения и локализации пифагоровых троек чисел, разложения числа на множители (факторизация), определять кратные клетки, содержащие одинаковые значения, и их местоположение и другие теоретико-числовые задачи. Помимо этого появляются хорошие возможности визуального отображения результатов.

Зависимости чисел в организованных клетках

Под организацией клеток будем понимать принадлежность некоторых (семантически выделенных) клеток некоторому изображению, задаваемому математической зависимостью либо координат, либо значений в клетках, либо того и другого. Свойства получаемых изображений будем использовать для решения теоретико-числовых задач, в частности для ЗФБЧ. Начнем рассмотрение с очень простых изображений прямых линий, лучей. Г^2- — модель обеспечивает их визуализацию.

Пример 1. Рассмотрим нижнюю полуплоскость Г^2- и значения чисел в клетках с координатами (х₁, х₀), где координата х₁ пропорциональна другой х₀ координате х₁ = kх₀, коэффициент пропорциональности изменяется монотонно k = 2,3,4,….∞, что кратко записывается так k=2(1)∞. С изменением координаты х₀ = 0(1)∞, т. е. от нуля до бесконечности с шагом 1 и при фиксированном значении k будут вычисляться клетки и натуральные значения в них, принадлежащие линиям (лучам) с разрывами. Так при k = 2, получаемые клетки располагаются посередине отрезков горизонталей нижней полуплоскости, а линия получает вид луча-биссектрисы (обозначена Б3) нижней полуплоскости. При k = 3 получаемые клетки располагаются посередине отрезков коротких диагоналей нижней полуплоскости, а линия получает вид другого луча-биссектрисы (обозначена Б8) нижней полуплоскости.

Пусть задано некоторое число N ∊ Г^2-, и оно лежит в одной из клеток наклонной прямой (луча), формируемой условиями примера. Тогда можно получить следующее соотношение для модели луча:
при k = 2, имеем N(x₁, x₀) = x₁² — x₀² = (kx₀)² — x₀² = x₀²(k² — 1) = 3x₀² . Луч Б3;
при k = 3, имеем N(x₁, x₀) = x₁² — x₀² = (kx₀)² — x₀² = x₀²(k² — 1) = 8x₀² . Луч Б8;
при k = 4, имеем N(x₁, x₀) = x₁² — x₀² = (kx₀)² — x₀² = x₀²(k² — 1) = 15x₀². Луч Б15;
при k = 5, имеем N(x₁, x₀) = x₁² — x₀² = (kx₀)² — x₀² = x₀²(k² — 1) = 24x₀². Луч Б24;

Основное свойство таких лучей для ЗФБЧ состоит в том, что числа в клетках лучей определяются одной координатой x₀, т.е. значение N(x₁, x₀) = N(kx₀, x₀) = (kx₀)² — x₀² = x₀²(k² — 1) в клетке, принадлежащей одному из лучей, становится функцией только одной координаты x₀. Наличие числа N, факта принадлежности его клетке конкретного луча, обеспечивают определение второй координаты и получение решения ЗФБЧ за время долей секунды, которое практически не зависит от разрядности числа. Значение второй координаты находится из соотношения модели луча полуплоскости х₁ = kx₀. Из наличия обеих координат клетки вытекает, что все числа линии в таких клетках факторизуются элементарными действиями и практически мгновенно. Приводимые простые наглядные примеры убеждают нас в этом.

Действительно, N(x₁,x₀) = x₁² — x₀²=(x₁+x₀)(x₁ -x₀)= р ∙ q.

Пример 2. Подтверждение работоспособности модели вычислительным экспериментом. Пусть заданы для факторизации числа N = 968 и N = 507 ∊ Г^2- — модели, и каждое лежит в одной из клеток наклонной прямой, формируемой соотношением при некотором k, например, k = 2 получаем N(x₁, x₀) = x₁² — x₀² = (kx₀)² — x₀² = x₀²(k² — 1) = 3x₀² = 968.

1. Выполняется проверка принадлежности заданного числа одному из возможных лучей полуплоскости Г^2-. Значение N = 968 проверяем на принадлежность лучу Б3, делим N на 3, число N = 968 не делится нацело на 3, проверяем принадлежность следующему лучу Б8, делим на 8. 968 / 8 = 121 = 11² = х₀².
2. Получили, что число N = 968 лежит в клетке, принадлежащей лучу Б8, и клетка имеет координату х₀ = 11. Вторая координата клетки определяется из соотношения модели луча х₁ = kx₀=3 ∙ 11 = 33. Наличие координат клетки обеспечивает факторизацию числа в ней: N(x₁, x₀) = x₁² — x₀²=(х₁+х₀)(х₁-х₀) = (33+11)(33-11) = 44 ∙ 22 = 968. Факторизация выполнена успешно.

Для второго числа N = 507 выполняем такие же действия.

1. Первая же проверка подтверждает принадлежность лучу Б3 клетки с числом N = 507, и дает результат деления 507 / 3 =169 = 13² = х₀². Координата клетки х₀ = 13. Другая координата х₁ = 2х₀ = 2 ∙ 13 = 26.
   Эту координату можно находить и другим путем. Он имеет самостоятельное значение (ценность) и применим в других ситуациях. Из общего соотношения N(x₁, x₀) = x₁² — x₀² = (kx₀)² — x₀² = x₀²(k² — 1) = 3x₀² = 507.
2. Находим делением N / 3=507 / 3 = 169 значение x₀² и суммированием с N этого квадрата находим квадрат другой координаты x₁²= N + x₀² = 507 + 169 = 676. Откуда х₁ = 26 и х₀ = 13. Тогда факторизация числа N, представимого разностью квадратов, N = 507 = x₁² — x₀²= (26 — 13)(26 + 13) = 13 ∙ 39 = 507, успешно выполняется и завершается.

Использованные источники

1. Гельфонд А.О., Линник Ю.В. Элементарные методы в аналитической теории чисел. -М.: ГИФМЛ, 1962.-272с.
2. Линник Ю.В. О представлении больших чисел суммою семи кубов, Матем. сб. 12(54),(1943),220-224.
3. Линник Ю.В. О разложении больших чисел на семь кубов, ДАН 36 (1942), 179-180
4. Манин Ю.Н, Панчишкин А.А. Введение в современную теорию чисел. –М.: МЦНМО, 2013. – 552с.