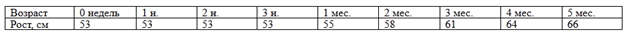Ôункциональные зависимости между величинами могут задаваться различными способами: с помощью формул, графиков, таблиц, словесных описаний. Совершенствованию умений пользоваться этими способами, получать из них необходимую информацию посвящен данный параграф.
1. Понятие функции, способы ее задання


ния t по формуле s = 3t – 1 можно найти лишь одно значение s. Напомним сначала то, что изучалось о функциональных зависимостях ранее.
Пусть заданы две переменные х и у, принимающие числовые значения, и D — множество значений переменной х.
Зависимость между переменными х и у, которая для каждого значения х из D определяет единственное значение у, называется функциональной зависимостью или функцией у от х с областью определения D.
Переменную х в таких зависимостях называют независимой переменной или аргументом, переменную у — зависимой переменной. Функции обычно обозначают латинскими (иногда греческими) буквами — f, g, F, ϕ и т. п.
Функция — от латинского function — действие, выполнение.

|
Функциональные зависимости |
47 |
Область определения функции f часто обозначают D(f). Значение переменной у, которое соответствует х, называют значением функции f в точке х и обозначают f(х). Запись «у = f(х)» означает, что задана функция f. Функциональную зависимость переменной у от х иногда записывают так: у = у(х).
Множество значений, которые принимает зависимая переменная у, если х пробегает область определения функции f, называют
множеством значений этой функции и обозначают Е(f).
!Фраза «задать функцию у от х» означает сформулировать правило, с помощью которого для каждого допустимого значения переменной х можно найти соответствующее ему значение переменной у.
Существуютразличныеспособызаданняфункции.Вматематике функциональная зависимость чаще всего задается формулами.
Какизвестно,линейнаяфункциязадаетсяформулой:y = kx +b, где k и b — некоторые числа, х — аргумент. Например, функции
у=2х–3(здесь k = 2, b = – 3), у = –0,5х + 2 (здесь k = – 0,5, b = 2), у = 4х (здесь k = 4, b = 0), у = 5 (здесь k = 0, b = 5) являются линейными.
Квадратичная функция задается формулой: y = ax2 + bx + c,
где a, b, c – некоторые числа, а ≠ 0, х — аргумент. Например, функции у = х2, у = 3х2 + 1, у = 2х2 + х – 4 являются квадратичными. (Укажите для каждой из этих функций, чему равняются коэффициенты a, b, c.)
Обратная пропорциональность задается формулой y = kx ,
где k ≠ 0 — некоторое число, х — аргумент.
Такой способ задания функции называется аналитическим. Заметим, что не всякая зависимость между переменными является функциональной. Например, зависимость между переменными у и х, заданная уравнением х2 + у2 = 1, не является функциональной, так как, например, значению х = 0 соответствуют два
значения у: у1 = –1, у2 = 1.
!Если функция задана формулой, то при отсутствии дополнительных замечаний или условий считают, что ее областью определения является множество всех значений независимой переменной, при которых эта формула имеет смысл. Её иногда называют естественной областью определения функции.
|
48 |
Функции, их свойства и графики |
Так, линейная функция y = kx + b, квадратичная функция y = ax2 + + bx + c определены при всех значениях х, то есть D(y) = (–∞; +∞).
Обратная пропорциональность y = kx определена при всех зна-
чениях х, кроме х = 0, то есть D(y) = (– ∞; 0) (0; + ∞). Естественной областью определения функции у = x является промежуток [0; + ∞), поскольку извлечение квадратного корня возможно толь-
ко из неотрицательных чисел.
3
1)область определения функции; x2 −1 . Найти:
2)значение функции в точке х = –2;
3)значения аргумента, при которых функция принимает значение 1.
1) Функция определена при всех значениях х, для которых знаменатель дроби не равен нулю, то есть при всех х, кроме х = ±1.
Следовательно, D(y) = (−∞;−1) (−1;1) (1;+∞).
|
2) Значение функции в точке х = – 2 равно: |
y(−2) = |
3 |
= |
|
(−2)2 −1 |
=43−1 =1 .
3)Чтобы найти значения аргумента, при которых функция
|
принимает значение 1, |
решим уравнение 1 = |
3 |
. Получим: |
||
|
x2 |
−1 |
||||
|
х2 – 1 = 3, х2 = 4, х1 = – 2, |
|||||
|
х2 = 2. Следовательно, в этих точках фун- |
|||||
|
кция принимает значение 1. |
Ответ. 1) (−∞;−1) (−1;1) (1;+∞); 2) 1; 3) – 2; 2.
При решении многих прикладных задач область определения функции устанавливают, исходя из физического или геометрического смысла задачи. Например, если рассматривать зависимость площади квадрата от длины его стороны х, то областью оп-
ределения этой функции будет интервал (0; + ∞), так как длина
стороны квадрата может выражаться только положительным числом. В таком случае иногда пишут: y = x2 , х > 0.
! Обратите внимание на то, что функции y = x2 и y = x2 ,
х > 0 различны. У них не только не совпадают области
|
Функциональные зависимости |
49 |
|
определения, они также обладают различными свойс- |
|
|
твами, в чем убедимся впоследствии. |
|
|
В математике и ее приложениях очень распространен графи- |
|
|
ческий способ задания функции. Существует много самопи- |
|
|
шущих приборов, которые вычерчивают кривые, устанавливая |
|
|
тем самым зависимость между исследуемыми величинами. Так, |
|
|
сейсмограф вычерчивает график колебания земной коры. По это- |
|
|
му графику можно, например, изучать силу и характер толчков |
|
|
при землетрясении. |
|
|
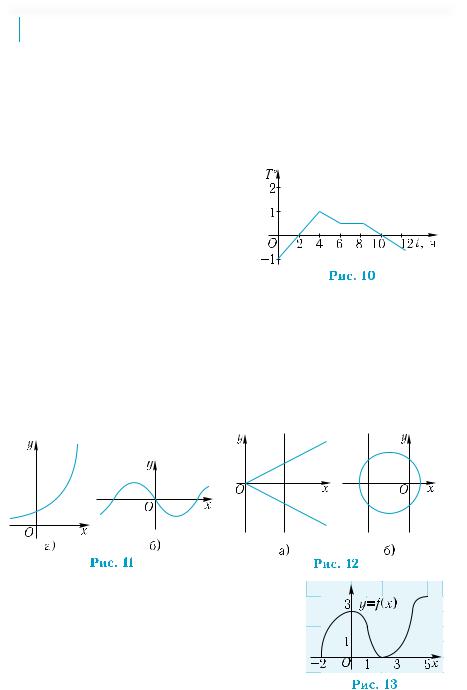
С помощью линии, изображен- |
|
|
ной на рис. 10, можно для каждого |
|
|
момента времени 0 ≤ t ≤ 12 указать |
|
|
единственное значение |
температу- |
|
ры среды Т, то есть эта линия задает |
|
|
функциональнуюзависимостьмежду |
|
|
переменными t и Т. |
|
|
Не всякая линия на координатной плоскости задаёт некоторую |
|
|
функцию. Чтобы некоторая линия определяла функциональную |
|
|
зависимость у от х, необходимо и достаточно, чтобы каждая пря- |
|
|
мая, параллельная оси у, и ось у пересекали эту линию не более |
|
|
чем в одной точке. Так, линии на рис. 11 определяют функцио- |
|
|
нальные зависимости у |
от х. Линии, изображённые на рис. 12, |
|
не задают функции у от |
х, так как можно указать вертикальные |
|
прямые, пересекающие линию в двух точках. |
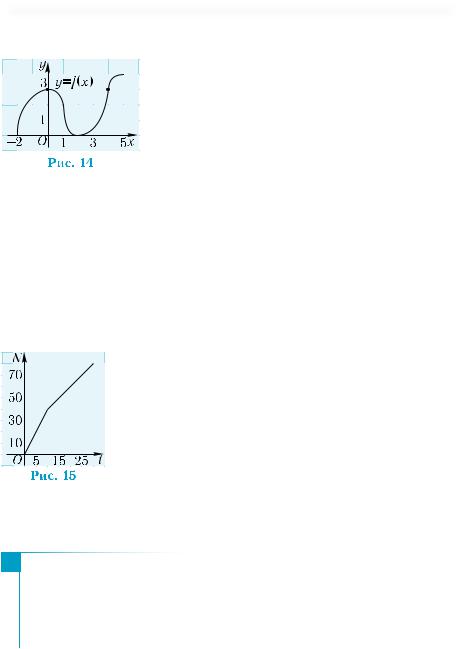
Пример 2. Функция y = f(x) задана гра-
фически (рис. 13). Указать:
1) её область определения;
2) её множество значений;
3) значение функции при х = 5;
|
50 |
Функции, их свойства и графики |
|
4) значение аргумента х, при котором функция принимает значе- |
|
|
ние 3. |
1) Областью определения функции яв- |
|
ляется отрезок [–2; 5]. |
|
|
2) Множеством значений функции явля- |
|
|
ется отрезок [0; 4]. |
|
|
3) f(5) = 4. |
|
|
4) Проведем прямую у = 3 и найдем ее |
|
|
точки пересечения с графиком функции |
|
|
у = f(x) (рис. 14). Это точки с координатами |
|
|
(0; 3) и (4; 3). Следовательно, значение 3 функция принимает при |
|
|
х = 0 и при х |
= 4. |
|
Ответ. 1) [–2; 5]; 2) [0; 4]; 3) 4; 4) 0; 4. |
|
|
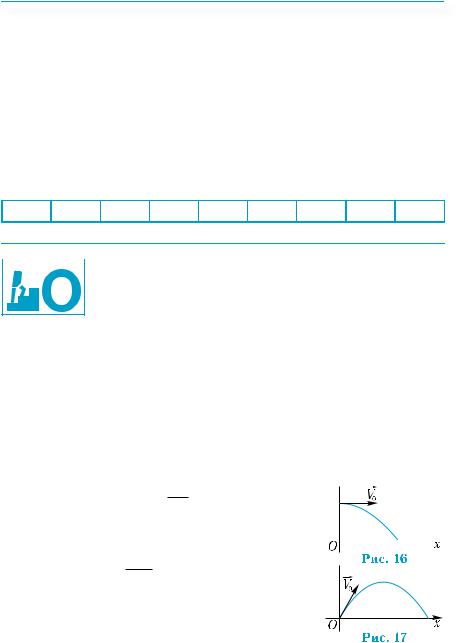
Пример 3. |
На рис. 15 изображена зависимость N(t) количест- |
|
ва деталей, изготовленных рабочим, от времени t (в днях). |
|
|
1) Сколько деталей изготовил рабочий за первые 10 дней? |
|
|
2) За какие 10 дней — первые или последние — рабочий изгото- |
|
|
вил больше деталей? |
|
|
3) За сколько дней рабочий изготовил 50 деталей? |
|
|
1) Найдем значение функции N(t) при t = 10. |
|
|
Обратите внимание на масштаб по оси t и оси N. |
|
|
Имеем: N(10) = 40, то есть за первые 10 дней из- |
|
|
готовлено 40 деталей. |
|
|
2) За последние десять дней изготовлено |
|
|
N(30) – N(20) = 80 – 60 = 20 деталей, то есть мень- |
|
|
ше, чем за первые 10 дней. |
|
|
3) Необходимо найти значение аргумента, при |
|
|
которомфункцияпринимаетзначение50. Прове- |
|
|
дем прямую N = 50 до пересечения с графиком функции N = N(t). |
|
|
Получим, что 50 деталей рабочий изготовил за 15 дней. |
|
|
Ответ. 1) 40; 2) за первые; 3) 15. |
!В рассмотренном примере функция N(t) определена для натуральных значений аргумента. Её графиком являетсяконечнаясовокупностьточек.Длянаглядностионисоединены отрезками. Такой приём построения изображения зависимостей будем использовать и в дальнейшем, если он не приводит к недоразумениям.
Кроме аналитического и графического способов задания функций, применяется также табличный способ. В физике и технике час-
|
Функциональные зависимости |
51 |
то зависимости между переменными фиксируются на шкалах измерительных приборов. В таких случаях функцию задают в виде таблицы, в первой строке которой содержатся значения независимой переменной x1, x2, x3, …, во второй — соответствующие им значения функции. Наиболее распространёнными являются таблицы с постояннымиразностямиx2 –x1,x3 –x2,…,причемзначениеразности называется шагом таблицы. Для таких таблиц независимая переменная принимает значения x0, x0 + h, x0 + 2h, …, где h — шаг таблицы.Так,приведеннаянижетаблицапоказываетдинамикуизменения объема пассажирских перевозок (в млн. людей) в нашей стране по железным дорогам, начиная с 2000 года.
2000 2001 2002 2003 2004 2005 2006 2007 2008











величины ее растяжения х имеет вид F = – kx (закон Гука). Немало физических зависимостей моделируются с помощью
квадратичной функции. Например, закон движения тела вдоль координатнойпрямой поддействиемпостояннойсилы можно предста-
вить в виде: x = x0 +v0t + at22 , зависимость кине-
тической энергии тела W, масса которого равняется m, от скорости движения v выражает-
ся формулой: W = mv22 . Тела, брошенные гори-
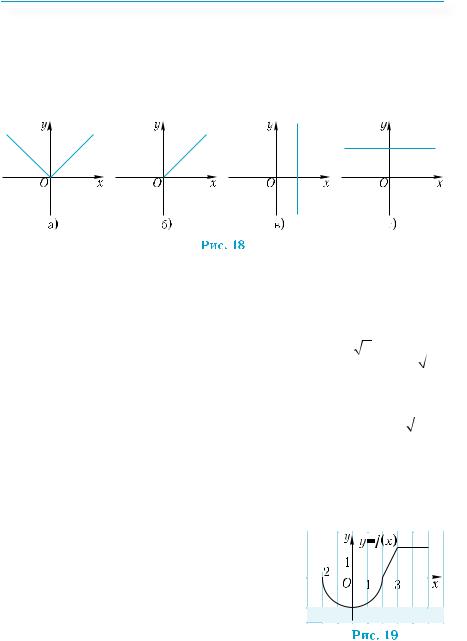
зонтально или под углом к горизонту, будут двигаться под действием силы тяжести по
параболическим траекториям (рис. 16, 17). Обратно пропорциональными являются:
— зависимость времени, необходимого на преодоление данного пути, от скорости;

|
52 |
Функции, их свойства и графики |
—зависимость между сторонами прямоугольника при заданной площади;
—зависимость между давлением газа и его объемом при постоянной температуре.
Пример 4. При свободном падении тела с достаточно большой высоты с начальной скоростью v0 = 10 м/с зависимость пройденного
пути от времени t ≥ 0 выражается формулой: s = v0t + gt22 , де s — путь, м; t — время, с; g ≈ 10 м/с2 — ускорение свободного падения.
1)Какой путь пройдет тело за первые 2 с?
2)За какое время тело пройдет 15 м?
1) Чтобы ответить на первый вопрос, нужно вычислить значение функции s при t = 2: s(2) ≈10 2+ 10222 = 40 (м).
2)Чтобы ответить на второй вопрос, нужно решить квадратное
уравнение: 10t + 5t2 =15 . Оно имеет два корня: –3 и 1, но условию задачи удовлетворяет только значение t = 1. Следовательно, тело преодолеет 15 м примерно за 1 с.
Ответ. 1) ≈40 м; 2) ≈1 с.
Пример 5. Некоторая масса газа при температуре 20°С имела объем 107 см3, а при 40°С объем равнялся 114 см3.
1) Опираясь на закон Гей-Люссака, найти функциональную зависимость объема газа от температуры.
2) Каким будет объем газа при 0°С?
1) По закону Гей-Люссака, объем газа V линейно зависит от температуры t: V = a + bt, где a и b — некоторые числа. Найдем эти числа, используя условие задачи. Так как V(20) = 107, V(40) = 114, то имеем систему уравнений относительно a и b:
107 = a + 20b, Отсюда: b = 0,35, a = 100. Итак, V = 100 + 0,35t.114 = a + 40b.
2) V(0) = 100 + 0,35 0 = 100 (см3). Ответ. 1) V = 100 + 0,35t; 2) 100 см3.
9 Контрольные вопросы
1°. Какие из следующих зависимостей являются функциональными:
а) каждому двузначному числу ставится в соответствие сумма его цифр;
|
Функциональные зависимости |
53 |
б) каждому числу, не равному нулю, ставится в соответствие обратное к нему число; в) каждому числу ставится в соответствие целое число, меньшее его?
2°. Какая из линий, изображенных на рис. 18, а)–г), не задаёт функциональную зависимость у от х?
|
3. |
x |
в точке х = – 1; х = 0? |
||||||||||||||||||
|
2x −1 |
||||||||||||||||||||
|
4. |
||||||||||||||||||||
|
В скольких точках функция у = х2 – 2х принимает значение 0; |
||||||||||||||||||||
|
–1; –2? |
1 ; 2) |
1 |
||||||||||||||||||
|
5. |
Длякакойизследующихфункций:1) y = |
y = |
x;3) y = |
; |
||||||||||||||||
|
x |
x |
|||||||||||||||||||
|
4) y = x2 областью определения служит промежуток (0; + ∞)? |
||||||||||||||||||||
|
1 − x |
2 |
2 |
; 4) y = ( |
2 |
||||||||||||||||
|
6. |
Даны функции: 1) y = |
2 |
; 2) |
y = x ;3) y = (1 − x) |
x ) . |
|||||||||||||||
|
а) Какая из них является линейной; квадратичной; обратной |
||||||||||||||||||||
|
пропорциональностью? |
||||||||||||||||||||
|
б) В каких точках квадратичная функция принимает значе- |
||||||||||||||||||||
|
ние 1? |
||||||||||||||||||||
|
в) Какая из функций не обращается в 0? |
||||||||||||||||||||
|
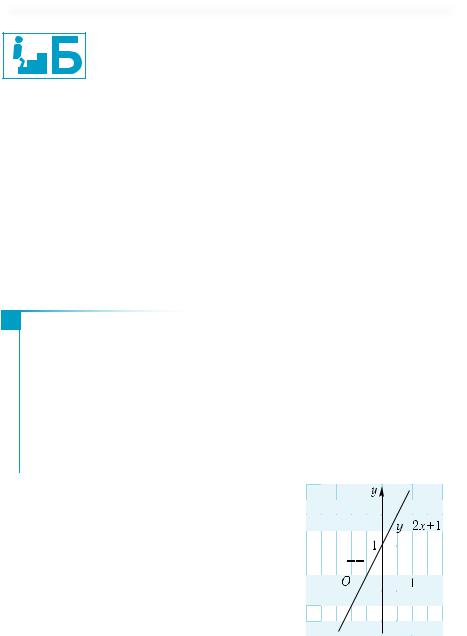
7. |
Для графически заданной |
функции |
||||||||||||||||||
|
y = f(x) (рис. 19) найдите: |
||||||||||||||||||||
|
а) область определения; |
||||||||||||||||||||
|
б) множество значений; |
||||||||||||||||||||
|
в) значения функции в точке х |
= 0; х = 4; |
г) нули функции, то есть точки, в которых функция обращается в 0.
|
54 |
Функции, их свойства и графики |
2. График функции
Графической способ задания функции более на- 

График функции y = f(x) — это множество точек координатной плоскости с координатами (х; f(x)), где х — произвольное число из области определения функции.
Для построения графика функции y = f(x) на плоскости вводят прямоугольную систему координат и строят точки с координата-
ми (x; f(x)).
!Абсолютноточнопостроитьграфикфункцииневозможно, так как невозможно точно изобразить даже одну точку (х0; f(х0)) на координатной плоскости, а тем более если их бесконечное множество. Поэтому под построением графика функции понимают построение линии, отображающей основные особенности «идеального» графика. Такую линию называют эскизом графика. Следовательно, построить график функции — значит построить эскиз графика, то есть отобразить графически все основные свойства функции.
Графиком линейной функции y = kx + b является, как вам уже известно, прямая линия. Для ее построения достаточно найти 



|
1 |
и проведем через |
|||||
|
точки А(0; 1) и |
B |
− |
2 |
; 0 |
||
них прямую (рис. 20). 
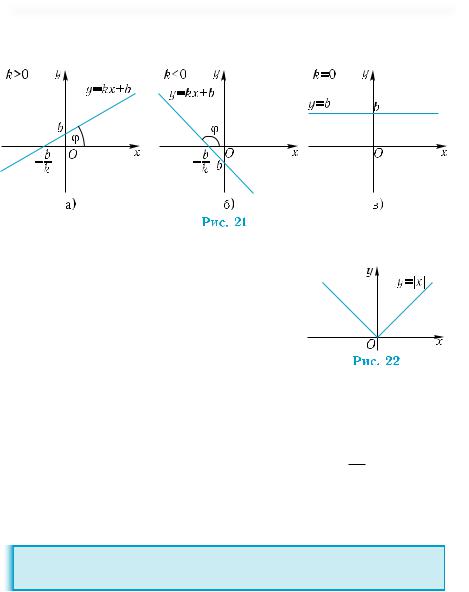
х и называется ее угловым коэффициентом. На рис. 21, а), б)
|
Функциональные зависимости |
55 |
изображены графики линейных функций в зависимости от знака k. Если k = 0, то имеем постоянную функцию y = b, график которой изображен на рис. 21, в).
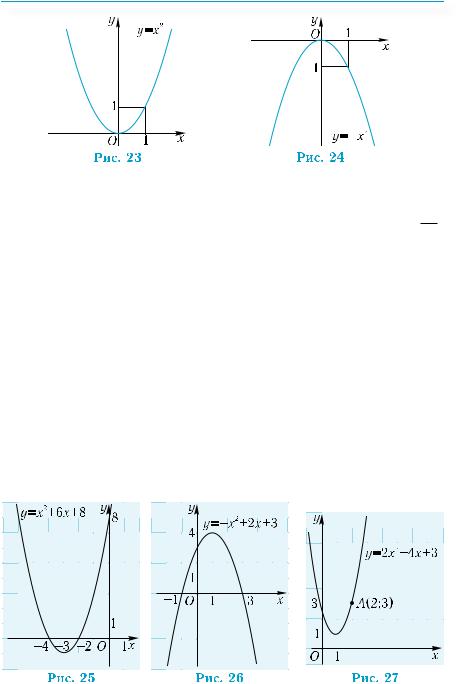
Пример 6. Построить график функции y = |x|.
|
Так как |
x |
x,eсли x ≥ 0, |
то для неот- |
|
|
= |
||||
|
−x,eсли x < 0, |
||||
|
рицательных значений х график функции |
||||
|
y = |x| совпадает с графиком функции у = х, а |
||||
|
для отрицательных — с графиком функции |
||||
|
у = –х (рис. 22). |
Графиком квадратичной функции у = ах2 + bх + с является парабола. Ее расположение на координатной плоскости зависит от коэффициентов a, b, c. Направление ее ветвей определяется знаком числа а: при а > 0 они направлены вверх, при а < 0 — вниз.
Вершина ее находится в точке с абсциссой x0 = − 2ba . Парабола
может не иметь общих точек с осью х, а может иметь с ней одну или две общие точки. Это зависит от количества корней квадратного уравнения ах2 + bх + с = 0.
Парабола — по гречески παραβολη (parabole) от παραβολλειν (parabollein) — прикладываю, сравниваю.
Параболу обычно строят по ее характерным точкам: вершине и точкам пересечения с осями координат. Графики функций у = х2 и у = –х2 изображены на рис. 23, 24.
Рассмотрим на конкретных примерах построение графиков квадратичных функций.
|
56 |
Функции, их свойства и графики |
||||
Пример 7. Построить график функции:
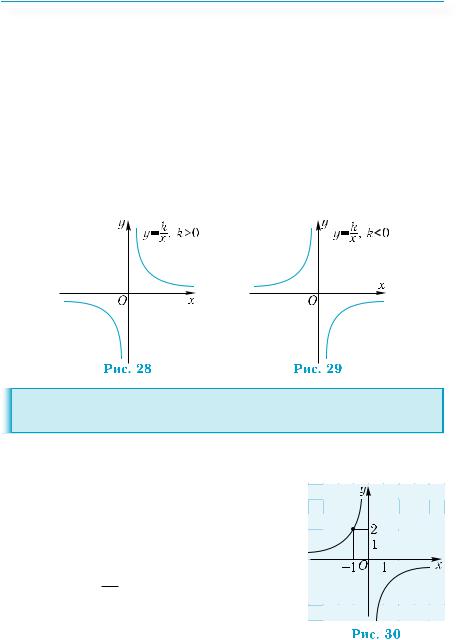
1) у = х2 + 6х + 8; 2) у = – х2 + 2х + 3; 3) у = 2х2 – 4х + 3.
1) Найдем абсциссу вершины параболы по формуле x0 = −2ba : x0 = −62 = −3.
Ордината вершины находится вычислением значения квадратичной функции при х0 = – 3: у0 = у(– 3) = 9 – 18 + 8 = – 1. Итак, координаты вершины — (–3; –1). Найдем точки пересечения графика с осью абсцисс. Для этого решим уравнение: х2 + 6х + 8 = 0. Получим: х1 = –4; х2 = –2. Найдем точку пересечения графика с осью у. Для этого вычислим значение функции у = х2 + 6х + 8 при х = 0: у(0) = 8. График пересекает ось у в точке с координатами (0; 8). Ветви параболы направлены вверх, так как коэффициент при х2 положителен. На основании полученных результатов построим график (рис. 25).
2) Вершина параболы находится в точке с координатами (1; 4). Точки пересечения параболы с осью абсцисс имеют координаты (–1; 0) и (3; 0). График функции пересекает ось у в точке с коорди-
|
Функциональные зависимости |
57 |
натами (0; 3). Ветви параболы направлены вниз. График изображен на рис. 26.
3) Вершина параболы находится в точке с координатами (1; 1). Парабола не пересекает ось х, поскольку уравнение 2х2 – 4х + 3 = 0 не имеет корней. Парабола пересекает ось у в точке с координатами (0; 3). Для уточнения положения графика вычислим значение функции в точке х = 2: у(2) = 3, то есть парабола проходит через точку А(2; 3). График изображен на рис. 27.
Графиком обратной пропорциональности y = kx является гипербола, расположение которой зависит от знака k (рис. 28, 29).
|
Гипербола (по гречески νπερβολη) — избыток, преуве- |
|
|
личение. |
|
|
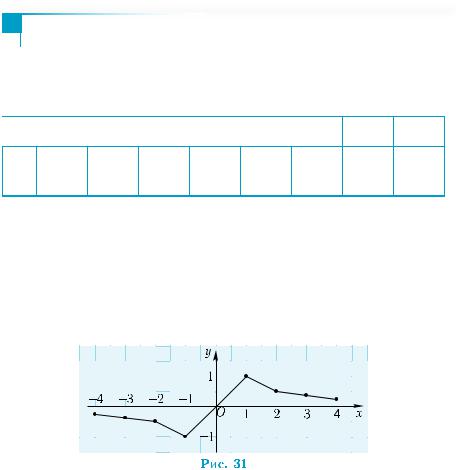
Пример 8. |
На рис. 30 изображен график обратной пропорци- |
|
ональности. Задать эту зависимость формулой. |
|
|
Обратная пропорциональность задает- |
|
|
ся формулой y = k . Необходимо найти чис- |
|
|
x |
|
|
ло k. График функции проходит через точку |
|
|
с координатами (–1; 2), то есть имеет место |
|
|
равенство: 2 = |
k . Отсюда k = – 2. |
|
−1 |
|
|
Ответ. y = − 2 . |
|
|
x |
|
|
Существуют различные способы построе- |
|
|
ния графиков функций. Один из них — построение по несколь- |
|
|
ким точкам. |
|
58 |
Функции, их свойства и графики |
!Произвольной выбор точек и построение графика по этим точкам может привести к существенным ошибкам.
Например, чтобы построить график функции некоторую таблицу ее значений.







|
у |
− |
1 |
− |
1 |
− |
1 |
–1 |
1 |
1 |
|
4 |
3 |
2 |
2 |
Теперь изобразим соответствующие точки на координатной плоскости и, соединив их, получим кривую, изображенную на
рис. 31. Однако она совсем не похожа на график функции y = 1x .
Вы его хорошо знаете — это гипербола (см. рис. 28). Какие мы допустили ошибки? Дело в том, что график функции нужно строить не по произвольно взятым точкам, а по характерным для данной функции точкам.
Проще всего построить график линейной функции. Для этого достаточно найти две точки, принадлежащие графику, и через них провести прямую. Характерными точками для квадратичной функции являются вершина параболы и точки пересечения параболы с осями координат. А для обратной пропорциональности характерной является точка х = 0, в которой ее график «разрывается».
В дальнейшем вы познакомитесь с общими методами нахождения характерных точек.
Другой способ построения графиков функций основан на гео-
метрических преобразованиях. Так, зная график функции
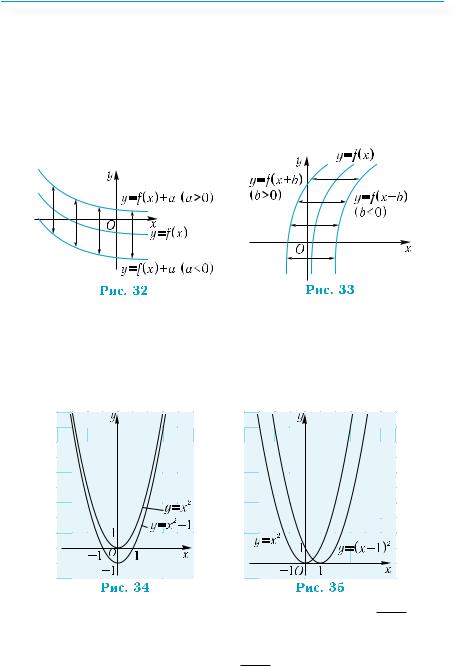
у=f(х),можнопостроитьграфикифункций у=f(х)+аиу= f(х+b), где а и b — некоторые числа, по следующим правилам.
|
Функциональные зависимости |
59 |
График функции у = f (х) + а можно получить из графика функции у = f (х) параллельным переносом его вдоль оси у на |а| единиц: в направлении оси у, если а > 0 и в
противоположном направлении, если а < 0 (рис. 32). График функции у = f(х + b) можно получить из графика функции у = f (х) параллельным переносом его вдоль оси х на |b| единиц: в направлении оси х, если b < 0 и в
противоположном направлении, если b > 0 (рис. 33).
Например,графикфункцииу= х2 –1можнополучитьпараллель- нымпереносомграфикафункцииу= х2 наоднуединицувнаправлении, противоположном направлению оси у, так как х2 – 1 = х2 + (–1) (рис. 34). График функции у = (х – 1)2 можно получить из графика функции у = х2 параллельным переносом последнего на одну единицу в направлении оси х, так как (х – 1)2 = (х + (–1))2 (рис. 35).
|
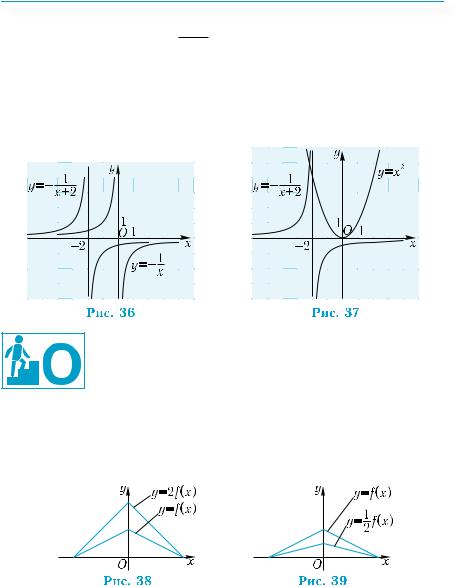
Пример 9. |
Сколько корней имеет уравнение x2 = − |
1 |
? |
||
|
x + 2 |
|||||
|
Уравнение имеет столько корней, сколько общих точек име- |
|||||
|
ют графики функций у = х2 и y = − |
1 |
. Построим графики этих |
|||
|
x + 2 |
|||||
|
функций в одной системе координат. |
|
60 |
Функции, их свойства и графики |
График функции y = − x 1+ 2 можно получить из графика фун-
кции y = − 1x параллельным переносом последнего вдоль оси х на
2 единицы влево (рис. 36). Тогда из рис. 37 видно, что уравнение имеет один корень.
Ответ. Один корень.
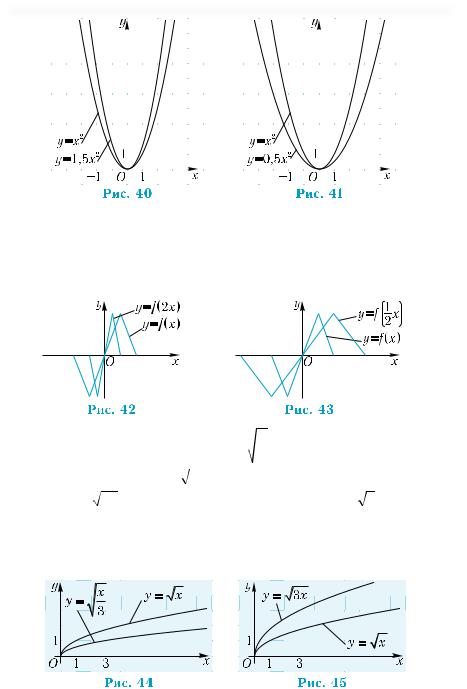
Теперь напомним, как зная график функции у = f(х) можнопостроитьграфикифункцийу=kf(х)иу=f(ωх),
где k и ω — некоторые положительные числа.
График функции у = kf(x) (k > 0) можно получить из графика функции y = f(x) растяжением его в k раз от
оси х при k > 1 (рис. 38) и сжатием в 1 раз к оси х при k
0<k<1(рис.39).
Пример 10. Построить графики функций у = 1,5 х2, у = 0,5х2.
График функции у = 1,5 х2 получим из графика функции
у= x2 растяжением от оси х в 1,5 раза (рис. 40). График функции
у= 0,5х2 получим из графика у = x2 сжатием его к оси х в 2 раза
(рис. 41).
|
Функциональные зависимости |
61 |
|||||||||||||||||||||||
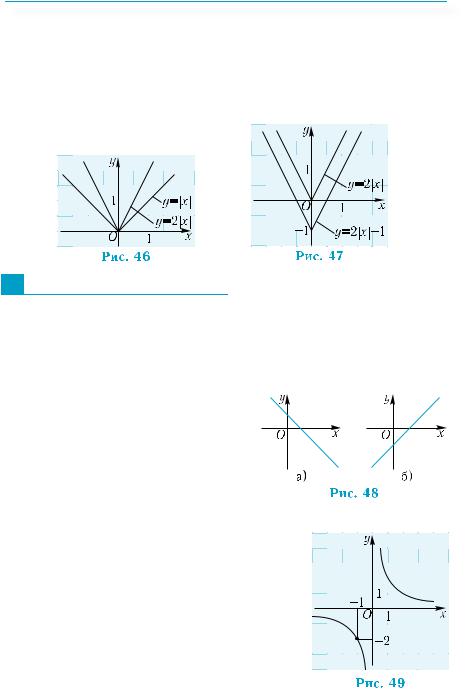
График функции y = f(ωx) (ω > 0) можно получить из графика функции у = f (х) сжатием его к оси у в ω раз
при ω > 1 (рис. 42) и растяжением его в 1 раз от оси у
ω
при 0 < ω < 1 (рис. 43).
|
Например, график функции y = |
x |
можно построить, растя- |
|
3 |
нув график функции у = x от оси у в 3 раза (рис. 44). График функции y = 3x получим из графика функции у = x , сжав его
к оси у в 3 раза (рис. 45).
При построении графика функции иногда приходится выполнять несколько геометрических преобразований.
|
62 |
Функции, их свойства и графики |
|
Пример |
11. Построить график функции у = 2|х| – 1. |
Построение выполняется в два этапа, исходя из графика функции у = |х|:
1) график функции у = |х| растягивается от оси х вдвое (рис. 46); 2) полученный график параллельно переносится на одну еди-
ницу в отрицательном направлении оси у (рис. 47).
|
9 |
Контрольные вопросы |
||||
|
1°. |
Проходит ли график функции у= 5х + 2 через точку: |
||||
|
а) А(0; 5); |
б) В(0; 2); |
в) С(–1; –2); |
г) D(–1; –3)? |
||
|
2°. |
В каких точках прямая у = 1 – 4х пересекает оси координат? |
||||
|
3°. |
Укажите несколько точек, через которые проходит график ли- |
||||
|
нейной функции у = –2. |
и b, |
||||
|
4°. |
Какие знаки имеют числа k |
||||
|
если график линейной функции |
|||||
|
у = kх + b |
изображен на рис. 48? |
||||
|
5°. |
У каких из следующих парабол |
||||
|
ветви направлены вверх: |
|||||
|
а) у = 1 – |
х + 2х2; |
||||
|
б) у = 5х – 3х2 – 1; |
|||||
|
в) у = 1 – |
х2? |
||||
|
6°. |
Чему равна абсцисса вершины параболы: |
||||
|
а) у = 1 – 3х + 2х2; |
|||||
|
б) у = – 5х2 + х |
– 2; |
||||
|
в) у = (х + 5)(х |
– 1)? |
||||
|
7°. |
Найдите обратную пропорциональность, |
||||
|
график которой изображен на рис. 49. |
|||||
|
8°. |
Сколько точек пересечения имеют гра- |
||||
|
фики функций: |
|
Функциональные зависимости |
63 |
||||||||||||||||||
|
2 |
2 |
2 |
|||||||||||||||||
|
9°. |
а) у = |
x , у |
= х; |
б) у = x |
, у = –х; |
в) у = – x , у = х2? |
|||||||||||||
|
На сколько единиц и в каком направлении следует параллель- |
|||||||||||||||||||
|
но перенести гиперболу y = 1 |
, чтобы получить гиперболу: |
||||||||||||||||||
|
1 |
x |
б) y = 1 |
|||||||||||||||||
|
а) y = |
; |
+ 4? |
|||||||||||||||||
|
x + 4 |
|||||||||||||||||||
|
x |
|||||||||||||||||||
|
10°.На сколько единиц и в каком направлении следует парал- |
|||||||||||||||||||
|
лельно перенести параболу |
у = х2, чтобы ее вершина оказа- |
||||||||||||||||||
|
лась в точке с координатами: а) (–2; 0); |
б) (0; 2)? |
||||||||||||||||||
|
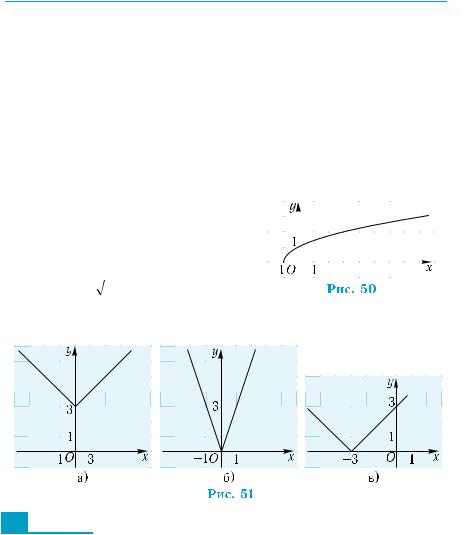
11°.Какой формулой может быть за- |
|||||||||||||||||||
|
дана функция, график которой |
|||||||||||||||||||
|
изображен на рис. 50, если он по- |
|||||||||||||||||||
|
лучен с помощью геометрических |
|||||||||||||||||||
|
преобразований из графика фун- |
|||||||||||||||||||
|
кции y = |
x ? |
12.Для каждой из функций y = |x + 3|, y = |x| + 3, y = 3|x| подберите соответствующий график на рис.51, а) – в).
Задачи
|
46. |
Дана функция f(x) = x2 − 2x −3. Найдите: |
|||||
|
1°) f(−2), f(3), |
1 |
; |
||||
|
f |
2 |
|||||
|
3) корни уравнения f(x) = f(0). |
||||||
|
2°) нули функции; |
2x +1 |
|||||
|
47°.Дана функция y = |
. Найдите значения аргумента, при |
|||||
|
x +1 |
||||||
|
которых функция принимает значения: 1) – 2; 2) 2; 3) 3. |
|
64 |
Функции, их свойства и графики |
|||||||||
|
48. Найдите область определения функции: |
||||||||||
|
1°) |
y = |
5x +1; |
2°) |
y = |
5x +1 ; |
3°) |
y = |
1 |
; |
|
|
x2 + 4 |
x2 −4 |
2− x |
||||||||
|
4°) |
y = |
3−2x ; |
5) |
y = |
x |
+ |
2− x ; 6) |
y = |
1 − x2 . |
|
|
x +3 |
x |
|||||||||
|
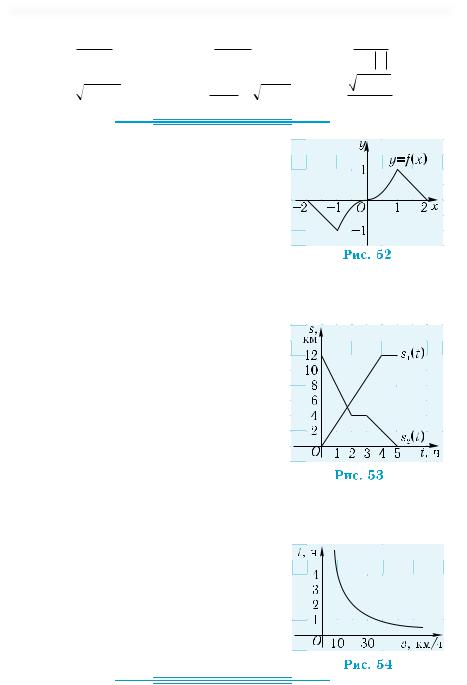
49. Функция у = f(х) задана графически |
||||||||||
|
(рис. 52). |
||||||||||
|
1°) Какова её область определения? |
||||||||||
|
2°) Каково множество значений фун- |
||||||||||
|
кции? |
||||||||||
|
3°) Сколько нулей имеет функция? |
||||||||||
|
4°) Укажите все значения |
х, при ко- |
|||||||||
|
торых функция принимает положи- |
||||||||||
|
тельные (отрицательные) значения? |
||||||||||
|
5) Чему равно наибольшее (наименьшее) значение функции? |
||||||||||
|
6) Сколько корней имеет уравнение f(x) = 0,5? |
||||||||||
|
50. На рис. 53 изображены графики дви- |
||||||||||
|
жений двух пешеходов навстречу друг |
||||||||||
|
другу по шоссе, соединяющему пункты |
||||||||||
|
А и Б; s1(t) и s2(t) — расстояния от А, со- |
||||||||||
|
ответственно, до первого и второго пе- |
||||||||||
|
шеходов в момент времени t. |
||||||||||
|
1°)Каковорасстояниемеждупунктами? |
||||||||||
|
2°) Сколько километров прошел пер- |
||||||||||
|
вый пешеход за первые два часа? |
||||||||||
|
3) Какой из пешеходов к моменту |
||||||||||
|
встречи преодолел большее расстоя- |
||||||||||
|
ние? |
||||||||||
|
4) Какой из пешеходов пришел в пункт назначения первым? |
||||||||||
|
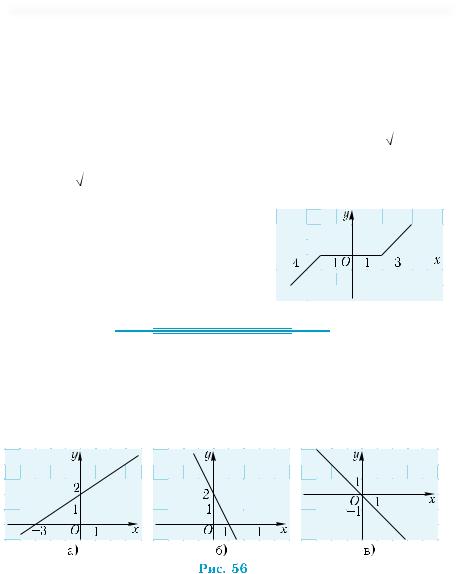
51. На рис. 54 приведен график зависи- |
||||||||||
|
мости |
времени |
t, необходимого на |
||||||||
|
путь из пункта А в пункт Б, от скоро- |
||||||||||
|
сти движения v. С какой скоростью |
||||||||||
|
нужно двигаться, чтобы добраться из |
||||||||||
|
А в Б менее чем за 2 часа? |
|
Функциональные зависимости |
65 |
|||||||
|
52°.Постройте график функции: |
||||||||
|
1) y = |
x −3 |
; |
2) |
y = −3; |
3) y = − |
2 |
; |
4) y = x2 −5x + 4; |
|
x |
||||||||
|
2 |
||||||||
|
5) y = −3x2 −2x +1; |
6) y = x2 −4x + 4; |
7) y = (x + 2)(x −4). |
53.Постройте график функции с помощью геометрических преобразований:
|
1°) |
y = (x −0,5) |
2 |
2°) |
2 |
−0,5; |
3) y = |
x2 |
4°) |
x + 2; |
|||||
|
; |
y = x |
; |
y = |
|||||||||||
|
2 |
||||||||||||||
|
5°) |
y = x −2; |
6°) |
1 |
7°) y |
1 |
|
x 2 |
|||||||
|
y = |
; |
= |
+3; |
y = |
. |
|||||||||
|
x −3 |
x |
|||||||||||||
|
2 |
54.На рис. 55 изображен график функции y = f(x). Постройте график фун-
кции: 

3)y = f(2x);
4)y = 2f(x).
55.Найдите линейную функцию, если:
1°) ее график проходит через точки А(1; –1) и В(2; –1);
2)ее график составляет угол 135° с осью х и проходит через точку А(0; 2).
Задайте с помощью формулы функции, графики которых изображены на рис. 56, а)–в).
57.Напряжение в электрической цепи равномерно растет, то есть линейно зависит от времени. В начале опыта напряжение равнялось 10 В, а в конце опыта, длившегося 5 с, напряжение увеличилось в 1,5 раза.
1)Выразите зависимость напряжения от времени и постройте график этой функции.
2)Каким было напряжение через 3 с после начала опыта?

|
66 |
Функции, их свойства и графики |
58°.Найдите обратную пропорциональность, если известно, что ее график проходит через точку А(–1; 3). Постройте ее график.
59. По закону Бойля–Мариотта, давление р и объем газа V связаны формулой p = Vc , где с — некоторое число, постоянное для дан-
ной массы и температуры газа. Постройте график этой зависимости, если при давлении р = 10 Па объем газа равен 0,5 л.
|
60. |
Какие из следующих пар точек симметричны относительно |
||||||
|
оси у, а какие — относительно начала координат: |
|||||||
|
1) |
А(0; 1), |
В(1; 0); |
2) |
А(0; 1), |
В(0; –1); |
||
|
3) |
А(1; 2), |
В(–1; 2); |
4) |
А(1; 2), |
В(–1; –2)? |
||
|
Упражнения для повторения |
|||||||
|
61. |
Укажите функции, графики которых симметричны относи- |
||||||
|
тельно оси у, а которых — относительно начала координат: |
|||||||
|
1) у = х; |
2) у = – х + 1; 3) у = |
1 |
|||||
|
62. |
х2; 4) у = х3; |
5) y = x . |
|||||
|
Докажите, что большему значению аргумента соответствует |
|||||||
|
большее значение функции: 1) у = 2х+ 1; 2) y = |
x. |
63. Чему равно расстояние между точками координатной прямой: 1) А(х) и В(2); 2) А(а) и В(–3); 3) А(а) и B(b); 4) A(a) и B(–b)?
Итог
Основные понятия
|
Определение |
Геометрическая интерпре- |
||
|
тация, примеры |
|||
|
Зависимость |
между перемен- |
Например, высота от самолета |
|
|
ными х и у, которая для каж- |
до поверхности земли является |
||
|
дого значения х из D опреде- |
функцией времени его пребы- |
||
|
ляет единственное значение у, |
вания в полете. |
||
|
называется |
функциональной |
||
|
зависимостью у от х с областью |
|||
|
определения D. |
|
График функции у = f(х) — это |
График линейной функции — |
||
|
множество |
точек координат- |
прямая. |
квадратичной функ- |
|
ной плоскости с координатами |
График |
||
|
(х; f(х)), где |
х — произвольное |
ции — парабола. |
|
|
число из области определения |
График |
обратной пропорцио- |
|
|
функции. |
нальности –— гипербола. |
Содержание
- Функции
- Функциональная зависимость функция область ее определения способы задания функций
- Что такое Функция?
- Понятие функции
- Функция. Способы задания функций.
Функции
Если две переменные величины находятся между собой в такой зависимости, что каждому значению одной переменной соответствует строго определённое значение другой, то первая величина называется аргументом, а вторая его функцией.
Функция — это зависимая переменная величина. Аргумент — это независимая переменная. Зависимость функции от аргумента называется функциональной зависимостью.
Если нужно указать на тот факт, что y функция от x, не акцентируя внимания на то, в какой именно зависимости находится функция от аргумента, то пишут просто:
где f (начальная буква слова function — функция) заменяет слово функция , y — это функция, а x — аргумент.
Иногда, чтобы показать, что y зависит от x, пишут просто:
Обратите внимание, что вместо y и x могут использоваться любые другие буквы.
Значение y, соответствующее заданному значению x, называют значением функции. Все значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют множество значений функции. Для функции f приняты следующие обозначения:
D(f) — область определения функции
(множество значений аргумента).
E(f) — множество значений функции.
Пример. Возьмём формулу нахождения расстояния по скорости и времени:
где S — это расстояние, v — скорость, а t — время. Если взять скорость, равную 50 км/ч, то каждому неотрицательному значению t будет соответствовать строго определённое значение S:
| t (ч) | 1 | 1,5 | 2 | 2,5 | 3 |
|---|---|---|---|---|---|
| S (км) | 50 | 75 | 100 | 125 | 150 |
Следовательно, S является функцией от t — S(t) , область определения функции — D(S) ⩾ 0, так как время не может быть отрицательным, но при этом можно не затратить времени вообще, если не двигаться, в этом случае t = 0. Значение этой функции в точке t0 можно обозначить в виде S(t0), то есть записать таблицу со значениями в таком виде:
Источник
Функциональная зависимость функция область ее определения способы задания функций
Функция — это одно из основных общенаучных и математических понятий, выражающее зависимость между переменными величинами. Это закон, по которому каждому значению элемента x из некоторого множества X ставится в соответствие единственный элемент y из множества Y.
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом, а переменную у — зависимой переменной. Значение у, соответствующее заданному значению х, называют значением функции.
Записывают: у = f (х). Буквой f обозначается данная функция, т. е. функциональная зависимость между переменными х и у; f (х) есть значение функции, соответствующее значению аргумента х. Говорят также, что f (х) есть значение функции в точке х. Все значения, которые принимает независимая переменная, образуют область определения функции. Все значения, которые принимает функция f (х) (при х, принадлежащих области ее определения), образуют область значений функции.
Способы задания функции
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у = f (х),
где f (х) — некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
Пусть функция задана аналитически формулой у = f (х). Если на координатной плоскости отметить все точки, обладающие следующим свойством: абсцисса точки принадлежит области определения функции, а ордината равна соответствующему значению функции, то множество точек (х; f (x)) есть график функции. В физике и технике функции нередко задаются графически, причем иногда гарфик является единственным доступным средством задания функции. Чаще всего это бывает при употреблении самопишущих приборов, автоматически записывающих изменение одной величины в зависимости от изменения другой. В результате на ленте прибора получается линия, графически задающая регистрируемую прибором функцию.
Также функцию можно задать таблично. Рассмотрим примеры функциональной зависимости в реальной жизни.
Таблицей заданы данный о росте ребенка в течении первых 5 месяцев жизни:
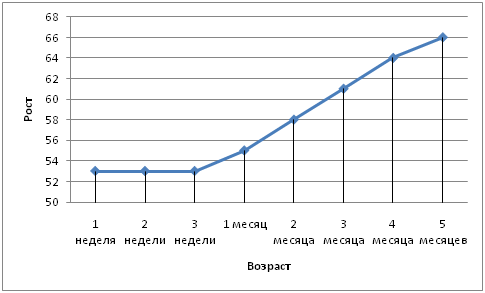
Имея таблицу значений функциональной зависимости роста от возраста, можно по точкам построить график:
Вот яркий пример функции, заданной графически. На графике можно увидеть максимум и минимум, фрагменты линейной функции, сглаживание линий и т.д.
Кардиограмма — график работы сердца.
Кардиограмма — это запись сокращений сердца человека, которая осуществляется при помощи какого-либо инструментального способа. Во время сокращения сердце передвигается в пределах грудной клетки, оно вращается вокруг своей оси слева направо.
Суть электрографии заключается в том, чтобы зарегистрировать разности потенциала во времени. Кривая, которая показывает нам эти изменения и есть кардиограмма. Прибор, который записывает эту кривую, именуется электрокардиографом. Кардиограмма сердца показывает возбуждение сердца и его сокращение. Во время снятия кардиограммы к телу человека прикрепляются специальные электроды, благодаря которым аппарат и получает необходимые данные.
Суть обработки сигналов данного исследования заключается в том, чтобы диагностировать имеющиеся проблемы в работе сердечных мышц, используя при этом различные аналитические методы.
Переход вещества из твердого состояние в жидкое называется плавлением. Для того чтобы тело начало плавиться, его необходимо нагреть до определенной температуры. Температура, при которой вещество плавится, называют температурой плавления вещества.
Каждое вещество имеет свою температуру плавления. У каких-то тел она очень низкая, например, у льда. А у каких-то тел температура плавления очень высокая, например, железо. Плавление кристаллического тела это сложный процесс.
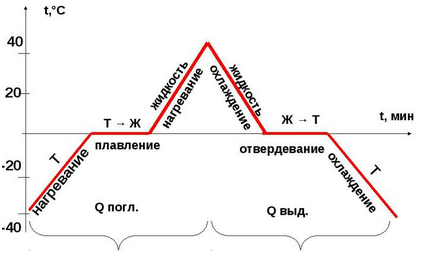
На рисунке представлен известный из курса физики график плавления льда.
График показывает зависимость температуры льда от времени, которое его нагревают. На вертикальной оси отложена температура, по горизонтальной — время.
Из графика видно, что изначально температура льда была -40 градусов. Потом его начали нагревать. С течением времени, температура увеличилась до 0 градусов. Эта температура считается температурой плавления льда. При этой температуре лед начал плавиться, но при этом перестала возрастать его температура, хотя при этом лед также продолжали нагревать. Затем, когда весь лед расплавился и превратился в жидкость, температура воды снова стала увеличиваться. Во время плавления температура тела не изменяется, так как вся поступающая энергия идет на плавление. После нагревания (пик графика) жидкость стали охлаждать, процесс пошел в обратную сторону до затвердевания.
Рассмотрим задачу
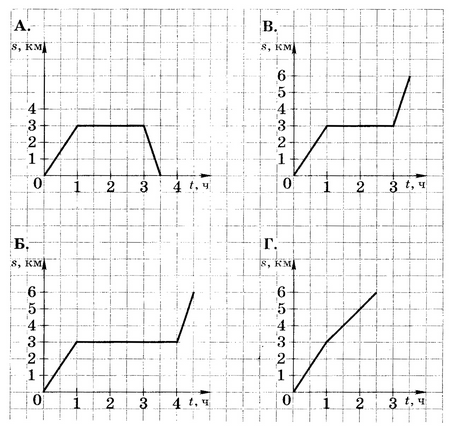
Туристы отправились с турбазы на озеро, провели там 2 часа и вернулись обратно. Выберите график, описывающий зависимость пройденного расстояния от времени:
Верным будет ответ А., т.к. в течении двух часов туристы находились на озере, добравшись до него, а затем снова вернулись в лагерь, т.е. в нулевую точку отсчета.
Источник
Что такое Функция?
О чем эта статья:
7 класс, 11 класс, ЕГЭ/ОГЭ
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
- х ≠ 0 (потому что на ноль делить нельзя)
И записать это можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.
Источник
Функция. Способы задания функций.
Функция является заданной, иначе говоря, известной, если для каждого значения возможного числа аргументов можно узнать соответствующее значение функции. Наиболее распространенные три способа задания функции: табличный, графический, аналитический, существуют еще словесный и рекурсивный способы.
1. Табличный способ наиболее широко распространен (таблицы логарифмов, квадратных корней), основное его достоинство – возможность получения числового значения функции, недостатки заключаются в том, что таблица может быть трудно читаема и иногда не содержит промежуточных значений аргумента.
Аргумент х принимает заданные в таблице значения, а у определяется соответственно этому аргументу х.
2. Графический способ заключается в проведении линии (графика), у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции. Часто для наглядности масштабы на осях принимают разными.
Например: для нахождения по графику у, которому соответствует х = 2,5 необходимо провести перпендикуляр к оси х на отметке 2,5. Отметку можно довольно точно сделать с помощью линейки. Тогда найдем, что при х = 2,5 у равно 7,5, однако если нам необходимо найти значение у при х равном 2,76, то графический способ задания функции не будет достаточно точным, т.к. линейка не дает возможности для столь точного замера.
Достоинства этого способа задания функций заключаются в легкости и целостности восприятия, в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.
3. Аналитический способ состоит в задании функции одной или несколькими формулами. Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента, а недостатком является затрата времени на проведение дополнительных математических операций.
Функцию можно задать с помощью математической формулы y=x 2 , тогда если х равно 2, то у равно 4, возводим х в квадрат.
4. Словесный способ состоит в задании функции обычным языком, т.е. словами. При этом необходимо дать входные, выходные значения и соответствие между ними.
Словесно можно задать функцию (задачу), принимающуюся в виде натурального аргумента х с соответствующим значением суммы цифр, из которых состоит значение у. Поясняем: если х равно 4, то у равно 4, а если х равно 358, то у равен сумме 3 + 5 + 8, т. е 16. Далее аналогично.
5. Рекурсивный способ состоит в задании функции через саму себя, при этом значения функции определяются через другие ее же значения. Такой способ задания функции используется в задании множеств и рядов.
При разложении числа Эйлера задается функцией:
Ее сокращение приведено ниже:
При прямом расчёте возникает бесконечная рекурсия, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо f(n) единицу.
Источник
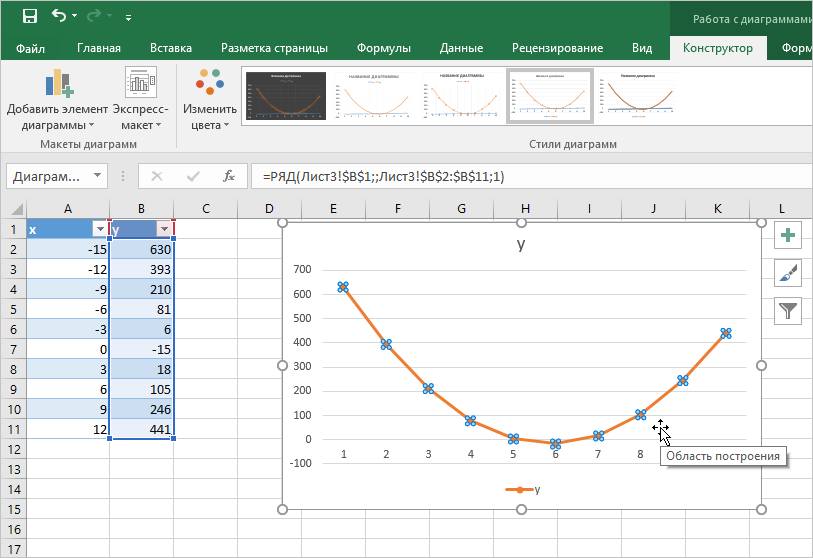
Когда перед пользователем стоит задача качественно оформить учебный документ, часто приходится работать с таблицами и графиками, которые строятся на ее основе. Рассмотрим несколько актуальных методик, как построить график зависимости в Excel.
Как постороить одноосевой график
Для каждого случая построения графиков существуют индивидуальные условия, но практически всегда должна быть независимая переменная функция. На практике такую обозначают символами «х» или «у».
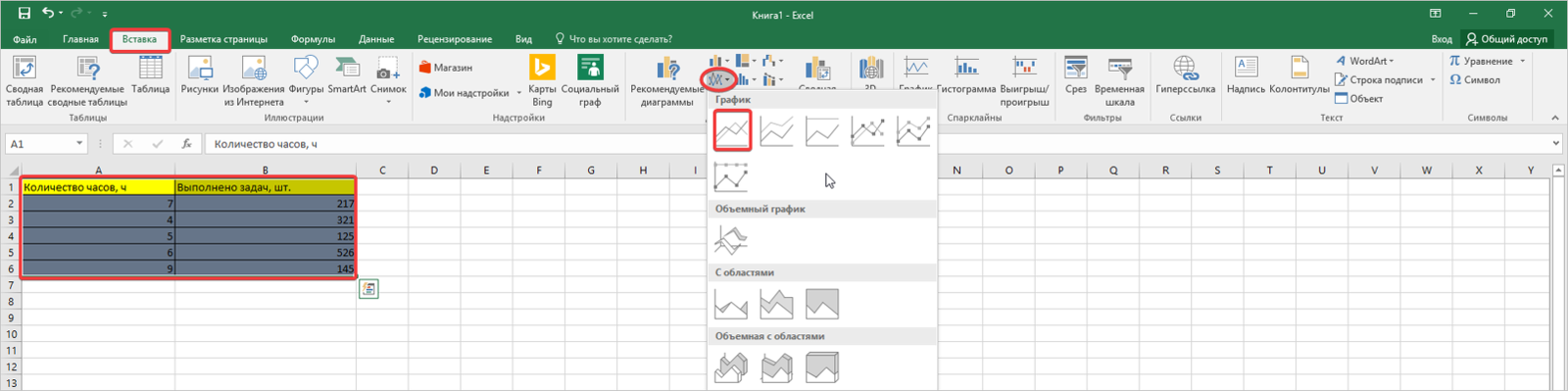
- Предположим, у нас есть таблица с двумя известными составляющими. Построим график зависимости на ее основе. Выделяем весь диапазон ячеек, которые охватывает наша таблица, затем переходим во вкладку «Вставка». Находим блок с диаграммами и нажимаем на инструмент «Вставить график». Для начала подойдёт самый простой.
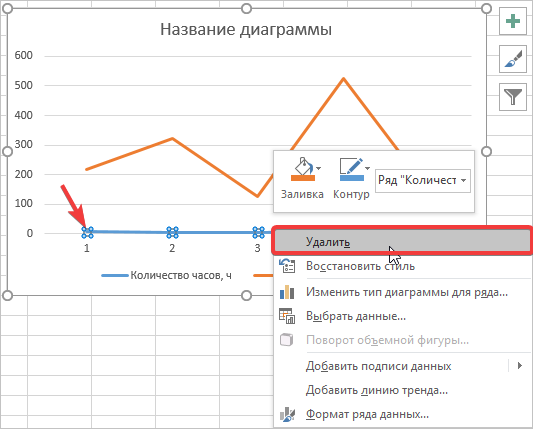
- Автоматически система произвела построение графика с ломаными линиями, однако нам понадобится лишь одна, поэтому ненужную ось (с количеством часов) можно удалить. Для этого сделаем выделяем её мышью, а затем нажмем правой кнопкой вызовем меню редактирования. Нажимаем «Удалить».
- На данном этапе можно считать первый способ построения графика завершенным. Мы удалили ось временного промежутка и получили значение, которое нас интересует: «Зависимость выполненных задач за заданное время».
Для более сложных систем зависимости можно использовать графическую диаграмму с маркерами. Она поможет более точно определить сегмент данных и выстроить аналитическую картину таблицы.
Как постороить осложненный график зависимости
При наличии двух или трех неизменных данных в таблице, график зависимости выполняет сложную функцию. Рассмотрим способ построения графика зависимости для нескольких значений:
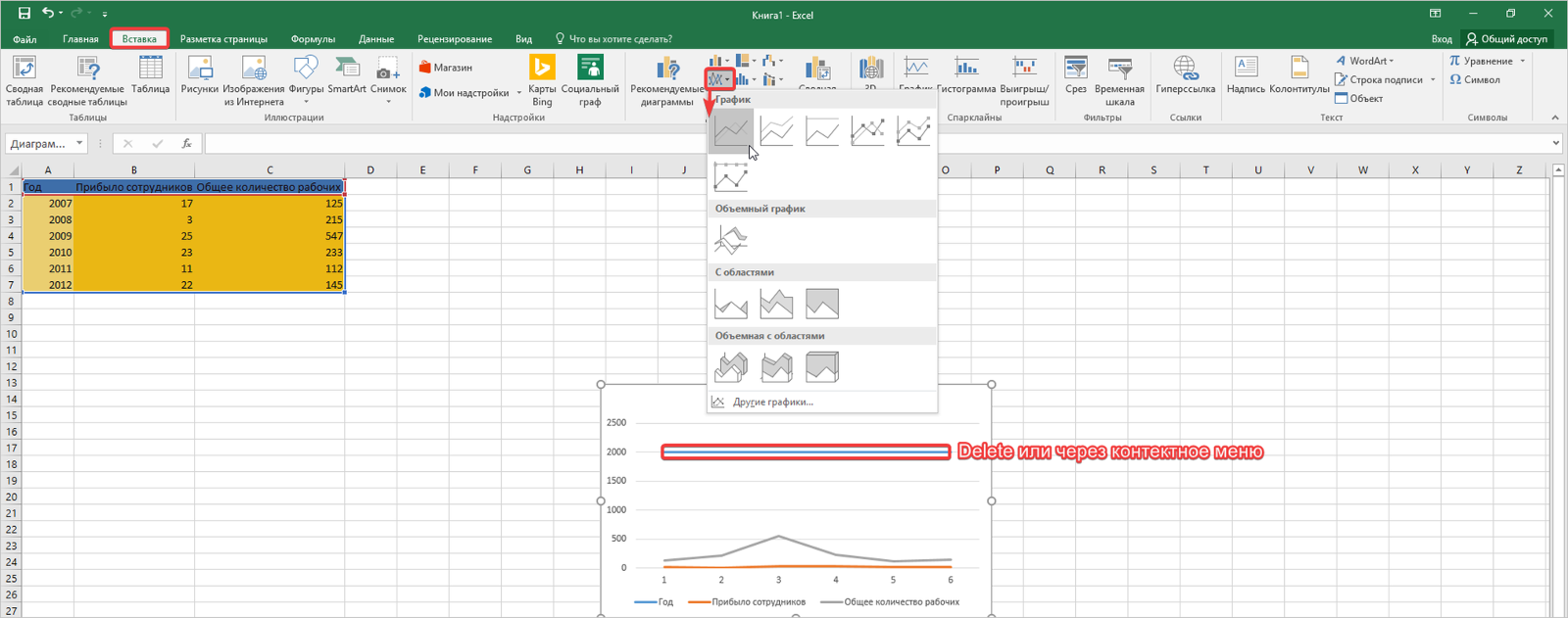
- Выделим всю область нашей таблицы и снова запустим первый график. Перед вами появился объект, в котором одна линия, отвечающая за год, отображается некорректно. Удаляем ее, как в предыдущем способе.
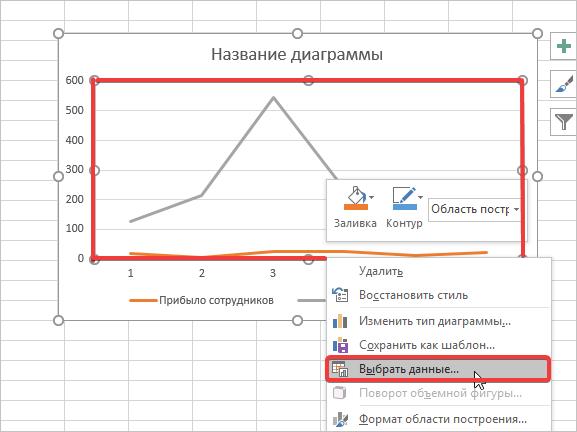
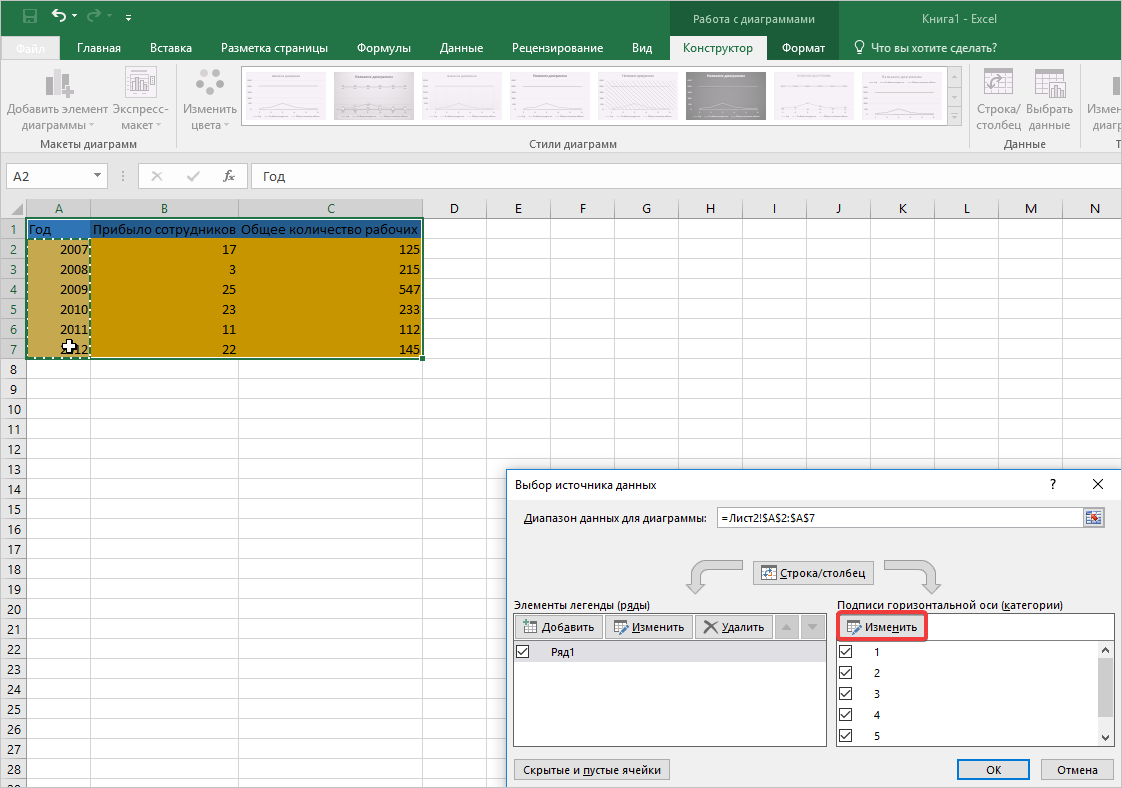
- График отобразился иначе, однако одна из линий все равно неправильно отвечает за свои функции. Для исправления этой ошибки выбираем область построения (активируем ее так, чтобы видны были элементы перемещения). Затем сделаем клик правой кнопкой мыши и нажмем на пункт «Выбрать данные».
- Открывается дополнительное окно настроек. В нем находим кнопку «Изменить», после ее нажатия автоматически открывается окно поменьше.
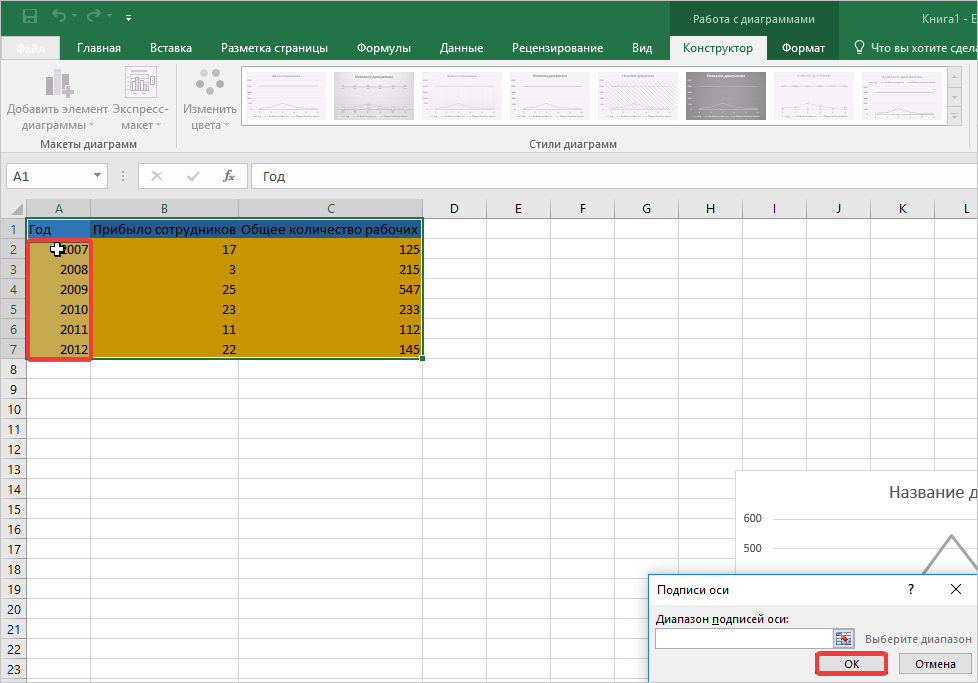
- Теперь выделяем диапазон ячеек, где отображаются года. Только не вносите в адрес заголовок этого столбца. Затем нажмите кнопку «ОК.
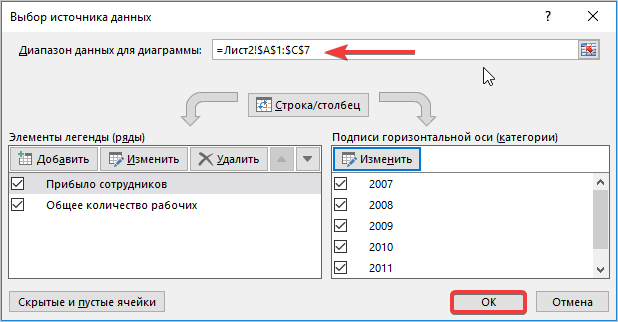
- Снова нажмите «ОК», чтобы сохранить изменения, внесенные в график зависимости. Обратите внимание, что адреса обрабатываемых ячеек автоматически перенеслись в поле диапазона.
После произведенных манипуляций все данные на листе получили четкую позицию, соответственно, отображаются корректно. Можно заметить, никаких сложностей с оформлением графиков зависимости нет.
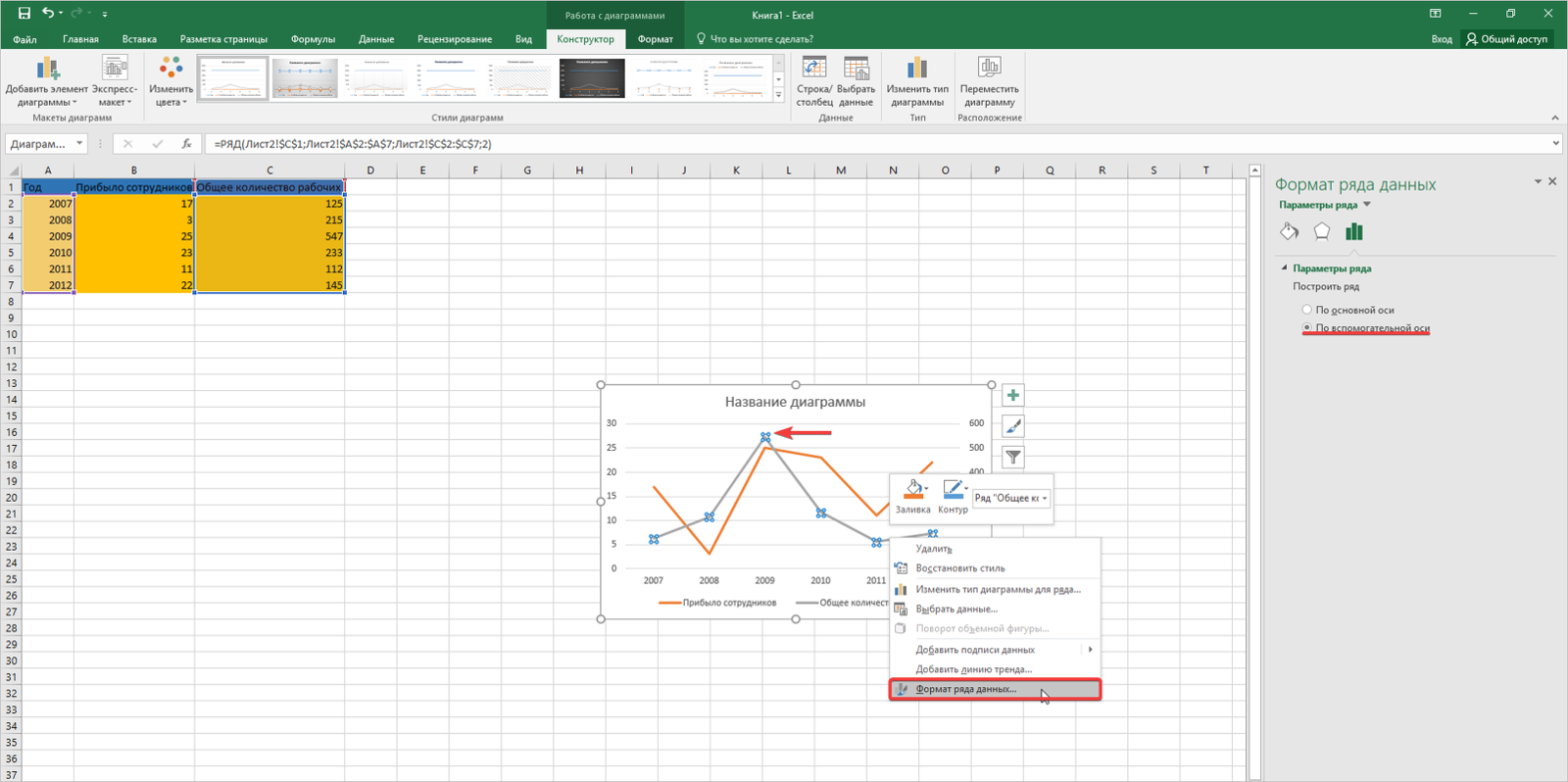
Если на графике отображается несоответствие величин, необходимо построить вспомогательную ось. Для этого нажмите на область изменения оси, а затем сделайте клик правой кнопкой мыши.
Выберите «Формат ряда данных». В окне мастера справа отметьте флажок «По вспомогательной оси». Изменения будут активированы.
Алгебраическая функция и график зависимости
Этот способ построения графика зависимости используют студенты и те, кто работают в области статистики. Прежде чем выстроить график зависимости, необходимо посчитать значение «х» и прописать его в таблице с определенным шагом.
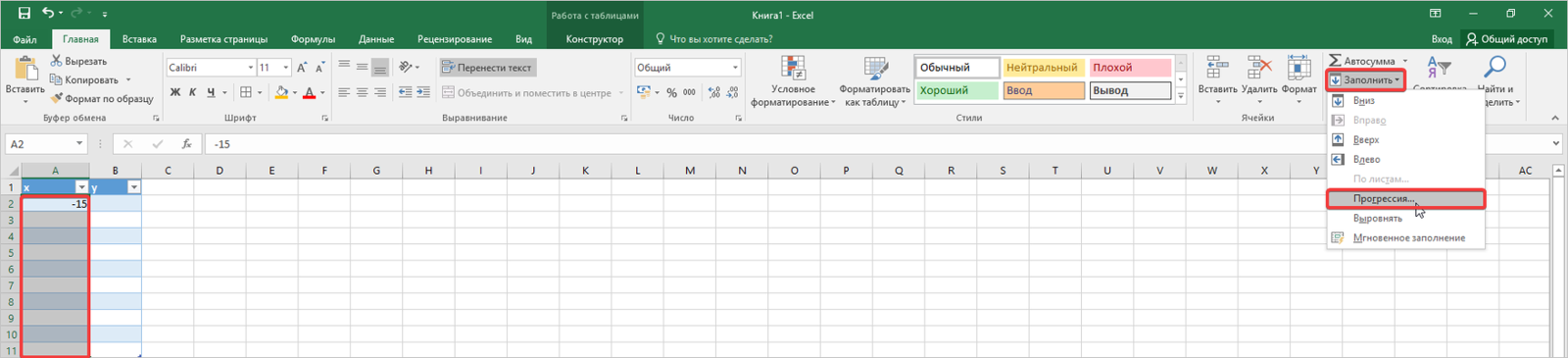
- Для начала построим таблицу и впишем в нее единственное значение. Вставляем в первую ячейку «х» число -15. Затем заполним оставшиеся данные вниз через три шага. Для этого воспользуемся автоматическим инструментом. Выделяем весь столбец «х», затем во вкладке «Главная» нажимаем на пункт «Заполнить». Высветится список, в котором выбираем «Прогрессия».
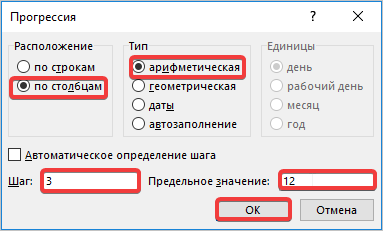
- В следующем открывшемся окне редактируем все так, как указано на фото. Обязательно проставляем величину шага «3», затем отмечаем предельное значение, в нашем случае будет число «12». Нажимаем кнопку «ОК».
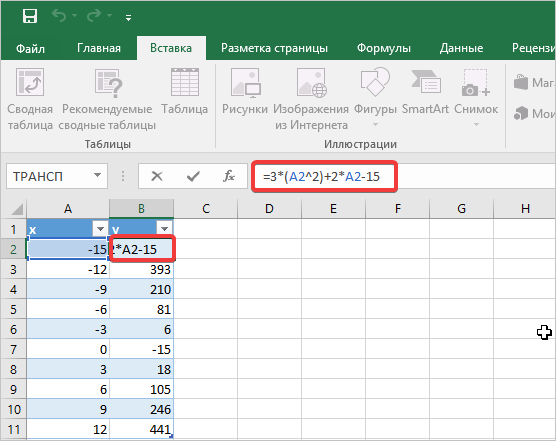
- Выполняем преобразование обычной формулы в формулу Excel. Для этого вставим нашу формулу в первую ячейку столбца «у», где вместо значения «х» пропишем адрес ячейки, в котором оно прописано. Затем в конце формулы нажимаем кнопку «Enter».
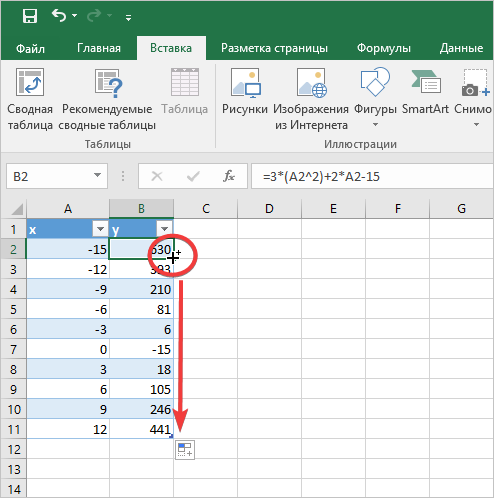
- Как вы видите, все значения автоматически посчитались для каждой отдельно взятой ячейки. Если в вашей версии Excel значения не заполнились, необходимо использовать маркер автозаполнения. Наведите на нижний угол до появления крестика. Нажмите и протяните вниз до последней ячейки.
- Как в предыдущих способах, выстраиваем графики. В данном случае, необходимо выбрать маркированный объект. Обязательно удаляем лишнюю ось.
Если вам малопонятны функции Microsoft Excel, вы можете вручную прописать каждое значение выражения, однако автоматизированный процесс поможет сберечь ваше время.
Подробнее о функциях Excel и их применении читайте в инструкции Справочника.
Тест по теме «Альтернативные способы построения графика зависимости в Excel»
Урок 67 (Р)
Тема урока: «Функциональная зависимость между величинами. Способы
задания функции».
Основные цели:
Личностные:
Сформировать
готовность и способность к выполнению моральных норм в отношении взрослых и
сверстников в школе, дома и т.д.
Метапредметные:
1)
Сформировать представления о семье как о ценности жизни любого человека.
2)
Сформировать понимание значимости ученика, его чувств, действий, поступков и
результатов для его семьи.
3)
Формировать ответственность за свою семью, за создание доверительных отношений
в семье уже сегодня, а также в своей семье в будущем.
4)
Тренировать умение разрешать конфликтные ситуации в семье.
6)
Тренировать умение анализировать собственную деятельность.
7) Тренировать умение проводить контроль и коррекцию.
Предметные:
1)
Организовать самоконтроль умения определять функциональную зависимость,
задавать функции разными способами, находить значения функций по данным
значений аргументов и значения аргумента по данному значению функции.
2) Тренировать умение решать текстовые задачи доказывать
общие утверждения.
 |
Вариант
проведения урока
Оборудование.
1) Эталоны из
курса «Мир деятельности»
Д—67.1 План работы на уроке.
Д—67.2 Алгоритм самопроверки и работы над ошибками.
2)
Демонстрационный материал
Д—67.3
Определение функциональной зависимости (из урока 64, Д−64.1).
Д—67.4
Обозначения функции (из урока 65, Д—65.2).
Д—67.5 Условия
задания функции (из урока 65, Д−65.3).
Д—67.6 Способы
задания функции (из урока 65, Д−65.4).
Д—67.7 Алгоритм
нахождения значения функции в некоторой точке (из урока 65, Д−65.5).
Д—67.8 Карточка
с заданиями для актуализации знаний.
Д—67.9 Вопросы для этапа рефлексии.
3) Раздаточный
материал
Р—67.1 Алгоритм
самопроверки и работы над ошибками (из урока 10, Р−10.1).
Р—67.2 Подробный образец выполнения заданий из домашней работы.
Р—67.3
Самостоятельная работа № 1.
Р—67.4 Образец
выполнения самостоятельной работы № 1.
Р—67.5 Подробный образец для самопроверки
самостоятельной работы № 1.
Р—67.6 Таблица
результатов.
Р—67.7
Самостоятельная работа № 2.
Р—67.8 Подробный
образец для самопроверки самостоятельной работы № 2.
Р—67.9 Подробный
образец выполнения дополнительных заданий.
Р—67.10 Задания
для выбора.
Р—67.11 Образец
выполнения заданий для выбора.
Р—67.12 Карточка
рефлексии.
Р—67.13 Карточка
для локализации затруднений в группах.
4) Презентация к
уроку 67: слайды 1-5.
5) Электронная форма
учебника, 7 класс, 3 часть.
Ход
урока:
1. Мотивация к учебной
деятельности.
На
доске пронумерованные эталоны Д−67.1 – Д−67.7,
у учащихся на партах карточки Р−67.1, Р−67.6, Р−67.12.
−
Сегодня вы проведёте самопроверку умений определять, является ли зависимость
функцией, определять область определения и область значения, использовать
разные способы задания функции, находить значение функции по данному значению
аргумента.
−
Как вы будете работать на уроке?
−
С чего начнёте работу?
2. Самостоятельная
деятельность по известной норме и фиксация индивидуальных затруднений в
самостоятельной работе.
Группам
раздаются карточки с подробным образцом выполнения заданий из домашней работы (Р−67.2):
 |
№ 56.
 |
№ 61.
= 1
= 3
= − 2
2х – 3 = 17 2х – 3 = 2х
– 3 = −
2х = 20 2х
= 2х = −
х = 10 х = х
= −
х
= 4 х = − 2,75
№ 63 (а). у = 0,5х + 1.
Учащиеся
проводят самопроверку. Проговаривают способы, эталоны решения каждого задания,
при необходимости ошибки обсуждаются и исправляются. На доску вывешивается
карточка с заданиями для актуализации знаний (Д−67.8,
слайд 2-3):
1. Зависимости
между Х и Y заданы
нижеприведенными схемами. Определите, какие из указанных зависимостей
являются функциональными и обоснуйте свой ответ:

2. Задайте зависимость пути S,
который автомобилист проехал со скоростью 80 км/ч от времени движения t.
Укажите область определения и область значений для этой зависимости.
Определите, является ли данная зависимость функцией. Найдите значение
величины зависимой переменной при указанных значениях независимой переменной:
a) t = 5 ч; б)
t = 45
мин; в) t = 1ч 30
мин; г) t = 7 ч
15 мин.
Группы
выполняют задания, каждое задание озвучивается одной из групп.
Выполнение заданий:
1. а) является функцией, т.к. каждому значению множества Х
соответствует одно значение множества Y;
б)
не является функцией, т.к. элементу (числу 7) множества Х нет элемента в
множестве Y.
2. s = 80t
T – неотрицательные числа, S – неотрицательные числа, зависимость
является функцией.
a) t = 5 ч б)
t = 45 мин
s = 80 ∙ 5 = 400 (км); s = 80 ∙ 0,75 = 60 (км);
в) t = 1ч 30
мин г) t = 7 ч 15 мин
s = 80 ∙ 1,5 = 120 (км); s = 80 ∙ 7,25 = 580 (км).
− Что вы повторили?
− Сейчас вы будете работать самостоятельно, с какой целью вы будете
выполнять самостоятельную работу?
Для
самостоятельной работы учащимся раздаются карточки (Р−67.3):

нижеприведенными схемами. Определите, какие из указанных зависимостей
являются функциональными и обоснуйте свой ответ:
а)
б)
2. Задайте зависимость выполненной работы А
от времени работы t, если
известно, что производительность равна 60 ед. в час Укажите область
определения и область значений для этой зависимости. Определите, является ли
данная зависимость функцией. Найдите значение величины зависимой переменной
при указанных значениях независимой переменной: t = 15
мин.
3. Функция задана словесным описанием,
найдите ее значение в точках х1, х2, и х3:
Всем
целым числам поставлено в соответствие число 7, а всем нецелым
числам – число
(– 1).
х1 = – 9; х2
= 7,4; х3 = – 3,7.
4. Функция задана с помощью таблицы,
задайте ее графически:
|
х |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
|
у |
1 |
–1 |
2 |
–2 |
3 |
–3 |
4 |
–4 |
5 |
5. Функция
задана формулой у = 6 – 5х.
Найдите ее значение в точках х1, х2, и х3:
х1 = 0; х2
= 3; х3 = –3.
6*.
Функция задана формулой у = 9х – 4. Найдите значение аргумента, при котором значение функции
равно у1, у2, и у3:
у1 = 0; у2
= 2; у3 = –5.
На
работу отводится 10 минут.
− Вы выполнили работу, что теперь вы должны сделать?
− С какой целью вы будете сопоставлять работу с образцом?
Учащимся
раздаются образцы выполнения самостоятельной работы № 1 (Р−67.4):
1. Ответ: а) не является функцией, т.к. числу 9 соответствует
два числа 5 и 7;
б) является функцией, т.к. каждому элементу множества Х
соответствует один элемент множества Y.
2. Ответ: А = 60t. T – все неотрицательные числа, А – все неотрицательные числа.
Является функцией. А = 15 ед.
3. Ответ:
|
х |
− 9 |
7,4 |
− 3,7 |
|
у |
7 |
− 1 |
− 1 |

5. Ответ: у1 = 6; у2
= − 9; у3
= 21.
− Что теперь вы должны сделать?
− Сегодня вы будете сопоставлять свои работы с подробным образцом. С
какой целью вы будете это делать?
3. Локализация
индивидуальных затруднений.
Каждый
учащийся получает подробный образец для самопроверки самостоятельной работы № 1
(Р−67.5):

а)
б)
Используем
определение функции:
не является функцией, т.к. числу 9 является функцией,
т.к. каждому элементу
соответствует два числа 5 и 7 множества
Х соответствует один элемент множества Y.
Ответ: а) не является
функцией; б) является функцией.
2. А = pt p = 60 ед./ч А = 60t. T – все неотрицательные числа, А – все неотрицательные числа. Является функцией, т.к. каждому значению времени Если t = 15 мин = 0,25 ч, то А = 60 ∙ 0,25 = 15 |
||||||||||||||||||||
|
3.
По − 9 число целое, 7,4; |
||||||||||||||||||||
|
|
||||||||||||||||||||
|
5. у = 6 – 5х Если х1 Если х2 Если х3 |
Учащиеся
самостоятельно сопоставляют свои работы с подробным образцом для самопроверки,
фиксируя результаты в карточках (Р−67.6):
|
№ (виды) заданий |
Результат выполнения самостоятельной работы № 1 |
Эталоны, в которых допущены ошибки |
Результат работы над ошибками |
Результат выполнения самостоятельной работы № 2 |
|
|
По образцу |
По эталону для самопроверки |
||||
|
Определение является зависимость функцией |
|||||
|
Построение зависимости |
|||||
|
Указание области определения |
|||||
|
Указание области значения |
|||||
|
Нахождение значения функции по данному значению аргумента |
|||||
|
Задание функции с помощью таблицы по словесному описанию |
|||||
|
Графическое задание функции по таблицы |
|||||
|
Вычислительные ошибки |
|||||
|
Дополнительное задание |
Результат выполнения |
||||
|
6* |
После
того, как учащиеся проведут самопроверку, они объединяются в группы. Каждый в
группе проговаривает место и причину возникших затруднений или фиксирует, что
затруднений нет. Организатор вносит ответы учащихся в таблицу (Р−67.13):
|
№ задания |
Выполнено |
Используемые эталоны |
Вызвало |
|
|
Места |
Причины |
|||
|
1 |
||||
|
2 |
||||
|
3 |
||||
|
4 |
||||
|
5 |
По
окончании работы каждый руководитель группы анализирует результаты самопроверки
во внешней речи.
Можно
локализацию затруднений провести фронтально.
−
Какие эталоны использовали при выполнении первого задания?
−
У кого возникли затруднения в первом задании?
−
В каких местах возникли затруднения?
−
В чём причина возникших затруднений в первом задании?
Аналогичные
вопросы задаются по остальным заданиям?
−
У кого работа выполнена правильно?
−
Какой вывод вы можете сделать?
4. Коррекция выявленных затруднений.
−
Что дальше будут делать те, кто выяснил, что затруднений нет? (Мы будем
работать с дополнительными заданиями.)
Учащиеся
продолжают работать с текстом самостоятельной работы и выполняют задание 6*.
−
Посмотрите на задания и сформулируйте цель своей деятельности.
−
Сформулируйте цель своей дальнейшей работы, те, у кого затруднения
зафиксированы.
−
Что вам будет помогать при работе над ошибками? (Алгоритм исправления ошибок.)
Учащиеся,
используя алгоритм исправления ошибок, самостоятельно работают над ошибками.
Для тренинга им предлагаются карточки с заданиями (Р−67.10):

нижеприведенными схемами. Определите, какие из указанных зависимостей являются
функциональными и обоснуйте свой ответ:
а)
б)
2. Задайте
зависимость выполненной работы А от времени работы t, если
известно, что производительность равна 100 ед. в час Укажите область
определения и область значений для этой зависимости. Определите, является ли
данная зависимость функцией. Найдите значение величины зависимой переменной
при указанных значениях независимой переменной.
a) t = 15
мин; б) t = 7 ч; в)
t = 2 ч
30 мин; г) t = 3 ч.
3. Функция
задана словесным описанием, найдите ее значение в точках х1,
х2, и х3:
Всем
правильным дробям поставлено в соответствие число 7,
а
всем неправильным – число (–1).
х1 = –; х2 =
; х3 =
.
4. Функция
задана с помощью таблицы, задайте ее графически:
|
х |
–6 |
–4 |
–2 |
0 |
2 |
4 |
6 |
8 |
10 |
|
у |
–8 |
–6 |
–4 |
–2 |
0 |
2 |
4 |
6 |
8 |
5.
Функция задана формулой у = 7 –
3х. Найдите ее значение в точках х1, х2,
и х3:
х1 = 0; х2
= 5; х3 = –4.
Для
самопроверки учащимся, которые работали с тренировочными заданиями раздаются
карточки с подробными образцами (Р−67.11):
|
1. Ответ: а) не |
|
2. Ответ: А а) |
|
3. |
|
|
|
5. у = 7 – 3х Если х1 Если х2 Если х3 Ответ: у1 |
В конце
работы подводится результат.
−
Кому удалось выполнить задания для тренинга без ошибок?
5.
Обобщение затруднений во внешней речи.
−
В каких местах были допущены ошибки?
−
На какие эталоны были допущены ошибки?
Эталоны,
при использовании которых были допущены ошибки, озвучиваются.
6. Самостоятельная работа с самопроверкой по эталону.
−
Кто будет выполнять вторую самостоятельную работу? (Те, кто допустил ошибки в
первой самостоятельной работе.)
−
С какой целью вы будете выполнять вторую самостоятельную работу?
−
Как вы будете работать со второй самостоятельной работой? (Мы выполним только
те задания, которые выполнили неправильно.)
Для
работы учащимся предлагаются карточки (Р−67.7):
1. Зависимости
между Х и Y заданы
нижеприведенными схемами. Определите, какие из указанных зависимостей
являются функциональными и обоснуйте свой ответ:

2. Задайте
зависимость пути S,
который автомобилист проехал со скоростью 60 км/ч от времени движения t.
Укажите область определения и область значений для этой зависимости.
Определите, является ли данная зависимость функцией. Найдите значение
величины зависимой переменной при указанных значениях независимой переменной:
t = 4 ч
3. Функция
задана словесным описанием, найдите ее значение в точках х1,
х2, и х3:
Всем числам,
делящимся на 3, поставлено в соответствие число 9, а всем остальным числам –
число (–4).
х1 = 28; х2
= 36; х3 = 41.
4. Функция
задана с помощью таблицы, задайте ее графически:
|
х |
–7 |
–5 |
–3 |
–1 |
0 |
1 |
3 |
5 |
7 |
|
у |
–5 |
–3 |
–1 |
0 |
1 |
2 |
5 |
7 |
9 |
5. Функция
задана формулой у = 6х –
1. Найдите ее значение в точках х1, х2, и
х3:
х1 = 0; х2
= 3; х3 = –3.
На
работу отводится 5 минут. После выполнения работы учащиеся сопоставляют свои
работы с подробным образцом для самопроверки (Р−67.8):

а)
б)
Используем
определение функции:
является функцией, т.к. каждому элементу не является
функцией, т.к. числу 4
множества Х соответствует один элемент не
соответствует никакой элемент.
множества Y.
Ответ: а) является
функцией; б) не является функцией.
2. s = vt v = 60 км/ч s = 60t. T – все положительные числа, S – все неотрицательные числа. Является функцией, т.к. каждому значению времени Если t = 4 ч, то s = |
||||||||||||||||||||
|
3. По 36 28; |
||||||||||||||||||||
|
|
||||||||||||||||||||
|
5. у = 6х – 1 Если х1 Если х2 Если х3 |
Результаты
фиксируют в таблице (Р−67.6).
Учащиеся,
которые работали с дополнительными заданиями проводят самопроверку по
подробному образцу (Р−67.9):

−
Кто справился с затруднениями в задании 1?
−
Кому удалось исправить ошибки в задании 2?
−
Кому удалось правильно выполнить задание 3?
−
Кому удалось правильно выполнить задание 4?
−
Кому удалось правильно выполнить задание 5?
−
С какими заданиями справились те, кто работал с дополнительными заданиями?
−
В каких заданиях вы столкнулись с затруднениями?
−
Вы смогли справиться с затруднениями, что вам в этом помогло?
7. Включение в
систему знаний и повторение.
− А теперь я
предлагаю повторить, как решать текстовые задачи и доказывать общие
утверждения.
Предлагаемые
задания целесообразно выполнять в группах с дальнейшим отчётом групп.
№ 52 (б), стр. 17.
Пусть расстояние между Москвой и Самарой х км,
тогда первый теплоход был в пути ч, а второй −
ч. По
условию первый теплоход был на 3 часа дольше в пути, чем второй теплоход:
−
= 3 | ×120
6х – 5х
= 360
х = 360
Ответ: искомое расстояние 360 км.
№ 53, стр. 17.
а) а4 + 2а3
– а2 – 2а = (а4
+ 2а3) – (а2 + 2а)
= а3(а + 2) – а(а +
2) = (а + 2)(а3 – а) =
= а(а + 2)(а2
– 1) = а(а + 2)(а – 1)(а + 1) = (а – 1)а(а + 1)(а
+ 2).
Получилось произведение четырёх
последовательных чисел, а среди них есть число, которое делится на 3.
б) b5 – 5b3 + 4b = b(b4 – 5b2 + 4) = b(b4 – 4b2 + 4 – b2) = b((b2 – 2)2 – b2) =
= b(b2 – 2 – b)(b2 – 2 + b) = b(b – 1)(b + 1)(b – 2)(b + 2) = (b – 2)(b – 1)b(b + 1)(b + 2).
Получилось произведение пяти
последовательных чисел, а среди них есть число, которое делится на 5.
8. Рефлексия деятельности на уроке.
−
Что необходимо сделать в конце работы?
На
доску вывешивается карточка с вопросами (Д−67.9,
слайд 4).
−
Обсудите в группах предложенные вопросы.
−
А теперь каждый проанализируйте свою работу на уроке.
Учащиеся
работают с карточками рефлексии (Р−67.12):
|
Понятия |
Знаю |
Умею |
|
Определение |
||
|
Области |
||
|
Область значения |
||
|
Нахождение значения |
||
|
Задание функции |
||
|
Задание функции |
Домашнее задание: № 54; №
55; № 68.
Введение в функциональные зависимости
Время на прочтение
11 мин
Количество просмотров 26K
В этой статье мы поговорим о функциональных зависимостях в базах данных — что это такое, где применяются и какие алгоритмы существуют для их поиска.
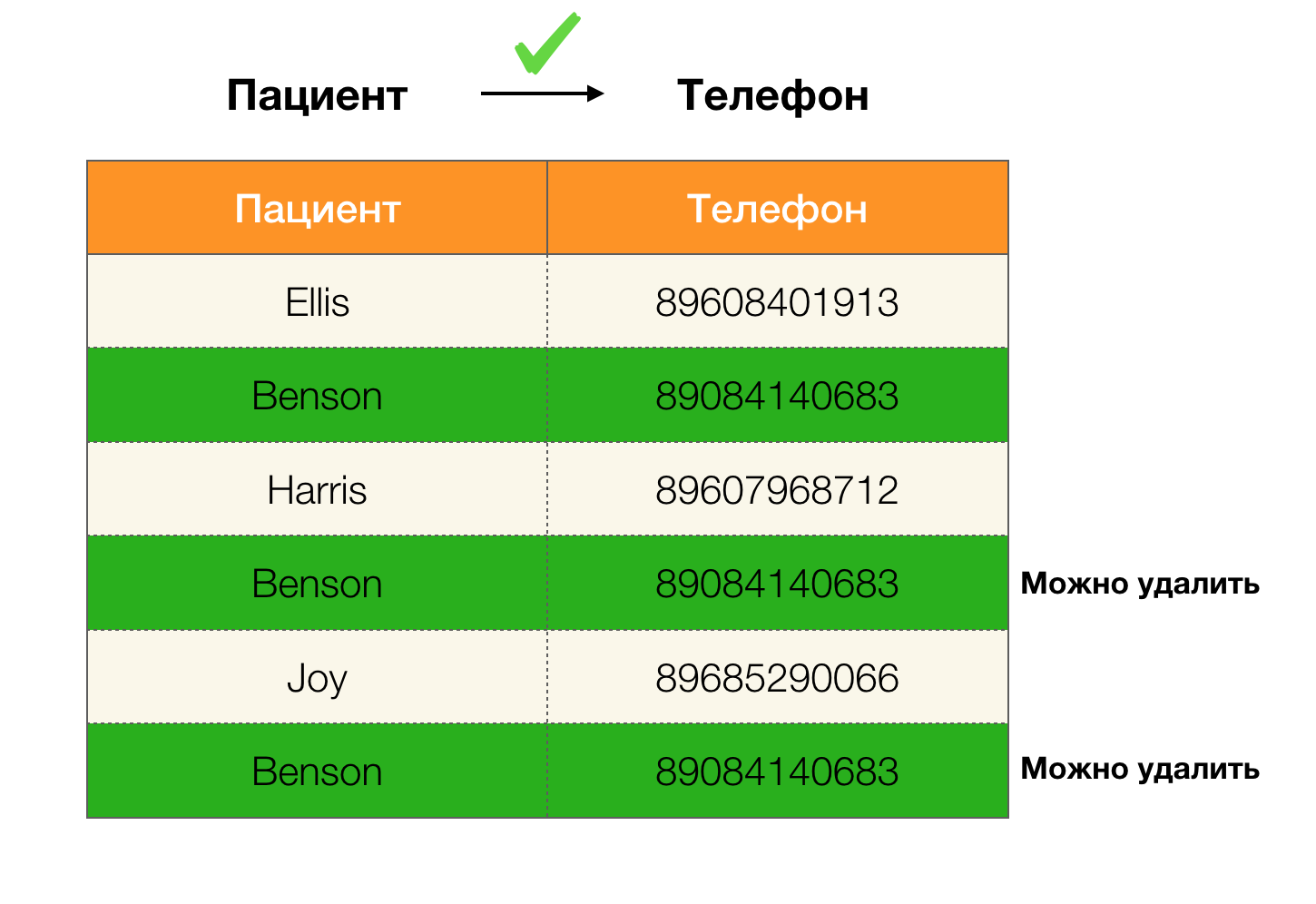
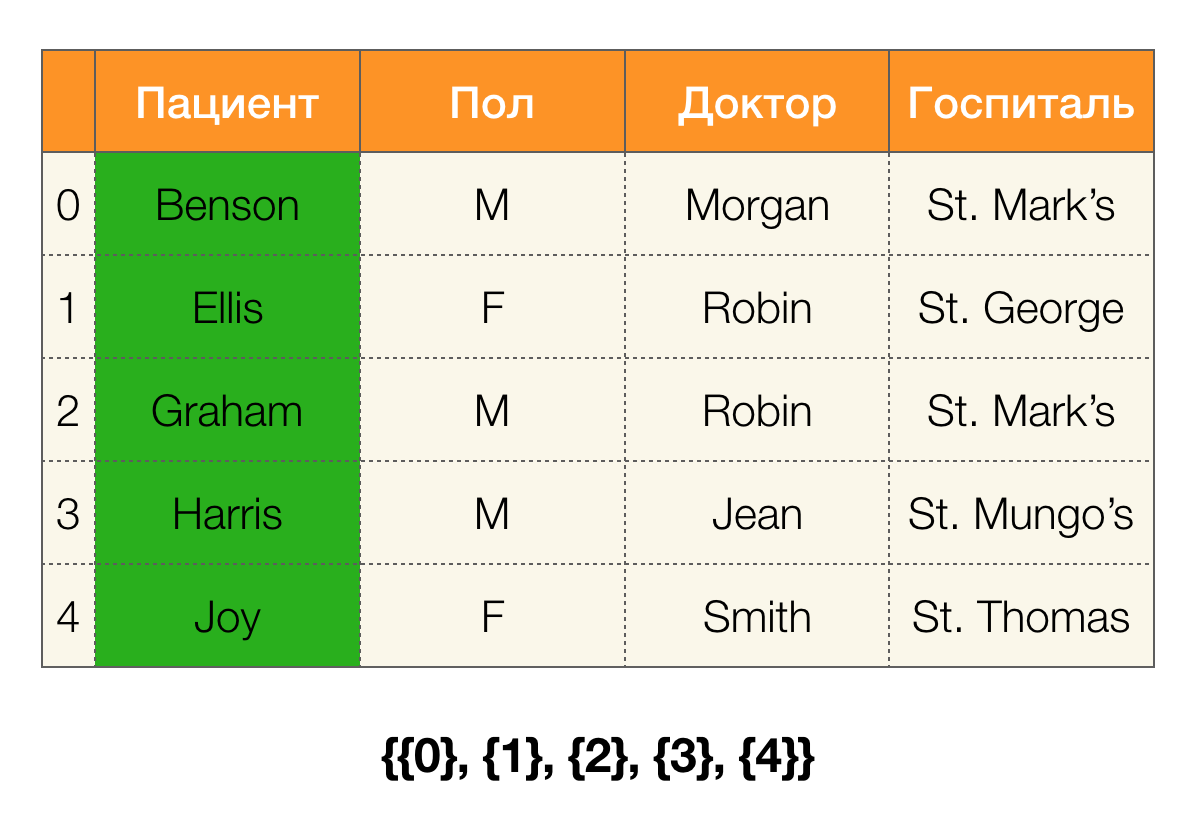
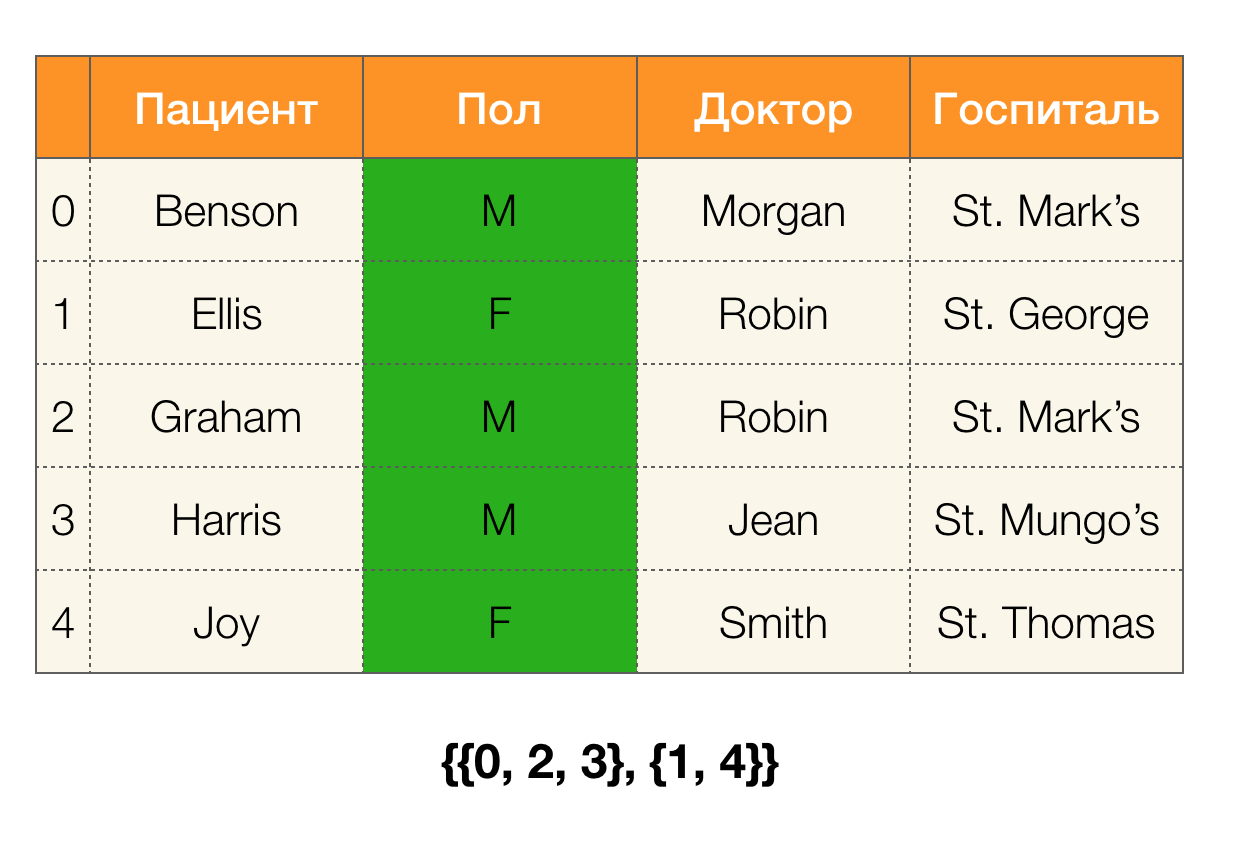
Рассматривать функциональные зависимости мы будем в контексте реляционных баз данных. Если говорить совсем грубо, то в таких базах данных информациях хранится в виде таблиц. Далее мы используем приближенные понятия, которые в строгой реляционной теории не являются взаимозаменяемыми: саму таблицу будем называть отношением, столбцы — атрибутами (их множество — схемой отношения), а набор значений строки на подмножестве атрибутов — кортежем.
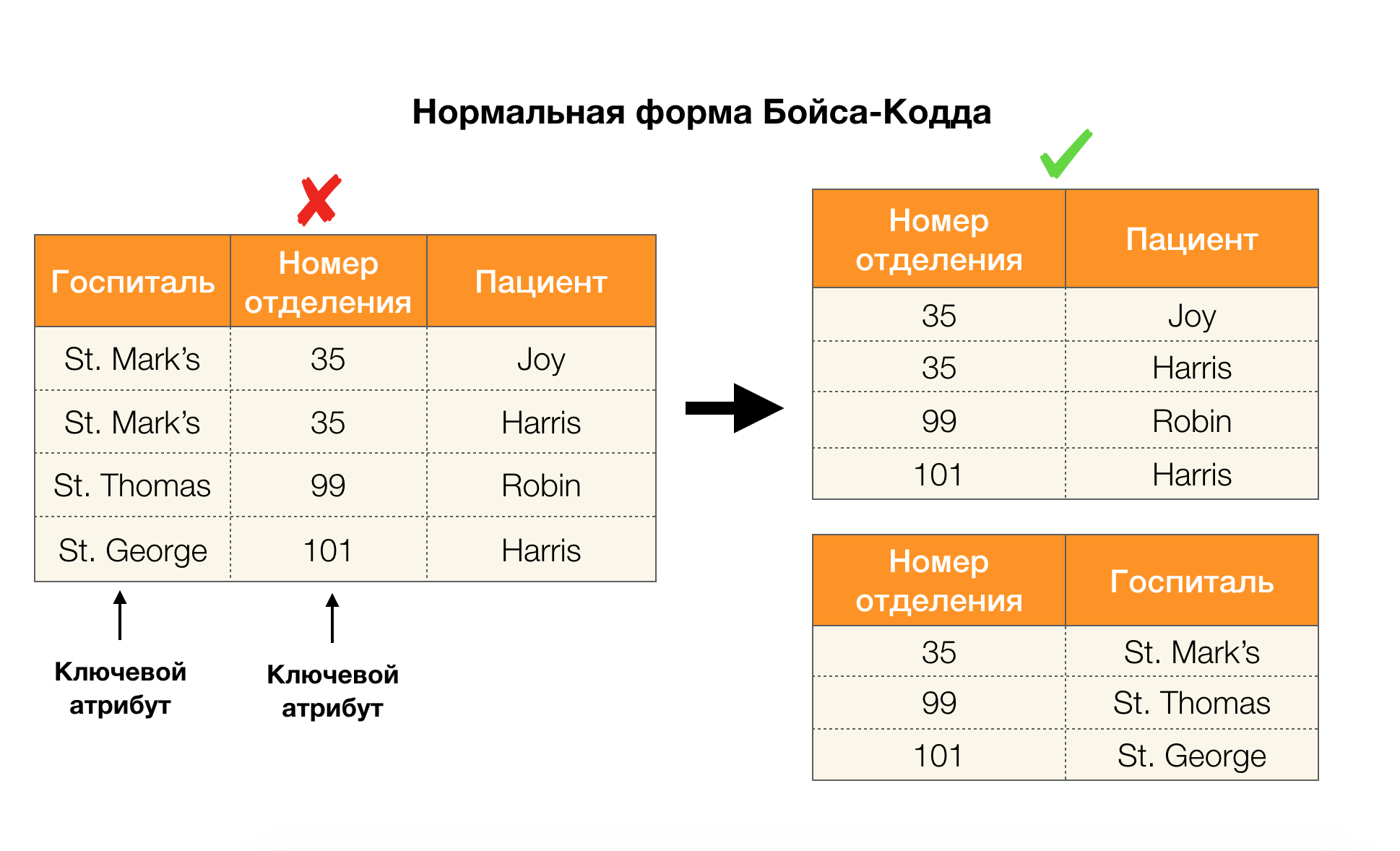
Например, в таблице выше, (Benson, M, M organ) является кортежем по атрибутам (Пациент, Пол, Доктор).
Более формально это записывается в следующем виде:
[Пациент, Пол, Доктор] = (Benson, M, M organ).
Теперь мы можем ввести понятие функциональной зависимости (ФЗ):
Определение 1. Отношение R удовлетворяет ФЗ X → Y (где X, Y ⊆ R) тогда и только тогда, когда для любых кортежей ,
∈ R выполняется: если
[X] =
[X], то
[Y ] =
[Y ]. В таком случае говорят, что X (детерминант, или определяющее множество атрибутов) функционально определяет Y (зависимое множество).
Иными словами, наличие ФЗ X → Y означает, что если мы имеем два кортежа в R и они совпадают по атрибутам X, то они будут совпадать и по атрибутам Y.
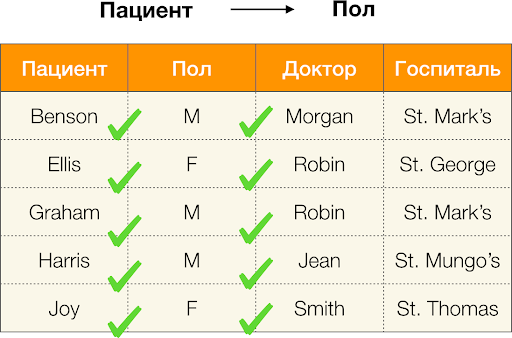
А теперь по порядку. Рассмотрим атрибуты Пациент и Пол для которых хотим узнать, есть ли между ними зависимости или нет. Для такого множества атрибутов могут существовать следующие зависимости:
- Пациент → Пол
- Пол → Пациент
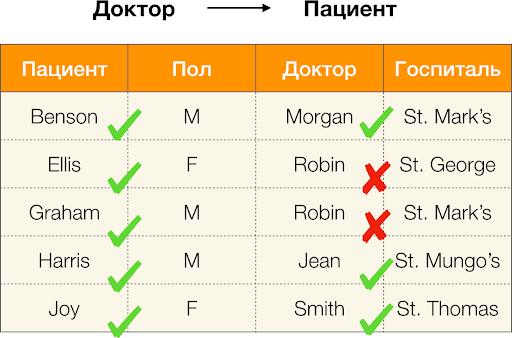
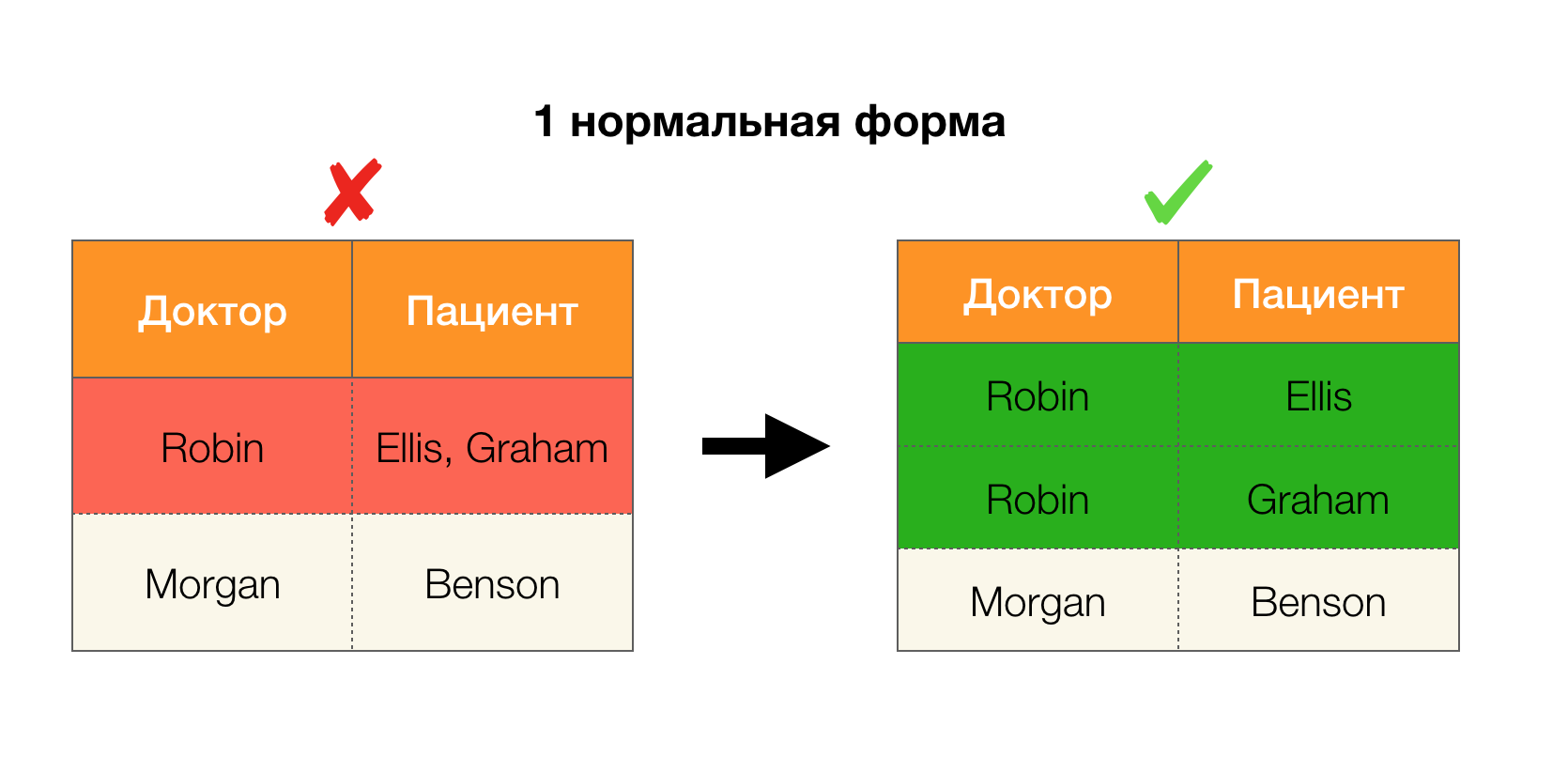
Согласно определению выше, для того чтобы удержалась первая зависимость, каждому уникальному значению столбца Пациент должно соответствовать только одно значение столбца Пол. И для таблицы-примера это действительно так. Однако в обратную сторону это не работает, то есть вторая зависимость не выполняется, а атрибут Пол не является детерминантом для Пациента. Аналогично, если взять зависимость Доктор → Пациент, можно заметить, что она нарушается, так как значение Robin по этому атрибуту имеет несколько разных значений — Ellis и Graham.
Таким образом, функциональные зависимости позволяют определить имеющиеся связи между множествами атрибутов таблицы. Отсюда и впредь мы будем рассматривать наиболее интересные связи, а точнее такие X → Y, что они являются:
- нетривиальными, то есть правая часть зависимости не является подмножеством левой (Y ̸⊆ X);
- минимальными, то есть нет такой зависимости Z → Y, что Z ⊂ X.
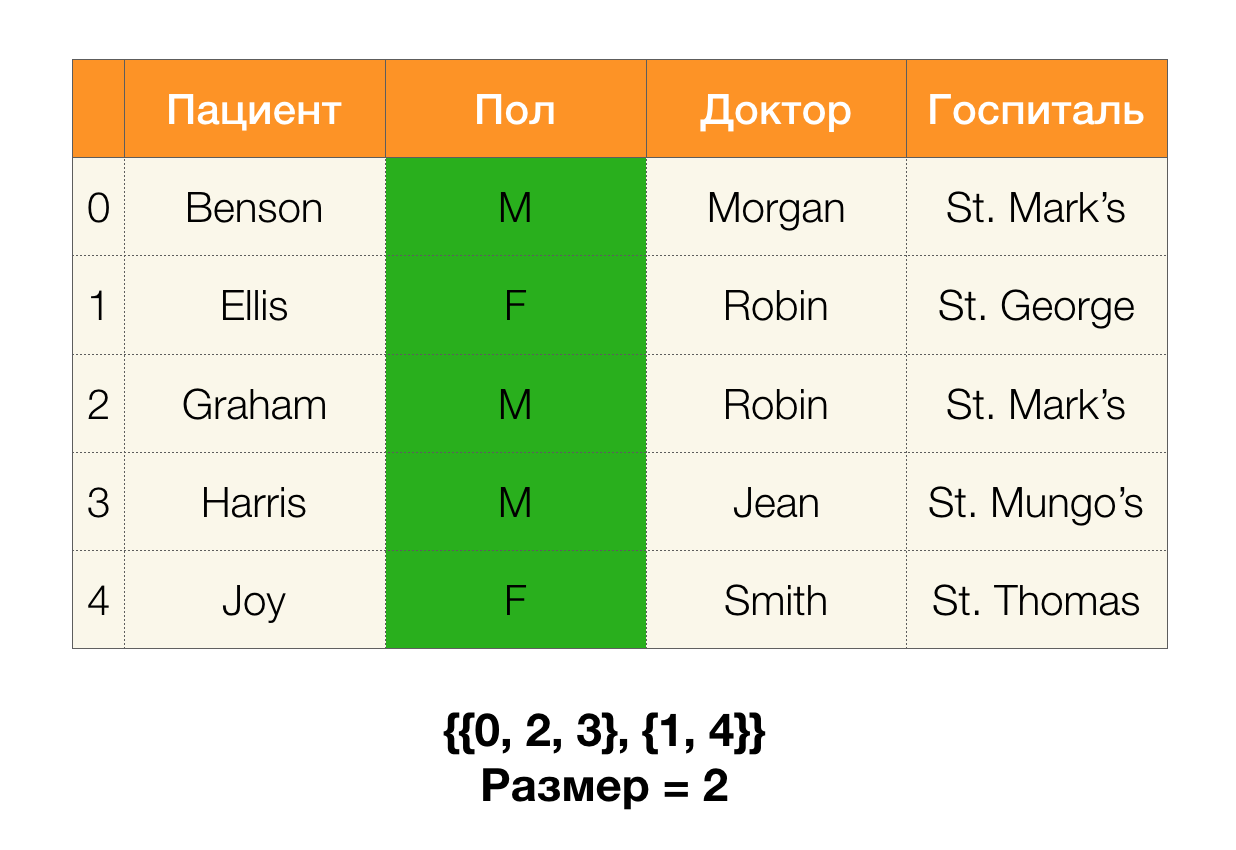
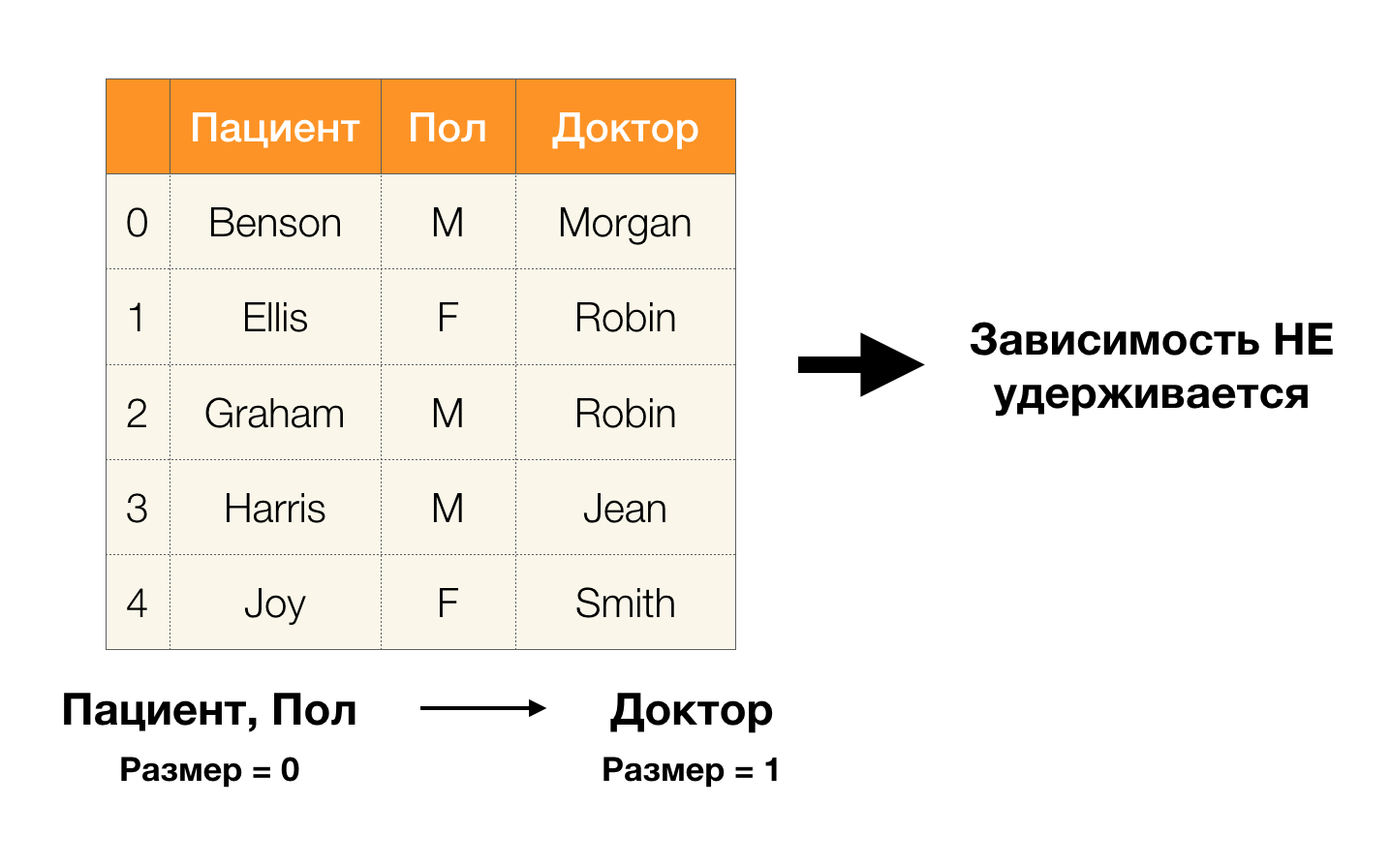
Рассматриваемые до этого момента зависимости были строгими, то есть не предусматривающими никаких нарушений на таблице, но помимо них есть и такие, которые допускают некоторую несогласованность между значениями кортежей. Такие зависимости выносят в отдельный класс, называют приближенными и разрешают им нарушаться на определенном количестве кортежей. Это количество регулируется показателем максимальной ошибки emax. Например, доля ошибки
= 0.01 может означать, что зависимость может нарушаться на 1% от имеющихся кортежей на рассматриваемом множестве атрибутов. То есть для 1000 записей максимум 10 кортежей могут нарушать ФЗ. Мы же будем рассматривать немного иную метрику, основанную на попарно-различных значениях сравниваемых кортежей. Для зависимости X → Y на отношении r она считается так:
Посчитаем ошибку для Доктор → Пациент из примера выше. Имеем два кортежа, значения которых разнятся на атрибуте Пациент, но совпадают на Докторе:
[Доктор, Пациент] = (Robin, Ellis) и
[Доктор, Пациент] = (Robin, Graham). Следуя определению ошибки, мы должны учитывать все конфликтующие пары, а значит таковых будет две: (
,
) и ее инверсия (
,
). Подставим в формулу и получим:
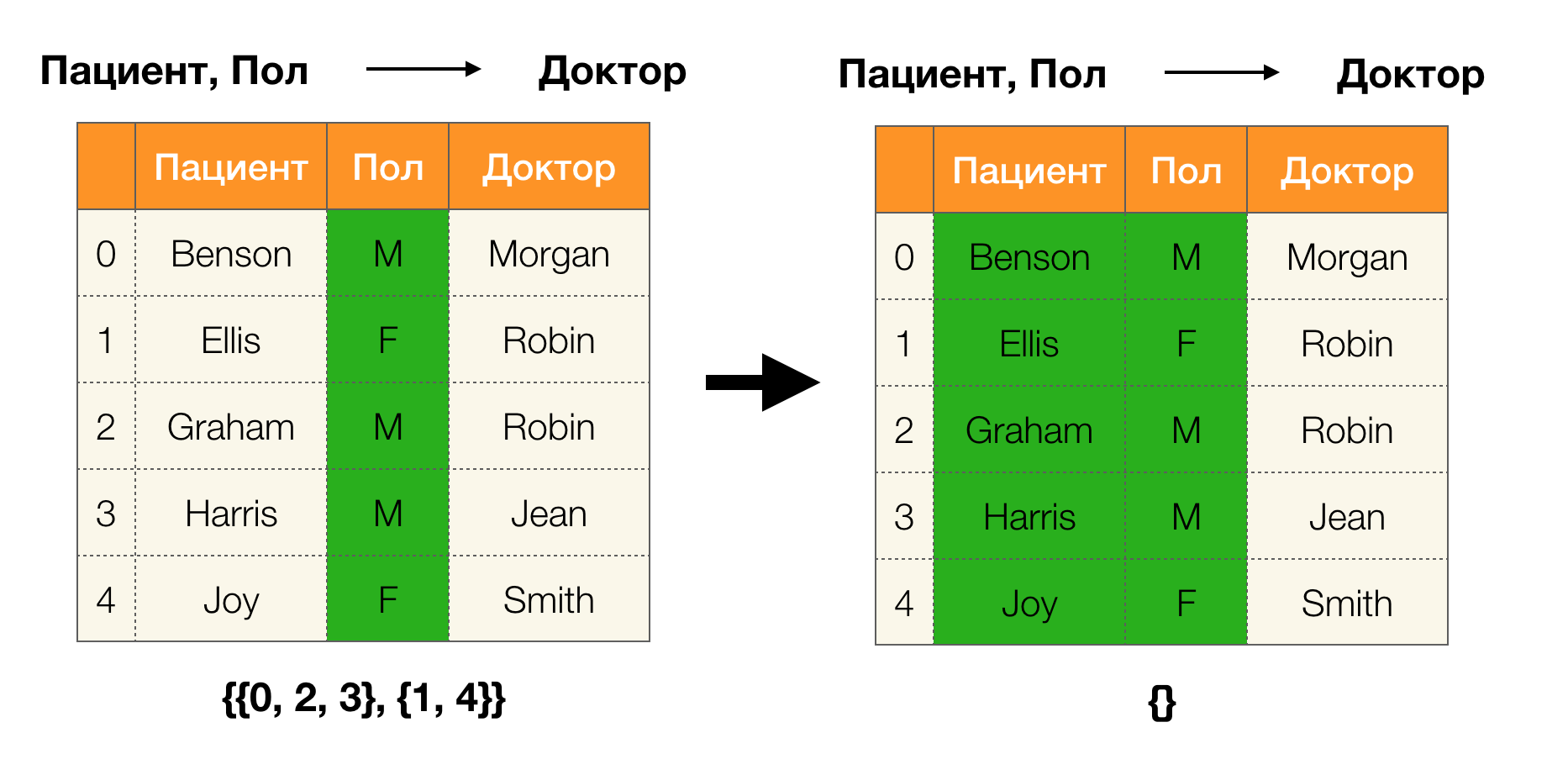
А теперь попытаемся ответить на вопрос: «А зачем оно все?». На самом деле, ФЗ бывают разные. Первый тип — это такие зависимости, которые определяются администратором на этапе проектирования базы данных. Их обычно немного, они строгие, а основное применение — нормализация данных и дизайн схемы отношения.
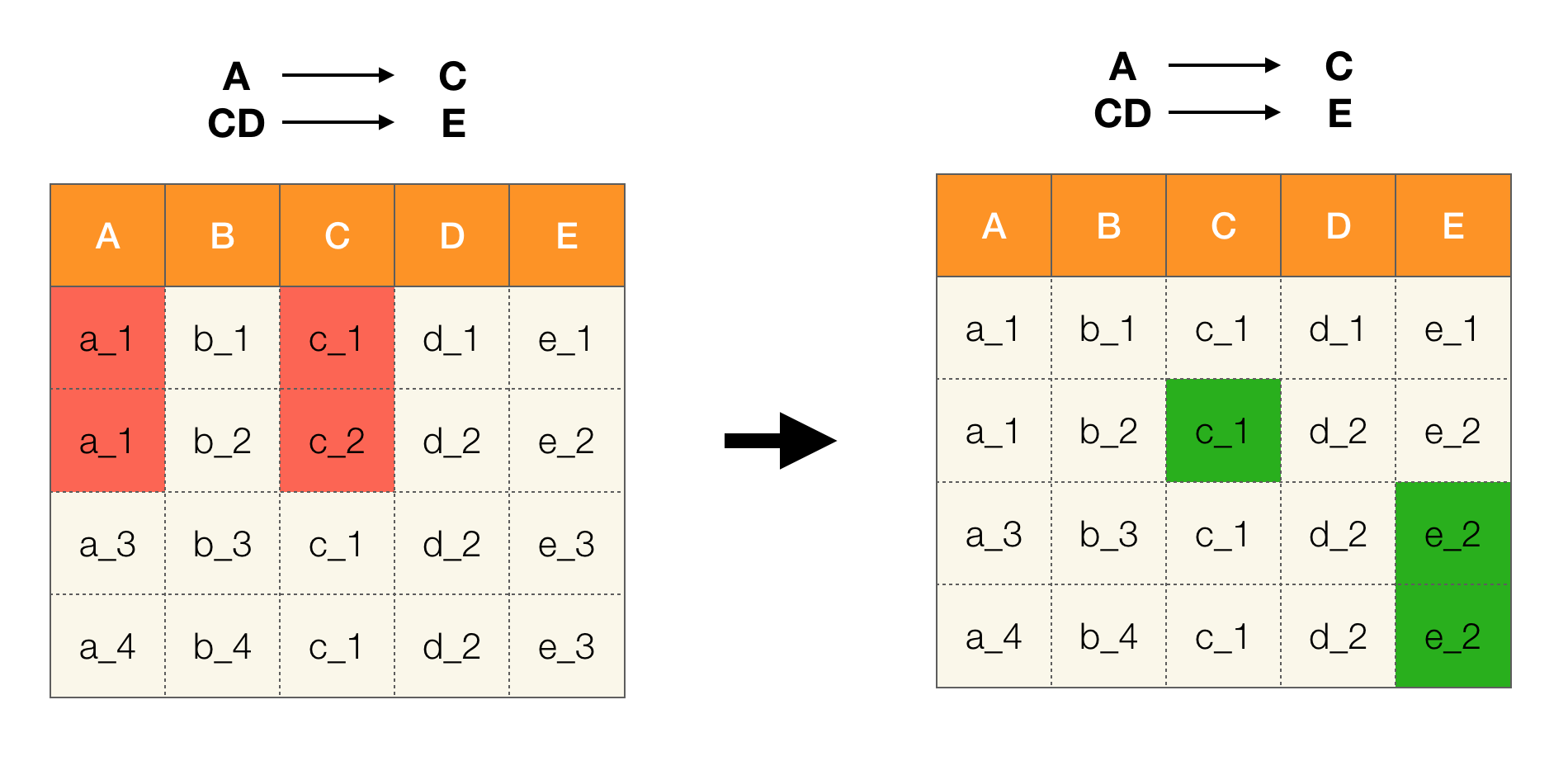
Второй тип — зависимости, представляющие «скрытые» данные и ранее неизвестные связи между атрибутами. То есть о таких зависимостях не думали в момент проектирования и их находят уже для имеющегося набора данных, чтобы потом на основе множества выявленных ФЗ сделать какие-либо выводы о хранимой информации. Как раз с такими зависимостями мы и работаем. Ими занимается целая область дата майнинга с различными техниками поиска и построенными на их основе алгоритмами. Давайте разбираться, чем могут быть полезны найденные функциональные зависимости (точные или приближенные) в каких-либо данных.
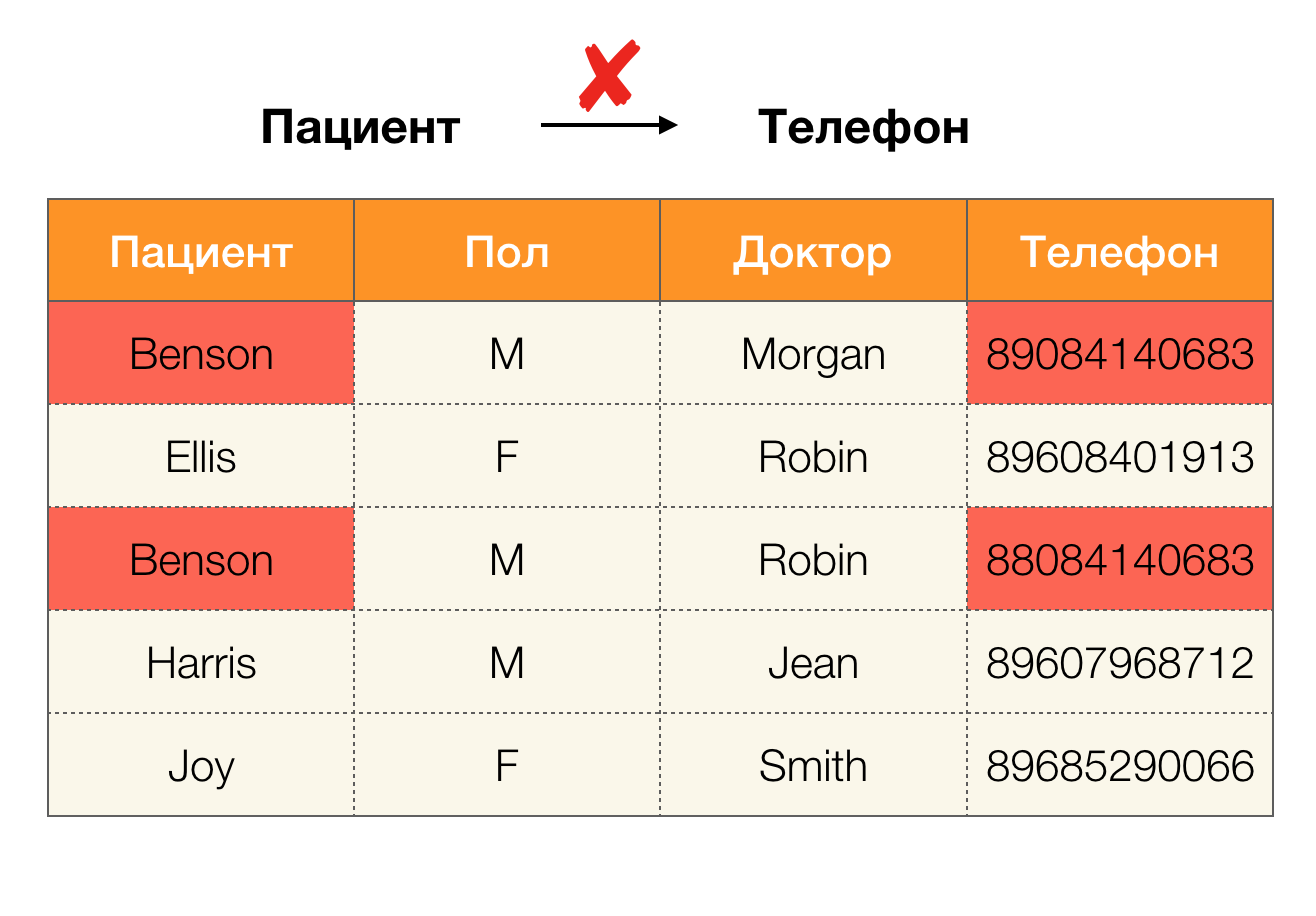
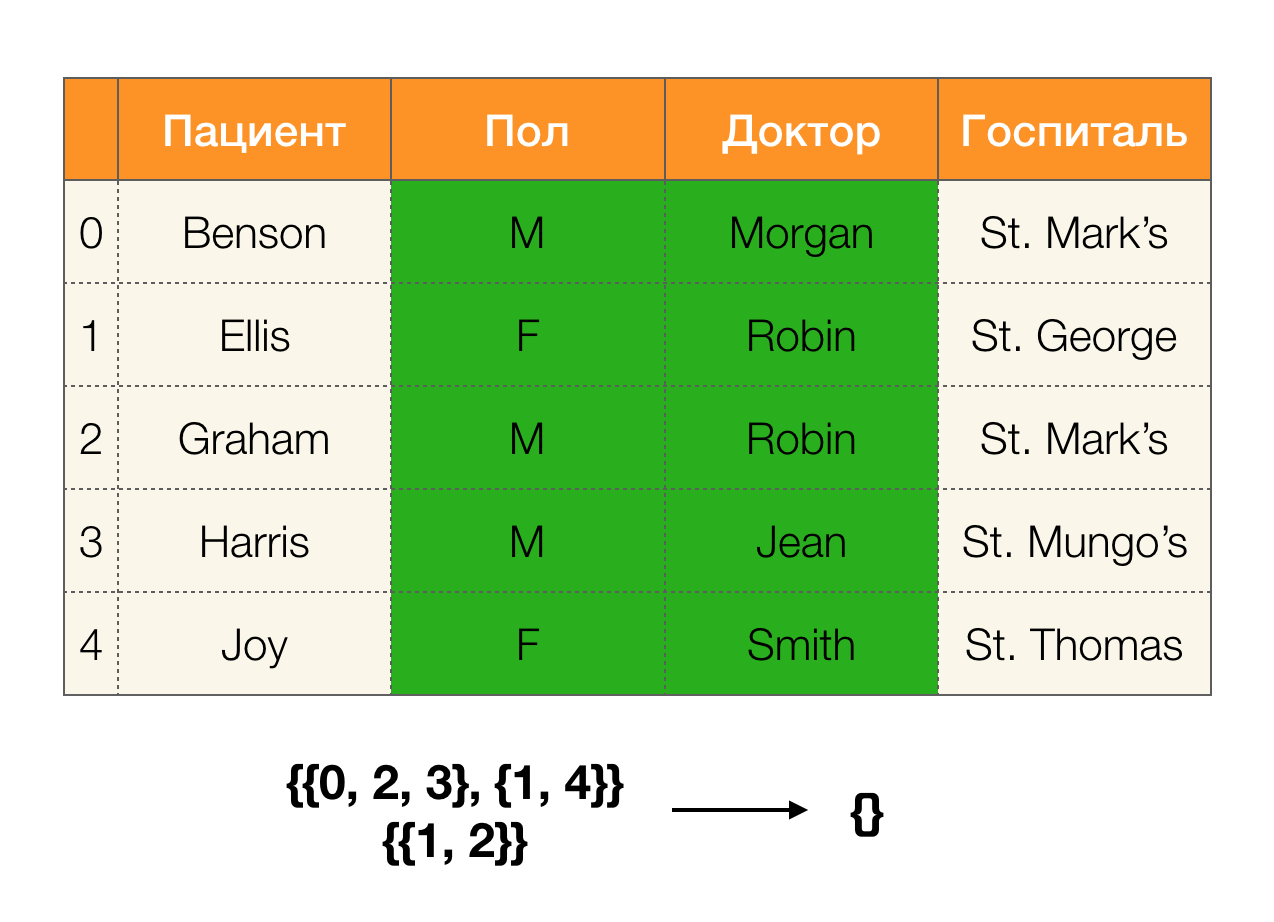
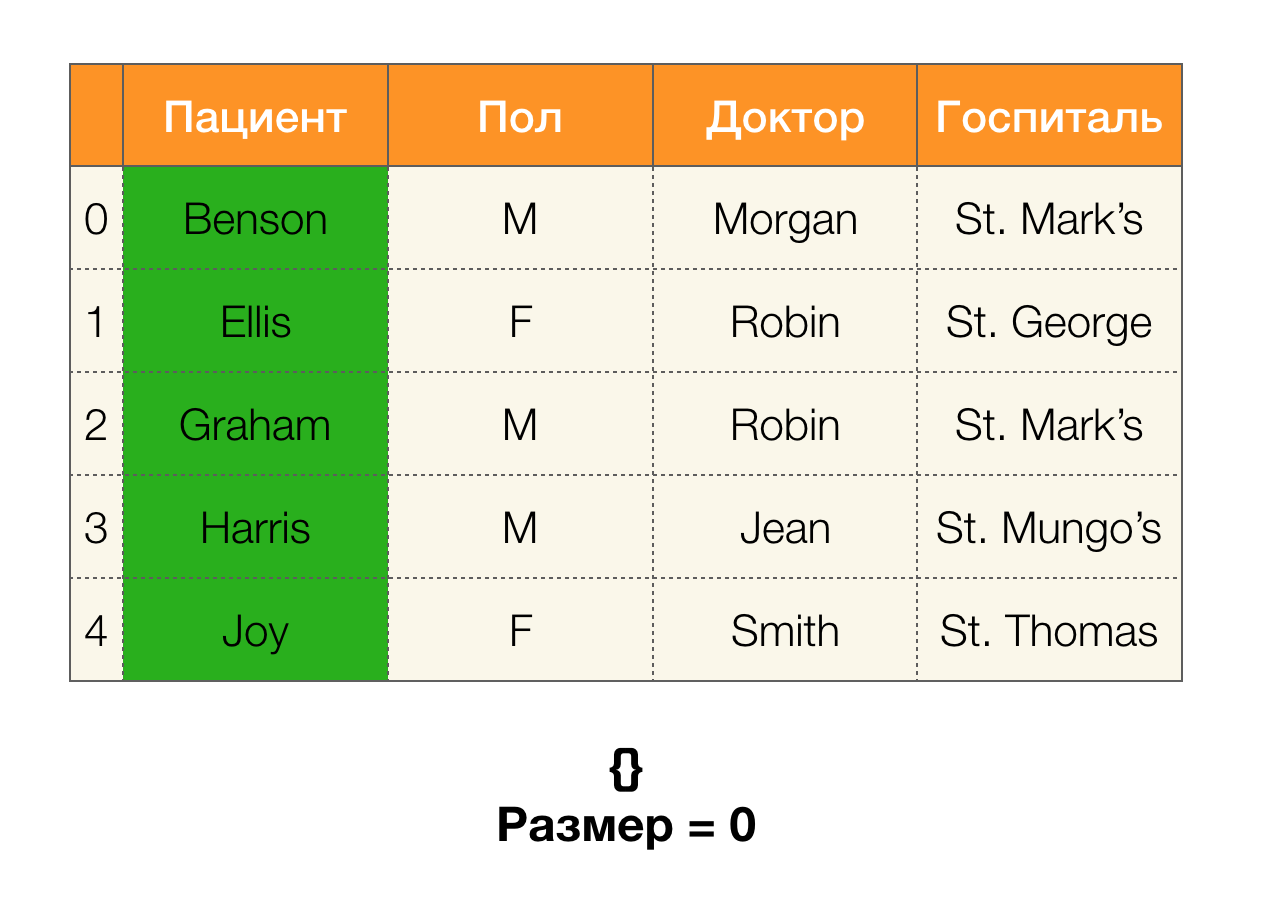
Сегодня среди основных областей применения зависимостей выделяют очистку данных. Она подразумевает разработку процессов выявления «грязных данных» с последующим их исправлением. Яркими представителями «грязных данных» являются дубликаты, ошибки в данных или опечатки, пропущенные значения, устаревшие данные, лишние пробелы и тому подобное.
Пример ошибки в данных:
Пример дубликатов в данных:
Например, мы имеем таблицу и набор ФЗ, которые должны выполняться. Очистка данных в данном случае предполагает изменить данные таким образом, чтобы ФЗ стали верны. При этом число модификаций должно быть минимально (для данной процедуры существуют свои алгоритмы, на которых мы не будем сосредотачивать внимание в данной статье). Ниже приведен пример такого преобразования данных. Слева исходное отношение, в котором, очевидно, не выполняются необходимые ФЗ (красным цветом выделен пример нарушения одной из ФЗ). Справа представлено обновленное отношение, в котором зеленые ячейки показывают измененные значения. После проведения такой процедуры необходимые зависимости стали удерживаться.
Другой популярной областью применения является дизайн базы данных. Здесь стоит напомнить про нормальные формы и нормализацию. Нормализация — это процесс приведения отношения в соответствие некоторому набору требований, каждый из которых определяется нормальной формой по-своему. Расписывать требования различных нормальных форм мы не станем (это делается в любой книге по курсу БД для начинающих), а лишь заметим, что каждая из них по-своему использует концепцию функциональных зависимостей. Ведь ФЗ по своей сути являются ограничениями целостности, которые учитываются при проектировании базы данных (в контексте этой задачи ФЗ иногда называют суперключами).
Рассмотрим их применение для четырех нормальных форм на картинке ниже. Напомним, что нормальная форма Бойса-Кодда является более строгой, чем третья форма, но при этом менее строгой, чем четвертая. Последнюю пока не рассматриваем, поскольку для ее постановки нужно понимание многозначных зависимостей, которые в данной статье нам не интересны.
Еще одной областью, в которой зависимости нашли свое применение, является понижение размерности пространства признаков в таких задачах как построение наивного байесовского классификатора, выделение значимых признаков и репараметризация регрессионной модели. В оригинальных статьях эта задача называется определением избыточных признаков (feature redundancy) и релевантных (feature relevancy) [5, 6], и решается она с активным использованием концепций баз данных. С появлением таких работ мы можем говорить, что сегодня наблюдается запрос на решения, позволяющие объединить базу данных, аналитику и реализацию вышеперечисленных проблем оптимизации в один инструмент [7, 8, 9].
Для поиска ФЗ в наборе данных существует множество алгоритмов (как современных, так и не очень).Такие алгоритмы можно разделить на три группы:
- Алгоритмы, использующие обход алгебраических решеток (Lattice traversal algorithms)
- Алгоритмы, основанные на поиске согласованных значений (Difference- and agree-set algorithms)
- Алгоритмы, основанные на попарных сравнениях (Dependency induction algorithms)
Краткое описание каждого типа алгоритмов представлено в таблице ниже:
Подробнее о данной классификации можно почитать [4]. Ниже представлены примеры алгоритмов на каждый из типов:
В настоящее время появляются новые алгоритмы, которые сочетают в себе сразу несколько подходов к поиску функциональных зависимостей. Примерами таких алгоритмов являются Pyro [2] и HyFD [3]. Разбор их работы предполагается в следующих статьях данного цикла. В этой статье мы лишь разберем основные понятия и лемму, которые необходимы для понимания техник выявления зависимостей.
Начнем с простого — difference- и agree-set, используемые во втором типе алгоритмов. Difference-set представляет собой множество кортежей, которые не совпадают по значениям, а agree-set наоборот — кортежи, совпадающие по значениям. Стоить отметить, что в данном случае мы рассматриваем только левую часть зависимости.
Также важным понятием, которое встречалось выше, является алгебраическая решетка. Так как многие современные алгоритмы оперируют данным понятием, нам нужно иметь представление о том, что это такое.
Для того чтобы ввести понятие решетки, необходимо определение частично упорядоченного множества (или partially ordered set, сокращенно — poset).
Определение 2. Говорят, что множество S частично упорядочено бинарным отношением ⩽, если для всяких a, b, c ∈ S выполнены свойства:
- Рефлексивность, то есть a ⩽ a
- Антисимметричность, то есть, если a ⩽ b и b ⩽ a, то a = b
- Транзитивность, то есть для a ⩽ b и b ⩽ c следует, что a ⩽ c
Такое отношение называется отношением (нестрогого) частичного порядка, а само множество — частично упорядоченным множеством. Формальное обозначение: ⟨S, ⩽⟩.
В качестве простейшего примера частично упорядоченного множества можно взять множество всех натуральных чисел N с обычным отношением порядка ⩽. Нетрудно проверить, что все необходимые аксиомы выполняются.
Более содержательный пример. Рассмотрим множество всех подмножеств {1, 2, 3}, упорядоченное отношением включения ⊆. Действительно, это отношение удовлетворяет всем условиям частичного порядка, поэтому ⟨P ({1, 2, 3}), ⊆⟩ — частично упорядоченное множество. На рисунке ниже изображена структура этого множества: если из одного элемента можно дойти по стрелочкам до другого элемента, то они находятся в отношении порядка.
Нам потребуются еще два простых определения из области математики — супремум (supremum) и инфимум (infimum).
Определение 3. Пусть ⟨S, ⩽⟩ — частично упорядоченное множество, A ⊆ S. Верхняя граница A — это такой элемент u ∈ S, что ∀x ∈ A: x ⩽ u. Пусть U — множество всех верхних границ A. Если в U существует наименьший элемент, тогда он называется супремумом и обозначается как sup A.
Аналогично вводится понятие точной нижней границы.
Определение 4. Пусть ⟨S, ⩽⟩ — частично упорядоченное множество, A ⊆ S. Нижняя граница A — это такой элемент l ∈ S, что ∀x ∈ A: l ⩽ x. Пусть L — множество всех нижних границ A. Если в L существует наибольший элемент, тогда он называется инфимумом и обозначается как inf A.
Рассмотрим в качестве примера приведенное выше частично упорядоченное множество ⟨P ({1, 2, 3}), ⊆⟩ и найдем в нем супремум и инфимум:
Теперь можно сформулировать определение алгебраической решетки.
Определение 5. Пусть ⟨P, ⩽⟩ — частично упорядоченное множество, такое что всякое двухэлементное подмножество имеет точные верхнюю и нижнюю границы. Тогда P называется алгебраической решеткой. При этом sup{x, y} записывают как x ∨ y, а inf {x, y} — как x ∧ y.
Проверим, что наш рабочий пример ⟨P ({1, 2, 3}), ⊆⟩ является решеткой. Действительно, для всяких a, b ∈ P ({1, 2, 3}), a∨b = a∪b, а a∧b = a∩b. Например, рассмотрим множества {1, 2} и {1, 3} и найдем их инфимум и супремум. Если мы их пересечем, то получим множество {1}, которое и будет являться инфимумом. Супремум же получим их объединением — {1, 2, 3}.
В алгоритмах выявления ФЗ пространство поиска зачастую представляется в форме решетки, где множества из одного элемента (читай первый уровень решетки поиска, где левая часть зависимостей состоит из одного атрибута) являют собой каждый атрибут исходного отношения.
В начале рассматриваются зависимости вида ∅ → Одиночный атрибут. Данный шаг позволяет определить, какие атрибуты являются первичными ключами (для таких атрибутов не бывает детерминантов, а потому левая часть пуста). Далее такие алгоритмы двигаются по решетке вверх. При этом стоит отметить, что решетку можно обходить не всю, то есть если на вход передать желаемый максимальный размер левой части, то дальше уровня с таким размером алгоритм идти не будет.
На рисунке ниже показано, как можно использовать алгебраическую решетку в задаче поиска ФЗ. Здесь каждое ребро (X, XY) представляет собой зависимость X → Y. Например, мы прошли первый уровень и знаем, что удерживается зависимость A → B (отобразим это зеленой связью между вершинами A и B). Значит далее, когда будем продвигаться по решетке вверх, мы можем не проверять зависимость A, C → B, потому что она будет уже не минимальной. Аналогично мы бы не стали ее проверять, если бы удерживалась зависимость C → B.
Кроме того, как правило, все современные алгоритмы по поиску ФЗ используют такую структуру данных, как партиция (в первоисточнике — stripped partition [1]). Формальное определение партиции выглядит следующим образом:
Определение 6. Пусть X ⊆ R — набор атрибутов для отношения r. Кластер представляет собой набор индексов кортежей из r, которые имеют одинаковое значение для X, то есть c(t) = {i|ti[X] = t[X]}. Партиция представляет собой множество кластеров, исключающее кластеры единичной длины:
Простыми словами, партиция для атрибута X представляет собой набор списков, где каждый список содержит номера строк с одинаковыми значениями для X. В современной литературе структура, представляющая партиции, называется position list index (PLI). Кластеры единичной длины исключаются в целях сжатия PLI, потому что это кластеры, содержащие лишь номер записи с уникальным значением, которое всегда будет легко установить.
Рассмотрим пример. Вернемся все к той же таблице с пациентами и построим партиции для столбцов Пациент и Пол (слева появился новый столбец, в котором отмечены номера строк таблицы):
При этом, согласно определению, партиция для столбца Пациент на самом деле будет пустая, так как одиночные кластеры исключаются из партиции.
Партиции можно получать по нескольким атрибутам. И для этого существует два пути: пройдясь по таблице, построить партицию сразу по всем необходимым атрибутам, или же построить ее с помощью операции пересечения партиций по подмножеству атрибутов. Алгоритмы поиска ФЗ используют второй вариант.
Простыми словами, чтобы, например, получить партицию по столбцам ABC, можно взять партиции для AC и B (или любой другой набор непересекающихся подмножеств) и пересечь их между собой. Операция пересечения двух партиций выделяет кластеры наибольшей длины, общие для обеих партиций.
Давайте рассмотрим пример:
В первом случае мы получили пустую партицию. Если присмотреться к таблице, то действительно, одинаковых значений по двум атрибутам там нет. Если же мы немного модифицируем таблицу (случай справа), то уже получим непустое пересечение. При этом строки 1 и 2 и правда содержат одинаковые значения по атрибутам Пол и Доктор.
Далее нам понадобится такое понятие, как размер партиции. Формально:
Проще говоря, размер партиции представляет собой количество кластеров, входящих в партицию (помним, что единичные кластеры в партицию не входят!):
Теперь мы можем определить одну из ключевых лемм, которая для заданных партиций позволяет установить, удерживается зависимость или нет:
Лемма 1. Зависимость A, B → C удерживается, если и только если
Согласно лемме, для определения, удерживается ли зависимость, необходимо выполнить четыре шага:
- Вычислить партицию для левой части зависимости
- Вычислить партицию для правой части зависимости
- Вычислить произведение первого и второго шага
- Сравнить размеры партиций, полученных на первом и третьем шаге
Ниже представлен пример проверки, удерживается ли зависимость по данной лемме:
В данной статье мы разобрали такие понятия, как функциональная зависимость, приближенная функциональная зависимость, рассмотрели, где они применяются, а также какие алгоритмы поиска ФЗ существуют. Также мы подробно разобрали базовые, но важные понятия, активно используемые в современных алгоритмах по поиску ФЗ.
Ссылки на литературу:
- Huhtala Y. et al. TANE: An efficient algorithm for discovering functional and approximate dependencies //The computer journal. – 1999. – Т. 42. – №. 2. – С. 100-111.
- Kruse S., Naumann F. Efficient discovery of approximate dependencies //Proceedings of the VLDB Endowment. – 2018. – Т. 11. – №. 7. – С. 759-772.
- Papenbrock T., Naumann F. A hybrid approach to functional dependency discovery //Proceedings of the 2016 International Conference on Management of Data. – ACM, 2016. – С. 821-833.
- Papenbrock T. et al. Functional dependency discovery: An experimental evaluation of seven algorithms //Proceedings of the VLDB Endowment. – 2015. – Т. 8. – №. 10. – С. 1082-1093.
- Kumar A. et al. To join or not to join?: Thinking twice about joins before feature selection //Proceedings of the 2016 International Conference on Management of Data. – ACM, 2016. – С. 19-34.
- Abo Khamis M. et al. In-database learning with sparse tensors //Proceedings of the 37th ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems. – ACM, 2018. – С. 325-340.
- Hellerstein J. M. et al. The MADlib analytics library: or MAD skills, the SQL //Proceedings of the VLDB Endowment. – 2012. – Т. 5. – №. 12. – С. 1700-1711.
- Qin C., Rusu F. Speculative approximations for terascale distributed gradient descent optimization //Proceedings of the Fourth Workshop on Data analytics in the Cloud. – ACM, 2015. – С. 1.
- Meng X. et al. Mllib: Machine learning in apache spark //The Journal of Machine Learning Research. – 2016. – Т. 17. – №. 1. – С. 1235-1241.
Авторы статьи: Анастасия Бирилло, исследователь в JetBrains Research, студентка CS центра и Никита Бобров, исследователь в JetBrains Research